梁横向振动的近似解法

梁的横向弯曲振动试验原理
梁的横向弯曲振动试验的原理是:
1. 将梁的两端固定,使其形成简支梁。

2. 在梁的中部施加一个短时的冲击力,使梁产生横向弯曲振动。

3. 根据牛顿第二定律,力的冲击会使梁发生位移和振动。

4. 梁的振动属于强迫谐振,振动周期取决于其本身的质量和刚度分布。

5. 通过测量梁的振动周期,可以计算出其横向振动的固有频率。

6. 调节激励力的参数,可以获得梁在不同激励下的响应规律。

7. 使用传感器测量梁的位移、应变等,结合信号分析,可以确定梁的动态特性和模态参数。

8. 控制梁的边界条件,使其接近理想的简支状态。

9. 进行多次试验取平均,可以提高结果准确性。

10. 试验符合梁横向弯曲振动的工程动力学理论。

通过该试验可以研究梁的动力学行为,获得其横向弯曲振动的动态特性。

任意跨弹性支承直梁横向自振的一个新解法
周叮
【期刊名称】《工程力学》
【年(卷),期】1991(8)4
【摘要】本文给出了任意跨弹性支承(包括扭转弹性支承)直梁横向自由振动的一个新解析解法,将弹性支承反力看作是作用于梁上的未知外力,求得了直梁横向受迫振动响应的解析解,由边界条件确定待定的积分常数,利用支承处支承反力与梁位移间的线性关系导出频率方程,频率方程是以阶数等于弹性支承个数的行列式表示的,振型函数则以统一的解析式表示,刚性支承是本文特例。

本文具体导出了几种常见边界条件下的频率方程,最后给出了一个算例。

【总页数】15页(P111-125)
【关键词】梁;振动;直梁;弹性支座
【作者】周叮
【作者单位】华东工学院
【正文语种】中文
【中图分类】O327
【相关文献】
1.考虑支承质量时弹性支承连续梁的固有横振 [J], 吴晓;郭作杰
2.弹性支承连续梁法在斜梁桥葆载横向分布计算中的应用 [J], 黄平明;夏淦
3.用弹性支承连续梁法求桥跨结构横向分布系数的研究——弹性支承连续梁修正法
[J], 梁忠滨
4.弹性支承连续梁法在斜梁桥荷载横向分布计算中的应用 [J], 黄平明;夏淦;邵容光
5.受任意个同心弹性环支圆板横向自由振动的一个新的解析解法 [J], 周叮
因版权原因，仅展示原文概要，查看原文内容请购买。

振动理论及工程应用_天津大学中国大学mooc课后章节答案期末考试题库2023年1.振动问题属于动力学问题中的第二类问题，即已知主动力求（）。

答案:运动2.振动是指物体在平衡位置附近所做的（）。

答案:往复运动3.弹簧串联、等效刚度（），弹簧并联，等效刚度（）。

答案:减小增加4.在建立单自由度弹簧—质量系统的运动微分方程时，当选择物块的静平衡位置为坐标原点，假设x轴正方向垂直向下，则物块的位移、速度和加速度的正方向如何确定（）。

答案:都垂直向下5.质点或质点系的运动相互影响的现象叫做（）。

答案:耦联6.激振力与受迫振动的位移相位差为（）时，振动系统达到共振状态。

答案:90°7.小车重P在斜面自高度h处滑下与缓冲器相撞，斜面倾角为α，缓冲弹簧刚度系数为k。

如缓冲质量不计，斜面摩擦不计，小车碰撞后，系统的自由振动周期为（）。

答案:8.在图示振动系统中，已知重为P的AB杆对O轴的回转半径为ρ，物块重为Q，两个弹簧的刚度系数均为k，当系统静止时，杆处于水平。

则此系统微振动的圆频率为：（）答案:9.关于主振型的正交性，下列说法错误的是（）答案:零固有圆频率对应的主振型不与系统的其他主振型关于质量矩阵和刚度矩阵正交10.关于主振型矩阵和正则振型矩阵的关系是（）。

答案:将主振型矩阵的各列除以其对应主质量矩阵元素的平方根，得到的振型就是正则振型11.关于主振型矩阵和正则振型矩阵下列说法错误的是（）。

答案:将主振型矩阵的各列除以其对应主刚度的平方根，得到的振型就是正则振型12.瑞利第一商用（）方程求解，瑞利第二商用（）方程求解。

答案:作用力位移13.瑞利法估算基频的结果是精确值的（），邓克莱法估算基频的结果是精确值的（）答案:上限下限14.子空间迭代法是将（）与（）结合起来的计算方法，它对自由度数较大系统的前若干阶固有频率及主振型非常有效。

答案:里兹法矩阵迭代法15.一维单元应变位移关系矩阵B为：（）答案:16.在杆的纵向振动中，要考虑的边界条件是（）答案:位移和轴向力17.以下不属于梁横向振动的近似解法的是（）答案:传递矩阵法18.下列哪些是主动控制的特点（）。

非均匀弹性地基上梁横向振动的渐近解法
周叮
【期刊名称】《强度与环境》
【年(卷),期】1994(000)001
【摘要】研究非均匀弹性地基上梁的横向振动，提供了一种既能保证较高精度、计算又非常简单的固有频率的渐近解法，作为算例，给出了非均匀弹性地基上悬臂梁固有频率的一级近似计算公式并将计算结果与连续质量有限元素法的计算结果作了比较。

【总页数】5页(P8-12)
【作者】周叮
【作者单位】无
【正文语种】中文
【中图分类】TU323.301
【相关文献】
1.非均质变截面弹性直杆横向振动自主频率的渐近解法 [J], 周叮
2.横向荷载作用下弹性地基上梁的主共振分析 [J], 王连华;马建军;刘齐建
3.弹性地基上梁的GDQ振动分析 [J], 宋丽红;陈殿云;张传敏
4.非均匀弹性地基上梁的弯曲 [J], 陈浩;何芳社
5.非均匀温度场中弹性直杆横向、纵向及扭转振动固有频率的渐近解法 [J], 周叮因版权原因，仅展示原文概要，查看原文内容请购买。

梁横向振动的近似解法弹性体的固有振动有两种提法，一种是微分方程的特征值问题，另一种是泛函的驻值问题。

从精确解得角度看，两者完全等价，从近似解得角度看，求泛函驻值问题比求微分方程的近似解容易。

精确解法主要是分离变量法，此处略去不谈。

一方程的建立假设：梁的各截面中心主惯性轴在同一平面，外载也在同一平面，梁在该平面内的横向振动引起弯曲变形，低频振动时可以忽略剪切变形及截面绕中性轴转动惯量的影响。

∂2∂x 2 EJ ∂2y ∂x 2 +ρA ∂2y ∂t 2=p x,t −∂∂xm x,t (1) p(x,t),m(x,t)分别为单位长度梁上分布的外力和外力矩。

假设：y(x,t)=Y(x)bsin(ωt +ϕ)代入(1)式的齐次形式，有：(EJY ′′)′′−ω2ρAY =0 (2)上式改写成：(EJY ′′i )′′=ω2ρAY i上式两边同时乘以Y i 并在全梁上积分，i ，j 互换得到两个式子并相减等于0可以得到主振型的关于质量和刚度正交性，并且可以得到相应的频率p378。

固有频率的变分式命题：这个式子与边界条件的组合所确定的特征值ω2及相应的特征函数Y(x) 等价于下列泛函所取驻值及相应的自变函数，该自变函数满足位移边界条件P389。

ω2=st EJ(Y ′′)2dx l 0ρAY 2dx l 0 (3)证明：1，(3)式各驻值及相应的函数Y(x)是(2)式的的特征值和特征函数。

驻值时，一阶变分等于0，δ(ω2)=0展开后，得到三个item 相加得0：EJY ′′ ′′−ω2ρAY δYdx − EJY ′′ ′l0δY ︱0l +EJY ′′δY ‘︱0l=0 (∗) 由δY 的任意性，第一个item 等于0，可以得到(2)式，由第二、三项可以得到Y(x)的边界条件。

2，(3)式加(2)式后反过来可以得到δ(ω2)=0。

从而证明泛函的驻值问题与微分方程的特征值问题完全等价。

另外，可以由泛函(3)证明主振型的正交性。

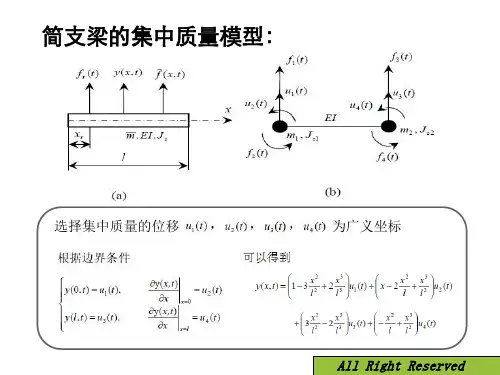
简支梁横向振动的固有频率及振型函数的推导一．等截面细直梁的横向振动取梁未变形是的轴线方向为X 轴（向右为正），取对称面内与x 轴垂直的方向为y 轴（向上为正）。

梁在横向振动时，其挠曲线随时间而变化，可表示为y=y(x,t) (1)除了理想弹性体与微幅振动的假设外，我们还假设梁的长度与截面高度之比是相当大的（大于10）。

故可以采用材料力学中的梁弯曲的简化理论。

根据这一理论，在我们采用的坐标系中，梁挠曲线的微分方程可以表示为：22y EI M x ∂=∂(2) 其中，E 是弹性模量，I 是截面惯性矩，EI 为梁的弯曲刚度，M 代表x 截面处的弯矩。

挂怒弯矩的正负，规定为左截面上顺时针方向为正，右截面逆时针方向为正。

关于剪力Q 的正负，规定为左截面向上为正，右截面向下为正。

至于分布载荷集度q 的正向则规定与y 轴相同。

在这些规定下，有：M QQ q x x ∂∂==∂∂， (3)于是，对方程（2）求偏导，可得：222222(EI )(EI )y M y Q Q q x x x x x x ∂∂∂∂∂∂====∂∂∂∂∂∂， (4)考虑到等截面细直梁的EI 是常量，就有：3434y yEI Q EI q x x ∂∂==∂∂， (5)方程（5）就是在等截面梁在集度为q 的分部李作用下的挠曲微分方程。

应用达朗贝尔原理，在梁上加以分布得惯性力，其集度为22yq t ρ∂=-∂(6)其中ρ代表梁单位长度的质量。

假设阻尼的影响可以忽略不计，那么梁在自由振动中的载荷就仅仅是分布的惯性力。

将式（6）代入（5），即得到等截面梁自由弯曲振动微分方程：4242y yEI x t ρ∂∂=--∂∂ (7)其中2/a EI ρ=。

为求解上述偏微分方程（7），采用分离变量法。

假设方程的解为：y(x,t)=X(x)Y(t)(8)将式（8）代入（7），得：224241Y a d XY t X dx ∂=-∂ (9) 上式左端仅依赖于t,而右端仅依赖于x ，因此要使对于任何x,t 上式均成立，必须二者均等于一个常数。

总第285期2〇17年第6期交通科技Transportation Science &TechnologySerial No. 285No.6 Dec. 2017DOI10.3963/j.i ssn.1671-7570.2017.06.020固端梁横向自振频率的简化计算方法周小苏(中铁第一勘察设计院集团有限公司西安710043)摘要跨座式轨道交通轨道梁的横向自振频率是此类交通形式安全性及舒适性的关键性指标。

为准确、便捷地计算轨道梁自振频率，将轨道梁简化为固端梁，以瑞利法基本原理，采用单位均布力下的挠曲线和正弦曲线2种振型曲线推导得到固端梁一阶自振频率计算公式，通过有限元程序对工程实例对比验证。

结果证明此简化公式精度满足工程需要且方便应用。

关键词固端梁瑞利法振型曲线自震频率结构设计跨座式轨道交通系统近年来不仅在旅游区被 逐步使用，由于其造价低、土地占用量少、噪声小、能适应较小的曲线半径和较大坡度，在城市复杂的 建筑地形和对施工速度要求较高、对交通影响要求 严苛的市政交通领域也得到越来越广泛的应用[1]。

因为跨座式轻轨交通车辆是骑跨在梁体之 上，故其轨道梁为既充当了轨道也承担车辆荷载 的受力梁体，且其断面为宽度小于高度的窄梁[]。

钢梁相较于混凝土梁本身存在刚度较小的问 题，加之轨道梁又为宽度小于高度的窄梁，因此其 横向刚度需要特别关注。

相关规范[3]也对轨道梁 桥的横向自振频率做了要求。

轨道梁在横向振动平面内其边界条件为固 结，对于简支梁的自振频率，相关规范都给出了简 化计算公式[45,但目前固端梁的计算在设计中多 采用有限元软件建模分析，往往花费较多时间，且 因操作复杂也较容易出错。

关于梁体横向自振特 性的简化计算方法已有一些研究成果[67,但大多 基于简支边界条件，本文在这些研究成果的基础 上对固端梁这一特殊但又常见的工程实际给出便 捷实用的简化计算公式。

1计算公式推导1.1计算模型原理简化计算模型见图1。

梁横向弯曲振动的振型正交性),(]),()([),(222222t x p x t x u x EI x t t x u m =∂∂∂∂+∂∂齐次方程为：0]),()([),(222222=∂∂∂∂+∂∂x t x u x EI x t t x u m ]),()([),(222222x t x u x EI x t t x u m ∂∂∂∂-=∂∂根据分离变量法，设：)()(),(t q x t x u φ=，可得：0)()(2=+t q t qω )(])()([22222x m dxx d x EI dx d φωφ= 上式即为分析频率和振型的特征方程。

设对于第i 、j 两阶频率，有：)(])()([22222x m dx x d x EI dx d i i i φωφ= )(])()([22222x m dx x d x EI dx d j j j φωφ= 上面第一式两边乘以)(x j φ，并沿杆长积分得：)()(])()([)(22222x x m dx x d x EI dx d x j i i i j φφωφφ=⎰⎰⎰==l j i i l j i i li j dx x x m dx x x m dx dx x d x EI dx d x 020202222)()()()(])()([)(φφωφφωφφ⎰⎰⎰⎰⎰⎰⎰+-=+-=-=-=-==l j i li j li j l j i li j li j i l j l i j l j i li j l j i li j l i j li j dx dx x d dx x d x EI dx x d x EI dx x d dx x d x EI dx d x dx x d d dx x d x EI dx x d x EI dx x d dx x d x EI dx d x dx x d x EI d dx x d dx x d x EI dx d x xd dx x d dx x d x EI dx d dx x d x EI dx d x x d dx x d x EI dx d dx x d x EI dx d x dx x d x EI dx d d x dx dx x d x EI dx d x 0222202222022022022220022022*********02202222)()()(])()([)(])()([)()()()(])()([)(])()([)(])()([)(])()([)()(])()([])()([)()(])()([])()([)(]))()([()(])()([)(φφφφφφφφφφφφφφφφφφφφφφφφφφφφ 对于基本边界条件，有：0])()([)(022=li j dx x d x EI dx d x φφ0])()([)(022=li j dx x d x EI dx x d φφ 则有：⎰⎰⎰==lj i i l j i li j dx x x m dx dx x d dx x d x EI dx dx x d x EI dx d x 020222202222)()()()()(])()([)(φφωφφφφ 同理有：⎰⎰⎰==lj i j l j i lj i dx x x m dx dx x d dx x d x EI dx dx x d x EI dx d x 020222202222)()()()()(])()([)(φφωφφφφ 两式相减得到：0)()()(022=-⎰lj i j i dx x x m φφωω当22j i ωω≠时，有：0)()(0=⎰ljidx x x m φφ令：iliiM dx x x m =⎰0)()(φφ为振型i 对应的广义质量。