运筹学教案_排队论1讲解
- 格式:ppt
- 大小:556.50 KB
- 文档页数:39









运筹学排队论1. 简介排队论是运筹学中重要的一个分支,它研究了在人员、物品或信息流动过程中产生的排队现象,并通过建立数学模型和分析这些模型来探讨和优化系统中的排队行为。
排队论在各个领域都有广泛的应用,如交通运输、电信网络、生产制造等。
2. 排队模型排队论中常用的模型包括M/M/1模型、M/M/s模型、M/G/1模型等。
其中,M表示到达过程的分布,而G表示服务时间的分布。
而数字1或s则表示系统中的服务通道数。
2.1 M/M/1模型M/M/1模型是排队论中最简单的一个模型,它假设到达过程和服务时间都服从指数分布。
该模型中只有一个服务通道。
2.2 M/M/s模型M/M/s模型是M/M/1模型的扩展,它假设到达过程和服务时间仍然服从指数分布,但有s个服务通道。
M/M/s模型适用于有多个并行服务通道的排队系统。
2.3 M/G/1模型M/G/1模型假设到达过程服从泊松分布,而服务时间服从一般分布。
该模型在实际应用中更为常见,因为服务时间往往不服从指数分布。
3. 排队论的性能度量排队论的性能度量是对排队模型进行定量分析和评估的重要手段,常见的性能度量指标包括平均等待时间、平均逗留时间、系统繁忙率等。
3.1 平均等待时间平均等待时间是指在排队系统中,每个顾客平均等待的时间长度。
通过对排队模型的分析和计算,可以得到平均等待时间的具体数值。
3.2 平均逗留时间平均逗留时间是指每个顾客在排队系统中逗留的平均时间长度。
它等于平均等待时间加上服务时间。
3.3 系统繁忙率系统繁忙率是指服务通道在单位时间内处于工作状态的比例。
它可以用来评估系统是否能够满足顾客的需求。
4. 排队论的应用4.1 交通运输排队论在交通运输领域的应用非常广泛。
例如,交通信号灯的控制就可以通过排队论进行优化,以减少车辆的等待时间和交通拥堵。
4.2 电信网络在电信网络中,排队论被用于研究数据包的传输和路由机制。
通过对排队论模型的分析,可以提高网络的传输效率和质量。

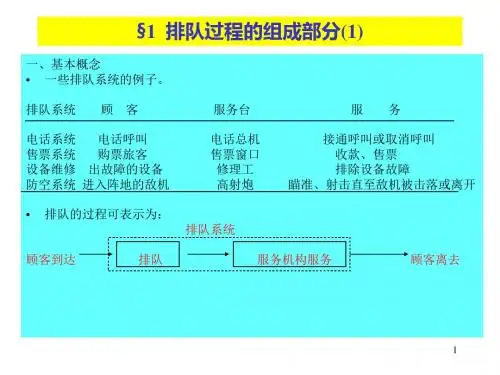
《运筹学Ⅱ》课程教案第1次排队系统的描述:排队系统的描述 实际中的排队系统各不相同,但概括起来都由三个基本部分组成:输入过程,排队及排队规则和服务机构。
(一)输入过程:描述顾客按照什么样的规律到达系统,从三个方面描述一个输入: 顾客总体(顾客源)数:可能是有限,也可能是无限。
到达方式:是单个到达还是成批到达。
库存问题中,若把进来的货看成顾客,则为成批到达的例子。
顾客(单个或成批)相继到达的时间间隔分布:这是刻划输入过程的最重要内容。
令0T =0,n T 表示第n 顾客到达的时刻,则有012u T T T T ≤≤≤≤记1,1,2,n n n X T T n -=-=,则n X 是第n 顾客与第n-1顾客到达的时间间隔。
一般假定{}n X 是独立同分布,并记分布函数为()A t 。
{}n X 的分布()A t 常见的有:定常分布(D ):顾客相继到达的时间间隔为确定的。
如产品通过传送带进入包装箱就是定常分布。
最简流(或称Poisson)(M :Markov 的字头):顾客相继到达的时间间隔{}n X 为独立的,同为负指数分布,其密度函数为:t 0()0 t<0t e a t λλ-⎧≥=⎨⎩ k 介爱尔朗(Erlang )分布:(二) 排队及排队规则 (1)排队有限排队——排队系统中顾客数是有限的。
无限排队——顾客数是无限,队列可以排到无限长(等待制排队系统)。
有限排队还可以分成:损失制排队系统:排队空间为零的系统,即不允许排队。
(顾客到达时,服务台占满,顾客自动离开,不再回来)(电话系统)混合制排队系统:是等待制与损失制结合,即允许排队,但不允许队列无限长。
B :排队规则当顾客到达时,若所有服务台都被占有且又允许排队,则该顾客将进入队列等待。
服务台对顾客进行服务所遵循的规则通常有: 先来先服务(FCFS )后来先服务(LCFS)。
在许多库存系统中就会出现这种情况,如钢板存入仓库后,需要时总是从最上面取出;又如在情报系统中,后来到达的信息往往更重要,首先要加以分析和利用。