大学物理-磁场能量

磁场的能量与磁场能的计算磁场是物质周围的物理场，对于我们的生活和科学研究具有重要的意义。

了解磁场的能量和如何计算磁场能量对于深入理解磁场的本质和应用具有重要的意义。

本文将介绍磁场的能量及其计算方法。

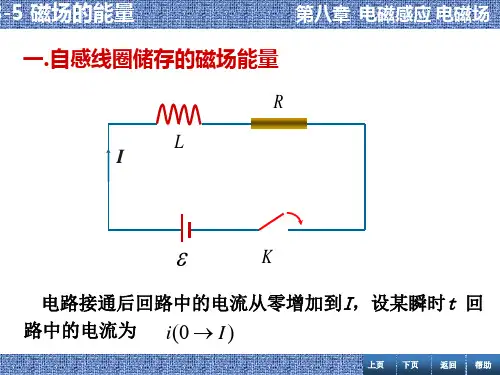
一、磁场的能量磁场是由带电粒子的运动产生的，磁场能量即为磁场中储存的能量。

磁场能量可以分为两种类型：势能和动能。

1. 势能磁场具有势能的体现是磁场对带电物体产生力的能力。

当带电物体在磁场中运动时，磁场力将对其进行做功，从而将能量转化为势能。

势能的计算公式如下：E_p = -m · B其中，E_p表示势能，m表示带电物体的磁矩，B表示磁感应强度。

在SI国际单位制中，磁感应强度的单位为特斯拉（T），磁矩的单位为安培-米²（A·m²）。

2. 动能磁场中的动能是带电粒子在磁场力的作用下所具有的能量。

当带电粒子在磁场中做加速运动时，由于受到磁场力的作用，其动能将被转化为磁场能量。

动能的计算公式如下：E_k = 1/2mv²其中，E_k表示动能，m表示带电物体的质量，v表示带电物体在磁场中的速度。

在SI单位制中，质量的单位为千克（kg），速度的单位为米/秒（m/s）。

二、磁场能的计算磁场能的计算涉及到磁场强度、磁通量和磁场能量密度等多个参数。

下面将介绍一些常见的磁场能计算方法。

1. 对于匀强磁场在匀强磁场中，磁感应强度是恒定的，磁场能计算比较简单。

磁场能可以通过下列公式计算：W = V · B²/2μ₀其中，W表示磁场能，V表示磁场体积，B表示磁感应强度，μ₀表示真空磁导率。

2. 对于非匀强磁场在非匀强磁场中，磁感应强度随位置的变化而变化，计算磁场能稍微复杂。

一种常见的方法是将非匀强磁场分解为无穷小体积，然后对每个小体积进行磁场能的计算，最后将所有小体积的磁场能相加得到总的磁场能量。

三、总结本文介绍了磁场的能量及其计算方法。

磁场的能量可以分为势能和动能，势能是磁场对带电物体产生力的能力，动能是带电粒子在磁场中具有的能量。

磁场能量公式磁场能量（MagneticFieldEnergy，MFE）是一种能量，它是围绕着磁场产生的，也称为磁性能量。

磁场能量是无穷无尽的，在宇宙的每个角落都存在着磁场和磁场能量。

它是一种可以被利用的能量，可以用来激发电子，分子，原子等，从而得到物理和化学反应。

磁场能量有一个简单的公式来表示它，这个公式就是MFE（磁场能量）=（电荷*电荷）/（2*电荷间距），其中MFE是磁场能量，电荷是指磁场中同类电荷的数量，电荷间距是指电荷之间的距离。

磁场能量的大小取决于电荷的数量和电荷间距。

如果电荷数量增加，磁场能量也会增加；如果电荷间距增加，磁场能量就会减少。

磁场能量的另一个重要因素是磁场的大小，磁场越大，磁场能量就越大。

磁场能量可以用来制造电磁元件，例如电路，变压器，电磁炉，磁力棒等。

它也可以用来制造磁性材料，例如电磁铁，电磁铁和磁碟机等。

此外，磁场能量还可以用来制造可控磁场，如磁场探测器，磁场压缩机等。

磁场能量也可以用于电能的转换。

例如，磁场能量可以用于动力发电，运用的原理是将磁场能量转换成机械能和电能。

此外，磁场能量还可以转换成光能和热能，因此，它有许多应用领域，如电子领域，照明领域，能源领域等。

磁场能量在宇宙中是非常普遍的，但很多人都认为它是一种抽象的能量。

实际上，它是一种可以用来提高能源利用效率的有用能量。

磁场能量在我们的日常生活中也有许多应用，它可以用来生产磁带，磁贴等，也可以用来改善居住环境，消除辐射，减少噪声等，从而给人们带来更加舒适的生活环境。

综上所述，磁场能量是宇宙中最丰富的能量之一，它不仅具有多种应用，而且对于改善我们的日常生活也有着重要作用。

因此，要解决当今能源紧张的问题，我们应该积极利用磁场能量，实现能源的高效利用。

磁场的能量公式
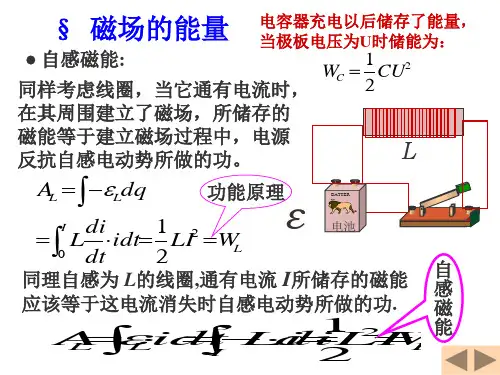
1. 自感线圈磁场能量公式。

- 对于一个自感系数为L的线圈，当通过的电流为I时，其储存的磁场能量W = (1)/(2)LI^2。

- 推导过程：当电路中的电流I发生变化时，自感电动势E = - L(di)/(dt)。

在建立电流I的过程中，电源克服自感电动势做功，这个功就转化为磁场的能量。

根据能量守恒定律，设电流从0增加到I，电源克服自感电动势做的功W=∫_0^tEidt=∫_0^ILi
di=(1)/(2)LI^2。

2. 磁场能量密度公式。

- 在均匀磁场中，磁场能量密度w=(1)/(2)frac{B^2}{μ}，其中B是磁感应强度，μ是磁导率（对于真空μ=μ_0，对于介质μ = μ_rμ_0，μ_r是相对磁导率）。

- 推导过程：对于长直螺线管，内部磁场B=μ nI（n是单位长度的匝数），自感系数L=μ n^2V（V是螺线管的体积）。

根据W=(1)/(2)LI^2，将L和I=(B)/(μ n)代入可得W=(1)/(2)frac{B^2}{μ}V，所以磁场能量密度w = (W)/(V)=(1)/(2)frac{B^2}{μ}。

对于非均匀磁场，可以通过对体积元dV积分W=∫_Vw dV=∫_V(1)/(2)frac{B^2}{μ}dV
来计算磁场的总能量。