乐山市五通桥区初中2015届中考调研考试数学试卷及答案
- 格式:doc
- 大小:754.50 KB
- 文档页数:15

2015年四川省乐山市中考数学试卷一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求.1.(3分)(2015•乐山)3的相反数是( ) ﹣2.(3分)(2015•乐山)下列几何体中,正视图是矩形的是( )CD3.(3分)(2015•乐山)某班开展1分钟仰卧起坐比赛活动,5名同学的成绩如下(单位:个):37、38、40、40、42.这组数据的众数是() 4.(3分)(2015•乐山)下列说法不一定成立的是( )5.(3分)(2015•乐山)如图,l 1∥l 2∥l 3,两条直线与这三条平行线分别交于点A 、B 、C 和D 、E 、F .已知,则的值为( )C D6.(3分)(2015•乐山)二次函数y=﹣x 2+2x+4的最大值为( ) 7.(3分)(2015•乐山)如图,已知△ABC 的三个顶点均在格点上,则cosA 的值为( )C D8.(3分)(2015•乐山)电影《刘三姐》中,秀才和刘三姐对歌的场面十分精彩.罗秀才唱到:“三百条狗交给你,一少三多四下分,不要双数要单数,看你怎样分得均?”刘三姐示意舟妹来答,舟妹唱道:“九十九条打猎去,九十九条看羊来,九十九条守门口,剩下三条财主请来当奴才.”若用数学方法解决罗秀才提出的问题,设“一少”的狗有x条,“三多”的狗有y条,则解此问题所列关系式正确的是()A.B.C.D.9.(3分)(2015•乐山)已知二次函数y=ax2+bx+c的图象如图所示,记m=|a﹣b+c|+|2a+b+c|,n=|a+b+c|+|2a﹣b﹣c|.则下列选项正确的是()10.(3分)(2015•乐山)如图,已知直线y=x﹣3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是()D二、填空题:本大题共6小题,每小题3分,共18分.11.(3分)(2015•湘潭)的倒数是.12.(3分)(2015•乐山)函数的自变量x的取值范围是.13.(3分)(2015•乐山)九年级1班9名学生参加学校的植树活动,活动结束后,统计每人植树的情况,植了2棵树的有5人,植了4棵树的有3人,植了5棵树的有1人,那么平均每人植树棵.14.(3分)(2015•乐山)如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,已知∠ADE=40°,则∠DBC=°.15.(3分)(2015•乐山)如图,已知A(2,2)、B(2,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2,2)的位置,则图中阴影部分的面积为.16.(3分)(2015•乐山)在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).(1)若点(﹣1,﹣2)是一次函数y=x+3图象上点M的“可控变点”,则点M的坐标为.(2)若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,则实数a的取值范围是.三、本大题共3小题,每小题9分,共27分.17.(9分)(2015•乐山)计算:|﹣|+﹣4cos45°+(﹣1)2015.18.(9分)(2015•乐山)求不等式组的解集,并把它们的解集在数轴上表示出来.19.(9分)(2015•乐山)化简求值:÷(﹣a),其中a=﹣2.四、本大题共3小题,每小题10分,共30分.20.(10分)(2015•乐山)如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.(1)求证:△DCE≌△BFE;(2)若CD=2,∠ADB=30°,求BE的长.21.(10分)(2015•乐山)某班开展安全知识竞赛活动,班长将所有同学的成绩分成四类,并制作了如下的统计图表:根据图表信息,回答下列问题:(1)该班共有学生人;表中a=;(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.22.(10分)(2015•乐山)“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:(1)小张如何进货,使进货款恰好为1300元?(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.五、本大题共2小题,每小题10分,共20分.23.(10分)(2015•乐山)如图1,四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=.(1)求CD边的长;(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q(点Q运动到点B停止).设DP=x,四边形PQCD的面积为y,求y与x的函数关系式,并求出自变量x的取值范围.24.(10分)(2015•乐山)如图,正比例函数y=2x的图象与反比例函数y=的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.(1)求k的值;(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.六、本大题共2小题,第25题12分,第26题13分,共25分.25.(12分)(2015•乐山)已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O于点E.(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)26.(13分)(2015•乐山)如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.(1)求二次函数的解析式;(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.①求点P的运动路程;②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;(3)在(2)的条件下,连结EF,求△PEF周长的最小值.2015年四川省乐山市中考数学试卷参考答案与试题解析一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求.1.(3分)(2015•乐山)3的相反数是()﹣2.(3分)(2015•乐山)下列几何体中,正视图是矩形的是()C D3.(3分)(2015•乐山)某班开展1分钟仰卧起坐比赛活动,5名同学的成绩如下(单位:个):37、38、40、40、42.这组数据的众数是()4.(3分)(2015•乐山)下列说法不一定成立的是()5.(3分)(2015•乐山)如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C 和D、E、F.已知,则的值为()C D根据平行线分线段成比例定理得出=,===,6.(3分)(2015•乐山)二次函数y=﹣x2+2x+4的最大值为()时,时,y=7.(3分)(2015•乐山)如图,已知△ABC的三个顶点均在格点上,则cosA的值为()C D=,=2cosA==8.(3分)(2015•乐山)电影《刘三姐》中,秀才和刘三姐对歌的场面十分精彩.罗秀才唱到:“三百条狗交给你,一少三多四下分,不要双数要单数,看你怎样分得均?”刘三姐示意舟妹来答,舟妹唱道:“九十九条打猎去,九十九条看羊来,九十九条守门口,剩下三条财主请来当奴才.”若用数学方法解决罗秀才提出的问题,设“一少”的狗有x条,“三多”的狗有y条,则解此问题所列关系式正确的是()条,可得:,9.(3分)(2015•乐山)已知二次函数y=ax2+bx+c的图象如图所示,记m=|a﹣b+c|+|2a+b+c|,n=|a+b+c|+|2a﹣b﹣c|.则下列选项正确的是()≤>≤>10.(3分)(2015•乐山)如图,已知直线y=x﹣3与x轴、y轴分别交于A、B两点,P 是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是()Dx的距离是=,y=1+=面积的最大值是××=,二、填空题:本大题共6小题,每小题3分,共18分.11.(3分)(2015•湘潭)的倒数是2.根据倒数的定义,的倒数是的倒数是12.(3分)(2015•乐山)函数的自变量x的取值范围是x≥2.13.(3分)(2015•乐山)九年级1班9名学生参加学校的植树活动,活动结束后,统计每人植树的情况,植了2棵树的有5人,植了4棵树的有3人,植了5棵树的有1人,那么平均每人植树3棵.解:平均每人植树=314.(3分)(2015•乐山)如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,已知∠ADE=40°,则∠DBC=15°.C=(15.(3分)(2015•乐山)如图,已知A(2,2)、B(2,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2,2)的位置,则图中阴影部分的面积为π.,)的位置易得旋转,可得出阴影部分的面积.22,2Sπ×﹣)故答案为:π16.(3分)(2015•乐山)在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).(1)若点(﹣1,﹣2)是一次函数y=x+3图象上点M的“可控变点”,则点M的坐标为(﹣1,2).(2)若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,则实数a的取值范围是0≤a≤4..x=4.三、本大题共3小题,每小题9分,共27分.17.(9分)(2015•乐山)计算:|﹣|+﹣4cos45°+(﹣1)2015.+2﹣×﹣.18.(9分)(2015•乐山)求不等式组的解集,并把它们的解集在数轴上表示出来.19.(9分)(2015•乐山)化简求值:÷(﹣a),其中a=﹣2.÷•,﹣=四、本大题共3小题,每小题10分,共30分.20.(10分)(2015•乐山)如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.(1)求证:△DCE≌△BFE;(2)若CD=2,∠ADB=30°,求BE的长.BC=2CE=EC=.,CE=EC=.21.(10分)(2015•乐山)某班开展安全知识竞赛活动,班长将所有同学的成绩分成四类,并制作了如下的统计图表:根据图表信息,回答下列问题:(1)该班共有学生40人;表中a=20;(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.==22.(10分)(2015•乐山)“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:(1)小张如何进货,使进货款恰好为1300元?(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.五、本大题共2小题,每小题10分,共20分.23.(10分)(2015•乐山)如图1,四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=.(1)求CD边的长;(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q(点Q运动到点B停止).设DP=x,四边形PQCD的面积为y,求y与x的函数关系式,并求出自变量x的取值范围.tanA=,tanA=,cosA=,ECD==,即问题可得;ECD=,,求得PQ=y=DC﹣=DM=ED= tanA=tanA=,得cosA=,ECD==,CD=ECD=,PQ=PQ DC﹣=DM=ED=,≤24.(10分)(2015•乐山)如图,正比例函数y=2x的图象与反比例函数y=的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.(1)求k的值;(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.的比例系数的面积等于|k|联立成方程组,OD=AB=OAy=图象上的点,且|k||k|=1;联立成方程组得:解得:x+bb=x+,﹣,x,OD==OD=,(﹣,)或(﹣,六、本大题共2小题,第25题12分,第26题13分,共25分.25.(12分)(2015•乐山)已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O于点E.(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)CDCED===,DCEC=DC==.DCEC=DC==26.(13分)(2015•乐山)如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.(1)求二次函数的解析式;(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.①求点P的运动路程;②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;(3)在(2)的条件下,连结EF,求△PEF周长的最小值.∠PFA=PE PE=AD)AD=AD解得:y=x xHK=,∴HK=;PE=AD=PAPEA=∠PFA=PE=AD PF=ADEPC=BAC==,=PE EF=PE=AD1+ADBCAD=3最小值为:AD=.。

2015年兰州市初中毕业生学业考试数 学(A )满分150分,考试时间120分钟一、选择题(本题有15小题,每小题4分,共60分)1. 下列函数解析式中,一定为二次函数的是A. 13-=x yB. c bx ax y ++=2C. 1222+-=t t sD. xx y 12+= 2. 由五个同样大小的立方体组成如图的几何体,则关于此几何体三种视图叙述正确的是A. 左视图与俯视图相同B. 左视图与主视图相同C. 主视图与俯视图相同D. 三种视图都相同3. 在下列二次函数中,其图象的对称轴为2-=x 的是A. 2)2(+=x yB. 222-=x yC. 222--=x yD. 2)2(2-=x y4. 如图,△ABC 中,∠B=90°,BC=2AB ,则cosA= A. 25 B. 21 C. 552 D. 55 5. 如图,线段CD 两个端点的坐标分别为C (1,2),D (2,0),以原点为位似中心,将线段CD 放大得到线段AB ,若点B 的坐标为(5,0),则点A 的坐标为A.(2,5)B.(2.5,5)C. (3,5)D.(3,6)6. 一元二次方程0182=--x x 配方后可变形为A. 17)4(2=+xB. 15)4(2=+xC. 17)4(2=-xD. 15)4(2=-x7. 下列命题错误..的是 A. 对角线互相垂直平分的四边形是菱形 B. 平行四边形的对角线互相平分C. 矩形的对角线相等D. 对角线相等的四边形是矩形8. 在同一直角坐标系中,一次函数k kx y -=与反比例函数)0(≠=k xk y 的图象大致是9. 如图,经过原点O 的⊙P 与x 、y 轴分别交于A 、B 两点,点C 是劣弧上一点,则∠ACB=A. 80°B. 90°C. 100°D.无法确定10. 如图,菱形ABCD 中,AB=4,∠B=60°,AE ⊥BC ,AF ⊥CD ,垂足分别为E ,F ,连结EF ,则△AEF 的面积是 A. 34 B. 33 C. 32 D. 311. 股票每天的涨、跌幅均不超过10%,即当涨了原价的10%后,便不能再张,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停。

四川省乐山市五通桥区2014届九年级数学调研考试试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至 10页,共150分.考试时间为120分钟.考试结束后第Ⅱ卷和答题卡按规定装袋上交.第Ⅰ卷(选择题30分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案,不能答在本试题卷上.3.考试结束后,本试卷由考场统一收回,集中管理不上交.一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求1. 如果汽车向东行驶3公里记作3公里,向西2公里应记作()A.+2公里 B.-2公里C.+3公里D.-3公里2. 一个立体图形三视图如图(1)所示,那么这个立体图形的名称是()A.三棱柱 B.四棱柱C.三棱锥 D.四棱锥3. 为参加阳光体育运动,有9位同学去购买运动鞋,他们的鞋号由小到大是: 20, 21, 21, 22,22, 22, 22, 23, 23.这组数据的中位数和众数是()A.21和22 B.21和23C.22和22D.22和234. 如图,在平行四边形ABCD中,AE垂直于CD,E是垂足.如果∠B=55°,那么∠DAE 的角度为()A.25° B.35°C.45°D.55°5. 如图(3)所示的梯形梯子,AA′∥EE′,AB=BC=CD=DE,图(2)正视图侧视图俯视图图(1)A′B′=B′C′=C′D′=D′E′,AA′=60cm ,EE′=80cm .则BB′的长为( ) A .0.65cm B .0.675cmC .0.725cmD .0. 75cm6.轮船在顺水中航行80千米所需的时间和逆水航行60千米所需的时间相同. 已知水流的速度是3千米/时,求轮船在静水中的速度.设轮船在静水中的速 度为x 千米/时,由题意列出方程,其中正确..的是( ) A .803603+=-x x B .360380+=-x xC .803603-=+x xD .360380-=+x x 7. 如图,点M 是等腰梯形ABCD 底边AB 的中点,下例说法正确的是( )A .∠DA M =∠DCMB .DM ∥BCC .△AMD ≌△BMC D .△AMD ≌△DMC 8. 已知()2320x y x y -+++=,则x y +的值为A .1- B .1 C . 2D .39.如图,⊙O 的半径OD ⊥弦AB 于点C ,连结AO 并延长交⊙O 于 点E ,连结EC .若AB =8,CD =2,则EC 的长为( )A .8B .102 C .132D .15210.如图,M 为双曲线xy 3=上的一点,过点M 作x 轴、y 轴的垂线,分别交直线m x y +-=于点D 、C 两点,若直线m x y +-=与y 轴交于点A ,与x 轴相交于点B ,则AD•BC 的值为( )A .32B .23C .22D .22EABCO图(5)图(6)绝密★启用前【考试时间: 9:00——11:00】五通桥区2011年中考复习调研考试数学 第Ⅱ卷(非选择题共120分)注意事项:1.第Ⅱ卷共8页,用钢笔或圆珠笔直接答在试卷上.2.答卷前将密封线内的项目填写清楚. 题 号 二 三 四 五 六 第Ⅱ卷 总分人满分值 18分 27分 30分 20分 25分 120分得 分得分 评卷人11. 地球离太阳约有150000000千米,这个数字用科学记数法记为 12. 在解关于x 的方程02)12(3)12(2=+-+-x x 时,若设)12(-=x y ,则方程可以转化为关于y 的方程:13. 如图,在△ABC 中,∠BAC =40°,BP 平分∠ABC ,CP 平分 ∠ACB ,则∠BPC的度数为 度.14. 已知2<x <3,化简:3)2(2-+-x x = 15. 如图(8-1),在正方形铁皮上剪下一个扇形和一个半径为1cm 的圆形,使之恰好围成图(8-2)所示的一个圆锥,则这个圆锥的高为 .16.如果10b=n ,那么称b 为n 的“拉格数”,记为d (n),由定义可知:d (n)=b.如100102=,则d (100)= d (210)=2,给出下列关于“拉格数”d (n)的结论:①d(10)=10,②d(102-)=-2,③)10()10(3d d =3,④d(mn) =d(m)+d(n),⑤d(n m )=d(m )÷d(n).二、填空题(本大题共6小题,每小题3分,共18分.把答案填在题中的横线上)图(7)图(8-1) 图(8-2)其中,正确的结论有(填写所有正确的序号)。

乐山市市中区2015年初中毕业会考暨高中阶段统一招生适应性考试数 学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第一部分1至2页,第二部分3至6页,共150分.考试时间为120分钟.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题 共30分)注意事项:1.答第一部分前,考生务必将自己的姓名、报名号用0.5毫米的黑色签字笔填写在答题 卡上.并将条形码粘在答题卡的指定位置.2.选择题用2B 铅笔填涂在答题卡对应题目标号的位置上,其它试题用0.5毫米黑色签 字笔书写在答题卡对应框内,不得超越题框区域.在草稿纸、试卷上答题无效.3.考试结束后,监考人员将本试题卷和答题卡分别收回并装袋.一、选择题:本大题共10题,每题3分,共30分.在每题给出的四个选项中,只有一个选项是符合题目要求的. 1.下面的数中,比0小1的实数是(A )2 (B )0 (C )1- (D )2- 2. 函数124y x =-中,自变量x 的取值范围是(A )2x ≠ (B )2x > (C )2x < (D )4x ≠3. 如图,以O 为圆心,任意长为半径画弧,与射线OM 交于点A,再以A 为圆心,AO 长 为半径画弧,两弧交于点B ,画射线OB . 则cos ∠AOB 的值等于(A (B )12(C (D4. 如图甲所示的几何体的左视图是(A ) (B ) (C ) (D )5. 为参加阳光体育运动,有9位同学去购买运动鞋,他们的鞋号由小到大是: 20, 21, 21, 22, 22, 22, 22, 23, 23.这组数据的中位数和众数是 (A )21和22 (B )21和23 (C )22和22 (D )22和23图甲B MO A6. 如图,直线y kx b =+交坐标轴于A (-3,0)、B (0,1)两点,则不等式0kx b --< 的解集为(A )x >3- (B )x <3- (C )x >3 (D )x <37. 如图,已知△ADE 与△ABC 的相似比为1:2,则△ADE 与四边形BCED的面积 比为(A )1:2 (B )1:3 (C )1:4 (D )3:48. 已知一元二次方程032=--x x 的较小根为1x ,则下面对1x 的估计正确的是 (A )231-<<-x (B )121-<<-x (C )011<<-x (D )321<<x9. 如图,点D 为AC 上一点,点O 为边AB 上一点,AD =DO .以O 为圆心,OD 长为半 径作圆,交AC 于另一点E ,交AB 于点F ,G , 连接EF .若∠BAC =22°,则∠EFG = (A )55︒ (B )44︒ (C )38︒ (D )33︒10. 已知二次函数)0(2≠++=a c bx ax y 的图象如图所示,有下列结论:①0abc >; ②20b a +=; ③80a c +>; ④930a b c ++>. 其中,正确结论的个数是 (A )1个 (B )2个 (C )3个 (D )4个乐山市市中区2015年初中毕业会考暨高中阶段统一招生适应性考试数 学第二部分(非选择题 共120分)注意事项:1.考生需用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答,作图题 可先用铅笔画线,确认后用0.5毫米黑色墨迹签字笔描清楚,答在试题卷上无效.2.本部分共16小题,共120分.二、填空题:(本大题共6题.每题3分,共18分)11. yxB AOCEDBG OFAEDCBA y xOx =1–1–212.因式分解:2242a a -+= . 13. 如图,过正五边形ABCDE 的顶点A 作直线l ∥CD ,则∠1=____________.14. 如图,△ABC 是等腰直角三角形,∠ACB 90=︒,AC =BC ,把△ABC 绕点A 按顺时针方向旋转45︒后得到△''AB C ,若AB =2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是(结果保留π).15. 在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3,现从中任意摸出一个小球,将其上面的数字作为点M 的横坐标;将球放回袋中搅匀,再从中任 意摸出一个小球,将其上面的数字作为点M 的纵坐标.则点M 在直线y =x 上的概率 是 .16. 定义[a ,b ,]c 为函数2y ax bx c =++的特征数,下面给出特征数[2m ,1m -,1]m -- 的函数的一些结论:①当3m =-时,函数图象的顶点坐标是1(3,8)3;②当2m =时,函数图象的对称轴方程是18x =-;③当0m >时,函数图象截x 轴所得的线段长度大于32;④当0m <时,函数在14x <时,y 随x 的增大而增大. 其中正确的结论有 .(请填写所有正确的序号)三、(本大题共3题.每题9分,共27分)17.12sin 452015-++︒-.18. 先化简,再求值:22244(4)2x x x x x+--÷+,其中1x =-. 19. 如图,在平面直角坐标系xOy 中,点A (0,3),点B (4,3).(1)只用直尺(没有刻度)和圆规,求作一点P ,使点P 同时满足下列两个条件(要求保留作图痕迹,不必写出作法): ①点P 到A 、B 两点的距离相等; ②点P 到∠xOy 的两边距离相等. (2)在(1)作出点P 后,写出点P 的坐标.四、(本大题共3题.每题10分,共30分)20. 如图,将□ABCD 的边DC 延长到点E ,使CE =DC ,连接AE ,交BC 于点F .l C'B'CBABAy xO D(1)求证:△ABF ≌△ECF ;(2)若∠AFC =2∠D ,连接AC 、BE . 求证:四边形ABEC 是矩形.21.为鼓励创业,省政府制定了小型企业的优惠政策,许多小型企业应运而生,某镇统计 了该镇1﹣5月新注册小型企业的数量,并将结果绘制成如下两种不完整的统计图:(1)某镇今年1﹣5月新注册小型企业一共有 家.请将折线统计图补充完整; (2)在扇形统计图中,4月部分所对应的圆心角是 度;(3)该镇今年3月新注册的小型企业中,只有2家是餐饮企业,现从3月新注册的小型企业中随机抽取2家企业了解其经营状况,请用列表或画树状图的方法求出所抽取的2 家企业恰好都是餐饮企业的概率.22.如图,在直角坐标系xOy 中,直线y mx =与双曲线ny x=相交于A (-1,a )、B 两点, AC ⊥x 轴,垂足为C ,BD ⊥x 轴,垂足为D , 且满足tan ∠AOC 2=. (1)求m 、n 的值;(2)求直线AD 的解析式和△ABD 的面积.五、(本大题共2题.每题10分,共20分)23. 已知关于x 的一元二次方程2()20x k x k --+=有两个实数根1x 、2x . (1)求实数k 的取值范围;xyDC B A O25%1月2月3月4月5月数量(家)65432105月4月3月2月1月今年1—5月各月新注册小型企业数量占今年前五月新注册小型企 业总量的百分比扇形统计图今年1—5月各月新注册小 型企业数量折线统计图(2)当实数k 为何值时,代数式2212121x x x x +-⋅+取得最小值,并求出该最小值.24. 如图,已知等边△ABC ,以AB 为直径的圆与BC 边交于点D ,过点D 作DF ⊥AC ,垂足为F ,过点F 作FG ⊥AB ,垂足为G ,连结G D . (1)求证:DF 是⊙O 的切线; (2)若AB =12,求FG 的长;(3)在(2)问条件下,求点D 到FG 的距离.六、(本大题共2题.25题12分,26题13分,共25分)25. 如图,tan ∠QCF 2=,点E 在射线CQ 上,CE =12.点P 是∠QCF 内一点,PE ⊥QC 于点E ,PE =4.在射线CQ 上取一点A ,连AP 并延长交射线CF 于点B ,作BD ⊥QC 于 点D .(1)若AB ⊥FC ,求AE 的长; (2)若△APE ∽△CBD ,求AE 的长;(3)当点P 是线段AB 中点时,试判断△ABC 的形状,并说明理由;(4)连结BE . 当APE EBC S S =△△时,求AE 的长.26. 如图,在平面直角坐标系中,四边形OABC 是平行四边形,直线经过O 、C 两点.点 A 的坐标为(8,0),点B 的坐标为(11,4),动点P 在线段OA 上从点O 出发以每秒1 个单位的速度向点A 运动,同时动点Q 从点A 出发以每秒2个单位的速度沿A →B →C 的方向向点C 运动,过点P 作PM 垂直于x 轴,与折线O 一C —B 相交于点M .当M 、 Q 两点相遇时停止运动,设点P 、Q 运动的时间 为t 秒(0t >).△MPQ 的面积为S . (1)点C 的坐标为___________,直线的解析式为 ;(2)若抛物线'C 经过O 、A 、C 三点,则抛物线'C 的开口方向: ,对称轴OFG D CBAy xl QPCBAO EF Q PDCBA方程: ;(3)试求点Q 与点M 相遇前S 与t 的函数关系式,并求出S 的最大值.乐山市市中区2014~2015学年度下期适应性试题九年级数学参考答案一、选择题(本大题共10小题.每小题3分,共30分)1.C2.A3.B4.B5.C6.A7.B8.B9.D 10.C二、填空题(本大题共6小题.每小题3分,共18分)11. 2 12. 22(1)a - 13. 36︒14.4π15.1316. ①③④ 三、(本大题共3小题,每小题9分,共27分)17. 132.18. 化简得:2x -;代值得3-.(化简正确7分,代值并计算正确2分) 19. (1)作图; (7分)(评分说明:作AB 的中垂线3分;作∠xOy 的角平分 线3分;指明点P 的位置1分)(2)点P 的坐标为(2,2). (9分)四、(本大题共3小题,每小题10分,共30分) 20. (1)问(5分);(2)问(5分). 【(2)问需说明四边形ABEC 是平行四边形,AE =BC .】 21. (1)16;(2分) 折线统计图如下(2分) (2)67.5︒;(1分)(3)设该镇今年3月新注册的小型企业为甲、乙、丙、丁,其中甲、乙为餐饮企业. 画树状图:(3分)∵共有12种等可能的结果,甲、乙2家企业恰好被抽到的有2种,POx y AB今年1—5月各月新注册小型企业数量折线统计图1月2月3月4月5月0123456数量(家)∴所抽取的2家企业恰好都是餐饮企业的概率为16.……………………(2分)22. (1)2m =-,2n =;(各2分,共4分)(2)直线AD 的解析式为1y x =-+,△ABD 的面积为2. 【评分说明:求解析式正确得4分,面积正确得2分.】五、(本大题共2小题,每小题10分,共20分)23. (1)实数k 的取值范围是14k ≤; ………………………………(4分)(2)利用根与系数的关系,化简2212121x x x x +-⋅+得2(1)1k -+;当14k =时,代数式的最小值为2516. …………………………(10分)24.(1)证明:连结OD ,如图,∵△ABC 为等边三角形,∴∠C =∠A =∠B =60°. 而OD =OB ,∴△ODB 是等边三角形,∠ODB =60°, ∴∠ODB =∠C ,∴OD ∥AC ,∵DF ⊥AC ,∴OD ⊥DF ,∴DF 是⊙O 的切线. ………………(4分) (2)解:∵OD ∥AC ,点O 为AB 的中点,∴OD 为△ABC 的中位线.∴BD =CD =6.在Rt △CDF 中,∠C =60°,∴∠CDF =30°,∴CF =CD =3. ∴AF =AC ﹣CF =12﹣3=9,在Rt △AFG 中,∵∠A =60°,∴FG =AF ×sinA =9×=. ………(7分)(3)解:过D 作DH ⊥AB 于H .∵FG ⊥AB ,DH ⊥AB ,∴FG ∥DH , 在Rt △BDH 中,∠B =60°,∴∠BDH =30°,∴BH =BD =3,DH =BH =3.在Rt △AFG 中,∵∠AFG =30°,∴AG =AF =,∵GH =AB ﹣AG ﹣BH =12﹣﹣3=,FG ⊥AB ,∴点D 到FG 的距离是92. ……………………………………………………………………………(10分)六、(25题12分,26题13分,共25分) 25.解:(1)∵AB ⊥FC ,QC PE ⊥,∴APE C ∠=∠. ∵tan 2QCF ∠=,∴tan 2APE ∠=. 在Rt △APE 中,4=PE ,∴tan 428AE PE APE =⋅∠=⨯=.……(3分)(2)∵△APE ∽△CBD ,∴C PAE ∠=∠. ∴tan 2PAE ∠=.在Rt △APE 中,4=PE ,∴42tan 2PE AE PAE ===∠. …………………………………………(6分) (3)ABC ∆为直角三角形.理由如下: …………………………………(7分) ∵PE ∥BD ,得BDPEAD AE AB AP ==,得8=BD ,4=DC , ∴8412=-=DE . ∴8=AE . ∴APE ∆∽BCD ∆,PAE DBC ∠=∠.∴90ABC ABD DBC ABD BAD ∠=∠+∠=∠+∠=︒.∴△ABC 为直角三角形. ………………………………………………(9分) (4)连接BE ,设a DC =,则a BD 2=,a S EBC 12=∆.由APE EBC S S ∆∆=,则a AE 6=. 由APE ∆∽ABD ∆,得AD AE BD PE =,aa aa -+=126624. 解得31=a ,342-=a (舍去). 所以18=AC .…………………………………………………………(12分)26. 解:(1)点C 的坐标是(3,4),直线l 的解析式为43y x =.……(每空1分)(2)开口方向: 向下 ,对称轴方程:4x =.…………(每空1分) (3)根据题意,得OP =t ,AQ =2t .分三种情况讨论:①当502t <≤时,如图1,M 点的坐标是(43t t ,). 过点C 作CD ⊥x 轴于D ,过点Q 作QE ⊥ x 轴于E ,可得△AEQ ∽△ODC .EF Q PDCBAEF Q PDCB A图1EDMyxl Q P CB AO∴AQ AE QE OC OD CD ==,∴2AE QE ==534t ,∴65t AE =,85EQ t =. ∴Q 点的坐标是(68855t t +, ),∴PE =618855t t t +-=+.∴S =21141216(8)2235153MP PE t t t t ⋅⋅=⋅⋅+=+. ……………………(7分)∴222162160(20)153153S t t t =+=+-∵ 当502t <≤时,S 随t 的增大而增大,∴ 当52t =时,S 有最大值,最大值为856. ……………………(8分)②当532t <≤时,如图2,过点Q 作QF ⊥x 轴于F ,∵25BQ t =-,∴OF =11(25)162t t --=- ∴Q 点的坐标是(1624t -, ), ∴PF =162163t t t --=-.∴S =211432(163)22233MP PF t t t t ⋅⋅=⋅⋅-=-+. ……………………(10分)2232812822()339S t t t =-+=--+. ∴当83t =时,S 有最大值,最大值为1289. ……………………(11分)③当1633t <<时,如图3,∴MQ=162163t t t --=-,MP=4.∴S=114(163)63222MP PF t t ⋅⋅=⋅⋅-=-+.∵60k =-<.∴S 随t 的增大而减小. 又∵当3t =时,S =14.当163t =时,S=0.∴014S <<. 综上所述,S 与t 函数关系式为222165(0)15323252(3)3216632(3)3t t t S t tt t t ⎧+<≤⎪⎪⎪=-+<≤⎨⎪⎪-+<<⎪⎩ 当83t =时,S 有最大值,最大值为1289. ……………………(13分)O ABC PQlxy MF图2图3M y xlQPC BAO。

准考证号:五通桥区2018年中考复习调研考试数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至6页,共150分.考试时间为120分钟.考试结束后第Ⅱ卷和答题卡按规定装袋上交.第Ⅰ卷(选择题30分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案,不能答在本试题卷上.3.考试结束后,本试卷由考场统一收回,集中管理不上交.一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求1.若)3()2(a ,则a 的值为(▲).A .5B .5C .6D .62.据媒体报道,我国最新研制的“察打一体”无人机的速度极快,经测试最高速度可达每分钟204000米,这个数用科学记数法表示,正确的是(▲).A .61004.2B .51004.2C .4104.20D .3102043.如图(1)是由五个相同的小正方体搭成的几何体,则它的主视图是(▲).4.如图(2),下列选项中,哪个不可以得到1l ∥2l (▲).A .21B .32C .53D .180435.下列说法正确的是(▲)A .在抽样调查过程中,样本容量越大,对总体的估计就越准确B .投一个骰子的得数是6是必然事件C .要考察一个班级中的学生对建立图书角的看法适合用抽样调查D .甲、乙两人射中环数的方差分别为2S2甲,4S 2乙,说明乙的射击成绩比甲稳定图(1)A .B .C .D .图(2)。
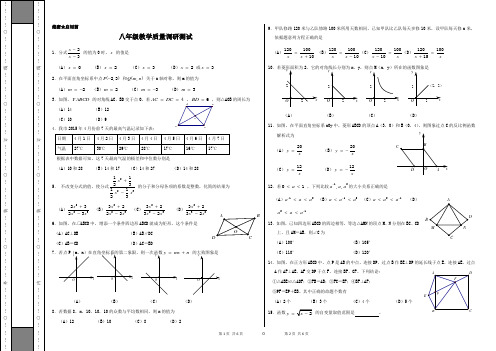
第1页共6页◎第2页共6页绝密★启用前八年级教学质量调研测试1.分式23x x -- 的值为0时,x 的值是 (A )0x = (B )2x = (C )3x = (D )2x = 或3x = 2.在平面直角坐标系中点(2,3)P - 和(,)Q m n 关于x 轴对称,则m 的值为 (A )2m =- (B )2m = (C )3m =- (D )3m =3.如图,ABCD 的对角线AC 、BD 交于点O ,若4AC DC == ,6BD = ,则△AOB 的周长为(A )14 (B )12 (C )10 (D )94.我市2015年4月份前7天的最高气温记录如下表:根据表中数据可知,这7天最高气温的极差和中位数分别是(A )10和28 (B )14和17 (C )14和27 (D )14和285. 不改变分式的值,使分式22311231123x x x +- 的分子和分母各项的系数是整数,化简的结果为 (A )2232323x x x +- (B )2233223x x x +- (C )2233232x x x +- (D )2323232x x x +-6.如图,在□ABCD 中,增添一个条件四边形ABCD 就成为矩形,这个条件是 (A )AC ⊥DB (B )AB ∥DC (C )AB =CD (D )AC =BD7.若点P (m ,n(A ) (B ) (C ) (D )8.若数据8,x ,10,10,10的众数与平均数相同,则x 的值为 (A )12 (B )10 (C )8(D )29.甲队修路120米与乙队修路100米所用天数相同,已知甲队比乙队每天多修10米,设甲队每天修x 米,依据题意列方程正确的是 (A )12010010x x =+ (B)12010010x x =-(C )12010010x x =-(D )12010015x x=+ 10x ,y ,则点M (x ,y )所在的函数图象是(A ) (B ) (C ) (D )11.如图,在平面直角坐标系xOy中,菱形ABCD 的顶点A (3,0)和B (0,4),则图象过点C 的反比例函数解析式为(A )20y x = (B )20y x=-(C )12y x =(D )12y x=- 12.若01a << ,下列比较12,,a a a -的大小关系正确的是(A )12aa a -<< (B )12a a a -<< (C )21a a a -<< (D )21a a a -<<13.如图,已知四边形ABCD 的四边相等,等边△AMN 的顶点M 、N 分别在BC 、CD上,且AM =AB ,则∠C 为(A )100° (B )105° (C )110° (D )120°14.如图,在正方形ABCD 中,点P 是AB 的中点,连接DP ,过点B 作BE ⊥DP 的延长线于点E ,连接AE ,过点A 作AF ⊥AE ,AF 交DP 于点F ,连接BF 、CF 。
准考证号:五通桥区2018年中考复习调研考试数 学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至6页,共150分.考试时间为120分钟.考试结束后第Ⅱ卷和答题卡按规定装袋上交.第Ⅰ卷(选择题 30分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案,不能答在本试题卷上.3.考试结束后,本试卷由考场统一收回,集中管理不上交.一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求1.若)3()2(-⨯-=a ,则a 的值为( ▲ ). A .5B .5-C .6D .6-2.据媒体报道,我国最新研制的“察打一体”无人机的速度极快,经测试最高速度可达每分钟204000 米,这个数用科学记数法表示,正确的是( ▲ ).A .61004.2⨯ B .51004.2⨯ C . 4104.20⨯ D .310204⨯ 3.如图(1)是由五个相同的小正方体搭成的几何体,则它的主视图是( ▲ ).4.如图(2),下列选项中,哪个不可以得到1l ∥2l ( ▲ ).A .21∠=∠B .32∠=∠C .53∠=∠D .︒=∠+∠18043 5.下列说法正确的是( ▲ )A .在抽样调查过程中,样本容量越大,对总体的估计就越准确B .投一个骰子的得数是6是必然事件C .要考察一个班级中的学生对建立图书角的看法适合用抽样调查D .甲、乙两人射中环数的方差分别为2S 2=甲,4S 2=乙,说明乙的射击成绩比甲稳定A .B .C .D .图(1)图(2)6.若03)2(2=-+-y x ,则y x -的正确结果是( ▲ )A . 1-B .1C .5-D .57.如图(3),扇形纸扇完全打开后,外侧两竹条AB 、AC 夹角为︒120,AB 的长为cm 30,贴纸部分BD 的长为cm 20,则贴纸部分的面积为( ▲ ) A.23400cm π B .23800cm πC .2100cm π D .2800cmπ8.如图(4),网格中的四个格点组成菱形ABCD ,则DBC ∠tan 的值为( ▲ )A .31B .22C .3D .29. 如图(5),在平面直角坐标系中,A (3-,1),以点O 为直角顶点作等腰直角三角形AOB ,双曲线xk y 11=在第一象限内的图象经过点B ,设直线AB 的解析式为b x k y -=22,当21y y >时,x 的取值范围是( ▲ )A .15<<-xB .10<<x 或5-<xC .16<<-xD .10<<x 或6-<x10. 如图(6)中是抛物线形拱桥,P 处有一照明灯,水面OA 宽m 4,从O 、A 两处观测P 处,仰角分别为α、β,且21tan =α,23tan =β,以O 为原点,OA 所在直线为x 轴建立直角坐标系.若水面上升m 1,水面宽为( ▲ ) A .22 B .32 C .223 D .321图(4)图(3)图(5)图(6)绝密★启用前【考试时间: 9:00——11:00】五通桥区2018年中考复习调研考试数 学第Ⅱ卷(非选择题 共120分)注意事项:1.第Ⅱ卷共4页,用钢笔或圆珠笔答在答题卡上. 2.答卷前将密封线内的项目填写清楚.题 号 二 三 四 五 六 第Ⅱ卷 总分人满分值 18分 27分 30分 20分 25分 120分得 分得分 评卷人11.如图(7)所示,数轴上点A 所表示的数的相反数是 ▲ .12.函数2-=x xy 中,自变量x 的取值范围是 ▲ .13.小明把如图(8)所示的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是 ▲ . 14.若一个圆锥的底面积为π9,锥高为4,则这个圆锥侧面展开的扇形面积为 ▲ .15.如图(9),矩形AOCB 的两边OC 、OA 分别位于x 轴、y 轴上,点B 的坐标为(320-,5),D 是AB 边上的一点.将ADO ∆沿直线OD 翻折,使A 点恰好落在对角线OB 上的点E 处,若点E 在反比例函数xky =的图像上,那么k 的值是 ▲ 16.抛物线截直线所得的线段长度叫做抛物线的弦长.如图(10),线段AB 的长为抛物线截直线l 所得的弦长.(1)求抛物线1412-=x y 截x 轴所得的弦长为 ▲ (2)已知抛物线1412-=x y 截两条经过原点直线的弦长为a 和b ,若这两条直线互相垂直,则b a 11+为定值.则这个定值=+ba 11 ▲二、填空题(本大题共6小题,每小题3分,共18分.把答案填在答题卡上相应位置)-1A01图(7)图(8)图(10)图(9)得分 评卷人17.()2)2018(360sin 23312-+-︒--+π18.解不等式组⎪⎩⎪⎨⎧-≥-+<-.4221,15)1(3x x x x ,并求所有的非负整数解.19.如图(11),D 、E 、F 、B 在一条直线上,CD AB =,D B ∠=∠,DE BF =,求证:AE ∥CF . 得分 评卷人20.先化简,再求值:114411222-++-+⋅--x x x x x x ,其中x 从1-,0,1,2中选取的一个合适的数.21.某校举行“足球在身边”的专题调查活动,采取随机抽样的方法进行问卷调查,调查结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,并将调查结果绘制成两幅不完整的统计图(如图),请根据图中提供的信息,解答下列问题:(1)被调查的学生共有___人.在扇形统计图中,表示“比较了解”的扇形的圆心角度数为___度 (2)请用列表法或树状分析从2名男生和2名女生中随机抽取2名学生参加“足球在身边”的知识竞赛,抽中1男1女的概率.22.如图(12),在数学活动课中,小敏为了测量校园内旗杆CD 的高度.先在教学楼的底端A 点处,观测到旗杆顶端C 得︒=∠60CAD ,然后爬到教学楼上的B 处,观测到旗杆底端D 的俯角是︒30.已知教学楼中A 、B 两处高度为4米.(1)求教学楼与旗杆的水平距离AD ;(结果保留根号......); 三、(本大题共3小题,每小题9分,共27分)四、(本大题共3小题,每小题10分,共30分.)CEBDFA图(11)图(12)(2)求旗杆CD 的高度.得分 评卷人23.图(13)中的折线ABC 表示某汽车的耗油量y (单位:km L /)与速度x (单位:h km /)之间的函数关系(12030≤≤x ),已知线段BC 表示的函数关系中,该汽车的速度每增加h km /1,耗油量增加km L /002.0.(1) 当速度为h km /50、h km /100时,该汽车的耗油量分别为_____km L /、____km L /; (2) 速度是多少时,该汽车的耗油量最低?最低是多少?24.如图(14),在ABC ∆中,a BC =,b AC =,c AB =,⊙D 与BC 、AC 、AB 都相切,切点分别是E 、F 、G ,BA 、ED 的延长线交于点H ,a 、b 是关于x 的方程084)4(2=+++-c x c x 的两个根.(1)求证:ABC ∆是直角三角形;(2)若c BAC a 9sin 25=∠⋅,求四边形CEDF 的面积.五、(本大题共2小题,每小题10分,共20分.)图(13)A CFGDE图(14)得分 评卷人25.如图(15),已知在ABC ∆中,5==AC AB ,54cos =B ,P 是边AB 上一点,以P 为圆心,PB 为半径的⊙P 与边BC 的另一个交点为D ,连结PD 、AD .(1)求△ABC 的面积;(2)设x PB =,APD ∆的面积为y ,求y 关于x 的函数关系式,并写出自变量x 的取值范围; (3)如果APD ∆是直角三角形,求PB 的长.26.如图(16-1),已知菱形ABCD 的边长为32,点A 在x 轴负半轴上,点B 在坐标原点,点D 的坐标为(3-,3),抛物线)0(2≠+=a b ax y 顶点在DC 边上,并经过AB 边的中点.(1)求这条抛物线的函数解析式;(2)点C 关于直线)0(3≠+=k kx y 的对称点是'C ,求点'C 到点A 的最短距离;(3)如图(16-2)将菱形ABCD 以每秒1个单位长度的速度沿x 轴正方向匀速平移,过点B 作CD BE ⊥于点E ,交抛物线于点F ,连接DF 、AF .设菱形ABCD 平移的时间为t 秒(30<<t ),问是否存在这样的t ,使ADF ∆与DEF ∆相似?若存在,求出t 的值;若不存在,请说明理由.六、(本大题共2小题,第25题12分,第26题13分,共计25分).DACBP 图(15)ACB(备用图)图(16-1)图(16-2)参考答案及评分意见一、选择题:每小题3分,10小题,共计30分1.C 2.B 3.D 4.C 5.A 6.A 7.B 8.C 9.D 10.A 二、填空题:每小题3分,6小题,共计18分 11.2 12.2≠x 13.41 14.π15 15.-12 16.(1)4(2)41(第一空1分,第二空2分)三、本大题共3小题,每小题9分,共27分17.解:原式=132323332+-⨯--+………………………8分 =1 …………………………………………………………………………………………………9分 18.解:①解15)1(3+<-x x 得2->x……………………………………………………………………3分②解4221-≥-x x 得37≤x …………………………………………………………………………6分 得不等式解集:372≤<-x ……………………………………………………………………………8分所有非负整数解为:0,1,2………………………………………………………………………9分19.证明:∵DE BF =∴EF DE EF BF +=+DF BE =…………………………………………2分在ABE ∆和CDF ∆中⎪⎩⎪⎨⎧=∠=∠=DF BE D B CDAB∴ABE ∆≌CDF ∆……………………………………………………………………6分 ∴CFD AEB ∠=∠∴AE ∥CF ……………………………………………………………………………9分四、本大题共3小题,每小题10分,共30分20.解:原式=11)2(1)1)(1(22-+-+⋅-+-x x x x x x ……………………4分 =11)2)(1(1-+--x x x ……………………6分 =21-x ………………………………………………………………………………………………7分 当0=x时,原式=21-(若直接代入运算,可给答案分)………………………………………………10分 21.(1)被调查的学生共有300人.在扇形图中,表示“比较了解”的圆心角度数为108度………………4分(2) ……………………8分由树状图:P (抽中一男一女)=128=32…………………………………………………10分 E DFA图(11)男女女22.解:(1)∵教学楼点B 处的俯角是30° ∴∠ADB =30°在Rt △ABD 中,∠BAD =90°,∠ADB =30°,AB =4 ∴3430tan 4tan =︒=∠=ADB AB AD∴教学楼与旗杆的水平距离是34………………………………………………………………5分 (2)在Rt △ACD 中,∠ADC =90°,∠CAD =60°,AD =34 ∴1233460tan =⨯=︒⋅=AD CD∴旗杆的高度是12……………………………………………………………………………………10分五、本大题共2小题,每小题10分,共20分.23.(1)13.0,14.0……………………………………………………………………………………………2分(2)根据题意,线段AB 所表示的y 与x 之间的函数表达式为18.0001.0+-=x y ……………………5分根据题意,线段BC 所表示的y 与x 之间的函数表达式为06.0002.0-=x y ……………………8分由图像可知,B 是折线ABC 的最低点. 解方程组⎩⎨⎧-=+-=,06.0002.0,18.0001.0y x y 得⎩⎨⎧==1.0,80y x 因此,速度是h km /80时,该汽车的耗油量最低,最低是km L /1.0.………………………………………10分 24.(1)证明:∵a 、b 是关于x 的方程084)4(2=+++-c x c x 的两个根,∴4+=+c ba ,84+=c ab ,∴22)4()(+=+c b a ,即1682222++=++c c b ab a ,∴222c b a =+,∴△ABC 是直角三角形;……………………………………………………………………………4分(2)解:连DB ,如图∵c BAC a 9sin 25=∠⋅,即ac BAC 259sin =∠,又∵在ABC Rt ∆中,ca BAC ∠sin , ∴acc a 259=,得a c 53= 设x c5=,则x a 3=,x b 4=, ∴4+=+c b a∴4543+=+x x x ,解得2=x ,∴6=a ,8=b ,10=c ……………………………………7分∵⊙D 与BC 、AC 、AB 都相切,切点分别是E 、F 、G , ∴DE=DF=DG ,DE ⊥BC ,DG ⊥AB , ∴四边形DECF 为正方形,设DE=DF=DG=r ,则BE =6+r ,BH =)6(35+r ,EH =)6(34+r ∵BEH BHD BED S S S ∆∆∆=+∴)6()6(3421)6(3521)6(21+⋅+⨯=+⨯++r r r r r r ,解得6=r ∴362==r S CEDF四边形.…………………………………………………………………………………10分六、本大题共2小题,第25小题12分,第26小题13分,共计25分25.解:(1)∵5==AC AB ,54cos =B ∴8=BC ,3=h∴123821=⨯⨯=∆ABCS …………………………………………………………………………3分 (2)如图,作AB DM⊥垂足为M∵x PB =,54cos =B 得x BD 58=∴x x DM 25245853=⨯=又∵5=AB ,x PB =得x AP -=5 ∴()x x DM AP S APD 252452121-=⋅=∆ ∴x x y 51225122+-=)50(<<x ………………………………………………………………7分 ………………………………12分M26.解:(1)由题意得AB 的中点坐标为(3- ,0),CD 的中点坐标为(0,3),分别代入b ax y +=2,得⎩⎨⎧==+-30)3(2b b a ,解得⎩⎨⎧=-=31b a∴这条抛物线的函数解析式为32+-=x y ………………………………………………………3分(2)∵点C (3-,3)关于直线)0(3≠+=k kx y 的对称点是'C又∵)0(3≠+=k kx y 过点(0,3) ∴'C 一定在点(0,3)为圆心,3为半径的圆上∴点'C 到点A 的最短距离为321- …………………………………………………………6分(3)如图2所示,在Rt △BCE 中,∠BEC=90°,BE=3,BC=23 ,∴BE 33sinC =BC 223== ∴∠C=60°,∠CBE=30°。
数 学 试 卷 第1页(共4页)OP图3图2 乐山市五通桥区初中2019届中考调研考试数学试卷第Ⅰ卷(选择题 共30分)一、选择题:(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个选项符合题意.1A .9B .±9C .3D .±3 2.若点(,2)P a a -在第四象限,则a 的取值范围是( )A .20a -<<B .02a <<C .2a >D .0a <3.函数y ax b =+与cy x=的图象,如图1所示,则A .a >0,b >0,c >0B . a <0,b <0,c <0C .a <0,b >0,c >0D . a <0,b <0,c >04.全民健身活动中,组委会组织了长跑队和自行车队进行宣传,全程共10千米,自行车队的速度是长跑队速度的2.5倍,自行车队出发半小时后,长跑队才出发,结果长跑队比自行车队晚到了2小时,如果设长跑队跑步的速度为x 千米/时,那么根据题意可列方程为A.x10+2=x 5.210+21 B.x 5.210-x 10=20.5-C.x 10-x 5.210= 20.5-D.x 10-x 5.210=2+0.55.如图2,在长为a 的正方形中挖掉一个边长为b 的小正方形(a >b ),把余下的部分剪拼成一个矩形,通过计算两个图形的面积,验证了一个等式,则这个等式是A .a 2-b 2=(a-b )(a+b )B .(a+b )2=a 2+2ab+b 2C .(a-b )2=a 2-2ab+b 2D .(a +2b )(a -b )=a 2+ab-2b 2[②二班的优秀人数多于一班的优秀人数(成绩≥80分为优秀);③一班成绩波动情况比二班成绩波动大.上述结论正确的是 A.①②③ B.①② C.①③ D.②③7.如图3,⊙O 的半径为5,若OP =3,,则经过点P 的弦长可能是图1数 学 试 卷 第2页(共4页)图4 DABCE图6( )A .3B .6C .9D .128.如图4,在菱形ABCD 中,DE ⊥AB ,,AE =3,则tan ∠DBE 的值是A .B .2C .D .9.在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形又能拼成三角形和梯形的是A. B. C. D 10.二次函数y=ax 2+bx+c (a ≠0)的图象如图5所示,则下列结论中正确的是( ) A .a >0 B .当﹣1<x <3时,y >0 C .c <0 D .当x ≥1时,y 随x 的增大而增大第Ⅱ卷(非选择题 共90分)二、填空题:(本大题共6个小题,每小题3分,共18分)把答案直接填在题中横线上.11.已知关于x 的方程21x mx +=-的解是正数,则m 的范围是 12.一个口袋中装有4个白色球,1个红色球,7个黄色球,搅匀后随机从袋中摸出1个球是白色球的概率是________________.13.如图6,边长为a 的正方形发生形变后成为边长为a 的菱形,如果这个菱形的一组对边之间的距离为h ,记ak h=,我们把k 叫做这个菱形的“形变度”.若变形后的菱形有一个角是060,则形变度k = .14.如图7是某几何体的三视图,3cos 5A =125图 5图7数 学 试 卷 第3页(共4页)图/岁图10 图11该几何体的表面积是 . 15.一个正方体的每个面分别标 有数字1,2,3,4,5,6.根据如图8中该正方 体A 、B 、C 三种状态所显示的数字, 可推出“?”处的数字是 .16.请阅读下列语句:①一个数的相反数是它本身,则这个数一定是正数;②方程20ax bx c ++=,当240b ac ->时,方程一定有两个不等实根;③函数y kx b =+,当0k >时,图象有可能不经过第二象限; ④两边一角对应相等的两个三角形全等;⑤某校对A B 、两个班在一次数学测试中成绩统计为:A 班的方差2A S >B 班的方差2B S ,得出结论是:B 班的成绩比A 班的好.其中正确的是 (只填序号) 三、解答题:(本大题共8个小题,共72分)解答应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分6分)求:222(2)4ab a b -+-的值.18.(本小题满分8分)如图9,在A 岛周围25海里水域有暗礁,一轮船由西向东航行到O 处时,发现A 岛在北偏东60°方向,轮船继续前行20海里到达B 处,发现A 岛在北偏东45°方向,该船若不改变航向继续前进,有无触礁的危险? (参考数据:2≈1.4143≈1.732)19.(本小题满分8分)如图10是某训练班全体学生年龄的统计图。
准考证号:五通桥区2019年中考调研考试数 学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至 10页,共150分.考试时间为120分钟.考试结束后第Ⅱ卷和答题卡按规定装袋上交.第Ⅰ卷(选择题 30分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案,不能答在本试题卷上.3.考试结束后,本试卷由考场统一收回,集中管理不上交.一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求1.2-的倒数是( ▲ ). A .21 B .21- C .2 D .2- 2.如图(1)所示的物体是一个几何体,其主视图是( ▲ ).A .B .C .D . (图1)3.某中学参加全区中学小学生运动会的12名队员的年龄情况如下,则这个队队员年龄的众数是( ▲ ).A .13B .14C .15D .16 4.下列运算正确的是( ▲ ).A .532x x x =+B .222)(y x y x +=+ C .632x x x =⋅ D .632)(x x =DAB (图3)5.如图(2)所示,在平面直角坐标系中,半径均为1个单位长度的半圆1O ,2O ,3O ,…组成一条平滑的曲线.点P 从原点O 出发,沿这条曲线向右运动,速度为每秒2π个单位长度,则第15秒时,点P 的坐标是( ▲ ).A .(15,1)B .(15,1-)C .(30,1)D .(30,1-) 6.不等式组⎩⎨⎧-≥+1305>x x 的解集在数轴上表示为( ▲ )A .B .C .D . 7.如图(3),ABC ∆中,点D ,E 分别在边AB ,BC 上,DE ∥AC .若4=BD ,2=DA ,3=BE ,则=BC ( ▲ ). A .23 B .25 C .27 D .298.如图(4), 平行四边形ABCD 中,P 是形内任意一点,ABP ∆,BCP ∆,CDP ∆,ADP ∆的面积分别为4321,,,S S S S ,则一定成立的是( ▲ ).A .4321S S S S +=+B .4321S S S S +>+C .4231S S S S +=+D .4321S S S S +<+ 9. 如图(5),ABC ∆中,︒=∠60A ,AB 和AC 两边的长度分别是关于x 的方程0212=++mx x 的两根,若这个方程的有一个根为3,则ABC ∆的面积为( ▲ ).A .43 B .47C .421D .473 10. 如图(6),ABC ∆在平面直角坐标系中,点A 、B 分别在x 轴和y轴上,且OB OA =,边AC 所在直线解析式为2121-=x y ,若ABC ∆的内心在y 轴上,则ACB ∠tan 的值为( ▲ ). A .21 B .31 C .41D .51OPO 4O 3O2O 1DPB(图4)60°AB(图5)xy CB OA(图6)绝密★启用前【考试时间: 9:00——11:00】五通桥区2016年中考复习调研考试数 学第Ⅱ卷(非选择题 共120分)注意事项:1.第Ⅱ卷共8页,用钢笔或圆珠笔直接答在试卷上.11.在平面直角坐标系中,点P (3,1+x )在第四象限,那么x 的取值范围为 ▲ 12.5.2PM 是指大气中直径小于或等于5.2微米的颗粒,已知1米1000000=微米,则5.2微米0000025.0=米,用科学记数法可以表示为 米. 13.若数据1、2-、3、x 的平均数为2,则=x .14.如图(7),正六边形ABCDEF 的边长为2,则该正六边形的外接圆与内切圆所形成的圆环面积为 . 15.已知关于x ,y 的二元一次方程组⎩⎨⎧=+=-1153by x ay x 的解为⎩⎨⎧==65y x ,那么关于x ,y 的二元一次方程组⎩⎨⎧=-++=--+11)(5)()(3y x b y x y x a y x 的解为 .16.若平面直角坐标系中,两点关于过原点的一条直线对称,则这两点就是互为镜面点,这条直线叫镜面直线,如A (2,3)和B (3,2)是以x y =为镜面直线的镜面点. (1)M (4,1)和N (1-,4-)是一对镜面点,则镜面直线为 ; (2)以x y 3=为镜面直线,E (2-,0)的镜面点为 .二、填空题(本大题共6小题,每小题3分,共18分.把答案填在题中的横线上)(图7)17. 计算:()o 45cos 4582120+----π18.已知:如图(8),在ABC ∆中,︒=∠90ACB ,CD AB ⊥于点D ,点E 在AC 上,BC CE =,过E 点作AC 的垂线,交CD 的延长线于点F .求证:FC AB =19. 先化简,再求值:11122---x x x ,其中12-=x .三、(本大题共3小题,每小题9分,共27分)A (图8)20.如图(9),平行四边形ABCD 中,对角线BD AC ,交于O ,AC EO ⊥, (1)若ABE ∆的周长为cm 10,求平行四边形ABCD 的周长;(2)若︒=∠78ABC ,AE 平分BAC ∠,试求DAC ∠的度数.21.学校开展了“读一本好书”的活动,校团委对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:类别频数 (人数)频率小说 0.5 戏剧 4 散文 10 0.25 其他 6 合计 m 1(1)计算m = ;(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是乙和丙的概率.22.公司为了运输的方便,将生产的产品打包成件,运往同一目的地.其中A 产品和B 产品共320件,A 产品比B 产品多80件.(1)求打包成件的A 产品和B 产品各多少件?(2)现计划租用甲、乙两种货车共8辆,一次性将这批产品全部..运往同一目的地.已知甲种货车最多可装A 产品40件和B 产品10件,乙种货车最多可装A 产品和B 产品各20件.如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.则公司安排甲、乙两种货车时有几种方案?并说明公司选择哪种方案可使运输费最少?.四、(本大题共3小题,每小题10分,共30分.)OB(图9)23.如图(10),在四边形ABCD 中,AD ∥BC ,︒∠90=B ,8=AB ,34CAD t =∠an ,CD CA =, E 、F 分别是AD 、AC 上的动点(点E 与A 、D 不重合),且ACB FEC ∠=∠. (1)求CD 的长;(2)若2=AF ,求DE 的长.24.如图(11),已知反比例函数xky =(0>k )的图像与一次函数图像4+-=x y 交于A 、B 两点,点A 的纵坐标为3.(1)求反比例函数的解析;(2)y 轴上是否存在一点P ,使AOB APB ∠=∠21?若存在, 求出点P 的坐标,若不存在,请说明理由.五、(本大题共2小题,每小题10分,共20分,其中第24题为选做题.)DBCEF (图10)(图11)25.已知,是⊙O 的直径,8=AB ,点C 在⊙O 的半径OA 上运动,AB PC ⊥ B ,垂足为C ,5=PC ,PT 为⊙O 的切线,切点为T . (1)如图(11-1),当C 点运动到O 点时,求PT 的长; (2)如图(11-2),当C 点运动到A 点时,连接PO 、BT ,求证:PO ∥BT ; (3)如图(11-3),设y PT =,x AC =,求y 与x 的解析式并求出y 的最小值.(图11-1) (图11-2) (图11-3)六、(本大题共2小题,第25题12分,第26题13分,共计25分).26.如图(12),边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P 是抛物线上点A,C间的一个动点(含端点),过点P作BCPF⊥于点F,点D,E的坐标分别为(0,6),(4-,0),连接PD,PE,DE.(1)求抛物线的解析式;(2)若PFPDd-=.请说明d是否为定值,若是定值,请求出其大小;若不是定值,请说明其变化规律?(3)求出PDE∆周长取值范围.(图12)五通桥区2019年初三毕业复习适应性检测数学参考答案及评分意见一、选择题:每小题3分,10小题,共计30分1.B 2.C 3.A 4.D 5.A 6.C 7.B 8.D 9.C 10.B 二、填空题:每小题3分,6小题,共计18分11.1-<x ; 12.6105.2-⨯; 13.6; 14.π; 15.⎪⎪⎩⎪⎪⎨⎧-==21211y x ;16.(1)x y -=(2))3,1(- 三、本大题共3小题,每小题9分,共27分17.解:原式22122+--=……………………………………………8分 21+=………………………………………………………9分 18.证明:∵AB CD ⊥,AC FE ⊥∴︒=∠+∠=∠+∠90ACF F ACF A∴F A ∠=∠…………………………………………2分又∵AC FE ⊥,︒=∠90ACB∴︒=∠=∠90FEC ACB ……………………………4分在ABC ∆和FCE ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠CE BC FEC ACB F A ∴ABC ∆≌FCE ∆……………………………………8分∴FC AB =……………………………………………9分 19.解:原式=)1)(1(1)1)(1(2-++--+x x x x x x ………………………3分11+=x ………………………………………………6分 当12-=x 时,原式=22=22……………………………9分 四、本大题共3小题,每小题10分,共30分 20.解:(1)∵平行四边形ABCD∴OC OA = ……………………………………2分又∵AC EO ⊥∴EC AE =………………………………………4分 ∴10=+=++=∆BC AB AE BE AB C ABE∴cm BC AB C ABCD 201022=)(四边形⨯=+= ……5分 (2)∵A(图8)B∴ECA EAC ∠=∠……………………………………………7分又∵︒=∠78ABC ,AE 平分BAC ∠∴︒=-=∠=∠=∠34)78180(3100ECA EAC BAE ……………9分又∵AD ∥BC∴︒=∠=∠34ECA DAC …………………………10分21.解:(1)40=m ………………………………………………………4分 (2)画树状图,如图所示:………………8分所有等可能的情况有12种,其中恰好是丙与乙的情况有2种,∴61122==P . ………………………………………10分22.解(1)设打包成件的A 产品有x 件,B 产品有y 件,则⎩⎨⎧=-=+80320y x y x 解得⎩⎨⎧==120200y x 答:打包成件的A 产品有200件,B 产品有120件.………4分 (2)设租用甲种货车x 辆,则⎩⎨⎧≥-+≥-+120)8(2010200)8(2040x x x x 解得42≤≤x …………………7分 方案 甲车 乙车 运 费① 2 6 2×4000+6×3600=29600 ② 3 5 3×4000+5×3600=30000 ③444×4000+4×3600=3040010分五、本大题共2小题,每小题10分,共20分, 23.解:(1)∵AD ∥BC∴CB A CAD ∠=∠………………………………………………2分又∵︒∠90=B ,34CAD t =∠an ,8=AB∴6=BC ,54CAD s =∠in∴10=AC∴10==CA CD …………………………4分(2)作AD CM ⊥于点M∵10=AC ,54CAD s =∠in ∴CM=8∴AM=6,∴AD=2AM=12 ………………5分∵CD CA =∴CDA ∠=∠CAD又∵ACB FEC ∠=∠=∠CAD∴DEC ∠=∠AFE∴AEF ∆∽DCE ∆………………………………………………7分 ∴AECD AF DE = 又∵2=AF ,6=BC ,CD=10,AD=12设DE x =,得xx -=12102 整理解得2=x 或10=x ………………9分即2=DE 或10=DE …… ………………………………10分24. 解:(1)由A 在4+-=x y 上,且点A 的纵坐标为3,得点A (3,1),由点A 在反比例函数y=x k 的图象上 ,得 ∴x y 3=…………………………………………6分(2)由A (3,1)得10=OA根据圆周角定理,得P (0,10)或P (0,10-)…………10分六、本大题共2小题,第25小题12分,第26小题13分,共计25 分25.解:(1)连接OT∵PC =5,OT =4,∴由勾股定理得,PT =22OT PC -=1625-=3;………3分(2)证明:连接OT∵PT ,PC 为⊙O 的切线,∴OP 平分劣弧AT ,∴∠POA =∠POT ,∵∠AOT =2∠B ,∴∠AOP =∠B ,∴PO ∥BT ;…………………………………………7分(3)连接PO ,PT∵AB 是⊙O 的直径,8=AB ,x AC =∴CO =4-x ;又∵AB PC ⊥∴PO =225)4(+-x∴y = PT =22OT PO -=22245)4(-+-x =2582+-x x ∴39)4(2min =+-=x y …………………………………12分26.解:(1)抛物线解析式为8812+-=x y .……………………………2分 (2)设P(x , -81x 2+8), 则PF = 8- ( - 81x 2+8)=81x 2. PD 2 =x 2+[6-(-81x 2+8)]2 = 2224)281(421641+=++x x x ∴PD =2812+x …………………………5分 ∴PF PD d -= 2281281x x -+==2 ∴PF PD d -=为定值2 ………………………………………7分(3)由PF PD d -=为定值2得2+++=++=∆PF PE ED PD PE ED C PDE)(2PF PE ED C PDE +++=∆又∵D (0,6),E (4-,0)∴132524622==+=DE∴)(2132PF PE C PDE +++=∆…………………………10分当PE 和PF 在同一直线时PE +PF 最小∴过E 作EF ⊥x 轴,交抛物线于点P ,得PDE C ∆最小值1013282132+=++当P 与A 重合时,PE +PF 最大,得PDE C ∆最大值14132+ ∴1413210132+≤≤+∆PDE C …………………………………13分注:不同的正确解法,参照给分。