当前位置：文档之家 › 9.5因式分解(一)

9.5因式分解(一)

  • 格式：doc
  • 大小：84.50 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

9.5因式分解(一)(第2课时)教案 苏科版

9.5因式分解(一)(第2课时)教案 苏科版
=(9x2-4y)2
=[(3x+2y) (3x-2y)]2
=(3x+2y)2(3x-2y)2
师生阅读88页
学生归纳总结
作业
第92页第2(1)②④(3)①③题
板书设计
复习 例3板演
………………
………………
……例4……
………………
………………
教 学后 记
2把81x4-72x2y2+16y4分 解因式.
（本题用了两次乘法公式，难度稍大，教师要鼓励学生大胆尝试，敢于创新）
将乘法公式反过来就得到多项式因式分解的公式。运用这些公式把一个 多项式分解因式的方法叫做运用公式法。
练习：第88页练一练第1、2题
小结：
这节课你学到了什么知识，掌握什么方法？
教学素材：
a2+8a+16=a2+2×4a+42=(a+4)2
a2-8a+16=a2-2×4a+42=(a-4)2
（要强调注意符号）
首先我们来试一试：(投影：牛刀小试)
1.把下列 各式分解因式：
(1)x2+8x+16 ; ; (2)25a4+10a2+1
(3)（ m+n）2-4（m+n）+4
（教师强调步骤的重要性，注意 发现学生易错点，及时纠正）
3、把下列各式分解因式：
（1）、 （2）、1-x2+4xy-4y2
（学生阅读课本，可以互相讨论，然后回答）
类似地把乘法公式
(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2
反过来，就得到
a2+2ab+b2=(a+b)2a2-2ab+b2=(a-b)2

【最新】苏科版七年级数学下册第九章《9.5多项式的因式分解(1)》公开课课件.ppt

【最新】苏科版七年级数学下册第九章《9.5多项式的因式分解(1)》公开课课件.ppt

。2021年1月12日星期二2021/1/122021/1/122021/1/12
• 15、会当凌绝顶，一览众山小。2021年1月2021/1/122021/1/122021/1/121/12/2021
• 16、如果一个人不知道他要驶向哪头，那么任何风都不是顺风。2021/1/122021/1/12January 12, 2021
•
THE END 17、一个人如果不到最高峰，他就没有片刻的安宁，他也就不会感到生命的恬静和光荣。2021/1/122021/1/122021/1/122021/1/12
谢谢观看
三看指数：相同字母的指数取次数最低的．
9.5 多项式的因式分解（1）
填空并说说你的方法：
（1）a2b＋ab2＝ab（
）
（2）3x2－6x3＝3x2（
）
（3）9abc－6a2b2＋12abc2＝3ab（
）
像这样，把一个多项式写成几个整式的积的 形式叫做多项式的因式分解．
想一想 ：因式分解的依据是什么?
9.5 多项式的因式分解（1）
例2 分解因式 -2m3－8m2－12m
当多项式的第一项的系数为“－”时,先把“－” 当作公因式的负号写在括号外,使括号内第一项的系 数为“＋”.
9.5 多项式的因式分解（1）
例3 把下列各式分解因式 （1）3a（x＋y）－2b（x＋y）；
（2）3a（x－y）－2b（y－x）
9.5 多项式的因式分解（1）
下列各式由左到右的变形哪些是因式分解, 哪些不是?
(1) ab＋ac＋d＝a（b＋c）＋d (2) a2－1＝(a＋1)(a－1) (3) （a＋1）（a－1）＝a2－1 (4) 8a2b3c＝2a2·2b3·2c

苏教版七下9.5多项式的因式分解(一)

苏教版七下9.5多项式的因式分解(一)

公因式
4 4a 4a2b
给就上面的填表过程，你能归纳出 找一个多项式的公因式的方法吗？
总结
找一个多项式的公因式的方法一 般分三个步骤：
一看系数：当多项式的各项系数 的绝对值都是整数时，公因式的 系数应取各项系数的最大公约数。 二看字母：公因式的字母应取多项 式中各项都含有的相同字母。 三看指数：相同字母的指数取次数 最低的。
观察上面从左到右与从右到左的变形 过程，你能说出因式分解和整式乘法 的区别和联系吗？
区别： 整式乘法： 有几个整式积的形式转化 成一个多项式的形式。 因式分解： 有一个多项式的形式转化成 几个整式的积的形式。 联系： 多项式的因式分解与整式乘法是两种 相反方向的变形，它们互为逆过程。
4a3b-8a2b2
练一练
填表
多项式 公因式
a2b+ab2
3x2-6x3 9abc-6a2b2+12ab2c
ab
3x2 3ab
填空并说说你的方法： （1）a2b+ab2=ab（ a+b ） （2）3x2-6x3=3x（ X-2x2 ） （3）9abc-6a2b2+12abc2=3ab(3c-2ab+4c ) 像这样，把一个多项式写成几个整 式的积的形式叫做多项式的因式分解。
例2：把 3a(x+y)-2b(x+y) 分解因式； 分析：这个多项式就整体而言可分为两大项，
即3a(x+y)与-2ab(x+y)每项中都含有(x+y)
因此，可把（x+y）作为公因式提出来。 解： 3a(x+y)-2b(x+y)
=(x+y)〃3a-(x+y)〃2b
=(x+y)(3a-2b) 总结：用提公因式法分解因式时，公因式可以 是一个单项式也可以是一个多项式。

苏科初中数学七下《9.5 因式分解(一)》word教案 (11)

苏科初中数学七下《9.5 因式分解(一)》word教案 (11)
学生回答
完成“想一想”由学生自己先做(或互相讨论)，然后回答，若有答不全的，教师(或其他学生)补充．
让学生自己先做，同桌互相纠错，
作业
第87页第1、2题
教学后 记
关键是确定多项式各项的公因式,然后,将多项式各项写成公因式与其相应的因式的积,最后再提 公因式,把公因式 写在括号外面,然后再确定括号里的因式,这个因式(括号里的)的项数与原多项式的 项数相同,如果项数不一致就漏 项了.
完成“议一议”
因式分解：
把一个多项式写成几个整式积的形式叫做多项式的因式分解。
例题1：把 分解因式
9.5因式分解（一）-提公因式法
课题
课时分配
本课（章节）需11课时
本节课为第7课时
因式分解（一）--提公因式法
教学目标
1、理解因式分解的意义及其与整式乘法的区别和联系
2、了解公因式的概念，掌握提公因式的方法
3、培养学生的观察、分析、判断及自学能力
重点
掌握公因式的概念，会使用提公因式法进行因式分解。
难点
确定多项式的公因式的方法,对数字系数取各项系数的最大公约数,各项都含有的字母取最低次幂的积作为多项式的公因式,公因式可以是单项式,也可以是多项式,如:ax+bx中的公因式是x.多项式a(x+y)+b(x+y)的公因式是(x+y).如果多项式的第一项系数是负的,一般要先提出“一”号,使括号内的首项系数变为正,在提出“一”号时,注意括号里的各项都要变号.
⑶2x(x+y)2-(x+y)3
2、先因式分解，再求值．
(1)x(a-x)(a-y)-y(x-a)(y-a)，
其中a=3，x=2，y=4；
(2)-ab(a-b)2+a(b-a)2-ac(a-b)2，

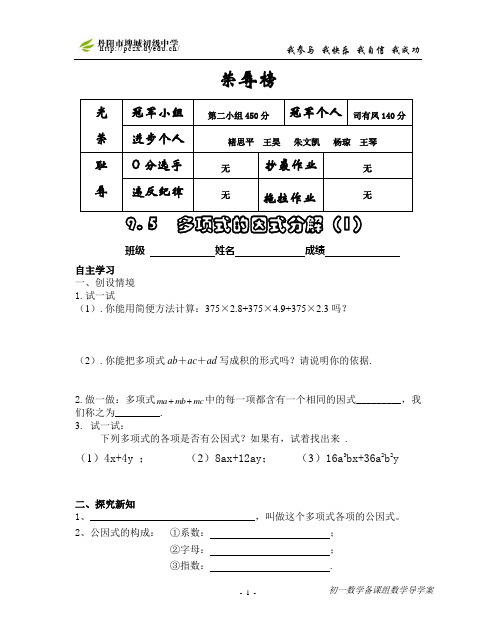
苏教版9.5因式分解1

苏教版9.5因式分解1

荣辱榜9. 5 多项式的因式分解（1）班级姓名成绩自主学习一、创设情境1.试一试（1）.你能用简便方法计算：375×2.8+375×4.9+375×2.3吗？（2）.你能把多项式ab＋ac＋ad写成积的形式吗？请说明你的依据.2.做一做：多项式mc+中的每一项都含有一个相同的因式_________，我mbma+们称之为_________.3.试一试：下列多项式的各项是否有公因式？如果有，试着找出来.（1）4x+4y；（2）8ax+12ay；（3）16a3bx+36a2b2y二、探究新知1、_________________________________，叫做这个多项式各项的公因式。

2、公因式的构成：①系数：；②字母：；③指数： .3、练一练：下列多项式的各项是否有公因式？如果有，试着找出来.（1）a2b＋ab2；（2）3x2－6x3；（3）9abc－6a2b2＋12abc24、填空并说说你的方法：（1）a2b＋ab2=ab( ) （2）3x2－6x3=3x2( ) （3）9abc－6a2b2＋12abc2=3ab( )5、归纳：（1）.因式分解的定义：. （2）.因式分解与整式乘法的联系和区别：趁热打铁：下列各式从左到右的变形，是不是因式分解？（1）6x2y3＝2x2y·3y；（2）ab＋ac＋d=a(b＋c)＋d（3）a2－1=(a＋1)(a－1) （4）(a＋1)(a－1) = a2－1（5）x2＋1=x(x＋1 x)例题讲解：例1：把（1）5x3－10x2分解因式；分析：1、多项式5x3－10x2各项的公因式是什么？2、你能把多项式5x3－10x2说你是如何得到另一个因式的？归纳：叫做提公因式法．把12ab2c－6ab分解因式变式练习1：把6a3b－9a2b2c+3a2b分解因式变式练习2：把－2m3＋8m2－12m因式分解练习：－8a2b2＋4a2b－2ab变式练习3：把3a(x+y)-2b(x+y)分解因式练习：（1）x(a-b)+y(b-a) （2）6(m-n)3-12(n-m)2变式练习4：把m(5ax+a y－1)+m(ay+1－3ax)因式分解拓展应用：（1）.计算 39×37-13×81；（2）20042+2004能被2005整除吗?三、通过本节课的学习，你有哪些收获？9.5单项式乘多项式的再认识－因式分解(一)反馈练习：1. 下列式子由左到右的变形中，属于因式分解的是（ ）A ．22244)2(y xy x y x ++=+ B.3)1(4222+-=+-x y x C. )1)(13(1232-+=--x x x x D.mc mb ma c b a m ++=++)(2.多项式－5mx 3+25mx 2－10mx 各项的公因式是A.5mx 2B.－5mx 3C. mxD.－5mx 3. 20082009)8()8(-+-能被下列数整除的是（ ）A ．3B ．5C ．7D ．94．把下列各式因式分解：（1）20a －15ab ； （2）m m m 216423-+-（3）10(a －b )2－5(b －a )3 （4）2m (m －7)－(7－m )(m －3)5.已知312=-y x ，2=xy ，求 43342y x y x -的值.你对本节课还有哪些问题和要求： 。

初中数学七年级下册《9.5 因式分解(一)》PPT课件 (14)

初中数学七年级下册《9.5 因式分解(一)》PPT课件 (14)

——十字相乘法
你能用什
1.口答计算结果：
么方法将
ห้องสมุดไป่ตู้
(1) (x+2)(x+3)= x2+5x+6 这类题目
(2) (x+2)(x－3)= x2－x－6 做得又快
(3) (x－2)(x+3)= x2+x－6 又准确的 (4) (x－2)(x－3)= x2－5x+6 呢？
归纳((65：)) ((xx(x+－+1a2)())x((xx+++4b5)=))==
(1) x2－7x+6 (2) t2－2t－8 (3) m2+4m－12 (4) x2+12x+32
变式 把下列各式分解因式：
(1) x4－6x2－7 (2) m2n2－8mn+15 (3) (a+b)2+7(a+b)+12 (4) x2+3xy－28y2
把下列各式分解因式：
(1) m4+4m2－12 (2) x2y2－13xy+36 (3) x2－6xy+8y2 (4) (a+b)2－(a+b)－12
例2 把2x2+x－6分解因式.
把下列各式分解因式：
(1) 3x2－5x－2 (2) 2x2－5xy－12y2
这节课你有什么收获？
4.若x2－x+m分解得到两个因式x－2与 x－ n ，求(m－n)2008的值.
5.已知y－x=2，x－3y=－1，求x2－4xy+3y2
的值．
思考1: 多项式4x2－4x+1能用十字相
因式分解
1.提公因式：ma+mb+mc=m(a+b+c)

多项式的因式分解(1)


（2）12ab2c－6ab ； （3） -2m3－8m2－12m
； (4)原式=(x＋y )(3a－2b)
（4）3a（x＋y）－2b（x＋y）.
学以致用： 1.把下列各式分解因式：
（1）8x4y3z2－6x5y2; (1)2x4y2(4yz2－3x) （2）-2m3+6m2－18m; (2) -2m(m2－3m+9) （3）3a(x－y)－2b(y－x); (3) (3a+2b)(x－y) （4）5m(a+b)－a－b; (4) (a+b)(5m－1)
初中数学 七年级(下册)
9.5 多项式的因式分解（1）
9.5 多项式的因式分解（1）
教学目标：
1.了解因式分解的意义，能用提公因式 法进行分解因式。
2.体会单项式乘多项式与提取公因式之 间的联系，发展逆向思维的能力。
看谁算得巧：
1.求999+9992的值。
999（1+999）=999×1000=999000
4x+4y=4(x+y)
公因式
另一个因式
4
x+y
x
m－n
a－b
m－n
4a
3x+2y
6a2b
2ax+3by
mx－nx=x(m－n)
m(a－b)－n(a－b)=(a－b)(m－n) 12ax+8ay=4a(3x+2y)
12a3bx+18a2b2y=6a2b(2ax+3by)
如果多项式的各项含有公因式，那么就可以把这个公因式 提到括号外，把多项式写成公因式与另一个多项式的积的
，叫做这个多项式的公因式。
练一练：

9.5单项式乘多项式的再认识-因式分解(一)


用提取公因式分解因式的一般步骤： 第一步：找出多项式各项的公因式； 第二步：把多项式各项写成公因式
与另一个因式的积的形式；
第三步：逆用单项式乘多项式法则写 成公因式与另一个多项式的积。
（2）把6a3b-9a2b2c+3a2b分解因式 解： 6a3b-9a2b2c+3a2b =3a2b.2a-3a2b.3bc+3a2b.1 =3a2b（2a-3bc+1） 注意：1、如果提取公因式与多项式中的某一项 相同，那么提取后多项式中的这一项剩下“1”结 果中的“1”不能漏写； 2、多项式有几项，提取公因式后另一项 也有几项。
下列各式由左到右的变形那些是因式分解
(1) ab+ac+d=a(b+c)+d
(2) a2-1=(a+1)(a-1)
(3) (a+1)(a-1) = a2-1 (4) x2+1=x(x+
1 )x
答案（1）不是；（2）是； （3）不是；（4）不是
课堂练习： 把下列各式分解因式：
（1）4x2-12x3
初中数学七年级下册 （苏科版）
9.5单项式乘多项式的再认识 －因式分解(一)
计算与交流
计算：375×2.8+375×4.9+375×2.3
如何计算上面的算式？请把你的想 法与你的同伴交流。 小明很快就能报出答案，你知道他 是怎么想的吗？
小明的方法：
375×2.8+375×4.9+375×2.3 =375×（2.8+4.9+2.3） =375×10 =3750 为什么375×2.8+375×4.9+375×2.3 可以写成375×（2.8+4.9+2.3）？依 据是什么？ 乘法分配率

9.5因式分解(一)(第2课时)教案 苏科版

重 点
运用完全平方公式分解因式
难点
灵活运用完全平方公式分解因式
教学方法
对比发现法
课型
新授课
教具
投影仪
教师活动
学生活动
复习巩固：上节课我们学习了运用平方差公式分解因式，请同学们先阅读课本87—88页，看看你能有什么发现？
新课讲解：
（投影）我们把形如a2+2ab+b2与a2-2ab+b2叫做完全平方式，和平方差公式一样，我们也可以利用它把一些多项式因式分解。例如：
3、把下列各式分解因式：
（1）、 （2）、1-x2+4xy-4y2
（学生阅读课本，可以互相讨论，然后回答）
类似地把乘法公式
(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2
反过来，就得到
a2+2ab+b2=(a+b)2a2-2ab+b2=(a-b)2
学生上台板演：
解：(1)x2+8x+16
2把81x4-72x2y2+16y4分 解因式.
（本题用了两次乘法公式，难度稍大，教师要鼓励学生大胆尝试，敢于创新）
将乘法公式反过来就得到多项式因式分解的公式。运用这些公式把一个 多项式分解因式的方法叫做运用公式法。
练习：第88页练一练第1、2题
小结：
这节课你学到了什么知识，掌握什么方法？
教学素材：
=x2+2×4x+42
=(x+4)2
(2)25a4+10a2+1
=(5a2)2+2×5a2+1
=(5a2+1)2
(3)（m+n）2-4（m+n）+4

9.5_因式分解(1)

初中数学七年级下册 （苏科版）
9.5_因式分解(1)
思考
能不能把多项式ab+ac+ad化成积的形式？ 因为 a(b+c+d)=ab+ac+ad
所以 ab+ac+ad=a(b+c+d)
a是多项式ab+ac+ad中各项ab﹑ac﹑ad 都有的因式，称为多项式各项的公因式．
议一议
下列多项式的各项是否有公因式？ 如果有，是什么？ (1)a2b+ab2 (2)3x2-6x3 (3)9abc-6a2b2
ab 3x2 3ab
试一试
找出下列各式的公因式，填在横线上． (1)ab,2a2b,3ab2＿＿＿＿＿＿＿＿＿． ab (2)6mn2,-18m2n2,24m3n＿＿＿＿＿＿． 6mn
7xy (3)7x2y,14xy2z,-35xyz2＿＿＿＿＿＿＿． 1.公因式系数应取各项系数的最大公约数 2.字母取各项相同的字母,且各字母的指数 取次数最低的．
P90-91 1-4
思考
如果n是自然数，那么n2+n是奇数还是 偶数？
从一块直径为(a+b)的圆形钢板上 截出直径分别为a和b的两个圆， 求出剩余钢板的面积．
小
结
１.什么是公因式． ２.如何提公因式.(先找后提） 3 .提公因式法分解因式的方法.
作业
P 91
习题
注意：当多项式的第一项的系数为负数时， 把“-”作为公因式的符号写在括号外，使 括号内第一项的系数为正.
你知道吗？
如果多项式的各项有公因式， 那么就可以把这个公因式提出来，把 多项式化成公因式与另一个多项式的 积的形式，这种分解因式的方法叫做 提公因式法．
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

9.5因式分解（一）教案
一、教学目标：
1.了解因式分解的意义，会用提公因式法进行因式分解；
2.提高学生逆向思考问题的能力和推理能力。

二、教学重点：
会用提公因式法进行因式分解
三、教学难点：
提高学生逆向思考问题的能力和推理能力
四、教学过程：
1.复习回顾：
单项式乘多项式的法则
2.自学质疑：
阅读书本P70—71回答下列问题
1.把单项式乘多项式的法则()ad ac ab d c b a ++=++反过来得 。

这个式子左边是 ，它是几个单项式的 形式；这个式子的右边是 和 的乘积，它是积的形式。

2.这里 是多项式ad ac ab ++各项都含有的 ，称为这个多项式各项的 。

3.如何找一个多项式的公因式？
4.什么叫做因式分解？什么叫提公因式法？
3.例题选讲：
例1把下列各式分解因式：
（1）c b a b a 22396- (2)m m m 12822
3-+- 补充例题：（1）()()a b y b a x ---63
（2）3.23759.43758.2375⨯+⨯+⨯
4.检测反馈：
1.下列各式由左边到右边的变形，哪些是因式分解，哪些不是？
（1）()d c b a d ac ab ++=++（2）)1)(1(12-+=-a a a （3）()()1112-=-+a a a 2.（1）将多项式ab a 352
+-提出公因式a -后，另一个因式是 ；
（2）把多项式()()b a a b a +-+24分解因式，应提出公因式 。

3.把下列各式分解因式：
（1）32124x x - （2）y y y x 542-+- 4.计算：5.5245.5263.05.5237.2⨯-⨯+⨯
5.小结：学生总结
五、教学反思：
9.5因式分解（一）学案
一、学习目标：
1.了解因式分解的意义，会用提公因式法进行因式分解；
2.提高自己逆向思考问题的能力和推理能力。

二、复习回顾：
单项式乘多项式的法则
三、自学质疑：
阅读书本P70—71回答下列问题
1.把单项式乘多项式的法则()ad ac ab d c b a ++=++反过来得 。

这个式子左边是 ，它是几个单项式的 形式；这个式子的右边是 和 的乘积，它是积的形式。

2. 这里 是多项式ad ac ab ++各项都含有的 ，称为这个多项式各项的 。

3.如何找一个多项式的公因式？
4.什么叫做因式分解？什么叫提公因式法因式分解？
四、例题选讲：
例1把下列各式分解因式：
（1）c b a b a 22396- (2)m m m 12822
3-+-
补充例题：（1）()()a b y b a x ---63 （2）3.23759.43758.2375⨯+⨯+⨯
五、检测反馈：
1.下列各式由左边到右边的变形，哪些是因式分解，哪些不是？
（1）()d c b a d ac ab ++=++（2）)1)(1(12-+=-a a a （3）()()1112-=-+a a a 2.（1）将多项式ab a 352
+-提出公因式a -后，另一个因式是 ；
（2）把多项式()()b a a b a +-+24分解因式，应提出公因式 。

3.把下列各式分解因式：
（1）32124x x - （2）y y y x 542-+-
4.计算：
5.5245.5263.05.5237.2⨯-⨯+⨯
9.5因式分解（一）巩固案
1.把下列各式分解因式：
（1）qm aq ap +- （2）x xy x 2842+-
（3）y x xyz 2912- （4）y xy y 2532
--
（5）ab ab b a 159622+- （6）234264a a a +--
（7）a ab a 3962+- （8）3228122xy xy x +--
2.先化简，再求值：
321IR IR IR ++,其中5.2,4.35,2.39,4.25321====I R R R
3.计算：
（1）14.32214.36114.317⨯+⨯+⨯
（2）234232214210⨯+⨯+⨯
4.已知7,6==+ab b a ，求22ab b a +的值。