伯努利定律

伯努利吸盘原理
伯努利吸盘原理是指在流体力学中，当流体通过管道或流经物体表面时，流速增大，压力就会减小，这就是伯努利定律。

而伯努利吸盘就是利用这一原理制成的一种吸盘装置，它可以通过气流的流动产生负压，从而实现吸附物体的目的。

伯努利吸盘主要由吸盘体、进气口、出气口等部分组成。

当气流通过进气口进入吸盘内部时，由于吸盘内部的形状设计和出气口的设置，气流在流动过程中会加速，从而使得吸盘内部的压力降低。

根据伯努利定律，流速增大，压力就会减小，因此在吸盘的作用下，外部大气压力就会将物体压附在吸盘上。

伯努利吸盘广泛应用于工业生产中，比如在自动化生产线上，可以利用伯努利吸盘来进行物料的吸取和传送。

由于伯努利吸盘不需要额外的能源，只需要通过气流就能产生负压，因此在一些特殊环境下，比如易燃易爆的场所，伯努利吸盘就显得更加安全可靠。

另外，伯努利吸盘也被广泛应用于机器人领域。

在一些需要进行物体抓取和搬运的场合，机器人可以通过安装伯努利吸盘来实现对物体的抓取和固定。

由于伯努利吸盘对物体表面的要求并不高，因此可以适用于各种不同材质和形状的物体，这为机器人的灵活应用提供了可能。

此外，伯努利吸盘还可以应用于一些特殊的领域，比如在医疗器械上，可以利用伯努利吸盘来实现对一些脆弱的组织或器官的抓取和固定，从而为医生的手术操作提供更大的便利和安全保障。

总的来说，伯努利吸盘作为一种利用流体力学原理制成的吸附装置，具有结构简单、使用方便、安全可靠等优点，在工业生产、机器人领域以及医疗器械等领域都有着广泛的应用前景。

随着科学技术的不断发展，相信伯努利吸盘在未来会有更多的创新和应用，为人们的生产和生活带来更多的便利和效益。

伯努利定律和伯努利定理
一、伯努利定律
伯努利定律是流体力学中的基本原理，由瑞士物理学家丹尼尔·伯努利于1738年提出。

定律指出，在理想流体中，流速大的地方压力小，流速小的地方压力大。

这是因为流体的压力与流速和重力之间存在相互关系。

在不可压缩的稳定流中，流体的动能和势能之和保持不变，即总机械能守恒。

这个定律可以用来解释和分析很多流体动力学现象，如飞机的升力、管道中的水流等。

二、伯努利定理
伯努利定理是热力学中的一个基本定理，由瑞士物理学家丹尼尔·伯努利于1757年提出。

定理指出，在没有外部力量作用的情况下，流体内部各点的速度和压力是连续变化的，但在同一水平面上，流体的速度和压力具有相同的值。

这个定理可以用来分析流体在管道中的流动和扩散现象，以及流体在容器中的等压和等温变化等。

总结：
伯努利定律和伯努利定理是两个不同的物理原理，分别应用于流体力学和热力学领域。

尽管它们的应用范围不同，但它们都涉及到流体的速度和压力之间的关系。

在实际应用中，需要根据具体的物理环境和现象选择合适的原理进行分析和计算。

伯努利定理的意义伯努利定理是流体力学中的一个基本定律，描述了流体在运动过程中压力和速度之间的关系。

这个定理的重要性在于它能够解释很多现象，例如飞机起飞、水泵工作等，同时也为设计和控制流体系统提供了基础和指导。

伯努利定理简单来说，就是在不考虑粘性阻力和外力作用的情况下，当流体沿着管道或容器中的不同位置流动时，其速度和压力之间存在一个反比例关系。

也就是说，当速度增大时，压力降低，反之亦然。

这个规律可以通过物理方程式来表达，即P + ½ρv² = 常数，其中 P 表示压力、ρ 表示流体密度、v 表示流体速度。

这个定理的应用非常广泛。

在空气动力学中，飞机的升力是由空气在机翼上流动、速度变化和压力产生的。

伯努利定理可以用来说明机翼上下表面所受到的压强不平衡是导致升力产生的原因之一。

在水力工程中，水泵的工作原理也是基于该定理：当水从进水口进入泵中，随着流速增加，压力会降低，从而产生一个向上的力，将水送至出水口。

伯努利定理还可以用来解释很多其他的现象，例如爬山气球的升力、船行驶时的动力、喷气式发动机的推力等。

此外，该定理也为工程设计提供了理论基础。

在流体系统的设计中，提高流速可以降低管道或容器的截面积，从而节约材料和成本。

此外，根据该定理，流体的速度和压力变化可以实现流量控制、氧气传输、空气过滤等应用。

综上所述，伯努利定理是流体力学中的一个重要定理，不仅能够解释很多现象，而且为工程设计和流体系统的控制提供了基础和指导。

通过深入研究和应用伯努利定理，我们可以更好地理解流体的运动规律，优化流体系统的设计和运作，从而促进科技进步和社会发展。

伯努利定律内容
伯努利定律是流体力学中的一个基本定律，它描述了在不同截面积上的流速不同的流体，其压力和动能之间的关系。

伯努利定律是流体力学的基础，对于理解流体运动和流体机械的设计有着重要的意义。

伯努利定律的内容可以简单地概括为：在流体运动过程中，当流体通过不同截面积时，流速的变化会引起压力和动能的变化，压力和动能之间的变化是相互关联的，即当流体速度增加时，压力就会降低，反之亦然。

伯努利定律的数学表达式为：P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2，其中P1和P2分别表示流体通过不同截面积的压力，ρ为流体密度，v1和v2分别表示流体通过不同截面积的速度，h1和h2分别表示流体通过不同截面积的高度。

伯努利定律的实际应用非常广泛，例如在流体机械中，伯努利定律可以用于设计流量计、涡轮机、喷气发动机等；在气象学中，伯努利定律可以用于解释风的形成和变化；在生物学中，伯努利定律可以用于研究血流动力学等。

伯努利定律的应用还可以帮助我们理解一些日常生活中的现象。

例如，当我们在喝吸管饮料时，吸管内的压力会降低，而外部的大气压力会将液体推向吸管内，这就是伯努利定律的应用；当我们在开车行驶时，车前方的空气会流经车身，形成气流，而车身的形状和速度会影响气流的流速和压力分布，这也是伯努利定律的应
用。

总之，伯努利定律是流体力学中的一个基本定律，它描述了流体在不同截面积上的压力和动能之间的关系，具有广泛的应用价值。

对于工程技术、气象学、生物学等领域的研究和应用，伯努利定律都有着重要的作用。

伯努利定律表达式
伯努利定律是流体力学中的一个基本定律，描述了在流体中沿流线上流速变化和压力变化之间的关系。

伯努利定律的数学表达式如下：
P + 1/2ρv²+ ρgh = 常数
其中：
- P 表示流体的压力（单位：帕斯卡，Pa），
-ρ表示流体的密度（单位：千克/立方米，kg/m³），
- v 表示流体的速度（单位：米/秒，m/s），
- g 表示重力加速度（单位：米/秒²，m/s²），
- h 表示流体在重力场中的高度（单位：米，m）。

上述表达式中的每一项分别代表了流体的压力能、动能和重力势能，它们在沿流线上的不同位置可能会发生变化，但总和保持不变。

这意味着当流体在流动过程中速度增加时，压力会下降；反之，当速度减小时，压力会增加。

伯努利定律适用于理想流体（无粘性和无压缩性）在稳态流动条件下的情况。

它可以用于解释多种现象，例如飞机升力产生、水管中水流速度和压力的关系等。

需要注意的是，伯努利定律的适用范围有限，
对于涉及湍流、粘性流体或复杂流动情况的问题，可能需要考虑其他因素和扩展模型。

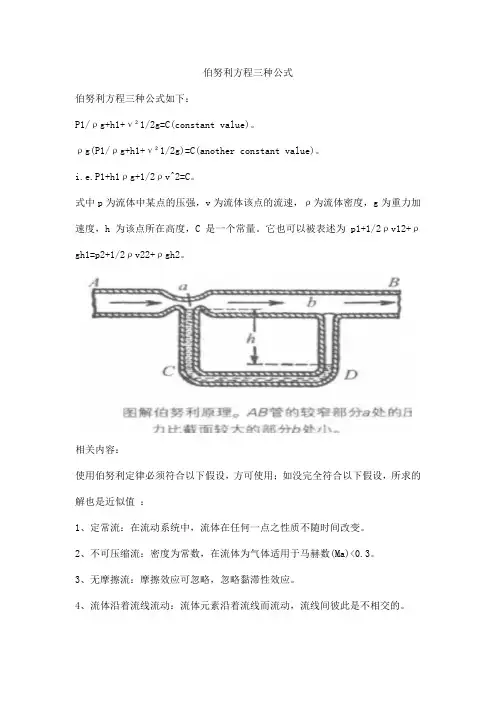
伯努利方程三种公式
伯努利方程三种公式如下：
P1/ρg+h1+ν²1/2g=C(constant value)。

ρg(P1/ρg+h1+ν²1/2g)=C(another constant value)。

i.e.P1+h1ρg+1/2ρv^2=C。

式中p为流体中某点的压强，v为流体该点的流速，ρ为流体密度，g为重力加速度，h为该点所在高度，C是一个常量。

它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。

相关内容：
使用伯努利定律必须符合以下假设，方可使用；如没完全符合以下假设，所求的解也是近似值：
1、定常流：在流动系统中，流体在任何一点之性质不随时间改变。

2、不可压缩流：密度为常数，在流体为气体适用于马赫数(Ma)<0.3。

3、无摩擦流：摩擦效应可忽略，忽略黏滞性效应。

4、流体沿着流线流动：流体元素沿着流线而流动，流线间彼此是不相交的。

伯努利试验公式
伯努利试验公式是描述管道或管道中流体流动的基本物理定律之一。

其公式表示为：
P + 1/2ρv^2 + ρgh = 常数
其中，P为流体静压力，ρ为流体密度，v为流体流速，g为重力加速度，h为流体高度。

这个公式说明了在管道或管道中，流体静压力、动能和位能之和是一个常数。

换句话说，当流速增加时，静压力会下降，而动能和位能则会增加，以保持总能量不变。

这个公式在航空、汽车、液压和水力工程等领域中都得到了广泛应用。

例如，它可以用来计算飞机、汽车或船只的速度、液压系统的压力、水力发电厂的效率等等。

需要注意的是，伯努利试验公式只适用于稳态流动的情况，即流体的速度和压力分布不随时间变化。

在非稳态流动或湍流中，该公式的适用性可能会受到限制。

伯努利反比定律伯努利反比定律是流体力学中的重要定律之一，它描述了在静止流体中，速度和压力之间的关系。

该定律是由瑞士数学家丹尼尔·伯努利在18世纪提出的，基于能量守恒的原理。

伯努利反比定律可以用以下公式表示：P + 1/2ρv² + ρgh = 常量其中，P是流体的压力，ρ是流体的密度，v是流体的速度，g是重力加速度，h是流体的高度。

该公式表示了在流体沿着流动路径上的某一点的总压力，即静压、动压和势能之和是一个常量。

通过伯努利反比定律，可以得出以下结论：1. 当速度增加时，压力降低。

根据公式可知，速度的增加导致动压项1/2ρv²的增加，而压力的减小则是为了保持总压力不变。

这就解释了为什么当流体通过管道缩窄或通过障碍物时，流体速度增加，而压力降低。

2. 当高度增加时，压力增加。

根据公式可知，高度的增加导致势能项ρgh的增加，而压力的增加则是为了保持总压力不变。

这就解释了为什么在山上气温较低、气压较高，而在山下气温较高、气压较低。

3. 当密度增加时，压力增加。

根据公式可知，密度的增加会导致静压项ρ的增加，而压力的增加则是为了保持总压力不变。

这就解释了为什么在深海中，水的压力比在海平面上更高，因为水的密度在深海中更大。

4. 伯努利反比定律适用于理想流体。

理想流体是指没有粘性和黏滞性的流体，实际流体在一些情况下可能不完全符合伯努利反比定律。

例如，在流体通过狭窄管道或穿过小孔时会产生湍流，这就会使得流体的速度和压力分布不均匀。

伯努利反比定律在许多实际应用中都有重要的意义。

例如，在航空工程中，该定律可以用来解释飞机上升或下降时的气动性能变化。

在涡轮机械中，该定律可以用来分析流体的能量转换和传输过程。

在建筑工程中，该定律可以用来设计水力工程和通风系统。

总之，伯努利反比定律是流体力学中一条基本原理，通过它可以理解速度和压力之间的关系。

这个定律对于解释和设计许多实际问题具有重要意义，是流体力学研究中的基础之一。

bernoulli定律Bernoulli定律Bernoulli定律是流体力学中的一个基本定律，它描述了在不可压缩流体中，速度增加时压力降低的现象。

Bernoulli定律可以应用于许多领域，如飞机、汽车、水管等。

1. Bernoulli定律的基本原理Bernoulli定律的基本原理是：在不可压缩流体中，当速度增加时，压力降低；当速度减小时，压力升高。

这个原理可以用以下公式表示：P + 1/2ρv^2 = constant其中，P表示静压力，ρ表示密度，v表示速度。

该公式表明，在不可压缩流体中，在一条流线上沿着流动方向速度越大，则静压力越小；反之亦然。

2. Bernoulli定律的应用Bernoulli定律可以应用于许多领域。

(1) 飞机在飞机上，通过改变机翼形状和倾斜角度来改变气流的速度和方向，从而产生升力和推力。

这就是所谓的“伯努利效应”。

(2) 汽车在汽车运动中，空气会沿着汽车表面流动，并且会在汽车的前部形成高压区域，而在汽车的后部形成低压区域。

这种压力差会产生阻力，从而减慢汽车的速度。

因此，在设计汽车时，需要考虑流体力学因素，以减小阻力。

(3) 水管Bernoulli定律也可以应用于水管中。

当水流通过水管时，由于速度的变化，水的压力也会发生变化。

如果水管中存在狭窄的部分，则在这个部分中速度会增加，从而降低压力。

这种现象被称为“Venturi效应”。

3. Bernoulli定律的局限性虽然Bernoulli定律可以描述不可压缩流体中速度与静压力之间的关系，但它有一些局限性。

(1) 仅适用于不可压缩流体Bernoulli定律只适用于不可压缩流体。

对于可压缩流体（如气体），在速度变化较大时需要考虑流动中气体密度和温度等因素。

(2) 忽略摩擦和粘滞Bernoulli定律忽略了摩擦和粘滞等因素对流体运动的影响。

在实际情况中，这些因素可能会对流体运动产生重要影响。

(3) 仅适用于定常流动Bernoulli定律只适用于定常流动。

概率论十大经典定理？1、伯努利大数定律：伯努利大数定律，即在多次重复试验中，频率有越趋稳定的趋势。

在相同的条件下,进行了n次试验,在这n次试验中,事件A发生的次数nA称为事件A发生的频数.比值nA/n称为事件A发生的频率,并记为fn(A).⒈当重复试验的次数n逐渐增大时,频率fn(A)呈现出稳定性,逐渐稳定于某个常数,这个常数就是事件A的概率.这种“频率稳定性”也就是通常所说的统计规律性.⒉频率不等同于概率.由伯努利大数定理,当n趋向于无穷大的时候,频率fn(A)在一定意义下接近于概率P(A).通俗地说，这个定理就是，在试验不变的条件下，重复试验多次，样本数量越多，随机事件的频率越近似于它的概率，偶然中包含着某种必然。

2、中心极限定理：大量相互独立的随机变量，其求和后的平均值以正态分布（即钟形曲线）为极限。

数学定义：设从均值为μ、方差为σ^2（有限）的任意一个总体中抽取样本量为n的样本，当n充分大时，样本均值的抽样分布近似服从均值为μ、方差为（σ^2）/n 的正态分布。

关于正态分布的核心结论是：μ、σ为均值和标准差，那么μ±1σ、μ±2σ、μ±3σ的命中概率分别是68.3%、95.5%、99.73%！中心极限定理最早由法国数学家棣莫弗在1718年左右发现。

他为解决朋友提出的一个赌博问题而去认真研究二项分布（每次试验只有“是/非”两种可能的结果，且两种结果发生与否互相对立）。

他发现：当实验次数增大时，二项分布（成功概率p=0.5）趋近于一个看起来呈钟形的曲线。

后来，著名法国数学家拉普拉斯对此作了更详细的研究，并证明了p不等于0.5时二项分布的极限也是高斯分布。

之后，人们将此称为棣莫弗-拉普拉斯中心极限定理。

是概率论中讨论随机变量序列部分和分布渐近于正态分布的一类定理。

比如，全国人口寿命、成年男女的身高分布、人在一天中情绪高低点对应的时间分布、金融市场中涨跌的时间周期及趋势的寿命等等，无不遵循此定理。

简单解释伯努利定律-概述说明以及解释1.引言1.1 概述伯努利定律是一个流体力学中的基本原理，它描述了在稳态条件下，流体在不同速度下经过不同截面积的管道或管道内部形状改变时，其压力和速度之间存在的定量关系。

这一原理由瑞士数学家伯努利于18世纪提出，并被广泛应用于各个领域，如液体和气体的流体力学、航空航天工程、水力学、管道系统设计等。

简单来说，伯努利定律表明了当流体通过截面积变化的管道或管道时，流体的压力、速度和高度之间存在着一种平衡关系。

按照伯努利定律，当流体在管道的较窄区域中流速增大时，流体的压力就会减小。

相反地，当流体在管道的较宽区域中流速减小时，流体的压力就会增加。

伯努利定律的应用非常广泛。

在工程学中，伯努利定律可以用于计算流体在管道中的流速和压力分布，从而帮助设计和优化管道系统。

在航空航天工程中，伯努利定律可以解释飞机机翼下表面的气压降低，进而产生升力，使飞机得以飞行。

在水力学中，伯努利定律可以解释水流在缓降地带加速的现象，以及流速变化对河流床形态和水力工程的影响。

总的来说，伯努利定律不仅是流体力学中的重要原理，而且在我们的日常生活和各个工程领域中都有着广泛的应用。

深入理解伯努利定律将有助于我们更好地理解和应用流体力学，从而提高我们对流体行为的认识和掌握。

1.2文章结构文章结构部分的内容可以包括以下几点：1.2 文章结构本篇文章将按照以下结构进行阐述伯努利定律的定义和原理，并探讨其应用和意义。

2.正文部分2.1 伯努利定律的定义本部分将介绍伯努利定律的基本定义。

伯努利定律是气体或液体在流动过程中的一种基本物理定律，它表明了流体在流动过程中压力、速度和高度之间的关系。

2.2 伯努利定律的原理本部分将详细阐述伯努利定律的原理。

伯努利定律是基于质量守恒原理和动量守恒原理推导而来的，它可以通过数学公式进行表达。

文章将深入解释伯努利定律的原理，并通过实例进行说明，帮助读者更好地理解。

3.结论部分3.1 伯努利定律的应用本部分将详细探讨伯努利定律的应用领域。

应用伯努利原理的例子1. 简介伯努利原理是描述流体运动时的一个重要物理定律，该定律可以应用于多个领域，包括航空、流体力学、声学等。

本文将介绍几个应用伯努利原理的例子，并说明其原理和应用。

2. 了解伯努利原理伯努利原理是由瑞士数学家伯努利在1738年提出的，它描述了在流体运动中速度增加时，压力将减小，速度减小时，压力将增加的关系。

这个原理可以用以下公式表示：P + 1/2 * ρ * v² + ρ * g * h = 常数其中，P表示压力，ρ表示密度，v表示流体的速度，g表示重力加速度，h表示流体的高度。

根据这个公式，我们可以推导出流体在不同速度下的压力差。

3. 应用伯努利原理的例子以下是几个应用伯努利原理的例子及其原理说明：3.1. 飞机飞行在飞机飞行中，机翼上下表面的气流速度不同，根据伯努利原理，当气流在机翼上流动时，速度增加，压力减小，而在机翼下表面流动时，速度减小，压力增加。

这种压力差产生了升力，使得飞机能够飞行。

应用伯努利原理，飞机翼型可以被设计成上表面较为凸起，下表面较为平坦，以使得上表面的气流速度更快，从而产生更大的升力。

3.2. 吸管喝水当我们用吸管喝水时，我们先用嘴吸住吸管一端，形成一个低气压区域。

根据伯努利原理，低气压将引起液体的压力，使得液体被吸起。

当液体进入吸管时，压力逐渐增加，直到与大气压力平衡。

3.3. 喷嘴出水当水从喷嘴中流出时，根据伯努利原理，流体速度增加，压力减小。

因此，喷嘴的压力将比周围环境低，使得液体从喷嘴被迫喷出。

3.4. 运动球的飞行当我们踢足球或打篮球时，球在空中飞行。

根据伯努利原理，球在飞行过程中，顶部气流速度更快，压力更低。

而底部气流速度较慢，压力较高。

这种压力差使得球在空中保持了稳定的飞行轨迹。

3.5. 跑道的闷浪现象在一些赛车比赛中，跑道上的车辆会出现闷浪现象。

根据伯努利原理，当车辆高速行驶时，车底的气流速度更快，压力更低，而车顶的气流速度较慢，压力较高。

流体力学伯努利定律一、伯努利定律的基本内容1. 定义- 对于理想流体（不可压缩、无黏性的流体）在稳定流动时，同一流线上的各点的压强p、流速v和高度h满足关系：p+(1)/(2)ρ v^2+ρ gh = C（C为常量）。

- 其中ρ是流体的密度，g是重力加速度。

2. 物理意义- 伯努利定律实际上是能量守恒定律在流体力学中的体现。

- 等式左边三项分别表示单位体积流体的压力能p、动能(1)/(2)ρ v^2和重力势能ρ gh。

在同一流线上的不同点，这三种能量可以相互转化，但它们的总和保持不变。

- 例如，当流体流速增大时，其动能(1)/(2)ρ v^2增大，根据伯努利定律，压强p会减小，或者高度h会降低（在某些情况下是两者同时变化），以保证三项之和不变。

二、伯努利定律的推导（简单理解版）1. 从功能原理出发- 考虑一段细流管中的流体，设流管的横截面积在不同位置有所变化。

- 在Δ t时间内，流入某一截面的流体质量Δ m=ρ V=ρ S_1v_1Δ t（S_1为流入截面面积，v1为流入速度）。

- 对这部分流体做功，外力做功包括压力做功。

流入端压力p_1做正功W_1 = p_1S_1v_1Δ t，流出端压力p_2做负功W_2=-p_2S_2v_2Δ t。

- 根据功能原理，外力做功等于流体机械能的增量。

流体的动能增量ΔE_k=(1)/(2)Δ m(v_2^2 - v_1^2)，重力势能增量Δ E_p=Δ mg(h_2 - h_1)。

- 由W_1+W_2=Δ E_k+Δ E_p，经过一系列推导（代入Δ m=ρ S_1v_1Δ t=ρS_2v_2Δ t等关系），可以得到伯努利方程p_1+(1)/(2)ρ v_1^2+ρgh_1=p_2+(1)/(2)ρ v_2^2+ρ gh_2。

三、伯努利定律的应用1. 飞机机翼升力原理- 飞机机翼的上表面是弧形，下表面相对较平。

- 当飞机飞行时，空气流过机翼。

由于机翼上表面的路程较长，空气流速v较大，根据伯努利定律p+(1)/(2)ρ v^2+ρ gh = C，在同一高度h下（可近似认为机翼上下表面高度差引起的重力势能变化可忽略），上表面空气流速大则压强p小，下表面空气流速相对较小则压强较大。

伯努利定律是流体力学中的一个重要原理，由瑞士物理学家丹尼尔・伯努利于1726年提出。

其核心内容是在流体系统中，如气流、水流等，流速越快的地方，流体产生的压力就越小；反之，流速越慢的地方，压力就越大。

这一原理可以用一个简单的实验来理解：拿着两张纸，往两张纸中间吹气，会发现纸不但不会向外飘去，反而会被一种力挤压在了一起。

这是因为两张纸中间的空气被吹得流动速度快，压力就小，而两张纸外面的空气没有流动，压力就大，所以外面力量大的空气就把两张纸“压”在了一起。

从数学表达式来看，伯努利方程为P+1/2ρv²+ρgh=常数，其中P 表示流体的压力，ρ是流体的密度，v表示流体速度，g是重力加速度，h代表流体相对于参考点的高度。

此方程表明，对于流动的流体元素，其机械能（包括压力能、动能和位能）在没有外力作用的情况下是守恒的。

伯努利定律仅适用于粘度可以忽略、不可被压缩的理想流体。

虽然在实际情况中，流体往往不是完全理想的，但伯努利定律在很多实际工程问题中仍提供了重要的参考价值。

例如，在处理高速流动或低粘度流体时，伯努利定律可以较好地近似实际情况。

飞机机翼升力如何应用伯努利定律飞机机翼的设计利用了伯努利定律来产生升力。

飞机机翼的横截面形状上下不对称，机翼上方的流线密，流速大，下方的流线疏，流速小。

根据伯努利方程可知，机翼上方的压强小，下方的压强大，这样就产生了作用在机翼上的升力。

具体来说，当气流经过机翼上下表面时，由于机翼上表面是圆弧形，路程比下表面长，气流在上表面的流速要比在下表面流速快。

例如湖北荆门“晨龙天使/Angel”多用途通勤飞机在漳河机场首飞成功，其飞行过程中，机翼周围空气的流动就遵循了伯努利定律。

飞机升力的大小还跟飞机的机翼面积、空气密度、飞行速度以及飞行迎角等因素有关。

机翼面积越大，升力越大，因为压强与面积的乘积才是压力的大小。

空气密度越大，升力也越大。

飞行速度越大，由伯努利原理给出的压强差就越大，升力也就越大。

伯努利大数定律和辛钦大数定律伯努利大数定律和辛钦大数定律是概率论中的两个重要定律，它们描述了大量独立重复实验中事件发生的频率趋于稳定的现象。

这两个定律对于理解概率与统计的基本原理具有重要意义。

伯努利大数定律，又称大数定律或弱大数定律，由瑞士数学家雅各布·伯努利在17世纪提出。

该定律表明，当独立重复实验次数足够多时，事件发生的频率将接近其概率。

换句话说，当实验次数足够多时，事件发生的频率将趋于稳定，并且接近于事件发生的概率。

以一个简单的掷硬币实验为例，我们假设硬币正面朝上的概率为p，反面朝上的概率为1-p。

当我们进行大量的掷硬币实验时，根据伯努利大数定律，正面朝上的频率将接近于p。

也就是说，如果我们掷硬币1000次，正面朝上的次数大约为1000*p。

当我们掷硬币10000次，正面朝上的次数大约为10000*p。

随着实验次数的增加，正面朝上的频率将逐渐稳定在p附近。

辛钦大数定律，又称强大数定律，由俄罗斯数学家阿列克谢·尼古拉耶维奇·辛钦于20世纪初提出。

该定律扩展了伯努利大数定律，更加详细地描述了频率的稳定性。

辛钦大数定律指出，对于独立重复实验，事件发生的频率将以极高的概率收敛于其概率。

也就是说，当实验次数趋于无穷大时，事件发生的频率几乎肯定会收敛到事件发生的概率。

回到掷硬币的例子，根据辛钦大数定律，随着实验次数的增加，正面朝上的频率将以极高的概率收敛于p。

这意味着，当我们进行足够多的掷硬币实验时，正面朝上的频率将几乎肯定会接近于硬币正面朝上的概率。

伯努利大数定律和辛钦大数定律的意义不仅限于掷硬币实验，它们在概率论和统计学中有广泛的应用。

无论是在自然科学还是社会科学领域，我们经常需要通过实验或观察来获取数据，并对数据进行统计分析。

伯努利大数定律和辛钦大数定律告诉我们，通过大量的独立重复实验，我们可以获得可靠的统计结果，这为科学研究和决策提供了重要的依据。

然而，需要注意的是，伯努利大数定律和辛钦大数定律只适用于独立重复实验。

伯努利定理是质量守恒定律在流体流动中的应用伯努利定理是流体力学中的重要定理之一，它描述了流体在不同位置和速度下的压力和动能之间的关系。

伯努利定理被广泛应用于流体力学、气象学、航空航天学等领域，在实际应用中具有重要的意义。

一、伯努利定理的基本概念伯努利定理是基于质量守恒定律和能量守恒定律推导出来的。

质量守恒定律是指在任何封闭系统中，质量是不会发生减少或增加的，而能量守恒定律是指在任何封闭系统中，能量是不会发生减少或增加的。

在流体力学中，这两个定律被称为连续方程和伯努利方程。

伯努利定理的基本概念是：在稳定的流体中，当流速增加时，压力会降低；当流速减小时，压力会增加。

这个定理的实质是：当流体通过一定截面时，其速度越大，单位时间内通过该截面的质量就越大，因此单位面积上承受的压力就越小；反之，当流体速度减小时，单位面积上承受的压力就越大。

二、伯努利定理的应用伯努利定理的应用非常广泛，下面我们就来看看它在实际应用中的一些例子。

1、飞机的升力飞机在飞行时，翼面上方的气流速度比下方的气流速度快，因此上方的气流压力会降低，而下方的气流压力会增加。

这就产生了一个向上的升力，使得飞机能够离开地面飞行。

这个现象正是伯努利定理的应用，因为在飞行时，翼面上方的气流速度比下方的气流速度快，所以上方的气流压力会降低，而下方的气流压力会增加。

2、水泵和水管在水泵和水管中，伯努利定理也有着重要的应用。

当水流通过水泵时，水流的速度会增加，因此水的压力会降低。

而当水流通过水管时，水的速度会减小，因此水的压力会增加。

这个现象正是伯努利定理的应用，因为当水流通过水泵时，水流的速度会增加，所以水的压力会降低；而当水流通过水管时，水的速度会减小，所以水的压力会增加。

3、汽车的行驶汽车在行驶时，车辆前面的气流速度要比车辆后面的气流速度快，因此车辆前面的气流压力会降低，而车辆后面的气流压力会增加。

这就产生了一个向后的阻力，使得汽车需要消耗更多的能量才能行驶。