(新教材)【人教A版】20版《高中全程学习方略》必修二6.3.1(数学)
- 格式:ppt
- 大小:12.62 MB
- 文档页数:61


单元素养评价(二)(第八章)(120分钟150分)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.cos215°+cos275°+cos15°cos75°的值是 ( )A. B. C. D.【解析】选D.原式=++=.2.若tan α=2,则的值等于( )A.-B.C. -D.【解析】选B.====.3.若sin=,sin=,则= ( )A.2B.4C.6D.8【解析】选B.sin=sin αcos β+cos αsin β=,sin=sin αcos β-cos αsin β=,由此得sin αcos β=,cos αsin β=,所以=5,所以=4.4.若sin θ<0,cos2θ<0,则在(0,2π)内θ的取值范围是( )A.π<θ<B.<θ<C.<θ<2πD.<θ<【解析】选B.因为cos 2θ<0,所以1-2sin2θ<0,即sin θ>或sin θ<-,又已知sin θ<0,所以-1≤sin θ<-,由正弦曲线得满足条件的θ取值为<θ<.5.三角形ABC中,若C>90°,则tan A·tan B与1的大小关系为( )A.tan A·tan B>1B.tan A·tan B<1C.tan A·tan B=1D.不能确定【解析】选B.在三角形ABC中,因为C>90°,所以A,B都为锐角.则有tan A>0,tan B>0,tan C<0.又因为C=π-(A+B),所以tan C=-tan(A+B)=-<0易知1-tan A·tan B>0,即tan A·tan B<1.6.若a,b是非零向量且满足(a-2b)⊥a,(b-2a)⊥b ,则a与b的夹角θ是( )A. B. C. D.【解析】选B.因为a2-2a·b=0,b2-2a·b=0,所以a2=b2=2a·b ,|a|=|b|,所以cos θ===.所以θ=.7.已知0<α<<β<π,又sin α=,cos(α+β)=-,则sin β等于( ) A.0 B.0或C. D.±【解析】选C.因为0<α<<β<π且sin α=,cos(α+β)=-,所以cos α=,<α+β<π,所以sin(α+β)=±,当sin(α+β)=时,sin β=sin[(α+β)-α]=sin(α+β)cos α-cos(α+β)sin α=×-×=;当sin(α+β)=-时,sin β=sin[(α+β)-α]=sin(α+β)cos α-cos(α+β)sin α=-×-×=0.又β∈,所以sin β>0,故sin β=.8.设△ABC的三个内角为A,B,C,向量m=(sin A,sin B),n=(cos B,cos A),若m·n=1+cos(A+B),则C= ( )A. B. C. D.【解析】选C.因为m·n=sin Acos B+sin B·cos A=sin(A+B)=sin C=1-cos C,所以sin=,又因为0<C<π,所以C+=,故C=.二、多项选择题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,选对但不全的得3分,有选错的得0分)9.下列计算正确的是( )A.=1B.1-2sin275°=C.cos4-sin4=D.cos275°+cos215°+cos75°c os 15°=【解析】选A、C、D. 对于选项A,=tan 45°=1;对于选项B,1-2sin275°=cos 150°=-,对于选项C,cos4-sin4==cos=;对于选项D,原式=sin215°+cos215°+sin 15°cos 15°=1+sin 30°=1+=.10.若函数y=sin cos+cos·sin,则( )A.函数的周期为2πB.函数的一个对称中心为C.函数的一条对称轴为x=πD.函数的值域为【解析】选A,C,D.y=sin·cos-cos sin=sin=sin=cos x,故周期为2π,x=π是函数y=cos x的一条对称轴,值域为.11.△ABC是边长为2的等边三角形,已知向量a,b满足=2a,=2a+b,则下列结论不正确的是 ( )A.|b|=1B.a⊥bC.a·b=1D.(4a+b)⊥【解析】选A,B,C.在△ABC中,由=-=2a+b-2a=b,得|b|=2.又|a|=1, 所以a·b=|a||b|cos 120°=-1,所以(4a+b)·=(4a+b)·b=4a·b+|b|2=4×(-1)+4=0,所以(4a+b)⊥.12.已知锐角α,β满足sin α-cos α=,tan α+tanβ+tan αtanβ=,则( )A.<α<B.β<<αC.<α<βD.<β<α【解析】选A,B.因为α为锐角,sin α-cos α=>0,所以<α<.又tan α+tan β+tan αtan β=,所以tan(α+β)==,所以α+β=,又α>,所以β<<α.三、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)13.函数f(x)=sin2的最小正周期是________.【解析】因为f(x)==(1-sin 4x),所以最小正周期T=.答案:14.tan+tan+tan·tan的值是________.【解析】因为tan=tan==,所以tan+tan+tan tan=.答案:15.若=2 020,则+tan 2α=________.【解析】+tan 2α======2 020.答案:2 02016.已知向量a,b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是________,最大值是________.【解析】设a,b的夹角为θ.因为|a|=1,|b|=2,所以|a+b|+|a-b|=+=+.令y=+,则y2=10+2.因为θ∈[0,π],所以cos2θ∈[0,1],所以y2∈[16,20],所以y∈[4,2],即|a+b|+|a-b|∈[4,2].答案:4 2四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(10分)(1)求值:.(2)已知sin θ+2cosθ=0,求的值.【解析】(1)原式====2+.(2)由sin θ+2cos θ=0,得sin θ=-2cos θ,又cos θ≠0,则tan θ=-2,所以====.18.(12分)已知向量a=(sin θ,-2)与b=(1,cos θ)互相垂直,其中θ∈.(1)求sin θ和cos θ的值.(2)若sin(θ-φ)=,0<φ<,求cos φ的值.【解析】(1)因为a与b互相垂直,则a·b=sin θ-2cos θ=0,即sin θ=2cos θ,代入sin2θ+cos2θ=1得, sin θ=±,cos θ=±,又θ∈,所以sin θ=,cos θ=.(2)因为0<φ<,0<θ<,所以-<θ-φ<,则cos(θ-φ)==,cos φ=cos[θ-(θ-φ)]=cos θcos(θ-φ)+sin θsin(θ-φ)=. 19.(12分)求函数f(x)=sin x的最小正周期与最值. 【解析】f(x)=sin x=sin x·2cos sin=-sin xcos=-=-sin+.所以最小正周期为T==π.因为sin∈[-1,1],所以f(x)max=,f(x)min=-.20.(12分)已知ω>0,a=(2sinωx+cosωx,2sinωx-cos ωx),b=(sin ωx,cosωx),f(x)=a·b,f(x)图像上相邻的两个对称轴的距离是.(1)求ω的值.(2)求函数f(x)在区间上的最大值和最小值.【解析】f(x)=a·b=(2sin ωx+cos ωx)sin ωx+(2sin ωx-cos ωx)cos ωx =2sin2ωx+3sin ωxcos ωx-cos2ωx=1-cos 2ωx+sin2ωx-(1+cos 2ωx)=(sin 2ωx-cos 2ωx)+=sin+.(1)因为函数f(x)的图像上相邻的两个对称轴间的距离是,所以函数f(x)的最小正周期T=π,则ω=1.(2)f(x)=sin+.因为x∈,所以∈,则当2x-=-,即x=0时,f(x)取得最小值-1;当2x-=,即x=时,f(x)取得最大值.21.(12分)如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为.(1)求tan(2α-β)的值.(2)若<α<π,0<β<,求α+β.【解析】(1)由三角函数的定义知tan α=-,所以tan 2α==.又由三角函数线知sin β=.因为β为第一象限角,所以tan β=,所以tan(2α-β)==.(2)因为cos α=-,sin β=,<α<π,0<β<,所以sin α=,cos β=.<α+β<.因为sin(α+β)=sin αcos β+cos αsin β=×-×=.又因为<α+β<,所以α+β=.22.(12分)如图,四边形ABCD是边长为10的正方形,以点A为圆心,9为半径画弧,分别交AB、AD于点E,F,P为上一动点,过点P分别作PM⊥BC,PN⊥CD,垂足分别为M,N,求矩形PMCN的面积的最小值.【解析】连接PA,设∠PAE=θ,如图所示.设矩形PMCN的面积为S,延长NP交AB于点H,则PM=HB=AB-AH=10-9cos θ,PN=HN-HP=10-9sin θ.所以S=PM·PN=(10-9cos θ)(10-9sin θ)=100-90sin θ-90cos θ+81sin θcos θ.设sin θ+cos θ=t.则S=100-90t+(t2-1)=t2-90t+=+.因为θ∈,所以t=sin θ+cos θ=sin∈[1,],所以当t=时,S min=,故矩形PMCN的面积的最小值为.关闭Word文档返回原板块。


1. 1.2集合的基本关系汉聲提示如果您在现石木年件旳辻芳中出"••字他泉・折吳同幷宥幻灯片・可正*恋・新版课程标准学业水平要求★水平一I.能从教材实例中抽象出子集、真子集的概念・(数学抽象)1.理解集合之间包含与相等的含义•能识别给定集2.能识别给定集合的子集、真子集・(逻辑推理)合的子集:3.会判断集合间的关系•并能用符号和维恩图表小.(直观想象)2•能使用维恩图表达集合的皋本关系•体会图形对★水平二理解抽象概念的作用;1・掌握列举冇限集的所冇子集的方法•(逻辑推理)2 •能根据集合之间的关系•利用数形结合的思想求参数的值或取1必备知识•素养奠基1・维恩图用平面上一条封闭曲线的内部来表示集合的示意图.2 •子集和真子集【思考】(1) 任意两个集合之间是否有包含关系?提示:不一定,如集合A={1 z 3} z B={2 , 3} z这两个集合就没有包含关系.(2) 符号与乜”有什么区别?提示:① y 是表示元素与集合之间的关系,比如IWN , -ieN.②y”是表示集合与集合之间的关系,比如NUR ,{1,2, 3}C{3 , 2 , 1}・③的左边是元素,右边是集合,而 V 的两边均为集合.3 •关于子集和真子集的结论⑴空集是任意一个集合A 的子集,即0CA.(2) 对于集合A, B, C,如果A C B, B C C,(3) 对于集合A, B, C,如果A B, B C,呈辜 2贝ijAcC.4 •集合相等与子集的关系⑴如果ACB且BCA,贝iJA=B. ⑵如果A=B,贝iJAcB-SBcA.【素养小测】1 •思维辨析(对的打“十',错的打“X”)(1) 任何集合至少有两个子集. ((2) {0, 1, 2}c{2, 0, 1}.()(3) 若AcB,且AHB,则A B. ((4) 集合{0, 1}的子集是{0},⑴,{0, 1}.提示:⑴x.0只有一个子集.z2}c (2)<{0 , 1 , 2}={2 ,0,1},所以{0 , 1 {2,0,1}.⑶7.若AcB z且AHB z则A B.(4) x.0也是集合{0 , 1}的子集.2下列图形中,表示MCN的是()C D【解析]选C・根据题意可知z M中的任意一个元素都是N中的元素,故C正确.3•已知集合A={・1, 3, m}, B={3, 4},若BcA,则实数________________【解析】因为BCA , B={3 z 4} z A={-1 , 3 z m} z比较A , B中的元素可知m=4. 答案:4关键能力类型一集合间夫:乐tl'J刊助【典例】1 •下列各个关系式中,正确的是A.0={O} B. WQC.{3, 5}#{5, 3}D.{1}C{X|X2=X}•素养形成^三()2•己知集合A={x|x<-2或x>0}, B={x|0<x<1},则(A.A=B B.A BC.B AD.AcB辜3 •判断下列各组中集合之间的关系:(1)A={x|x是12的约数}, B={x|x是36的约数};6= Rix2+1 =01 •⑶A={x|x是平寻四边形}, B={x|x是爰形}, C={x|x是四边形}, D={x|x是正方形};(4)M= f , N=< xlx=-, neZ >2< xlx=一- n, neZ2【思维•引】1 •先确定是元素与集合的关系还是集合与集合的关系,然后根据集合中元素的特征逐项判断.2画出数轴,观察数轴判断集合A与B的关系.3•首先确定集合由哪些元素构成,然后判断集合之间的关系.【解析】1 •选D•因为0 {0} , GQ, {3 , 5}={5 , 3} z所以A , B z C错误,{x|xM={0 , 1] 所以{1}C{X|X2=X}成立2选C.由数轴知B A.Bo --------- 1 ------- 6 -------- 6-23.(1)因为若x是12的约数,则必定是36的约数,反之不成立,所以A B.(2) 因为A={x|x2-x=0}={0, 1}, B={xeR|x2+1=O}=0, 所以B A.(3) 由图形的特点可画出维恩图如图所示,从而C A BD.呈w(4) 方法一:对于集合M ,其组成元素是,分子部分表示所有的整数;对于集合N ,其组成元素是H + n二,分子部分表示所有的奇数•由真子集的概- 念知z N M. 212n+l2方法二:用列举法表示集合如下:M=N= 所以N M.< ---1 -1 0 - 1 - 2 -〔2 2 2 2 2[3 113 5 ]I・・・・・・,,2 2 2 2 2…厶【内化•悟】1・区别属于关系和包含关系的关键是什么?提示:关键是结合具体情境识别集合还是元素.2当集合中元素有无限多个时,常用哪些方法判断集合之间的关系?提示:常用的方法有以下两种(1)画数车由,⑵适当变韧寻找联系,例如:对于集合 A= B= /将集合A 变为A= 不难观察出A B.2k X = 一 6< x x 二一,kwZ> 1 6 J【类题•通】1 •集合间基本关系判定的两种方法和一个关键2证明集合相等的两种方法(1)用两个集合相等的定义,证明两个集合A, B中的元素全部相同,即可证明心8・⑵证明A C B,同时B C A,推出A=B.【习练•破】1 •已知集合A={x|x=3k, kGZ}, B={x|x=6k, kGZ}, 则A与B之间最适合的关系是()A.AcBB.AaBC.A BD.A B【解析】选D.因为A中元素是3的整数倍,而B中元素是3的偶数倍z所以集合B是集合A的真子集.2已知集合U, S, T, F之间的关系如图所示,下列关系中错误的有____________ ・(只填序号)2T;F; )F s ②④ — s s F【解析】根据子集、真子集的定义, 由维恩图的关系,可以看出S U,S T ②④错误.答案:②④,F U正确,【加练個】1 •已知集合A=B=则集合A, B的关系为< xlx 壬1』3Vxlx = 2n + l,neZ。
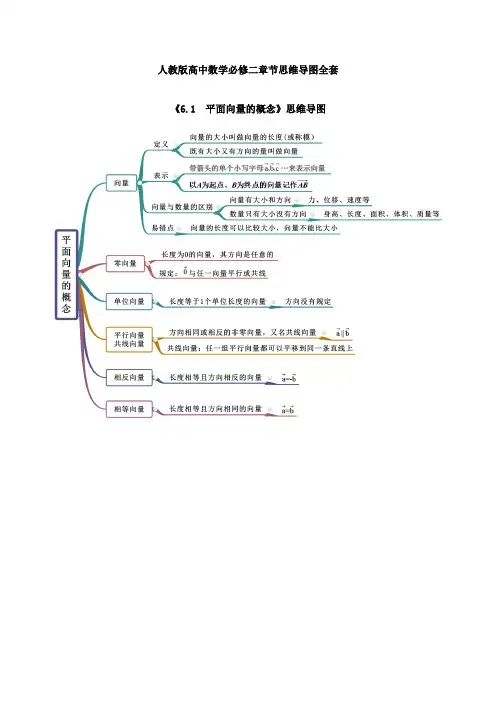
人教版高中数学必修二章节思维导图全套《6.1 平面向量的概念》思维导图
《6.3.1 平面向量的基本定理及加减数乘坐标运算》思维导图
《6.3.2 平面向量数量积的坐标表示》思维导图
《6.4.1平面向量在几何和物理中的运用》思维导图
《6.4.2 余弦定理、正弦定理》思维导图
《6.4.3 余弦定理、正弦定理的实际运用》思维导图
《7.1 复数的概念》思维导图
《7.2 复数的四则运算》思维导图
《7.3 复数的三角表示》思维导图
《8.1 基本立体图形》思维导图
《8.2 立体图形的直观图》思维导图
《8.3 简单几何体的表面积与体积》思维导图
《8.4 空间点、直线、平面之间的位置关系》思维导图
《8.5 空间直线、平面的平行》思维导图
《9.1 随机抽样》思维导图
《10.2 事件的相互独立性》思维导图
《10.3 频率与概率》思维导图。






人教版A版高中数学必修二全册课件【完整版】一、直线与方程1. 直线的斜率定义:直线斜率是指直线上任意两点之间的纵坐标之差与横坐标之差的比值。
计算公式:k = (y2 y1) / (x2 x1)性质:斜率k与直线倾斜角度的关系为k = tan(θ),其中θ为直线与x轴正方向的夹角。
2. 直线的截距定义:直线截距是指直线与y轴的交点的纵坐标。
计算公式:b = y kx,其中k为直线斜率,x为直线与x轴的交点的横坐标,y为直线与y轴的交点的纵坐标。
3. 直线方程点斜式:y y1 = k(x x1),其中k为直线斜率,(x1, y1)为直线上的一点。
斜截式:y = kx + b,其中k为直线斜率,b为直线截距。
一般式:Ax + By + C = 0,其中A、B、C为常数,且A、B 不同时为0。
4. 两条直线的位置关系平行:两条直线的斜率相等。
垂直:两条直线的斜率互为负倒数。
相交:两条直线的斜率不相等。
二、圆与方程1. 圆的定义定义:圆是平面上所有与一个固定点(圆心)距离相等的点的集合。
2. 圆的标准方程方程:(x a)² + (y b)² = r²,其中(a, b)为圆心坐标,r 为半径。
3. 圆的一般方程方程:x² + y² + Dx + Ey + F = 0,其中D、E、F为常数。
4. 圆与直线的位置关系相离:直线与圆没有交点。
相切:直线与圆有且仅有一个交点。
相交:直线与圆有两个交点。
三、椭圆与方程1. 椭圆的定义定义:椭圆是平面上所有与两个固定点(焦点)距离之和等于常数的点的集合。
2. 椭圆的标准方程方程:(x h)²/a² + (y k)²/b² = 1,其中(h, k)为椭圆中心坐标,a为椭圆长轴的一半,b为椭圆短轴的一半。
3. 椭圆的一般方程方程:Ax² + By² + Cx + Dy + E = 0,其中A、B、C、D、E 为常数,且A、B不同时为0。
1.2常用逻辑用语1.2.1命题与量词溟聲提示如果您在现石木年件旳辻芳中出"••字他泉・折吳同幷宥幻灯片・定义可供真假判断的陈述语句分类真命题:判断为真的语句假命题:判断为假的语句注意数学中的命题,经常借助符号和式子来表送一个命题,要么是真命题,要么是假命题,不能同时既是真命题又是假命题1 •命题必备知识•素养奠基2全称量词与全称量词命题(1)全称量词:“任意” “所有”“每一个, 称量词,用符号表示."在陈述中表示所述事物的全体,称为全(2)全称量词命题:含有全称量词的命题,叫做全称量词命题.(3)符号表示:“对集合M中的所有元素x,「(x)”.可简记为:VxeM, r(x).【思考】常见的全称量词还有哪些?提示:常见的全称量词还有〃一切〃〃全部"〃任给〃〃凡是"等.3 •存在量词与存在量词命题⑴存在量词:“存在”“有”“至少有一个^ 称为存在量词,用符号“丁‘表示.”在陈述中表示所述事物的个体或部分,(2)存在量词命题:含有存在量词的命题,叫做存在量词命题.(3)符号表示:“存在集合M中的元素x, s(x)”.可简记为:3xGM, s(x).s【思考】常见的存在量词还有哪些?提示:常见的存在量词还有〃有些"〃有一个〃〃对某些〃等.【素养小测】1 •思维辨析(对的打“十',错的打“X”)(1)全称量词命题是陈述某集合中所有元素都具有某种性质的命题. ((2)存在量词命题是陈述某集合中存在一个或部分元素具有某种性质的命题.()(3)全称量词命题一定含有全称量词.()提示:(1)/全称量词命题中的全称量词表明给定范围内所有对象都具有某一性质Z 无一例外,强调〃整体、全部〃•_ _ _ (2)/存在量词命题中的存在量词则表明给定范围内的对象有例外,强调〃个别、部分〃・(3)x.有些命题虽然没有写出全称量词,但其意义具备称量词命题z如〃正数大于0”即〃所有正数都大于0”任意性〃,这类命题也是全 ,故说法是错误的.2.卜列命题中是存在量词命题的是A.VxeR, x2>0B.axeR, x2<0C・平行四边形的对边不平行D.矩形的任一组对边都不相等【解析]选B.A , C z D是全称量词命题,B是存在量词命题.3 •下列命题中是全称量词命题并且是真命题的是()A•每个二次函数的图象都开口向上B.存在实数X,平方为8C.所有菱形的四条边都相等D.存在一个实数X。