数学模型电子教案(2)

数学建模教案设计一、教学内容本节课选自《数学建模》教材第四章第一节，详细内容为多变量线性规划及其应用。

主要包括多变量线性规划模型的建立、求解方法以及实际应用案例。

二、教学目标1. 理解多变量线性规划的概念，掌握其数学表达形式。

2. 学会使用单纯形法求解多变量线性规划问题。

3. 能够将实际问题抽象为多变量线性规划模型，并运用所学知识解决实际问题。

三、教学难点与重点教学难点：多变量线性规划模型的建立与求解。

教学重点：单纯形法的应用以及实际问题的建模。

四、教具与学具准备1. 教具：多媒体教学设备、黑板、粉笔。

2. 学具：数学建模教材、练习本、计算器。

五、教学过程1. 实践情景引入（5分钟）利用多媒体展示一个实际生产问题，引导学生思考如何优化生产方案。

2. 知识讲解（15分钟）讲解多变量线性规划的基本概念、数学表达形式及求解方法。

3. 例题讲解（20分钟）通过一个具体例题，演示如何将实际问题抽象为多变量线性规划模型，并运用单纯形法求解。

4. 随堂练习（15分钟）学生独立完成一道类似例题的练习，教师巡回指导。

6. 课堂小结（5分钟）回顾本节课所学内容，强调重点、难点。

六、板书设计1. 多变量线性规划概念及数学表达形式2. 单纯形法求解步骤3. 实际问题建模过程4. 例题解答过程七、作业设计1. 作业题目：（1）求解下列多变量线性规划问题：max z = 2x1 + 3x2s.t. x1 + 2x2 ≤ 4x1 + x2 ≤ 3x1, x2 ≥ 0某工厂生产两种产品，产品A和产品B。

生产一个A产品需要2小时工时和3小时机器时，生产一个B产品需要1小时工时和2小时机器时。

工厂每天有8小时工时和12小时机器时可用，问如何安排生产计划，才能使每天生产的A产品和B产品总价值最大？答案：（1）max z = 4x1 = 2, x2 = 0（2）max z = 18x1 = 3, x2 = 2八、课后反思及拓展延伸1. 反思：本节课学生对多变量线性规划的建模和求解掌握程度，以及课堂互动情况。

模板电子教案模板格式(5篇一、教学内容本节课我们将学习《高中数学》教材第四章第一节《函数的基本概念》。

详细内容包括函数的定义、函数的表示方法、函数的图像以及基本函数的性质。

二、教学目标1. 理解并掌握函数的基本概念及其表示方法。

2. 能够根据实际情境，运用函数模型解决相关问题。

3. 培养学生的逻辑思维能力和抽象思维能力。

三、教学难点与重点教学难点：函数的定义及其表示方法，函数图像的绘制。

教学重点：函数的基本概念，函数性质的探讨。

四、教具与学具准备教具：黑板、粉笔、多媒体设备。

学具：函数图像绘制模板、直尺、圆规。

五、教学过程1. 导入新课通过引入实际情境，如气温变化、人口增长等，让学生感受函数在现实生活中的应用，激发学习兴趣。

2. 知识讲解（1）讲解函数的定义，通过示例让学生理解函数的内涵。

（2）介绍函数的表示方法，如列表法、解析法、图像法等。

（3）分析基本函数的性质，如线性函数、二次函数等。

3. 例题讲解讲解典型例题，引导学生运用所学知识解决问题。

4. 随堂练习让学生独立完成练习题，巩固所学知识。

5. 课堂小结六、板书设计1. 板书函数的定义、表示方法、图像及性质。

2. 在黑板上展示典型例题及解题过程。

3. 在黑板上呈现随堂练习题目。

七、作业设计1. 作业题目：（1）列举生活中遇到的函数实例，并分析其性质。

a. f(1)=2, f(2)=4, f(3)=6b. 函数图像过点(1,2), (2,4), (3,6)2. 答案：（1）生活中的函数实例：气温变化、人口增长等。

（2）a. f(x)=2xb. f(x)=2x八、课后反思及拓展延伸1. 反思本节课的教学效果，针对学生的掌握情况，调整教学策略。

2. 拓展延伸：（1）研究其他类型的函数，如分段函数、复合函数等。

（2）探讨函数在实际问题中的应用，如最大值、最小值问题等。

重点和难点解析1. 教学内容的难点与重点；2. 教学过程中的实践情景引入、例题讲解、随堂练习；3. 作业设计中的题目设置及答案；4. 课后反思及拓展延伸。

高中数学教案电子版(通用19篇)（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如工作总结、工作计划、心得体会、条据文书、合同协议、规章制度、应急预案、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays, such as work summaries, work plans, insights, normative documents, contract agreements, rules and regulations, emergency plans, teaching materials, complete essays, and other sample essays. If you want to learn about different sample formats and writing methods, please pay attention!高中数学教案电子版(通用19篇)2024年人教版高中数学电子课本教案是教学活动中对于整个课程内容和过程的安排和设计，它具有指导教师教学行为、促进学生学习的重要作用。

数学建模教案修订版一、教学内容本节课选自《数学建模》教材第二章第三节，详细内容为多变量线性回归模型的构建与求解。

通过本节内容的学习，使学生了解多变量线性回归模型的基本概念，掌握模型构建和求解的方法。

二、教学目标1. 知识与技能：理解多变量线性回归模型的基本原理，掌握模型参数的求解方法。

2. 过程与方法：培养学生运用数学知识解决实际问题的能力，提高团队协作能力。

3. 情感态度与价值观：激发学生学习数学的兴趣，培养学生的科学素养。

三、教学难点与重点1. 教学难点：多变量线性回归模型的求解方法。

2. 教学重点：多变量线性回归模型的构建与应用。

四、教具与学具准备1. 教具：多媒体教学设备、黑板、粉笔。

2. 学具：教材、计算器、草稿纸。

五、教学过程1. 实践情景引入（5分钟）利用多媒体展示实际案例，如房屋价格与面积、楼层等因素的关系，引导学生思考如何建立数学模型来描述这些关系。

2. 知识讲解（15分钟）讲解多变量线性回归模型的基本概念、构建方法和求解步骤。

3. 例题讲解（15分钟）选取一道与实际案例相关的例题，详细讲解模型构建和求解的过程。

4. 随堂练习（10分钟）让学生独立完成一道与例题类似的题目，巩固所学知识。

5. 小组讨论（10分钟）7. 课堂小结（5分钟）强调多变量线性回归模型在实际应用中的重要性，鼓励学生在课后继续探索相关知识。

六、板书设计1. 多变量线性回归模型的基本概念2. 模型构建方法与求解步骤3. 例题及解答七、作业设计1. 作业题目：利用多变量线性回归模型分析某城市房屋价格与面积、楼层等因素的关系。

2. 答案：根据实际情况，给出模型的参数估计值和预测结果。

八、课后反思及拓展延伸1. 反思：本节课的教学效果，学生的掌握程度，教学过程中的不足之处。

2. 拓展延伸：引导学生了解其他类型的回归模型，如非线性回归、岭回归等，激发学生的求知欲。

重点和难点解析1. 教学难点：多变量线性回归模型的求解方法。

《数学模型电子教案》PPT课件第一章：数学模型概述1.1 数学模型的定义与分类1.2 数学模型的构建步骤1.3 数学模型在实际应用中的重要性1.4 数学模型与数学建模的区别与联系第二章：数学模型建立的基本方法2.1 直观建模法2.2 解析建模法2.3 统计建模法2.4 计算机模拟建模法第三章：线性方程组与线性规划模型3.1 线性方程组的求解方法3.2 线性规划的基本概念与方法3.3 线性规划模型的应用案例3.4 线性规划模型的求解算法第四章：微分方程与差分方程模型4.1 微分方程的基本概念与分类4.2 微分方程的求解方法4.3 差分方程的基本概念与分类4.4 差分方程的求解方法与应用第五章：概率论与统计模型5.1 概率论基本概念与随机变量5.2 概率分布与数学期望5.3 统计学基本概念与推断方法5.4 统计模型的应用案例第六章：最优化方法与应用6.1 无约束最优化问题6.2 约束最优化问题6.3 最优化方法的应用案例6.4 遗传算法与优化问题第七章：概率图与贝叶斯模型7.1 概率图的基本概念7.2 贝叶斯定理及其应用7.3 贝叶斯网络与推理方法7.4 贝叶斯模型在实际应用中的案例分析第八章：时间序列分析与预测模型8.1 时间序列的基本概念与分析方法8.2 自回归模型（AR）与移动平均模型（MA）8.3 自回归移动平均模型（ARMA）与自回归积分滑动平均模型（ARIMA）8.4 时间序列预测模型的应用案例第九章：排队论与网络流量模型9.1 排队论的基本概念与模型构建9.2 排队论在服务系统优化中的应用9.3 网络流量模型的基本概念与方法9.4 网络流量模型的应用案例第十章：随机过程与排队网络模型10.1 随机过程的基本概念与分类10.2 泊松过程与Poisson 排队网络10.3 马克威茨过程与随机最优控制10.4 排队网络模型的应用案例第十一章：生态学与种群动力学模型11.1 生态学中的基本概念11.2 种群动力学模型的构建11.3 差分方程在种群动力学中的应用11.4 种群动力学模型的案例分析第十二章：金融数学模型12.1 金融市场的基本概念12.2 金融数学模型概述12.3 定价模型与风险管理12.4 金融数学模型在实际应用中的案例分析第十三章：社会经济模型13.1 社会经济系统的基本特征13.2 经济数学模型的构建方法13.3 宏观经济模型与微观经济模型13.4 社会经济模型的应用案例第十四章：神经网络与深度学习模型14.1 人工神经网络的基本概念14.2 深度学习模型的构建与训练14.3 神经网络在数学建模中的应用案例14.4 当前神经网络与深度学习的发展趋势第十五章：数学模型在工程中的应用15.1 工程问题中的数学建模方法15.2 数学模型在结构工程中的应用15.3 数学模型在流体力学中的应用15.4 数学模型在其他工程领域中的应用案例重点和难点解析本《数学模型电子教案》PPT课件涵盖了数学模型概述、建模方法、线性方程组与线性规划、微分方程与差分方程、概率论与统计、最优化方法、概率图与贝叶斯模型、时间序列分析、排队论与网络流量模型、随机过程、生态学与种群动力学模型、金融数学模型、社会经济模型、神经网络与深度学习模型以及数学模型在工程中的应用等多个领域。

2024年七年级数学整册教案电子版教案一、教学内容详细内容包括：1. 有理数的概念、分类、运算及性质；2. 整式的概念、分类、加减运算及性质；3. 一元一次方程的解法及应用；4. 不等式与不等式组的解法及应用；5. 几何图形的基本概念，如点、线、面的认识；6. 数据的收集、整理、描述和分析。

二、教学目标1. 让学生掌握有理数、整式、一元一次方程、不等式与不等式组的基本概念和运算方法；2. 培养学生运用数学知识解决实际问题的能力，提高逻辑思维和分析问题的能力；3. 培养学生几何图形的观察能力，激发对数学学习的兴趣。

三、教学难点与重点教学难点：有理数的运算、整式的加减、一元一次方程的解法、不等式与不等式组的解法。

教学重点：培养学生的数学思维能力、几何图形观察能力以及解决实际问题的能力。

四、教具与学具准备1. 教具：多媒体教学设备、几何模型、计算器；2. 学具：教材、练习本、直尺、圆规。

五、教学过程1. 实践情景引入：通过生活中的实例，引导学生学习有理数、整式等概念；2. 例题讲解：针对每个知识点，选择典型例题进行讲解；3. 随堂练习：针对讲解的例题，设计相应的随堂练习，巩固所学知识；5. 课后作业布置：布置适量的课后作业，巩固所学知识。

六、板书设计1. 知识点；2. 重要概念、性质、公式；3. 典型例题及解答；4. 课堂小结。

七、作业设计1. 作业题目：（1）计算题：有理数的混合运算；（2）填空题：整式的加减运算；（3）应用题：一元一次方程、不等式与不等式组的实际应用；（4）作图题：几何图形的绘制。

八、课后反思及拓展延伸1. 课后反思：对本节课的教学过程、学生学习情况进行反思，找出不足，及时调整教学方法；2. 拓展延伸：针对学有余力的学生，设计一些拓展题，提高学生的数学素养。

如：（1）有理数的乘方运算；（2）整式的乘法运算；（3）一元一次方程的整数解、分数解；（4）不等式与不等式组的整数解、分数解。

《初中数学几何模型------“手拉手”模型》教学设计教学目标：1.了解并熟悉“手拉手”模型，掌握基本特征。

2.借助“手拉手”模型，利用旋转有关知识解决相关问题。

3.通过小组合作学习，培养学生的合作意识，从中体验到学数学的快乐。

教学重难点：1.能熟练的找出“手拉手”模型，并能解决问题。

2.掌握“手拉手”模型的方法。

教学方法：探究发现法，鼓励学生自主学习。

课前准备：多媒体课件，几何画板教学过程：本节课贯穿四个问题“为什么”、“是什么”、“怎么做”、“注意什么”【设计意图】对本节内容的梳理，引起学生的好奇心与求知欲。

一．“为什么”模型可以让学生更快的进入到几何之中，产生兴趣,也是学习初中几何不可或缺的一种重要方法。

其中一种经典的几何模型---“手拉手”模型，这也是历年数学中考常考的几何压轴题型之一。

【设计意图】研究近几年中考题，发现“手拉手”模型是一个重要的考点，通过本节课的设计能帮助学生建立良好的解题思路，克服做题时的恐惧和盲目心理。

二．“是什么”“手拉手”模型的概念1.“手”的判别判断左右：将等腰三角形顶角顶点朝上，正对读者，读者左边为左手顶点，右边为右手顶点。

2、手拉手模型的定义：定义: 两个顶角相等且有共顶点的等腰三角形形成的图形。

（左手拉左手，右手拉右手）【设计意图】通过“手拉手”模型的概念，能让学生认识基本图型。

三．“怎么做”（一）知识应用（直击中考）如图1，在Rt ABC ∆中，90A ∠=︒，AB AC =，点D ，E 分别在边AB ，AC 上，AD AE =，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点.（1）观察猜想图1中，线段PM 与PN 的数量关系是 ，位置关系是 ；（2）探究证明把ADE ∆绕点A 逆时针方向旋转到图2的位置，连接MN ，BD ，CE ，判断PMN ∆的形状，并说明理由；（3）拓展延伸把ADE ∆绕点A 在平面内自由旋转，若4AD =，10AB =，请直接写出PMN ∆面积的最大值.（二）．巩固提升在矩形ABCD 中 ，AB=6，AD=8.E ，F 分别为AB ，AD 边的中点，四边形AEGF 为矩形，连接CG（1） 请直接写出CG 的长是（2） 如图2，当矩形AEGF 绕点A 旋转（比如顺时针旋转）至点G 落在边AB 上时，请计算DF 与CG 的长，通过计算试猜想DF 与CG 之间的数量关系。

《数学建模》课程教案一、教学内容本节课的教学内容选自《数学建模》教材的第五章，主要内容包括线性规划模型的建立、图与网络模型的建立、整数规划模型的建立以及非线性规划模型的建立。

通过本节课的学习，使学生掌握数学建模的基本方法和技巧，培养学生解决实际问题的能力。

二、教学目标1. 让学生掌握线性规划、图与网络、整数规划和非线性规划模型的建立方法。

2. 培养学生运用数学知识解决实际问题的能力。

3. 提高学生的团队协作能力和创新意识。

三、教学难点与重点1. 教学难点：线性规划、图与网络、整数规划和非线性规划模型的建立及求解。

2. 教学重点：线性规划模型的建立和求解。

四、教具与学具准备1. 教具：多媒体教学设备、黑板、粉笔。

2. 学具：教材、笔记本、文具。

五、教学过程1. 实践情景引入：以一个工厂生产安排的问题为例，引入线性规划模型的建立和求解。

2. 知识点讲解：（1）线性规划模型的建立：讲解目标函数的设定、约束条件的确定以及线性规划模型的标准形式。

（2）图与网络模型的建立：讲解图的概念、图的表示方法以及网络模型的建立。

（3）整数规划模型的建立：讲解整数规划的概念和建立方法。

（4）非线性规划模型的建立：讲解非线性规划的概念和建立方法。

3. 例题讲解：选取具有代表性的例题，讲解模型建立和求解的过程。

4. 随堂练习：让学生分组讨论并解决实际问题，巩固所学知识。

六、板书设计板书设计如下：1. 线性规划模型：目标函数约束条件标准形式2. 图与网络模型：图的概念图的表示方法网络模型的建立3. 整数规划模型：整数规划的概念整数规划的建立方法4. 非线性规划模型：非线性规划的概念非线性规划的建立方法七、作业设计1. 作业题目：（1）根据给定的条件，建立线性规划模型，并求解。

（2）根据给定的条件，建立图与网络模型，并求解。

（3）根据给定的条件，建立整数规划模型，并求解。

（4）根据给定的条件，建立非线性规划模型，并求解。

2. 答案：（1）线性规划模型的目标函数为：Z = 2x + 3y，约束条件为：x + y ≤ 6，2x + y ≤ 8，x ≥ 0，y ≥ 0。

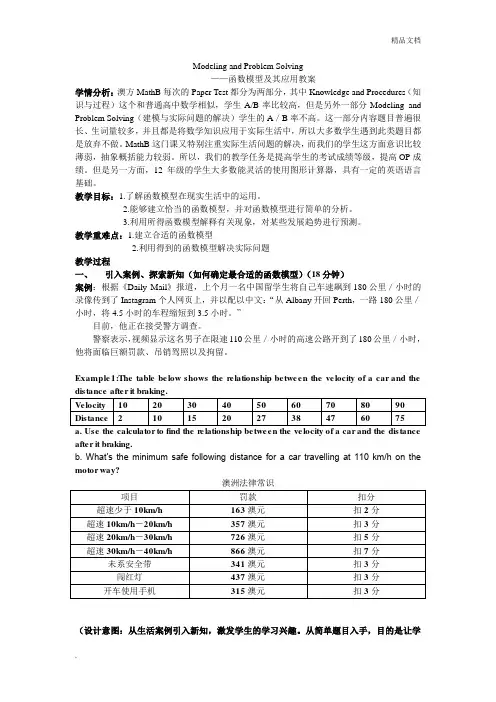
Modeling and Problem Solving——函数模型及其应用教案学情分析：澳方MathB每次的Paper Test都分为两部分，其中Knowledge and Procedures（知识与过程）这个和普通高中数学相似，学生A/B率比较高，但是另外一部分Modeling and Problem Solving（建模与实际问题的解决）学生的A／B率不高。

这一部分内容题目普遍很长、生词量较多，并且都是将数学知识应用于实际生活中，所以大多数学生遇到此类题目都是放弃不做。

MathB这门课又特别注重实际生活问题的解决，而我们的学生这方面意识比较薄弱，抽象概括能力较弱。

所以，我们的教学任务是提高学生的考试成绩等级，提高OP成绩。

但是另一方面，12年级的学生大多数能灵活的使用图形计算器，具有一定的英语语言基础。

教学目标：1.了解函数模型在现实生活中的运用。

2.能够建立恰当的函数模型，并对函数模型进行简单的分析。

3.利用所得函数模型解释有关现象，对某些发展趋势进行预测。

教学重难点：1.建立合适的函数模型2.利用得到的函数模型解决实际问题教学过程一、引入案例、探索新知（如何确定最合适的函数模型）（18分钟）案例：根据《Daily Mail》报道，上个月一名中国留学生将自己车速飙到180公里／小时的录像传到了Instagram个人网页上，并以配以中文：“从Albany开回Perth，一路180公里／小时，将4.5小时的车程缩短到3.5小时。

”目前，他正在接受警方调查。

警察表示，视频显示这名男子在限速110公里／小时的高速公路开到了180公里／小时，他将面临巨额罚款、吊销驾照以及拘留。

Example1:The table below shows the relationship between the velocity of a car and thea. Use the calculator to find the relationship between the velocity of a car and the distance after it braking.b. What’s the minimum safe following distance for a car travelling at 110 km/h on the motor way?澳洲法律常识（设计意图：从生活案例引入新知，激发学生的学习兴趣。

九年级数学下册电子版教案（人教版）一、教学目标1. 知识与技能：（1）能理解并掌握电子版的制作方法和技巧。

（2）能熟练运用电子版进行数学题目的解答和分析。

（3）能运用电子版进行数学知识的探索和研究。

2. 过程与方法：（1）通过自主学习，掌握电子版的操作方法和技巧。

（2）通过合作学习，提高运用电子版解决数学问题的能力。

（3）通过研究性学习，培养运用电子版进行数学探索和研究的能力。

3. 情感态度与价值观：（1）培养对数学学习的兴趣和热情。

（2）培养运用现代技术手段进行学习的习惯。

（3）培养团队协作和自主探究的精神。

二、教学内容第一章：电子版的初步使用1. 电子版的启动与退出2. 电子版的界面认识3. 电子版的文件操作第二章：电子版的编辑技巧1. 文字的输入与编辑2. 公式的输入与编辑3. 图片的插入与处理第三章：电子版的解题方法1. 运用电子版进行几何题目的解答2. 运用电子版进行代数题目的解答3. 运用电子版进行概率题目的解答第四章：电子版的探索与研究1. 运用电子版进行数学知识的探索2. 运用电子版进行数学问题的研究3. 运用电子版进行数学实验的设计与实施第五章：电子版的合作学习1. 运用电子版进行数学小组合作学习2. 运用电子版进行数学课题的研究3. 运用电子版进行数学成果的展示与评价三、教学重点与难点1. 教学重点：（1）电子版的操作方法和技巧。

（2）运用电子版进行数学题目的解答和分析。

（3）运用电子版进行数学知识的探索和研究。

2. 教学难点：（1）电子版的深入运用和操作。

（2）运用电子版解决较复杂的数学问题。

（3）运用电子版进行数学探索和研究。

四、教学方法与手段1. 教学方法：（1）任务驱动法：通过设置具体任务，引导学生自主学习电子版的操作方法和技巧。

（2）合作学习法：通过小组合作，提高学生运用电子版解决数学问题的能力。

（3）研究性学习法：引导学生运用电子版进行数学知识的探索和研究。

2. 教学手段：（1）电子版的操作演示。

引言欢迎同学们选修“数学建模”公选课！一、什么是数学：1、定义数学是研究现实世界的数量关系和空间形式的科学。

即研究“数”和“形”的科学（恩格斯）数学经过长期的发展和不断完善，现代数学不仅研究具体的数量关系和空间形式，而且“数”和“形”的概念已发展到很高的境地：，如非“数”之“数”的众多代数结构（群、环、域……）,无形之“形”的大量抽象空间（线性空间，拓扑空间……）。

因此，数学研究现实世界的任何关系和形式，数学还研究在逻辑上可能的关系和形式（数理逻辑），当今若还用过去意义下的数量关系和空间形式来理解数学，已远不能反映该学科的实质，更确切一点说法应该是：数学是研究各种抽象的“数”和“形”的模式结构的科学。

2、数学的特点高度的抽象性严谨的逻辑性广泛的应用性3、数学科学的地位目前学术界认可的观点是，科学分为如下三类：自然科学、社会科学、数学科学。

当今高科技时代，自然科学和社会科学各领域的研究进入到更深的层次和更广的范畴，在这些研究中数学的运用往往是实质性的，数学与自然科学和社会科学的关系从来没有像今天这样密切，数学在自然科学和社会科学中的渗透和应用日益广泛。

·当代自然科学的研究正在日益呈现出数学化趋势（美国自然科学基金会）；·计算机的发明和广泛应用以数学为基础；·信息技术已被广泛应用于方方面面（医学的CT技术、印刷排版自动化、飞行器模拟设计、指纹识别、石油地震勘探数据处理、信息安全……）本质上是一种数学技术；·用数学模型研究宏观经济和微观经济；·用数学手段进行社会和市场调查与预测；·用数学理论进行风险分析、指导金融投资；……·诺贝尔经济学奖的获得者中，数学家和有数学研究经历的经济学家占半数以上；4、数学教育的作用数学是人类社会进步的产物，也是推动社会发展的动力。

数学与人类文明、人类文化有着密切关系，在人类文明的进步和发展中一直在文化层面上发挥着重要的作用，主要体现在以下三个方面：·数学不仅是一种工具或方法，也是一种思维模式——数学方式的理性思维；·数学不仅是一门科学，也是一种文化——数学文化；·数学不仅是一些知识，也是一种素质——数学素质。

2.2 建立概率模型整体设计教学分析本节教材通过例2的四种模型的所有可能结果数越来越少，调动起学生思考探究的兴趣；教师在教学中要注意通过引导学生体会不同模型的特点以及对各种方法进行比较，提高学生分析和解决问题的能力.三维目标1.使学生能建立概率模型来解决简单的实际问题，提高学生分析问题和解决问题的能力.2.通过学习建立概率模型，培养学生的应用能力.重点难点教学重点：建立古典概型.教学难点：建立古典概型.课时安排1课时教学过程导入新课思路1.计算事件发生概率的大小时，要建立概率模型，把什么看成一个基本事件是人为规定的.今天我们学习如何建立概率模型，教师点出课题.思路2.解决实际应用问题时，要转化为数学问题来解决，即建立数学模型，这是高中数学的重点内容之一，也是高考的必考内容，同样解决概率问题也要建立概率模型，教师点出课题.推进新课新知探究提出问题1.回顾解应用题的步骤？2.什么样的概率属于古典概型？讨论结果：1.解应用题的一般程序：①读：阅读理解文字表达的题意，分清条件和结论，理顺数量关系，这一关是基础.②建：将文字语言转化为数学语言，利用数学知识，建立相应的数学模型.熟悉基本数学模型，正确进行建“模”是关键的一关.③解：求解数学模型，得到数学结论.一要充分注意数学模型中元素的实际意义，更要注意巧思妙作，优化过程.④答：将数学结论还原给实际问题的结果.2.同时满足以下两个条件的概率属于古典概型：①试验的所有基本事件只有有限个，每次试验只出现其中一个基本事件；②每一次试验中，每个基本事件出现的可能性相等.应用示例思路1例1 口袋里装有2个白球和2个黑球,这4个球除颜色外完全相同,4个人按顺序依次从中摸出一球.试计算第二个人摸到白球的概率.分析：我们只需找出4个人按顺序依次摸球的所有可能结果数和第二个人摸到白球的可能结果数.为此考虑用列举法列出所有可能结果.解法一：用A 表示事件“第二个人摸到白球”.把2个白球编上序号1,2;2个黑球也编上序号1,2.于是,4个人按顺序依次从袋中摸出一球的所有可能结果,可用树状图直观地表示出来(如图1).图1树状图是进行列举的一种常用方法.从上面的树状图可以看出,试验的所有可能结果数为24.由于口袋内的4个球除颜色外完全相同,因此,这24种结果的出现是等可能的,试验属于古典概型.在这24种结果中,第二个人摸到白球的结果有12种,因此“第二个人摸到白球”的概率P(A)=2412=21, 这与第一节的模拟结果是一致的.还可以建立另外的模型来计算“第二个人摸到白球”的概率.如果建立的模型能使得试验的所有可能结果数变少,那么我们计算起来就更简便.解法二：因为是计算“第二个人摸到白球”的概率,所以我们可以只考虑前两人摸球的情况.前两人依次从袋中摸出一球的所有可能结果可用树状图列举出来(如图2).图2从上面的树状图可以看出,这个模型的所有可能结果数为12,因为口袋里的4个球除颜色外完全相同,因此,这12种结果的出现是等可能的,这个模型也是古典概型.在上面12种结果中,第二个人摸到白球的结果有6种,因此“第二个人摸到白球”的概率P(A)=126=21. 这里,我们是根据事件“第二个人摸到白球”的特点,利用试验结果的对称性,只考虑前两人摸球的情况,从而简化了模型.还可以从另外一个角度来考虑这个问题.因为口袋里的4个球除颜色外完全相同,因此,可以对2个白球不加区别,对2个黑球也不加区别,这样建立的模型的所有可能结果数就会更少,由此得到例2的另一种解法.解法三：只考虑球的颜色,4个人按顺序依次从袋中摸出一球的所有可能结果可用树状图列举出来(如图3).图3试验的所有可能结果数为6,并且这6种结果的出现是等可能的,这个模型是古典概型.在这6种结果中,第二个人摸到白球的结果有3种,因此“第二个人摸到白球”的概率P(A)=63=21. 下面再给出一种更为简单的解法.解法四：只考虑第二个人摸出的球的情况,他可能摸到这4个球中的任何一个,这4种结果出现的可能性是相同的.第二个人摸到白球的结果有2种,因此“第二个人摸到白球”的概率P(A)=42=21. 点评：画树状图进行列举是计算结果个数的基本方法之一.解法一利用树状图列出了4个人依次从袋中摸出一球的所有可能结果，共有24种，其中第二个人摸到白球的结果有12种，因此算得“第二个人摸到白球”的概率为21. 解法二利用试验结果的对称性，只考虑前两人摸球的情况，所有可能结果减少为12种，简化了模型.解法三只考虑球的颜色，对2个白球不加区别，对2个黑球也不加区别，所有可能结果只有6种.解法四只考虑第二个人摸出的球的情况，所有可能结果变为4种，这个模型最简单.尽管解法二,三,四建立的模型在解决该问题时比解法一简便，但解法一也有它的优势，利用解法一可以计算出4个人顺次摸球的任何一个事件的概率，而解法二,三,四却不能做到.教师要提醒学生，本章古典概率的计算，解法一是最基本的方法.对于一个实际问题，有时从不同的角度考虑，可以建立不同的古典概型来解决.变式训练小明和小刚正在做掷骰子游戏，两人各掷一枚骰子，当两枚骰子点数之和为奇数时，小刚得1分，否则小明得1分.这个游戏公平吗？分析：计算双方获胜的概率，来判断游戏是否公平.解：设(x,y)表示小明抛掷骰子点数是x ，小刚抛掷骰子点数是y ，则该概率属于古典概型.所有的基本事件是：(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3), (4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3), (6,4),(6,5),(6,6),即有36种基本事件.其中点数之和为奇数的基本事件有：(1,2),(1,4),(1,6),(2,1),(2,3),(2,5),(3,2),(3,4),(3,6),(4,1),(4,3),(4,5),(5,2),(5,4),(5,6),(6,1),(6,3),(6,5).即有18种.所以小刚得1分的概率是3618=21. 则小明得1分的概率是1-21=21. 则小明获胜的概率与小刚获胜的概率相同，游戏公平.思路2例1 （2007广东高考,文8）在一个袋子中装有分别标注数字1，2，3，4，5的五个小球，这些小球除标注的数字外完全相同.现从中随机取出2个小球，则取出的小球标注的数字之和为3或6的概率是( ) A.103 B.51 C.101 D.121 分析：用(x,y)(x≠y)表示从这5个球中随机取出2个小球上数字的结果，其结果有： (1，2)、(1，3)、(1，4)、(1，5)、(2，3)、(2，4)、(2，5)、(3，4)、(3，5)、(4，5)，即共有10种，取出的小球标注的数字之和为3或6的结果有：(1，2)、(1，5)、(2，4)，共有3种，所以取出的小球标注的数字之和为3或6的概率为P(A)= 103. 答案：A点评：求古典概型的概率的步骤：①利用枚举法计算基本事件的总数;②利用枚举法计算所求事件所含基本事件的个数;③代入古典概型的概率计算公式求得.变式训练1.（2007全国高考卷Ⅰ,文13）从某自动包装机包装的食盐中，随机抽取20袋，测得各袋的质量分别为(单位：g)：该自动包装机包装的食盐质量在497.5 g —501.5 g 之间的概率约为___________.分析：观察表格可得在497.5 g —501.5 g 之间的食盐有：498，501，500，501，499共5袋，则食盐质量在497.5 g —501.5 g 之间的概率P(A)=205=0.25. 答案：0.252.某校要从高一、高二、高三共2 007名学生中选取50名组成访问团，若采用下面的方法选取：先用分层抽样的方法从2 007人中剔除7人，剩下的2 000人再按简单随机抽样的方法进行，则每人入选的概率( ) A.不全相等 B.均不相等C.都相等且为200750D.都相等且为401 分析：按分层抽样抽取样本时，每个个体被抽到的概率是相等的，都等于200750. 答案：C知能训练1.袋中有4个红球，5个白球，2个黑球，从里面任意摸2个小球，不是基本事件.( )A.｛正好2个红球｝B.｛正好2个黑球｝C.｛正好2个白球｝D.｛至少一个红球｝分析：至少一个红球包含：一红一白或一红一黑或2个红球，所以｛至少一个红球｝不是基本事件，其他事件都是基本事件.答案：D2.抛掷一枚质地均匀的硬币，如果连续抛掷10 000次，那么第9 999次出现正面朝上的概率是( )A.99991B.100001C.100009999D.21 答案：D3.有4条线段,长度分别为1、3、5、7,从这四条线段中任取三条,则所取三条线段能够成一个三角形的概率是( )A.41B.31C.21D.52 答案：A4.（2007全国高考卷Ⅱ,文13）一个总体含有100个个体，以简单随机抽样方式从该总体中抽取一个容量为5的样本，则指定的某个个体被抽到的概率为____________.分析：按简单随机抽样抽取样本时，每个个体被抽到的概率是相等的，都等于1005,即201. 答案：201 5.某小组有5名女生，3名男生，现从这个小组中任意选出一名组长，则其中一名女生小丽当选为组长的概率是__________.答案：81 6.袋中有6个球，其中4个白球，2个红球，从袋中任意取出两球，求下列事件的概率：(1)事件A ：取出的两球都是白球；(2)事件B ：取出1个是白球，另1个是红球.分析：首先应求出任取两球的基本事件的总数，然后需分别求出事件A 的个数和事件B 的个数，运用公式求解即可.解：设4个白球的编号为1，2，3，4，两个红球的编号为5，6.从袋中的6个小球中任取两个的基本事件有：(1，2)，(1，3)，(1，4)，(1，5)，(1，6)，(2，3)，(2，4)，(2，5)，(2，6)，(3，4)，(3，5)，(3，6)，(4，5)，(4，6)，(5，6)共15个.(1)取出的全是白球的基本事件，共有6个，即为(1，2)，(1，3)，(1，4)， (2，3)，(2，4)，(3，4)，∴取出的两个球都是白球的概率为P(A)=156. (2)取出一个红球，而另一个为白球的基本事件，共有8个，即为(1，5)，(1，6)， (2，5)，(2，6)， (3，5)，(3，6)， (4，5)，(4，6),∴取出的两个球一个是白球，另一个是红球的概率为P(B)=158. 拓展提升1.连续掷两次骰子，以先后得到的点数m,n 为点P(m,n)的坐标，设圆Q 的方程为x 2+y 2=17.(1)求点P 在圆Q 上的概率；(2)求点P 在圆Q 外部的概率.解：m 的值的所有可能是1，2，3，4，5，6，n 的值的所有可能是1，2，3，4，5，6，所以,点P(m ，n)的所有可能情况有6×6=36种，且每一种可能出现的可能性相等，本问题属古典概型问题.(1)点P 在圆Q 上只有P(1,4)，P(4,1)两种情况，根据古典概型公式，点P 在圆Q 上的概率为181362=. (2)点P 在圆Q 内的坐标是：(1,1)，(1,2)，(1,3)，(2,1)，(2,2)，(2,3)，(3,1)，(3,2),共有8点，所以点P 在圆Q 外部的概率为1-18133682=+. 2.将一枚质地均匀的硬币连续投掷3次，求以下事件的概率：(1)3次正面向上;(2)2次正面向上,1次反面向上.解：(1)将一枚质地均匀的硬币连续投掷3次的基本事件总数为8,又事件“3次正面向上”共有基本事件数为1,设事件“3次正面向上”为A, ∴P(A)=81. ∴事件“3次正面向上”发生的概率为81. (2)又事件“2次正面向上，1次反面向上”共有基本事件数为3,设事件“2次正面向上，1次反面向上”为B,∴P(B)=83. ∴事件“2次正面向上，一次反面向上”发生的概率为83. 课堂小结本节课学习了同一个古典概型的概率计算问题，可以建立不同的概率模型来解决. 作业习题3－2 A 组 7、8.设计感想本节教学设计过程中，注重培养学生的应用能力，以及古典概型的计算方法.在实际教学过程中，教师要根据学生的实际，重点指导学生如何建立古典概型.。

3.2.4 函数模型的应用实例（二）（一）教学目标1．知识与技能掌握应用指数型，拟合型函数模型解答实际应用问题的题型特征，提升学生解决简单的实际应用问题的能力.2．过程与方法经历实际应用问题的求解过程，体验指数函数模型、拟合函数模型的题型特征，学会运用函数知识解决实际问题.3．情感、态度与价值观了解数学知识来源于生活，又服务于实际，从而培养学生的数学应用意识，提高学生学习数学的兴趣.（二）教学重点与难点重点：指数函数模型、拟合函数模型的应用难点：依据题设情境，建立函数模型.（三）教学方法师生合作探究解题方法，总结解题规律.老师启发诱导，学生动手尝试相结合.从而形式应用指数函数模型，似合函数模型解决实际问题的技能.（四）教学过程教学环节教学内容师生互动设计意图例1某桶装水经营部每天的房租、人员工资等固定成本为200元，每桶水的进价是5元.销售单价与日均销售量的关系如表所示：销售单价/元6789师生合作回顾一元一次函数，一元二次函数.分段函数建模实际问题的求解思路“审、建、解、检”生：尝试解答例1解：根据表，销售单价每日均销售量/桶480440400360销售单价/元101112日均销售量/桶320280240请据以上数据作出分析，这个经营部怎样定价才能获得最大利润？增加1元，日均销售量就减少40桶.设在进价基础上增加x元后，日均销售利润为y元，而在此情况下的日均销售量就为480–40(x–1)=520–40x(桶)由于x＞0且520–40x＞0，即0＜x＜13，于是可得y=(520–40x)x–200= –40x2+520x–200，0＜x＜13易知，当x=6.5时，y有最大值.所以，只需将销售单价定为11.5元，就可获得最大的利润.师：帮助课本剖析解答过程，回顾反思上节课的学习成果4．指数型函数模型的应用例1人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律，可以为有效控制人口增长提供依据.早在1798年，英国经济学家马尔萨斯(T.R.Malthus,1766—1834)就提出了自然状态下的人口增长模型：y=y0e rt，其中t表示经过的时间，y0表示t=0时的人口数，r表示人口的年平均增长率.下表是1950~1959年我国的人口数据资料：年份19501951195219531954人数/万人5519656300574825879660266年份19551956195719581959人数/万人6145662828645636599467207（1）如果以各年人口增长率的平均值作为我国这一时期的人口增长率（精确到0.0001），用马尔萨斯人口增长师：形如y=ba cx函数为指数型函数，生产生活中以此函数构建模型的实例很多（如例1）生：在老师的引导下审题、建模、求解、检验、尝试完成此例师生合作总结解答思路及题型特征师生：共同完成例1 解答：（1）设1951~1959年的人口增长率分别为r1，r2，…，r9.由55196(1 + r1) = 56300，可得1951年的人口增长率r1≈0.0200.同理可得，r2≈0.0210，r3≈0.0229，r4≈0.0250，r5≈0.0197，r6≈0.0223，r7≈0.0276，r8≈0.0222，r9≈0.0184.模型建立我国在这一时期的具体人口增长模型，并检验所得模型与实际人口数据是否相符；（2）如果按表的增长趋势，大约在哪一年我国的人口达到13亿？例2某地区不同身高的未成年男性的体重平均值如表身高/cm 60708090100110体重/kg 6.137.909.9012.1515.0217.50身高/cm 120130140150160170体重/kg 20.9226.8631.1138.8547.2555.05（1）根据表提供的数据，能否建立恰当的函数模型，使它能比较近似地反映这个地区未成年男性体重y kg 与身高x cm 的函数关系？试写出这个函数模型的解析式.（2）若体重超过相同身高男性体重平均值的1.2倍为偏胖，低于0.8倍为偏瘦，那么这个地区一名身高为175cm ，体重为78kg 的在校男生的体重是否正常？例2 解答：（1）以身高为横坐标，体重为纵坐标，画出散点图.根据点的分布特征，可考虑以y =a ·b x 作为刻画这个地区未成年男性的体重与身高关系的函数模型.如果取其中的两组数据(70，7.90)，(160，47.25)，代入y =a ·b x 得：701607.947.25a b a b⎧=⋅⎪⎨=⋅⎪⎩，用计算器算得a ≈2，b ≈1.02.这样，我们就得到一个函数模型：y =2×1.02x .将已知数据代入上述函数解析式，或作出上述函数的图象，可以发现，这个函数模型与已知数据的拟合程度较好，这说明它能较好地反映这个地区未成年男性体重与身高的关于是，1951~1959年期间，我国人口的年均增长率为r (r 1+r 2+…+r 9)÷9≈0.0221.令y -0=55196，则我国在1950~1959年期间的人口增长模型为y =55196e 0.0221t ，t ∈N .根据表中的数据作出散点图并作出函数y =55196e 0.0221t (t ∈N )的图象由图可以看出，所得模型与1950~1959年的实际人口数据基本吻合.（2）将y =130000代入y =55196e 0.0221t ，由计算器可得t ≈38.76.所以，如果按表的增长趋势，那么大约在1950年后的第39年（即1989年）我国的人口就已达到13亿.由此可以看到，如果不实行计划生育，而是让人口自然增长，今天我国将面临难以承受的人口压力.系.（2）将x=175代入y=2×1.02x得y=2×1. 02175，由计算器算得y≈63.98.由于78÷63.98≈1.22＞1.2，所以，这个男生偏胖.归纳总结：通过建立函数模型，解决实际实际问题的基本过程：巩固练习练习1已知1650年世界人口为5亿，当时人口的年增长率为0.3%；1970年世界人口为36亿，当时人口的年增长率为2.1%.（1）用马尔萨斯人口模型计算，什么时候世界人口是1650年的2倍？什么时候世界人口是1970年的2倍？（2）实际上，1850年以前世界人口就超过了10亿；而2003年世界人口还没有达到72亿.你对同样的模型得出的两个结果有何看法？解答：（1）已知人口模型为y = y0e n，其中y0表示t=0时的人口数，r表示人口的年增长率.若按1650年世界人口5亿，年增长率为0.3%估计，有y = 5e0.003t.当y = 10时，解得t≈231.所以，1881年世界人口约为1650年的2倍.同理可知，2003年世界人口数约为1970年的2倍.（2）由此看出，此模型不太适宜估计跨度时间非常大的人口增长情况.固化能力强化技巧4．拟合函数模型例3某皮鞋厂从今年1月份开始投产，并且前4个月的产量分别为1万双，1.2万双，1.3万双，1.37万双.由于产品质量好，款式新颖，前几个月的销售生：动手实践解题此例学生四个代表分别板书四种函数模型.师：点评学生解答，总结，回答问题解析：本题是通过数据验（2）画散点图.（3）确定函数模型.甲：y 1= –x 2 +12x +41，乙：y 2 = –52.07×0.778x + 92.5（4）做出函数图象进行比较.计算x = 6时，y 1 = 77，y 2 = 80.9.可见，乙选择的模型较好.归纳总结1．数学模型所谓数学模型是指对客观实际的特征或数量关系进行抽象概括，用形式化的数学语言表述的一种数学结构.数学模型剔除了事物中一切与研究目标无本质联系的各种属性，在纯粹状态下研究数量关系和空间形式，函数就是最重要的数学模型，用函数解决方程问题，使求解变得容易进行，这是数学模型间的相互转换在发挥作用.而用函数解决实际问题，则体现了数学模型是联系数学与现实世界的桥梁.2．关于数学建模中的假设就一般的数学建模来说，是离不开假设的，如果在问题的原始状态下不作任何假设，将所有的变化因素全部考虑进去，对于稍复杂一点的师生合作交流归纳知识，整合解题体会整合理论培养学习能问题就无法下手了.假设的作用主要表现在以下几个方面：（1）进一步明确模型中需要考虑的因素和它们在问题中的作用.通常，初步接触一个问题，会觉得围绕它的因素非常多，经仔细分析筛查，发现有的因素并无实质联系，有的因素是无关紧要的，排除这些因素，问题则越发清晰明朗.在假设时就可以设这些因素不需考虑.（2）降低解题难度.由于每一个解题者的能力不同，经过适当的假设就可以有能力建立数学模型，并且得到相应的解.一般情况下，是先在最简单的情形下组建模型，然后通过不断地调整假设使模型尽可能地接近实际，得到更满意的解.课后练习 3.2 第四课时习案学生独立完成固化知识提高能力。

数学建模教案设计第一章：数学建模概述1.1 数学建模的定义与意义1.2 数学建模的基本步骤1.3 数学建模的应用领域1.4 数学建模的方法与技巧第二章：数学建模的基本技能2.1 数学符号与表达式的运用2.2 数学模型的构建与分析2.3 数学模型的求解与验证2.4 数学建模软件的使用第三章：数学建模实例解析3.1 线性规划问题3.2 微分方程问题3.3 概率论与统计问题3.4 网络优化问题第四章：数学建模竞赛与实践4.1 数学建模竞赛简介4.2 数学建模竞赛的准备与策略4.3 数学建模竞赛案例分析4.4 数学建模实践活动的组织与实施第五章：数学建模在实际问题中的应用5.1 数学建模在经济学中的应用5.2 数学建模在工程问题中的应用5.3 数学建模在生物学中的应用5.4 数学建模在其他领域中的应用第六章：数学建模中的数学方法6.1 初等数学方法6.2 微分方程方法6.3 差分方程方法6.4 概率论与数理统计方法第七章：数学建模中的模型构建7.1 连续模型7.2 离散模型7.3 随机模型7.4 混合模型第八章：数学建模中的数据分析8.1 数据整理与描述8.2 数据分析方法8.3 数据可视化8.4 模型验证与拟合第九章：数学建模软件与应用9.1 MATLAB 在数学建模中的应用9.2 Python 在数学建模中的应用9.3 R 在数学建模中的应用9.4 其他数学建模软件简介第十章：数学建模竞赛案例解析10.1 国内外数学建模竞赛简介10.2 数学建模竞赛题目类型与解题策略10.3 数学建模竞赛案例分析10.4 数学建模竞赛经验分享与启示第十一章：数学建模在自然科学中的应用11.1 物理学中的数学建模11.2 化学中的数学建模11.3 生物学中的数学建模11.4 地球科学中的数学建模第十二章：数学建模在社会科学与人文学科中的应用12.1 经济学中的数学建模12.2 政治学中的数学建模12.3 社会学中的数学建模12.4 人文学科中的数学建模第十三章：数学建模在工程技术中的应用13.1 电子与信息技术中的数学建模13.2 机械工程中的数学建模13.3 建筑学中的数学建模13.4 交通运输工程中的数学建模第十四章：数学建模在商业与管理中的应用14.1 运筹学中的数学建模14.2 金融学中的数学建模14.3 营销学中的数学建模14.4 管理科学中的数学建模第十五章：数学建模的挑战与发展趋势15.1 数学建模面临的挑战15.2 数学建模的新方法与新技术15.3 数学建模在跨学科研究中的应用15.4 数学建模的未来发展趋势重点和难点解析本文主要介绍了数学建模教案设计，包括数学建模的基本概念、方法、技巧以及在不同领域的应用。

教学设计一.教学目标：知识与技能：经历用数学眼光发现现实生活中的数学问题，尝试提出问题，并加以解决的全过程，体会模型思想，发展应用意识，提高实践能力，了解数学的价值.过程与方法：综合运用一元一次不等式与方程、一次函数的相关知识解决问题，体会三者之间的内在联系.情感态度与价值观：会反思参与活动的全过程，将研究的过程和结果形成结论并能进行交流，进一步积累数学活动经验.教学重点：根据情境提出问题并会运用一元一次不等式、一元一次方程与一次函数解决实际问题.教学难点：体会一元一次不等式与一元一次方程、一次函数之间的内在联系，形成对数学知识系统性的认识.二.教学设计思路和过程设计：（一）设计思路：到目前为止，学生已经学习了一元一次不等式、一元一次方程与一次函数，积累了一定的知识基础和活动经验，也初步发现了它们彼此之间的内在联系，但本综合与实践是以一种新的形式呈现，且教科书给出的任务比较宽泛，没有给定的背景，没有具体的安排，只是规定了一个大的方向：要求将一元一次方程、一元一次不等式和一次函数集体融入到一个问题情境.由于对多数同学来说，从事这样开放性比较强的综合与实践活动的经验可能还一些不足，因此，教师选取了生活中常见的相遇问题进行研究，给定学生一个情境，让学生自己提出问题并解答，同过三个问题的解决，让学生体会一次方程、一元一次不等式与一次函数的内在联系.最后学生自己总结，可以用“一次模型”解决的行程问题，必须是匀速的行程问题.（二）教学过程：【第一环节】创设情境，引出课题数学源于生活，我们学习数学是为了更好地服务于生活。

通过一个生活中常见的情境：A、B两地相距180千米，甲、乙两人分别从A、B 两地相向而行.假设他们始终保持匀速行驶.教师询问学生：接下来，甲乙两人会怎样？通过提问，让学生自己想象接下来会发生的情境.从而引出我们要研究的行程问题是相遇问题.然后教师继续提问，两人相遇的地点确定吗？一定是A、B两地的中点吗？让学生意识到相遇地点与他们各自的速度有关.然后，让学生根据情境自己提出问题.【第二环节】实践探究（一）——建立一元一次方程与一元一次不等式模型解决问题教师选取了几个有代表性的问题让学生解决：①经过多长时间两人相遇？②何时两人相距20千米？③何时两人相距小于20千米？学生在解决问题的过程中发现，情境中缺少甲、乙两人速度这个条件，通过添加条件，让学生自己画线段图解决问题.对于问题一，学生通过画线段图用算术法或列一元一次方程都可以解决，相遇的时间为x=3.6小时.对于问题二，学生借助线段图分析两人相距20千米会有两种情况，一种是相遇前两人相距20千米，一种是相遇后两人相距20千米，学生列一元一次方程可以求出相距20千米有两个答案x=3.2或x=4.第三个问题，何时两人相距小于20千米？学生通过线段图可以分析得到，从第一次相距20千米之后，两人距离越来越小，直到相遇时两人之间距离最小为0，随后两人之间距离逐渐拉大，直到再次相距20千米.所以，对于第三问，很多同学会直接写出答案3.24<<，然后由老师分析，这其实是一个不等式问x题，只要将两人之间的距离表示出来，然后让其小于20千米即可，通过列出的两个不等式并解答，发现最终答案确实是3.24<<.x【第三环节】实践探究（二）——建立一次函数模型解决问题教师总结，对于刚才的问题，我们借助线段图分析，运用一元一次方程和一元一次不等式可以解决，那么有没有更加直观的方法描述刚才的情境从而更直观的解决问题？让学生意识到，可以画函数图像.让学生小组活动，自己讨论如何画函数图像.学生能想到画出甲、乙两人到某地距离的函数图像：通过分析图像，分别求出两条函数图像的解析式，明确两个解析式中的k分别是甲、乙的速度.从而借助解析式，最终也是转化成一元一次方程或一元一次不等式解决刚才提出的三个问题，并且让学生明确两条图像的交点的含义，明确图像与坐标轴交点的含义.可以让学生再提出几个问题借助图像解决.个别小组想到，可以画出两人之间距离的函数图像：然后通过分析这个图像，求出这个图像各段的表达式，仍然可以解决刚才的问题.需要注意的是，这个图像的解析式在求解过程中，学生会遇到困难，例如图像的第一段，只知道一个点并不能求出函数解析式，需要引领学生分析，相遇问题两人之间距离的减少是两人共同运动造成的，类比第一个图像的斜率k分别是甲、乙两人的速度，可以得出此线段的斜率k是甲、乙两人的速度和，又因为y随x的增大而减小，所以k=-180,从而可以直接写出第一段的解析式为y=-50x+180.以此类推，可以得到后面两段的函数解析式.从而借助此图像，仍然可以解决刚才的问题.最后引导学生找到这两个图像之间的关系，让学生分别在两个图像中可以找到，表示两人相遇的点是哪个点，表示乙到达终点的点是哪个，表示甲到达终点的点是哪个.【第四环节】课堂小结，指导概括教师总结，通过图像，也就是“型”的角度，解决了数的问题，这就是“数形结合”的思想，鼓励学生在今后的学习中灵活运用这种思想.教师继续提问，为什么列出的方程和不等式一定是一元一次的？为什么画出的函数图像一定是一条直线？或者说，为什么函数关系一定是一次函数？学生通过讨论探究，发现只有是匀速运动才是一次的，是因为在整个过程中，速度不变，路程只和时间这一个变量有关，且路程随着时间的变化而均匀变化，所以，路程与时间的变化率不变，所以路程与时间的关系才一定是一次函数.回顾整个探究过程，可以得到，对于匀速的行程问题，我们可以用一元一次方程、一元一次不等式或者是一次函数去解决，那么这个过程就是在建立“一次模型”.然后鼓励学生，能否在匀速的追及问题中建立“一次模型”解决问题.【第五环节】随堂练习，跟踪检测例题：A、B两地相距50km，甲于某日下午13：00骑自行车从A地出发驶往B地，乙也于同日下午骑摩托车从A地出发驶往B地。

数学教案电子完整版一、教学内容本节课选自《高中数学》第二册第三章，具体内容为“复数及其四则运算”。

主要包括复数的定义、复数的几何意义、复数的四则运算及其性质。

二、教学目标1. 理解复数的定义，掌握复数的标准形式，能准确区分实数与复数。

2. 掌握复数的几何意义，能将复数与坐标系中的点对应起来。

3. 学会复数的四则运算，并能运用其解决实际问题。

三、教学难点与重点难点：复数的几何意义及其在坐标系中的应用。

重点：复数的定义、复数的四则运算及其性质。

四、教具与学具准备1. 教具：多媒体教学设备、坐标系图、复数运算示例。

2. 学具：练习本、笔。

五、教学过程1. 实践情景引入通过展示心电图、机械振动等实际例子，引导学生思考这些现象背后的数学模型。

2. 教学内容讲解（1）复数的定义：引导学生回顾实数的概念，进而引出复数的定义。

（2）复数的标准形式：讲解复数的代数表示方法，以及复数与实数的关系。

（3）复数的几何意义：将复数与坐标系中的点对应起来，解释复数的模长和幅角。

（4）复数的四则运算：讲解复数的加减乘除运算，并通过示例进行演示。

3. 例题讲解选取具有代表性的例题，讲解解题思路，引导学生运用复数的四则运算解决问题。

4. 随堂练习设计难易适中的练习题，让学生当堂巩固所学知识。

六、板书设计1. 复数的定义2. 复数的标准形式3. 复数的几何意义4. 复数的四则运算（1）加法和减法（2）乘法（3）除法5. 例题及解答七、作业设计1. 作业题目（1）计算下列复数的和、差、积、商：1+i, 32i; 2+3i, 4+5i; 1i, 2+i; 3+4i, 23i。

（2）已知复数z1=3+4i，z2=25i，求z1+z2, z1z2, z1z2,z1/z2。

（3）在坐标系中表示出复数1+2i, 34i, 1+3i。

（4）已知复数z满足|z1|<|z+1|，求复数z在复平面上的位置。

2. 答案（1）直接计算得出结果。

（2）z1+z2=5i；z1z2=1+9i；z1z2=2+23i；z1/z2=0.41.4i。