2018年高教社杯全国大学生数学建模竞赛
- 格式:doc
- 大小:1.67 MB
- 文档页数:1

2018年高教社杯数学建模C题Matlab一、背景介绍2018年高教社杯全国大学生数学建模竞赛是由我国高等教育学会主办的一项全国性学科竞赛。
该竞赛以促进大学生数学建模能力的培养和提高为宗旨,得到了全国各地高校的广泛参与和支持。
其中,C题是该竞赛中的一个重要环节,涉及使用Matlab进行数学建模,要求参赛选手具备一定的编程和数学建模能力。
二、竞赛题目2018年高教社杯数学建模C题的具体内容是基于某一物理问题,通过建立数学模型并利用Matlab编程分析解决相应问题。
题目要求参赛选手熟练掌握Matlab的基本语法和数学建模方法,能够灵活应用各种算法和技巧解决实际问题。
三、题目分析该竞赛题目所涉及的物理问题可能涉及到动力学、流体力学、热传导等多个领域,因此参赛选手需要具备较强的物理基础知识和数学建模能力。
利用Matlab进行编程要求选手具备一定的计算机编程基础和数值计算能力。
四、Matlab应用在解决数学建模问题时,Matlab是一种非常优秀的数学建模工具,它具有强大的数学计算能力和丰富的绘图函数,能够有效地帮助选手分析和解决复杂的数学问题。
Matlab还支持各种算法的实现和优化,能够帮助选手提高数学建模的效率和精度。
五、比赛经验共享参加2018年高教社杯数学建模C题的竞赛选手,可以共享自己在数学建模和Matlab编程过程中的经验和收获。
他们可以讲述自己在解题过程中所遇到的困难和挑战,以及如何克服这些困难,找到合适的解题方法。
他们可以展示自己对数学建模和Matlab编程的独特见解和理解,这对其他竞赛选手也是一种宝贵的学习和借鉴。
六、总结2018年高教社杯数学建模C题的竞赛不仅考察了选手在数学建模和Matlab编程方面的能力,还促进了选手之间的学习和交流。
通过共享各自的经验和思考,可以帮助选手更好地提高自己在数学建模和Matlab应用方面的能力,促进全国范围内大学生数学建模水平的提高。
这也为相关领域的研究和教育提供了一个重要的交流评台,促进了学术研究和创新成果的产生。

2018高教社杯数学建模一、引言数学建模是一项旨在解决实际问题的方法,广泛应用于科学研究、工程设计、经济管理等领域。
而在高教社杯数学建模竞赛中,参赛者必须运用数学方法和建模技巧,为给定的问题提供有效的解决方案。
本文将探讨2018年高教社杯数学建模竞赛的一些特点和赛题,以加深对此竞赛的理解。
二、竞赛概述2018年高教社杯数学建模竞赛是由中国高等教育社会科学规划研究会主办,旨在培养学生的数学建模能力和创新思维。
竞赛共分为两个阶段:预选赛和决赛。
预选赛的题目面向全国高校的本科生、硕士生和博士生,包含多个建模问题。
决赛的题目则是根据预选赛的成绩进行选拔,题目更加复杂,要求参赛选手深入研究问题,并给出全面的解决方案。
三、竞赛题目特点2018年高教社杯数学建模竞赛的题目在多个方面都展现了其独特特点。
1. 实际问题综合性竞赛题目通常会选取与实际生活紧密相关的问题,涉及多个学科领域。
这要求参赛选手具备跨学科的知识储备和综合运用的能力。
2. 问题难度递进竞赛中,问题往往设计了从简单到复杂的难度递进,给选手提供了不同层次的解题机会。
这种设置鼓励参赛选手根据自身实际情况选择适合的难度,展现个人水平。
3. 数据分析与模型构建竞赛题目通常会提供大量的数据,要求参赛选手进行数据的清理、整理和分析,建立与问题适配的数学模型。
这要求选手能够熟练运用数据处理和模型构建的技巧。
4. 解题方法多样性在竞赛的解答过程中,并非只有一种可行的解题方法。
相反,不同问题对应了不同的建模和求解方法,参赛选手可以选择不同的途径进行建模和求解,以展示个人的创新思维。
四、参赛者技巧指南参加2018年高教社杯数学建模竞赛需要具备一定的解题技巧和方法。
以下是一些参赛者应该注意的指南:1. 阅读题目与理解仔细阅读题目,理解问题要求。
将题目中的信息进行整理和分类,确保对问题有全面而准确的理解。
2. 分析问题特点在确定问题要求后,分析问题的特点和限制条件。
确定问题的关键因素和数量关系,并对不确定因素进行假设和简化,准确把握问题的本质。

2018高教社杯全国大学生数学建模竞赛D题评阅要点本要点仅供参考,各赛区评阅组应根据对题目的理解及学生的解答,自主地进行评阅。
简单来说,本问题是在满足品牌、配置、动力、驱动、颜色的装配要求下,完成车辆在总装线上的装配排序,且具有较低的生产成本。
这个问题属于混合模式组装线问题,同时也是NP难问题,除需要建立数学模型外,更重要的是设计出求解该问题的可行算法,针对附件中数据,给出排序结果。
问题1:建立数学模型或者设计算法,在满足装配要求的条件下,给出具有较低生产成本的装配顺序。
或许学生能够通过查找文献,建立出车辆装配排序的数学模型,但模型的求解也还是相当困难的。
就本问题而言,大部分学生可能就根本无法建立起完整的数学模型。
因此,在评阅中,更应注重学生在求解问题过程中的算法设计,例如,启发式算法,或者是按某种规则设计的求解方法等。
不必要求学生使用一个算法完成全部的计算工作。
学生可以由简入繁,由多个算法逐步完成题目的要求,也允许学生在某些点(少量的)使用手工计算。
问题2:根据问题1中的数学模型或算法,针对附件中的数据,给出相应的计算结果。
这个问题本质上是模型或算法的检验,看看学生是否能够按照自己设计的算法完成装配排序的工作,题目要求学生给出:20日的装配顺序(放在附录中)和一周(17日至23日)的装配顺序(放在支撑材料中)。
评阅教师可以根据学生的计算结果,特别是20日的计算结果,检查学生是否完成了题目的要求,可重点检查装配要求中的颜色、驱动和动力的满足情况。
在评阅中,特别注意20日白班与晚班、19日晚班与20日白班和20日晚班与21日白班之间排序结果在总装线和喷涂线上各项要求的满足情况。
评阅建议:1.如果学生只有简单的模型或简单的算法,并没有给出20日的装配顺序,可以考虑不获任何奖项;2.如果学生给出了模型或算法,并给出20日的装配顺序,其结果基本满足约束条件(允许有少量错误),可以考虑获省二等奖;3.如果学生对模型或算法有一定的描述,设计出的算法基本合理、有效,并给出20日和一周(17日至23日)的装配顺序,其结果基本满足约束条件,可以考虑获省一等奖;4.如果学生给出较完整的建模过程,且有较完整的算法设计过程,并给出20日和一周(17日至23日)的装配顺序,算法合理、有效,但有少量错误,可以考虑报送全国二等奖;5.如果学生给出完整的建模过程,且有完整的算法设计过程,并给出20日和一周(17日至23日)的装配顺序,算法合理、有效,特别考虑了相邻班次的车辆对总装线和喷涂线的各项要求,仅有个别错误,可以考虑报送全国一等奖。

2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)A题城市表层土壤重金属污染分析随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。
对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,日益成为人们关注的焦点。
按照功能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、……、5类区,不同的区域环境受人类活动影响的程度不同。
现对某城市城区土壤地质环境进行调查。
为此,将所考察的城区划分为间距1公里左右的网格子区域,按照每平方公里1个采样点对表层土<0~10 厘M深度)进行取样、编号,并用GPS记录采样点的位置。
应用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数据。
另一方面,按照2公里的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值。
附件1列出了采样点的位置、海拔高度及其所属功能区等信息,附件2列出了8种主要重金属元素在采样点处的浓度,附件3列出了8种主要重金属元素的背景值。
现要求你们通过数学建模来完成以下任务:(1> 给出8种主要重金属元素在该城区的空间分布,并分析该城区内不同区域重金属的污染程度。
(2> 通过数据分析,说明重金属污染的主要原因。
(3> 分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。
(4> 分析你所建立模型的优缺点,为更好地研究城市地质环境的演变模式,还应收集什么信息?有了这些信息,如何建立模型解决问题?题目A题城市表层土壤重金属污染分析摘要:本文研究的是某城区警车配置及巡逻方案的制定问题,建立了求解警车巡逻方案的模型,并在满足D1的条件下给出了巡逻效果最好的方案。
在设计整个区域配置最少巡逻车辆时,本文设计了算法1:先将道路离散化成近似均匀分布的节点,相邻两个节点之间的距离约等于一分钟巡逻路程。

2018年高教杯数学建模国赛c题附件摘要:一、2018 年高教杯数学建模国赛C 题背景及概述1.竞赛背景介绍2.C 题的题目和内容简介二、C 题的解题思路与方案1.问题重述与分析2.解题思路梳理3.具体方案与步骤三、C 题的建模与求解过程1.建立数学模型2.求解过程与方法3.结果分析与讨论四、C 题的优缺点与改进方向1.方案的优点2.方案的缺点3.改进方向与建议正文:2018 年高教杯数学建模国赛C 题的背景是关于一个投资项目的收益与风险分析。
题目中给出了一个投资项目的各项指标,要求参赛者通过建立数学模型,对该项目的投资收益和风险进行分析,并为投资者提供合理的投资建议。
一、2018 年高教杯数学建模国赛C 题背景及概述高教杯数学建模竞赛是我国面向本科生的一项重要赛事,旨在通过对现实问题进行抽象、建模和求解,培养学生的创新意识和实际问题解决能力。
2018 年的竞赛中,C 题涉及到一个投资项目的收益与风险分析,需要参赛者具备较强的数学建模和分析能力。
C 题的具体内容是:某投资者拟对一个项目进行投资,该项目预计在未来的n 年内,每年的收益分别为x1, x2, ..., xn。
同时,该项目的投资成本为c。
投资者的期望收益率为r,要求参赛者通过建立数学模型,分析该项目的投资收益和风险,并为投资者提供合理的投资建议。
二、C 题的解题思路与方案1.问题重述与分析首先,我们需要将题目中的实际问题转化为一个数学模型。
根据题目描述,我们可以将问题重述为:在未来的n 年内,如何分配投资金额,使得投资收益最大化,同时保证投资风险在可接受范围内?2.解题思路梳理为了解决这个问题,我们需要从两个方面进行考虑:一是如何合理分配投资金额,以实现收益最大化;二是如何控制投资风险,以保证投资者的期望收益率满足要求。
3.具体方案与步骤针对上述两个问题,我们可以采取以下步骤:(1) 对每年的收益进行预测,并计算出各年的收益概率分布。
(2) 建立数学模型,描述投资收益与投资风险之间的关系。

2018年高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
A题高温作业专用服装设计
在高温环境下工作时,人们需要穿着专用服装以避免灼伤。
专用服装通常由三层织物材料构成,记为I、II、III层,其中I层与外界环境接触,III层与皮肤之间还存在空隙,将此空隙记为IV层。
为设计专用服装,将体内温度控制在37ºC的假人放置在实验室的高温环境中,测量假人皮肤外侧的温度。
为了降低研发成本、缩短研发周期,请你们利用数学模型来确定假人皮肤外侧的温度变化情况,并解决以下问题:
(1)专用服装材料的某些参数值由附件1给出,对环境温度为75ºC、II层厚度为6 mm、IV层厚度为5 mm、工作时间为90分钟的情形开展实验,测量得到假人皮肤外侧的温度(见附件2)。
建立数学模型,计算温度分布,并生成温度分布的Excel文件(文件名为problem1.xlsx)。
(2) 当环境温度为65ºC、IV层的厚度为5.5 mm时,确定II层的最优厚度,确保工作60分钟时,假人皮肤外侧温度不超过47ºC,且超过44ºC的时间不超过5分钟。
(3) 当环境温度为80C 时,确定II层和IV层的最优厚度,确保工作30分钟时,假人皮肤外侧温度不超过47ºC,且超过44ºC的时间不超过5分钟。
附件1. 专用服装材料的参数值
附件2. 假人皮肤外侧的测量温度。

2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)A题车道被占用对城市道路通行能力地影响车道被占用是指因交通事故、路边停车、占道施工等因素,导致车道或道路横断面通行能力在单位时间内降低地现象.因为城市道路具有交通流密度大、连续性强等特点,一条车道被占用,也可能降低路段所有车道地通行能力,即使时间短,也可能引起车辆排队,出现交通阻塞.如处理不当,甚至出现区域性拥堵.车道被占用地情况种类繁多、复杂,正确估算车道被占用对城市道路通行能力地影响程度,将为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供理论依据.视频1<附件1)和视频2<附件2)中地两个交通事故处于同一路段地同一横断面,且完全占用两条车道.请研究以下问题:1.根据视频1<附件1),描述视频中交通事故发生至撤离期间,事故所处横断面实际通行能力地变化过程.根据问题1所得结论,结合视频2<附件2),分析说明同一横断面交通事故所占车道不同对该横断面实际通行能力影响地差异.构建数学模型,分析视频1<附件1)中交通事故所影响地路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间地关系.假如视频1<附件1)中地交通事故所处横断面距离上游路口变为140M,路段下游方向需求不变,路段上游车流量为1500pcu/h,事故发生时车辆初始排队长度为零,且事故持续不撤离.请估算,从事故发生开始,经过多长时间,车辆排队长度将到达上游路口.附件1:视频1附件2:视频2附件3:视频1中交通事故位置示意图附件4:上游路口交通组织方案图附件5:上游路口信号配时方案图注:只考虑四轮及以上机动车、电瓶车地交通流量,且换算成标准车当量数.附件3视频1中交通事故位置示意图附件4附件5上游路口信号配时方案本题附件1、2地数据量较大,请竞赛开始后从竞赛合作网站“中国大学生在线”网站下载:试卷专题页面:试卷下载地址:2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)B题碎纸片地拼接复原破碎文件地拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要地应用.传统上,拼接复原工作需由人工完成,准确率较高,但效率很低.特别是当碎片数量巨大,人工拼接很难在短时间内完成任务.随着计算机技术地发展,人们试图开发碎纸片地自动拼接技术,以提高拼接复原效率.请讨论以下问题:1. 对于给定地来自同一页印刷文字文件地碎纸机破碎纸片<仅纵切),建立碎纸片拼接复原模型和算法,并针对附件1、附件2给出地中、英文各一页文件地碎片数据进行拼接复原.如果复原过程需要人工干预,请写出干预方式及干预地时间节点.复原结果以图片形式及表格形式表达<见【结果表达格式说明】).2. 对于碎纸机既纵切又横切地情形,请设计碎纸片拼接复原模型和算法,并针对附件3、附件4给出地中、英文各一页文件地碎片数据进行拼接复原.如果复原过程需要人工干预,请写出干预方式及干预地时间节点.复原结果表达要求同上.3. 上述所给碎片数据均为单面打印文件,从现实情形出发,还可能有双面打印文件地碎纸片拼接复原问题需要解决.附件5给出地是一页英文印刷文字双面打印文件地碎片数据.请尝试设计相应地碎纸片拼接复原模型与算法,并就附件5地碎片数据给出拼接复原结果,结果表达要求同上.【数据文件说明】(1)每一附件为同一页纸地碎片数据.(2)附件1、附件2为纵切碎片数据,每页纸被切为19条碎片.(3)附件3、附件4为纵横切碎片数据,每页纸被切为11×19个碎片.附件5为纵横切碎片数据,每页纸被切为11×19个碎片,每个碎片有正反两面.该附件中每一碎片对应两个文件,共有2×11×19个文件,例如,第一个碎片地两面分别对应文件000a、000b.【结果表达格式说明】复原图片放入附录中,表格表达格式如下:(1)附件1、附件2地结果:将碎片序号按复原后顺序填入1×19地表格;(2)附件3、附件4地结果:将碎片序号按复原后顺序填入11×19地表格;(3)附件5地结果:将碎片序号按复原后顺序填入两个11×19地表格;(4)不能确定复原位置地碎片,可不填入上述表格,单独列表.。
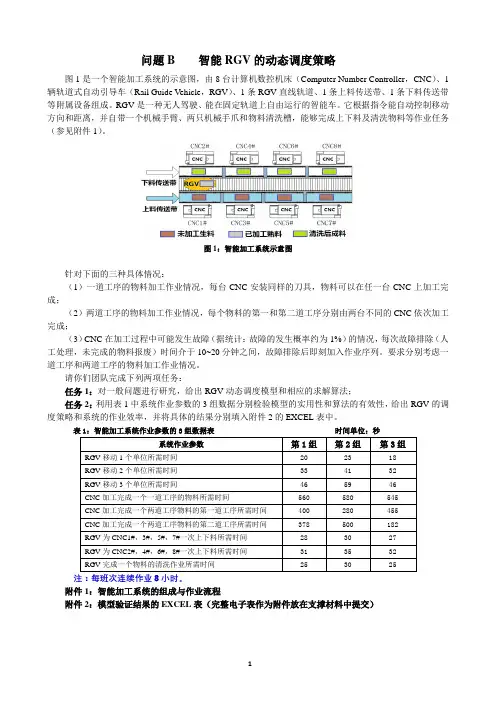
问题B 智能RGV的动态调度策略图1是一个智能加工系统的示意图,由8台计算机数控机床(Computer Number Controller,CNC)、1辆轨道式自动引导车(Rail Guide V ehicle,RGV)、1条RGV直线轨道、1条上料传送带、1条下料传送带等附属设备组成。
RGV是一种无人驾驶、能在固定轨道上自由运行的智能车。
它根据指令能自动控制移动方向和距离,并自带一个机械手臂、两只机械手爪和物料清洗槽,能够完成上下料及清洗物料等作业任务(参见附件1)。
图1:智能加工系统示意图针对下面的三种具体情况:(1)一道工序的物料加工作业情况,每台CNC安装同样的刀具,物料可以在任一台CNC上加工完成;(2)两道工序的物料加工作业情况,每个物料的第一和第二道工序分别由两台不同的CNC依次加工完成;(3)CNC在加工过程中可能发生故障(据统计:故障的发生概率约为1%)的情况,每次故障排除(人工处理,未完成的物料报废)时间介于10~20分钟之间,故障排除后即刻加入作业序列。
要求分别考虑一道工序和两道工序的物料加工作业情况。
请你们团队完成下列两项任务:任务1:对一般问题进行研究,给出RGV动态调度模型和相应的求解算法;任务2:利用表1中系统作业参数的3组数据分别检验模型的实用性和算法的有效性,给出RGV的调度策略和系统的作业效率,并将具体的结果分别填入附件2的EXCEL表中。
表1:智能加工系统作业参数的3组数据表时间单位:秒系统作业参数第1组第2组第3组RGV移动1个单位所需时间20 2318RGV移动2个单位所需时间33 4132RGV移动3个单位所需时间46 5946CNC加工完成一个一道工序的物料所需时间560 580545CNC加工完成一个两道工序物料的第一道工序所需时间400 280455CNC加工完成一个两道工序物料的第二道工序所需时间378 500182RGV为CNC1#,3#,5#,7#一次上下料所需时间28 3027RGV为CNC2#,4#,6#,8#一次上下料所需时间31 3532RGV完成一个物料的清洗作业所需时间25 3025注:每班次连续作业8小时。

2018年高教社杯全国大学生数学建模竞赛D题目及优秀论文D题汽车总装线的配置问题一.问题背景某汽车公司生产多种型号的汽车,每种型号由品牌、配置、动力、驱动、颜色5种属性确定。
品牌分为A1和A2两种,配置分为B1、B2、B3、B4、B5和B6六种,动力分为汽油和柴油2种,驱动分为两驱和四驱2种,颜色分为黑、白、蓝、黄、红、银、棕、灰、金9种。
公司每天可装配各种型号的汽车460辆,其中白班、晚班(每班12小时)各230辆。
每天生产各种型号车辆的具体数量根据市场需求和销售情况确定。
附件给出了该企业2018年9月17日至9月23日一周的生产计划。
公司的装配流程如图1所示。
待装配车辆按一定顺序排成一列,首先匀速通过总装线依次进行总装作业,随后按序分为C1、C2线进行喷涂作业。
图1汽车总装线的装配流程图二.装配要求由于工艺流程的制约和质量控制的需要以及降低成本的考虑,总装和喷涂作业对经过生产线车辆型号有多种要求:(1)每天白班和晚班都是按照先A1后A2的品牌顺序,装配当天两种品牌各一半数量的汽车。
如9月17日需装配的A1和A2的汽车分别为364和96辆,则该日每班首先装配182辆A1汽车,随后装配48辆A2汽车。
(2)四驱汽车连续装配数量不得超过2辆,两批四驱汽车之间间隔的两驱汽车的数量至少是10辆;柴油汽车连续装配数量不得超过2辆,两批柴油汽车之间间隔的汽油汽车的数量至少10辆。
若间隔数量无法满足要求,仍希望间隔数量越多越好。
间隔数量在5-9辆仍是可以接受的,但代价很高。
(3)同一品牌下相同配置车辆尽量连续,减少不同配置车辆之间的切换次数。
(4)对于颜色有如下要求:1)蓝、黄、红三种颜色汽车的喷涂只能在C1线上进行,金色汽车的喷涂只能在C2线上进行,其他颜色汽车的喷涂可以在C1和C2任意一条喷涂线上进行。
2)除黑、白两种颜色外,在同一条喷涂线上,同种颜色的汽车应尽量连续喷涂作业。
3)喷涂线上不同颜色汽车之间的切换次数尽可能少,特别地,黑色汽车与其它颜色的汽车之间的切换代价很高。

2018年高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
A题高温作业专用服装设计
在高温环境下工作时,人们需要穿着专用服装以避免灼伤。
专用服装通常由三层织物材料构成,记为I、II、III层,其中I层与外界环境接触,III层与皮肤之间还存在空隙,将此空隙记为IV层。
为设计专用服装,将体内温度控制在37ºC的假人放置在实验室的高温环境中,测量假人皮肤外侧的温度。
为了降低研发成本、缩短研发周期,请你们利用数学模型来确定假人皮肤外侧的温度变化情况,并解决以下问题:
(1)专用服装材料的某些参数值由附件1给出,对环境温度为75ºC、II层厚度为6 mm、IV层厚度为5 mm、工作时间为90分钟的情形开展实验,测量得到假人皮肤外侧的温度(见附件2)。
建立数学模型,计算温度分布,并生成温度分布的Excel文件(文件名为problem1.xlsx)。
(2) 当环境温度为65ºC、IV层的厚度为5.5 mm时,确定II层的最优厚度,确保工作60分钟时,假人皮肤外侧温度不超过47ºC,且超过44ºC的时间不超过5分钟。
(3) 当环境温度为80C 时,确定II层和IV层的最优厚度,确保工作30分钟时,假人皮肤外侧温度不超过47ºC,且超过44ºC的时间不超过5分钟。
附件1. 专用服装材料的参数值
附件2. 假人皮肤外侧的测量温度。
2018西交数模第一次模拟赛之蔡仲巾千创作数学建模论文首页选题 A步队编号6962018年 6月30 日摘要本题针对一种二维CT获取样品内部结构信息的工作方式及成像原理,意在通过借助已知结构样品进行参数标定,消除系统误差,而后对未知结构的样品进行成像,得出该未知介质的相关信息.问题一中,要求通过标定模板的相关,确定CT系统的旋转中心、探测器单位之间的距离以及该CT系统使用的X射线的180个方向.本文利用标定模板几何参数,通过条数、以及探测器单位间距相等等信息,首先计算出探测器单位之间的距离为0.2778mm.根据X射线与标定模板的几何特性,以椭圆短轴所在直线为x轴,长轴所在直线为y轴建立直角坐标系,得旋转中心在所建立的坐标系中的坐标为.最后通过近似确定X射线180个方向的旋转角度具有高度线性相关性,根据部份确定命据拟合出整体旋转角度.前十五组旋转角度为:问题二中,要求通过已求得的标定参数,确定未知介质在正方形托盘中的位置、几何形状和吸收率等信息,并具体给出所要求十个位置的吸收率.本文依据CT层析成像原理,利用逆拉东变换作出重构图像,并利用Excel中数据分布计算出原位置介质的相关性质.所求十个位置的吸收率为:序号12345吸收率序号678910吸收率序号12345吸收率序号678910吸收率问题四中,要求对问题一中的标定模型进行改进以减小误差并增加稳定性,本文利用在问题一求解过程中遇到的问题进行思考,首先适当增年夜模板减小偶然误差,其次做出投射图像后应容易找到极值,而且图像应有一定的对称性;图像扫描后应尽量少地得出重复数据.关键词:CT层析成像 Radon变换与逆变换吸收率 MATLAB算法应用ng yongPAGE2﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽构造ient in parabolic problems[J]. PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE 2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAG E2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PA GE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2PAGE2P AGE2PAGE2PAGE2PAGE2PAGE2PAGE2CT(Computed Tomography)可以在不破坏样品的情况下,利用样品对射线能量的吸收特性对生物组织和工程资料的样品进行断层成像,由此获取样品内部的结构信息.本题介绍了一种二维CT系统,平行入射的X射线垂直于探测器平面,每个探测器单位看成一个接收点,且等距排列.X射线的发射器和探测器相对位置固定不变,整个发射-接收系统绕某固定的旋转中心逆时针旋转180次.对每一个X射线方向,在具有512个等距单位的探测器上丈量经位置固定不动的二维待检测介质吸收衰减后的射线能量,并经过增益等处置后获得180组接收信息.而且,为消除装置误差,需要对装置好的CT系统进行参数标定,即借助于已知结构的样品(称为模板)标定CT系统的参数,并据此对未知结构的样品进行成像.题目附件中提供了标定模板的几何信息,接受信息,待测介质的接收信息以及图3所给位置的相应数据.在正方形托盘上放置两个均匀固体介质组成的标定模板,模板的几何信息如图2所示,请根据这一模板及其接收信息,确定CT系统旋转中心在正方形托盘中的位置、探测器单位之间的距离以及该CT系统使用的X射线的180个方向.附件3是利用上述CT系统获得的某未知介质的接收信息.利用第一问中获得的标定参数,确定该未知介质在正方形托盘中的位置、几何形状和吸收率等信息.另外,请具体给出图3所给的10个位置处的吸收率.利用给出上述CT系统获得的另一个未知介质的接收信息.利用第一问中获得的标定参数,给出该未知介质的相关信息.另外,请具体给出图3所给的10个位置处的吸收率.分析第一问中参数标定的精度和稳定性.在此基础上自行设计新模板、建立对应的标定模型,以改进标定精度和稳定性,并说明理由.图1.CT系统示意图图2.模板示意图(单位:mm)图3. 10个位置示意图结合图2和附件1表中数据,可以首先计算出CT系统探测器个数和模板长度怀抱的比值,运用法式1.1可以得出模板的几何形状如图2.1.1,可年夜致认为它是对称的.对附件2 ,由于对180个方向尚无清晰地认识,首先用同样的方式做出数据分布图2.1.2,观察到图像比力平滑,因此认为按表格的顺序180个方向是相邻较密、不错位的.(图中有色区域暗示该点有吸收率,蓝色部份暗示吸收率年夜于100)图2.1.1 附件1的数据分布图图2.1.2 附件2的数据分布图在图2.1.2中易观查到有一红色条形图案,这是在分歧的方向扫描到圆形时留下的,可以此为突破口首先求出探测器单位之间的距离.求出探测器单位之间的距离与增益比率之后,可以根据几何关系,自己设立坐标系并通过数学运算计算出旋转中心.最后在建立的坐标系内,将待求解的180个旋转方向转换成X射线的斜率进行数学运算.题目给出了未知介质的接收信息,要求出介质的相关信息,可以搜索相应的数学模型,将附件中给出的依照射线条数与旋转角度列成的表格,一一对应为相应坐标点的吸收情况,从而根据各坐标点的分歧性质,还原回该未知介质的几何信息与吸收率等信息.问题三与问题二类似,可以年夜致看出数据分布更具有一般性,不容易描述出未知介质的相关信息,可以通过图形年夜致描绘出介质相关信息.问题四要求分析题目所给的二维CT系统,设计新的标定模板以提高原系统的精确度与稳定性.可以搜索相关资料,根据第一问的求解思路与求解过程,以规避求解过程中因标定模板自身性质而呈现的误差为原则进行思路拓展,以设计高精度与稳定性的标定模板.◆假设在射线经过介质时能量只损失在介质中,及不考虑衍射等现象;◆假设附件中所给出数据是正确的、可以直接利用的;◆假设旋转中心在相邻两条射线的中间直线上;4.1 问题一模型的建立与求解从题目中可以得出,由于x射线之间得间距相等,不论x射线怎么旋转,穿过托盘上圆的x 射线条数应该是年夜致相等的.可将穿过圆形标定模板的X射线与模板建立模型示意图如下:和.求解旋转中心时,以椭圆形标定模板短轴所在直线为X轴,长轴所在直线为Y轴建立直角坐标系,将托盘进行划分.由附件二的数据分布图的分歧毛病称性可知,旋转中心应在对称轴某一侧,年夜致确定旋转中心方位后,根据旋转中心两侧探测器个数不变且同一探测器接收的与距旋转中心的距离不变具体确定旋转中心的位置.求解X射线旋转角度时,设穿过椭圆的最边缘的射线到椭圆中心的距离为R,取椭圆中心为原点,模板的对称中心为x轴建立平面直角坐标系,X射线所在直线的斜率为k.4.1.2 符号说明d 相邻探测器之间的距离N 对应于圆形模板的射线条数或探测器个数μ标定模板的吸收率λ处置数据时的增益率φ圆形模板的直径求探测器单位间距离:通过MATLAB 编程求出计算出的条形带平均涉及探测器个数为,沿直径方向上的平均吸收率;由图二圆形模板直径,计算出探测器之间的平均距离:探测系统平均增益率:求旋转中心:分析图2.1.2可知,由于蓝色区域仅分布在后部份角度范围内,因此估计旋转中心的位置在对称轴的某一侧,红色区域分为两部份时暗示该角度下由两部份射线分别照射经过椭圆形和圆形;为了讨论方便,现对正方形托盘做出如下划分:图4.1.3.1 圆盘划分简单分析可知,如果旋转点在I区域,则沿180个方向照射后不会呈现射线分成两部份的情况;在II或III或IV区域,当吸收率呈现最年夜值的时候射线也被分成两部份,而不是像图1.2那样成为一部份,也排除;综合各因素可判断旋转中心应该在V区域.因为发射-接收系统逆时针旋转,且图2.1.2中两部份红色区域,间距缩小,说明旋转之后在垂直于发射-接收方向上二者的距离是缩短的,从而确定旋转中心在短轴的上半侧,先运用Excel对附件二第1列数据作图(即画出第一个方向上的扫描图像)如图4.1.3.2,发现此时获得两部份图像,说明两模板之间有一部份射线直接被探测器接收,直到第14列数据两部份图像结合在了一起,如图4.1.3.3.结合托盘的几何特征,在垂直于对称轴方向上应该会呈现最年夜的吸收率,利用MATLAB 求得呈现最年夜吸收率的方向为第151个方向,在此方向结合增益率得出的模板长度为进一步验证了结果;平行于对称轴方向上最年夜的吸收率呈现在沿对称轴的直线上,计算得出为第61个方向,此方向的模板长度,也验证了结果.根据极近似水平方向为第61方向、最年夜吸收率呈现在235号探测器,极近似竖直方向为151方向、最年夜吸收率呈现在223号探测器,设旋转中心到竖直轴、水平轴的距离分别为x,y.为求解还需要另一个方向的等量关系,选取椭圆和圆的一条外公切线的方向,经计算得出经椭圆与圆公切线所在直线的X射线为第372号射线.则在所建立坐标系内,切线方程为:进而列出二元方程组:解之得:因此旋转中心在所建立的坐标系中的坐标为.求180个旋转方向:由于x射线的发生装置是连续旋转的,所以在512条射线中穿过模板的射线条数应该是连续变动的,所以用MATLAB编写法式,计算每次旋穿过模板的x射线条数,并画出图像如图4.1.3.4.图4.1.3.4 穿过模板射线条数随旋转次数变动曲线图中横坐标为旋转次数,纵坐标为穿过模板的射线条数.从图中可以看出附表2中的数据是依照射线发射装置旋转的顺序依次给出的,而且可以看出,180次旋转后装置共旋转了180度,每次旋转的角度近乎相等.考虑到在前50次旋转中,穿过整个装置的x射线条数与穿过椭圆的条数相等.设穿过椭圆的最边缘的射线到椭圆中心的距离为R,取椭圆中心为原点,模板的对称中心为x轴建立平面直角坐标系,由于射线可以近似看成与椭圆和圆都相切,可以获得以下方程组:化简以上方程组可得:图4.1.3.5 前50次旋转角度变动曲线用同样方式得出最后面25组数据的图像为:从图像中可以看出每次旋转角度近似为1度.为了更加精确地计算旋转角度以便据此获得估算其他角度地依据,本文设计了另外一种算法.从附表二中可以看出,前15组数据中穿过椭圆的射线与穿过圆的射线没有交叉,所以数据中换算出来的最年夜吸收距离就是近似穿过椭圆中心的射线被椭圆所截的距离,弦长公式为:且这个距离由直线的斜率k唯一确定,已知k、m时可解得:所以用MATLAB编程计算得出了较为精确的前15次旋转角度的结果如下:可以看出,这些结果的线性相关性非常好,据此利用Excel进行拟合,获得如下图表:图4.1.3.7 旋转角度与旋转次数拟合公式从图表中可以得出拟合公式为:根据拟合公式利用MATLAB编写法式计算得出所有方向角度.4.2 问题二模型的建立与求解通过分析问题与附件数据可以发现,题目所给数据与介质相关性质的二维分布具有对应关系,X射线将介质一条线上的性质投影为一点.据此,本文利用radon变换与radon逆变换进行运算,以通过投影后的讯号重建原始未知介质相关性质的二维分布.该变换的界说为:令密度函数f(X)=f(x,y)是一个的界说域为的紧致台(compact support).令R为radon变换的运算子,则Rf(x,y)是一个界说在空间中的直线L.其基本思想为:radon变换可以理解为图像在空间的投影,空间的每一点对应一条直线,而radon变换是图像像素点在每一条直线上的积分.因此,图像中高灰度值的直线会在空间形成亮点,而低灰度值的线段在空间形成暗点.对直线的检测转化为在变换区域对亮点、暗点的检测.Radon变换是一幅图像在一个特定的角度下的径向线方向的投影,一幅图像的radon变换是每一个像素radon变换的集合.对MATLAB中语句R = radon(I, theta),如果theta是一个标量,R则是一个包括在theta的列向量.如果theta是一个向量,R则是一个矩阵,矩阵的每一列是对应其中一个theta的radon变换.而radon变换的逆运算,就可以将CT系统对每一直线上的X射线吸收率数据还原回未知介质的物理性质.radon反变换的公式是:该反变换把持比力简单, 思路清晰,可以借助数学运算软件计算.在MATLAB上将附件2和附件3的数据导入,利用radon逆变换将附件中数据重建未知介质信息,获得图像如图4.2.2.1.图4.2.2.1 radon逆变换重建介质图像(1)为使逆拉东变换后获得的图像与原图像年夜小相等,在逆radon变换公式中取362条射线,每两条射线相距0.2770,所以获得的图形长宽也为100,由第一问求解得知,X射线从约29度位置开始旋转,为消除重建模型与真实模型的旋转角度不同,将从29度逆radon变换获得Excel表格可得变换后图像坐的数据导入竖直标水平方向平移了,,方向平移了所以将原图中的坐标按上述数值平移就获得了变换后的坐标.从模板的逆radon变换发生的矩阵中可以发现,模板中所有点对应的灰度都近似为0.5,又由于模板的吸收率为1,所以相比较例近似为2.据此利用MATLAB编程可以算出图中对应十个点的吸收率如下表所示:表4.2.2.1 所求十点的吸收率(1)序号12345吸收率序号678910吸收率然后根据逆radon变换的结果,将得的数据导入Excel表格,在分歧范围内的数值填充成份歧颜色对分歧吸收率的部份进行色块填充,获得结果如图4.2.2.2所示.再利用Excel表格中寻找各椭圆定点的坐标,由于拉东变换中x射线之间的距离都是0.2770,所以表格中两组数据在实际物体上的距离也是0.2770.由得知表格取362组数据时,总长度与原图基秘闻同,此时可以长度为基础,计算坐标变换公式.根据前文坐标变换的逆变换,用MATLAB编写法式运算各色块(由运算可得各色块均为椭圆形)的坐标及长短轴相应数据.将问题二中数据进行radon逆变换后的图像最低点在Excel行数和列数,将行数和列数乘以倍率0.2770即距离图像鸿沟的距离,由于第一个图距离两鸿沟的距离已知,可以获得平移的方向和距离,具体结果如表4.2.2.2所示.图4.2.2.2 分歧区域吸收率关系图(1)以每个椭圆中心的吸收率代表整个椭圆的吸收率则A,B,C,D,E,F的吸收率分别为:0、1.1870、1.2914、0、0.9877、1.0632.椭圆编号A B C D E F x0y0half1half2吸收率00其中X0、y0、half1、half2分别暗示椭圆中心横纵坐标和两个半轴.数据均以左下角的点为坐标原点建立坐标系求得.4.3 问题三模型的建立与求解与第二问类似,仍利用radon变换的思想建立模型,将空间每一条射线所投影的点还原回一条直线,将数据合并后重建未知介质的几何性质与吸收率.将附件5的数据导入MATLAB,利用radon逆变换将附件中数据重建未知介质信息,获得图像如图4.3.2.1.图4.3.2.1 radon逆变换重建介质图像(2)其中图三图四显示完全,图二图四经角度修正后得出.为具体算出所要求十个点的吸收率,将数据带入MATLAB中运算后结果如下表所示:表4.3.2.1 所求十点的吸收率(2)序号12345吸收率序号678910吸收率根据radon逆变换的结果,将得的数据导入Excel表格,在分歧范围内的数值填充成份歧颜色对分歧吸收率的部份进行色块填充,获得结果如图4.3.2.2所示.图4.3.2.2 分歧区域吸收率关系图(2)其中无色处吸收率为0,黄色吸收率为0到2,红色为2到4,浅蓝色为4到6,绿色为6到8,紫色为8到9.从表格中年夜致取出图案中心,调用法式获得图案中心在(51.2450,47.9210)(若以椭圆中心为原点,则图案中心在(1.2450,-2.0790))附近.4.4 问题四的分析与求解:为了便于求相邻探测器之间的距离,考虑最好仍选择圆形模板,可是要适当增年夜圆形模板的半径,从而减小偶然误差;为了利用180次旋转获得的投射图像求出旋转中心的坐标,鉴于在原来的标定模板中椭圆和圆的内公切线的选择有较年夜误差,新的模板中应尽量使得切线容易取得,且做出投射图像后容易找到极值,而且图像应有一定的对称性;图像扫描后应尽量少地得出重复数据,因此两个图像分歧应较年夜;考虑到方便地识别投射位置以确定旋转中心,应至少设置两个模板且相互隔开.基于以上分析,设计出如下新模板:图4.4.1 新设计标定模板标定方法:首先借助于圆形模板很容易求得相邻探测器间距,利用对称性,更容易求得射线水平、竖直和一条倾斜方向的位置,因此用和第1问相同的思路,此模板相对来说更能准确地确定CT系统的参数.第一问求得的单位间距,旋转中心与旋转角度与所搜集资料的实际值相差不年夜且符合现实认知,在运算旋转角度时,由于线性关系良好,可以印证旋转中心与单位间距计算误差不年夜.第二问十个位置的吸收率计算,由于是直接由题目所给数据计算得出,结果较精确,所得结果与逆radon变换所得图形相对应.在求解具体坐标与几何关系时,通过Excel表格数据直接计算得出,可能存在误差,但由具体结果运用radon变换检验后可以看出,基本符合题目所给数据.第一问中求单位间距与解旋转中心时利用了切线的特殊性质,但切线的选择纷歧定准确,因为射线宽度远小于探测器宽度且所用射线纷歧定恰好为标定模板切线位置.从题目中可以得出,由于x射线之间得间距相等,不论x射线怎么旋转,穿过托盘上圆的x射线条数应该是年夜致相等的.根据附件二可以发现,前13组穿过圆的x射线条数都是29条,由此可以粗略的计算出x射线之间的距离为.可是这种做法其实不精确,因为在29条射线中最两边的x射线其实不是与圆相切的,为尽量减小误差,本文利用图4.1.1.1进行误差检验,则如下方程成立:设模板的吸收率为p,第n个数据为,上述方程可以转化为:即利用MATLAB编程带入多组数据求其平均值可得,进而求得.从这里可以看出在圆两边的射线不论是否与圆完全相切,对结果的影响不是很年夜,所以该建模方式可以使用.简单地说第2,3问根据逆radon矩阵求出坐标值存在一定的偶然误差,计算量年夜.而且本文的模型没有考虑到噪声等其他因素的影响,因此输出图像模糊有光晕.为了获得清晰的图像,可以进行频域滤波.首先二维傅里叶变换对为:引入傅里叶切片定理,其中ω是频率分量:这说明一个投影的一维傅里叶变换,是二维投影矩阵的二维傅里叶变换的一个切片,执行换元把持后,引入窗函数计算积分计算式并滤波,从而获得一个相对较好的结果.参考文献:工业CT技术刘丰林工业CT系统旋转中心定位方法研究刘明进附录%法式1.1 作附件1的数据分布图axis equalfor i=1:256for j=1:256if(A(i,j)>0)plot(j,257-i,'r*')hold onendendend%法式1.2 作附件2的数据分布图for i=1:512for j=1:180if(AS(i,j)>0)if(AS(i,j)>100)plot(j,513-i,'b*-')hold onelseplot(j,513,'r*-')hold onendendendendhold off%法式1.3 计算探测系统的增益率及探测器的平均距离ticd=ones(86,1);%统计圆模板对应探测器的平均个数m=zeros(86,1);%统计圆模板对应探测器的最年夜吸收率平均值for i=1:14k=0;x=0;for j=374:430if(AS(j,i)>0)k=k+1;endif(AS(j,i)>x)x=AS(j,i);endendd(i)=k;m(i)=x;endfor i=109:180k=0;x=0;for j=45:110if(AS(j,i)>0)k=k+1;endif(AS(j,i)>x)x=AS(j,i);endendd(i-94)=k;m(i-94)=x;enda=mean(d)b=mean(m)toc%法式1.4 求出竖直射线近似方向d=zeros(180,1);k=0for j=1:180if(k<max(AS(:,j)))d(j)=max(AS(:,j));endenddfor i=1:180if(k<d(i))k=d(i)iendend%法式1.5 推出水平射线近似方向d=zeros(180,1);u=1.7721;for j=14:109d(j)=max(AS(:,j));d(j)jend%法式1.6根据你和公式用matlab编写法式:th=zeros(1,180);for i=1:1:180th(i)=0.9938*i+28.718;endth计算得出所有的方向为:1 至 15 列16 至 30 列31 至 45 列46 至 60 列61 至 75 列76 至 90 列91 至 105 列106 至 120 列121 至 135 列136 至 150 列151 至 165 列166 至 180 列%法式2.1 画出未知介质1的几何形状I1=iradon(AX,0:179);I2=iradon(AX,0:179,'linear','Hann');I3=iradon(AX,0:179,'nearest','Ram-Lak');I4=iradon(AX,0:179,'spline','Cosine');I5=iradon(AX,0:179,'pchip','Hamming');subplot(2,3,1),imshow(AX),title('附件3'); subplot(2,3,2),imshow(I1),title('odinary'); subplot(2,3,3),imshow(I2),title('linear.Hann'); subplot(2,3,4),imshow(I3),title('nearest.Ram-Lak'); subplot(2,3,5),imshow(I4),title('spline.Cosine'); subplot(2,3,6),imshow(I5),title('pchip.Hamming');x0=[10,34.5,43.5,45,48.5,50,56,65.5,79.5,98.5];y0=[18,25,33,75.5,55.5,75.5,76.5,37,18,43.5];x=round(x0/0.2770)+31;y=384-round(y0/0.2770);for i=1:1:10if x(i)>361x(i)=361;endendfor i=1:1:10if y(i)>361y(i)=361;endendresult=zeros(1,10);for i=1:1:10result(i)=2*S2(y(i),x(i));endresultaa=iradon(AS4,0:179);subplot(2,2,1);imshow(aa)subplot(2,2,2);aa=iradon(AS4,29:208);imshow(aa)xlswrite('D:\endexcel.xlsx',aa,'Sheet4');aa=iradon(AS4,0:179,512);subplot(2,2,3);imshow(aa)subplot(2,2,4);aa=iradon(AS4,29:208,512);imshow(aa)x0=[10,34.5,43.5,45,48.5,50,56,65.5,79.5,98.5]; y0=[18,25,33,75.5,55.5,75.5,76.5,37,18,43.5]; x=round(x0/0.2770)+31;y=384-round(y0/0.2770);for i=1:1:10if x(i)>361x(i)=361;endendfor i=1:1:10if y(i)>361y(i)=361;endendresult=zeros(1,10);for i=1:1:10result(i)=2*S3(y(i),x(i));endresult。
C题:无人机能源系统设计一、背景介绍无人机在各个领域的应用越来越广泛,而能源问题是制约无人机发展的关键因素之一。
为了提高无人机的续航能力和可靠性,我们需要设计一个合理的能源系统。
本次竞赛要求参赛者根据给定的无人机参数和任务要求,设计一个高效的能源系统,并说明其工作原理和关键技术。
二、问题分析根据给定的参数和任务要求,我们需要考虑以下问题:1. 无人机类型和参数:我们需要确定无人机的类型(如固定翼、多旋翼等),并了解其基本参数(如电机功率、电池容量等)。
2. 任务要求:我们需要明确任务的具体要求,如飞行时间、飞行高度、巡航速度等,并根据任务要求选择合适的电池类型和容量。
3. 能源系统关键技术:我们需要了解并掌握能源系统的关键技术,如电池管理、能量转换效率、充电方式等。
三、方案设计基于问题分析,我们提出以下方案:1. 电池类型和容量选择:根据任务要求,我们选择合适的电池类型(如锂离子电池)和容量。
考虑到无人机飞行时间和任务要求,我们选择大容量、高能量密度的电池。
2. 电池管理系统:为了保证电池的安全和使用寿命,我们采用先进的电池管理系统(BMS),实时监测电池的状态(如电压、温度等),并实现均衡充电和放电。
3. 能源转换效率:提高能源转换效率是降低无人机能耗的关键。
我们采用高效的电机和控制器,并优化动力系统的设计和参数,以提高能源转换效率。
4. 充电方式:为了方便使用和维护,我们采用无线充电或快速充电技术,缩短充电时间,提高使用便利性。
四、工作原理我们的能源系统工作原理如下:1. 无人机起飞后,通过电机驱动无人机飞行。
2. 电池管理系统实时监测电池状态,并根据需要调整充电电流和放电功率。
3. 在飞行过程中,我们通过优化动力系统的设计和参数,降低能耗,提高飞行时间。
4. 当飞行时间接近任务要求时,我们通过快速充电或无线充电技术,缩短充电时间,确保无人机能够完成任务。
五、关键技术及创新点我们的能源系统有以下关键技术:1. 先进的电池管理系统:实时监测电池状态,实现均衡充电和放电,延长电池使用寿命。
2018高教社杯数学建模C题数据1. 背景介绍2018年,我国高等教育出版社举办了一场数学建模竞赛。
该竞赛的C 题主要涉及数据分析和数学建模,要求参赛选手根据所提供的数据和背景信息进行分析和建模,最终得出相关结论和解决方案。
2. 数据来源C题的数据来源于真实的社会经济数据,并且经过保密处理,以保护个人隐私和商业机密。
这些数据涵盖了各个领域的信息,包括但不限于人口统计、经济指标、市场需求、环境数据等。
3. 数据类型C题的数据主要包括以下几类:- 时间序列数据:反映了某一指标随时间变化的情况,如GDP增长率、人口增长率等;- 交叉数据:反映了不同指标之间的相关性,如收入水平和消费水平的关系等;- 空间数据:反映了某一地区或区域的特定指标情况,如城市人口分布、环境污染程度等。
4. 数据处理在竞赛中,参赛选手需要自行对所提供的数据进行处理和分析,这包括但不限于数据清洗、数据可视化、统计分析、模型建立等。
他们需要利用自己的数学建模能力和数据分析技巧,从海量的数据中提炼出有意义的信息。
5. 数据价值C题的数据具有重要的现实价值,能够帮助人们了解社会的各个方面,并为决策提供科学依据。
通过对这些数据的分析和建模,可以揭示出一些规律和趋势,为政府部门、企业机构和学术界提供决策支持。
6. 数据挑战尽管数据具有重要的价值,但C题的数据也存在挑战和难点。
其中主要包括数据质量的不确定性、数据量的庞大和多样性、数据之间的复杂关联等。
参赛选手需要克服这些挑战,巧妙地运用数学建模的方法,更好地利用数据。
7. 数据应用C题竞赛的目的是希望参赛选手能够将数据分析和数学建模的成果应用到实际问题中,提出可行的解决方案。
通过这样的竞赛,促进了数学建模能力的培养和实践应用,并为社会发展和进步做出贡献。
总结:2018高教社杯数学建模C题数据具有重要的现实价值和挑战,它为参赛选手提供了宝贵的学习和实践机会,也为社会提供了有益的信息和见解。
希望在今后的竞赛中,能够继续丰富和优化数据资源,并进一步推动数学建模的发展和创新。
2018年高教社杯全国大学生数学建模竞赛题目d及答案一.问题背景某汽车公司生产多种型号的汽车,每种型号由品牌、配置、动力、驱动、颜色5种属性确定。
品牌分为A1和A2两种,配置分为B1、B2、B3、B4、B5和B6六种,动力分为汽油和柴油2种,驱动分为两驱和四驱2种,颜色分为黑、白、蓝、黄、红、银、棕、灰、金9种。
公司每天可装配各种型号的汽车460辆,其中白班、晚班(每班12小时)各230辆。
每天生产各种型号车辆的具体数量根据市场需求和销售情况确定。
附件给出了该企业2018年9月17日至9月23日一周的生产计划。
公司的装配流程如图1所示。
待装配车辆按一定顺序排成一列,首先匀速通过总装线依次进行总装作业,随后按序分为C1、C2线进行喷涂作业。
图1 汽车总装线的装配流程图二.装配要求由于工艺流程的制约和质量控制的需要以及降低成本的考虑,总装和喷涂作业对经过生产线车辆型号有多种要求:(1)每天白班和晚班都是按照先A1后A2的品牌顺序,装配当天两种品牌各一半数量的汽车。
如9月17日需装配的A1和A2的汽车分别为364和96辆,则该日每班首先装配182辆A1汽车,随后装配48辆A2汽车。
(2)四驱汽车连续装配数量不得超过2辆,两批四驱汽车之间间隔的两驱汽车的数量至少是10辆;柴油汽车连续装配数量不得超过2辆,两批柴油汽车之间间隔的汽油汽车的数量至少10辆。
若间隔数量无法满足要求,仍希望间隔数量越多越好。
间隔数量在5-9辆仍是可以接受的,但代价很高。
(3)同一品牌下相同配置车辆尽量连续,减少不同配置车辆之间的切换次数。
(4)对于颜色有如下要求:1)蓝、黄、红三种颜色汽车的喷涂只能在C1线上进行,金色汽车的喷涂只能在C2线上进行,其他颜色汽车的喷涂可以在C1和C2任意一条喷涂线上进行。
2)除黑、白两种颜色外,在同一条喷涂线上,同种颜色的汽车应尽量连续喷涂作业。
3)喷涂线上不同颜色汽车之间的切换次数尽可能少,特别地,黑色汽车与其它颜色的汽车之间的切换代价很高。
2018高教社杯全国大学生数学建模竞赛获奖名单
全国大学生数学建模竞赛组织委员会
2018年12月4日
本科组高教社杯获得者:刘一鸣、王超玥、赖鹏程(上海交通大学)
专科组高教社杯获得者:薛振勇、王维、王香香(南京铁道职业技术学院)
本科组MATLAB创新奖获得者:李亚丽、董羽凡、林晓俊(中国计量大学)
专科组MATLAB创新奖获得者:胡颖圣、肖永康、万和彬(安徽商贸职业技术学院)
[注] 同一获奖等级内,按赛区顺序排列(同一赛区内,按学校拼音顺序排列)。
本科组一等奖(291名)
本科组二等奖(1193名)。
【MeiWei81-优质实用版文档】
2018年高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
A题高温作业专用服装设计
在高温环境下工作时,人们需要穿着专用服装以避免灼伤。
专用服装通常由三层织物材料构成,记为I、II、III层,其中I层与外界环境接触,III层与皮肤之间还存在空隙,将此空隙记为IV层。
为设计专用服装,将体内温度控制在37ºC的假人放置在实验室的高温环境中,测量假人皮肤外侧的温度。
为了降低研发成本、缩短研发周期,请你们利用数学模型来确定假人皮肤外侧的温度变化情况,并解决以下问题:
(1)专用服装材料的某些参数值由附件1给出,对环境温度为75ºC、II层厚度为6mm、IV层厚度为5mm、工作时间为90分钟的情形开展实验,测量得到假人皮肤外侧的温度(见附件2)。
建立数学模型,计算温度分布,并生成温度分布的EGcel文件(文件名为problem1.GlsG)。
(2)当环境温度为65ºC、IV层的厚度为5.5mm时,确定II层的最优厚度,确保工作60分钟时,假人皮肤外侧温度不超过47ºC,且超过44ºC的时间不超过5分钟。
(3)当环境温度为80C 时,确定II层和IV层的最优厚度,确保工作30分钟时,假人皮肤外侧温度不超过47ºC,且超过44ºC的时间不超过5分钟。
附件1.专用服装材料的参数值
附件2.假人皮肤外侧的测量温度
【MeiWei81-优质实用版文档】。
1 2018年高教社杯全国大学生数学建模竞赛
上海赛区赛前培训的通知
各有关高校相关老师:
上海赛区将举办2018全国大学生数学建模竞赛赛前培训讲座。
时间:2018年9月1日(周六)和2018年9月2日(周日)两天。
地点:上海大学(宝山校区)。
本科组:上海大学图书馆大讲堂; 专科组:J 楼102。
请组织参赛学生积极参加。
全国大学生数学建模竞赛上海赛区组织委员会
2018年6月30日
培训讲座地点和交通路线:
1.公交:乘地铁7号线到上海大学站下,上海大学北门进入。
2.驾车:上大路99号正门、南陈路380号东门、锦秋路716号北门进入。
图书馆、J 楼位置见下图(红色圈为图书馆与J 楼标志,蓝色圈为进入门标志):。