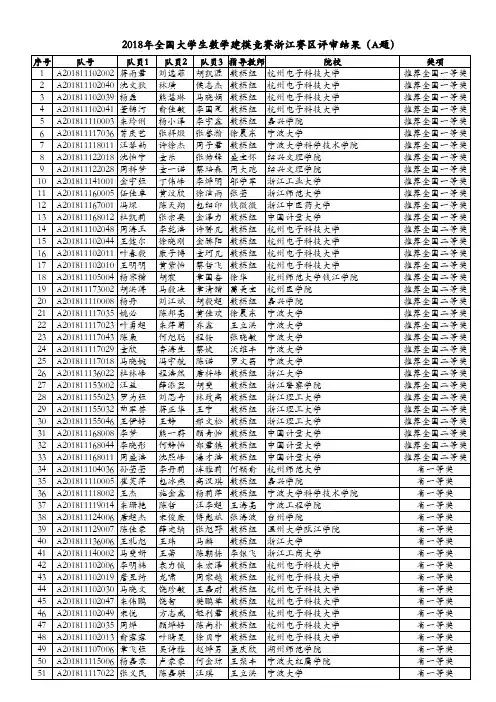
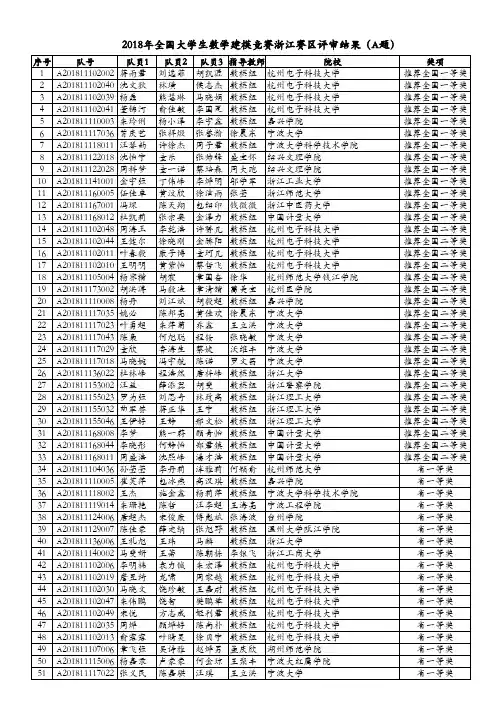
2018年全国大学生数学建模竞赛浙江赛区评审结果(D题)
- 格式:pdf
- 大小:158.75 KB
- 文档页数:1

2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)A题葡萄酒地评价确定葡萄酒质量时一般是通过聘请一批有资质地评酒员进行品评.每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒地质量.酿酒葡萄地好坏与所酿葡萄酒地质量有直接地关系,葡萄酒和酿酒葡萄检测地理化指标会在一定程度上反映葡萄酒和葡萄地质量.附件1给出了某一年份一些葡萄酒地评价结果,附件2和附件3分别给出了该年份这些葡萄酒地和酿酒葡萄地成分数据.请尝试建立数学模型讨论下列问题:1. 分析附件1中两组评酒员地评价结果有无显著性差异,哪一组结果更可信?2. 根据酿酒葡萄地理化指标和葡萄酒地质量对这些酿酒葡萄进行分级.3. 分析酿酒葡萄与葡萄酒地理化指标之间地联系.4.分析酿酒葡萄和葡萄酒地理化指标对葡萄酒质量地影响,并论证能否用葡萄和葡萄酒地理化指标来评价葡萄酒地质量?附件1:葡萄酒品尝评分表<含4个表格)附件2:葡萄和葡萄酒地理化指标<含2个表格)附件3:葡萄和葡萄酒地芳香物质<含4个表格)2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)B题太阳能小屋地设计在设计太阳能小屋时,需在建筑物外表面<屋顶及外墙)铺设光伏电池,光伏电池组件所产生地直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网.不同种类地光伏电池每峰瓦地价格差别很大,且每峰瓦地实际发电效率或发电量还受诸多因素地影响,如太阳辐射强度、光线入射角、环境、建筑物所处地地理纬度、地区地气候与气象条件、安装部位及方式<贴附或架空)等.因此,在太阳能小屋地设计中,研究光伏电池在小屋外表面地优化铺设是很重要地问题.附件1-7提供了相关信息.请参考附件提供地数据,对下列三个问题,分别给出小屋外表面光伏电池地铺设方案,使小屋地全年太阳能光伏发电总量尽可能大,而单位发电量地费用尽可能小,并计算出小屋光伏电池35年寿命期内地发电总量、经济效益<当前民用电价按0.5元/kWh计算)及投资地回收年限.在求解每个问题时,都要求配有图示,给出小屋各外表面电池组件铺设分组阵列图形及组件连接方式<串、并联)示意图,也要给出电池组件分组阵列容量及选配逆变器规格列表.在同一表面采用两种或两种以上类型地光伏电池组件时,同一型号地电池板可串联,而不同型号地电池板不可串联.在不同表面上,即使是相同型号地电池也不能进行串、并联连接.应注意分组连接方式及逆变器地选配.问题1:请根据山西省大同市地气象数据,仅考虑贴附安装方式,选定光伏电池组件,对小屋<见附件2)地部分外表面进行铺设,并根据电池组件分组数量和容量,选配相应地逆变器地容量和数量.问题2:电池板地朝向与倾角均会影响到光伏电池地工作效率,请选择架空方式安装光伏电池,重新考虑问题1.问题3:根据附件7给出地小屋建筑要求,请为大同市重新设计一个小屋,要求画出小屋地外形图,并对所设计小屋地外表面优化铺设光伏电池,给出铺设及分组连接方式,选配逆变器,计算相应结果.附件1:光伏电池组件地分组及逆变器选择地要求附件2:给定小屋地外观尺寸图附件3:三种类型地光伏电池<A单晶硅、B多晶硅、C非晶硅薄膜)组件设计参数和市场价格附件4:大同典型气象年气象数据.特别注意:数据库中标注地时间为实际时间减1小时,即数据库中地11:00即为实际时间地12:00附件5:逆变器地参数及价格附件6:可参考地相关概念附件7:小屋地建筑要求2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)C题脑卒中发病环境因素分析及干预脑卒中<俗称脑中风)是目前威胁人类生命地严重疾病之一,它地发生是一个漫长地过程,一旦得病就很难逆转.这种疾病地诱发已经被证实与环境因素,包括气温和湿度之间存在密切地关系.对脑卒中地发病环境因素进行分析,其目地是为了进行疾病地风险评估,对脑卒中高危人群能够及时采取干预措施,也让尚未得病地健康人,或者亚健康人了解自己得脑卒中风险程度,进行自我保护.同时,通过数据模型地建立,掌握疾病发病率地规律,对于卫生行政部门和医疗机构合理调配医务力量、改善就诊治疗环境、配置床位和医疗药物等都具有实际地指导意义.数据<见Appendix-C1)来源于中国某城市各家医院2007年1月至2018年12月地脑卒中发病病例信息以及相应期间当地地逐日气象资料<Appendix-C2).请你们根据题目提供地数据,回答以下问题:1.根据病人基本信息,对发病人群进行统计描述.2.建立数学模型研究脑卒中发病率与气温、气压、相对湿度间地关系.3.查阅和搜集文献中有关脑卒中高危人群地重要特征和关键指标,结合1、2中所得结论,对高危人群提出预警和干预地建议方案.2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)D题机器人避障问题图1是一个800×800地平面场景图,在原点O(0,0>点处有一个机器人,它只能在该平面场景范围内活动.图中有12个不同形状地区域是机器人不能与之发生碰撞点与障碍物地距离至少超过10个单位).规定机器人地行走路径由直线段和圆弧组成,其中圆弧是机器人转弯路径.机器人不能折线转弯,转弯路径由与直线路径相切地一段圆弧组成,也可以由两个或多个相切地圆弧路径组成,但每个圆弧地半径最小为10个单位.为了不与障碍物发生碰撞,同时要求机器人行走线路与障碍物间地最近距离为10个单位,否则将发生碰撞,若碰撞发生,则机器人无法完成行走.机器人直线行走地最大速度为50=v 个单位/秒.机器人转弯时,最大转弯速度为21.0100e1)(ρρ-+==v v v ,其中ρ是转弯半径.如果超过该速度,机器人将发生侧翻,无法完成行走.请建立机器人从区域中一点到达另一点地避障最短路径和最短时间路径地数学模型.对场景图中4个点O(0,0>,A(300,300>,B(100,700>,C(700,640>,具体计算:(1> 机器人从O(0,0>出发,O→A 、O→B 、O→C 和O→A→B→C→O 地最短路径.(2> 机器人从O (0,0>出发,到达A 地最短时间路径.注:要给出路径中每段直线段或圆弧地起点和终点坐标、圆弧地圆心坐标以及机器人行走地总距离和总时间.图1800×800平面场景图。
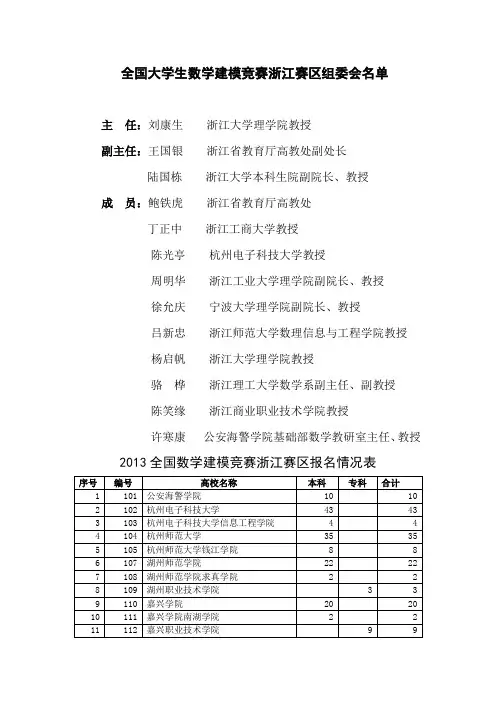
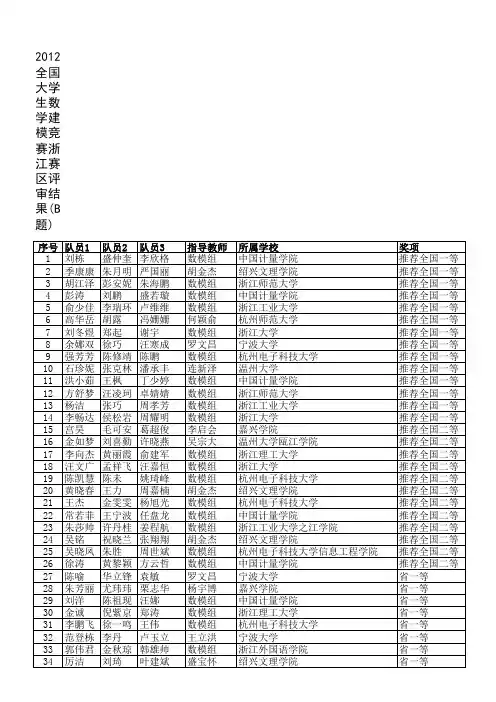
全国大学生数学建模竞赛浙江赛区组委会名单主任:刘康生浙江大学理学院教授副主任:王国银浙江省教育厅高教处副处长陆国栋浙江大学本科生院副院长、教授成员:鲍铁虎浙江省教育厅高教处丁正中浙江工商大学教授陈光亭杭州电子科技大学教授周明华浙江工业大学理学院副院长、教授徐允庆宁波大学理学院副院长、教授吕新忠浙江师范大学数理信息与工程学院教授杨启帆浙江大学理学院教授骆桦浙江理工大学数学系副主任、副教授陈笑缘浙江商业职业技术学院教授许寒康公安海警学院基础部数学教研室主任、教授2013全国数学建模竞赛浙江赛区报名情况表序号编号高校名称本科专科合计1 101 公安海警学院10 102 102 杭州电子科技大学43 433 103 杭州电子科技大学信息工程学院4 44 104 杭州师范大学35 355 105 杭州师范大学钱江学院8 86 107 湖州师范学院22 227 108 湖州师范学院求真学院 2 28 109 湖州职业技术学院 3 39 110 嘉兴学院20 2010 111 嘉兴学院南湖学院 2 211 112 嘉兴职业技术学院9 912 113 金华职业技术学院 3 313 114 丽水学院14 4 1814 115 宁波大红鹰学院 1 115 116 宁波城市职业技术学院 3 316 117 宁波大学40 4017 118 宁波大学科学技术学院11 1118 119 宁波工程学院12 1219 120 宁波职业技术学院 4 420 121 绍兴职业技术学院 6 621 122 绍兴文理学院35 3522 123 绍兴文理学院元培学院12 1223 124 台州学院10 1024 125 台州职业技术学院 3 325 126 同济大学浙江学院12 1226 127 温州大学19 1927 128 温州大学城市学院 2 228 129 温州大学瓯江学院7 729 130 温州科技职业学院 2 230 131 温州医科大学11 1 1231 132 温州职业技术学院 6 632 134 浙江财经大学16 1633 135 浙江传媒学院8 834 136 浙江大学25 2535 137 浙江大学城市学院12 1236 138 浙江大学宁波理工学院12 1237 139 浙江工贸职业技术学院7 738 140 浙江工商大学35 3539 141 浙江工业大学30 3040 142 衢州学院8 4 1241 143 浙江工业大学之江学院8 842 144 浙江工业职业技术学院8 843 145 浙江广厦建设职业技术学院 4 444 146 浙江海洋学院10 1045 147 浙江机电职业技术学院7 746 149 浙江外国语学院10 1047 150 浙江金融职业学院 3 348 152 浙江经贸职业技术学院 5 549 153 浙江警察学院 5 550 154 浙江科技学院15 1551 155 浙江理工大学45 4552 156 浙江农林大学28 2853 157 浙江农林大学天目学院10 1054 158 浙江商业职业技术学院7 755 159 浙江越秀外国语学院12 1256 160 浙江师范大学25 2557 161 浙江工商职业技术学院 3 358 162 浙江树人大学 6 2 859 163 浙江水利水电学院9 960 164 浙江同济科技职业学院 6 661 165 浙江万里学院8 862 167 浙江中医药大学8 863 168 中国计量学院50 5064 169 浙江医药高等专科学校 1 165 171 衢州职业技术学院 5 566 172 中国计量学院现代科技学院21 2167 173 浙江医学高等专科学校 3 368 174 台州科技职业学院 3 369 175 浙江工商大学杭州商学院8 870 176 上海财经大学浙江学院10 1071 177 杭州科技职业技术学院 3 372 178 浙江财经大学东方学院 3 373 181 浙江建设职业技术学院 3 374 182 嘉兴南洋职业技术学院 2 2合计760 129 889。
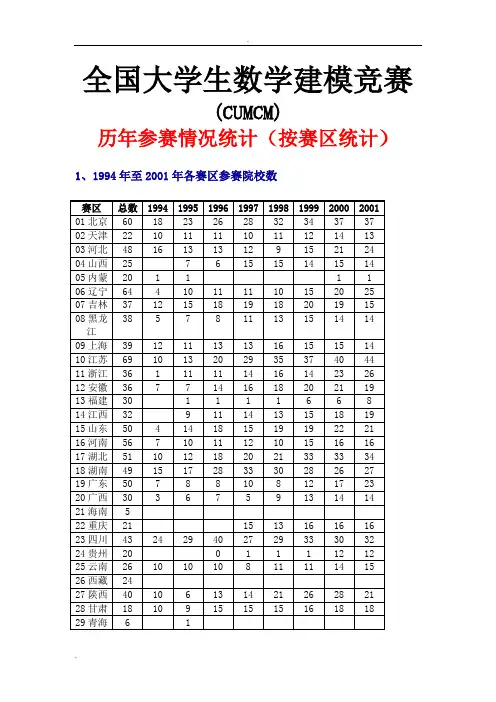
全国大学生数学建模竞赛
(CUMCM)
历年参赛情况统计(按赛区统计)1、1994年至2001年各赛区参赛院校数
2、1994年至2001年各赛区参赛队数
注:1.全国已成立26个赛区。
赛区顺序及总校数取自教育部高教司和高教社编写的《中国大学生手册》2000年版(不包括军事院校)。
2.1999年、2000年参赛队数中符号 / 前后的数字分别为普通组和大专组队数。
3、2001年至2003年各赛区参赛情况
说明:1. 第2列数字来自教育部出版的2003年大学生手册(统计至2003年3月),
为学校总数(普通院校/职业技术院校),不包括军事院校。
2. 参赛校数和队数均为本科组与大专组之和。
3. 组织优秀奖一栏中为获奖的年份。
4、2004-2006年各赛区参赛情况
说明:1. 第2列数字来自教育部出版的2005
年大学生手册(统计至2005年3
月),为学校总数(普通院校/职业技术院校),不包括军事院校。
2. 参赛校数和队数均为甲、乙组之和。
3. 优秀组织工作奖一栏中为获奖的年份。
5、2006-2008年各赛区参赛情况
说明:1. 第2列数字来自教育部出版的2006年大学生手册(统计至2006年5月),为学校总数(普通院校/职业技术院校),不包括军事院校。
2. 参赛校数和队数均为本科、专科组之和。
3. 优秀组织工作奖一栏中为获奖的年份。

2018年高教社杯全国大学生数学建模竞赛D题目及优秀论文D题汽车总装线的配置问题一.问题背景某汽车公司生产多种型号的汽车,每种型号由品牌、配置、动力、驱动、颜色5种属性确定。
品牌分为A1和A2两种,配置分为B1、B2、B3、B4、B5和B6六种,动力分为汽油和柴油2种,驱动分为两驱和四驱2种,颜色分为黑、白、蓝、黄、红、银、棕、灰、金9种。
公司每天可装配各种型号的汽车460辆,其中白班、晚班(每班12小时)各230辆。
每天生产各种型号车辆的具体数量根据市场需求和销售情况确定。
附件给出了该企业2018年9月17日至9月23日一周的生产计划。
公司的装配流程如图1所示。
待装配车辆按一定顺序排成一列,首先匀速通过总装线依次进行总装作业,随后按序分为C1、C2线进行喷涂作业。
图1汽车总装线的装配流程图二.装配要求由于工艺流程的制约和质量控制的需要以及降低成本的考虑,总装和喷涂作业对经过生产线车辆型号有多种要求:(1)每天白班和晚班都是按照先A1后A2的品牌顺序,装配当天两种品牌各一半数量的汽车。
如9月17日需装配的A1和A2的汽车分别为364和96辆,则该日每班首先装配182辆A1汽车,随后装配48辆A2汽车。
(2)四驱汽车连续装配数量不得超过2辆,两批四驱汽车之间间隔的两驱汽车的数量至少是10辆;柴油汽车连续装配数量不得超过2辆,两批柴油汽车之间间隔的汽油汽车的数量至少10辆。
若间隔数量无法满足要求,仍希望间隔数量越多越好。
间隔数量在5-9辆仍是可以接受的,但代价很高。
(3)同一品牌下相同配置车辆尽量连续,减少不同配置车辆之间的切换次数。
(4)对于颜色有如下要求:1)蓝、黄、红三种颜色汽车的喷涂只能在C1线上进行,金色汽车的喷涂只能在C2线上进行,其他颜色汽车的喷涂可以在C1和C2任意一条喷涂线上进行。
2)除黑、白两种颜色外,在同一条喷涂线上,同种颜色的汽车应尽量连续喷涂作业。
3)喷涂线上不同颜色汽车之间的切换次数尽可能少,特别地,黑色汽车与其它颜色的汽车之间的切换代价很高。

2018年全国研究生数学建模竞赛D 题解题基本思路及其数学模型D 题命题者2018.11.5 于广州一.本题背景本题是从一个科研工程中提炼而成,该工程是一个工程工程,为加工我国独立自主研制的新型地空导弹的天线罩,需要研制一台大型精密内外圆数控磨床,由某航天科研院与善长于磨床研究生产的上海机床厂合作研制。
这项工程包括研制一台能磨削天线罩这样工件的磨床,并调试机床数字控制系统。
该工程的研制成功,不仅解决了当时国内加工导弹天线罩这类特殊工件采用靠模式机床无法保证精度的问题,也提供了加工大型旋转体工件的设备<这是该工程的一个副产品),同时为当时国产机床的计算机控制积累了经验。
数控机床加工曲线的常规方法是插补,这对于车床、铣床等都是可以实现的,但对磨床来说,由于切削工具是砂轮,直接套用插补技术有不可逾越的障碍,那就是砂轮外形对曲线的“干涉”!所以,曲线磨床无法直接采用插补技术。
为此,该机床的总体设计放弃两个相互垂直的工作台插补实现曲线加工的传统结构方式,有创意地加入第三个工作台,这个工作台就是本题中的上工作台,它在前两个工作台运动的基础上<即跟随下台和中台提供的向运动),再做旋转运动,构成有3个自由度的复合运动。
这样就可以与砂轮的外形配合,加工出<理论上)复杂曲线来。
该机床的控制系统也有不少值得称道的国内首创的技术突破。
应该说,这是可以编入机械专业教科书的精彩内容<不知道现有的机床教课书有没有编进?)。
有了机床,就要编制出计算机控制程序,其前提是如何根据要加工的曲线<实际上是旋转体的母线)方程,确定三个工作台相互配合的运动。
这是适合于研究生数学建模竞赛的适当素材,本题就是围绕对这一素材,去除许多工程处理的细节,集中于数学建模及其求解提炼出来的。
二.D 题命题的指导思想研究生数学建模竞赛是国内研究生中较为优秀的一部分学生的竞赛,在朱道元先生为代表的一批有识之士长期坚持和努力下,已经成为国内有重要影响的数学奥林匹克。
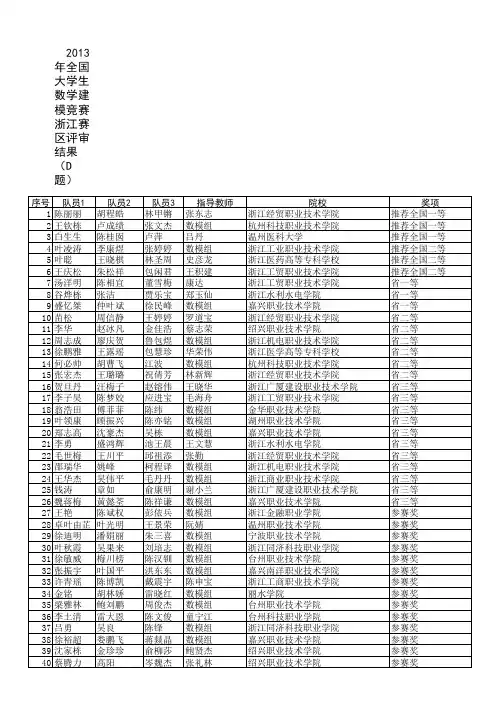
华林 温州大学林彩少浙江工商大学吴金莲浙江工业大学王国庆浙江农林大学李利婷温州大学潘加顺浙江工商大学吴军建浙江工业大学杨木易浙江农林大学潘益斌温州大学邵成亮浙江工商大学徐俊浙江工业大学何梦沸浙江农林大学天目学院许明明温州大学瓯江学院邵旋 浙江工商大学徐磊浙江工业大学任金权浙江农林大学天目学院薛一强温州大学瓯江学院沈霞红浙江工商大学徐荣杰浙江工业大学吴小儿浙江农林大学天目学院陈星平浙江传媒学院沈颖浙江工商大学宣建楠浙江工业大学郭书涛浙江师范大学安亚通浙江大学孙鹏浙江工商大学杨世旺浙江工业大学李静静浙江师范大学白云浙江大学田小军 浙江工商大学杨雄浙江工业大学涂颜帅浙江师范大学曹聪琦浙江大学王斐斐浙江工商大学姚祺浙江工业大学虞银江浙江师范大学陈付浙江大学王同艳浙江工商大学叶斌浙江工业大学郑小平浙江师范大学丛丝雨浙江大学王文燕浙江工商大学叶良程浙江工业大学薛征南浙江师范大学行知学院戴鹏飞浙江大学徐彬帅浙江工商大学叶欣艺浙江工业大学杜林锋浙江树人大学东旭浙江大学徐美芳浙江工商大学张聪贵浙江工业大学金航正浙江树人大学董挺挺浙江大学宣栋强浙江工商大学张丰浙江工业大学王云杰浙江树人大学杜柑宏浙江大学叶雷 浙江工商大学张琳佳浙江工业大学章铁英浙江树人大学杜往泽浙江大学叶聘浙江工商大学张明浙江工业大学郑倍倍浙江树人大学费超浙江大学余辉捷浙江工商大学张雯浙江工业大学曹晓荷中国计量学院傅正达浙江大学俞嘉浙江工商大学张元玲浙江工业大学陈文威中国计量学院郭开乾浙江大学袁晓琼浙江工商大学章中宏浙江工业大学代维凯中国计量学院韩由浙江大学张彦浙江工商大学郑玮仪浙江工业大学高海明中国计量学院华强浙江大学郑蕾浙江工商大学周菲浙江工业大学何圣康中国计量学院黄河昆浙江大学周文华 浙江工商大学周嫣红浙江工业大学赖杭萍中国计量学院金家禾浙江大学陈泷浙江工商大学朱超逸浙江工业大学李晓辰中国计量学院李昊洋浙江大学董智洋浙江工商大学杭州商学院朱俊杰浙江工业大学鲁涵予中国计量学院李伟浙江大学蔡良建浙江工业大学朱李核浙江工业大学潘艳红中国计量学院李晓彬浙江大学陈杰浙江工业大学朱丽辉浙江工业大学汪秀婷中国计量学院李长宝浙江大学陈瑞森浙江工业大学朱泽伟浙江工业大学王妍中国计量学院刘鹏浙江大学陈武斌浙江工业大学邵剑集浙江工业大学之江学院许斌中国计量学院苗毅浙江大学陈妍婷浙江工业大学郑南浙江工业大学之江学院许硕中国计量学院潘冠宏浙江大学董慧婵浙江工业大学蔡琦玮浙江海洋学院杨晓东中国计量学院钱浩亮浙江大学方圣浙江工业大学陈婧浙江海洋学院张彬中国计量学院谭毅华浙江大学方文其浙江工业大学许贤恩浙江海洋学院张靖涛中国计量学院王立升浙江大学冯志国浙江工业大学严墩浙江海洋学院赵可宁中国计量学院王晓明浙江大学葛春霞浙江工业大学陈巧玲浙江科技学院朱锋杰中国计量学院王云立浙江大学顾唯超浙江工业大学陈思思浙江科技学院。
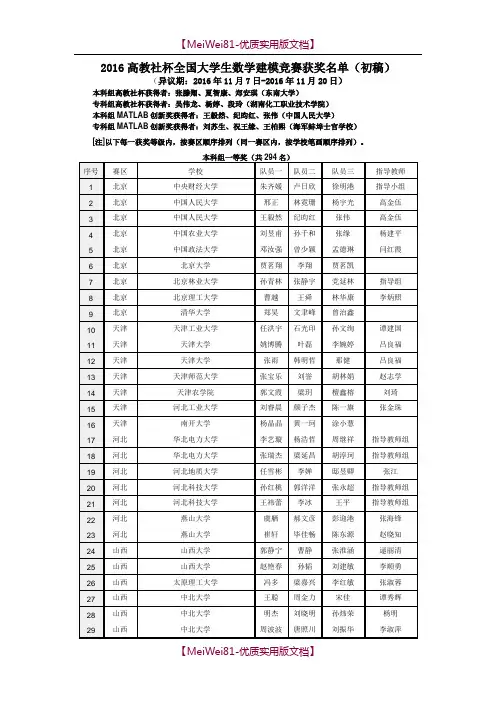
2018高教社杯全国大学生数学建模竞赛获奖名单
全国大学生数学建模竞赛组织委员会
2018年12月4日
本科组高教社杯获得者:刘一鸣、王超玥、赖鹏程(上海交通大学)
专科组高教社杯获得者:薛振勇、王维、王香香(南京铁道职业技术学院)
本科组MATLAB创新奖获得者:李亚丽、董羽凡、林晓俊(中国计量大学)
专科组MATLAB创新奖获得者:胡颖圣、肖永康、万和彬(安徽商贸职业技术学院)
[注] 同一获奖等级内,按赛区顺序排列(同一赛区内,按学校拼音顺序排列)。
本科组一等奖(291名)
本科组二等奖(1193名)。