汽车售后服务毛利率可达50%

真笔特殊符号大全Φ℡㊣㈱㎎㎏㎜㎝㎞㎡㏄㏎㏑㏒㏕─ ━│ ┃┄┅┆┇┈┉┊┋┌ ┍┎┏┐ ┑┒┓└ ┕┖┗┘ ┙┚┛├ ┝┞┟┠┡┢┣┤ ┥┦┧┨┩┪┫┬ ┭┮┯┰┱┲┳┴ ┵┶┷┸┹┺┻┼ ┽┾┿╀╁╂╃╄╅╆╇╈╉╊╋═ ║ ╒ ╓ ╔ ╕ ╖ ╗ ╘ ╙ ╚ ╛ ╜ ╝ ╞ ╟ ╠╡ ╢ ╣ ╤ ╥ ╦ ╧ ╨ ╩ ╪ ╫ ╬ ╭╮╯╰╱╲╳▁▂▃▄ ▅▆▇█ ▉▊▋▌ ▍▎▏▓ ▔▕■ □ ▲ △▼ ▽◆◇○ ◎● ◢◣◤◥★☆☉♀♂、。

〃々〆〇〈〉《》「」『』【】〒〓〔〕〖〗〝〞〡〢〣〤〥〦〧〨〩ぁあぃいぅうぇえぉおかがきぎくぐけげこごさざしじすずせぜそぞただちぢっつづてでとどなにぬねのはばぱひびぴふぶぷへべぺほぼぽまみむめもゃやゅゆょよらりるれろゎわゐゑをん゛゜ゝゞァアィイゥウェエォオカガキギクグケゲコゴサザシジスズセゼソゾタダチヂッツヅテデトドナニヌネノハバパヒビピフブプヘベペホボポマミムメモャヤュユョヨラリルレロヮワヰヱヲンヴヵヶーヽヾㄅㄆㄇㄈㄉㄊㄋㄌㄍㄎㄏㄐㄑㄒㄓㄔㄕㄖㄗㄘㄙㄚㄛㄜㄝㄞㄟㄠㄡㄢㄣㄤㄥㄦㄧㄨㄩ︰￠￡¤￥| §¨- ˉ ° ± ′ μ · 1 o à á è é ê ì í D ò ó ×ùúüY T àáa è é ê ì í e ò ó ÷ ù ú ü y t ā ā ē ē ě ě ī ī ń ň ō ō ū ū ∥ǎ ǎ ǐ ǐ ǒ ǒ ǔ ǔ ǖ ǖ ǘ ǘ ǚ ǚ ǜ ǜ ɑɡˇ ˉ ˊˋ˙ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ σ τ υ φ χ ψ ω Ё А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф ХЦ Ч Ш Щ ЪЫ Ь Э Ю Я а б в г д е ж з и й к л м н о п р с т у ф х ц ч ш щ ъ ы ь э ю яё‐–—― ‖‘ ’ “ ” ‥… ‰ ′ ″ ‵※￣€ ℃℅ ℉№ ℡ⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹ← ↑ → ↓ ↖↗↘↙∈∏ ∑ ∕ ° √ ∝∞ ∟ ∠∣∥∧∨∩ ∪∫ ∮∴∵∶∷～∽≈ ≌≒≠ ≡ ≤ ≥ ≦≧≮≯⊕⊙⊥⊿⌒①②③④⑤⑥⑦⑧⑨⑩⑴⑵⑶⑷⑸⑹⑺⑻⑼⑽⑾⑿⒀⒁⒂⒃⒄⒅⒆⒇⒈⒉⒊⒋⒌⒍⒎⒏⒐⒑⒒⒓⒔⒕⒖⒗⒘⒙⒚⒛㈠㈡㈢㈣㈤㈥㈦㈧㈨㈩︱︳︴︵︶︷︸︹︺︻︼︽︾︿﹀﹁﹂﹃﹄﹉﹊﹋﹌﹍﹎﹏﹐﹑﹒﹔﹕﹖﹗﹙﹚﹛﹜﹝﹞﹟﹠﹡﹢﹣﹤﹥﹦﹨﹩﹪﹫！＂＃＄％＆＇（）＊＋，－．／０１２３４５６７８９：；＜＝＞？＠ＡＢＣＤＥＦＧＨＩＪＫＬＭＮＯＰＱＲＳＴＵＶＷＸＹＺ［＼］＾＿｀ａｂｃｄｅｆｇｈｉｊｋｌｍｎｏｐｑｒｓｔｕｖｗｘｙｚ｛｜｝～￠￡￢￣￤￥o(╥﹏╥)o真笔个性符号大全兦亼亽亖亗盲凸凹卝卍卐匸皕旡玊尐幵木囘囙囚四囜囝回囟因女團団囤亢囦囧囨雲囪囫囬園化囯困囪囲図圍掄囶囷正囹固囻囼國圖囿圀圁圂圃吾圅圓圇圈幸青國圌圍園圏圐圑員圓圔圕圖圗團圙圚圛圈圝圞㈱㊣㊊㊋㊌㊍㊎㊏㊐㊑㊒㊓㊔㊕㊖㊗㊘㊜㊝㊞㊟㊠㊡㊢㊤㊥㊦㊧㊨㊩㊪㊫㊬㊭㊮㊯㊰✗✘✚✪✣✤✥✦✧✩✫✬✭✮✯✰✱✲✳❃❂❁❀✿✾✽✼✻✺✹✸✷✶✵✴❄❅❆❇❈❉❊❋❖☀☂☁❣✚✪✣✤✥✦❉❥❦❧❃❂❁❀✄☪☣☢☠☭♈➸✓✔✕✖｡✿*ﾟﾟ･✿｡真笔网提供▧▨▣▤▥▦▩◘◙▒░๑۞๑๑۩ﺴﺴ۩๑o (‧'''‧)o❆べò⊹⊱⋛⋋⋌⋚⊰⊹ⓛⓞⓥⓔべ☀☼☜☞◈♦◊◦教大家如何打特殊符号在“智能ABC”里先按v,再按0~9中任何一个数字就行了（下面真笔网将详细介绍这个方法）~~在“全拼”输入法图标的后面，有“键盘”的图标，在那上面“右键” 就出来特殊符号了~~在“搜狗”输入法图标的后面，有“扳手”的图标（Ctrl+Shift+M）；选择“软键盘”（Shift+S）就出来1-9排N多特殊符号了~~开始---程序---附件---造字程序;里面N多，自己设计吧~~真笔网独家详细讲解特殊符号首先在“智能ABC”里先按v,再按0~9中任何一个数字就行了（这个都不会？F了你了Q 320088518 吧）~~ /fuhao.htm独家提供∝╬══→选择输入法智能ABC打V1出现特殊的符号（真笔网提示：PgUp ；PgDn 多翻几页）：、。

2024～2025学年度第一学期期中试卷高二数学考试时长90分钟一、选择题：本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,(1,2,1)=-a ，(,4,2)x =b ，若⊥a b ，则x =()A ）2-（B ）2（C ）6-（D ）6已知为直线的一个方向向量，为平面的一个法向量，则下列选项中正确的是()A ）（B ）（C ）（D ）已知a ，b ，c 不共面，3e t =--a b c ，26+2t =-+d a b c ，若e 与d 共线，则实数t 的()A ）3-（B ）1（C ）3（D ）3-或3已知函数()sin(2)(0)f x x ϕϕπ=+<<的图像关于直线6x π=对称，则ϕ的值为()（A ）12π（B ）3π（C ）6π（D ）23π在空间直角坐标系中，已知长方体1111ABCD A B C D -的顶点()()0,0,0,3,0,0D A ,()()13,2,0,0,2,4C ，则直线11A B 与平面11ABC D 之间的距离为()A ）125（B ）43（C ）1（D ）2已知平面,αβ，直线l α⊂，直线m β⊂，//l β，则“//l m ”是“//m α”的()A ）充分而不必要条件（B ）必要而不充分条件C ）充分必要条件（D ）既不充分也不必要条件7.如图，在正方体1111ABCD A B C D -中，P 为对角线1BD 的三等分点，P 到各顶点的距离的不同取值有()（A ）3个（B ）4个（C ）5个（D ）6个8．已知一个正四棱锥的侧棱与底面所成角的正弦值为5，则该四棱锥侧面与底面所成角的余弦值为()（A ）2（B ）5（C ）13（D ）59.空间直角坐标系中，一定点到三个坐标轴的距离都是1，则该点到原点距离是()（A ）（B ）2（C ）3（D ）210．如图，在四棱柱1111ABCD A B C D -中，底面ABCD 为正方形，侧棱1AA ⊥底面ABCD ，3AB =，16AA =，P 是侧面11BCC B 内的动点，且1AP BD ⊥，记AP 与平面11BCC B 所成的角为θ，则tan θ的最大值为()．（A ）（B ）3（C ）2（D ）259二、填空题:本大题共5小题,每小题5分,共25分.11.已知a，b 是空间两向量，若||3,||2,||a b a b ==-=则a 与b 的夹角为__________.12.已知(1,1,1)A ，(2,1,1)B --，点P 在坐标平面xOy 上，且A 、B 、P 三点共线，则P 点的坐标为__________.13.在ABC 中，sin 53C =，AC 4=，1cos 9B =，则AB =__________.14.在棱长为2的正方体1111ABCD A B C D -中，E 为BC 的中点，点P 在线段1D E 上，则点P 到直线1AA 的距离的最小值为__________.15.如图，在三棱锥O ABC -中，三条侧棱OA ，OB ，OC 两两垂直，且2OA OB OC ===，M 为ABC 内部一动点，过M 分别作平面OAB ，平面OBC ，平面OAC 的垂线，垂足分别为P ，Q ，.R ①直线PR 与直线BC 是异面直线；||MP MQ MR ++②为定值；③三棱锥M PQR -的外接球表面积的最小值为43π；④当2||||3MP MQ ==时，平面PQR 与平面OBC 所成的锐二面角为45.︒则以上结论中所有正确结论的序号是______.三、解答题:本大题共4小题，共45分.解答应写出文字说明，演算步骤或证明过程.16.（本小题满分8分）已知函数2()sin(2)cos 6f x x x π=-+.（Ⅰ）求(0)f 的值；（Ⅱ）求函数)(x f 的单调递增区间.17.（本小题满分15分）如图，四边形ABCD 是边长为3的正方形，DE ABCD ⊥平面，//AF DE ，3,DE AF =BE 与平面ABCD 所成角为3π．（Ⅰ）求证：AC ⊥平面BDE ；（Ⅱ）平面FBE 与平面BED 所成角的余弦值；（Ⅲ）求三棱锥E BDF -的体积．18.（本小题满分12分）如图，在四棱锥P ABCD -中，底面A BCD 是菱形，点,E F 分别为,AB PD 的中点．60DAB ︒∠=，平面PDE ⊥平面ABCD ，2PD AD ==.（Ⅰ）求证：直线//AF 平面.PCE （Ⅱ）再从条件①、条件②这两个条件中选择一个作为已知，在线段PE 上是否存在点M ，使得DM ⊥平面ABF ？若存在，求出PMPE的值；若不存在，请说明理由．条件①：PE CE =;条件②：cos 7PED ∠=.19.（本小题满分10分）实数集上的函数，不妨称为“集合的标记函数”.对于两个集合和，定义集合．当集合且集合时，（Ⅰ）求与的值；（Ⅱ）求集合（用列举法表示）；（Ⅲ）用表示有限集合所包含元素的个数.已知集合C 是正整数集的有限子集，求的最小值，并说明理由．期中试题参考答案（高二数学）一、选择题:本大题共10小题,每小题5分,共50分.1~5CBCCA 6~10DBCDA二、填空题:本大题共5小题,每小题5分,共25分.11.3π；12.1,1,02⎛⎫- ⎪⎝⎭；13.3;14.；15②③.（0分/选对一个2分/选对两个5分）三、本大题共4小题，共45分.解答应写出文字说明，演算步骤或证明过程.16.（本小题满分8分）解：（I ）11(0)sin(cos 01622f π=-+=-+=..........3分(每个值1分，结论1分)22cos 16sin 2cos 6cos 2sin )(xx x x f ++-=ππ..........5分（一个公式给1分）212sin 23+=x （II ）当Z k k x k ∈+≤≤+-,22222ππππ，...........6分即Z k k k x ∈++-∈],4,4[ππππ时，)(x f 单调递增.所以，函数)(x f 的单调增区间是Z k k k ∈++-],4,4[ππππ...........8分（结论不规范扣1分）17.（本小题满分15分）证明：()Ⅰ因为DE ⊥平面ABCD ，AC ⊂平面ABCD ，所以.DE AC ⊥因为ABCD 是正方形，所以AC BD ⊥，,,BD DE D BD DE =⊂ 平面BDE ，从而AC ⊥平面.BDE ……………………………5分解：()Ⅱ因为DE ABCD ⊥平面，,DA DC ABCD ⊂平面,所以,.DE DA DE DC ⊥⊥又因为DA DC ⊥.,,DA DE DC 两两垂直，如图建系．因为BE 与平面ABCD 所成角为60︒，即60DBE ∠=︒，所以EDDB=由3AD =，可知DE =AF则(3,0,0)A ，(3,F ，(0,E ，(3,3,0)B ，(0,3,0)C ，所以(0,BF =-，(3,0,EF =-设平面BEF 的法向量为(,,)n x y z =，则00n BF n EF ⎧⋅=⎪⎨⋅=⎪⎩，即30.30y x ⎧-=⎪⎨-=⎪⎩令z =n =因为AC ⊥平面BDE ，所以CA 为平面BDE 的法向量，(3,3,0).CA =-所以cos ,||||n CA n CA n CA ⋅==平面FBE 与平面BED所成角的余弦值为13……………………12分()Ⅲ因为13E BDF F BDE BDE V V S h--∆==⋅又知1122BDE S BD DE ∆=⋅=⨯=|||cos ,|||||BF CA h BF BF CA CA ⋅=<>=所以E BDF V -=………………………………………15分18.（本小题满分12分）(1)证明：取PC 的中点G ，连接FG ，EG ，如图．F ，G 分别是PD ，PC的中点，，12FG DC =，又四边形ABCD 是菱形，E 是AB 的中点，，12AE DC =，//AE FG ∴=，∴四边形AEGF 是平行四边形，，又AF ⊂/平面PCE ，EG ⊂平面PCE ，//AF ∴平面.PCE (5)分(2)选择①：假设在线段PE 上存在点M ，使得DM ⊥平面.ABF 如图，连接DB ，DE ， 四边形ABCD 是菱形，60DAB ︒∠=，DAB ∴ 是等边三角形．E 是AB 的中点，DE AB ∴⊥，又//AB DC ，.DE DC ∴⊥则PE CE =又 222PD DE PE +=,所以PD DE ⊥.又 平面PDE ⊥平面ABCD ，平面PDE 平面ABCD=DE ，DC ⊂平面ABCD ,DC ∴⊥平面PDE.又PD ⊂平面PDE ,所以PD DC ⊥.,,DE DC DP 两两垂直，如图建系.另证：假设在线段PE 上存在点M ，使得DM ⊥平面.ABF 如图，连接DB ，DE ， 四边形ABCD 是菱形，60DAB ︒∠=，DAB ∴ 是等边三角形．E 是AB 的中点，DE AB ∴⊥，又//AB DC ，.DE DC ∴⊥则PE CE =又 222PD DE PE +=,所以PD DE ⊥.又 平面PDE ⊥平面ABCD ，平面PDE 平面ABCD=DE ，PD ⊂平面PDE ,PD ∴⊥平面ABCD.又DC ⊂平面ABCD ,所以PD DC ⊥.,,DE DC DP 两两垂直，如图建系.则(0,0,0)D ，(0,0,2)P，)B，)1,0A-，()0,0,1F，)E，1,1)FA =--，1)FB =-0,2)PE =-,.设[],0,1PM PE λλ=∈ ，[]0,1λ∈，),0,2PM λ=-则()))0,0,2,0,2,0,22DM DP PM λλ=+=+-=-，DM ⊥ 平面ABF ，00DM FA DM FB ⎧⋅=⎪∴⎨⋅=⎪⎩即32203220λλλλ+-=⎧∴⎨+-=⎩解得25λ=，∴在线段PE 上存在点M ，使得DM ⊥平面ABF ，此时25PM PE =.…………………………12分选择②：假设在线段PE 上存在点M ，使得DM ⊥平面.ABF 如图，连接DB ，DE ， 四边形ABCD 是菱形，60DAB ︒∠=，DAB ∴ 是等边三角形．E 是AB 的中点，DE AB ∴⊥，又//AB DC ，.DE DC ∴⊥在PDE中，2222cos 2PE DE PD PDE PE DE +-∠=⋅,解得：PE .又 222PD DE PE +=,所以PD DE ⊥.又 平面PDE ⊥平面ABCD ，平面PDE 平面ABCD=DE ，PD ⊂平面PDE ,PD ∴⊥平面ABCD.又DC ⊂平面ABCD ,所以PD DC ⊥.,,DE DC DP 两两垂直，如图建系.则(0,0,0)D ，(0,0,2)P，)B，)1,0A-，()0,0,1F，)E，1,1)FA =--，1)FB =-0,2)PE =-,.设[],0,1PM PE λλ=∈ ，[]0,1λ∈，),0,2PM λ=-则()))0,0,2,0,2,0,22DM DP PM λλ=+=+-=-，DM ⊥ 平面ABF ，00DM FA DM FB ⎧⋅=⎪∴⎨⋅=⎪⎩即32203220λλλλ+-=⎧∴⎨+-=⎩解得25λ=，∴在线段PE 上存在点M ，使得DM ⊥平面ABF ，此时25PM PE =.…………………………12分19.（本小题满分10分）解：（Ⅰ）由1∈知，由1∉知．……………………2分（Ⅱ）(p+(p=1，即实数属于且只属于集合、中的一个，故t={1,2,4,5,8,9}．……………………4分（Ⅲ）引理1.对于任意集合、，考虑添加集合中的元素对|tU的影响。

2024年沪科版高二数学上册月考试卷178考试试卷考试范围：全部知识点；考试时间：120分钟学校：______ 姓名：______ 班级：______ 考号：______总分栏题号一二三四五六总分得分评卷人得分一、选择题(共9题，共18分)1、从装有2支铅笔和2支钢笔的文具袋内任取2支笔；那么互斥而不对立的两个事件是（）A. 恰有1支钢笔；恰有2支铅笔。

B. 至少有1支钢笔；都是钢笔。

C. 至少有1支钢笔；至少有1支铅笔。

D. 至少有1个钢笔；都是铅笔。

2、（2x-sinx）dx的值是（）A.B.C.D.3、设不等的两个正数a，b满足a3﹣b3=a2﹣b2，则a+b的取值范围是（）A. （1，+∞）B.C.D. （0，1）4、设函数f（x）是定义在R上的奇函数，且f（x）= 则g[f（﹣7）]=（）A. 3B. ﹣3C. 2D. ﹣25、如图，底面为正方形且各侧棱长均相等的四棱锥V﹣ABCD可绕着棱AB任意旋转，若AB⊂平面α，M，N分别是AB，CD的中点，AB=2，VA= 点V在平面α上的射影为点O，则当ON的最大时，二面角C﹣AB﹣O的大小是（）A. 90°B. 105°C. 120°D. 135°6、已知z（1+2i）=4+3i，则|z|=（）A.B.C. 2D.7、已知函数f（x）=函数g（x）=-f（1-x），则函数y=f（x）-g（x）的零点的个数为（）A. 2C. 4D. 58、不同的直线m和n，不同的平面α，β，γ，下列条件中能推出α∥β的是（）A. α∩γ=n，β∩γ=m，n∥mB. α⊥γ，β⊥γC. n∥m，n⊥α，m⊥βD. n∥α，m∥β，n∥m9、事件A，B是相互独立的，P（A）=0.4，P（B）=0.3，下列四个式子：①P（AB）=0.12；②P（B）=0.18；③P（A）=0.28；④P（）=0.42．其中正确的有（）A. 4个B. 2个C. 3个D. 1个评卷人得分二、填空题(共9题，共18分)10、若函数是函数的反函数，其图象经过点则______________．11、【题文】在数列中，已知记为数列的前项和，则____.12、【题文】将函数的图象向左平移个单位，得到函数的图象，则____13、数列{a n}中，a1=1，a n+1=2a n+1，则通项a n=____14、已知等差数列{a n}中，a1+a13=10，则a3+a5+a7+a9+a11=____15、如果圆：x2+y2+2x+4y+m=0上恰有两点到直线l：x+y+1=0的距离为则m的取值范围是______ ．16、已知随机变量X～N（1，4）且P（X＜2）=0.72，则P（1＜X＜2）= ______ ．17、将二进制数10101（2）化为十进制是 ______ ．18、若实数xy满足{x鈮�1y鈮�0x+y鈮�4则z=2x+y的最大值是 ______ ．评卷人得分三、作图题(共6题，共12分)19、著名的“将军饮马”问题：有一位将军骑着马要从A地走到B地；但途中要到水边喂马喝一次水，则将军怎样走最近？20、A是锐角MON内部任意一点，在∠MON的两边OM，ON上各取一点B，C，组成三角形，使三角形周长最小．（如图所示）21、已知，A，B在直线l的两侧，在l上求一点，使得PA+PB最小．（如图所示）22、著名的“将军饮马”问题：有一位将军骑着马要从A地走到B地；但途中要到水边喂马喝一次水，则将军怎样走最近？23、A是锐角MON内部任意一点，在∠MON的两边OM，ON上各取一点B，C，组成三角形，使三角形周长最小．（如图所示）24、已知，A，B在直线l的两侧，在l上求一点，使得PA+PB最小．（如图所示）评卷人得分四、解答题(共3题，共6分)25、为了检测某条生产线上产品的尺寸．现从该条生产线上每隔一定时间取一件产品；共取了50件，测得其产品尺寸后，画得其频率分布直方图如图．（1）分别求尺寸在[10；15）和[20，25）内产品的频率．（2）求尺寸在[20；25）内产品的个数．26、在数列{a n}中，．（1）计算a2，a3，a4，猜想数列{a n}的通项公式并加以证明；（2）求证：．27、【题文】 (本题满分14分；其中第1小题6分，第2小题8分)在中，分别为角的对边，且满足(1)求角大小；(2)若求的面积的最大值.评卷人得分五、计算题(共3题，共6分)28、如图，正三角形ABC的边长为2，M是BC边上的中点，P是AC边上的一个动点，求PB+PM的最小值．29、解不等式组．30、在（1+x）6（1+y）4的展开式中，记x m y n项的系数为f（m，n），求f（3，0）+f（2，1）+f（1，2）+f（0，3）的值．评卷人得分六、综合题(共1题，共10分)31、已知S n为等差数列{a n}的前n项和，S6=51，a5=13．参考答案一、选择题(共9题，共18分)1、A【分析】A 恰有1支钢笔和恰有2支铅笔互斥但不对立．B至少有1支钢笔和都是钢笔不互斥．C至少有1支钢笔和至少有1支铅笔不互斥．D 至少有1个钢笔和都是铅笔是对立事件．故选 A．【解析】【答案】根据恰有1支钢笔和恰有2支铅笔互斥但不对立；至少有1支钢笔和都是钢笔不互斥，至少有1支钢笔和至少有1支铅笔不互斥，至少有1个钢笔和都是铅笔是对立事件，得到答案．2、A【分析】==．故选A．【解析】【答案】利用握微积分基本定理即可求出．3、B【分析】【解答】解：由a2+ab+b2=a+b；得：（a+b）2﹣（a+b）=ab；而所以得．故选B．【分析】根据题意及立方差公式的展开形式可得出a2+ab+b2=a+b的值，然后可求出ab与a+b的关系式，结合基本不等式即可得出答案．4、D【分析】【解答】解：函数f（x）是定义在R上的奇函数，且f（x）=设x＜0，则﹣x＞0，则f（﹣x）=log2（﹣x+1）；∵f（﹣x）=﹣f（x）；∴f（x）=﹣f（﹣x）=﹣log2（﹣x+1）；∴g（x）=﹣log2（﹣x+1）（x＜0）；∴f（﹣7）=g（﹣7）=﹣log2（7+1）=﹣3；∴g（﹣3）=﹣log2（3+1）=﹣2；故选：D．【分析】先设x＜0，则﹣x＞0，根据函数的奇偶性，即可求出g（x），再代值计算即可．5、B【分析】【解答】解：设∠VMO=θ；则∵M、N分别是AB、CD的中点，AB=2，VA=∴AM=1，VM= = =2；MN=BC=AB=2；VN=VM=2；则三角形VNM为正三角形；则∠NMV=60°；则OM=2cosθ；在三角形OMN中；ON2=MN2+OM2﹣2MN•OMcos（60°+θ）=4+4cos2θ﹣2×2×2cosθcos（60°+θ）=4+4cos2θ﹣8cosθ（cosθ﹣sinθ）=4+4cos2θ﹣4cos2θ+4 sinθcosθ=4+2 sin2θ；∴要使ON最大；则只需要sin2θ=1，即2θ=90°即可，则θ=45°；此时二面角C﹣AB﹣O的大小∠OMN=60°+θ=60°+45°=105°；故选：B【分析】根据条件确定二面角的平面角，结合余弦定理以及两角和差的余弦公式以及倍角公式进行求解即可．6、D【分析】【解答】解：∵z（1+2i）=4+3i；∴|z（1+2i）|=|4+3i|；即：|z||1+2i|=|4+3i|；即：|z|∴|z|=故选：D．【分析】利用积的模等于模的积，通过复数方程两边求模，化简即可．7、C【分析】解：函数f（x）= 可得则令f（x）-g（x）=0；可得f（x）+f（1-x）=画出y=f（1-x）+f（x）与y= 的图象如图所示：由图可得：y=f（1-x）+f（x）与y= 有4个交点。

三峡名校联盟2023年秋季联考高2026届数学试题（答案在最后）(考试范围：人教A 版2019必修第一册第一章、第二章、第三章满分：150时间：120分钟)一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.请把正确选项在答题卡中的相应位置涂黑.1.已知集合{}2,A x x =，若1A ∈，则x =（）A ．1或1-B ．1C ．1-D ．1-或02.“0xy >”是“0,0x y >>”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.函数()2xf x x =+的零点所在区间是（）A ．()2,1--B ．()1,0-C ．()0,1D ．()1,24.一元二次不等式20ax bx c ++>的解集为()2,3，则不等式20cx bx a ++<的解集为（）A ．()3,2-- B.1123,⎛⎫-- ⎪⎝⎭C.11,32⎛⎫ ⎪⎝⎭D.113,,2⎛⎫⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎭⎝⎭5.已知0.91.2313,log 0.7,3a b c -⎛⎫=== ⎪⎝⎭，则,,a b c 的大小关系是（）A.b<c<aB.<<C.c<a<bD.c b a<<6.著名数学家、物理学家牛顿曾提出：物体在空气中冷却，如果物体的初始温度为1θ℃，空气温度为0θ℃，则t 分钟后物体的温度θ（单位：℃)满足：010()e ktθθθθ-=+-.若常数0.05k =，空气温度为30℃，某物体的温度从110℃下降到40℃以下，至少大约需要的时间为（）（参考数据：ln 20.69≈）A.40分钟B.41分钟C.42分钟D.43分钟7.函数()f x 的定义域为R ，对任意的∈1,+∞)、∈0,+∞，都有+<成立，且函数()1f x +为偶函数，则（）A.()()()123f f f <-<B.()()()231f f f -<< C.()()()213f f f -<< D.()()()312f f f <<-二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，选对但不全的得2分，有选错的得0分.9.设a b >，则下列不等式一定成立的是（）A.−c >−B.33a b >C.a b> D.a c b c>10.下列说法正确的是（）A ．1Q3∈B ．若集合{}210A x ax x =++=中只有一个元素，则14a =C ．命题“∃x <3,2x −”的否定是“x ”D ．若命题“∀x ∈1,2,xC ．不等式[][]22x x -≤的解集为{}13x x -≤<三、填空题：本大题共4小题，每小题5分，共20分.其中第16题第一空2分，第二空3分.请把答案填在答题卡的相应位置上.13.若幂函数()()211m m m f x x +=+-在()0,∞+上是减函数，则m =________．14.1634+log 1212−log 123=________．15.函数()()log 231a f x x =-+（0a >且1a ≠）的图象恒过定点(),A m n ，若对任意正数x 、y 都有4mx ny +=，则121x y++的最小值是________．四、解答题：本大题共6小题，第17题10分，18、19、20、21、22题各12分，共70分.解答应写出文字说明、证明过程或演算步骤.必须把解答过程写在答题卡相应题号指定的区域内，超出指定区域的答案无效.21．已知函数()f x 的定义域为()()()()0,,1f xy f x f y +∞-=+，当1x >时，()1f x <-．（1）求()1f 的值；（2）证明：函数()f x 在()0,∞+上为单调减函数；（3）解不等式()()22f x f x -+>-．22．已知定义在R 上的函数1()421()xx f x m m m +=⋅-+-∈R ．（1）已知当m >0时，函数()f x 在0,2上的最大值为8，求实数m 的值；（2）若函数()y g x =的定义域内存在0x ，使得00()()2g a x g a x b ++-=成立，则称()g x 为局部对称函数，其中(,)a b 为函数()g x 的局部对称点．若(1,0)是()f x 的局部对称点，求实数m 的取值范围．三峡名校联盟2023年秋季联考22．【解析】（1）令t =2x ，则：t ∈1,4设g t =mt 2−2t +1−m (m >0)由题意，g t 在1,4的最大值为8.因为m >0，二次函数g t 图像开口向上，所以g t max=max g 1，g 4即:g 1=8或g 4=8解得：m =1经检验：m =1符合题意（2）根据局部对称函数的定义可知，(1)(1)0f x f x ++-=，即1111114214210xx x x m m m m +++--+⋅-+-+⋅-+-=，2424222210x x x x m m m --⋅+⋅--⋅-⋅+=，()()122122212124412414x x xx xxx x m --⎛⎫+- ⎪+-⎝⎭==⎛⎫+-+- ⎪⎝⎭，令12212xx s ⎛⎫=+- ⎪⎝⎭，则22229292922s s m s s s s s s ===+-+--+，因为1221132xx s ⎛⎫=+-≥= ⎪⎝⎭，当且仅当122xx=，0x =时等号成立，函数92y s s =-+在区间[3,)+∞上单调递增，所以9923223y s s =-+≥-+=，所以2(0,1]92m s s=∈-+，所以m 的取值范围是(0,1]．。

2024-2025学年北师大二附中高三数学上学期9月统练试卷全卷满分150分，考试时间120分钟一、单选题：本题共10小题，共40分．1．已知全集{}2,1,0,1,2,3U =--，集合{Z |2}A x x =∈<，则U C A =（）A ．{}1,0,1-B ．{}2,2,3-C ．{}2,1,2--D ．{}2,0,3-2．若i(1)1z -=，则z z +=（）A ．2-B ．1-C ．1D ．23．如果0a b >>，那么下列不等式一定成立的是（）A ．a b<B ．11a b>C ．1122ab⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭D ．ln ln a b>4．从分别写有1，2，3，4，5，6的6张卡片中无放回随机抽取2张，则抽到的2张卡片上的数字之积是4的倍数的概率为（）A ．15B ．13C ．25D ．235．“空气质量指数（AQI ）”是定量描述空气质量状况的无量纲指数．当AQI 大于200时,表示空气重度污染,不宜开展户外活动．某地某天0~24时的空气质量指数y 随时间t 变化的趋势由函数10290,01224,1224t t y t -+≤≤⎧⎪=⎨<≤⎪⎩描述,则该天适宜开展户外活动的时长至多为（）A ．5小时B ．6小时C ．7小时D ．8小时6．已知等差数列{}n a 的公差为d,前n 项和为n S ,则“d>0”是465"+2"S S S >的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件7．某地的中学生中有60%的同学爱好滑冰，50%的同学爱好滑雪，70%的同学爱好滑冰或爱好滑雪，在该地的中学生中随机调查一位同学，若该同学爱好滑雪，则该同学也爱好滑冰的概率为（）A ．0.8B ．0.4C ．0.2D ．0.18．有12个砝码，总质量为45g ，它们的质量从大到小依次构成等差数列，且最重的3个砝码质量之和是最轻的3个砝码质量之和的4倍．用这些砝码称一个质量为30g 的物体，则需要的砝码个数至少为（）A ．4B ．5C ．6D ．79．已知函数2()3log 2(1)f x x x =--，则不等式()0f x >的解集是（）A ．(1,4)B ．(,1)(4,)-∞+∞C ．(0,1)(4,)∞⋃+D ．(0,4)10．设,a b R ∈，数列{}n a 中，211,n n a a a a b +==+，N n *∈,则A ．当101,102b a =>B ．当101,104b a =>C ．当102,10b a =->D ．当104,10b a =->二、填空题：本题共5小题，每小题6分，共30分．11．函数1()21x f x =-的定义域是．12．在等差数列{}n a 中，公差d 不为0，19a =，且145,,a a a 成等比数列，则d =；当n =时，数列{}n a 的前n 项和n S 有最大值．13．在一次体育水平测试中，甲、乙两校均有100名学生参加，其中:甲校男生成绩的优秀率为70%，女生成绩的优秀率为50%;乙校男生成绩的优秀率为60%，女生成绩的优秀率为40%.对于此次测试，给出下列三个结论:①甲校学生成绩的优秀率大于乙校学生成绩的优秀率;②甲、乙两校所有男生成绩的优秀率大于甲、乙两校所有女生成绩的优秀率;③甲校学生成绩的优秀率与甲、乙两校所有学生成绩的优秀率的大小关系不确定.其中，所有正确结论的序号是.14．设函数2,(),x x a f x x x x a-≥⎧=⎨-+<⎩，当2a =时，()f x 的单调递增区间为，若x ∃∈R 且0x ≠，使得12f x ⎛⎫+= ⎪⎝⎭12f x ⎛⎫- ⎪⎝⎭成立，则实数a 的取值范围为.15．对于非空实数集合A ，记*{|,}A y x A y x =∀∈≤，设非空实数集合P 满足条件“若<1，则x P ∉”且M P ⊆，给出下列命题：①若全集为实数集，对于任意非空实数集合A ，必有*R A A =ð；②对于任意给定符合题设条件的集合M ，P ，必有**P M ⊆；③存在符合题设条件的集合M ，P ，使得*M P ⋂=∅；④存在符合题设条件的集合M ，P ，使得*M P ⋂≠∅．其中所有正确命题的序号是．三、解答题：本题共2小题，共30分．16．“稻草很轻，但是他迎着风仍然坚韧，这就是生命的力量，意志的力量”“当你为未来付出踏踏实实努力的时候，那些你觉得看不到的人和遇不到的风景都终将在你生命里出现”……当读到这些话时，你会切身体会到读书破万卷给予我们的力量．为了解某普通高中学生的阅读时间，从该校随机抽取了800名学生进行调查，得到了这800名学生一周的平均阅读时间（单位：小时），并将样本数据分成九组，绘制成如图所示的频率分布直方图．(1)求a 的值；(2)为进一步了解这800名学生阅读时间的分配情况，从周平均阅读时间在(]12,14，(]14,16，(]16,18三组内的学生中，采用分层抽样的方法抽取了10人，现从这10人中随机抽取3人，记周平均阅读时间在(]14,16内的学生人数为X ，求X 的分布列和数学期望；(3)以样本的频率估计概率，从该校所有学生中随机抽取20名学生，用()P k 表示这20名学生中恰有k 名学生周平均阅读时间在(]8,12内的概率，其中0,1,2,,20k =⋅⋅⋅．当()P k 最大时，写出k 的值．17．已知函数()ln sin f x x x =+．(1)求曲线()y f x =在点(1,(1))f 处的切线方程；(2)求函数()f x 在区间[1,e]上的最小值；(3)证明函数()f x 只有一个零点．1．B【分析】由补集的运算即可求解.【详解】解：{}{Z |2}1,0,1A x x =∈<=-，{}2,2,3U C A ∴=-，故选：B ．2．D【分析】利用复数的除法可求z ，从而可求z z +.【详解】由题设有21i1i i iz -===-，故1+i z =，故()()1i 1i 2z z +=++-=，故选：D3．D【分析】根据不等式的性质判断A 、B ，再根据指数函数的性质判断C ，根据对数函数的性质判断D ；【详解】解：因为0a b >>，所以0a b >>，故A 错误；因为0a b >>，所以11a b<，故B 错误；因为0a b >>，且12xy ⎛⎫= ⎪⎝⎭在定义域上单调递减，所以1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，故C 错误；因为0a b >>，且ln y x =在定义域()0,∞+上单调递增，所以ln ln a b >，故D 正确；故选：D4．C【分析】方法一：先列举出所有情况，再从中挑出数字之积是4的倍数的情况，由古典概型求概率即可.【详解】[方法一]：【最优解】无序从6张卡片中无放回抽取2张，共有()()()()()()()()()()()()()()()1,2,1,3,1,4,1,5,1,6,2,3,2,4,2,5,2,6,3,4,3,5,3,6,4,5,4,6,5,615种情况，其中数字之积为4的倍数的有()()()()()()1,4,2,4,2,6,3,4,4,5,4,66种情况，故概率为62155=.[方法二]：有序从6张卡片中无放回抽取2张，共有()()()()()()()()()()()()()()()1,2,1,3,1,4,1,5,1,6,2,3,2,4,2,5,2,6,3,4,3,5,3,6,4,5,4,6,5,6,(2,1),(3,1),(4,1),(5,1),(6,1),(3,2),(4,2),(5,2),(6,2),(4,3),(5,3),(6,3),(5,4),(6,4),(6,5)30种情况，其中数字之积为4的倍数有(1,4),(2,4),(2,6),(3,4),(4,1),(4,2),(4,3),(4,5),(4,6),(5,4),(6,2),(6,4)12种情况，故概率为122305=.故选：C.【整体点评】方法一：将抽出的卡片看成一个组合，再利用古典概型的概率公式解出，是该题的最优解；方法二：将抽出的卡片看成一个排列，再利用古典概型的概率公式解出；5．C 【分析】当AQI 大于200时,表示空气重度污染,不宜开展户外活动,即200y ≤时适合开展户外活动,根据分段函数的解析式,分情况讨论求出不等式解集,再求出区间长度即可.【详解】解:由题知,当AQI 大于200时,表示空气重度污染,不宜开展户外活动,即当AQI 小于等于200时,适宜开展户外活动,即200y ≤,因为10290,01224,1224t t y t -+≤≤⎧⎪=⎨-<≤⎪⎩,所以当012t ≤≤时,只需10290200t -+≤,解得:912t ≤≤,当1224t <≤时,只需24200≤,解得:1216t <≤,综上:适宜开展户外活动的时间段为916t ≤≤,共计7个小时.故选:C 6．C【详解】由46511210212(510)S S S a d a d d +-=+-+=，可知当0d >时，有46520S S S +->，即4652S S S +>，反之，若4652S S S +>，则0d >，所以“d >0”是“S 4+S 6>2S 5”的充要条件，选C ．【名师点睛】本题考查等差数列的前n 项和公式，通过套入公式与简单运算，可知4652S S S d +-=，结合充分必要性的判断，若p q ⇒，则p 是q 的充分条件，若p q ⇐，则p 是q 的必要条件，该题“0d >”⇔“46520S S S +->”，故互为充要条件．7．A【分析】根据题意，设某人爱好滑冰为事件A ，某人爱好滑雪为事件B ，由古典概型公式求出()P A 和()P AB ，进而由条件概率公式计算可得答案．【详解】根据题意，在该地的中学生中随机调查一位同学，设选出的同学爱好滑冰为事件A ，选出的同学爱好滑雪为事件B ，由于中学生中有60%的同学爱好滑冰，50%的同学爱好滑雪，70%的同学爱好滑冰或爱好滑雪，则()0.5P B =,而同时爱好两个项目的占50%60%70%40%+-=，即()0.4P AB =，则该同学爱好滑该同学也爱好滑冰的概率为()0.4(|)0.8()0.5P AB P A B P B ===．故选：A ．8．C【分析】设12个砝码的质量从大到小构成的等差数列为，公差为d ，<0，112n ≤≤，*N n ∈，由题意得到基本量的方程求解，然后由等差数列的前n 项和公式得到不等式求解即可.【详解】设12个砝码的质量从大到小构成的等差数列为，公差为d ，<0，112n ≤≤，*N n ∈，由题意可得()1231011124a a a a a a ++=++，12310111245a a a a a a ++++++= ，即()11334330a d a d +=⨯+，1126645a d +=，解得1132a =，12d =-，则()()211113127··22224n n n n n n n S na d n ---+⎛⎫=+=+-= ⎪⎝⎭，令227304n n nS -+=≥，又112n ≤≤，*N n ∈，解得612n ≤≤，*N n ∈，故需要的砝码个数至少为6．故选：C 9．A【分析】将不等式问题转化为函数图象问题，结合图象求得正确答案.【详解】依题意()2()3log 210f x x x =-->，()22log 13x x >-，由()2log 213y xy x =⎧⎪⎨=-⎪⎩解得1110x y =⎧⎨=⎩或2242x y =⎧⎨=⎩画出()22log ,13y x y x ==-的图象如下图所示，由图可知，不等式()0f x >的解集是(1,4).故选：A10．A【解析】若数列{}为常数列，101a a a ==，则只需使10a ≤，选项的结论就会不成立.将每个选项的b 的取值代入方程20x x b -+=，看其是否有小于等于10的解.选项B 、C 、D 均有小于10的解，故选项B 、C 、D 错误.而选项A 对应的方程没有解，又根据不等式性质，以及基本不等式，可证得A 选项正确.【详解】若数列{}为常数列，则1n a a a ==，由21n n a a b +=+，可设方程20x x b -+=选项A ：12b =时，2112n n a a +=+，2102x x -+=，1210∆=-=-<，故此时{}不为常数列，222112(22n n n n a a a +=+=+ ，且2211122a a =+≥，792(2)42a a ∴≥≥21091610a a >≥>，故选项A 正确；选项B ：14b =时，2114n n a a +=+，2104x x -+=，则该方程的解为12x =，即当12a =时，数列{}为常数列，12n a =，则101102a =<，故选项B 错误；选项C ：2b =-时，212n n a a +=-，220x x --=该方程的解为1x =-或2，即当1a =-或2时，数列{}为常数列，1n a =-或2，同样不满足1010a >，则选项C 也错误；选项D ：4b =-时，214n n a a +=-，240x x --=该方程的解为1172x ±=，同理可知，此时的常数列{}也不能使1010a >，则选项D 错误.故选：A.【点睛】遇到此类问题，不少考生会一筹莫展.利用函数方程思想，通过研究函数的不动点，进一步讨论a 的可能取值，利用“排除法”求解.11．{1x x ≥-且}0x ≠【分析】根据题意得到21010x x ⎧-≠⎨+≥⎩求解即可.【详解】由题知：210110x x x ⎧-≠⇒≥-⎨+≥⎩且0x ≠.故答案为：{1x x ≥-且}0x ≠.12．2-5【分析】根据等比数列得到2415a a a =，解得2d =-，再计算510a =>，610a =-<，得到答案.【详解】145,,a a a 成等比数列，故2415a a a =，即()()293994d d +=⨯+，解得2d =-或0d =（舍）.()921112n a n n =--=-，190a =>,510a =>，610a =-<，故5n =时，n S 有最大值.故答案为：2-；513．②③【解析】根据局部频率和整体频率的关系，依次判断每个选项得到答案.【详解】不能确定甲乙两校的男女比例，故①不正确；因为甲乙两校的男生的优秀率均大于女生成绩的优秀率，故甲、乙两校所有男生成绩的优秀率大于甲、乙两校所有女生成绩的优秀率，故②正确；因为不能确定甲乙两校的男女比例，故不能确定甲校学生成绩的优秀率与甲、乙两校所有学生成绩的优秀率的大小关系，故③正确.故答案为：②③.【点睛】本题考查局部频率和整体频率的关系，意在考查学生的理解能力和应用能力.14．1,2⎛⎤-∞⎥⎝⎦(1,)-+∞【分析】当2a =时，作出函数()f x 的图象，利用图象求出函数()f x 的递增区间；由12f x ⎛⎫+= ⎪⎝⎭12f x ⎛⎫- ⎪⎝⎭得()f x 关于12x =对称，结合二次函数的对称性及方程有解判断范围.【详解】当2a =时，2,2(),2x x f x x x x -≥⎧=⎨-+<⎩，其图象如下图：由图知，函数()f x 的单调递增区间为1,2⎛⎤-∞ ⎥⎝⎦；()2f x x x =-+，其图象关于12x =对称，显然当12a >时，由二次函数对称知x ∃∈R 且0x ≠，使得12f x ⎛⎫+= ⎪⎝⎭12f x ⎛⎫- ⎪⎝⎭成立，符合题意；则12a ≤时，当x a <时，y x =-关于12x =对称的曲线为1y x =-，联立21y x y x x =-⎧⎨=-+⎩，得12x y =-⎧⎨=-⎩或10x y =⎧⎨=⎩（舍去），所以当112a -<≤时，满足()()122f f -==-，即13312222f f ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭，符合题意；当1a ≤-时，曲线2y x x =-+，x a <与曲线1y x =-无公共点，不符合题意；综上，实数a 的取值范围为(1,)-+∞.故答案为：1,2⎛⎤-∞ ⎥⎝⎦；(1,)-+∞15．②③④【分析】根据新定义运算、补集、子集、交集和空集等知识对命题进行分析，从而确定正确答案.【详解】由于非空实数集A ，记*{|,}A y x A y x =∀∈≤，则*A 中元素为不大于A 中所有值的数，即不大于A 中最小元素的数组成的集合．①当A 集合下边界趋向负无穷大时，如(]()*R ,2,2,,A A A =-∞=+∞=∅ð，故①错误；②由于M P ⊆，假设M 中最小值为m ，P 最小值为p ，那么.m p ≥因此*M 表示不大于m 所有数组成的集合，*P 表示所有不大于p 的数组成的集合，则**P M ⊆，故②正确；③令3{|1}2M P x x ==<<，则*{|1}M x x =≤，故*M P ⋂=∅，故③正确；④令{|23}M P x x ==≤<，则*{|2}P x x =≤，故*{|2}M P x x ⋂==≠∅，故④正确；故答案为：②③④【点睛】思路点睛：解新定义题型的步骤：(1)理解“新定义”——明确“新定义”的条件、原理、方法、步骤和结论.(2)重视“举例”,利用“举例”检验是否理解和正确运用“新定义”;归纳“举例”提供的解题方法.归纳“举例”提供的分类情况.(3)类比新定义中的概念、原理、方法，解决题中需要解决的问题.16．(1)0.1a =(2)分布列见解析；数学期望()65E X =(3)10k =【分析】（1）根据频率和为1，可构造方程求得a 的值；（2）根据分层抽样原则可确定10人中，周平均阅读时间在(]12,14，(]14,16，(]16,18的人数，则可确定X 所有可能的取值，根据超几何分布概率公式可求得X 每个取值对应的概率，由此可得分布列；根据数学期望公式可求得期望值；（3）根据频率分布直方图可求得周平均阅读时间在(]8,12内的概率，利用二项分布概率公式可表示出()P k ，由此可确定结果.【详解】（1）()0.020.030.050.050.150.050.040.0121a ++++++++⨯= ，0.1a ∴=.（2）由频率分布直方图可得：周平均阅读时间在(]12,14，(]14,16，(]16,18三组的频率之比为0.05:0.04:0.015:4:1=，10∴人中，周平均阅读时间在(]12,14的人数为510510⨯=人；在(]14,16的人数为410410⨯=人；在(]16,18的人数为110110⨯=人；则X 所有可能的取值为0,1,2,3，()36310C 2010C 1206P X ∴====；()2164310C C 6011C 1202P X ====；()1264310C C 3632C 12010P X ====；()34310C 413C 12030P X ====；X ∴的分布列为：X123P1612310130∴数学期望()1131601236210305E X =⨯+⨯+⨯+⨯=.（3）用频率估计概率，从该校所有学生中随机抽取1名学生，周平均阅读时间在(]8,12内的概率()10.150.120.52p =+⨯==；则()()202020202020C 11C 1C 222k kk kk k k P k p p --=-=⨯⨯=，若()P k 最大，则20C k最大，∴当10k =时，()P k 取得最大值.17．(1)()1cos11sin1cos10x y +--+-=(2)()1sin1f =(3)见解析【分析】（1）对()f x 求导，求出()()1sin1,11cos1f f =+'=，由点斜式方程即可求出答案；（2）令()1()cos g x f x x x ==+'，()21sin g x x x-'=-，得出()g x 在[1,e]的单调性，结合零点存在性定理可得()f x 在()1,x α∈上单调递增，在(),e x α∈上单调递减，再比较()()1,e f f 的大小，即可得出答案.（3）利用导数判断函数的单调性，借助零点存在性定理，讨论01x <≤，1x π<≤和x π>时，()f x 的正负，即可得出证明.【详解】（1）()ln sin f x x x =+的定义域为()0,∞+，故1()cos f x x x'=+，()()1sin1,11cos1f f =+'=，所以曲线()y f x =在点(1,(1))f 处的切线方程为：()()sin11cos11y x -=+-，化简得：()1cos11sin1cos10x y +--+-=（2）令()1()cos g x f x x x ==+'，()21sin g x x x -'=-，当[]1,e x ∈时，()21sin 0g x x x '=--<，所以()g x 在[]1,e 上单调递减，且()11cos10g =+>，()11211e cos e<cos 0e e 3e 2g π=++=-<，所以由零点存在定理可知，在区间[1,e]存在唯一的α，使()()0g f αα'==又当()1,x α∈时，()()0g x f x '=>；当(),e x α∈时，()()0g x f x ='<；所以()f x 在()1,x α∈上单调递增，在(),e x α∈上单调递减，又因为()()()1ln1sin1sin1,e ln e sin e 1sin e 1,f f f =+==+=+>所以函数()f x 在区间[1,e]上的最小值为()1sin1f =.11（3）()ln sin f x x x =+，()0,x ∈+∞，若01x <≤，1()cos 0f x x x+'=>，所以()f x 在区间(]0,1上单调递增，又()1sin10f =>，111sin 0e e f ⎛⎫=-+< ⎪⎝⎭，结合零点存在定理可知，()f x 在区间(]0,1有且仅有一个零点，若1x π<≤，则ln 0,sin 0x x >≥，则()0f x >，若x π>，因为ln ln 1sin x x π>>≥-，所以()0f x >，综上，函数()f x 在()0,∞+有且仅有一个零点.【点睛】利用导数研究函数的零点，一方面利用导数判断函数的单调性，借助零点存在性定理判断；另一方面，也可将零点问题，转化为函数图象的交点问题，利用数形结合判断.。

整式的化简求值专项训练50题1．老师在黑板上书写了一个正确的演算过程，随后用一张纸挡住了一个二次三项式，形式如下：+3（x﹣1）＝x2﹣5x+1（1）求所挡的二次三项式；（2）若x＝﹣1，求所挡的二次三项式的值．2．阅读材料：我们知道，4x﹣2x+x＝（4﹣2+1）x＝3x，类似地，我们把（a+b）看成一个整体，则4（a+b）﹣2（a+b）+（a+b）＝（4﹣2+1）（a+b）＝3（a+b）．“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．尝试应用：（1）把（a﹣b）2看成一个整体，合并3（a﹣b）2﹣6（a﹣b）2+2（a﹣b）2的结果是．（2）已知x2﹣2y＝4，求3x2﹣6y﹣21的值；拓展探索：（3）已知a﹣2b＝3，2b﹣c＝﹣5，c﹣d＝10，求（a﹣c）+（2b﹣d）﹣（2b﹣c）的值．3．已知：关于x的多项式2ax3﹣9+x3﹣bx2+4x3中，不含x3与x2的项．求代数式3（a2﹣2b2﹣2）﹣2（a2﹣2b2﹣3）的值．4．已知含字母a，b的代数式是：3[a2+2（b2+ab﹣2）]﹣3（a2+2b2）﹣4（ab﹣a﹣1）（1）化简代数式；（2）小红取a，b互为倒数的一对数值代入化简的代数式中，恰好计算得代数式的值等于0，那么小红所取的字母b的值等于多少？（3）聪明的小刚从化简的代数式中发现，只要字母b取一个固定的数，无论字母a取何数，代数式的值恒为一个不变的数，那么小刚所取的字母b的值是多少呢？4．如果关于x的多项式（3x2+2mx﹣x+1）+（2x2﹣mx+5）﹣（5x2﹣4mx﹣6x）的值与x的取值无关，试确定m的值，并求m2+（4m﹣5）+m的值．5．已知：2x2+ax﹣y+6﹣bx2+3x﹣5y﹣1的值与x的取值无关，A＝4a2﹣ab+4b2，B＝3a2﹣ab+3b2，先化简3A﹣[2（3A﹣2B）﹣3（4A﹣3B）]再求值．7．（2022秋•南昌期中）已知天平左边托盘中的物体重量为x，右边托盘中的物体重量为y，其中x＝30（1+a2）﹣3（a﹣a2），y＝31﹣[a﹣2（a2﹣a）﹣31a2]（1）化简x和y；（2）请你想一想，天平会倾斜吗？如果出现倾斜，将向哪边倾斜？请说明理由．8．（2022秋•福田区校级期中）如下1□2□3□4…□（n+1）将1到n+1（n≥1，且n为正整数）一共n+1个连续正整数按从小到大的顺序排成一排，每相邻的两个数之间放置一个方格．（1）一共需要放置个方格；（2）如果第一个方格填入加号“+”，第二个方格填入减号“﹣”，第三个方格填入加号“+”，第四个方格填入减号“﹣”，…，按此规律轮流将加、减号从左向右依次填入方格中，问最后一个方格应填入什么符号？（3）按照（2）中的方法我们用加、减号将1到n+1一共n+1个连续正整数连接成一个算式，问这个算式的值等于多少？9.如果“三角”表示3（2x+5y+4z），“方框”表示﹣4[（3a+b）﹣（c﹣d）]．求的值．10．先化简，后求值（1）2（x2y+xy）﹣3（x2y﹣xy）﹣4x2y，其中x＝1，y＝﹣1；（2）|a﹣2|+（b+3）2＝0，求3a2b﹣[2ab2﹣2（ab﹣1.5a2b）+ab]+3ab2的值；（3）已知a2+5ab＝76，3b2+2ab＝51，求代数式a2+11ab+9b2的值；（4）已知ab＝3，a+b＝4，求3ab﹣[2a﹣（2ab﹣2b）+3]的值．11．课堂上老师给大家出了这样一道题，“当x＝2010时，求代数式x+（2x3﹣3x2y﹣2xy2）﹣（x3﹣2xy2+y3）+（﹣x3+3x2y+y3）的值”，小明一看，“x的值太大了，而且又没有y的值，怎么算呢？”你能帮小明解决这个问题吗？请写出过程．12．化简计算：（1）3a2﹣2a﹣a2+5a（2）14(−82+2−4)−12(−1)（3）根据下边的数值转换器，当输入的x与y满足|+1|+(−12)2=0时，请列式求出输出的结果．（4）若单项式232与﹣2x m y3是同类项，化简求值：（m+3n﹣3mn）﹣2（﹣2m﹣n+mn）13．化简或化简求值①3（x2﹣2xy）﹣[3x2﹣2y﹣2（3xy+y）]②已知A＝3a2+b2﹣5ab，B＝2ab﹣3b2+4a2，先求﹣B+2A，并求当a=−12，b＝2时，﹣B+2A的值．③如果代数式（2x2+ax﹣y+6）﹣（2bx2﹣3x+5y﹣1）的值与字母x所取的值无关，试求代数式133−22−(143−32)的值．④有这样一道计算题：“计算（2x3﹣3x2y﹣2xy2）﹣（x3﹣2xy2+y3）+（﹣x3+3x2y﹣y3）的值，其中=12，y＝﹣1”，甲同学把=12看错成=−12；但计算结果仍正确，你说是怎么一回事？14．一个四位数m＝1000a+100b+10c+d（其中1≤a，b，c，d≤9，且均为整数），若a+b＝k（c﹣d），且k为整数，称m为“k型数”．例如，4675：4+6＝5×（7﹣5），则4675为“5型数”；3526：3+5＝﹣2×（2﹣6），则3526为“﹣2型数”．（1）判断1731与3213是否为“k型数”，若是，求出k；（2）若四位数m是“3型数”，m﹣3是“﹣3型数”，将m的百位数字与十位数字交换位置，得到一个新的四位数m′，m′也是“3型数”，求满足条件的所有四位数m．15．对于整数a，b，定义一种新的运算“⊙”：当a+b为偶数时，规定a⊙b＝2|a+b|+|a﹣b|；当a+b为奇数时，规定a⊙b＝2|a+b|﹣|a﹣b|．（1）当a＝2，b＝﹣4时，求a⊙b的值．（2）已知a＞b＞0，（a﹣b）⊙（a+b﹣1）＝7，求式子34（a﹣b）+14（a+b﹣1）的值．（3）已知（a⊙a）⊙a＝180﹣5a，求a的值．16．先化简，再求值4x2y﹣[6xy﹣3（4xy﹣2）﹣x2y]+1，其中|x+1|+（y﹣2）2＝0．17．已知A﹣2B＝7a2﹣7ab，且B＝﹣4a2+6ab+7（1）求A等于多少？（2）若|a+1|+（b﹣2）2＝0，求A的值．18．已知A＝2x2﹣3xy+y2+2x+2y，B＝4x2﹣6xy+2y2﹣3x﹣y（1）当x＝2，y=−15时，求B﹣2A的值．（2）若|x﹣2a|+（y﹣3）2＝0，且B﹣2A＝a，求a的值．19．有这样一道计算题：3x2y+[2x2y﹣（5x2y2﹣2y2）]﹣5（x2y+y2﹣x2y2）的值，其中x=12，y＝﹣1．小明同学把“x=12”错看成“x=−12”，但计算结果仍正确；小华同学把“y＝﹣1”错看成“y＝1”，计算结果也是正确的，你知道其中的道理吗？请加以说明．20．若单项式235r2r23与−3463K2K1的和仍是单项式，求m，n的值．21．先化简，再求值：已知2（﹣3xy+y2）﹣[2x2﹣3（5xy﹣2x2）﹣xy]，其中x，y满足|x+2|+（y﹣3）2＝0．22．先化简，再求值：3（2x2﹣3xy﹣5x﹣1）+6（﹣x2+xy﹣1），其中x、y满足（x+2）2+|y−23|＝0．23．已知：A＝ax2+x﹣1，B＝3x2﹣2x+4（a为常数）．（1）若A与B的和中不含x2项，求出a的值；（2）在（1）的基础上化简：B﹣2A．24．已知M＝x2﹣ax﹣1，N＝2x2﹣ax﹣2x﹣1．（1）求N﹣（N﹣2M）的值；（2）若多项式2M﹣N的值与字母x取值无关，求a的值．25．已知多项式（a+3）x3﹣x b+x+a是关于x的二次三项式，求a b﹣ab的值．26．已知A＝x﹣2y，B＝﹣x﹣4y+1（1）求2（A+B）﹣（2A﹣B）的值；（结果用x、y表示）（2）当|x+12|与y2互为相反数时，求（1）中代数式的值．26．已知﹣2a m bc2与4a3b n c2是同类项，求多项式3m2n﹣2mn2﹣m2n+mn2的值．28．已知：A﹣2B＝7a2﹣7ab，且B＝﹣4a2+6ab+7．（1）求A．（2）若|a+1|+（b﹣2）2＝0，计算A的值．29．先化简，再求值：﹣2（mn﹣3m2）﹣[m2﹣5（mn﹣m2）+2mn]，其中|m﹣1|+（n+2）2＝030．已知m、n是系数，且mx2﹣2xy+y与3x2+2nxy+3y的差中不含二次项，求m+3n的值．31．阅读材料：对于任何数，我们规定符号的意义是=ad﹣bc．例如：1234=1×4﹣2×3＝﹣2（1）按照这个规定，请你计算56−28的值．（2）按照这个规定，请你计算当|m+3|+（n﹣1）2＝0时，23+2−12−2的值．31．如果代数式（﹣2x2+ax﹣y+6）﹣（2bx2﹣3x+5y﹣1）的值与字母x所取得的值无关，试求代数式13a3﹣2b2﹣（14a3﹣3b2）的值．32．学习了整式的加减运算后，老师给同学们布置了一道课堂练习题“a＝﹣2，b＝2017时，求（3a2b﹣2ab2+4a）﹣2（2a2b﹣3a）+2（ab2+12a2b）﹣1的值”．盈盈做完后对同桌说：“张老师给的条件b＝2017是多余的，这道题不给b的值，照样可以求出结果来．”同桌不相信她的话，亲爱的同学们，你相信盈盈的说法吗？说说你的理由．33．小红做一道数学题：两个多项式A，B＝4x2﹣5x﹣6，试求A+B的值．小红误将A+B看成A﹣B，结果答案为﹣7x2+10x+12（计算过程正确）．试求A+B的正确结果．34．有这样一道题，计算（2x4﹣4x3y﹣x2y2）﹣2（x4﹣2x3y﹣y3）+x2y2的值，其中x＝2，y ＝﹣1，甲同学把“x＝2”错抄成“x＝﹣2”，但他计算的结果也是正确的，请用计算说明理由．35．有三个多项式A、B、C分别为：A=12x2+x﹣1，B=12x2+3x+1，C=12x2﹣x，请你对A﹣2B﹣C进行化简，并计算当x＝﹣2时代数式A﹣2B﹣C的值．37．已知代数式A＝x2+xy+2y−12，B＝2x2﹣2xy+x﹣1（1）求2A﹣B；（2）当x＝﹣1，y＝﹣2时，求2A﹣B的值；（3）若2A﹣B的值与x的取值无关，求y的值．38．化简求值：（1）当a＝﹣1，b＝2时，求代数式﹣2（ab﹣3b2）﹣[6b2﹣（ab﹣a2）]的值（2）先化简，再求值：4xy﹣2（32x2﹣3xy+2y2）+3（x2﹣2xy），当（x﹣3）2+|y+1|＝0，求式子的值（3）若（2mx2﹣x+3）﹣（3x2﹣x﹣4）的结果与x的取值无关，求m的值39．课堂上李老师给出了一道整式求值的题目，李老师把要求的整式（7a3﹣6a3b）﹣（﹣3a3﹣6a3b+10a3﹣3）写完后，让小红同学顺便给出一组a、b的值，老师说答案．当小红说完：“a＝65，b＝﹣2014”后，李老师不假思索，立刻说出答案“3”．同学们莫名其妙，觉得不可思议，但李老师用坚定的口吻说：“这个答案准确无误”．你能说出其中的道理吗？40．化简求值：（1）（8x﹣7y）﹣3（4x﹣5y）其中：x＝﹣2，y＝﹣1．（2）已知多项式（﹣2x2+3）的2倍与A的差是2x2+2x﹣7，当x＝﹣1时，求A的值．40．已知整式﹣5x2y﹣[2x2y﹣3（xy﹣2x2y﹣mx4）]+2xy不含x4项，化简该整式，若|x+1|+（y ﹣2x）2＝0，求该整式的值．42．已知：A＝2a2+3ab﹣2a﹣1，B＝a2+ab﹣1（1）求4A﹣（3A﹣2B）的值．（2）当a取任何数值，A﹣2B的值是一个定值时，求b的值．43．莉莉在计算一个多项式A减去多项式2b2﹣3b﹣5的差时，因一时疏忽忘了对两个多项式用括号括起来，因此减式后面两项没有变号，结果得到的差是b2+3b﹣1．（1）据此请你求出这个多项式A；（2）求出这两个多项式运算的正确结果．44．已知一个三角形的第一条边长为2a+5b，第二条边比第一条边长3a﹣2b，第三条边比第二条边短3a（1）用含a，b的式子表示这个三角形的第二条边、第三条边及周长，结果要化简；（2）若a，b满足|a﹣5|+（b﹣3）2＝0，求出这个三角形的周长．45．填空题：（请将结果直接写在横线上）定义新运算“⊕”，对于任意有理数a，b有a⊕b=r32，（1）4（2⊕5）＝．（2）若A＝x2+2xy+y2，B＝﹣2xy+y2，则（A⊕B）+（B⊕A）＝．46．（1）若代数式﹣4x6y与x2n y是同类项，求（4n﹣13）2015的值．（2）若2x+3y＝2015，求2（3x﹣2y）﹣（x﹣y）+（﹣x+9y）的值．（3）已知A＝x3+3x2y﹣5xy2+6y3﹣1，B＝﹣6y3+5xy2+x2y﹣2x3+2，C＝x3﹣4x2y+3，试说明A+B+C的值与x，y无关．47．已知A＝3x﹣2y﹣3，B＝﹣4x+3y+2（1）求3A+2B；（2）将英文26个字母按以下顺序排列：a、b、c、d、e、f、g、h、i、j、k、l、m、n、o、p、q、r、s、t、u、v、w、x、y、z．规定a接在z后面，使26个字母排成圈，设计一个密码：若x代表其中一个字母，则x﹣3代表“把一个字母换成字母表中从它向前3位的字母”．如x表示字母m时，则x﹣3表示字母j．若（1）中求得的式子恰好是一个密码，请直接解读下列密文“Nqtajrfymx”的意思，并翻译成中文为．48．老师在黑板上书写一个正确的演算过程，随后用手掌捂住了一个二次三项式．形式如下：（1）求所捂的二次三项式；（2）若x=−32，求所捂的二次三项式的值．49．（1）设n表示任意一个整数，则用含有n的代数式表示任意一个偶数为，用含有n的代数式表示任意一个奇数为；（答案直接填在题中横线上）（2）用举例验证的方案探索：任意两个整数的和与这两个数的差是否同时为奇数或同时为偶数？你的结论是；（填“是”或“否”，答案直接填在题中横线上）（3）设a、b是任意的两个整数，试用“用字母表示数”的方法并分情况来说明a+b和a﹣b是否“同时为奇数”或“同时为偶数”？并进一步得出一般性的结论．例：①若a、b都是偶数，设a＝2m，b＝2n，则a+b＝2m+2n＝2（m+n）；a﹣b＝2m﹣2n ＝2（m﹣n）；此时a+b和a﹣b同时为偶数．请你仿照以上的方法并考虑其余所有可能的情况加以计算和说明；（4）以（3）的结论为基础进一步探索：若a、b是任意的两个整数，那么﹣a+b、﹣a ﹣b、a+b、a﹣b是否“同时为奇数”或“同时为偶数”？（5）应用第（2）、（3）、（4）的结论完成：在2016个自然数1，2，3，…，2015，2016的每一个数的前面任意添加“+”或“﹣”，则其代数和一定是．（填“奇数”或“偶数”，答案直接填在题中横线上）50．已知m、x、y满足（1）32（x﹣5）2+5|m|＝0；（2）﹣a2b y+1与3a2b3是同类项，求代数式；0.375x2y+5m2x﹣{−716x2y+[−14xy2+（−316x2y﹣3.475xy2）]﹣6.275xy2}的值．。

2024-2025学年度十月月度检测数学试题（答案在最后）时限：120分钟满分：150分命题人：一、选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1.已知集合1{(,)|||},(,)|||A x y y x B x y y x ⎧⎫====⎨⎬⎩⎭，则A B = （）A.{1,1}-B.{(1,1),(1,1)}- C.(0,)+∞ D.(0,1)【答案】B 【解析】【分析】先解方程组，得出点的坐标即可得出交集.【详解】,1y x y x ⎧=⎪⎨=⎪⎩，解得1,1x y =⎧⎨=⎩，或1,1x y =-⎧⎨=⎩，所以{(1,1),(1,1)}A B =- ，故选：B ．2.已知函数()*(2),nf x x n =-∈N ，则“1n =”是“()f x 是增函数”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】由当21,n k k =+∈N 时，′≥0，可得()(2)nf x x =-是增函数，即可得到答案.【详解】由()(2)nf x x =-，得()1(2)n f x n x --'=，则当21,n k k =+∈N 时，′≥0，()(2)nf x x =-是增函数，当1n =时，可得()f x 是增函数；当()f x 是增函数时，21,n k k =+∈N ，故“1n =”是“()f x 是增函数”的充分不必要条件.3.函数()sin cos f x a x b x =+图像的一条对称轴为π3x =，则a b =（）A.B. C.3D.3-【答案】A 【解析】【分析】直接利用对称性，取特殊值，即可求出a b.【详解】由()()sin cos 0f x a x b x ω=+>的图象关于π3x =对称，可知：2π(0)(3f f =，即sin0cos0=s 3o 2π3i 2πn c s a b a b ++，则a b=故选：A ．4.已知随机变量()2~2,N ξσ，且(1)()P P a ξξ≤=≥，则19(0)x a xa x+<<-的最小值为（）A.5B.112 C.203D.163【答案】D 【解析】【分析】根据正态分布的对称性求得a ，利用基本不等式求得正确答案.【详解】根据正态分布的知识得12243a a +=⨯=⇒=，则03,30x x <-，19119139(3)103333x x x x x a x x x x x -⎛⎫⎛⎫+=+-+=++ ⎪ ⎪---⎝⎭⎝⎭1161033⎛≥+= ⎝，当且仅当393x x x x -=-，即34x =时取等.故选：D5.已知函数()sin2cos2f x x a x =+，将()f x 的图象向左平移π6个单位长度，所得图象关于原点对称，则()f x 的图象的对称轴可以为（）．A.π12x = B.π6x =C.π3x =D.5π12x =【答案】D【分析】根据题意找到函数的对称点得()π03f x f x ⎛⎫+-= ⎪⎝⎭，结合特殊值法计算得a =角公式化简得()π2sin 23f x x ⎛⎫=-⎪⎝⎭，最后整体替换计算得到结果；【详解】由题意可得()f x 的图象关于点π,06⎛⎫⎪⎝⎭对称，即对任意x ∈R ，有()π03f x f x ⎛⎫+-=⎪⎝⎭，取0x =，可得()π300322a f f ⎛⎫+=+=⎪⎝⎭，即a =．故()πsin22sin 23f x x x x ⎛⎫=-=- ⎪⎝⎭，令ππ2π32x k -=+，k ∈Z ，可得()f x 的图象的对称轴为5ππ122k x =+，k ∈Z ．故选：D ．6.设37a =，ln 2b =，3sin 7c =，则（）A.b c a >>B.a c b>> C.a b c>> D.b a c>>【答案】D 【解析】【分析】构造函数()πsin (0)2f x x x x =-<<，利用导数探讨单调性并比较,a c ，再利用对数函数单调性比较大小即得.【详解】当π02x <<时，令()sin f x x x =-，求导得()1cos 0f x x '=->，则函数()f x 在π(0,)2上单调递增，有()(0)0f x f >=，即有sin x x >，因此33sin 77a c =>=，显然13ln 2ln 27b a =>=>=，所以b a c >>.故选：D7.已知函数()222cos (sin cos )(0)f x x x x ωωωω=-->的图象关于直线π12x =轴对称，且()f x 在π0,3⎛⎫⎪⎝⎭上没有最小值，则ω的值为（）A.12B.1C.32D.2【答案】C 【解析】【分析】先由三角恒等变换化简解析式，再由对称轴方程解得36,2k k ω=+∈Z ，再由()f x 在π0,3⎛⎫⎪⎝⎭上没有最小值得ω范围，建立不等式求解可得.【详解】()()2222cos sin 2sin cos cos f x x x x x x ωωωωω=--+22cos sin21cos2sin2x x x x ωωωω=+-=+π24x ω⎛⎫=+ ⎪⎝⎭，因为()f x 的图象关于直线π12x =轴对称，所以πππ1264f ω⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭故ππππ,642k k ω+=+∈Z ，即36,2k k ω=+∈Z ，当ππ22π42x m ω+=-+，m ∈Z ，0ω>,即当3ππ,8m x m ωω=-+∈Z 时，函数()f x 取得最小值，当1m =时，5π8x ω=为y 轴右侧第1条对称轴.因为()f x 在π0,3⎛⎫⎪⎝⎭上没有最小值，所以5ππ83ω≥，即158ω≤，故由3150628k <+≤，解得11416k -<≤，k ∈Z故0k =，得32ω=．故选：C.8.定义在R上的奇函数()f x ，且对任意实数x 都有()302f x f x ⎛⎫--+=⎪⎝⎭，()12024e f =．若()()0f x f x '+->，则不等式()11e xf x +>的解集是（）A.()3,+∞ B.(),3-∞ C.()1,+∞ D.(),1-∞【答案】C【解析】【分析】由()f x 是奇函数，可得()f x '是偶函数，得到()()0f x f x +'>，令()()e xg x f x =，得到()0g x '>，得出()g x 在R 上单调递增，再由()302f x f x ⎛⎫--+= ⎪⎝⎭，求得()f x 的周期为3的周期函数，根据()12024ef =，得到()2e g =，把不等式转化为()()12g x g +>，结合函数的单调性，即可求解.【详解】因为()f x 是奇函数，可得()f x '是偶函数，又因为()()0f x f x '+->，所以()()0f x f x +'>，令()()e x g x f x =，可得()()()e 0xg x f x f x ''=+>⎡⎤⎣⎦，所以()g x 在R 上单调递增，因为()302f x f x ⎛⎫--+=⎪⎝⎭且()f x 是奇函数，可得()()23f x f x f x ⎛⎫+=-=-⎪⎝⎭，则()()3333[()()222f x f x f x f x +=++=-+=，所以()f x 的周期为3的周期函数，因为()()()12024674322e f f f =⨯+==，所以()212e e eg =⨯=，则不等式()11e xf x +>，即为()1e 1e xf x ++>，即()()12g x g +>，又因为()g x 在R 上单调递增，所以12x +>，解得1x >，所以不等式()11ex f x +>的解集为()1,+∞．故选：C ．二、选择题（本大题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．）9.下列等式成立的是（）A.()21sin15cos152︒-︒=B.22sin 22.5cos 22.52︒-︒=-C.1cos28cos32cos62cos582︒︒-︒︒=-D.(3tan10cos502︒︒=-【答案】AB 【解析】【分析】应用倍角正余弦、和差角正余弦公式及诱导公式化简求值，即可判断各项的正误.【详解】A ：()21sin15cos1512sin15cos151sin 302︒-︒=-︒︒=-︒=，成立；B：22sin 22.5cos 22.5cos 452︒-︒=-︒=-，成立；C ：cos 28cos32cos62cos58cos 28cos32sin 28sin 32cos(2832)︒︒-︒︒=︒︒-︒︒=︒+︒1cos602=︒=，不成立；D：(sin102sin 50cos50sin100tan10cos50cos50cos10cos10cos10︒-︒-︒︒-︒︒-︒=⋅︒=︒︒︒cos101cos10︒=-=-︒，不成立.故选：AB10.已知抛物线()2:20C y px p =>，过C 的焦点F 作直线:1l x ty =+，若C 与l 交于,A B 两点，2AF FB =，则下列结论正确的有（）A.2p =B.3AF =C.t =或-D.线段AB 中点的横坐标为54【答案】ABD 【解析】【分析】由直线:1l x ty =+，可知焦点1,0，得p 的值和抛物线方程，可判断A 选项；直线方程代入抛物线方程，由韦达定理结合2AF FB =，求出,A B 两点坐标和t 的值，结合韦达定理和弦长公式判断选项BCD.【详解】抛物线()2:20C y px p =>的焦点F 在x 轴上，过F 作直线:1l x ty =+，可知1,0，则12p=，得2p =，A 选项正确；抛物线方程为24y x =，直线l 的方程代入抛物线方程，得2440y ty --=.设1,1，2,2，由韦达定理有124y y t +=，124y y =-，2AF FB =，得122y y=-，解得12y y =-=12y y ==，124y y t=+，则4t =或4t =-，C 选项错误；则1212,2x x ==，线段AB 中点的横坐标为121252242x x ++==，D 选项正确；12192222AB x x p =++=++=，2293332AF AB ==⨯=，B 选项正确.故选：ABD.11.已知()00,P x y 是曲线33:C x y y x +=-上的一点，则下列选项中正确的是（）A.曲线C 的图象关于原点对称B.对任意0x ∈R ，直线0x x =与曲线C 有唯一交点PC.对任意[]01,1y ∈-，恒有012x <D.曲线C 在11y -≤≤的部分与y 轴围成图形的面积小于π4【答案】ACD 【解析】【分析】将x ，y 替换为x -，y -计算即可判断A ；取0x =，可判断有三个交点即可判断B ；利用函数3y x x =-的单调性来得出300y y -的取值范围，再结合()3f x x x =+的单调性进行求解即可判断C ；利用图象的对称性和半圆的面积进行比较即可判断D ．【详解】A ．对于33x y y x +=-，将x ，y 替换为x -，y -，所得等式与原来等价，故A 正确；B ．取0x =，可以求得0y =，1y =，1y =-均可，故B 错误；C ．由330000x x y y +=-，[]01,1y ∈-，函数3y x x =-，故213y x '=-，令2130y x '=-=，解得：13x =±，在1,3x ⎡∈--⎢⎣⎦，,13⎤⎥⎣⎦时，0'<y ，函数单调递减，在,33x ⎛⎫∈- ⎪ ⎪⎝⎭时，0'>y ，函数单调递增，所以300,99y y ⎡-∈-⎢⎣⎦，又因为()3f x x x =+是增函数，15289f ⎛⎫=>⎪⎝⎭，所以有012x <，故C 正确；D ．当[]00,1y ∈时，3300000x x y y +=-≥，又320002x x x +≥，32000022y y y y -≤-，所以22000x y y ≤-．曲线22x y y =-与y 轴围成半圆，又曲线C 的图象关于原点对称，则曲线C 与y 轴围成图形的面积小于π4，故D 正确．故选：ACD ．三、填空题（本大题共3小题，每小题5分，共15分）12.若π,02α⎛⎫∈- ⎪⎝⎭，且πcos2cos 4αα⎛⎫=+ ⎪⎝⎭，则α=__________.【答案】π12-【解析】【分析】化简三角函数式，求出1sin 42πα⎛⎫+= ⎪⎝⎭，根据π,02α⎛⎫∈- ⎪⎝⎭即可求解.【详解】由πcos2cos 4αα⎛⎫=+⎪⎝⎭，得()22cos sin cos sin 2αααα-=-.因为π,02α⎛⎫∈- ⎪⎝⎭，所以cos sin 0αα-≠，则cos sin 2αα+=，则1sin 42πα⎛⎫+= ⎪⎝⎭.由π,02α⎛⎫∈- ⎪⎝⎭，得πππ,444α⎛⎫+∈- ⎪⎝⎭，则ππ46α+=，解得π12α=-.故答案为：π12-.13.海上某货轮在A 处看灯塔B ，在货轮北偏东75︒，距离为A 处看灯塔C ，在货轮的北偏西30︒，距离为海里C 处，货轮由A 处向正北航行到D 处时看灯塔B 在东偏南30︒，则灯塔C 与D 处之间的距离为______海里．【答案】【解析】【分析】由正弦定理和余弦定理求解即可．【详解】如图：由题意75DAB ∠=︒，903060ADB ∠=-︒=︒，所以180756045DBA ∠=︒-︒-︒=︒，在ABD △中，由正弦定理sin sin AD AB ABD ADB =∠∠，即306sin 45sin 60AD =︒︒，所以60AD =，在ADC △中，30DAC ∠=︒，所以20CD =.故答案为：14.若存在实数m ，使得对于任意的[],x a b ∈，不等式2πsin cos 2sin 4m x x x m ⎛⎫+≤-⋅ ⎪⎝⎭恒成立，则b a -取得最大值时，sin2a b+=__________．【答案】2【解析】【分析】以m 为变量，结合一元二次不等式的存在性问题可得1sin 22x ≤，解不等式结合题意得[]()7ππ,π,π,1212a b k k k ⎡⎤⊆-+∈⎢⎥⎣⎦Z ，由此可得答案.【详解】因为2πsin cos 2sin 4m x x x m ⎛⎫+≤-⋅ ⎪⎝⎭恒成立，即2π2sin sin cos 04m x m x x ⎛⎫--⋅+≤ ⎪⎝⎭恒成立，若存在实数m ，使得上式成立，则2πΔ4sin 4sin cos 04x x x ⎛⎫=--≥ ⎪⎝⎭，则πΔ22cos 22sin 222sin 22sin 224sin 202x x x x x ⎛⎫=---=--=-≥ ⎪⎝⎭，可得1sin 22x ≤，可得7ππ2π22π,66k x k k -≤≤+∈Z ，解得7ππππ,1212k x k k -≤≤+∈Z ，由[]()7ππ,π,π,1212a b k k k ⎡⎤⊆-+∈⎢⎥⎣⎦Z ，则b a -取得最大值时()7πππ,π,1212a k bk k =-=+∈Z ，此时()7ππππ1212sin sin ,222k k a b k -+++==∈Z .故答案为：2.【点睛】关键点点睛：双变量问题的解题关键是一次只研究其中一个变量，本题先以m 为变量，转化为存在性问题分析求解.四、解答题（本大题共5小题，共77分．解答应写出必要的文字说明、证明过程或演算步骤）15.已知函数()π4sin cos 6f x x x ⎛⎫=+ ⎪⎝⎭,x ∈R .（1）求函数()f x 的单调减区间;（2）求函数()f x 在π0,2⎡⎤⎢⎥⎣⎦上的最大值与最小值.【答案】（1）π2ππ,π,63k k k Z ⎡⎤++∈⎢⎥⎣⎦（2）()min 2f x =-，()max 1f x =【解析】【分析】（1）根据三角恒等变换化简函数()f x ，再根据正弦函数的单调性结合整体思想即可得解；（2）由x 的范围求得π26x +的范围，再根据正弦函数的性质即可得解.【小问1详解】解：()2π314sin cos 4sin cos sin cos 2sin 622f x x x x x x x x x ⎛⎫⎛⎫=+=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭1πcos212sin2cos212sin 21226x x x x x ⎛⎫⎛⎫=+-=+-=+- ⎪ ⎪ ⎪⎝⎭⎝⎭，令ππ3π2π22π,262k x k k +≤+≤+∈Z ，解得π2πππ63k x k +≤≤+，所以函数()f x 的单调减区间为π2ππ,π,63k k k Z ⎡⎤++∈⎢⎥⎣⎦；【小问2详解】解：因为π02x ≤≤，所以ππ7π2666x +≤≤，所以1πsin 2126x ⎛⎫-≤+≤ ⎪⎝⎭，于是π12sin 226x ⎛⎫-≤+≤ ⎪⎝⎭，所以()21f x -≤≤，当且仅当π2x =时，()f x 取最小值()min π22f x f ⎛⎫==- ⎪⎝⎭，当且仅当ππ262x +=，即π6x =时，()f x 取最大值()max π16f x f ⎛⎫== ⎪⎝⎭.16.已知0b >，函数2()((ln )1)f x x x x bx =---在点()(1,)1f 处的切线过点()0,1-.（1）求实数b 的值；（2）证明：()f x 在()0,∞+上单调递增；（3）若对())1,1(x f x a x ∀≥≥-恒成立，求实数a 的取值范围．【答案】（1）1b =（2）证明见解析（3）(,1]-∞【解析】【分析】（1）先求导函数再写出切线方程代入点得出参数值；（2）求出导函数1()2ln 2f x x x x'=+--，再根据导函数求出()(1)10f x f ''≥=>即可证明单调性；（3）根据函数解析式分1x =和1x >两种情况化简转化为ln x x a -≥恒成立，再求()ln (1)h x x x x =->的单调性得出最值即可求出参数范围.【小问1详解】()f x 的定义域为1(0,),()2ln()2f x x bx x'+∞=+--，故(1)1ln f b '=-，又(1)0f =，所以()f x 在点(1,(1))f 处的切线方程为(1ln )(1)y b x =--，将点(0,1)-代入得1ln 1b -=，解得1b =．【小问2详解】由（1）知2()(1)ln f x x x x x =---，则1()2ln 2f x x x x'=+--，令1()()2ln 2g x f x x x x '==+--，则22221121(1)(21)()2x x x x g x x x x x---+'=--==，当01x <<时，()0,()g x g x <'单调递减；当1x >时，()0,()g x g x >'单调递增，所以()(1)10f x f ''≥=>，所以()f x 在(0,)+∞上单调递增．【小问3详解】对())1,1(x f x a x ∀≥≥-恒成立，即对1,(1)(1)ln (1)x x x x x a x ∀≥---≥-恒成立，当1x =时，上式显然恒成立；当1x >时，上式转化为ln x x a -≥恒成立，设()ln (1)h x x x x =->，则11()10x h x x x'-=-=>，所以()h x 在(1,)+∞上单调递增；所以()(1)1h x h >=，故1a ≤，所以实数a 的取值范围为(,1]-∞．17.在ABC V 中，设内角A ，B ，C 所对的边分别为,,a b c ．（1）2b a =+，4c a =+，是否存在正整数a *N ，且ABC V 为钝角三角形？若存在，求出a ；若不存在，说明理由．（2）若4,a b c D ===为BC 的中点，E ，F 分别在线段,AB AC 上，且90EDF ︒∠=，CDF θ∠=()090θ︒︒<<，求DEF 面积S 的最小值及此时对应的θ的值．【答案】（1）存在,4a =（2）12-【解析】【分析】（1）分析可知，角C 为钝角，由cos 0C <结合三角形三边关系可求得整数a 的值；（2）由正弦定理可得出()sin 60DF θ=+︒，()sin 150DE θ=︒-，再利用三角形的面积公式和两角和与差的正弦公式化简即可求得结果.【小问1详解】假设存在正整数a 满足题设．ABC V 为钝角三角形，因为a b c <<，所以C 为钝角，根据题设，2b a =+，4c a =+，由余弦定理222cos 2a b c C ab+-=,所以()222(2)(4)1cos 022a a a C a a ++-+-<=<+，得24120a a --<，解得26a -<<．因为**a ∈N N ，所以1a =或4a =，当1a =时，ABC V 不存在，故存在4a =满足题设．所以4a =【小问2详解】如图，因为()90,090EDF CDF θθ∠=︒∠=︒<<︒，所以90BDE θ∠=︒-．在CDF V 中，因为()2sin60sin 60DF θ=︒+︒，所以()3sin 60DF θ=+︒在BDE V 中，因为()2sin 60sin 150DE θ=︒︒-，所以()sin 150DE θ=︒-．所以()()132sin 60sin 150S θθ=⨯+︒︒-，设()()()sin 60sin 150f θθθ=+︒︒-，()090θ︒<<︒，所以11()sin cos cos sin 2222f θθθθθ⎛⎫⎛⎫=++ ⎪⎪⎪⎪⎝⎭⎝⎭2213cos cos sin 444θθθθ+=++化简可得：()1sin 242f θθ=+所以1122S =-当45θ=︒时，S取得最小值12-18.已知椭圆22221(0)x y a b a b +=>>的左右焦点分别为12,F F ，离心率22e =，点,P Q 分别是椭圆的右顶点和上顶点，POQ 的边PQ上的中线长为2．（1）求椭圆的标准方程；（2）过点(2,0)H -的直线交椭圆C 于,A B 两点，若11AF BF ⊥，求直线AB 的方程；（3）直线12,l l 过右焦点2F ，且它们的斜率乘积为12-，设12,l l 分别与椭圆交于点,C D 和,E F ．若,M N 分别是线段CD 和EF 的中点，求OMN 面积的最大值．【答案】（1）2212x y +=（2）220x y -+-或220x y ++=（3）8【解析】【分析】（1）根据POQ △的边PQ上中线为2得PQ ==，再联立2222,2c e a b c a ===+即可求解；（2）设直线AB 的方程为(2)(0)y k x k =+≠，1122()A x y B x y ,,(,)，联立直线AB 与椭圆方程得1212,x x x x +，再由11AF BF ⊥，即110AF BF ⋅= ，最后代入即可求解；（3）设直线1l 的方程为(1)y k x =+,则直线2l 的方程为1(1)2y x k =-+，分别与椭圆方程联立，通过韦达定理求出中点,M N 的坐标，观察坐标知，MN 的中点坐标1(,0)2T 在x 轴上，则1||||2OMN M N S OT y y =- 整理后利用基本不等式即可得到面积的最值.【小问1详解】由题意，因为(,0),(0,)P a Q b ，POQ △为直角三角形，所以PQ ==.又2222,2c e a b c a ===+，所以1,1a b c ===，所以椭圆的标准方程为2212x y +=.【小问2详解】由（1）知，1(1,0)F -,显然直线AB 的斜率存在，设直线AB 的方程为(2)(0)y k x k =+≠，1122()A x y B x y ,,(,)，联立2212(2)x y y k x ⎧+=⎪⎨⎪=+⎩消去y 得，2222(12)8820k x k x k +++-=，所以22222(8)4(12)(82)8(12)0k k k k ∆=-+-=->，即2102k <<.且22121222882,1212k k x x x x k k-+=-=++，因为11AF BF ⊥，所以110AF BF ⋅= ，所以1122(1,)(1,)0x y x y ------=，即12121210x x x x y y ++++=，所以1212121(2)(2)0x x x x k x k x +++++⋅+=，整理得2221212(12)()(1)140k x x k x x k ++++++=，即22222228(1)(82)(12)()1401212k k k k k k k +-+-+++=++，化简得2410k -=，即12k =±满足条件，所以直线AB 的方程为1(2)2y x =+或1(2)2y x =-+，即直线AB 的方程为220x y -+=或220x y ++=.【小问3详解】由题意，2(1,0)F ,设直线1l 的方程为(1)y k x =+,3344(,),(,)C x y D x y ，则直线2l 的方程为1(1)2y x k=-+，5566(,),(,)E x y F x y ，联立2212(1)x y y k x ⎧+=⎪⎨⎪=-⎩消去y 得2222)202142(-=+-+x k x k k ，所以22343422422,1212k k x x x x k k -+==++所以23422,212M x x k x k +==+2(1)12M M k y k x k =-=-+所以2222(,)1212k k M k k -++，同理联立22121(1)2x y y x k ⎧+=⎪⎪⎨⎪=--⎪⎩消去y 得222(12)2140k x x k +-+-=，所以2565622214,1212k x x x x k k -+==++所以5621,212N x x x k +==+21(1)212N N k y x k k =--=+所以221(,)1212k N k k ++，即MN 的中点1(,0)2T .所以221121||11||||||12412212282||||OMN M N k k S OT y y k k k k =-==⨯=⨯+++ ，当且仅当12||||k k =，即22k =±时取等号，所以OMN的面积最大值为8.【点睛】关键点点睛：本题考查待定系数法求椭圆的标准方程，直线与椭圆综合应用问题，利用基本不等式求最值，第三问的解题关键是分类联立直线12,l l 与椭圆方程，求出,M N 的坐标，观察坐标知，MN 的中点坐标1(,0)2T 在x 轴上，则1||||2OMN M N S OT y y =- 整理后利用基本不等式得到面积的最值..19.正整数集{}1,2,3,,3A m m m m n =++++ ，其中,m n +∈∈N N .将集合A 拆分成n 个三元子集，这n 个集合两两没有公共元素.若存在一种拆法，使得每个三元子集中都有一个数等于其他两数之和，则称集合A 是“三元可拆集”.（1）若1,3m n ==，判断集合A 是否为“三元可拆集”，若是，请给出一种拆法；若不是，请说明理由；（2）若0,6m n ==，证明：集合A 不是“三元可拆集”；（3）若16n =，是否存在m 使得集合A 是“三元可拆集”，若存在，请求出m 的最大值并给出一种拆法；若不存在，请说明理由.【答案】（1）是，拆法见解析（2）证明见解析（3）答案见解析【解析】【分析】（1）{}2,3,4,,10A = ，可拆成{}{}{}10,7,39,5,48,6,2､､或{}10,6,4､{}{}9,7,28,5,3､；（2）三元可拆集”中所有元素和为偶数，A 中所有元素和为19181712⨯=，与和为偶数矛盾；（3）可以拆成16个三元子集，将这16个三元子集中的最大的数依次记为12316,,,,a a a a ，利用等差数列求和得到1231616648a a a a m ++++≤+ ，结合1231624588a a a a m ++++=+ ，得到不等式，求出152m ≤，当7m =时写出相应的集合A 以及具体拆法，得到答案.【小问1详解】是，{}2,3,4,,10A = ，可拆成{}{}{}10,7,39,5,48,6,2､､或{}10,6,4､{}{}9,7,28,5,3､；【小问2详解】对于“三元可拆集”，其每个三元子集的元素之和为偶数，则“三元可拆集”中所有元素和为偶数；而{}1,2,3,4,,18A = ，A 中所有元素和为19181712⨯=，与和为偶数矛盾，所以集合A 不是“三元可拆集”；【小问3详解】{}1,2,3,,48A m m m m =++++ 有48个元素，可以拆成16个三元子集，将这16个三元子集中的最大的数依次记为12316,,,,a a a a ，则()()()()1231648474633a a a a m m m m ++++≤++++++++ ()28116166482m m +⨯==+；另一方面，A 中所有元素和为()249484811762m m +⨯=+，所以212316481176245882m a a a a m +++++==+ ，所以2458816648m m +≤+，解得152m ≤，即7m ≤；当7m =时，{}8,9,10,,55A = ，可拆为{}{}55,40,1554,38,16､､{}{}{}{}{}{}53,39,1452,35,1751,31,2050,37,1349,25,2448,26,22､､､､､､{}{}{}{}{}{}47,29,1846,27,1945,34,1144,23,2143,33,1042,30,12､､､､､､{}{}41,32,9,36,28,8（拆法不唯一）；综上所述，m 的最大值是7.【点睛】关键点点睛：集合新定义问题，命题新颖，且存在知识点交叉，常常会和函数的性质，数列知识等进行结合，很好的考虑了知识迁移，综合运用能力，对于此类问题，一定要解读出题干中的信息，正确理解问题的本质，转化为熟悉的问题来进行解决.。

⽣僻字⼤全（加拼⾳标注）古汉语⽣僻字读史最让⼈头疼的莫过于⽣僻字和地名以及官衔，故下定决⼼将上述三者归纳。

（1）纛（⾳“道“）两种解释：⼀、古代⽤⽑⽻做的舞具或帝王车舆上的饰物。

⼆、古时军队或仪仗队的⼤旗。

（2）恚（⾳“会”） 意思为怨恨、愤怒。

（3）彖（⾳“团”、四声）《易经》中解释卦义的⽂字：彖辞。

（4）掾（⾳“院”）原为佐助的意思，后为副官佐或官署属员的通称。

（5）旒（⾳“留”）两种解释：⼀、古代旌旗下边或边缘上悬垂的装饰品：“旌旗垂旒”。

⼆、古代帝王礼帽前后悬垂的⽟串：“冕⽽前旒”。

（6）旱魃（⾳“拔”）传说中引起旱灾的怪物。

（7）杨思勖（⾳“序”）唐⽞宗时期宦官。

罗州⽯城⼈，本性苏，从⼩进宫，被杨姓宦官收养后改姓。

他跟随唐⽞宗平定了宫廷政变，升左监门卫将军。

开元年间，先后平定了安南梅叔鸾、五溪覃⾏章、邕州粱⼤海、泷州陈⾏范的叛乱，屡⽴战功，是⽞宗得⼒帮⼿。

专管征伐的事，所受到的宠信与⾼⼒⼠相似。

他虽然⾮常勇猛，不过性情也⽐较凶狠，对待俘虏⼗分残忍。

杨思勖虽然是太监，但⽣性刚毅果决，有军事才能，只是性情凶暴，每次俘虏敌⼈，⼤多⽣剥其⾯，甚⾄剥去头⽪，⼿下⼠卒，⽆不畏惧，也因此惟命是从，所向⽴功。

内给事⽜仙童出使幽州，被密报接受刺史张守珪的贿赂，唐⽞宗⼤怒，命杨思勖杀之。

杨思勖将⽜仙童绑起来，⽣挖其⼼，砍去⼿⾜，割其⾁⽽⽣吞，残酷⽆⽐。

（8）妫（⾳“归”）姓⽒。

（9）姒（⾳“四”）姓⽒。

（10）敕（⾳“⾚”）帝王的诏书、命令。

（11）薨（⾳“轰”）古代称诸侯之死。

后世有封爵的⼤官之死也称薨。

（12）虿（⾳“拆”四声）古书上说的蝎⼦⼀类的毒⾍。

（13）貔貅（⾳“⽪休”）古书上说的⼀种凶猛的野兽。

（14）彘（⾳“⾄”）猪的意思。

（15）⾘（⾳“⾄”）本指长脊兽,如猫、虎之类。

引申为⽆脚的⾍,体多长,如蚯蚓之类，有⾜谓之⾍,⽆⾜谓之⾘。

——《尔雅》（16）铉（⾳“眩”）古代举⿍器具，状如钩，铜制，⽤以提⿍两⽿。

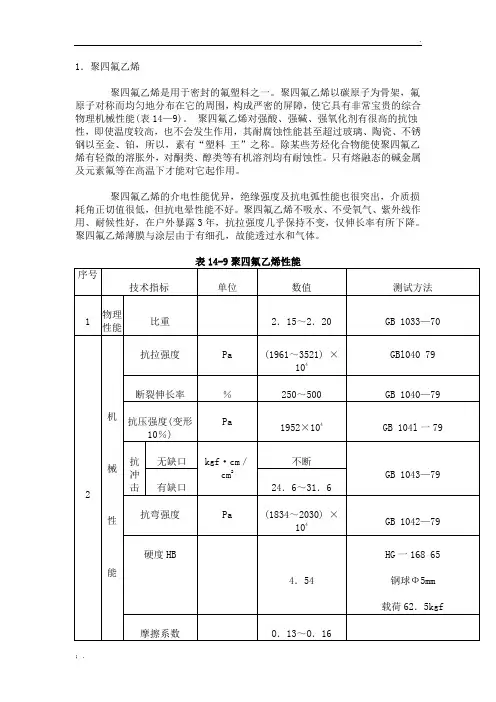
1．聚四氟乙烯聚四氟乙烯是用于密封的氟塑料之一。

聚四氟乙烯以碳原子为骨架，氟原子对称而均匀地分布在它的周围，构成严密的屏障，使它具有非常宝贵的综合物理机械性能(表14—9)。

聚四氟乙烯对强酸、强碱、强氧化剂有很高的抗蚀性，即使温度较高，也不会发生作用，其耐腐蚀性能甚至超过玻璃、陶瓷、不锈钢以至金、铂，所以，素有“塑料王”之称。

除某些芳烃化合物能使聚四氟乙烯有轻微的溶胀外，对酮类、醇类等有机溶剂均有耐蚀性。

只有熔融态的碱金属及元素氟等在高温下才能对它起作用。

聚四氟乙烯的介电性能优异，绝缘强度及抗电弧性能也很突出，介质损耗角正切值很低，但抗电晕性能不好。

聚四氟乙烯不吸水、不受氧气、紫外线作用、耐候性好，在户外暴露3年，抗拉强度几乎保持不变，仅伸长率有所下降。

聚四氟乙烯薄膜与涂层由于有细孔，故能透过水和气体。

聚四氟乙烯在200℃以上，开始极微量的裂解，即使升温到结晶体熔点327℃，仍裂解很少，每小时失重为万分之二。

但加热至400℃以上热裂解速度逐渐加快，产生有毒气体，因此，聚四氟乙烯烧结温度一般控制在375～380℃。

聚四氟乙烯分子间的范德华引力小，容易产生键间滑动，故聚四氟乙烯具有很低的摩擦系数及不粘性，摩擦系数在已知固体材料中是最低的。

聚四氟乙烯的导热系数小，该性能对其成型工艺及应用影响较大。

其不但导热性差，且线膨胀系数较大，加入填充剂可适当降低线膨胀系数。

在负荷下会发生蠕变现象，亦称作“冷流”，加入填充剂可减轻蠕变程度。

聚四氟乙烯可以添加不同的填充剂，选择的填充剂应基本满足下述要求：能耐380℃高温即四氟制品的烧结温度；与接触的介质不发生反应；与四氟树脂有良好的混入性；能改善四氟制品的耐磨性、冷流性、导热性及线膨胀系数等。

常用的填充剂有无碱无蜡玻璃纤维、石墨、碳纤维、MoS2、A123、CaF2、焦炭粉及各种金属粉。

如填充玻璃纤维或石墨，可提高四氟制品的耐磨、耐冷流性，填充MoS2可提高其润滑性，填充青铜、钼、镍、铝、银、钨、铁等，可改善导热性，填充聚酰亚胺或聚苯酯，可提高耐磨性，填充聚苯硫醚后能提高抗蠕变能力，保证尺寸稳定等。

2025届高三月考试卷（一）数学（答案在最后）本试卷共8页.时量120分钟.满分150分.一、选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.设集合[),A a =+∞，()1,2B =-，若A B =∅ ，则（）A.1>-aB.2a > C.1a ≥- D.2a ≥【答案】D 【解析】【分析】根据题意，结合集合的交集的运算，即可求解.【详解】由集合[),A a =+∞，()1,2B =-，因为A B =∅ ，则满足2a ≥.故选：D.2.已知复数z 满足22z -=，z 的取值范围为（）A.[]0,2 B.()0,2 C.[]0,4 D.()0,4【答案】C 【解析】【分析】根据题意，利用复数模的几何意义，得到复数z 在复平面内对应的轨迹，进而结合圆的性质，即可求解.【详解】由题意知复数z 满足22z -=，可得复数z 在复平面内对应的轨迹为以(2,0)A 为圆心，2r =为半径的圆，且z 表示圆上的点到原点(0,0)O 的距离，则max min 224,220z OA r z OA r =+=+==-=-=，所以z 的取值范围为0,4.故选：C.3.在ABC V 中，若2AB BC BC CA CA AB ⋅=⋅=⋅，则AB BC=A.1B.2C.2D.2【答案】C 【解析】【分析】根据题意，由AB BC BC CA ⋅=⋅uu u v uu u v uu u v uu v可以推得AB AC =，再利用向量运算的加法法则，即可求得结果．【详解】由题意得，AB BC BC CA ⋅=⋅uu u v uu u v uu u v uu v ，即A A =0+BC B C ⋅uu u v uu u v uuu v（），设BC 的中点为D ，则AD BC ⊥，即ABC V 为等腰三角形，B=C AB AC =∠∠，又因为2BC CA CA AB⋅=⋅uu u v uu v uu v uu u v即2222222C C cos 2C 2C cos 112C +22232C 2AB BC CA A B AB BC B A CA B C BC A BC A BC⋅=⋅-=-+-=-+⨯=uu u v uu u v uu v uu u v uuv uu u v uu u v uu u v uu v uuvuu u v uu u v uu u v uu u v uu u v （）所以2AB BC=uu u v uu u v ．【点睛】本题主要考查平面向量的线性运算．4.若函数()2211x x f x x ++=+的最大值为M ，最小值为N ，则M N +=（）A.1 B.2 C.3D.4【答案】B 【解析】【分析】将函数解析式化为()211xf x x =++，令()21xg x x =+，判断()g x 的奇偶性，然后利用函数的奇偶性求解即可.【详解】()2222221111111x x xf x x x x x x x +==+=+++++++，令()21x g x x =+，则其定义域为R ，又()()()2211x x g x g x x x --==-=-+-+，所以()21xg x x =+为奇函数，则()()max min 0g x g x +=，所以()()()()max min max min 112f x f x g x g x +=+++=，则2M N +=.故选：B.5.如图，点N 为正方形ABCD 的中心，ECD ∆为正三角形，平面ECD ⊥平面AB,是线段ED 的中点，则A.BM EN =，且直线,BM EN 是相交直线B.BM EN ≠，且直线,BM EN 是相交直线C.BM EN =，且直线,BM EN 是异面直线D.BM EN ≠，且直线,BM EN 是异面直线【答案】B 【解析】【分析】利用垂直关系，再结合勾股定理进而解决问题．【详解】如图所示，作EO CD ⊥于O ，连接ON ，过M 作MF OD ⊥于F ．连BF ， 平面CDE ⊥平面ABCD ．,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，MF ⊥平面ABCD ，MFB ∴∆与EON ∆均为直角三角形．设正方形边长为2，易知12EO ON EN ===，5,,22MF BF BM ==∴=．BM EN ∴≠，故选B ．【点睛】本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形．6.tan10tan503tan50︒+︒+︒︒的值为（）A.3B.3C.3D.33【答案】B 【解析】【分析】利用正切的和角公式，逆用即可求出结果.【详解】tan10tan503tan10tan50︒+︒︒︒()()tan 10501tan10tan 503tan 50=︒+︒-︒︒+︒︒)31tan10tan503tan 50=-︒︒+︒︒33tan10tan503tan50=-︒︒︒︒3=故选：B.7.一枚质地均匀的正方体骰子，其六个面分别刻有1，2，3，4，5，6六个数字，投掷这枚骰子两次，设事件M =“第一次朝上面的数字是奇数”，则下列事件中与M 相互独立的是（）A.第一次朝上面的数字是偶数B.第一次朝上面的数字是1C.两次朝上面的数字之和是8D.两次朝上面的数字之和是7【答案】D 【解析】【分析】根据题意，由相互独立事件的定义，对选项逐一判断，即可得到结果.【详解】抛掷骰子两次，共有6636⨯=个基本事件数，则()()()()()()()()()()()(){1,1,1,2,1,3,1,4,1,5,1,6,3,1,3,2,3,3,3,4,3,5,3,6M =，()()()()()()}5,1,5,2,5,3,5,4,5,5,5,6共18个基本事件，则()181362P M ==，设事件E 为第一次朝上面的数字是偶数，则事件M 与事件E 是对立事件，故A 错误；设事件F 为第一次朝上面的数字是1，则F M ⊆，故B 错误；设事件N 为两次朝上面的数字之和是8，则()()()()(){}2,6,3,5,4,4,5,3,6,2N =共5个基本事件，则()536P N =，且()(){}3,5,5,3MN =，则()213618P MN ==，()()()P MN P M P N ≠⋅，所以C 错误；设事件Q 两次朝上面的数字之和是7，则()()()()()(){}1,6,2,5,3,4,4,3,5,2,6,1Q =，则()61366P Q ==，且()()(){}1,6,3,4,5,2MQ =，则()313612P MQ ==，因为()()()P MQ P M P Q =⋅，所以事件M 与事件Q 相互独立.故选：D8.一只蜜蜂从蜂房A 出发向右爬，每次只能爬向右侧相邻的两个蜂房（如图），例如：从蜂房A 只能爬到1号或2号蜂房，从1号蜂房只能爬到2号或3号蜂房，…，以此类推，用n a 表示蜜蜂爬到n 号蜂房的方法数，则10a =（）A.10B.55C.89D.99【答案】C 【解析】【分析】根据给定条件，求出数列{}n a 的递推公式，再依次计算求出10a .【详解】依题意，12n n n a a a --=+（*n ∈N ，3n ≥），11a =，22a =，所以34567893,5,8,13,21,34,55,a a a a a a a =======1089a =.故选：C二、选择题（本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.）9.已知一组样本数据1x ，2x ，…，()201220x x x x ≤≤≤ ，下列说法正确的是（）A.该样本数据的第60百分位数为12x B.若样本数据的频率分布直方图为单峰不对称，且在右边“拖尾”，则其平均数大于中位数C.剔除某个数据i x （1i =，2，…，20）后得到新样本数据的极差不大于原样本数据的极差D.若1x ，2x ，…，10x 的均值为2，方差为1，11x ，12x ，…，20x 的均值为6，方差为2，则1x ，2x ，…，20x 的方差为5【答案】BC 【解析】【分析】由百分位数的定义即可判断A ；由极差的定义即可判断C ，由频率分布直方图中中位数、平均数的求法画出图形即可判断B ；由方差计算公式即可判断D.【详解】对于A ，由2060%12⨯=，所以样本数据的第60百分位数为12132x x +，故A 错误；对于B ，数据的频率分布直方图为单峰不对称，向右边“拖尾”，大致如下图，由于“右拖”时最高峰偏左，中位数靠近高峰处，平均数靠近中点处，此时平均数大于中位数，故B 正确；对于C ，剔除某个数据i x （1i =，2，…，20）后得到新样本数据的极差不大于原样本数据的极差，故C 正确；对于D ，由10102642020x =⨯+⨯=，则()()22210101112426420202s ⎡⎤⎡⎤=+-++-=⎣⎦⎣⎦，所以则1x ，2x ，…，20x 的方差为112，故D 错误.故选：BC.10.在平面直角坐标系中，O 为坐标原点，抛物线()220y px p =>的焦点为F ，点()1,2M ，()11,A x y ，()22,B x y 都在抛物线上，且0FA FB FM ++=ruu r uu r uuu r ，则下列结论正确的是（）A.抛物线方程为22y x= B.F 是ABM 的重心C .6FA FM FB ++= D.2223AFO BFO MFO S S S ++=△△△【答案】BCD 【解析】【分析】把点代入可得抛物线的方程，结合向量运算可得F 是ABM 的重心，利用抛物线的定义可得6FA FM FB ++= ，利用三角形面积公式及122x x +=，可得2223AFO BFO MFO S S S ++=△△△.【详解】对于A ，由()1,2M 在抛物线上可得42p =，即抛物线方程为24y x =，错误；对于B ，分别取,AB AM 的中点,D E ，则2FA FB FD +=uu u u r uu r u r ，2FM FD =-uuu r uu u r，即F 在中线MD 上，同理可得F 也在中线BE 上，所以F 是ABM 的重心，正确；对于C ，由抛物线的定义可得121,2,1FA x FM FB x =+==+uu r uuu r uu r，所以124++=++FA FM FB x x uu r uuu r uu r.由()10F ,是ABM 的重心，所以12113x x ++=，即122x x +=，所以1246++=++=FA FM FB x x uu r uuu r uu r，正确；对于D ，112AFO S OF y =△，221114AFO S y x ==△；同理222214BFOSy x ==△,21MFO S =△，所以2221213AFO BFO MFO S S S x x ++=++=△△△，正确.故选：BCD.11.已知函数()()()322,,R ,f x x ax bx c a b c f x =-++'∈是()f x 的导函数，则（）A.“0a c ==”是“()f x 为奇函数”的充要条件B.“0a b ==”是“()f x 为增函数”的充要条件C.若不等式()0f x <的解集为{1xx <∣且1}x ¹-，则()f x 的极小值为3227-D.若12,x x 是方程()0f x '=的两个不同的根，且12111x x +=，则0a <或3a >【答案】ACD 【解析】【分析】根据函数的奇偶性和充分、必要条件的判定方法，可判定A 正确；结合导数和函数的单调性间的关系，结合充分、必要条件的判定方法，可判定B 错误；利用导数求得函数()f x 的单调性，进而求得()f x 的极小值，可判定C 正确；结合二次函数的性质，结合0∆>，列出不等式，可判定D 正确．【详解】对于A 中，当0a c ==时，函数()3f x x bx =+，则满足()()3f x x bx f x -=--=-，所以()f x 为奇函数，所以充分性成立；若()f x 为奇函数，则()322f x x ax bx c -=---+=()322f x x ax bx c -=-+--，则24ax -20c =恒成立，所以0a c ==，所以必要性成立，所以A 正确；对于B 中，当0a b ==时，()3f x x c =+，可得()230f x x '=≥，所以()f x 为增函数；由()234f x x ax b =-+'，当()f x 为增函数时，216120a b ∆=-≤，所以“0a b ==”是“()f x 为增函数”的充分不必要条件，所以B 错误；对于C 中，由()234f x x ax b =-+'，若不等式()0f x <的解集为{|1x x <且1}x ¹-，则()f x 在R 上先增后减再增，则()1f '-=()()0,110f f =-=，解得21a b c ===-，故()()()232111f x x x x x x =+--=+-，可得()()()2321311f x x x x x '=+-=-+，令()0f x '=，解得=1x -或13x =，当(),1x ∈-∞-内，()0f x '>，()f x 单调递增；当11,3x ⎛⎫∈- ⎪⎝⎭内，()0f x '<，()f x 单调递减；当1,3x ⎛⎫∈+∞ ⎪⎝⎭内，()0f x '>，()f x 单调递增，所以()f x 的极小值为2111321133327f ⎛⎫⎛⎫⎛⎫=+⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以C 正确．对于D 中，由()234f x x ax b =-+'，因为12,x x 是方程()0f x '=的两个不同的根，所以216120a b ∆=->，即2430a b ->，且1x +2124,33a bx x x ==，由12111x x +=，可得1x +212x x x =，所以433a b =，即4b a =，联立方程组，可得230a a ->，解得0a <或3a >，所以D 正确．故选：ACD ．三、填空题（本大题共3小题，每小题5分，共15分.）12.点M 在椭圆221259x y +=上，F 是椭圆的一个焦点，N 为MF 的中点，3ON =，则MF =_________.【答案】4【解析】【分析】根据椭圆的对称性，利用三角形中位线定理求得||MF '，再由椭圆定义求解||MF 即可．【详解】如图，根据椭圆的对称性，不妨设F 为左焦点，F '为右焦点，由椭圆221259x y +=，得5a =，210a =，N Q 是MF 的中点，O 是FF '的中点，ON ∴为FMF ' 的中位线，||2||6MF ON ∴'==，∴由椭圆的定义得||2||1064MF a MF =-'=-=．故答案为：4．13.如图，将一个各面都涂了油漆的正方体切割为125个同样大小的小正方体.经过搅拌后，从中随机取一个小正方体，记它的涂漆面数为X ，则X 的均值()=E X ______.【答案】65【解析】【分析】根据题意得出X 的所有可能取值为0,1,2,3，然后分析出涂3面油漆，2面油漆，1面油漆，0面油漆的各有多少个小正方体，从而计算X 取每个值时的概率，从而求X 的均值.【详解】X 的所有可能取值为0,1,2,3，大正方体8个顶点处的8个小正方体涂有3面油漆；每一条棱上除了两个顶点处的小正方体外剩余的都涂有两面油漆，所以涂有两面油漆的有31236⨯=个；每个表面去掉四条棱上的16个小正方体，还剩9个小正方体，这9个都是一面涂漆，所以一共有9654⨯=个小正方体涂有一面油漆；剩余的()1258365427-++=个内部的小正方体6个面都没有涂油漆，所以()270125P X ==，()541125P X ==，()362125P X ==，()83125P X ==，()()()()()00112233E X P X P X P X P X =⨯=+⨯=+⨯=+⨯=2754368150601231251251251251255=⨯+⨯+⨯+⨯==.故答案为：65.14.若函数()()52cos sin 2f x a x x x =-+在R 上单调递增，则a 的取值范围是_________.【答案】11,22⎡⎤-⎢⎥⎣⎦【解析】【分析】求导，根据()0f x '≥在R 上恒成立，即可结合二次函数的性质求解.【详解】根据题意，()22259cos 2sin 2cos cos 4cos 22f x a x x x a x x '=+-+=-+，()f x 在R 上单调递增，()0f x '∴≥在R 上恒成立，令cos x t =，[]1,1t ∈-，则()f x '可写为()2942g t at t =-+，[]1,1t ∈-，根据题意()g t 在[]1,1-上的最小值非负，∴()()10,10,g g ⎧-≥⎪⎨≥⎪⎩解得1122a -≤≤.故答案为：11,22⎡⎤-⎢⎥⎣⎦四、解答题（本大题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.）15.△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知向量(),sin m b a C =-- ，(),sin sin n c b A B =++，满足//m n u r r ．（1）求A ；（2）若角A 的平分线交边BC 于点D ，AD 长为2，求△ABC 的面积的最小值．【答案】（1）23A π=（2）【解析】【分析】（1）由//m n u r r 得出等式，再由正、余弦定理即可解出；（2）把ABC 的面积用等积法表示可得,b c 关系，再利用基本不等式得出bc 的最小值，即得面积最小值．【小问1详解】因为//m n u r r ，所以()()()()sin sin sin b a A B c b C -+=+-，由正弦定理得()()()()b a a b c b c -+=+-，所以222b c a bc +-=-，所以2221cos 222b c a bc A bc ab +--===-，因为()0,A π∈，故23A π=.【小问2详解】∵AD 平分∠BAC ，∴123BAD CAD BAC π∠=∠=∠=，∵ABD ACD ABC S S S +=△△△，∴1sin 2AB AD BAD ⋅⋅∠11sin sin 22AC AD CAD c A +⋅⋅∠=⋅⋅，即22sin 2sin sin 333c b bc πππ+=，∴22c b bc+=由基本不等式可得：22bc b c =+≥，∴16bc ≥，当且仅当4b c ==时取“=”，∴1sin 2ABC S bc A ==≥ 即ABC V的面积的最小值为.16.如图，已知点P 在圆柱1OO 的底面圆O 上，120AOP ∠=o ，圆O 的直径4AB =，圆柱的高13OO =.（1）求点A 到平面1A PO 的距离；（2）求二面角1A PB O --的余弦值大小.【答案】（1）32；（2）277.【解析】【分析】（1）根据等体积法，由11A AOP A A OP V V --=即可求出点A 到平面1A PO 的距离；（2）先证明PB AP ⊥，1PB AA ⊥，由线面垂直的判定定理可得PB ⊥面1AA P ，进而可得1A PA ∠即为所求二面角的平面角，在1Rt A PA 中，计算11cos AP A PA A P∠=即可求解.【详解】（1）因为113AA OO ==，122AO AB ==，所以1AO ===在AOP中，由余弦定理可得：AP ===所以1A P ==，2OP =，在1AOP中，由余弦定理可得222111121cos 27A P OP A O A PO A P OP +-∠===⋅，所1sin7A PO∠==，所以11227A OPS=⨯=，设点A到平面1A PO的距离为d，由11A AOP A A OPV V--=，得111133AOP AO PS AA S d⋅⋅=⋅⋅，即1111233223d⨯⨯⨯⨯=，解得：32d=，所以点A到平面1A PO的距离为32；（2）二面角1A PB O--即二面角1A PB A--，因为AB是圆O的直径，点P在圆柱1OO的底面圆O上，所以PB AP⊥，因为1AA⊥面ABP，PB⊂面ABP，可得1PB AA⊥，因为1AP AA A⋂=，所以PB⊥面1AA P，因为1A P⊂面1AA P，AP⊂面1AA P，所以PB⊥AP，PB⊥1A P，所以1A PA∠即为二面角1A PB O--的平面角，在1Rt A PA中，1A P=，AP=所以11cos7APA PAA P∠===，所以二面角1A PB O--的余弦值为7.17.双曲线()2222:10,0x yC a ba b-=>>的左顶点为A，焦距为4，过右焦点F作垂直于实轴的直线交C于B、D两点，且ABD△是直角三角形．（1）求双曲线C的方程；（2）M、N是C右支上的两动点，设直线AM、AN的斜率分别为1k、2k，若122k k=-，求点A到直线MN的距离d的取值范围．【答案】（1）2213y x -=（2）(⎤⎦【解析】【分析】（1）根据等腰直角三角形的性质，转化为,,a b c 的方程，即可求解；（2）首先设直线MN 的方程为x my n =+，与双曲线方程联立，利用韦达定理表示122k k =-，并根据2m 的取值范围，求点到直线的距离的取值范围.【小问1详解】依题意，90BAD ∠=，焦半径2c =，由AF BF =，得2b ac a+=，得22222a a a +=-，解得：1a =（其中20a =-<舍去），所以222413b c a =-=-=，故双曲线C 的方程为2213y x -=；【小问2详解】显然直线MN 不可能与轴平行，故可设直线MN 的方程为x my n =+，联立2233x my n x y =+⎧⎨-=⎩，消去x 整理得()()222316310m y mny n -++-=，在条件2310Δ0m ⎧-≠⎨>⎩下，设()11,M x y ，()22,N x y ，则122631mn y y m +=--，()21223131n y y m -=-，由122k k =-，得()()12122110y y x x +++=，即()()12122110y y my n my n +++++=，整理得()()()()2212122121210m y y m n y y n ++++++=，代入韦达定理得，()()()()()22222312112121310n m m n n n m -+-+++-=，化简可消去所有的含m 的项，解得：5n =或1n =-（舍去），则直线MN 的方程为50x my --=，得d =又,M N 都在双曲线的右支上，故有2310m -<，2103m ≤<，此时1≤<，(d ⎤=⎦，所以点A 到直线MN 的距离d的取值范围为(⎤⎦.18.已知函数()()e xf x x a =-，a ∈R .（1）当1a =时，求()f x 的极值；（2）若函数()()ln g x f x a x =-有2个不同的零点1x ，2x .（i ）求a 的取值范围；（ii ）证明：12112e x x a x x +->.【答案】（1）极小值为0，无极大值（2）（i ）()e,+∞；（ii ）证明见解析【解析】【分析】（1）将1a =代入函数解析式，求导，判断其单调性，进而得出极值；（2）（i ）化简函数()g x 的解析式，令e x t x =，问题可转化为()ln h t t a t =-在(0,)t ∈+∞有2个零点1t ，2t ，再利用导数研究函数()h t 的性质即可得出答案；（ii ）等价于证明21e a t t >，再利用极值点偏移法即可得证．【小问1详解】1a =时，()()e 1xf x x =-，()()1e 1x f x x =+'- ，令()()()(),2e xm x f x m x x ''=∴=+，(),2x ∞∴∈--，()0m x '<；()2,x ∞∈-+，()0m x '>，()f x ∴'在(),2∞--单调递减，()2,∞-+单调递增，x →-∞ 时，10x +<，e 0x >，则′<0，()21210ef '--=-<，()00f '=，x →+∞时，()f x ∞'→+，(),0x ∞∴∈-时，′<0；∈0,+∞，′>0，∴在(),0∞-单调递减，在0,+∞单调递增，∴的极小值为()00f =，无极大值.【小问2详解】（i ）()()()()ln e ln e ln e x x x g x f x a x x a x x x a x =-=-+=-，∈0,+∞，令e x t x =，()0,t ∞∈+，()1e 0x t x =+'> ，e x t x ∴=在0,+∞单调递增，令()ln h t t a t =-，即()h t 在()0,t ∞∈+有2个零点1t ，2t ，且111e x t x =，222e xt x =，()1a t a h t t t-='-= ，0a ∴≤时，()0h t '>，()h t 在()0,t ∞∈+单调递增，不存在2个零点，0a ∴>，()0,t a ∈ 时，()0h t '<；(),t a ∞∈+时，()0h t '>，()h t ∴在()0,a 单调递减，在(),a ∞+单调递增，0t → 时，()h t ∞→+；t →+∞时，()h t ∞→+，()()()min 1ln 0h t h a a a ∴==-<，()e,a ∞∴∈+.（ii ）设12t t <，()110h => ，()e e 0h a =-<，∴由（i ）知，121e t a t <<<<，即证：12e t t a >，即证：21e a t t >，2t a > ，1e a a t >，()h t 在(),a ∞+单调递增，∴即证：()21e 0a h t h t ⎛⎫=> ⎪⎝⎭，11ln t a t = ，()1111111e e e e e e ln ln ln ln 1ln a a a h a a a t t t t t t t ⎛⎫⎛⎫⎡⎤∴=-=-=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，令()()111e ln ln 1p t t t =+-，()11,e t ∈，即证：()10p t <，()1112211111eln e 1ln ln t t p t t t t t t -=='-+，令()111eln q t t t =-，()11,e t ∈，()1111e e 10t q t t t -=-='< ，()1q t ∴在()1,e 单调递减，()()1e 0q t q >=，()10p t ∴'>，()1p t ∴在()1,e 单调递增，()()1e 0p t p ∴<=，【点睛】方法点睛：利用导数证明或判定不等式问题：1．通常要构造新函数，利用导数研究函数的单调性与极值（最值），从而得出不等关系；2．利用可分离变量，构造新函数，直接把问题转化为函数的最值问题，从而判定不等关系；3．适当放缩构造法：根据已知条件适当放缩或利用常见放缩结论，从而判定不等关系；4．构造“形似”函数，变形再构造，对原不等式同解变形，根据相似结构构造辅助函数.19.已知集合{}()1,2,3,,,3A n n n =∈≥ N ，W A ⊆，若W 中元素的个数为()2m m ≥，且存在u ，()v W u v ∈≠，使得()2k u v k +=∈N ，则称W 是A 的()P m 子集.（1）若4n =，写出A 的所有()3P 子集；（2）若W 为A 的()P m 子集，且对任意的s ，()t W s t ∈≠，存在k ∈N ，使得2k s t +=，求m 的值；（3）若20n =，且A 的任意一个元素个数为m 的子集都是A 的()P m 子集，求m 的最小值.【答案】（1）{}{}1,2,3,1,3,4；（2）2；（3）13.【解析】【分析】（1）根据()P m 子集的定义，即可容易求得；（2）取{}1,3W =，求得2m =，再利用反证法假设3m ≥，推得10a <与11a ≥矛盾即可；（3）令{}020,19,18,17,11,10,9,3,16,8,4,2W =，讨论12m ≤时不满足题意，再验证13m ≥时的情况满足题意，即可求得m 的最小值.【小问1详解】当4n =时，{}1,2,3,4A =，A 的所有()3P 子集为{}{}1,2,3,1,3,4.【小问2详解】当3n ≥时，取{}1,3W =，因为2132+=，所以W 是A 的()2P 子集，此时2m =；若3m ≥，设123,,a a a W ∈且1231a a a ≤<<，根据题意，3121213232,2,2kk k a a a a a a +=+=+=，其中123,,N k k k ∈；因为121323a a a a a a +<+<+，所以312222k k k <<，所以123k k k <<；又因为123,,N k k k ∈，所以321k k ≥+；因为()3121232222k k k a a a ++=++，所以()31212312222k k k a a a ++=++，所以()()3331212111222222222k k k k k k k a =++-=+-；因为3122221222222k k k k k k ++<+=≤，所以3122220k k k +-<，所以10a <，与11a ≥矛盾.综上所述，2m =.【小问3详解】设{}{}{}{}{}1234520,12,19,13,18,14,17,15,11,5,A A A A A ====={}{}{}{}{}{}{}678123410,6,9,7,1,3,2,4,8,16A A AB B B B =======，设W 的元素个数为m ，若W 不是A 的()P m 子集，则W 最多能包含1238,,,,A A A A 中的一个元素以及1234,,,B B B B 中的元素；令{}020,19,18,17,11,10,9,3,16,8,4,2W =，易验证0W 不是A 的()12P 子集，当12m ≤时，0W 的任意一个元素个数为m 的子集都不是A 的()P m 子集，所以，若A 的任意一个元素个数为m 的子集都是A 的()P m 子集，则13m ≥；当13m ≥时，存在{}1,2,3,4,5,6,7,8i ∈，使得W 中必有两个元素属于i A ，同时i A 中两个元素之和为2的某个正整数指数幂，P m子集；所以W是A的()所以，m的最小值为13.P m子集的定义，【点睛】关键点点睛：本题考查集合新定义问题，处理问题的关键是充分把握题中对()同时要熟练的使用证明方法，属综合困难题.。

2024年青岛版六三制新高二数学下册月考试卷997考试试卷考试范围：全部知识点；考试时间：120分钟学校：______ 姓名：______ 班级：______ 考号：______总分栏题号一二三四五六总分得分评卷人得分一、选择题(共9题，共18分)1、若圆始终平分圆的周长,则实数应满足的关系是（）A.B.C.D.2、抛物线x2=4y的准线方程是（）A. x=1B. x=-1C. y=1D. y=-13、【题文】若则A.B.C.D.4、【题文】设数列｛｝的前n项和=则的值为A. 15B. 16C. 49D. 645、【题文】在平面直角坐标系中，点A（1，2），B（3，1）到直线l的距离分别为1和2，则符合条件的直线条数有（）A. 3B. 2C. 4D. 16、设f′（x）是函数f（x）的导函数；y=f′（x）的图象如图，则y=f（x）的图象最有可能的是（）A.B.C.D.7、如果实数x，y满足（x-2）2+y2=3，那么的取值范围为（）A. （-）B. [-]C. []D. （-）8、若x，y∈R，且x2+y2=1．当x+y+c=0时，c的最大值是（）A.B.C.D.9、如图是某同学为求50个偶数：246100的平均数而设计的程序框图的部分内容，则在该程序框图中的空白判断框和处理框中应填入的内容依次是()A. i>50,x=x50B. i鈮�50,x=x100C. i<50,x=x50D. i鈮�50,x=x100评卷人得分二、填空题(共6题，共12分)10、在直角坐标系xOy中，设P为两动圆（x+2）2+y2=（r+2）2，（x-2）2+y2=r2（r＞1）的一个交点；记动点P 的轨迹为C．给出下列三个结论：①曲线C过坐标原点；②曲线C关于x轴对称；③设点P（x；y），则有|y|＜|2x|．其中，所有正确的结论序号是____．11、过直线2x-y-10=0和直线x+y+1=0的交点且平行于3x-2y+4=0的直线的方程为____．12、【题文】在中，则的面积是____.13、复数2-3i的实部是 ______ ．14、已知i是虚数单位，复数z满足|z-1|=1，则|z-2i|的最大值是 ______ ．15、有一个五边形ABCDE若把顶点ABCDE涂上红、黄、绿三种颜色中的一种，使得相邻的顶点所涂的颜色不同，则共有 ______ 种不同的涂色方法．评卷人得分三、作图题(共8题，共16分)16、著名的“将军饮马”问题：有一位将军骑着马要从A地走到B地；但途中要到水边喂马喝一次水，则将军怎样走最近？17、A是锐角MON内部任意一点，在∠MON的两边OM，ON上各取一点B，C，组成三角形，使三角形周长最小．（如图所示）18、已知，A，B在直线l的两侧，在l上求一点，使得PA+PB最小．（如图所示）19、著名的“将军饮马”问题：有一位将军骑着马要从A地走到B地；但途中要到水边喂马喝一次水，则将军怎样走最近？20、A是锐角MON内部任意一点，在∠MON的两边OM，ON上各取一点B，C，组成三角形，使三角形周长最小．（如图所示）21、已知，A，B在直线l的两侧，在l上求一点，使得PA+PB最小．（如图所示）22、分别画一个三棱锥和一个四棱台．评卷人得分四、解答题(共4题，共12分)23、若动点到定点的距离比到直线距离小1，求点的轨迹方程。

2024年北师大版八年级数学上册阶段测试试卷551考试试卷考试范围：全部知识点；考试时间：120分钟学校：______ 姓名：______ 班级：______ 考号：______总分栏题号一二三四五总分得分评卷人得分一、选择题(共5题，共10分)1、小聪将一个骰子随意抛5次，出现的点数分别为6，4，3，5，4；在这5次中“4”出现的频率是（）A. 5B.C. 2D.2、周末，几名同学包租一辆面包车前往“黄岗山”游玩，面包车的租价为180元，出发时，又增加了2名学生，结果每个同学比原来少分担3元车费，设原来参加游玩的同学为x人，则可得方程（）A. -=3B. -=3C. -=3D. -=33、如图, D是等腰Rt△ABC内一点, BC是斜边, 如果将△ABD绕点A逆时针方向旋转到△ACD′的位置, 则∠ADD′的度数（）A. 25°B. 30°C. 35°D. 45°4、计算÷的结果是（）.A. 1B. x+1C.D.5、(－2)2的算术平方根是（）A. 2B. ±2C. －2D.评卷人得分二、填空题(共7题，共14分)6、随着综艺节目“爸爸去哪儿”的热播，问卷调查公司为调查了解该节目在中学生中受欢迎的程度，走进某校园随机抽取部分学生就“你是否喜欢看爸爸去哪儿”进行问卷调查，并将调查结果统计后绘制成如下不完整的统计表：。

非常喜欢喜欢一般不知道频数200 30 10频率 a b 0.025则a-b=____．7、【题文】如图；点Q在直线y＝－x上运动，点A的坐标为（1，0）；当线段AQ最短时，点Q的坐标为__________________。

8、【题文】△ABC中，∠A与∠B的平分线相交于点P，若点P到AB的距离为10，则它到AC的距离为_______________．9、若（x2-x+m）（x-8）中不含x的一次项，则m的值为 ______ ．10、如图，在菱形ABCD中，EF分别是ABAC的中点，如果EF=2那么菱形的周长为 ______ ．11、如图所示，在鈻�ABC中，按以下步骤作图：垄脵分别以点BC为圆心，以大于BC的长为半径作弧，两弧相交于MN两点；垄脷作直线MN于点D连结CD若CD=AC隆脧B=25鈭�则隆脧ACB的度数为________。

2024年沪教版高一数学下册阶段测试试卷640考试试卷考试范围：全部知识点；考试时间：120分钟学校：______ 姓名：______ 班级：______ 考号：______总分栏题号一二三四五六总分得分评卷人得分一、选择题(共5题，共10分)1、设{a n}是公差为-2的等差数列，若a1+a4+a7+ +a97=50，则a3+a6+a9+ +a99等于（）A. 82B. -82C. 132D. -1322、下列函数图象中；能用二分法求零点的是（）A.B.C.D.3、一个几何体的三视图形状都相同，大小均相等，那么这个几何体不可以是（）A. 球,B. 三棱锥,C. 正方体,D. 圆柱4、【题文】设A,Ｂ,Ｉ均为非空集合，且满足则下列各式中错误的是（）A.B.C.D.5、设集合A={x|x＞1}，则（）A. ∅∈AB. 0∉AC. 0∈AD. A⊆{0}评卷人得分二、填空题(共5题，共10分)6、7、【题文】已知f(x)＝x2＋ax＋b，满足f(1)＝0，f(2)＝0，则f(－1)=________．8、【题文】已知f（x）是R上的奇函数，且f（x+4）=f（x），当x（0；2）时，f（x）=x2，则f（7）=___________.9、下列各数a=3E（16）、b=210（6）、c=1000（4）、d=111011（2）中，由大到小的顺序是 ______ ．10、对于函数f(x)在使f(x)鈮�M恒成立的所有常数M中，我们把M中的最大值称为函数f(x)的“下确界”，则函数f(x)=x2+1(x+1)2的下确界为 ______ ．评卷人得分三、解答题(共6题，共12分)11、已知平面向量．（1）当时，求的取值范围；（2）若的最大值是求实数的值；（3）（仅理科同学做，文科同学不做）若的最大值是对任意的都有恒成立，求实数的取值范围．12、若关于x的不等式（m-3）x2-2mx-8＞0（m∈R）的解集是一个开区间D，定义开区间（a，b）的长度l=b-a．（1）求开区间D的长度l（l用m表示）；并写出其定义域。

绝密＊考试结束前2023学年第二学期浙江精诚联盟适应性联考高三日语学科试题考生须知：l．本试题卷共8页，满分150分，考试时间120分钟。

2．答题前，在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号。

3．所有答案必须写在答题卷上，写在试卷上无效。

4．考试结束后，只需上交答题卷。

第一部分听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题纸上。

第一节（共7小题；每小题2分，满分14分）听下面7段录音，每段录音下面有1个小题，从题中所给的A、B、C三个选项中选出最佳选项。

例男(1)尺士E(T)<'G1t泪本i吾老勉强L去L尤力、。

A.6小月．、厂8.9办月 C.12小月1今日、二0唉茶店忱、何睹哇飞飞寸加。

A.11峙8.7峙 C.6峙2男仍人仍家过誰祁料理在作0去寸办。

A.夕y岂儿B．母 C.看眼卸3.二人以二九力迁迂甘护七之＾行艺哇寸办。

A.唤茶店8.映画航C．公圆4.男0）人过、二杠力屯洼于何在L去寸办。

A卜4匕＾行＜B．北金在出寸C．雄祜它靶忆入九石5.女0人煤、.:.(/)会括仍前忆何它L去Lt乙办。

A贸心物旮L尤8.台所仍摇除仓L左C料理宅Lt乙6．男0人过、EIv众料理在作0去寸办。

A. t凡芬'::,13.肉(l)力匕一 C.野菜0)力区一7女0人过、七才札它注文L去寸办。

A.木、y卜＝－七一B.冷t乙V亡3一七一C.=i－匕一70一卜第二节（共8小题；每小题2分，满分16分）听下面4段录音，每段录音后有2个小题，从题中所给的A、B、C三个选项中选出最佳选项。

8.女0）人过、七，5Lt力歹才夕忆行艺去甘Iv办。

A仕事赤忙LL、办G B.体(/)渊子力吐<tt.v、办G C.眠V吩屯9.女(/)人过、二(/)冼七c·?l.,哇寸朴oA会社飞仕事左寸石B．病院＾行< C. ?朽^,J帚石10男(/)尺土匕5L飞迎九去L,t:.汃A.寝坊Lt3力屯B．键在探L飞V吃边屯 C.部屋在片付讨飞V寸之力屯ll男幻人1之今L哎、会括O)内容七合？tL屯汛刃丈七令机飞寸办。

-:: 7”下列强；明中E ，晶（,f.cy 一辈立学试卷（噩科］λ15 且－� C.15）＇岛-.ll.l.抒问：120舟峙试革睛分.］50骨〉A 司10明：且15扭.2品,$,.,,. 告咀霄豆是喃喃用悔阜碍于J争咕嘻再马精品也喜量＃寺，国.！＇.，啡玛峰题时－研吝噎苟品h 』细画型SI f (:d =·t a n .::ie -!!i n 在跑卡ι，苟且本忧患A且提．ι B.C E 小圈「，，踵小圃5卦F 共60张在每小阻挡国的回i 1"选明申，只-3<.;r<刷』＝�y l y ＝主.r ��E A ）.罔A na 的无理＋酣由.3 且也C 寻2.=ll:6tl BC中，若AB =I AC =5 :::.ir'! A ＝� 1-:1Tti '"7i'f·=D. 6且－l l e � 且主10. A .喜 －”，、、h、:3.画瞌／Cr)』..zl -7..r 啻＋l 的回串在血U .. /(4））娃的国扭曲剖串芷『.t\. -8.. 且－7巳－6,且－5唱.J盟主;r ��节t 11响毡喃喃ll.W .咀.fflW •咄咄圳眶ti �口电.!l)ll.)'J • l [ll 』叫拙作a陪同剧咀回1－.；；；明取E t 曲吁唱国』：忆M 文F !.f.'.l 百rv .r 翩翩！棉军事也i:;!1.1'n 由U!'r.rr Ai\量臼耐性2肉同剧帘？町非金阳串串·M i ’圄嬉刷品件i ii 脑T 长挡住与陆曾任曲时l 制附1<f 』· 1 · ii 困〈川，（2).(3）中嗣囚的离心串分剧为且6 ..巴细雨阻／（x)-lg x－（吉）＂＂./(m ）同L且O＜户〈嗣＜11.�J '(,J l <l 且J （ρ＞I 盹f (n )>I 且f f p )>’t川＞-1且（，（p)<]:D .／（时＜l 且J(p.)<1－� --·l (a >o ,o >O ））剧左、在甜点1-t 别为’F',, ,f t 串』吁；为C左“「rr 为主ltllM F ，，上一点画且I M!\H -H \.!F -r • P 为蝇it N F �闺中品君l f \F d =41口1.P l (O 为血呈阳占，L时t幽1曲目啤肯固古A.y:a土2工y ＝土d 1且如阁，荫敢f (:r ）曲回串由一翩翩植物酶的－时附属咽卢；r )的罕点为－t .f(.t +a z 〕�J （�r ）阳＃的J.f .7E R 植成5『{i SJ吉儿〈一目，一T J U ［－；；－哩十四〉, ｛一惧噜－.／3]U （.／立．十∞）F 一？叫孚十四〉国｝:, --., 'to l 面＝』瞩暨咀巳$：＊II 典.�J j ＼圈中每小圈E 卦a 典现分嘈捆】菁靠墙在普噩卡翩翩且也置，1口.21:盟主」n -2i )o -sn的宝由为i-. J'ii . ';{:f :x .y i 罔iE 玉’且在组丐1'1"'i . .r .,.. ：）�.!o 画剧.z －｝·罔缸式也为血,,.:rf 申JI 的15司在撞到比1中•a l =2. vf +J )Q ,..H =2时－2国十跑马唱』则也＝－－主Z自I盐t m:’wt：斗1－-－－－·吨(1) 臼｝业肉踊A 』冒吁的边f ,a ，，（；� c .巴知.�＝、币，t,=2.’I •草�创茸的面.......· I 的蠕事3旷2日曲Y 副rr 2-2.21－叫:20. ( 12 #.)(]) (2) τ＝为='l.p:,,{p ＞的的1且JS..�II 盟t，回一『于点T �.日Z ）� -1-2�，1 x. 2童M 搞捏.2J 胃晤中任菌－BiJ;警二归..辙，i•J 撞fir 髓的篝－个国国副l mi醋’'i-41.：盟的吉;s;电帚卸阻刀副』H JJ '1') 在10）写出(2）毡，A(l ,0),,.8(-l ,O) ..且P为曲盟C I 耐动点础四．四＋2掘，．：静的-5�;f 暗直选t闸门，0卦f（耳）= 1..-c+f!!. I + I .i'+&1.R ./(x〕�l.如C-G 南1］萨$a ’•• b的－盟m 目并说t �c� tlfiT。

交、并、补集的混合运算·单选题50练（含详细答案）一、单选题1．已知集合=U =log 2，>1，=U =，>1，则A B =⋂（）A ．ΦB ．{}|01y y <<C ．1|12y y ⎧⎫<<⎨⎬⎩⎭D ．1|02y y ⎧⎫<<⎨⎬⎩⎭2．已知全集U ＝R ，集合A ＝{x|x 2－2x ＜0}，B ＝{x|x －1≥0}，那么集合A∩U B ð＝（）A ．{x|0＜x ＜1}B ．{x|x ＜0}C ．{x|x ＞2}D ．{x|1＜x ＜2}3．已知集合{}0,1,2A =，{}0,1,3B =，若全集U AB=⋃，则()U AB =⋂ð（）A ．{}2,3B ．{}0,1C ．{}0,1,2,3D ．∅4．已知全集{}0,1,2,3,4,5,6,7,8,9U =，集合{}0,1,3,5,8A =，集合{}2,4,5,6,8B =，则()()U U C A C B =⋂（）A ．{}5,8B ．{}7,9C ．{}0,1,3D ．{}2,4,65．设集合U={1，2，3，4，5}，A={1，2，3}，B={2，4}，则图中阴影部分所表示的集合是（）A ．{4}B ．{2，4}C ．{4，5}D ．{1，3，4}6．已知集合{|5}U x x x N =≤∈，，{}1245A =，，，，0123B =｛，，，｝，则()UA B =⋂ð（）A ．{}03，B ．{3}C ．{0}D ．{}12，7．设全集*{|6}U x N x =∈<，集合{}13A =，，{}35B =，，则()U A B ⋃ð（）A ．{}1 6，B ．{}15，C ．{}24，D ．{}23，8．已知集合{}(){}|24|lg 2A x x B x y x =-<<==-，，则()RAC B =⋂（）A ．()24，B ．()24-，C ．(]22-，D ．()2-+∞，9．设全集为R ，若{}|1M x x =≥，{}|05N x x =≤<，则()()U U C M C N ⋃是（）A ．{}|0x x ≥B ．{|1x x <或5}x ≥C ．{|1x x ≤或5}x >D ．{|0x x <或5}x ≥10．已知集合{}|06M x x =<<，2{|450}N x x x =--≤，则()R M N ⋂=ð（）A ．()56，B ．()05，C ．()16-，D ．()()1056⋃-，，11．已知集合A={x ∈R|0≤x≤4}，B={x ∈R|x 2≥9}，则A ∪（∁R B ）等于（）A ．[0，3）B ．（﹣3，4]C ．[3，4]D ．（﹣∞，﹣3）∪[0，+∞）12．已知全集U R =，集合{}|12A x x =-〉，{}2|680B x x x =-+<，则集合()UA B =⋂ð()A ．{}|23x x <≤B ．{}|14x x -≤≤C ．{}|23x x ≤<D ．{}|14x x -<<13．已知集合{|2}A x x = ，2{|60}B x x x =-- ，则RAB =⋂ð（）A ．{|23}x x <B ．{|23}x x <C ．{|23}x x -< D ．{|32}x x -< 14．已知全集{}1,2,3,4,5,6U =，集合{}1,2,5A =，集合{}1,3,4B =，则()U C A B =⋂（）A ．{}1B ．{}3,4C ．{}2,5D ．{}1,2,3,4,515．已知集合{}|14A x x =≤≤，(){}2|14B x x =-≥，则()R A B ⋂=ð（）A ．[]34，B ．[]14，C ．[)13，D ．[)3+∞，16．已知集合{}{}|1|ln 1A x x B x N x =<=∈<，，则()R C A B =⋂（）A ．{}2B ．{}12，C ．{}23，D ．{}123，，17．已知集合{}{}{}0,1,2,3,4,5,6,7,1,2,3,5,1,2,4,6U A B ===，则()UA B =⋃ð（）A ．{0,1,2,4,6,7}B ．{1,2,4,6,7}C ．{4,6}D ．{0,4,6,7}18．设全集为{}3,2,1,0,1,2,3U =---，集合{}3,0,1S =-，{}1,2T =-，则()U ST ⋃ð等于（）A ．0B ．{}2,3-C ．{}2,1,2,3--D ．{}3,1,0,1,2--19．已知全集U R =，集合{|(4)(1)0}A x x x =--<，{}3|log 1B x x =>，则()UAB =⋂ð（）A ．{13}xx ≤<∣B ．{13}x x <≤∣C ．13}x x <<D ．{14}xx ≤<∣20．已知全集{}12345U =，，，，，集合{}{}13124A B ==，，，，，则()U A B ⋂=ð（）A ．{}24，B ．{}15，C ．{}1245，，，D ．{}12345，，，，21．已知全集U R =，{}|22M x x =-≤≤，{}|1N x x =<，那么MN =⋃（）A ．{}|21x x -≤<B ．{}|21x x -≤≤C ．{}|2x x <-D ．{}|2x x ≤22．已知集合{}|24xA x =<，()(){}|410B x x x =--<，则()RA B =⋂ð（）A ．{}|12x x <<B ．{}|24x x <<C ．{}|24x x ≤<D ．{|2x x <或4}x ≥23．设全集U={1，2，3，4，5，6，7，8}，集合S={1，3，5}，T={3，6]，则()U C ST ⋃等于（）A ．∅B ．{2，4，7，8}C ．{1，3，5，6}D ．{2，4，6，8}24．已知全集{}1,0,1,2,3U =-，集合{}0,1,2A =，{}1,0,1B =-，则U ()A B =⋂ð（）A ．{}1-B ．{}0,1C ．{}1,2,3-D ．{}1,0,1-25．已知集合M={x|2x ≤1}，N={x|-2≤x ≤2}，则R C MN⋂（）A ．[-2，1]B ．[0，2]C ．（0，2]D ．[-2，2]26．全集{}{}3,24,|log 1xU R A X B x x ===<，则A B ⋂＝（）.A ．{}|2x x <-B ．{}|23x x <<C ．{}3x x D ．{|2x x <-或23}x <<27．设全集U {x N |x 6}=∈<，集合{}A l,3=，{}B 3,5=，则()()UU A B (=⋂)A ．{}2,4B ．{2,4，6}C ．{0,2，4}D ．{0,2，4，6}28．设全集为{}|7U x N x =∈<.集合A={1，3，6}，集合B={2，3，4，5}．则集合UAB =⋂ð（）．A ．{3}B ．{}1,3,6C ．{}2,4,5D ．{}1,629．已知集合{}{},1,0,1,2,3,2,0,3U Z A B ==-=--，则UAB =⋂ð（）A ．{3-，3}B ．{2-，0，2}C ．{0，2}D ．{1-，1，2}30．设全集{}2,1,0,1,2U =--，{}2,1A =--，{}2,1,0,1B =--，则()U C A B =⋂（）A ．{}2,1--B ．{}0,1C ．{}1,0,1-D ．{}2,1,0,1--31．已知全集U Z =，集合{}123A =-，，，{}34B =，，则()UA B =⋂ð（）A ．{}4B ．{}3C ．{}12，D ．∅32．已知集合{}1,2,3,4,5,6,7U ＝，{}2,3,4,5A =，{}2,3,6,7B =，则()UBA =⋂ð（）A ．{}1,6B ．{}1,7C ．{}6,7D ．{}1,6,733．设全集U=R ，集合A={x|x 2﹣3x≥0}，B={x ∈N|x≤3}，则（∁U A ）∩B 等于（）A ．∅B ．{0，1}C ．{1，2}D ．{1，2，3}34．图中阴影部分所对应的集合是（）A ．()()UAB B ⋃⋂ðB ．()U AB ⋂ðC ．()()()U AB A B ⋂⋂⋃ðD ．()()()U AB A B ⋃⋃⋂ð35．设全集为R ，集合A={x||x|≤2}，B={x|11x -＞0}，则A∩∁R B=（）A ．[﹣2，1）B ．[﹣2，1]C ．[﹣2，2]D ．[﹣2，+∞）36．已知全集{1,U =2，3，4，5，6}，集合{}1,4P =，{}3,5Q =，则()(U PQ =⋃ð)A ．B ．3，5，C ．3，4，D ．2，3，4，5，37．设全集U={x|x ＜4，x ∈N}，A={0，1，2}，B={2，3}，则B ∪∁U A 等于（）A ．{3}B ．{2，3}C ．∅D ．{0，1，2，3}38．已知集合{|48}A x x =≤<，{|210}B x x =<<，则()R C A B =⋂（）A ．{|48}x x ≤<B ．{|28}x x <<C ．{|410}x x <<D ．{|24}{|810}x x x x <<≤<⋃39．已知R 是实数集，M={x|2x＜1}，N={y|y=+1}，N∩∁R M=（）A ．（1，2）B ．[0，2]C ．∅D ．[1，2]40．已知全集{}0,1,2,3,4U =，集合{}1,2,3A =，{}2,4B =，则()UA B⋃ð为（）A ．{}0,2,3,4B ．{4}C ．{}1,2,4D ．{}0,2,441．若集合=0，，=1，2，∩=2，则PQ ⋃=()A ．{0，1}B ．{0，2}C ．{1，2}D ．{0，1，2}42．已知集合A={x|y=}，B={x|﹣1≤2x ﹣1≤0}，则（∁R A ）∩B=（）A ．（4，+∞）B ．102⎡⎤⎢⎣⎦，C ．142⎛⎤⎥⎝⎦，D ．（1，4]43．已知全集{}1,2,3,4,5,6,7,8,U =集合{}{}3,4,5,6,5,6,7,8A B ==，则()U A B =⋂ð（）A ．{}1,2B ．{}3,4C ．{}5,6D ．{}7,844．已知全集{}1,0,1,2,3U =-，集合{}0,1,2A =，{}1,0,1B =-，则()UA B =⋂ð（）A ．{}1-B ．{}0,1C ．{}1,2,3-D ．{}1,0,1,3-45．设{}2,{|21},log 0xU A x B x x ==>=R ,则CUAB =⋂（）A ．{|0}x x <B ．{}|1x x 〉C ．{|01}x x <≤D ．{|01}x x ≤<46．已知A ，B 均为集合U={1，3，5，7，9}的子集，且A∩B={3}，()U C B ∩A={9}，则A=（）A ．{1，3}B ．{3，7，9}C ．{3，5，9}D ．{3，9}47．已知全集U={x|x≤9，x ∈N +}，集合A={1，2，3}，B={3，4，5，6}，则∁U （A ∪B ）=（）A ．{3}B ．{7，8}C ．{7，8，9}D ．{1，2，3，4，5，6}48．若集合A={x|x 2﹣3x ﹣10＜0}，集合B={x|﹣3＜x ＜4}，全集为R ，则A∩（∁R B ）等于（）A ．（﹣2，4）B ．[4，5）C ．（﹣3，﹣2）D ．（2，4）49．设全集u={0，1，2，3，4}，集合A={1，2，3}，B={2，3，4}，则()UAC B =⋂（）A ．{0}B ．{1}C ．{0，1}D ．{0，1，2，3，4}50．已知集合U={1,2,3,4,5,6,7}，A={2,3,4,5}，B={2,3,6,7}则UBA⋂ð=（）A ．{1,6}B ．{1,7}C ．{6,7}D ．{1,6,7}答案解析部分1．【答案】D【知识点】交、并、补集的混合运算；指数函数的定义、解析式、定义域和值域；对数函数的值域与最值【解析】【分析】=，=，所以故选D.【点评】熟练掌握指数函数和对数函数的定义域、值域。

2024-2025学年第一学期期中南京市六校联合调研试题高一数学（答案在最后）一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合={U 2+=0}，则1与集合的关系为（）A．1∈B．1∉C．1⊆D．1⊈2．命题：2(4,),51x x m ∀∈+∞+>的否定是（）A．2(4,),51x x m ∀∈+∞+≤B．2(4,),51x x m ∃∈+∞+≤C．2(,4],51x x m∃∈-∞+≤D．2(4,),51x x m∃∈+∞+<3．已知命题:32p x -<≤，若命题p 是命题q 的必要条件，则命题q 可以为（）A．31x -≤≤B．1x <C．31x -<<D．3x <-4．若,,R a b c ∈，且,0,a b c a b c >>++>则下列命题正确的是（）A．11a b>B．11baa b <++C．33c a <D．若0ac <，则22cb ab <5．某工程需要向一个容器内源源不断地注入某种液体，有三种方案可以选择，这三种方案的注入量随时间变化如下图所示：横轴为时间（单位：小时），纵轴为注入量，根据以上信息，若使注入量最多，下列说法中错误的是（）A．注入时间在3小时以内（含3小时），采用方案一B．注入时间恰为4小时，不采用方案三C．注入时间恰为6小时，采用方案二D．注入时间恰为10小时，采用方案二6．已知1122a a --=，则22a a --=（）A．B．±C．D．±7．已知函数222,0()04814,4x x f x x x x x +<⎧⎪=≤≤⎨⎪-+>⎩，若()2f a =，则(5)f a -的值为（）A．1B．1或0C．1-或1或0D．1或1-8．已知()22f x x x =-+，若关于x 的方程()()()20,f x mf x n m n ⎡⎤++=∈⎣⎦R 恰好有三个互不相等的实根，则实数m 的取值范围为（）A．1m <-B．0m ≤C．1m <-或0m >D．0m =或1m <-二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对得6分，部分选对得部分分，有选错得0分．9．下列命题中为真命题的是（）A．对任意实数x ，均有21x x +>B．若0xy =，则0x y +=C．设,R a b ∈，则“0a ≠”是“0ab ≠”的必要不充分条件D．若0x >，则()22lg lg x x =10．如图，已知矩形U 表示全集，,A B 是U 的两个子集，则阴影部分可表示为（）A．()U A B ⋂ðB．()B A B ⋂ðC．()U A B ⋂ðD．()()A B A B ⋃⋂ð11．已知,a b 为正实数，且216ab a b ++=，则（）A．ab 的最大值为8B．2a b +的最小值为8C．1112a b +++的最小值为2D．19b a +-的最小值为110-三、填空题：本题共3小题，每小题5分，共15分．12．函数y =的定义域是______.13．42223log log 16log log 68⎛⎫-+= ⎪⎝⎭______.14．已知函数()2229f x x ax a =-+-，x ∈23,a a ⎡⎤-⎣⎦()0a >，若函数()f x 的值域为[]9,0-，则实数a 的取值范围是______.四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．（13分）已知集合{}360A x x =-<，24<1B x x x ⎧=-⎫⎨⎬⎩⎭，{}>3C x x a =-，全集U R =，求：（1）A B ⋂；（2）()R A B ð；（3）如果B C ⋂=∅，求a 的取值范围．16．（15分）已知关于x 的一元二次不等式20ax x b ++>的解集为()(),21,-∞-+∞ ．（1）求a 和b 的值；（2）求不等式()222210ax a b x c -+++-<的解集．17．（15分）最近南京某地登革热病例快速增长，登革热是一种由登革病毒引起的急性虫媒传染病，主要通过埃及伊蚊和白纹伊蚊传播，为了阻断传染源，南京卫建委在全市范围内组织了蚊虫消杀工作．某工厂针对市场需求开始生产蚊虫消杀工具，经过研究判断生产该工具的年固定成本为50万元，每生产x 万件，需另外投入成本()C x （万元），2130,050()81005140052,0x x x C x x x x ⎧+<<⎪⎪=⎨⎪+-≥⎪⎩，每件工具售价为50元，经过市场调研该厂年内生产的工具能全部销售完.（1）写出年利润L （万元）关于年产量x （万件）的函数解析式；（2）年产量为多少万件时，该厂在这一工具的生产中所获利润最大？18．（17分）已知一次函数()f x 和二次函数()g x 的图像都过点()0,0和()1,1，且()()g x g x -=．（1）求()f x 和()g x 的解析式；（2）设关于x 的不等式()()()()21123k f x k k g x ++>-++()k R ∈的解集为T ．①若T R =，求实数k 的取值范围；②是否存在实数k ，满足：“对于任意正整数t ，都有t T ∈；对于任意负整数s ，都有s T ∉”，若存在，求出k 的值，若不存在，说明理由．19．（17分）已知集合{}()122k A a a a k =≥ ,,，其中()Z 1,2,i a i k ∈= ，由A 中元素可构成两个点集P 和Q ：(){},,,P x y x A y A x y A =∈∈+∈，(){},,,Q x y x A y A x y A =∈∈-∈，其中P 中有m个元素，Q 中有n 个元素.新定义1个性质G ：若对任意的x A ∈，必有x A -∉，则称集合A 具有性质G ．（1）已知集合{}0,2,4J =与集合{}1,2,3K =-和集合{}2L y y x ==+，判断它们是否具有性质G ，若有，则直接写出其对应的集合P ，Q ；若无，请说明理由；（2）集合A 具有性质G ，若520k =，求：集合Q 最多有几个元素？（3）试判断：集合A 具有性质G 是m n =的什么条件，并证明．2024-2025学年第一学期期中六校联合调研试题高一数学参考答案及评分标准1、【答案】B2、【答案】B3、【答案】C4、【答案】C5、【答案】D6、【答案】C7、【答案】B8、【答案】D9、【答案】AC10、【答案】AB11、【答案】ABD12、【答案】()(),13,-∞-⋃+∞13、【答案】3214、【答案】11321a ≤+≤15、【答案】（1）由题意得集合{}|2A x x =<，（2分）集合{}|04B x x =<<，（4分）则{}|02A B x x ⋂=<<（5分）（2）由（1）知(){}R |2A x x =≥ð，{}|04B x x =<<，（7分）所以(){}R 0A B x x ⋃=>ð.（9分）由（1）知，集合{}|04B x x =<<，又{}>3C x x a =-，B C ⋂=∅,所以3034a a -≤+≥且.（12分）所以1 3.a ≤≤（13分）16、【答案】（1）由题意知2-和1是方程20ax xb ++=的两个根且0a >，（1分）由根与系数的关系得12121ab a ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩，解得12a b =⎧⎨=-⎩；（5分）（2）由1a =、2b =-，不等式可化为22210x x c -+-<，即()()110x c x c -+--<⎡⎤⎡⎤⎣⎦⎣⎦，则该不等式对应方程的实数根为1c +和1c -．（8分）当0c >时，11c c +>-，解得11-<<+c x c ，即不等式的解集为()1,1c c -+，（10分）当0c =时，11c c +=-，不等式的解集为空集，（12分）当0c <时，11c c +<-，解得11c x c +<<-，即不等式的解集为()1,1c c +-，（14分）综上：当0c >时，解集为()1,1c c -+，当0c =时，11c c +=-，不等式的解集为空集，当0c <时，11c c +<-，解得11c x c +<<-，即不等式的解集为()1,1c c +-．（15分）17、【答案】（1）当050x <<时221()503050L x x x x =---2102250x x =-+-（3分）当50x ≥8100()505140050L x x x x=--+-8100350x x ⎛⎫=-+ ⎪⎝⎭（6分）故()212050,050,8100350,520,x x x L x x x x ⎧-+-<<⎪⎪=⎨⎛⎫⎪-+≥ ⎪⎪⎝⎭⎩（7分）（2）当050x <<时，21()(202)150L x x =--+∴当20x =时，()L x 取得最大值(20)150L =（10分）当50x ≥时，8100()350350170L x x x ⎛⎫=-+≤-= ⎪⎝⎭（当且仅当8100x x=即90x =时取到等号）（13分）170150>Q 90x ∴=时，()L x 取得最大值（14分）答：(1)年利润L （万元）关于年产量x （万件）的函数解析式为()212050,050,8100350,520,x x x L x x x x ⎧-+-<<⎪⎪=⎨⎛⎫⎪-+≥ ⎪⎪⎝⎭⎩(2)年产量为90万件时，该厂在这一工具的生产中所获利润最大．（15分）18、【答案】（1）设()f x ax =，由()11f =得1a =，所以()f x x =；设()2g x bx cx =+由()g 11=得1b c +=；又因为()()g x g x -=，所以()()22bx cx b x c x +=-+-，得0c =；所以()2g x x=（4分）（2）原不等式化为()()()2223110R k k x k x k --+++>∈当202k k 3--=时，解得32k =，或1k =-，①当1k =-时，不等式化为10>，1k ∴=-时，解集为R ；（5分）②当32k =时，不等式化为5102x +>，对任意实数x 不等式不成立；（7分）③当()()22223014230k k k k k ⎧-->⎪⎨∆=+---<⎪⎩时，可得()()3,1,213,1,7k k ∞∞∞∞⎧⎛⎫∈--⋃+ ⎪⎪⎪⎝⎭⎨⎛⎫⎪∈--⋃+ ⎪⎪⎝⎭⎩，则k 的取值范围为()13,1,7k ⎛⎫∈-∞-+∞ ⎪⎝⎭；（10分）综上所述，实数k 的取值范围为(]13,17⎛⎫-∞-+∞ ⎪⎝⎭.（3）根据题意，得出解集(,)T r =+∞，[)1,1r ∈-，当202k k 3--=时，解得32k =，或1k =-，32k =时，不等式的解集为2,5⎛⎫-+∞ ⎪⎝⎭，满足条件，1k =-时，10>恒成立，不满足条件，当2230k k -->时，此时对应的一元二次不等式的解集形式不是(,)r ∞+的形式，不满足条件，当2230k k --<时，此时对应的一元二次不等式的解集形式不是(,)r ∞+的形式，不满足条件，综上，存在满足条件的k 的值为32．（17分）19．【答案】（1）①集合0J ∈，不符合定义故J 不具有性质G ；②集合K 具有性质G ，对应集合()(){}1,3,3,1P =--，()(){}2,1,2,3Q =-；③集合L 不是整数集所以不具有性质G .（4分）（2）由题意可知集合A 的元素构成有序数对(),i j a a ()*,N ,,i j i k j k ∈≤≤，共有2k 个，∵0A ∉，∴(),i i a a Q∉又∵a A ∈时，a A -∉，∴(),i j a a Q ∈时候，(),j i a a Q ∉，∴集合Q 的元素个数不超过21349402k k-=个，取{}1,2,,520A = ，则Q 中元素的个数为134940个，故Q 中元素的个数最多为134940.（10分）（3）1）当集合A 具有性质G 时，①对于(),a b P ∈，根据定义可知：,,a A b A a b A ∈∈+∈，又因为集合A 具有性质G ，则(),a b a Q +∈，如果(),a b ，(),c d 是P 中的不同元素，那么a c =，b d =中至少有一个不成立，于是b d =，a b c d +=+中至少有一个不成立，故(),a b b +和(),c d d +也是Q 中不同的元素，可见P 的元素个数不多于Q 的元素个数，即m n ≤，②对于(),a b Q ∈，根据定义可知：,,a A b A a b A ∈∈-∈，又因为集合A 具有性质G ，则(),a b b Q -∈，如果(),a b ，(),c d 是Q 中的不同元素，那么a c =，b d =中至少有一个不成立，于是b d =，a b c d -=-中至少有一个不成立，故(),a b b -和(),c d d -也是P 中不同的元素，可见Q 的元素个数不多于P 的元素个数，即m n ≤，由①②可知m n=2）集合{1,1,2,3}A =-，则{(1,2),(2,1),(1,3),(3,1),(1,1),(1,2),(2,1)}P =----，{(1,2),(2,3),(2,1),(3,2),(1,1),(3,1),(2,1)}Q =--，满足m n =，而集合A 不具有性质G ，所以集合A 具有性质G 是m n =的充分不必要条件.（17分）。