山东省滕州第七中学2015届高三11月考数学(理)试题 Word版含答案

山东省滕州市第七中学2015届高三1月月考数学（理）试题说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

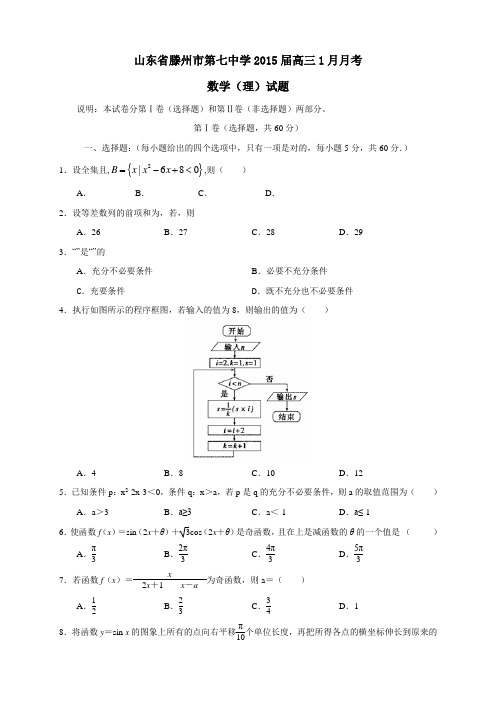
第Ⅰ卷（选择题，共60分）一、选择题：（每小题给出的四个选项中，只有一项是对的，每小题5分，共60分．） 1．设全集且,{}2|680B x x x =-+<,则（ ）A ．B ．C ．D ． 2．设等差数列的前项和为，若，则A ．26B ．27C ．28D ．293．“”是“”的 A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．执行如图所示的程序框图，若输入的值为8，则输出的值为（ ）A ．4B ．8C ．10D ．125．已知条件p ：x 2-2x-3＜0，条件q ：x ＞a ，若p 是q 的充分不必要条件，则a 的取值范围为（ ）A ．a ＞3B ．a≥3C ．a ＜-1D ．a≤-16．使函数f （x ）＝sin （2x ＋θ）＋3cos （2x ＋θ）是奇函数，且在上是减函数的θ的一个值是 （ ）A ．π3B ．2π3C ．4π3D ．5π37．若函数f （x ）＝x x ＋x －a为奇函数，则a ＝（ ）A ．12B ．23C ．34D ．18．将函数y ＝sin x 的图象上所有的点向右平移π10个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象的函数解析式是 （ ） A ． B ．C ．D ．9．已知关于x 的方程：a x x =-+242log )3(log 在区间（3，4）内有解，则实数a 的取值范围是 （ ）A ．B ．）C ．D ．10．在矩形ABCD 中，AB=，BC=4，点E 为BC 的中点，点F 在CD 上，若，则的值是（ ）A ．B ．C ．D ．11．已知函数：①，②，③．则以下四个命题对以上的三个函数都成立的是（ ） 命题是奇函数； 命题在上是增函数；命题； 命题的图像关于直线对称A ．命题B ．命题C ．命题D ．命题12．是上的偶函数,若将的图象向右平移一个单位后,则得到一个奇函数的图象,且,则)2011()3()2()1(f f f f ++++ 的值为（ ）A ．－1B ．C ．1D ．不能确定第Ⅱ卷（非选择题共90分）二、填空题：（本大题共4小题，每小题5分，共20分。

山东省滕州市第七中学2021届高三1月月考数学(理)试题
Word版含答
2021年山东省滕州市第七中学高三01月月考
数学（理）试题
说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷（选择题，共60分）
一、选择题：（每小题给出的四个选项中，只有一项是对的，每小题5分，共60分．）
2
1．设全集U R,且A x|x 1 2,B x|x 6x 8 0,则(CUA)
B （）
A．[ 1,4) B．(2,3) C．(2,3] D．( 1,4) 2．设等差数列{an}的前n项和为Sn，若S9 81，则a2 a5 a8
A．26
B．27
C．28
D．29
3．“ 30”是“sin
1”的 2
B．必要不充分条件 D．既不充分也不必要条件
A．充分不必要条件 C．充要条件
4．执行如图所示的程序框图，若输入n的值为8，则输出S的值为（）
A．4
B．8
C．10
D．12
5．已知条件p：x2-2x-3＜0，条件q：x＞a，若p是q的充分不必要条件，则a的取值范围为（）
A．a＞3
B．a≥3
C．a＜-1
D．a≤-1
6．使函数f（x）＝sin（2x＋θ）＋3cos（2x＋θ）是奇函数，且在区间 0 上是减函数的θ的一个值是（）
4。

山东省滕州第七中学2015届高三11月考（文）数学试题（文史类）共4页，满分150分，考试时间120分钟。

注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡相应的位置上。

2．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答，在试题卷上答题无效。

一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个备选项中，只有一项是符合题目要求的1．已知α是第二象限角，sin α＝513，则cos α＝（ ） A ．－1213 B ．－513 C ．513 D ．12132．已知双曲线x 225－y 29＝1的左、右焦点分别为F 1、F 2，若双曲线的左支上有一点M 到右焦点F 2的距离为18，N 是MF 2的中点，O 为坐标原点，则|NO |等于（ ）A ．23B ．1C ．2D ．43．下列说法正确的是A ．样本10，6，8，5，6的标准差是3．3．B ．“p q ∨为真”是“p q ∧为真”的充分不必要条件；C ．已知点()2,1A -在抛物线()220y px p =>的准线上，记其焦点为F ，则直线AF 的斜率等于4-D ．设有一个回归直线方程为ˆ2 1.5y x =-，则变量x 每增加一个单位，ˆy 平均减少1．5个单位；4．已知抛物线24y x =的准线与x 轴的交点为A ，焦点为F ，l 是过点A 且倾斜角为3π的直线，则点F 到直线l 的距离等于A ．1BC ．2D ．5．函数2()2log 3x f x x =+-在区间(1,2)内的零点个数是A ．0B ．1C ．2D ．36．一个几何体的三视图如图所示，其中正视图和侧视图均是边长为2的等边三角形，则该几何体的表面积是A B ． C ．12 D 7．运行如图所示的流程图，则输出的结果n a 是A ．1B ．1-C ．4-D ．5-8．函数112211()tan()log ()|tan()log ()|4242f x x x x x ππ=+----在区间1(,2)2上的图象大致为A B C D9．在锐角ABC ∆中，三个内角,,A B C 满足：2sin ()cos()B C A B +=-，则角A 与角B 的大小关系是A ．23AB π+= B ．A B <C ．A B =D ．A B >10．如图，已知,B C 是以原点O 为圆心，半径为1的圆与x 轴的交点，点A 在劣弧PQ （包含端点）上运动，其中60POx ∠=，OP OQ ⊥，作A H B C ⊥于H ．若记AH xAB yAC =+，则xy 的取值范围是A ．1(0,]4 B ．11[,]164 C ．13[,]1616 D ．31[,]164二、填空题：本大题共5小题，每小题5分，共25分.把答案填写在答题卡相应的位置上11．若i 为虚数单位，则复数31i i+=-． 12．在[3,3]-上随机取一个数x ，则(1)(2)0x x +-≤的概率为．13．满足约束条件⎪⎩⎪⎨⎧≤--≥-≥+3213y x y x y x 的变量,x y 使得230x y a ++≥恒成立，则实数a 的最小值为．14．已知点P 是双曲线2219y x -=上的一点，12,F F 是双曲线的左右焦点，且12120PF PF <>=︒，，则12=PF PF +．15．已知正项等差数列{}n a 的前n 项和为n S ，9=2S ，,*p q N ∈，且18p q +=，则p q S S ⋅的最大值为．三、解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤16．（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问7分）已知正项等比数列{}n a 满足：3454,24a a a =+=.（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）若(1)2n n na b n n =⋅+⋅，求数列}{n b 的前n 项和n S .17．（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问7分）某工厂对一批产品的质量进行了抽样检测，右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图.已知样本中产品净重在[70,75)克的个数是8个。

2014-2015学年度山东省滕州第七中学第一学期高三第11月考 语文试题 本试卷分为选择题和非选择题两部分。

共8页，150分。

考试时间150分钟。

注意事项：1．下列词语中加点的字，注音没有错误的一项是 A．广袤（mào） 靓（jìng）妆 豢（huàn）养 蟾宫（chán）宫折桂 B．道行（heng） 聒（guō）噪 跻（jī）身 胼手胝（dǐ）足 C．泥淖（nào） 龋（qǔ）齿 秸（jí）秆 沆（hàng）瀣一气 D．应（yīng）验 股肱（gōng） 勖（xù）勉 毋庸置喙（huì） 下列各句中成语使用恰当的一项是（ ） A．以牺牲环境来发展经济的做法，如果还不能引起各级政府的高度重视，后果将无法想象，这不是危言耸听。

B．小赵在这次技能大比武中荣获特等奖,确实值得表扬，但他旷工迟到、殴打同事等错误，绝不可一笔抹杀。

C．孔子曰：“学而不思则罔。

”“思”是消化知识的重要途径，可是许多学生没头没脑，学习时不加思考，结果事倍功半。

D．高中毕业以后，李小海没能考上理想的大学，也没有找到合适的工作，他便整天不学无术，在社会上瞎混。

下列有关《红楼梦》内容的说法中不正确的一项是 A．凤姐患病，一时难以痊愈。

王夫人便让尤氏、探春一同照管园中事物，又请来宝钗帮忙，托她各处小心。

B．宝玉不愿会客，湘云劝他谈讲仕途经济，宝玉马上放下脸，叫湘云到别处呆去，还说“林姑娘”从不说这些混帐话。

C．邢岫烟的家境贫苦，全家曾租借庙里的房子，一住十年，后来投靠亲戚来到贾府。

她的姑妈邢夫人不关痛痒地将她交给凤姐，凤姐冷眼旁观，发现她心性为人不像邢夫人及她的父母一样，觉得她是温厚可疼之人，又可怜她家贫命苦，反而比其他姐妹多疼她一些。

D．宝玉病后游园触景伤情，心生感慨之际忽见一股火光从山下那边冲出。

藕官在园子里烧纸钱被人发现，宝玉为之遮掩。

2014-2015学年度山东省滕州第七中学第一学期高三第11月考英语试题英语试题卷共10页。

满分120分。

考试时间100分钟。

注意事项:1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2．答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。

如需改动, 用橡皮擦擦干净后，再选涂其它答案标号。

3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答.在试题卷上答题无效。

5．考试结束后，将试题卷和答题卡一并交回。

第I卷一、单项填空（共15小题；每小题1分, 满分15分。

）请从A,B,C,D四个选顶中.选出可以填入空白处的最佳选项，并在答题卡上将该选项的标号涂黑。

1．During the rush hour they were in the heavy traffic．A．held on B．held up C．held down D．held out2.______ no bus, we had to walk home.A．There was B．There beingC．Because there being D．There were3．All of the children ______ in the school play and they are in high spirits.A．are involving B．involveC．are involved D．have involved4．As a result of the serious flood,two-thirds of the buildings in the areas ．A．need repairing B．need to repairC．needs repairing D．needs to repair5．---Would you like to go out for a walk?---- ．A．No,but I can’t aff ord the time B．No,I don’t feel in the mood for it nowC．You may ask your sister to go,too D．No,thank you6．—May I smoke here?—Choose a seat in the smoking section, if you ________.A．should B．must C．can D．may7．It is a wise father ________ knows his child.A．that B．which C．what D．whom 8．Knowing ________ you’re good at and doing even more of it creates excellence.A．where B．which C．what D．that9．Don’t you think the world would be an easier place to live in, if we all ________ the same language?A．speak B．had spoken C．spoke D．would speak 10．His wife was busy cooking while he watched TV ________ comfortably in the sofa.A．seat B．to seat C．seating D．seated 11．When our ancestors were hunters and gatherers 10,000 years ago, th ey didn’t have time to wonder much about ________ but finding food.A．everything B．anything C．nothing D．something 12．—Did you see ________ man in ________ black pass by just now?— No, sir. I was reading a newspaper.A．the; the B．the; a C．a; the D．a; / 13．The government promises that relief materials ________ to the flood-hit areas in no time.A．will be rushed B．will rushC．have rushed D．have been rushed14．—Why did Mr. Green take his 7th grade students to the river yesterday afternoon?—________ the river.A．Cleaned up B．Cleaning up C．To clean up D．Clean up 15．—Why are you going to the court?—________! I’ve been charged with parking my car in the wrong place.A．It’s ridiculous B．You don’t sayC．Tell me about it D．Leave me alone二、完形填空（共20小题；每小题1.5分，满分30分。

2014-2015学年度山东省滕州第七中学第一学期高三第11月考数学（文）试题数学试题（文史类）共4页，满分150分，考试时间120分钟。

注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡相应的位置上。

2．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答，在试题卷上答题无效。

一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个备选项中，只有一项是符合题目要求的1．已知α是第二象限角，sin α＝513，则cos α＝（ ）A ．－1213B ．－513C ．513D ．12132．已知双曲线x 225－y 29＝1的左、右焦点分别为F 1、F 2，若双曲线的左支上有一点M 到右焦点F 2的距离为18，N 是MF 2的中点，O 为坐标原点，则|NO |等于（ ）A ．23B ．1C ．2D ．43．下列说法正确的是A ．样本10，6，8，5，6的标准差是3．3．B ．“p q ∨为真”是“p q ∧为真”的充分不必要条件；C ．已知点()2,1A -在抛物线()220y px p =>的准线上，记其焦点为F ，则直线AF 的斜率等于4-D ．设有一个回归直线方程为ˆ2 1.5yx =-，则变量x 每增加一个单位，ˆy 平均减少1．5个单位；4．已知抛物线24y x =的准线与x 轴的交点为A ，焦点为F ，l 是过点A 且倾斜角为3π的直线，则点F 到直线l 的距离等于A ．1BC ．2D ．5．函数2()2log 3x f x x =+-在区间(1,2)内的零点个数是A ．0B ．1C ．2D ．36．一个几何体的三视图如图所示，其中正视图和侧视图均是边长为2的等边三角形，则该几何体的表面积是AB ．C ．12D 7．运行如图所示的流程图，则输出的结果n a 是A ．1B ．1-C ．4-D ．5-8．函数112211()tan()log ()|tan()log ()|4242f x x x x x ππ=+----在区间1(,2)2上的图象大致为ABCD9．在锐角ABC ∆中，三个内角,,A B C 满足：2sin ()cos()B C A B +=-，则角A 与角B 的大小关系是A ．23A B π+=B ．A B <C ．A B =D ．A B >10．如图，已知,B C 是以原点O 为圆心，半径为1的圆与x 轴的交点，点A 在劣弧PQ （包含端点）上运动，其中60POx ∠=，OP OQ ⊥，作A H B C ⊥于H ．若记AH xAB yAC =+，则xy 的取值范围是A ．1(0,]4B ．11[,]164C ．13[,]1616 D ．31[,]164二、填空题：本大题共5小题，每小题5分，共25分.把答案填写在答题卡相应的位置上 11．若i 为虚数单位，则复数31ii+=- ． 12．在[3,3]-上随机取一个数x ，则(1)(2)0x x +-≤的概率为 ．13．满足约束条件⎪⎩⎪⎨⎧≤--≥-≥+3213y x y x y x 的变量,x y 使得230x y a ++≥恒成立，则实数a 的最小值为 ．14．已知点P 是双曲线2219y x -=上的一点，12,F F 是双曲线的左右焦点，且12120PF PF <>=︒，，则12=PF PF + ．15．已知正项等差数列{}n a 的前n 项和为n S ，9=2S ，,*p q N ∈，且18p q +=，则p q S S ⋅的最大值为 ．三、解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤 16．（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问7分）已知正项等比数列{}n a 满足：3454,24a a a =+=.（Ⅰ）求数列{}n a 的通项公式；17．（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问7分）某工厂对一批产品的质量进行了抽样检测，右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图.已知样本中产品净重在[70,75)克的个数是8个。

2014-2015学年度山东省滕州第七中学第一学期高三第11月考理综试题物理部分一、选择题（本大题共5小题，每小题6分，共30分．在每小题给出的四个答案中，只有一项符合题目要求）1．如图实线是一簇未标明方向的由点电荷产生的电场线，虚线是某一带电粒子通过该电场区域时的运动轨迹，a 、b 是轨迹上的两点，若带电粒子在运动中只受电场力作用，根据此图不可确定的是A ．带电粒子所带电荷的符号B ．带电粒子在a 、b 两点的受力方向C ．带电粒子在a 、b 两点的速度何处较大D ．带电粒子在a 、b 两点的电势能何处较大2．如图，电荷量为q 1和q 2的两个点电荷分别位于P 点和Q 点。

已知在P 、Q 连线至某点R 处的电场强度为零，且PR=2RQ 。

则A ．q 1=2q 2B ．q 1=4q 2C ．q 1=-2q 2D ．q 1=-4q 23．U 23892经过多次α、β衰变最终变为稳定核Pb 20682．则在此衰变过程中不可能出现的原子核为A ．Rn 22286B ．Po 21884C ．Bi 21483D ．At 216854．如图所示，A 、B 、C 是匀强电场中的三点，AB 垂直于BC ，AB =4cm ，BC =3cm ．AC 与电场方向平行，A 、B 两点的电势分别为5V 和1.8V ．则电场强度大小和C 点的电势分别为A ．100N/C 和0VB ．80N/C 和4VC ．100N/C 和10VD ．80N/C 和1V5．如图所示，太阳和地球组成“日地双星系统”，两者绕共同的圆心C 点（图中未画出）做周期相同的圆周运动．数学家拉格朗日发现，处在拉格朗日点（如题5图所示）的航天器在太阳和地球引力的共同作用下可以绕“日地双星系统”的圆心C 点做周期相同的圆周运动，从而使日、地、航天器三者在太空的相对位置保持不变．不考虑航天器对日地双星系统的影响，不考虑其它天体对该系统的影响．已知：太阳质量为M ，地球质量为m ，太阳与地球球心距离为d ．则下列说法正确的是A ．位于拉格朗日点的绕C 点稳定运行的航天器，其向心加速度小于地球的向心加速度B ．日地双星系统的周期为GMmd T 32π=C ．圆心C 点在太阳和地球的连线上，距离太阳和地球球心的距离之比等于太阳和地球的质量之比D ．拉格朗日点距地球球心的距离x 满足关系式)()(322m M dMx dm M G x m G x d M G+++=++ 二、非选择题（本大题共4小题，共68分） 6．（19分）（1）在实验室里为了验证动量守恒定律，可以采用如图所示的装置．若入射小球质量为1m ，半径为1r ；被碰小球质量为2m ，半径为2r ，则A ．21m m >，21r r >B ．21m m >，21r r <C ．21m m >，21r r =D ．21m m <，21r r =（2）小欢在实验室中利用各种仪器探索由电源和电阻组成的黑箱，如图甲所示． I ．为了探测黑箱，小欢进行了以下几步测量： ①用多用电表的电阻挡测量a 、b 间的电阻； ②用多用电表的电压挡测量a 、b 间的输出电压； ③用多用电表的电流挡测量a 、b 间的输出电流．你认为以上测量中哪2项不妥： （填序号），理由是： II ．含有电源的黑箱相当于一个等效电源（a 、b 是电源的两极），小欢想测定这个等效电源的电动势和内阻，设计了如图乙所示的测量电路，此电路同时能测出电阻0R 的阻值．小欢将滑动变阻器的滑片移动到不同位置时，记录了三个电表的一系列示数．记录在下面两个表格中． 表格一电压表示数/V 1.21 0.90 0.60 0.29 0.01 电流表示数/A0.100.200.300.400.50表格二电压表示数/V 1.40 1.31 1.22 1.08 1.00 电流表示数/A0.100.200.300.400.50①在图丙的坐标纸中分别作出0R 的I U -图象和等效电源的I U -图象；②根据作出的图象可以求出定值电阻0R =________Ω，电源电动势E =_______V ，内电阻r =__________Ω③若实验中的所有操作和数据处理无错误，不考虑读数等偶然误差，实验中测得的定值电阻0R 值_____实际值（横线上选填“大于、等于、小于”）．7．如图所示的钢板由倾斜部分和水平部分组成，水平部分足够长，两部分之间由一小段圆弧面相连接．在钢板的中间有位于竖直面内的光滑圆槽轨道，斜面的倾角为θ．现有两个质量均为m 、半径均为r （不能忽略）的均匀球沿圆槽轨道排列，在施加于1号球的水平外力作用下均静止，此时1号球球心距它在水平槽运动时的球心高度差为h ．现撤去外力使小球开始滑动，然后两个小球均以相同速度滑动到水平槽内．已知整个过程中系统无机械能损失，重力加速度为g ．求：（1）两球在水平槽中一起匀速运动的速度．（2）从开始运动到两球在水平槽中一起匀速运动的过程中，1号球机械能的变化量 8．如图所示，纸面内有一固定的金属导轨，它由长为r 的直线段ON 和以O 点为圆心、半径为r 、在NF 处开有小缺口的圆环两部分组成. 另一直导线OP 以O 为圆心，沿逆时针方向匀速转动,周期为T .直导线OP 与导轨接触良好，导轨和直导线单位长度电阻均为λ．整个空间有磁感应强度为B 、方向垂直于纸面向外的匀强磁场．当直导线OP 转动到与ON 的夹角为θ（只考虑P 到达F 点之前的情况）时，求（1）固定导轨消耗的电功率；（2）圆环缺口NF 两端的电势差NF U ．9．平时擦玻璃时，我们经常会用到如图甲所示的“魔力刷”．使用时，两个一样的刷子分别位于玻璃窗户玻璃板的两侧，两刷子靠磁铁的吸引力吸在玻璃上，当移动其中一块刷子时，另一块刷子会跟到移动，达到同时清洁玻璃内外侧的目的．已知：某种品牌玻璃刷的每个刷子的质量都为m ，与玻璃的滑动摩擦因数均为63=μ，且最大静摩擦力等于滑动摩擦力，重力加速度取g ．（1）将其中一个刷子用与竖直方向成3πθ=的推力压在竖直玻璃上，如图乙所示，现要把刷子沿竖直方向向上推动，求推力的最小值（2）把两个刷子对齐分别放在竖直玻璃板的两侧，如图丙所示，现用与竖直方向成3πα=，大小为mg F 60=的拉力向下拉动内侧的刷子时，外侧刷子将立即跟着移动且很快与内侧刷子保持相对静止．此时刷子磁铁间的吸引力在垂直玻璃板面方向的分量恒为mg 36，求刷子间的磁铁吸引力在沿玻璃板面切线方向的分量．（3）假设玻璃是边长为L 的正方形，刷子是边长为d 的正方形；当两刷子的正对面积大于一半时，刷子磁铁间的吸引力的垂直分量和切向分量均不变，当两刷子的正对面积小于或等于一半时，两刷子就无法吸引在一起．在（2）的情况下，若拉力方向不变，大小变为mg 45271，要使一次性向下拉动刷子就可以完成清理玻璃的竖边，求Ld的取值范围． 三、选做题 10．（12分）（1）图为“研究一定质量气体在压强不变的条件下，体积变化与温度变化的关系”的实验装置图．粗细均匀的弯曲玻璃管的A 管插入烧瓶，B 管与玻璃管C 下部用橡胶管连接，C 管开口向上，一定质量的气体被水银封闭于烧瓶内．开始时，B 、C 内的水银面等高，外界大气压恒定，下列判断正确的是A ．保持B 、C 两管不移动，若烧瓶内气体温度降低，则瓶内气体密度增大，对外做正功 B ．保持B 、C 两管不移动，若烧瓶内气体温度降低，则C 管中水银柱将升高 C ．若烧瓶内气体温度升高，为使瓶内气体的压强不变，应将C 管向下移动D ．若烧瓶内气体温度升高，为使瓶内气体的压强不变，应将C 管向上移动（2）如图，喷雾器内有一定体积的水，初始时上部封闭有压强为0p 、体积为1V 的空气．关闭喷雾阀门，用打气筒向喷雾器内再充入压强为0p 、体积为2V 的空气（设外界环境温度一定，空气可看作理想气体）．①当水面上方被封气体温度与外界温度相等时，求气体压强．②打开喷雾阀门，喷雾过程中封闭气体可以看成等温膨胀，此过程气体是“吸热”、“放热”或“既不吸热也不放热”？2014-2015学年度山东省滕州第七中学第一学期高三第11月考理综试题物理部分参考答案1-5 A D D A D 6．（1）C （2分）（2）I ， ① ③ （2分）,多用表不能测含电源的电阻；直接用多用电表测电流可能电流过大（3分）II ①如下图（4分）②0R =__2.00___Ω（2分）；E =__1.50__V （2分）；r =__1.00_Ω（2分） ③0R 值___大于__实际值（2分） 7．（15分）解：（1）两球组成的系统机械能守恒，2221)sin (2mv r h mg =+θ （7分） 解得)sin (2θr h g v +=（1分）（2）取1号球为研究对象，其机械能变化量为mgh mv E -=∆2121 （6分） 解得θsin 1mgr E =∆ （1分）8．（16分）解：（1）设回路ONPO 电阻为R ，经时间t ∆，回路面积改变S ∆，磁通量改变φ∆，产生电动势E .由法拉第电磁感应定律，有 tE ∆∆=φ①（1分） S B ∆=∆φ ②（1分）由几何关系，有221r S θ∆=∆ ③（1分） 匀速圆周运动角速度为Tt πθ2=∆∆ ④（1分）由①、②、③、④有Tr BE 2π= ⑤（1分）据题意，有()2+=θλr R ⑥（1分） 由欧姆定律，有REI =⑦（1分） 由⑤、⑥、⑦得：()2+=θλπT BrI ⑧（1分）设固定导轨ONP 的电阻为1R ，消耗的电功率为1P .()11+=θλr R ⑨（1分）由电功率公式，有121R I P = ⑩（1分）由⑧、⑨、⑩得()()22322121++=θλθπT r B P ⑪（2分） （2）设圆弧NP 的电阻为2R ，则r R λθ=2 ⑫（1分）2IR U NF -= ⑬（1分）由⑧、⑫、⑬得()TBr U NF 22πθθ⋅+-= ⑭（2分）9．（18分）解：（1）如图由受力分析知：水平方向sin N F F α= ①（1分）； 竖直方向：cos N F G F αμ=+ ②（1分） 由①②得4F mg =（1分）（2）设磁力刷垂直玻璃板方向的分力为2F ，切向方向的分力为1F . 如图对左右两刷子受力分析可知：左侧磁刷：水平方向12N F F = ③（1分）； 竖直方向11N G F F ma μ+-= ④（2分）； 右侧磁刷：水平方向22sin N F F F θ=+ ⑤（1分）； 竖直方向12cos (sin )ma G F F F F θμθ+---= ⑥（2分）；由③④⑤⑥得4g a =；194mgF =（2分） （3）因为271645F mg mg =>，所以左侧磁刷14ga = ⑦，右侧磁刷122cos (sin )4a 15G F F F F g m θμθ+---== ⑧（2分）由运动分析知：右侧磁刷从上到下运动的位移22212x L d a t =-= ⑨（2分）；当右侧到达下面时，左侧磁刷运动的位移2113122x L d a t =-= ⑩（2分），由⑦⑧⑨⑩得19d L =（1分）10．（1）C （6分）（2）解①设末态压强为p ，则0121()p V V pV += （2分） 解得：0121()p V V p V +=（2分）②吸热 （2分）。

2015年普通高等学校招生全国统一考试（山东卷）数学（理科）第Ⅰ卷(共50分）一、选择题：本大题共10小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． （1）【2015年山东,理1】已知集合2{|430}x x x -+<,{|24}B x x =<<，则A B =（ )（A)()1,3 （B ）()1,4 （C ）()2,3 (D ）()2,4 （2）【2015年山东，理2】若复数z 满足i 1iz=-，其中i 是虚数单位，则z =( ） (A ）1i - (B ）1i + (C)1i -- （D ）1i -+（3）【2015年山东，理3】要得到函数sin(4)3y x π=-的图象,只需将函数sin 4y x =的图像（ ）（A ）向左平移12π个单位(B ）向右平移12π个单位（C)向左平移3π个单位（D ）向右平移3π个单位 (4）【2015年山东,理4】已知菱形ABCD 的边长为a ，60ABC ∠=,则BD⃗⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ =（ ) （A ）232a - （B)234a - （C)234a （D ）232a（5）【2015年山东,理5】不等式|1||5|2x x ---<的解集是（ )(A ）(,4)-∞ （B ）(,1)-∞ （C)(1,4) （D ）(1,5)（6）【2015年山东，理6】已知,x y 满足约束条件020x y x y y -≥⎧⎪+≤⎨⎪≥⎩若z ax y =+的最大值为4,则a =（ )（A ）3 (B ）2 （C ）-2 (D ）—3 (7）【2015年山东，理7】在梯形ABCD 中，2ABC π∠=，//AD BC ,222BC AD AB ===．将梯形ABCD绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为（ ）(A)23π （B ）43π （C ）53π （D ）2π（8)【2015年山东，理8】已知某批零件的长度误差（单位:毫米）服从正态分布2(0,3)N ,从中随机取一件,其长度误差落在区间()3,6内的概率为（ ）（附:若随机变量ξ服从正态分布2(,)N μσ，则()68.26%P μσξμσ-<<+=,(22)95.44%P μσξμσ-<<+=）（A)4.56% （B ）13.59% （C ）27.18% （D ）31.74%（9)【2015年山东,理9】一条光线从点(2,3)--射出，经y 轴反射与圆22(3)(2)1x y ++-=相切，则反射光线所在的直线的斜率为（ ）(A)53-或35- （B ）32-或23- （C ）54-或45- (D)43-或34-(10）【2015年山东,理10】设函数31,1,()2,1.x x x f x x -<⎧=⎨≥⎩则满足()(())2f a f f a =的取值范围是（ )（A ）2[,1]3 (B ）[0,1] （C ）2[,)3+∞ （D ）[1,)+∞第II 卷（共100分）二、填空题：本大题共5小题,每小题5分 （11）【2015年山东,理11】观察下列各式:0010113301225550123377774;4;4;4;C C C C C C C C C C =+=++=+++=照此规律，当*n ∈N 时,012121212121n n n n n C C C C -----++++= ．（12）【2015年山东，理12】若“[0,],tan 4x x m π∀∈≤”是真命题,则实数m 的最小值为 ．（13）【2015年山东，理13】执行右边的程序框图，输出的T 的值为 ．（14）【2015年山东,理14】已知函数()x f x a b =+(0,1)a a >≠的定义域和值域都是[1,0]-,则a b += ．（15）【2015年山东，理15】平面直角坐标系xOy 中，双曲线22122:1(0,0)x y C a b a b-=>>的渐近线与抛物线22:2(0)C x py p =>交于点,,O A B ,若OAB ∆的垂心为2C 的焦点，则1C 的离心率为 ．三、解答题：本大题共6题，共75分．(16)【2015年山东，理16】(本小题满分12分)设2()sin cos cos ()4f x x x x π=-+．（Ⅰ）求()f x 的单调区间；（Ⅰ）在锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ，若()0,12Af a ==,求ABC ∆面积．（17）【2015年山东，理17】(本小题满分12分)如图,在三棱台DEF ABC -中，2,,AB DE G H =分别为,AC BC 的中点． (Ⅰ）求证：//BD 平面FGH ；（Ⅰ）若CF ⊥平面ABC ，,,45AB BC CF DE BAC ⊥=∠=，求平面FGH 与平面ACFD 所成角（锐角)的大小．（18）【2015年山东，理18】(本小题满分12分）设数列{}n a 的前n 项和为n S ，已知233nn S =+．(Ⅰ）求数列{}n a 的通项公式；（Ⅰ）若数列{}n b 满足3log n n n a b a =,求数列{}n b 的前n 项和n T ．（19）【2015年山东,理19】（本小题满分12分）若n 是一个三位正整数，且n 的个位数字大于十位数字，十位数字大于百位数字，则称n 为“三位递增数"（如137,359，567等）．在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取一个数，且只能抽取一次,得分规则如下：若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分；若能被5整除，但不能被10整除，得—1分；若能被10整除，得1分．（Ⅰ)写出所有个位数字是5的“三位递增数";（Ⅰ)若甲参加活动,求甲得分X 的分布列和数学期望EX ．（20）【2015年山东，理20】（本小题满分13分）平面直角坐标系xOy 中，已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别是12,F F ，以1F 为圆心，以3为半径的圆与以2F 为圆心，以1为半径的圆相交,交点在椭圆C 上． (Ⅰ）求椭圆C 的方程;（Ⅰ）设椭圆2222:144x y E a b+=,P 为椭圆C 上的任意一点，过点P 的直线y kx m =+交椭圆E 于,A B 两点，射线PO 交椭圆E 于点Q ．（i)求||||OQ OP 的值；（ii)求ABQ ∆面积最大值．（21）【2015年山东，理21】（本题满分14分）设函数2()ln(1)()f x x a x x =++-,其中a R ∈．（Ⅰ）讨论函数()f x 极值点的个数，并说明理由； (Ⅱ)若0x ∀>，()0f x ≥成立，求a 的取值范围．2015年普通高等学校招生全国统一考试（山东卷）数学（理科）第Ⅰ卷（共50分）一、选择题：本大题共10小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． (1）【2015年山东，理1】已知集合2{|430}x x x -+<，{|24}B x x =<<，则A B =（ ）（A ）()1,3 （B ）()1,4 （C ）()2,3 （D ）()2,4 【答案】C【解析】2{|430}{|13}A x x x x x =-+<=<<,(2,3)A B =，故选C ．（2）【2015年山东，理2】若复数z 满足i 1iz=-，其中i 是虚数单位，则z =（ ） (A)1i - （B ）1i + (C)1i -- （D ）1i -+ 【答案】A【解析】2(1i)i i i 1i z =-=-+=+，1i z =-，故选A ．（3）【2015年山东，理3】要得到函数sin(4)3y x π=-的图象，只需将函数sin 4y x =的图像（ ）（A ）向左平移12π个单位（B ）向右平移12π个单位（C)向左平移3π个单位（D ）向右平移3π个单位 【答案】B【解析】sin 4()12y x π=-，只需将函数sin 4y x =的图像向右平移12π个单位，故选B ．(4）【2015年山东，理4】已知菱形ABCD 的边长为a ，60ABC ∠=,则BD⃗⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ =( ） （A ）232a - （B ）234a - （C ）234a (D)232a【答案】D【解析】由菱形ABCD 的边长为a ，60ABC ∠=可知18060120BAD ∠=-=，2223()()cos1202BD CD AD AB AB AB AD AB a a a a ⋅=-⋅-=-⋅+=-⋅+=，故选D ．（5）【2015年山东，理5】不等式|1||5|2x x ---<的解集是( )（A ）(,4)-∞ (B)(,1)-∞ （C ）(1,4) （D ）(1,5) 【答案】A【解析】当1x <时，1(5)42x x ---=-<成立;当15x ≤<时,1(5)262x x x ---=-<，解得4x <,则14x ≤<；当5x ≥时，1(5)42x x ---=<不成立．综上4x <,故选A ． （6）【2015年山东，理6】已知,x y 满足约束条件020x y x y y -≥⎧⎪+≤⎨⎪≥⎩若z ax y =+的最大值为4,则a =( ）（A ）3 （B)2 （C ）-2 （D ）-3【答案】B【解析】由z ax y =+得y ax z =-+，借助图形可知：当1a -≥，即1a ≤-时在0x y ==时有最大值0，不符合题意;当01a ≤-<,即10a -<≤时在1x y ==时有最大值14,3a a +==，不满足10a -<≤；当10a -<-≤,即01a <≤时在1x y ==时有最大值14,3a a +==，不满足01a <≤;当1a -<-，即1a >时在2,0x y ==时有最大值24,2a a ==，满足1a >，故选B ． (7）【2015年山东，理7】在梯形ABCD 中，2ABC π∠=，//AD BC ，222BC AD AB ===．将梯形ABCD绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为（ ）(A ）23π （B)43π （C ）53π （D ）2π 【答案】C【解析】2215121133V πππ=⋅⋅-⋅⋅=,故选C ．（8)【2015年山东，理8】已知某批零件的长度误差(单位:毫米）服从正态分布2(0,3)N ，从中随机取一件，其长度误差落在区间()3,6内的概率为（ )（附：若随机变量ξ服从正态分布2(,)N μσ,则()68.26%P μσξμσ-<<+=，(22)95.44%P μσξμσ-<<+=）（A ）4.56% （B)13.59% （C ）27.18% （D ）31.74% 【答案】D【解析】1(36)(95.44%68.26%)13.59%2P ξ<<=-=，故选D ．（9)【2015年山东，理9】一条光线从点(2,3)--射出，经y 轴反射与圆22(3)(2)1x y ++-=相切，则反射光线所在的直线的斜率为( ）（A ）53-或35- (B ）32-或23- （C ）54-或45- （D ）43-或34-【答案】D【解析】(2,3)--关于y 轴对称点的坐标为(2,3)-，设反射光线所在直线为3(2),y k x +=-即230kx y k ---=，则22|3223|1,|55|11k k d k k k ----==+=++，解得43k =-或34-，故选D ． （10）【2015年山东，理10】设函数31,1,()2,1.x x x f x x -<⎧=⎨≥⎩则满足()(())2f a f f a =的取值范围是（ ）（A ）2[,1]3 (B ）[0,1] (C ）2[,)3+∞ （D ）[1,)+∞【答案】C【解析】由()(())2f a f f a =可知()1f a ≥，则121a a ≥⎧⎨≥⎩或1311a a <⎧⎨-≥⎩，解得23a ≥，故选C ．第II 卷（共100分）二、填空题:本大题共5小题,每小题5分（11）【2015年山东，理11】观察下列各式：010113301225550123377774;4;4;4;C C C C C C C C C C =+=++=+++=照此规律，当*n ∈N 时，012121212121n n n n n C C C C -----++++= ．【答案】14n -【解析】0121012121212121212121211(2222)2n n n n n n n n n n C C C C C C C C ----------++++=++++021122223121212121212121210121212112121212121211[()()()()]211()2422n n n n nn n n n n n n n n n n n n n n n n n n C C C C C C C C C C C C C C ----------------------=++++++++=+++++++=⋅= (12）【2015年山东，理12】若“[0,],tan 4x x m π∀∈≤"是真命题，则实数m 的最小值为 ．【答案】1【解析】“[0,],tan 4x x m π∀∈≤”是真命题,则tan 14m π≥=，于是实数m 的最小值为1．（13)【2015年山东，理13】执行右边的程序框图,输出的T 的值为 ．【答案】116【解析】11200111111236T xdx x dx =++=++=⎰⎰．（14）【2015年山东，理14】已知函数()x f x a b =+(0,1)a a >≠的定义域和值域都是[1,0]-,则a b += ．【答案】32-【解析】当1a >时1010a b a b -⎧+=-⎨+=⎩，无解；当01a <<时1001a b a b -⎧+=⎨+=-⎩,解得12,2b a =-=,则13222a b +=-=-．(15）【2015年山东，理15】平面直角坐标系xOy 中，双曲线22122:1(0,0)x y C a b a b-=>>的渐近线与抛物线22:2(0)C x py p =>交于点,,O A B ，若OAB ∆的垂心为2C 的焦点，则1C 的离心率为 ． 【答案】32【解析】22122:1(0,0)x y C a b a b -=>>的渐近线为b y x a =±，则22222222(,),(,)pb pb pb pb A B a a a a-22:2(0)C x py p =>的焦点(0,)2pF ，则22222AFpb pa a k pb b a-==，即2254b a =,2222294c a b a a +==，32c e a ==． 三、解答题：本大题共6题，共75分．（16）【2015年山东,理16】(本小题满分12分)设2()sin cos cos ()4f x x x x π=-+．（Ⅰ)求()f x 的单调区间；（Ⅰ）在锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ，若()0,12Af a ==，求ABC ∆面积．解：（Ⅰ）由111111()sin 2[1cos(2)]sin 2sin 2sin 22222222f x x x x x x π=-++=-+=-,由222,22k x k k Z ππππ-≤≤+∈得,44k x k k Z ππππ-≤≤+∈，则()f x 的递增区间为[,],44k k k Z ππππ-+∈； 由3222,22k x k k Z ππππ+≤≤+∈得3,44k x k k Z ππππ+≤≤+∈，则()f x 的递增区间为3[,],44k k k Z ππππ++∈．（Ⅰ）在锐角ABC ∆中，11()sin 0,sin 222A f A A =-==，6A π=，而1a =,由余弦定理可得2212cos 23(23)6b c bc bc bc bc π=+-≥-=-，当且仅当b c =时等号成立，即12323bc ≤=+-，11123sin sin 22644ABC S bc A bc bc π∆+===≤故ABC ∆面积的最大值为234+．（17）【2015年山东，理17】（本小题满分12分）如图,在三棱台DEF ABC -中，2,,AB DE G H =分别为,AC BC 的中点． （Ⅰ)求证：//BD 平面FGH ;（Ⅰ）若CF ⊥平面ABC ，,,45AB BC CF DE BAC ⊥=∠=，求平面FGH 与平面ACFD 所成角（锐角）的大小．解:(Ⅰ）证明：连接DG ，DC ，设DC 与GF 交于点T ，在三棱台DEF ABC -中,2AB DE =，则2AC DF =， 而G 是AC 的中点，DF AC ,则//DF GC ,所以四边形DGCF 是平行四边形，T 是DC 的中点,DG FC ． 又在BDC ∆,是BC 的中点，则TH DB ，又BD ⊄平面FGH ，TH ⊂平面FGH ，故//BD 平面FGH ．（Ⅰ）由CF ⊥平面ABC ,可得DG ⊥平面ABC 而，AB BC ⊥，45BAC ∠=，则GB AC ⊥,于是,,GB GA GC 两两垂直，以点G 为坐标原点，,,GA GB GC 所在的直线，分别为,,x y z 轴建立空间直角坐标系，设2AB =,则1,22,2DE CF AC AG ====,22(0,2,0),(2,0,0),(2,0,1),(,,0)22B C F H ---， 则平面ACFD 的一个法向量为1(0,1,0)n =，设平面FGH 的法向量为 2222(,,)n x y z =，则2200n GH n GF ⎧⋅=⎪⎨⋅=⎪⎩，即22222202220x y x z ⎧-=⎪⎨⎪-+=⎩， 取21x =,则221,2y z ==，2(1,1,2)n =,1211cos ,2112n n <>==++，故平面FGH 与平面ACFD 所成角（锐角)的大小为60．（18）【2015年山东,理18】(本小题满分12分）设数列{}n a 的前n 项和为n S ，已知233nn S =+．（Ⅰ）求数列{}n a 的通项公式；(Ⅰ）若数列{}n b 满足3log n n n a b a =,求数列{}n b 的前n 项和n T ．解：（Ⅰ）由233n n S =+可得111(33)32a S ==+=，11111(33)(33)3(2)22n n n n n n a S S n ---=-=+-+=≥，而11133a -=≠，则13,13,1n n n a n -=⎧=⎨>⎩．（Ⅰ)由3log n n n a b a =及13,13,1n n n a n -=⎧=⎨>⎩，可得3111log 3113n n n n n a b n a n -⎧=⎪⎪==⎨-⎪>⎪⎩ 2311123133333n n n T --=+++++，2234111123213333333n n n n n T ---=++++++，22312231211111111111111()3333333333333331121213113213319392233182313n n n n n n n n n nn n T n n n ----=+-++++-=-+++++----+=+-=+--=-⋅⋅- 113211243n n n T -+=-⋅ (19）【2015年山东,理19】（本小题满分12分)若n 是一个三位正整数,且n 的个位数字大于十位数字，十位数字大于百位数字,则称n 为“三位递增数"(如137,359，567等)．在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取一个数，且只能抽取一次，得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除，参加者得0分;若能被5整除，但不能被10整除，得-1分；若能被10整除，得1分． (Ⅰ）写出所有个位数字是5的“三位递增数”;(Ⅰ）若甲参加活动，求甲得分X 的分布列和数学期望EX ． 解：（Ⅰ）125，135，145，235，245，345;（Ⅰ）X 的所有取值为—1，0,1．32112844443339992111(0),(1),(1)31442C C C C C P X P X P X C C C ⋅+====-=====0(1)13144221EX =⨯+⨯-+⨯=．（20）【2015年山东,理20】（本小题满分13分）平面直角坐标系xOy 中，已知椭圆2222:1(0)x y C a b a b+=>>的离左、右焦点分别是12,F F ，以1F 为圆心,以3为半径的圆与以2F 为圆心，以1为半径的圆相交，交点在椭圆C 上． (Ⅰ)求椭圆C 的方程；（Ⅰ)设椭圆2222:144x y E a b+=,P 为椭圆C 上的任意一点，过点P 的直线y kx m =+交椭圆E 于,A B 两点，射线PO 交椭圆E 于点Q ．（i ）求||||OQ OP的值;（ii ）求ABQ ∆面积最大值．解：(Ⅰ)由椭圆2222:1(0)x y Ca b a b+=>>可知c e a ==，而222a b c =+则2,a b c ==， 左、右焦点分别是12(,0),,0)F F ，圆1F：22()9,xy +=圆2F ：22()1,x y += 由两圆相交可得24<<,即12<，交点在椭圆C 上，则224134b b +=⋅,整理得424510b b -+=，解得21b =,214b =（舍去）, 故21b =,24a =，椭圆C 的方程为2214x y +=．（Ⅰ）（i ）椭圆E 的方程为221164x y +=,设点00(,)P xy ，满足220014x y +=，射线000:(0)y PO y x xx x =<， 代入221164x y +=可得点00(2,2)Q x y --,于是||2||OQ OP ==． （ii ）点00(2,2)Q x y --到直线AB 距离等于原点O 到直线AB 距离的3倍:d ==221164y kx mx y =+⎧⎪⎨+=⎪⎩，得224()16xkx m ++=，整理得222(14)84160k x kmx m +++-=．2222226416(41)(4)16(164)0k m k m k m ∆=-+-=+->,||AB = 211||||32214m S AB d k ∆==⋅⋅⋅+ 22221646122(41)m k m k ++-≤⋅=+，当且仅当22||82m m k ==+等号成立．而直线y kx m =+与椭圆22:14x C y +=有交点P ,则2244y kx m x y =+⎧⎨+=⎩有解，即222224()4,(14)8440x kx m k x kmx m ++=+++-=有解，其判别式22222216416(14)(1)16(14)0k m k m k m ∆=-+-=+-≥，即2214k m +≥，则上述2282m k =+不成立，等号不成立，设(0,1]t =，则S ∆==(0,1]为增函数，于是当2214k m +=时max S ∆=故ABQ ∆面积最大值为12．（21）【2015年山东，理21】（本题满分14分)设函数2()ln(1)()f x x a x x =++-,其中a R ∈．（Ⅰ)讨论函数()f x 极值点的个数,并说明理由；（Ⅱ)若0x ∀>，()0f x ≥成立,求a 的取值范围．解：（Ⅰ）2()ln(1)()f x x a x x =++-，定义域为(1,)-+∞，21(21)(1)121()(21)111a x x ax ax a f x a x x x x -++++-'=+-==+++,设2()21g x ax ax a =++-， 当0a =时,1()1,()01g x f x x '==>+，函数()f x 在(1,)-+∞为增函数，无极值点． 当0a >时，228(1)98a a a a a ∆=--=-， 若809a <≤时0∆≤，()0,()0g x f x '≥≥,函数()f x 在(1,)-+∞为增函数,无极值点． 若89a >时0∆>，设()0g x =的两个不相等的实数根12,x x ，且12x x <， 且1212x x +=-，而(1)10g -=>,则12114x x -<<-<，所以当1(1,),()0,()0,()x x g x f x f x '∈->>单调 递增；当12(,),()0,()0,()x x x g x f x f x '∈<<单调递减；当2(,),()0,()0,()x x g x f x f x '∈+∞>>单调递增．因此此时函数()f x 有两个极值点;当0a <时0∆>，但(1)10g -=>，121x x <-<,所以当2(1,),()0,()0,()x x g x f x f x '∈->>单调递増；当2(,),()0,()0,()x x g x f x f x '∈+∞<<单调递减，所以函数只有一个极值点．综上可知当809a ≤≤时()f x 的无极值点；当0a <时()f x 有一个极值点；当89a >时,()f x 的有两个 极值点．（Ⅰ)由（Ⅰ)可知当809a ≤≤时()f x 在(0,)+∞单调递增，而(0)0f =， 则当(0,)x ∈+∞时，()0f x >，符合题意； 当819a <≤时，2(0)0,0g x ≥≤，()f x 在(0,)+∞单调递增，而(0)0f =, 则当(0,)x ∈+∞时，()0f x >，符合题意；当1a >时，2(0)0,0g x <>，所以函数()f x 在2(0,)x 单调递减,而(0)0f =,则当2(0,)x x ∈时,()0f x <，不符合题意；当0a <时,设()ln(1)h x x x =-+，当(0,)x ∈+∞时1()1011x h x x x'=-=>++, ()h x 在(0,)+∞单调递增，因此当(0,)x ∈+∞时()(0)0,ln(1)0h x h x >=+<,于是22()()(1)f x x a x x ax a x <+-=+-,当11x a>-时2(1)0ax a x +-<， 此时()0f x <，不符合题意．综上所述，a 的取值范围是01a ≤≤．另解：（Ⅰ）2()ln(1)()f x x a x x =++-，定义域为(1,)-+∞ 21(21)(1)121()(21)111a x x ax ax a f x a x x x x -++++-'=+-==+++，当0a =时，1()01f x x '=>+，函数()f x 在(1,)-+∞为增函数，无极值点． 设222()21,(1)1,8(1)98g x ax ax a g a a a a a =++--=∆=--=-,当0a ≠时,根据二次函数的图像和性质可知()0g x =的根的个数就是函数()f x 极值点的个数．若(98)0a a ∆=-≤，即809a <≤时，()0g x ≥，()0f x '≥函数在(1,)-+∞为增函数，无极值点． 若(98)0a a ∆=->，即89a >或0a <，而当0a <时(1)0g -≥ 此时方程()0g x =在(1,)-+∞只有一个实数根，此时函数()f x 只有一个极值点； 当89a >时方程()0g x =在(1,)-+∞都有两个不相等的实数根，此时函数()f x 有两个极值点； 综上可知当809a ≤≤时()f x 的极值点个数为0；当0a <时()f x 的极值点个数为1；当89a >时， ()f x 的极值点个数为2． (Ⅰ）设函数2()ln(1)()f x x a x x =++-，0x ∀>，都有()0f x ≥成立,即2ln(1)()0x a x x ++-≥当1x =时，ln 20≥恒成立；当1x >时，20x x ->，2ln(1)0x a x x++≥-； 当01x <<时，20x x -<，2ln(1)0x a x x++≤-；由0x ∀>均有ln(1)x x +<成立． 故当1x >时，,2ln(1)11x x x x +<--(0,)∈+∞，则只需0a ≥； 当01x <<时，2ln(1)1(,1)1x x x x +>∈-∞---,则需10a -+≤,即1a ≤．综上可知对于0x ∀>,都有 ()0f x ≥成立，只需01a ≤≤即可，故所求a 的取值范围是01a ≤≤．另解：(Ⅰ）设函数2()ln(1)()f x x a x x =++-，(0)0f =，要使0x ∀>，都有()0f x ≥成立，只需函数函数()f x 在(0,)+∞上单调递增即可,于是只需0x ∀>,1()(21)01f x a x x '=+-≥+成立， 当12x >时1(1)(21)a x x ≥-+-，令210x t -=>，2()(,0)(3)g t t t =-∈-∞+, 则0a ≥；当12x =时12()023f '=>；当102x <<,1(1)(21)a x x ≤-+-， 令21(1,0)x t -=∈-，2()(3)g t t t =-+关于(1,0)t ∈-单调递增， 则2()(1)11(13)g t g >-=-=--+，则1a ≤，于是01a ≤≤． 又当1a >时，2(0)0,0g x <>，所以函数()f x 在2(0,)x 单调递减，而(0)0f =，则当2(0,)x x ∈时，()0f x <,不符合题意；当0a <时，设()ln(1)h x x x =-+，当(0,)x ∈+∞时1()1011x h x x x'=-=>++， ()h x 在(0,)+∞单调递增，因此当(0,)x ∈+∞时()(0)0,ln(1)0h x h x >=+<，于是22()()(1)f x x a x x ax a x <+-=+-，当11x a>-时2(1)0ax a x +-<，此时()0f x <，不符合题意． 综上所述,a 的取值范围是01a ≤≤．【评析】求解此类问题往往从三个角度求解：一是直接求解，通过对参数a 的讨论来研究函数的单调性，进一步确定参数的取值范围；二是分离参数法，求相应函数的最值或取值范围以达到解决问题的目的;三是凭借函数单调性确定参数的取值范围，然后对参数取值范围以外的部分进行分析验证其不符合题意,即可确定所求．。

2014-2015学年度山东省滕州第七中学第一学期高三第11月考数学（理）试题本试卷分选择题和非选择题两部分。

满分150分，考试时间120分钟。

注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答，在试题卷上答题无效。

5．考试结束后，只将答题卡交回。

第I 卷（选择题 共50分）一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个备选项中，只有一项是符合题目要求的）1、设集合{12345}U =，，，，，{13}A =，，{234}B =，，，则（C U A ）∩（C U B ）= A ．{1} B ．{5}C ．{24}，D ．{1,2,4,5}2．函数)(x f y =在[0，2]上单调递增，且函数)2(+x f 是偶函数，则下列结论成立的是A ．f （1）＜f （25）＜f （27） B ．f （27）＜f （1）＜f （25） C ．f （27）＜f （25）＜f （1）D ．f （25）＜f （1）＜f （27）3．已知数列{}n a 是等差数列，若91130a a +<，10110a a ⋅<，且数列{}n a 的前n 项和n S 有最大值，那么n S 取得最小正值时n 等于A ．20B ．17C ．19D ．214．如果执行如图所示的框图，则输出n 的值为A ．9B ．8C ．7D ．65．若62x ⎛ ⎝展开式中的常数项是60，则实数a 的值是A ．1±B ．C ．2±D ．±6．已知函数()sin()(0,)22f x x ππωϕωϕ=+>-<<，其部分图象如图所示，则,ωϕ的值分别为A ．2,3πωϕ==B ．2,6πωϕ==C ．1,3πωϕ==D ．1,6πωϕ==7．在等腰ABC ∆中，120,2BAC AB AC ︒∠===，2,3BC BD AC AE == ，则AD BE ⋅的值为 A ．23-B ．13-C ．13D ．438．已知某几何体的三视图如图所示（单位cm ），则此几何体的体积为A ．2123cm B ．1523cmC ．163cmD ．123cm9．对于函数()f x 和()g x ，设(){}0m x R f x ∈∈=，(){}0n x R g x ∈∈=，若存在m 、n ，使得1m n -≤，则称()()f x g x 与互为“零点关联函数”．若函数()12x f x e x -=+-与()23g x x ax a =--+互为“零点关联函数”，则实数a 的取值范围为A ．7[2,]3B ．7[,3]3C ．[2,3]D ．[2,4]10．过原点的直线交双曲线xy P Q 、两点，现将坐标平面沿x 轴折成直二面角，则折后线段PQ 的长度的最小值等于 A ．4B．C ．2D ．第Ⅱ卷（非选择题 共100分）二、填空题（本大题共6小题，每小题5分，请按要求作答5小题，共25分，把答案填写在答题卡相应位置上．） 11．已知i 是虚数单位，则复数3+1ii=-________． 12．已知实数,x y 满足10200,0x y x y x y -+≥⎧⎪+-≤⎨⎪≥≥⎩，则2z x y =+的最大值是________．13．假设乒乓球团体比赛的规则如下：进行5场比赛，除第3场为双打外，其余各场为单打，参赛的每个队选出3名运动员参加比赛，每个队员打两场，且第1,2场与第4,5场不能是某个运动员连续比赛．某队有4名乒乓球运动员，其中A 不适合双打，则该队教练安排运动员参加比赛的方法共有________种．考生注意：14~16题为选做题，请从中任选两题作答，若三题全做，则按前两题给分． 14．如图，,PAB PCD 为圆O 的两条割线，若5,7,PA AB ==11,CD =2AC =，则BD 的长为________．15．在直角坐标系xOy 中，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系．若极坐标方程为4cos 3ρθ=的直线与曲线1cos sin x y θθ=+⎧⎨=⎩（θ为参数）相交于A 、B ，则AB =________．16．若存在实数x ，使得13x a x -+-≤成立，则实数a 的取值范围是________． 三、解答题（本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．） 17．（本题共13分，第（Ⅰ）问5分，第（Ⅱ）问8分）今年3月1日，重庆某中学50位学生参加了“北约联盟”的自主招生考试．这50位同学的数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[)[)60,70,70,80,[)[)[)[]80,90,90,100,100,110,110,120．（Ⅰ）求图中a 的值；（Ⅱ）从成绩不低于100分的学生中随机选取2人，该2人中成绩在110分以上（含110分）的人数记为X ，求X 的分布列和数学期望．18．（本题共13分，第（Ⅰ）问6分，第（Ⅱ）问7分）已知向量2(cos ,1),,cos )222xx x m n =-=，函数()1f x m n =⋅+． （Ⅰ）若[0,]2x π∈，11()10f x =，求cos x 的值；（Ⅱ）在ABC ∆中，角,,A B C 的对边分别是,,a b c ，且满足2cos 2b A c ≤，求()f B 的取值范围．19．（本题共13分，第（Ⅰ）问6分，第（Ⅱ）问7分）已知函数()()21()2142ln 2f x x a x a x =-++- ()a R ∈． （Ⅰ）若函数()f x 在3x =处取得极值，求曲线()f x 在点()()1,1f 处的切线方程； （Ⅱ）当32a ≤时，讨论()f x 的单调区间． 20．（本题共12分，第（Ⅰ）问6分，第（Ⅱ）问6分）如图所示，已知三棱柱111ABC A B C -，点1A 在底面ABC 上的射影恰为AC 的中点D ，1190,2,BCA AC BC BA AC ︒∠===⊥．（Ⅰ）求证：1AC ⊥平面1A BC ； （Ⅱ）求二面角111B A B C --的余弦值．21．（本题共12分，第（Ⅰ）问4分，第（Ⅱ）问8分）设P 为圆221:2C x y +=上的动点，过P 作x 轴的垂线，垂足为Q ，点M PQ =． （Ⅰ）求点M 的轨迹2C 的方程；（Ⅱ）过直线2x =上的点T 作圆1C 的两条切线，设切点分别为,A B ，若直线AB 与 点M 的轨迹2C 交于,C D 两点，若CD AB λ=，求实数λ的取值范围． 22．（本题共12分，第（Ⅰ）问4分, 第（Ⅱ）问8分） 已知数列{}n a 满足：112k k k a a a -++≥()2,3,k = ． （Ⅰ）若12a =，25a =，411a =，求3a 的值； （Ⅱ）若12014a a a ==，证明：11k k k a aa a k++--≥且k a a ≤，()1,2,,2014k = ．参考答案一、选择题 1-5 BBACC6-10 CABCC第10题解析：设0000(,,(,P x Q x x x -0(0)x >，则折后有2222000||(2)PQ x =++22044x x =+8≥，所以||PQ的最小值为， 此时01x =。

山东省滕州第七中学2015届高三11月月考英语试题英语试题卷共10页。

满分120分。

考试时间100分钟。

注意事项:1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2．答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。

如需改动, 用橡皮擦擦干净后，再选涂其它答案标号。

3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答.在试题卷上答题无效。

5．考试结束后，将试题卷和答题卡一并交回。

第I卷一、单项填空（共15小题；每小题1分, 满分15分。

）请从A,B,C,D四个选顶中.选出可以填入空白处的最佳选项，并在答题卡上将该选项的标号涂黑。

1．During the rush hour they were in the heavy traffic．A．held on B．held up C．held down D．held out2.______ no bus, we had to walk home.A．There was B．There beingC．Because there being D．There were3．All of the children ______ in the school play and they are in high spirits.A．are involving B．involveC．are involved D．have involved4．As a result of the serious flood,two-thirds of the buildings in the areas ．A．need repairing B．need to repairC．needs repairing D．needs to repair5．---Would you like to go out for a walk?---- ．A．No,but I can’t afford the t ime B．No,I don’t feel in the mood for it now C．You may ask your sister to go,too D．No,thank you6．—May I smoke here?—Choose a seat in the smoking section, if you ________.A．should B．must C．can D．may7．It is a wise father ________ knows his child.A．that B．which C．what D．whom 8．Knowing ________ you’re good at and doing even more of it creates excellence.A．where B．which C．what D．that 9．Don’t you think the world would be an easier place to live in, if we all ________ the same language?A．speak B．had spoken C．spoke D．would speak 10．His wife was busy cooking while he watched TV ________ comfortably in the sofa.A．seat B．to seat C．seating D．seated 11．When our ancestors were hunters and gatherers 10,000 years ago, they didn’t have time to wonder much about ________ but finding food.A．everything B．anything C．nothing D．something 12．—Did you see ________ man in ________ black pass by just now?— No, sir. I was reading a newspaper.A．the; the B．the; a C．a; the D．a; / 13．The government promises that relief materials ________ to the flood-hit areas in no time.A．will be rushed B．will rushC．have rushed D．have been rushed14．—Why did Mr. Green take his 7th grade students to the river yesterday afternoon?—________ the river.A．Cleaned up B．Cleaning up C．To clean up D．Clean up 15．—Why are you going to the court?—________! I’ve been charged with parking my car in the wrong place.A．It’s ridiculous B．You don’t sayC．Tell me about it D．Leave me alone二、完形填空（共20小题；每小题1.5分，满分30分。