常微分方程_理学思维导图

考研高等数学知识点整理（附思维导图）被考研高数折磨过的小伙伴一定都知道那种痛苦：泰勒展开、麦克劳林展开、夹逼定理、定积分不定积分、微分多元微分......作为成功登陆的一员，我觉得有义务帮对岸的朋友考研一把。

下面这张考研高数知识图我之前用过，希望能给你带来好运。

我不多说了。

一、函数先明确一些基本概念，比如函数的定义，函数的性质，什么是复合函数，反函数，隐函数。

理解概念很重要！理解概念很重要！理解概念很重要！重要的事情说三遍~很多问题我们不会做。

其实不是我们解决问题的能力不好，而是我们连基本概念都没搞清楚，自然无从下手，或者说解决问题的方向是偏了！这是我十几年应试的血泪教训！熟悉基本初等函数，包括幂函数、指数函数、对称函数、三角函数、反三角函数，要把公式和参数适用范围记住；常用的函数有绝对值函数、符号函数、整数函数、狄利克雷函数、极大值函数、可变积分上限函数(我认为是最变态的)和双曲函数。

二、极限同样的，先厘清极限的定义了解数列极限的基本性质：极限的唯一性，收敛数列的有界性和保号性，收敛数列与子数列间的关系了解函数极限（区别于数列极限）的基本性质：极限的唯一性，局部有界性和局部保号性（这是和数列极限很大的不同）无穷小量和无穷大量极限的四则运算极限存在的判别方法：单调有界定律和夹迫定律（也有叫夹逼定理的，说的都是一个意思），这两个定律很常见，注意熟练使用三、函数的连续性四、导数与微分基本初等函数的导数公式都得背下来五、中值定理这部分很难(可能只是对我来说，我是个坏学生)，也是常规考试的重点。

六、函数单调性与凹凸性这部分也是重点。

七、渐近线与曲率八、不定积分和微分一样，基本积分公式也得去记九、定积分重点理解定积分的定义和性质（再次强调）然后去记重要的定理、公式和关系十、无穷级数功能扩展很烦人，但是很重要。

大家可能都看过这些表情包。

十一、常微分方程与差分方程要记公式十二、空间解析几何与向量代数理解向量运算，后面的平面方程也就很容易理解了十三、多元函数微分学条件极值经常考十四、重积分这部分主要注意一点：从里层到外层展开的过程要细心，不然展开到最后发现错了又得重新开始十五、曲线积分与曲面积分我当年没考这个，没什么发言权。

大一数学知识点思维导图数学是一门重要的学科，大一学生正式接触数学课程时，常常会感到有些吃力。

为了帮助大家更好地掌握大一数学知识，我整理了一份思维导图，以系统地呈现大一数学的重要知识点。

以下是思维导图的内容：1. 微积分1.1 极限与连续性- 数列极限- 函数极限- 连续函数与间断1.2 导数与微分- 导数的定义- 导数的性质- 微分的应用1.3 积分与不定积分- 不定积分的定义- 不定积分的计算法则- 定积分及其应用2. 线性代数2.1 矩阵与线性方程组- 矩阵的基本概念- 矩阵的运算法则- 线性方程组的求解方法 2.2 行列式与特征值- 行列式的性质与计算方法 - 特征向量与特征值- 对角化与相似矩阵2.3 向量空间与线性变换- 向量空间的基本概念- 线性变换的定义与性质 - 线性变换的矩阵表示3. 概率论与数理统计3.1 概率的基本理论- 随机试验与样本空间- 事件与概率- 条件概率与独立性3.2 随机变量与概率分布- 随机变量的概念- 离散型随机变量与概率分布- 连续型随机变量与概率密度函数 3.3 统计推断与假设检验- 参数估计- 假设检验的基本原理- 常见的假设检验方法4. 微分方程4.1 常微分方程基础- 微分方程的基本概念- 一阶常微分方程的解法- 高阶常微分方程的解法4.2 线性常微分方程与特殊函数 - 齐次线性常微分方程- 非齐次线性常微分方程- 常见的特殊函数及其应用5. 数学分析5.1 数列与级数- 数列的极限- 级数的收敛与发散- 常见的级数及其性质5.2 函数与极限- 函数的极限与连续性- 函数的一致连续性- 函数的一致收敛5.3 多元函数微分学- 偏导数与全微分- 多元函数的极值- 隐函数与参数方程以上是大一数学的主要知识点思维导图，通过整理这份导图，希望能够帮助大家更好地理清数学知识的脉络，并对各个知识点有一个整体的认识。

当然，在实际学习中，还需要深入学习每个知识点的具体内容，理解其定义、原理及应用方法。

高数大一上知识点思维导图高等数学是大一学生必修的一门课程，因为其抽象性和难度较大，对很多同学来说是一项挑战。

为了更好地掌握高等数学的知识点，提高学习效果，我整理了一份高等数学大一上知识点的思维导图。

下面就让我们一起来看看这份思维导图吧！在高等数学大一上的学习中，主要包含了导数与微分、积分与不定积分、微分方程三个部分。

首先，让我们从导数与微分这一部分开始。

在导数与微分这一部分中，首先介绍了函数与极限的概念。

函数是高等数学的基础，它是自变量和因变量之间的关系。

而极限则是函数无限逼近某一点的过程，通过极限我们可以研究函数在一个点的性质。

接着介绍了导数的概念，导数是函数变化率的度量，表示函数在某一点的瞬时变化率。

在导数的求解中，我们需要掌握一些常用的导数公式和运算法则。

通过这些工具，我们可以求解导数问题，如求函数的导函数、求曲线的切线等。

接下来是积分与不定积分这一部分。

积分是导数的逆运算，表示函数在一定区间内的累积变化量。

不定积分则是求积分的一种方法，其中的不定积分常数表示在不同点处的积分结果可能不同。

在积分与不定积分的学习中，我们需要熟练掌握换元法、分部积分法和定积分的计算。

这些方法可以帮助我们解决一些复杂的积分问题，如求某个函数的原函数、求曲线下的面积等。

最后是微分方程这一部分。

微分方程是含有未知函数及其导数的方程，通过求解微分方程我们可以得到函数的解析表达式。

在微分方程的求解中，我们需要掌握一些基本的解法，如可分离变量法、一阶线性微分方程的求解方法等。

此外，对于高阶微分方程，我们还需要熟悉齐次线性微分方程、非齐次线性微分方程和常系数线性齐次微分方程的特解等的求解方法。

通过这份思维导图，我们可以更好地了解高等数学大一上的知识点，并掌握相关的考点和解题技巧。

但是仅仅依靠思维导图是不够的，我们还需要辅以大量的练习，不断总结和思考，加深对知识点的理解和运用。

总之，高等数学是一门需要思维和逻辑能力的课程，通过合理的学习方法和不懈的努力，我们一定能够掌握好这门课程。

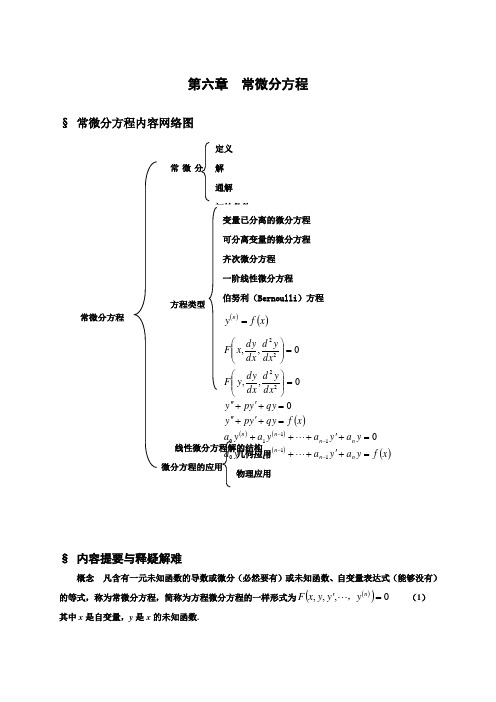
第六章 常微分方程§ 常微分方程内容网络图线性微分方程解的结构§ 内容提要与释疑解难概念 凡含有一元未知函数的导数或微分（必然要有）或未知函数、自变量表达式（能够没有）的等式，称为常微分方程，简称为方程微分方程的一样形式为()()0,,,='n y y y x F ， （1）其中x 是自变量，y 是x 的未知函数.变量已分离的微分方程 可分离变量的微分方程 齐次微分方程 一阶线性微分方程伯努利（Bernoulli ）方程()()x f y n =()()()()()()x f y a y a y a y a y a y a y a y a x f qy y p y qy y p y dx y d dx dy y F dx y d dx dy x F n n n n n n n n =+'+++=+'+++=+'+''=+'+''=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛----111011102222000,,0,,常微分方程常微分定义 解 通解初始条件方程类型微分方程的应用几何应用物理应用在方程中显现的各阶导数中最高的阶数，称为微分方程的阶。

若是将某一函数y=y(x)代入微分方程（1），能使方程成为恒等式，那么函数y=y(x)称为微分方程（1）的解。

若是微分方程的解中所含独立的任意常数的个数（即这些常数归并非了）与方程的阶数相同，那么该解为微分方程的通解（全部解）。

若是指定通解中的一组任意常数等于某一组固定的数，那么取得的微分方程的解，叫做微分方程的特解或说知足某些条件的方程的解，称为微分方程的特解，该条件称为初始条件。

概念 关于概念在某非空实数集D 上的n 个函数()()()x y x y x y n ,,,21 ，假设存在n 个不全为零的常数n k k k ,,,21 ，便得在D 上有恒等式()()()D x x y k x y k x y k n n ∈≡+++,02211 成立，那么称函数()()()x y x y x y n ,,,21 在D 上是线性相关的，假设上式仅当021====n k k k 时才能成立，那么称()()()x y x y x y n ,,,21 线性无关。

大一下高数知识点思维导图大一下学期高等数学是大部分理工科学生需要学习的一门重要课程。

为了更好地复习和掌握高数的知识点，下面将以思维导图的形式，系统地总结大一下学期高等数学的重点知识点。

1. 函数与极限在函数与极限这一部分，我们需要掌握函数的定义和性质，如增减性、奇偶性、周期性等。

同时，也要了解极限的定义、性质和计算方法，例如极限存在准则、夹逼定理等。

除此之外，还要熟练掌握一些常见函数的极限，如幂函数、指数函数、对数函数、三角函数等的极限运算。

2. 导数与微分导数与微分是高等数学的重要基础知识，需要掌握导数的定义、性质和计算方法。

特别是常见函数的导数，如幂函数、指数函数、对数函数、三角函数等的导数计算。

此外，还需了解一阶导数与二阶导数的关系、隐函数的求导、高阶导数等相关内容。

3. 微分中值定理与应用在微分中值定理与应用部分，掌握拉格朗日中值定理、柯西中值定理以及罗尔定理，并能灵活运用这些中值定理解决实际问题。

此外，还需了解泰勒展开式的概念和计算方法，以及利用泰勒展开逼近函数值的相关知识。

4. 不定积分与定积分不定积分与定积分是高等数学的核心内容之一，需要掌握不定积分的定义、性质和基本的计算方法。

特别是基本的不定积分公式、换元积分法和分部积分法的运用。

对于定积分，要熟悉定积分的定义、性质和基本的计算方法，掌握定积分的几何意义和物理应用，如求面积、求弧长、求体积等。

5. 微分方程微分方程是高等数学的重要应用部分，需要掌握常微分方程的基本概念、分类和一阶微分方程的解法。

特别是常见的一阶线性微分方程、二阶线性齐次微分方程和二阶线性非齐次微分方程的解法。

此外，还需了解高阶微分方程和常系数线性微分方程的解法。

总结起来，大一下学期高等数学的重点知识点可以归纳为函数与极限、导数与微分、微分中值定理与应用、不定积分与定积分以及微分方程。

通过对这些知识点的系统学习和复习，能够帮助我们更好地掌握高数的基础知识，为后续学习打下坚实的基础。

高等数学大一知识点思维导图高等数学是大一学生必修的一门课程，它是一门关于数学的基础理论和方法的课程。

在学习高等数学的过程中，我们需要掌握一系列的基础知识点。

为了更好地帮助大家理解和掌握这些知识点，我制作了以下思维导图，来帮助大家系统地梳理高等数学的重要概念。

导数与微分- 函数的极限与连续性- 导数的定义与性质- 基本导数公式- 高阶导数与导数的应用- 微分与近似计算不定积分与定积分- 不定积分的定义与性质- 基本积分表与常用积分公式- 定积分的定义与性质- 微积分基本定理及其应用- 变限积分与定积分的应用级数与数项级数- 数列的概念与性质- 数项级数的概念与性质- 收敛级数与发散级数的判定- 常见级数求和方法- 幂级数及其收敛区间多元函数与偏导数- 二元函数的概念与性质- 偏导数的定义与计算- 高阶偏导数与混合偏导数- 隐函数与参数方程的偏导数- 多元函数的极值与条件极值重积分与曲线积分- 重积分的概念与性质- 常见坐标系下的重积分计算- 曲线积分的概念与性质- 基本曲线积分公式与应用- 曲线积分与重积分的关系常微分方程- 微分方程的概念与分类- 一阶常微分方程的解法- 可解性与解的存在唯一性- 变量可分离方程与一阶线性方程- 常系数线性齐次与非齐次方程以上思维导图是我根据高等数学大一知识点整理的，通过这些思维导图，你可以更加清晰地看到各个知识点之间的联系和重要性。

这些导图可以作为你学习高等数学的参考资料，帮助你更好地理解和记忆知识点。

当然，高等数学的学习还需要进行大量的练习和实践，只有在实践中不断加深对知识点的理解和应用，我们才能真正掌握高等数学的知识。

希望这些思维导图对你在学习高等数学中有所帮助，祝你在高等数学学习中取得好成绩！。