初中数学知识点思维导图(北师大版)
- 格式:docx
- 大小:21.99 KB
- 文档页数:19
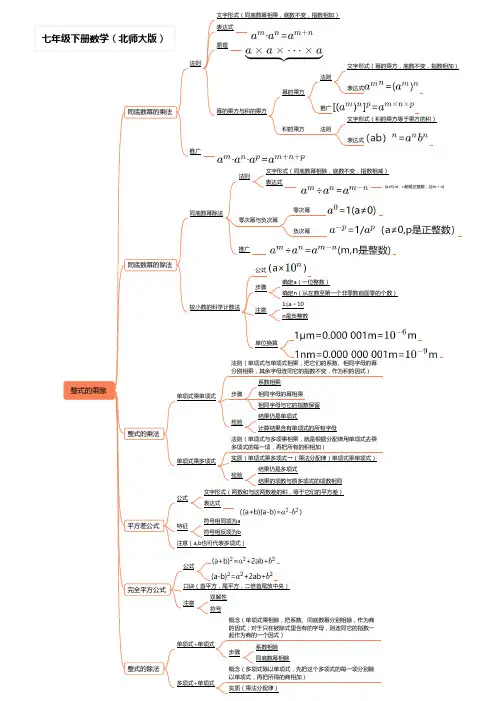
法则表达式推广文字形式(积的乘方等于乘方的积)表达式法则文字形式(同底数幂相除,底数不变,指数相减)表达式零次幂公式确定a(一位整数)确定n(从左数至第一个非零数前面零的个数)法则(单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式)符号相同项为a口诀(首平方,尾平方,二倍首尾放中央)双解性相交线与平行线两条直线的位置关系位置关系相交平行注意:同一平面内,不相交的两条直线平行定义(两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直)垂直交点叫做垂足,一条直线称作另一条直线的垂线公理平面内,过一点有且只有一条直线与已知直线垂直角对顶角直线外一点与直线上各点连接的所有线段中,垂线段最短定义(∠1与∠2有公共顶点O,它们的两边互为反向延长线)定理对顶角相等补角余角公理证明(同角的补角相等)定义(两角之和180°)证明(∵∠1+∠2=180°∴∠1与∠2互为补角)定义(两角之和90°)证明(∵∠1+∠2=90°∴∠1与∠2互为余角同角或等角的补角相等同角或等角的余角相等探索直线平行的条件同位角在第三条直线同旁特点两条直线的同侧形状(“F”型)平行条件两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行简称(同位角相等,两直线平行)证明∵∠1=∠2公理∴l1∥l2(同位角相等,两直线平行)过直线外一点有且只有一条直线与已知直线平行平行于同一条直线的两直线平行(平行的传递性)内错角在第三条直线两侧特点两条直线的两侧形状(“Z”型)平行条件两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行证明简称(内错角相等,两直线平行)∵∠1=∠2∴l1∥l2(内错角相等,两直线平行)同旁内角在第三条直线同旁特点两条直线内部形状(“C”型)平行条件两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行证明简称(同旁内角互补,两直线平行)∵∠1+∠2=180°∴l1∥l2(同旁内角互补相等,两直线平行)平行线的性质两条直线被第三条直线所截,如果这两条直线平行那么同位角相等两条直线被第三条直线所截,如果这两条直线平行那么内错角相等两条直线被第三条直线所截,如果这两条直线平行,那么同旁内角互补用尺规作图概念(在变化过程中,数值发生改变的量)定义(由不在同一条直线上的三条线段首尾顺次相接所组成实质(八字对顶全等)轴对称图形(如果一个平面图行沿一条直线折叠后,直线两。
平面丰富的图形叶界但械任相等他慢C 交线底直正方体 口嗔柱箕方体五蹦■相红两百 怕等■•多受市谢相等 心相芾正多边形面知扇形相交0囱 曲面可水面黑板 理面 而上下面三棱把 在同一平面且不在同一 直衰上的三条式三届以 J ■的教段首星连接且不 相交拒成的剑网图版三边用、种彝五边彬 ------- 、欧拉足谀直校性 和橙总,缱汨一个平面上•戴 一个几何体,然 出来的面口 I 的截点 相交 生活中的图形-展不与折叠也不同方「句看酝一•件几何悻正团 主战图 左面 左祝图 上面独视图正方体I几何好'、回鞋/\棱柱J 0 ■ N -圆柱■ ・胴I 卷方体■ L -W#.椎悻胃一 ------- 性能晓功戢面 面动成静个曲的交线叫做辕,相 落两个吃面的交靓叫做 恻梭.性柱的所节以械 长都框寻,梗柱的上下 花状相间,恻面的形状 加最平行四边修力方的用斗加 原叫做第方正数O ttox正故的Wig----- \比砰 负糊杆就正益为正得分玩 ..... .......... 若号J1—I —有理效及其 运尊乘法箔对怛 相如同丹相E---交时值大遑仃值小不相等.1*1= h3 | - | 1 I -2 备网善"身与沏T用反散 扣上和 I ⑴-2 = 1-3l3+bi*c-fl+ib*<^ 洁言堂4口中7 交拉室 ------------------ -—-P£tt>0正堂上为效襁苗谷dWW£if<&S=fl山,,产河葩时他大.会号电对把异号相加 持由 数太小 右边工至过相雍 胞时书 就近,P ・bP 交提事值冲声:7中『0 劫合津 运翼法.川 占也*“7皿&分配用相索二芝1 国祖 赛以赵拉 法时1目号神正 寻号算乌得女西S [相除法国历泊利值相结 数修存白 怕发较 间敷字〔-L^l^Z直国卫.匚这争对修 正显 再干E 本身 负哥蟀于它本身数伯 右边下左边有理票比鞋书也性空任何鼎等于仃正方晌向心卮苴律育理盥案效法定义:数告字母的糊L {单破一个献一个 字书也是羊困;;卜多项式的次蕊e 次磬震前的:卷f串项式0r 聿项式的至毂e 平攻五■中凶数字因装学会弓笛号表不穿激毒勺芝房 表亍殷姓地渔,解邑一骰性结论r 多项直的项已至顶比白个徵r 军用苴国次茎日哈有学者的指皴和至义:JLT 单^直闺和川帕多西探索与表达规律->代数式卜言义:目老箕汗言杷知咛耳互接而就 ★单独一个数或一个字母也是代数式 字母表示数口 .手里二合天任区道★所含手号相同:拒同字四的指他也旧同◎ o 同类项 ---------------------,把一柒项,并戒一项 口❷合并同奖项 口 整式的加减曰多项式可★着他加端点旋转再成同角度量法/角的比较聿雪法*角的计篁线段向一个方向无限延长就是前珑❷蹦q -------------------- :——: ----------------------------- 有一线匿向两个方向无延长就县直线Or --------------:-----------___r~ 1 r t~~~—兀师忘国心生国瓢. 说形挖F 】M 葭用以FA 式乐别我水线院,对战 由些r恃 I 4-1时视村1514-2EE4-3jB,畿汉”或或■ J ” (])BH 蛾和i & K* । t H&临出痂祖记柞,即1埼嚓 他」七为1秒.记他11即「西'多边形o线的表示n雌口线段有■两个端点两点之闰的距离两点之间浅段最短比较线段的长短6r -------------基本平面图形左万冰 正方体秘不变 0水箱登高了圆柱球 ---------------------------- 检骁检提回桂体交E 捎生、季榜•数星-总•价 日 箝更工程鹘程=时间M 速度 日三与赶,卜,京葡U ;孤启种变装按限本陛提高“r 。
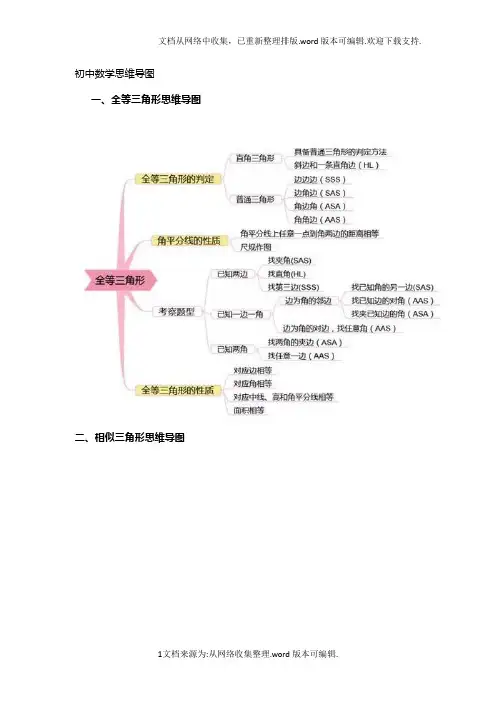
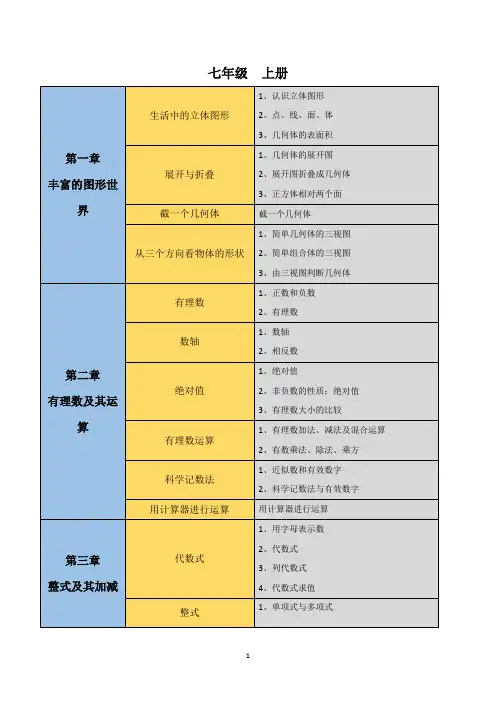
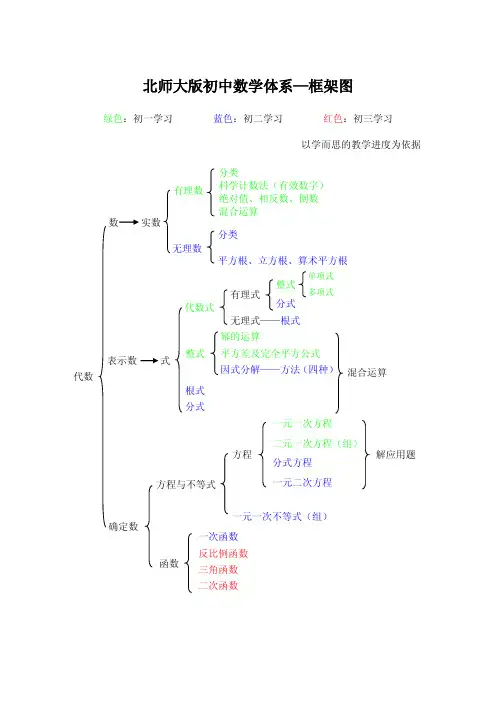
北师大版初中数学体系—框架图绿色:初一学习蓝色:初二学习红色:初三学习以学而思的教学进度为依据分类科学计数法(有效数字)绝对值、相反数、倒数混合运算幂的运算平方差及完全平方公式因式分解——方法(四种)分类平方根、立方根、算术平方根整式根式分式式实数有理数混合运算代数数表示数一元一次方程二元一次方程(组)分式方程一元二次方程解应用题方程一元一次不等式(组)方程与不等式一次函数反比例函数三角函数二次函数确定数函数代数式有理式无理式——根式整式分式单项式多项式无理数线——平行、相交、垂直角三角形四边形多边形——内/外角和平面直角坐标系轴对称图形/中心对称图形三视图,投影——平行投影、中心投影性质全等相似矩形正方形性质菱形圆各种判定图形变换等腰三角形等边三角形直角三角形——勾股定理轴对称——将军饮马,一次函数的对称,折叠平移——线、图(三角形等)旋转——三要素,图(三角形等),半角模型点与圆的位置关系线与圆的位置关系圆与圆的位置关系平行四边形梯形性质、概念(圆心角、圆周角等)垂径、切线长、切割线、弦切角、相交线定理扇形的面积(圆锥的侧面积)弧长性质特殊的平行四边形圆相关位置关系确定图变换图等腰梯形性质直角梯形图(图形及性质)几何性质、辅助线特殊梯形特殊三角形用“数、表示数、确定数”以及“图、确定图、变换图”这十四个字来概括初中代数与几何的方法是深圳学而思张明颂校长提出的。
统计与概率平均数、中位数、众数方差、标准差、极差频数、频率(频数分布直方图,频数分布表)统计图统计概率扇形统计图条形统计图折线统计图概念应用比例法列表法树状图确定事件不确定事件——等可能事件必然事件不可能事件常用判定特殊的线特殊三角形特殊四边形平行线角平分线垂直平分线切线等腰三角形等边三角形直角三角形三角形全等三角形相似平行四边形梯形矩形正方形菱形等腰梯形直角梯形。
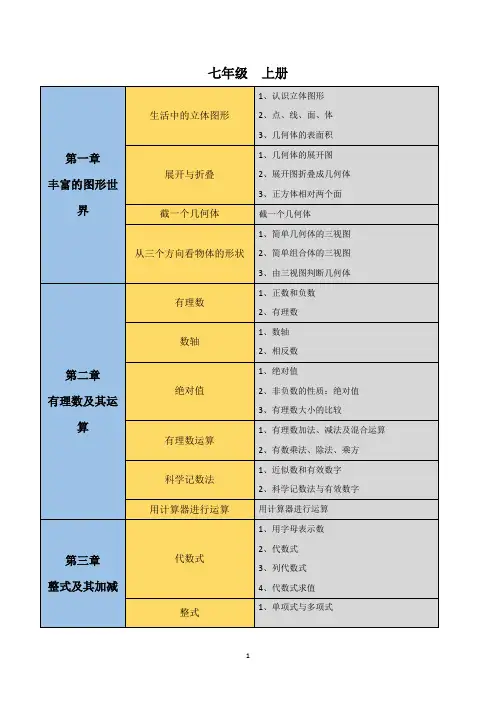
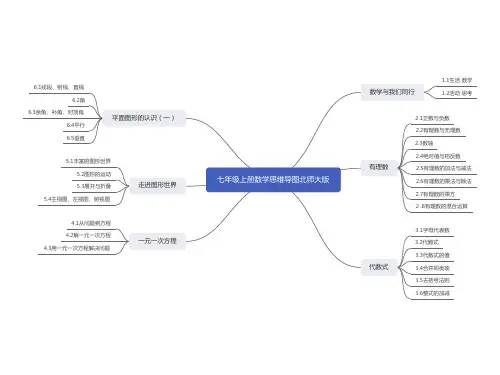
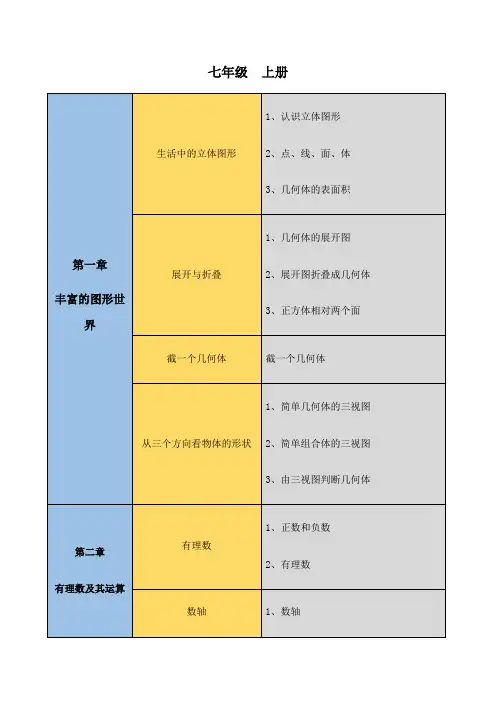
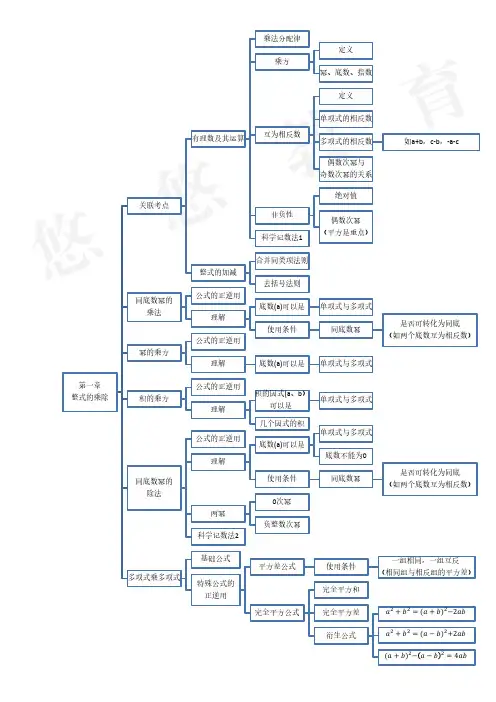
第一章整式的乘除关联考点有理数及其运算乘法分配律乘方定义幂、底数、指数互为相反数定义单项式的相反数多项式的相反数如a+b,c-b,-a-c偶数次幂与奇数次幂的关系非负性绝对值偶数次幂(平方是重点)科学记数法1整式的加减合并同类项法则去括号法则同底数幂的乘法公式的正逆用理解底数(a)可以是单项式与多项式使用条件同底数幂是否可转化为同底(如两个底数互为相反数)幂的乘方公式的正逆用理解底数(a)可以是单项式与多项式积的乘方公式的正逆用理解积的因式(a、b)可以是单项式与多项式几个因式的积同底数幂的除法公式的正逆用理解底数(a)可以是单项式与多项式底数不能为0使用条件同底数幂是否可转化为同底(如两个底数互为相反数)两幂0次幂负整数次幂科学记数法2多项式乘多项式基础公式特殊公式的正逆用平方差公式使用条件一组相同,一组互反(相同组与相反组的平方差)完全平方公式完全平方和完全平方差衍生公式a2+b2=(a+b)2−2aba2+b2=(a−b)2+2ab(a+b)2−a−b2=4ab第二章相交线与平行线平面内两条直线的位置关系相交定义对顶角定义性质对顶角相等余角和补角定义余角补角(特殊的补角:邻补角)性质同角的余角或补角相等等角的余角或补角相等特殊的相交(垂直)定义垂直垂线垂足垂线的画法垂线的性质在同一平面内,过一点有且只有一条直线与已知直线垂直垂线段最短点到直线的距离平行定义平行公理及推论过直线外一点有且只有一条直线与这条直线平行平行于同一条直线的两条直线平行平行线的判定同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行平行线的性质(与判定相反)两直线平行,同位角相等两直线平行,内错角相等两直线平行,同旁内角互补用尺规作角什么尺什么规尺规作角步骤第三章变量之间的关系变量辨析与常量的区别分类自变量因变量关系谁与谁的关系自变量与因变量关系的种类因变量随自变量的增长而增长因变量随自变量的增长而减小因变量随自变量的增长而保持不变关系的变化趋势不变一直增长量与速一直减小量与速一直不变趋势有变先增长后减小后不变先减小后增长后不变先不变后增长后减小关系的表示方法表格法关系式法图像法如何看出如何表示第四章三角形定义由不在同一条直线上的三条线段首尾顺次相接所组成的图形符号表示基本要素边、内角、顶点稳定性角内角分类(最大内角的度数)锐角三角形直角三角形符号表示三边名称钝角三角形内角和外角定义三角形的一条边与另一条边的反向延长线组成的角与内角关系等于与它不相邻的两个内角的和线段边对边定义三边关系任意两边之和大于第三边任意两边之差小于第三边三角形的中线定义交于一点重心三角形的角平分线定义交于一点内心三角形的高定义交于一点垂心全等图形定义能够完全重合的两个图形性质形状和大小都相同重点:全等三角形符号表示性质对应边相等对应角相等判定SSSASAAASSAS应用尺规作图第五章生活中的轴对称轴对称现象轴对称图形定义对称轴定义(注意是直线)条数成轴对称定义轴对称性质对应点连线被对称轴垂直平分对应角相等对应线段相等简单的轴对称图形等腰三角形定义有两条边相等的三角形基本要素一顶角和两底角一底边和两条腰性质三线合一两个底角相等对称轴顶角的平分线(底边上的中线、底边上的高)所在直线特殊的等腰三角形等边三角形三边相等三个内角均为60°线段对称轴线段垂直平分线(中垂线)定义性质尺规作图角对称轴角平分线所在直线角平分线性质尺规作图轴对称的应用1. 如何找角相等题目中给定的减去公共角依然相等加上公共角依然相等公共角对顶角相等同角或等角的余角相等同角或等角的补角相等两直线平行同位角相等内错角相等角平分线垂直全等三角形对应角相等等边对等角(同一三角形中)2. 如何找边相等题目中给定的减去公共边依然相等加上公共边依然相等公共边中线/中点全等三角形对应边相等等边对等角(同一三角形中)线段垂直平分线性质线段垂直平分线上的点到这条线段两端的距离相等角平分线性质角平分线上的点到这个角两边的距离相等。
