直齿圆柱齿轮接触接触分析

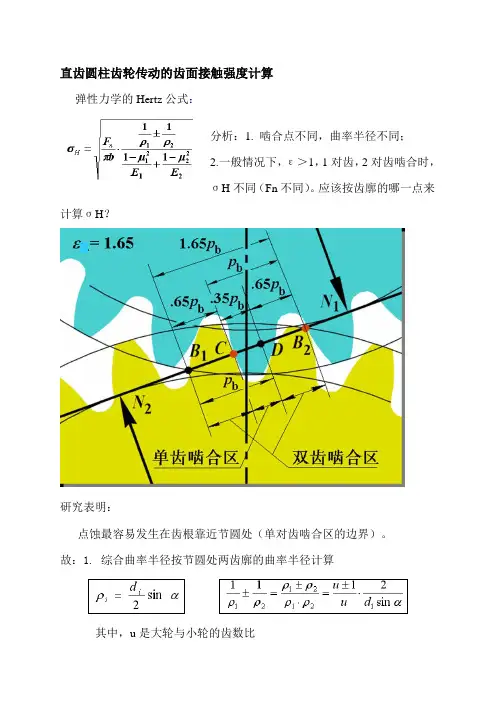
直齿圆柱齿轮传动的齿面接触强度计算
弹性力学的Hertz公式：
分析：1. 啮合点不同，曲率半径不同；
2.一般情况下，ε＞1，1对齿，2对齿啮合时，
σH不同（Fn不同）。

应该按齿廓的哪一点来计算σH？
研究表明：
点蚀最容易发生在齿根靠近节圆处（单对齿啮合区的边界）。

故：1. 综合曲率半径按节圆处两齿廓的曲率半径计算
其中，u是大轮与小轮的齿数比
2. Fn按单对齿啮合计算
针对钢制齿轮，引入钢的泊松比μ1= μ2 =0.3，钢的弹性模量
E=2.06×105 MPa，载荷系数K，中心距a，得齿面接触强度的验算公式：令齿宽系数ψa ＝b／d1，代入上式得中心距：
分析：当一对齿轮的材料、传动比、齿宽系数一定时，接触应力σH 仅取决于分度圆直径d或中心矩a，与模数m无关。

即：两对分度圆直径对应相等的齿轮传动，具有相同的接触强度，与各自模数无关。

即：增大模数m（但d不改变），不能提高齿面接触强度。

关于齿宽系数ψa
理论上讲，ψa越大，a越小，结构越紧凑。

但实际上，ψa↑，可能降低结构的刚性，载荷分布越不均匀，轮齿更易折断。

许用接触应力按下式计算：
式中: σHlim为试验齿轮的接触疲劳强度
极限，按图11－7查得；
S H为齿面接触疲劳安全系数，查表11－4得到。

图11－7。

直齿圆柱齿轮参数测定实验报告数据渐开线直齿圆柱齿轮参数的测定与分析渐开线直齿圆柱齿轮参数的测定与分析一、实验目的1．掌握测量渐开线直齿圆柱变位齿轮参数的方法。

2．通过测量和计算，进一步掌握有关齿轮各几何参数之间的相互关系和渐开线性质。

二、实验内容对渐开线直齿园柱齿轮进行测量，确定其基本参数(模数m和压力角α)并判别它是否为标准齿轮，对非标准齿轮，求出其变位系统X。

三、实验设备和工具1．待测齿轮分别为标准齿轮、正变位齿轮、负变位齿轮，齿数各为奇数、偶数。

2．游标卡尺，公法线千分尺。

3．渐开线函数表(自备)。

4．计算器(自备)。

四、实验原理及步骤渐开线直齿圆柱齿轮的基本参数有：齿数Z、模数m、分度圆压力角?齿顶高系数h*a、顶隙系数C*、中心距α和变位系数x等。

本实验是用游标卡尺和公法千分尺测量，并通过计算来确定齿轮的基本参数。

1．确定齿数Z齿数Z从被测齿轮上直接数出。

．确定模数m和分度圆压力角??在图4-1中，由渐开线性质可知，齿廓间的公法线长度AB与所对应的基圆弧长Α0Β0相等。

根据这一性质，用公法线千分尺跨过n个齿，测得齿廓间公法线长度为Wn′，然后再跨过n+1个齿测得其长度为Wn??1。

Wn??(n?1)Pb?Sb,Pb?Wn??1?Wn?Wn??1?nPb?Sb式中，Pb为基圆齿距，Pb??mcos? (mm)，与齿轮变位与否无关。

Sb为实测基圆齿厚，与变位量有关。

由此可见，测定公法线长度Wn?和Wn??1后就可求出基圆齿距Pb，实测基圆齿厚Sb，进而可确定出齿轮的压力角?、模数m和变位系数x。

因此，齿轮基本参数测定中的关键环节是准确测定公法线长度。

图4－1 公法线长度测量（1）测定公法线长度W?n和Wn??1根据被齿轮的齿数Z，按下式计算跨齿数：a?n?Z?0.5180?式中：??—压力角；z —被测齿轮的齿数我国采用模数制齿轮，其分度圆标准压力角是20°和15°。

若压力角为20°可直接参照下表确定跨齿数n。

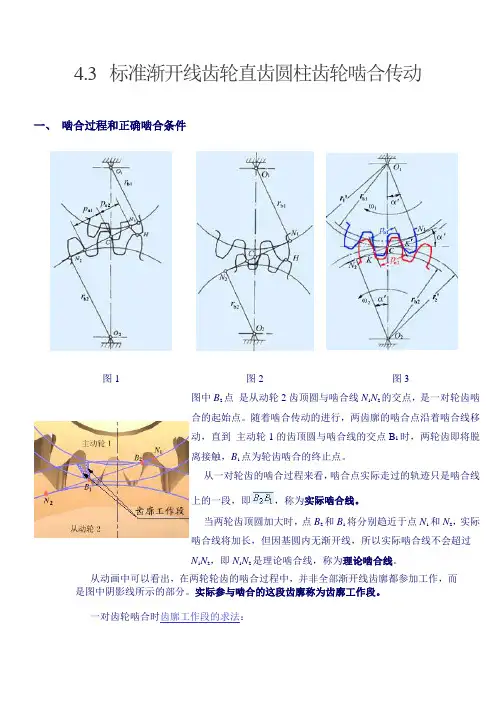
4.3 标准渐开线齿轮直齿圆柱齿轮啮合传动一、啮合过程和正确啮合条件图1 图2 图3图中B2点是从动轮2齿顶圆与啮合线N1N2的交点，是一对轮齿啮合的起始点。

随着啮合传动的进行，两齿廓的啮合点沿着啮合线移动，直到主动轮1的齿顶圆与啮合线的交点B1时，两轮齿即将脱离接触，B1点为轮齿啮合的终止点。

从一对轮齿的啮合过程来看，啮合点实际走过的轨迹只是啮合线上的一段，即，称为实际啮合线。

当两轮齿顶圆加大时，点B2和B1将分别趋近于点N1和N2，实际啮合线将加长，但因基圆内无渐开线，所以实际啮合线不会超过N1N2，即N1N2是理论啮合线，称为理论啮合线。

从动画中可以看出，在两轮轮齿的啮合过程中，并非全部渐开线齿廓都参加工作，而是图中阴影线所示的部分。

实际参与啮合的这段齿廓称为齿廓工作段。

一对齿轮啮合时齿廓工作段的求法：三个图中的齿轮都是渐开线齿轮，但图1和图2中的主动轮只能带动从动轮转过一个小角度就卡死不能动了，而图3中的主动轮可以带动从动轮整周转动，看来并不是任意两个渐开线齿轮都能正确地进行啮合，而是必须满足一定的条件，即正确啮合条件。

那么，这个条件是什么？从图3中可以看出：两个渐开线齿轮在啮合过程中，参加啮合的轮齿的工作一侧齿廓的啮合点都在啮合线N1N2上。

而在图1和图2中，工作一侧齿廓的啮合点H不在啮合线N1N2上，这就是两轮卡死的原因。

从图3中可以看出是齿轮1的法向齿矩，是齿轮2的法向齿矩，亦即:这个式子就是一对相啮合齿轮的轮齿分布要满足的几何条件,称为正确啮合条件。

由渐开线性质可知，法向齿距与基圆齿距相等，故上式也可写成将和代入式中得：由于模数m和压力角均已标准化，不能任意选取，所以要满足上式必须使：结论：一对渐开线齿轮，在模数和压力角取标准值的情况下，只要它们分度圆上的模数和压力角分别相等，就能正确啮合。

二、齿轮传动的正确安装条件1、齿侧间隙为了避免齿轮在正转和反转两个方向的传动中齿轮发生撞击,要求相啮合的轮齿的齿侧没有间隙。

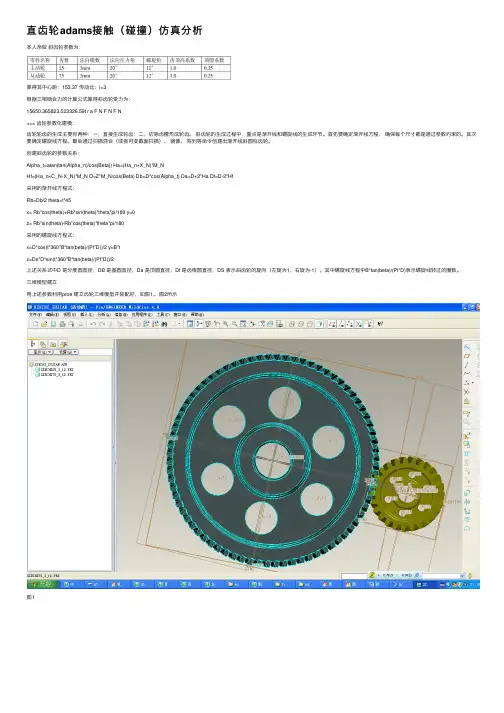
直齿轮adams接触（碰撞）仿真分析本⼈亲做斜齿轮参数为：算得其中⼼距：153.37 传动⽐：i=3根据三相啮合⼒的计算公式算得斜齿轮受⼒为：15650.365823.523326.59t r a F N F N F N=== 齿轮参数化建模：齿轮轮齿的⽣成主要有两种：⼀，直接⽣成轮齿；⼆，切除齿槽形成轮齿。

斜齿轮的⽣成过程中，重点是渐开线和螺旋线的⽣成环节。

⾸先要确定渐开线⽅程，确保每个尺⼨都是通过参数约束的。

其次要确定螺旋线⽅程。

最后通过扫描混合（或者可变截⾯扫描）、镜像、阵列等命令创建出渐开线斜圆柱齿轮。

创建斜齿轮的参数关系：Alpha_t=atan(tan(Alpha_n)/cos(Beta)) Ha=(Ha_n+X_N)*M_NHf=(Ha_n+C_N-X_N)*M_N D=Z*M_N/cos(Beta) Db=D*cos(Alpha_t) Da=D+2*Ha Df=D-2*Hf采⽤的渐开线⽅程式：Rb=Db/2 theta=t*45x= Rb*cos(theta)+Rb*sin(theta)*theta*pi/180 y=0z= Rb*sin(theta)-Rb*cos(theta)*theta*pi/180采⽤的螺旋线⽅程式：x=D*cos(t*360*B*tan(beta)/(PI*D))/2 y=B*tz=Ds*D*sin(t*360*B*tan(beta)/(PI*D))/2上述关系式中D 是分度圆直径，DB 是基圆直径，Da 是顶圆直径，Df 是齿根圆直径，DS 表⽰斜齿轮的旋向（左旋为1，右旋为-1）。

其中螺旋线⽅程中B*tan(beta)/(PI*D)表⽰螺旋线转过的圈数。

三维模型建⽴⽤上述参数利⽤proe 建⽴齿轮三维模型并装配好，如图1,、图2所⽰图1图2将三维模型导⼊adams定义导⼊模型后，逐步进⾏：材料属性定义，添加约束，添加驱动，添加负载，添加接触⼒，然后得到仿真处理前期⼯作，如图3，图4所⽰图3图4、仿真后处理仿真后处理得到斜齿轮三个⽅向上波动图和均值。

外啮合的直齿圆柱标准齿轮,小轮的齿根厚度和大轮的齿根厚度关系1. 引言1.1 概述直齿圆柱标准齿轮是一种常见的机械传动元件，广泛应用于各个领域。

在齿轮啮合过程中，齿根厚度是当今研究的一个重要方面，因为它对齿轮的强度和工作性能有着重要的影响。

而在外啮合直齿圆柱标准齿轮中，小轮的齿根厚度与大轮的齿根厚度之间存在着一定的关系。

1.2 文章结构本文将首先介绍外啮合的直齿圆柱标准齿轮的基本概念和特性，包括其定义、特点以及应用领域。

接下来，将详细讨论小轮的齿根厚度与大轮的齿根厚度之间的关系，并分析其中的影响因素。

随后，将介绍相关计算模型及仿真验证方法，以进一步验证前述理论分析结果。

最后，通过总结研究结果提出结论，并展望未来该领域研究可能发展的方向。

1.3 目的本文旨在深入研究外啮合的直齿圆柱标准齿轮中小轮的齿根厚度与大轮的齿根厚度之间的关系，探讨影响因素，并提出相关计算模型和仿真验证方法。

通过该研究，可以为设计者提供有关在不同应用场景中优化选择齿根厚度的参考指导，以提高齿轮传动系统的可靠性和工作效率。

此外，本文也希望培养读者对于直齿圆柱标准齿轮特性及其在机械传动中的应用领域有更全面的了解。

2. 外啮合的直齿圆柱标准齿轮介绍:2.1 定义与特性:外啮合的直齿圆柱标准齿轮是一种常见的机械传动元件, 具有两个相互啮合的齿轮: 大轮和小轮。

它们由金属材料加工而成，具有相对简单的结构。

其中大轮拥有较大的直径，而小轮则比大轮尺寸更小。

这种齿轮常用于各种工业领域，如汽车、机床等，用于实现速度转换、扭矩传递和运动分配。

2.2 齿轮应用领域:外啮合的直齿圆柱标准齿轮广泛应用于许多行业。

在汽车行业中，它们被用作变速箱和传动系统中关键组件，实现不同挡位之间的变速。

此外，在航空航天、能源发电以及其他工程应用中也可以找到这种类型的齿轮。

2.3 标准规范概述:为了确保外啮合的直齿圆柱标准齿轮在各种应用中具有良好的兼容性和互换性，相关机构制定了一系列标准规范。

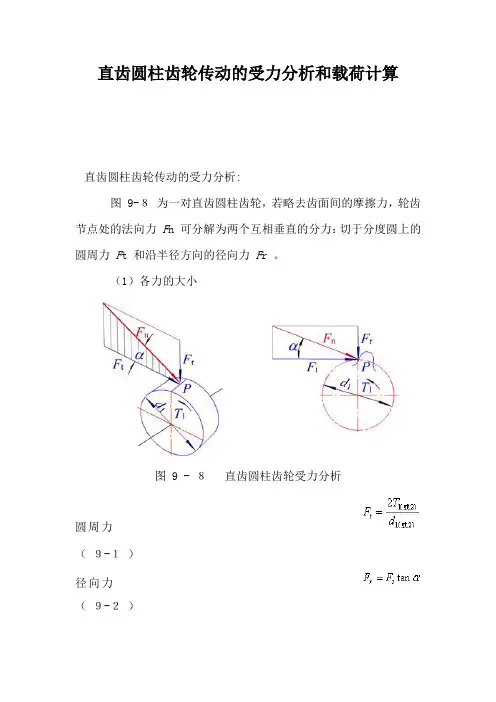
直齿圆柱齿轮传动的受力分析和载荷计算直齿圆柱齿轮传动的受力分析:图 9-８为一对直齿圆柱齿轮，若略去齿面间的摩擦力，轮齿节点处的法向力F n 可分解为两个互相垂直的分力：切于分度圆上的圆周力F t 和沿半径方向的径向力F r 。

（1）各力的大小图 9 - ８直齿圆柱齿轮受力分析圆周力（９-１）径向力（９-２）法向力（９-３）其中转矩（９-４）式中：T1 ，T2 是主、从动齿轮传递的名义转矩，N.mm ；d1 ，d2 是主、从动齿轮分度圆直径， mm ；为分度圆压力角；P是额定功率， kW ；n1 ，n2 是主动齿轮、从动轮的转速， r/min 。

作用在主动轮和从动轮上的各对应力大小相等，方向相反。

即：，，（2）各力的方向主动轮圆周力的方向与转动方向相反；从动轮圆周力的方向与转动方向相同；径向力F r 分别指向各自轮心 ( 外啮合齿轮传动 ) 。

9.4.2 计算载荷前面齿轮力分析中的F n 、F t 和F r 及F a 均是作用在轮齿上的名义载荷。

原动机和工作机性能的不同有可能产生振动和冲击；轮齿在啮合过程中会产生动载荷；制造安装误差或受载后轮齿的弹性变形以及轴、轴承、箱体的变形，会使载荷沿接触线分布不均，而同时啮合的各轮齿间载荷分配不均等，因此接触线单位长度的载荷会比由名义载荷计算的大。

所以须将名义载荷修正为计算载荷。

进行齿轮的强度计算时，按计算载荷进行计算。

（９－４）计算载荷(９ - ５)载荷系数(９- ６)式中：K是载荷系数；K A 是使用系数；K v 是动载系数；是齿向载荷分布系数；是齿间载荷分配系数。

1 ．使用系数K A使用系数K A 是考虑由于齿轮外部因素引起附加动载荷影响的系数。

其取决于原动机和工作机的工作特性、轴和联轴器系统的质量和刚度以及运行状态。

其值可按表 9 - ３选取。

表 9-３使用系数K A工作机的工作特性工作机器原动机的工作特性及其示例电动机、均匀运转的蒸气机、燃气轮机蒸气机、燃气轮机液压装置电动机（经多缸内燃机单缸内燃机（小的，启动转矩大）常启动启动转矩大）均匀平稳发电机、均匀传送的带式或板式运输机、螺旋输送机、轻型升降机、机床进给机构、通风机、轻型离心机、均匀密度材料搅拌机等1.00 1.101.251.50轻微冲击不均匀传送的带式输送机、机床的主传动机构、重型升降机、工业与矿用风机、重型离心机、变密度材料搅拌机、给水泵、转炉、轧机、1.25 1.351.51.75中等冲击橡木工机械、胶积压机、橡胶和塑料作间断工作的搅拌机、轻型球磨机、木工机械、钢坯初轧机、提升装置、单缸活塞泵等1.50 1.601.752.00严重挖掘机、重型球磨机、橡 1.75 1.85 2.0 2.25冲击胶揉合机、落沙机、破碎机、重型给水泵、旋转式钻探装置、压砖机、带材冷轧机、压坯机等0或更大注： 1. 对于增速传动，根据经验建议取表中值的 1.1 倍。

圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效，应进行齿面接触疲劳强度计算。

因此，齿轮接触疲劳强度计算准则为：齿面接触应力σH小于或等于许用接触应力σHP，即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区，轮齿受力较大，故点蚀首先出现在节点附近。

因此，通常计算节点的接触疲劳强度。

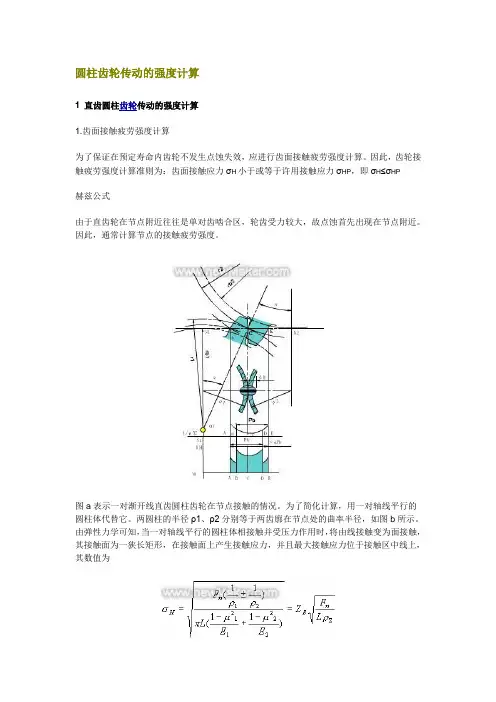
图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。

为了简化计算，用一对轴线平行的圆柱体代替它。

两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径，如图b所示。

由弹性力学可知，当一对轴线平行的圆柱体相接触并受压力作用时，将由线接触变为面接触，其接触面为一狭长矩形，在接触面上产生接触应力，并且最大接触应力位于接触区中线上，其数值为式中σH-接触应力（Mpa）Fn-法向力（N）L-接触线长度（mm）rS-综合曲率半径（mm）；±-正号用于外接触，负号用于内接触ZE-材料弹性系数（），，其中E1、E2分别为两圆柱体材料的弹性模量（MPa）；m1、m2分别为两圆柱体材料的泊松比。

上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同，且靠近节点的齿根处最大（图c、d）。

但为了简化计算，通常控制节点处的接触应力。

节点处的参数（1）综合曲率半径由图可知，，代入rE公式得式中：，称为齿数比。

对减速传动，u=i；对增速传动，u=1/i。

因，则有（2）计算法向力（3）接触线长度L引入重合度系数Ze，令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令，称为节点区域系数。

则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数，并将代入上式，则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径（mm）；ZE-材料弹性系数()，按下表查取；注：泊松比m1＝m2＝0.3Z H-节点区域系数，考虑节点处轮廓曲率对接触应力的影响，可由下左图查取。

2004年9月 陕　西　工　学　院　学　报Sept.2004第20卷第3期 Journal of Shaanxi Institute of Technology Vol.20　No.3[文章编号]1002-3410(2004)03-0004-03渐开线直齿圆柱齿轮有限元仿真分析刘道玉,　迟毅林,　徐兆红,　张春卿(昆明理工大学机电工程学院,　云南昆明　650093)[摘　要]　利用ANSYS 软件对齿轮变形和齿根应力进行了有限元计算,建立了一对齿轮接触仿真分析的模型,利用ANSYS 的面面接触单元进行齿轮接触仿真分析,计算了齿轮啮合中的接触应力和接触变形,说明了ANSYS 在齿轮计算尤其在接触分析上的有效性,为齿轮的优化设计和可靠性设计及CAE 奠定了基础。

[关　键　词]　有限元法;　轮齿变形;　接触应力;　仿真分析[中图分类号]　TH132.4;O241.82 [文献标识码]　A收稿日期:2004-05-14作者简介:刘道玉(1979—),男,河南永城人,昆明理工大学硕士生,主要研究方向为机械CAD/CAE ,虚拟仪器技术。

齿轮是机械中最重要的零件之一。

由于其形状比较复杂,用传统的计算方法不能确定其真实的应力及变形分布规律,因此从弹性力学出发,用现代设计方法研究齿轮的受载变形情况和接触强度,具有广泛的用途,它可以提高整个齿轮结构的设计水平。

相对于传统的计算方法,有限元由于其能快速、准确可靠、灵活地分析计算,在国内外齿轮设计和计算中已得到广泛应用。

齿轮变形的有限元分析七十年代已开始,但仅仅计算挠曲变形,接触变形和接触应力的有限元分析在九十年代才真正开始,主要方法有罚函数法,拉格朗日乘子法等,其中罚函数法由于其经济和方便,得到了广泛使用。

齿轮计算中的有限元法是建立在最小能量基础上的方法,最终形成一组平衡方程,即{K}{D}={R},{K}为刚度矩阵(它与齿轮的材料、几何形状和单元特性有关),{D}为位移向量,{R}为载荷向量,构成并求解这个方程就是齿轮计算的有限元法过程。

渐开线直齿圆柱齿轮参数测定实验报告1. 背景渐开线直齿圆柱齿轮是机械传动中常用的一种元件，其参数的准确测定对于设计和制造具有重要意义。

本实验旨在通过测量渐开线直齿圆柱齿轮的几何参数，如模数、齿数、压力角等，来评估其性能和适用范围。

2. 分析2.1 渐开线直齿圆柱齿轮的基本概念渐开线直齿圆柱齿轮是由一系列等距离排列的齿形构成，其特点是在啮合过程中两个相互啮合的齿面接触点在整个啮合过程中速度和方向均发生变化。

这种设计可以减小噪声和振动，并提高传动效率。

2.2 测量参数为了确定渐开线直齿圆柱齿轮的性能和适用范围，需要测量以下几个关键参数：•模数（Module）：模数是指每个齿所占据的长度，在计算机辅助设计（CAD）和计算机数值控制（CNC）中常用到。

模数的测量可以通过测量齿轮的直径和齿数来计算得出。

•齿数（Number of teeth）：齿数是指齿轮上的齿的数量，也是计算渐开线直齿圆柱齿轮参数的重要参数之一。

可以通过直接数数或使用光电传感器等设备来测量。

•压力角（Pressure angle）：压力角是指啮合面与法线之间的夹角，影响着传动效率和载荷分布。

可以通过测量两个相邻齿的啮合点坐标来计算压力角。

2.3 测量方法本实验使用以下步骤来测量渐开线直齿圆柱齿轮的参数：1.使用卡尺或测微仪等工具测量齿轮外径，根据外径计算模数。

2.使用光电传感器等设备对齿轮进行旋转，并记录每个周期内的脉冲数量，从而得到准确的齿数。

3.将两个相邻齿的啮合点坐标记录下来，并根据坐标计算出压力角。

4.根据上述测量结果，计算出渐开线直齿圆柱齿轮的几何参数。

3. 结果根据实验测量数据，得到以下结果：•齿数：20•外径：50mm•模数：2.5mm•压力角：20°4. 建议根据上述测量结果，可以得出渐开线直齿圆柱齿轮的参数。

根据实际应用需求和设计要求，可以进一步优化参数，如调整模数和压力角等，以满足特定的传动效果和载荷要求。

基于ANSYS 的直齿面齿轮的接触应力分析作者：李亚平来源：《中国科技纵横》2013年第18期【摘要】本文在Ansys软件的接触分析模块基础上，建立了面齿轮三维有限元非线性接触分析模型，对面齿轮齿面的接触状态进行了分析，并进行了承载状况下的接触状态分析。

同时对面齿轮在不同载荷条件下一个啮合周期内的接触情况进行了研究。

对同类产品的分析设计具有指导意义。

【关键词】直齿面齿轮接触分析 ANSYS 承载接触分析1 概述随着齿轮传动向重载、高速、低噪、高可靠性方向发展，现代齿轮设计对齿轮传动系统的静、动态特性提出了更高的要求。

齿轮设计的主要内容之一是强度设计，因此，建立比较精确的分析模型，准确的掌握齿轮应力的分布特点和变化规律具有重要的意义。

①③④设计模型的几何尺寸及边界条件如下表所示，大齿轮与小齿轮的齿厚为10mm，两个齿轮的中心距离为81mm。

小齿轮为主动齿轮，大齿轮为从动齿轮，小齿轮均匀转速0.2rad/s，大齿轮承受600N.m的阻力扭矩，计算时间为1s.（如表1表2）2 模型的建立定义小齿轮渐开线，定义小齿轮根部过渡曲线，定义小齿轮齿廓线，建立小齿轮模型，同理建立大齿轮模型，调整两个齿轮的位置，如图1所示。

3 齿轮有限元网格模型的建立在Ansys中对齿轮副进行分析，首先要建立齿轮的有限元网格模型。

依据齿轮啮合模型参数，把根据齿面方程设计的专有程序计算结果导人Ansys，建立齿轮单齿有限元网格模型如图2所示。

针对所建齿轮模型，在齿高方向划分了17层单元，过渡部分划分4层单元，齿厚方向划分41层单元，为节省计算资源，省略了齿轮的辐板和轮载部分等对接触分析结果影响不大的部分。

该模型共有7896个节点，7678个单元，轮齿采用Solid45八节点线性等参元，将生成的单齿模型数据导人到Ansys中，并对其进行旋转复制等操作，把单齿模型拓展为有限元网格模型。

4 齿面接触情况及分析过程在上述模型上施加扭矩，对面齿轮副进行分析计算。

基于ANSYS有限元软件的直齿轮接触应力分析一、本文概述随着现代机械工业的飞速发展，齿轮作为机械设备中的关键传动元件，其性能的稳定性和可靠性对于设备的长期运行和维护至关重要。

直齿轮作为齿轮传动的一种基本形式，其接触应力的分布与大小直接影响着齿轮的工作性能和使用寿命。

因此，对直齿轮接触应力的深入研究与分析，对于提高齿轮的设计水平、优化制造工艺以及提升设备的整体性能具有重要意义。

本文旨在利用ANSYS有限元软件对直齿轮的接触应力进行分析。

简要介绍了直齿轮的基本结构和传动原理，阐述了接触应力分析的必要性和重要性。

详细阐述了ANSYS有限元软件在齿轮接触应力分析中的应用，包括建模、网格划分、材料属性设定、接触设置、求解及后处理等关键步骤。

通过实例分析，展示了ANSYS软件在直齿轮接触应力分析中的具体操作流程，并对分析结果进行了详细的解读。

总结了利用ANSYS进行直齿轮接触应力分析的优势和局限性，并对未来的研究方向进行了展望。

本文旨在为齿轮设计师和工程师提供一种有效的直齿轮接触应力分析方法，帮助他们更好地理解直齿轮的应力分布特性，优化齿轮设计，提高齿轮的工作性能和可靠性。

本文也为相关领域的学者和研究人员提供了一种有益的参考和借鉴。

二、直齿轮接触应力的理论基础在直齿轮传动过程中，接触应力是决定齿轮使用寿命和性能的关键因素之一。

因此，对其进行准确的接触应力分析至关重要。

接触应力的分析主要基于弹性力学、材料力学和摩擦学的基本理论。

弹性力学是研究弹性体在外力作用下变形和应力分布规律的学科。

在直齿轮接触问题中，通常假设齿轮材料为线性弹性材料，满足胡克定律。

齿轮在啮合过程中，由于接触力的作用，齿面会产生弹性变形，进而产生接触应力。

材料力学是研究材料在受力作用下的应力、应变和强度等性能表现的学科。

对于直齿轮，材料的选择对齿轮的接触应力分布和承载能力有重要影响。

通常，齿轮材料需要具备较高的弹性模量、屈服强度和疲劳强度等。