最新stata初级入门5线性回归模型估计
- 格式:ppt
- 大小:1.14 MB
- 文档页数:45

stata中预测值命令Stata中预测值命令是数据分析中常用的功能之一,它可以根据已有的数据模型,利用模型参数对新的数据进行预测。
本文将介绍Stata中常用的预测值命令,并结合实例说明如何使用这些命令进行预测分析。
一、回归模型预测在Stata中,最常用的预测命令是regress或areg,它们用于估计回归模型的参数,并可以通过predict命令生成预测值。
例如,我们可以使用以下命令估计一个简单的线性回归模型:```regress y x```其中,y是因变量,x是自变量。
估计完成后,我们可以使用以下命令生成预测值:```predict yhat```这样,Stata会生成一个新的变量yhat,其中包含了根据回归模型预测的y的值。
二、时间序列预测Stata也提供了一些专门用于时间序列分析的命令,如arima、arma 等。
这些命令可以用于估计时间序列模型的参数,并生成预测值。
例如,我们可以使用以下命令估计一个ARIMA模型:```arima y, arima(1,1,1)```估计完成后,我们可以使用以下命令生成预测值:```predict yhat, dynamic(n)```其中,n是我们希望预测的时间点的个数。
Stata会生成一个新的变量yhat,其中包含了根据ARIMA模型预测的y的值。
三、分类模型预测除了回归和时间序列模型,Stata还可以用于分类模型的预测。
例如,我们可以使用以下命令估计一个logistic回归模型:```logit y x```估计完成后,我们可以使用以下命令生成预测值:```predict yhat, p```这样,Stata会生成一个新的变量yhat,其中包含了根据logistic 回归模型预测的y的概率。
四、交互效应预测在一些情况下,我们需要考虑自变量之间的交互效应。
Stata提供了一些命令用于估计交互效应模型,并生成预测值。
例如,我们可以使用以下命令估计一个包含交互效应的回归模型:```regress y x1 x2 x1*x2```估计完成后,我们可以使用以下命令生成预测值:```predict yhat```Stata会生成一个新的变量yhat,其中包含了根据包含交互效应的回归模型预测的y的值。
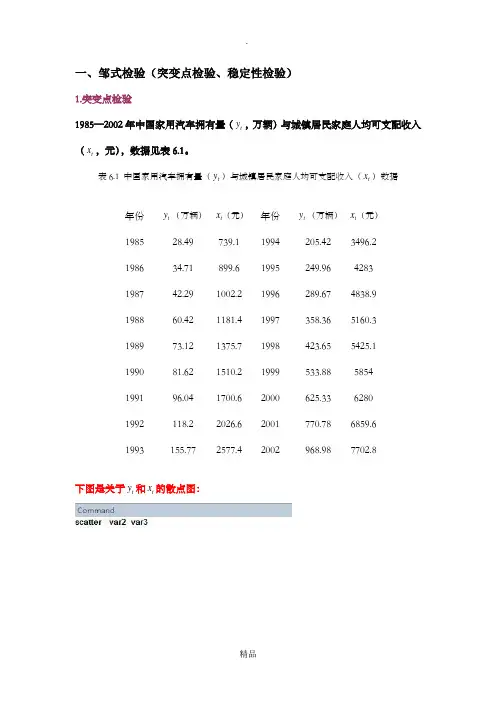
一、邹式检验(突变点检验、稳定性检验)1.突变点检验1985—2002年中国家用汽车拥有量(t y ,万辆)与城镇居民家庭人均可支配收入(t x ,元),数据见表6.1。
表6.1 中国家用汽车拥有量(t y )与城镇居民家庭人均可支配收入(t x )数据年份 t y (万辆) t x (元)年份 t y (万辆) t x (元)1985 28.49 739.1 1994 205.42 3496.2 1986 34.71 899.6 1995 249.96 4283 1987 42.29 1002.2 1996 289.67 4838.9 1988 60.42 1181.4 1997 358.36 5160.3 1989 73.12 1375.7 1998 423.65 5425.1 1990 81.62 1510.2 1999 533.88 5854 1991 96.04 1700.6 2000 625.33 6280 1992 118.2 2026.6 2001 770.78 6859.6 1993155.772577.42002968.987702.8下图是关于t y 和t x 的散点图:从上图可以看出,1996年是一个突变点,当城镇居民家庭人均可支配收入突破4838.9元之后,城镇居民家庭购买家用汽车的能力大大提高。
现在用邹突变点检验法检验1996年是不是一个突变点。
H0:两个字样本(1985—1995年,1996—2002年)相对应的模型回归参数相等H1:备择假设是两个子样本对应的回归参数不等。
在1985—2002年样本范围内做回归。
在回归结果中作如下步骤(邹氏检验):1、Chow 模型稳定性检验(lrtest)用似然比作chow检验,chow检验的零假设:无结构变化,小概率发生结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* 用似然比检验检验结构没有发生变化的约束得到结果如下;(如何解释?)2.稳定性检验(邹氏稳定性检验)以表6.1为例,在用1985—1999年数据建立的模型基础上,检验当把2000—2002年数据加入样本后,模型的回归参数时候出现显著性变化。

stata中最小二乘法最小二乘法(Ordinary Least Squares, OLS)是一种常见的回归分析方法,用于估计线性回归模型的参数。
该方法通过最小化观测值与模型预测值之间的残差平方和来找到最佳的模型参数估计值。
在接下来的内容中,我们将详细介绍最小二乘法的原理、应用、计算方法以及在Stata软件中的实际操作。
最小二乘法的原理最小二乘法的原理基于残差平方和的最小化。
在一个线性回归模型中,我们假设因变量Y与自变量X之间存在线性关系,即Y = βX + ε,其中β是系数,ε是误差项。
最小二乘法的目标是找到最佳的β估计值,使得实际观测值与模型预测值之间的残差平方和最小化。
具体来说,最小二乘法通过求解以下最小化问题来得到β的估计值:min Σ(yi - βxi)²其中,yi是第i个观测值的因变量取值,xi是第i个观测值的自变量取值。
通过对上述问题进行求导,可以得到最小二乘法的估计公式:β = (Σ(xi - x̄)(yi - ȳ)) / (Σ(xi - x̄)²)其中,x̄和ȳ分别是自变量X和因变量Y的均值。
上述公式即为最小二乘法的估计公式,用于估计线性回归模型的系数。
最小二乘法的应用最小二乘法在统计学和经济学中被广泛应用于线性回归模型的参数估计。
例如,我们可以使用最小二乘法来估计收入与消费之间的关系、股票价格与市盈率之间的关系、甚至是生产成本与产量之间的关系。
通过最小二乘法,我们可以得到线性回归模型的系数估计值,从而确定自变量对因变量的影响程度。
此外,最小二乘法也常用于时间序列分析和面板数据分析中。
在时间序列分析中,我们可以使用最小二乘法来估计变量随时间变化的趋势和季节性影响;在面板数据分析中,最小二乘法可以用来估计不同个体或单位之间的差异和影响因素。
最小二乘法的计算方法在实际应用中,最小二乘法的计算通常通过矩阵运算来进行。
对于简单的一元线性回归模型,最小二乘法的计算比较简单,只需要计算自变量X和因变量Y的均值,然后代入上述的估计公式即可得到系数的估计值。


一、Stata简介Stata是一款统计分析软件,广泛应用于社会科学和健康科学领域。
其强大的数据分析功能和直观的操作界面深受用户喜爱。
在Stata中,回归分析是常见的统计方法之一,通过回归分析可以探究自变量和因变量之间的关系,进而进行预测和解释。
二、回归系数估计回归分析中,我们经常关注的是回归系数的估计值。
回归系数代表了自变量对因变量的影响程度,是回归分析的核心参数之一。
在Stata 中,我们可以通过命令来计算回归系数的估计值,从而进行数据分析和解释。
三、命令输入在Stata中,计算回归系数估计值的命令非常简单,一般为“regress”命令,具体格式为:```regress dependent_variable independent_variable1 independent_variable2…```其中,dependent_variable代表因变量,independent_variable1、independent_variable2等代表自变量。
通过输入这样的命令,Stata 会自动进行回归分析并输出回归系数的估计值。
四、命令解释1. dependent_variable:因变量是回归分析中必不可少的部分,它代表了我们要探究的现象或变量。
在Stata中,这一部分通常是一个连续型变量。
2. independent_variable1、independent_variable2…:自变量则是我们用来解释因变量的变量,可以是一个或多个。
自变量可以包括连续型变量和分类变量。
五、命令示例为了更好地理解如何使用“regress”命令计算回归系数估计值,以下是一个具体的命令示例:```regress height weight age```在这个示例中,我们想要探究身高(height)和体重(weight)对芳龄(age)的影响。
通过输入上述命令,Stata会对这些变量进行回归分析并输出相应的回归系数估计值。

stata估计的斜率系数
在 Stata 中,可以使用各种回归命令来估计斜率系数。
下面是一个示例,说明如何使用 Stata 估计线性回归模型的斜率系数:
假设我们有一个名为`mpg`的数据集,其中包含了汽车的燃料效率(`mpg`)和汽车的重量(`weight`)等变量。
首先,我们可以使用`regress`命令进行简单线性回归,估计燃料效率与汽车重量之间的关系:
```stata
regress mpg weight
```
执行上述命令后,Stata 会输出回归的结果,包括斜率系数的估计值。
如果需要查看斜率系数的具体数值,可以使用以下命令:
```stata
display _b[weight]
```
这将显示回归模型中`weight`变量的斜率系数估计值。
如果回归模型中包含多个自变量,你可以使用`_b[varname]`来查看特定变量的斜率系数。
需要注意的是,斜率系数的估计值会受到数据、模型设定和估计方法等因素的影响。
在分析结果时,应结合实际背景和统计推断来解释斜率系数的意义。
此外,Stata 还提供了其他回归命令和选项,可以根据具体的研究问题和数据特点选择合适的方法来估计斜率系数。
如果你有特定的 Stata 命令或数据集,请提供更多细节,我将尽力帮助你估计斜率系数。

简单线性回归模型的公式和参数估计方法以及如何利用模型进行数据预测一、简单线性回归模型的公式及含义在统计学中,线性回归模型是一种用来分析两个变量之间关系的方法。
简单线性回归模型特指只有一个自变量和一个因变量的情况。
下面我们将介绍简单线性回归模型的公式以及各个参数的含义。
假设我们有一个自变量X和一个因变量Y,简单线性回归模型可以表示为:Y = α + βX + ε其中,Y表示因变量,X表示自变量,α表示截距项(即当X等于0时,Y的值),β表示斜率(即X每增加1单位时,Y的增加量),ε表示误差项,它表示模型无法解释的随机项。
通过对观测数据进行拟合,我们可以估计出α和β的值,从而建立起自变量和因变量之间的关系。
二、参数的估计方法为了求得模型中的参数α和β,我们需要采用适当的估计方法。
最常用的方法是最小二乘法。
最小二乘法的核心思想是将观测数据与模型的预测值之间的误差最小化。
具体来说,对于给定的一组观测数据(Xi,Yi),我们可以计算出模型的预测值Yi_hat:Yi_hat = α + βXi然后,我们计算每个观测值的预测误差ei:ei = Yi - Yi_hat最小二乘法就是要找到一组参数α和β,使得所有观测值的预测误差平方和最小:min Σei^2 = min Σ(Yi - α - βXi)^2通过对误差平方和进行求导,并令偏导数为0,可以得到参数α和β的估计值。
三、利用模型进行数据预测一旦我们估计出了简单线性回归模型中的参数α和β,就可以利用这个模型对未来的数据进行预测。
假设我们有一个新的自变量的取值X_new,那么根据模型,我们可以用以下公式计算对应的因变量的预测值Y_new_hat:Y_new_hat = α + βX_new这样,我们就可以利用模型来进行数据的预测了。
四、总结简单线性回归模型是一种分析两个变量关系的有效方法。
在模型中,参数α表示截距项,β表示斜率,通过最小二乘法估计这些参数的值。

stata面板数据re模型回归结果解释Stata是一种统计分析软件,可用于面板数据的回归分析。
在使用Stata进行面板数据的回归模型分析时,常见的面板数据回归模型是随机效应模型(Random Effects Model)和固定效应模型(Fixed Effects Model)。
回归结果解释通常包括以下几个方面:1. 模型拟合度:回归结果中的R-squared(决定系数)可以用来衡量模型对观测数据的拟合程度。
R-squared越接近1,说明模型对数据的解释能力越强。
2. 系数估计:回归结果中的各个系数估计值表示自变量与因变量之间的关系。
系数的正负和显著性可以告诉我们自变量对因变量的影响方向和程度。
通常,系数的显著性可以通过查看t统计量或者P值来确定。
显著性水平一般为0.05或0.01,如果P值小于显著性水平,则表示该系数是显著的。
3. 解释变量:回归结果中可能包含多个解释变量,每个解释变量的系数表示该变量对因变量的影响。
系数的正负可以告诉我们该变量对因变量的影响方向,而系数的大小可以表示该变量对因变量的影响程度。
4. 控制变量:回归模型中可能还包含一些控制变量,这些变量用于控制其他可能对因变量产生影响的因素。
通过控制这些变量,可以更准确地评估自变量对因变量的影响。
5. 随机效应和固定效应:如果采用了随机效应模型,回归结果中可能会显示随机效应的方差或标准差。
这些参数可以用来评估不同个体之间的随机差异。
而固定效应模型则将个体固定效应纳入考虑,回归结果中可能包括各个个体的固定效应系数。
6. 模型诊断:在解释回归结果时,还需要进行模型诊断,以评估回归模型是否满足模型假设。
常见的模型诊断包括残差分析、异方差性检验、多重共线性检验等。
需要注意的是,面板数据回归模型的解释需要结合具体的研究背景和问题进行分析,确保结果的可靠性和有效性。
同时,了解Stata软件的使用方法和相关统计知识也是进行面板数据回归分析的基础。

线性回归计算方法及公式线性回归是一种用于建立连续变量之间关系的统计模型。
它假设变量之间存在线性关系,并且通过最小化预测值和实际观测值之间的差异来确定最佳拟合线。
在本篇文章中,我们将讨论线性回归的计算方法和公式。
线性回归模型的数学表示如下:Y=β0+β1*X1+β2*X2+...+βn*Xn+ε在上述公式中,Y表示我们要预测的因变量,X1到Xn表示自变量,β0到βn表示线性回归模型的回归系数,ε表示误差项。
线性回归的目标是找到最佳拟合线,使预测值和实际值之间的平方差最小化。
最常用的方法是普通最小二乘法(Ordinary Least Squares, OLS)。
它通过最小化残差平方和来确定回归系数的最佳值。
残差(Residual)指的是观测值与预测值之间的差异。
残差平方和(Residual Sum of Squares, RSS)表示所有残差平方的总和。
OLS的目标是通过最小化RSS来找到最佳的回归系数。
要计算OLS,我们需要以下步骤:1.准备数据:收集自变量和因变量的数据。
2.设定模型:确定线性回归模型的形式。
3.拟合模型:使用OLS估计回归系数。
4.评估模型:根据一些指标评估模型的表现。
下面我们将详细描述上述步骤。
1.准备数据:收集自变量和因变量的数据。
确保数据集包含足够的样本数量和各种数值。
常见的方法是通过观察和实验来收集数据。
2.设定模型:确定线性回归模型的形式。
根据问题的背景和数据的特点,选择适当的自变量和因变量。
确保自变量之间没有高度相关性(多重共线性)。
3.拟合模型:使用OLS估计回归系数。
OLS的公式为:β=(X^T*X)^(-1)*X^T*Y其中,β是回归系数矩阵,X是自变量矩阵,Y是因变量矩阵,并且^T表示矩阵的转置,^(-1)表示矩阵的逆。
4. 评估模型:根据一些指标评估模型的表现。
常见的评估指标包括均方误差(Mean Squared Error, MSE)、判定系数(Coefficient of Determination, R^2)、残差分析等。
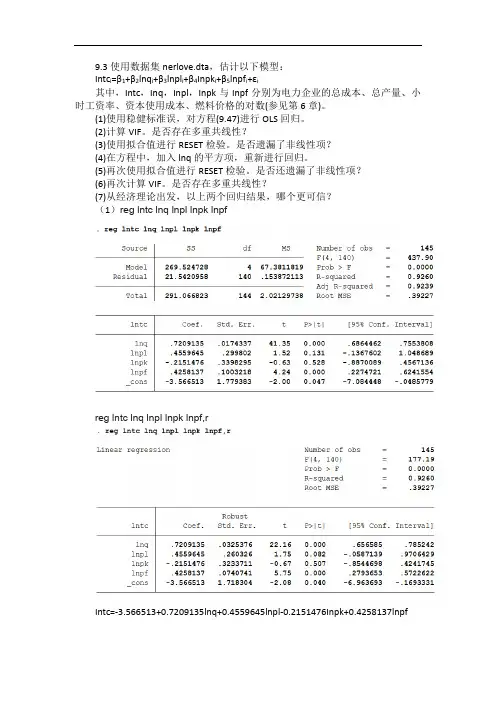
9.3使用数据集nerlove.dta,估计以下模型:
Intc i=β1+β2lnq i+β3lnpl i+β4Inpk i+β5lnpf i+εi
其中,Intc,Inq,Inpl,Inpk与Inpf分别为电力企业的总成本、总产量、小时工资率、资本使用成本、燃料价格的对数(参见第6章)。
(1)使用稳健标准误,对方程(9.47)进行OLS回归。
(2)计算VIF。
是否存在多重共线性?
(3)使用拟合值进行RESET检验。
是否遗漏了非线性项?
(4)在方程中,加入lnq的平方项,重新进行回归。
(5)再次使用拟合值进行RESET检验。
是否还遗漏了非线性项?
(6)再次计算VIF。
是否存在多重共线性?
(7)从经济理论出发,以上两个回归结果,哪个更可信?
(1)reg lntc lnq lnpl lnpk lnpf
reg lntc lnq lnpl lnpk lnpf,r
Intc=-3.566513+0.7209135lnq+0.4559645lnpl-0.2151476Inpk+0.4258137lnpf
(2)
最大VIF为1.21,远小于10,故不必担心存在多重共线性。
(3)
遗漏了非线性项。
(4)
Intc=-0.1627064+0.1166562lnq+0.536124lnq2+0.0206146lnpl-0.568725Inpk+0. 4804816lnpf
(5)
没遗漏了非线性项。
(6)
最大VIF为22.21,远大于10,故存在多重共线性。
(7)第一个更可信。

stata有序逻辑回归模型(最新版)目录1.介绍有序逻辑回归模型2.有序逻辑回归模型的假设和原理3.有序逻辑回归模型的步骤4.有序逻辑回归模型的应用实例5.总结正文一、介绍有序逻辑回归模型有序逻辑回归模型(Ordered Logistic Regression Model)是一种用于解决有序变量问题的统计分析方法。
它基于 Logistic 回归模型,但可以处理有序变量,如等级评分、排名等。
在社会学、心理学、医学等领域,研究者经常需要对这类有序变量进行分析,因此有序逻辑回归模型具有很高的实用价值。
二、有序逻辑回归模型的假设和原理1.假设:有序逻辑回归模型假设自变量与因变量之间存在线性关系,且因变量为有序变量。
2.原理:有序逻辑回归模型通过引入虚拟变量,将有序变量转换为多个二分类变量,然后运用 Logistic 回归模型进行分析。
具体操作包括:对每个有序变量类别的中点进行赋值,计算每个类别的累计概率,并以此作为虚拟变量的取值。
最后,利用 Logistic 回归模型估计参数,并根据参数解释变量对因变量的影响。
三、有序逻辑回归模型的步骤1.确定因变量为有序变量,并确定变量类别。
2.计算每个类别的累计概率,并计算虚拟变量。
3.运行 Logistic 回归模型,得到参数估计值。
4.根据参数估计值,解释自变量对因变量的影响。
5.检验模型的拟合度,如使用拟合优度(R)等指标。
四、有序逻辑回归模型的应用实例以学生学习成绩为例,研究者关心学生成绩等级(优秀、良好、及格、不及格)与学习时间、学习方法等因素之间的关系。
通过有序逻辑回归模型,可以分析这些因素如何影响学生成绩等级。
五、总结有序逻辑回归模型是一种有效的分析有序变量问题的方法,通过引入虚拟变量,将有序变量转换为多个二分类变量,然后运用 Logistic 回归模型进行分析。
第1页共1页。
STATA 回归估计常见问题及解决方法一、多重共线问题//多重共线性并不会改变OLS估计量BULE的性质,但会使得对系数的估计变得不准确。
//Stata检查是否存在多重共线的方法:estat vif//VIF值越大说明多重共线性问题越严重。
一般认为,最大的VIF不超过10,则不存在明显的多重共线性。
/*解决办法:1.如果只关心方程的预测能力,则在整个方程显著的条件下,可以不必关心具体的回归系数。
2.增加样本容量,剔除导致多重共线性的变量或者修改模型设定形式。
3.对于时间序列样本,通过使用差分模型可以一定程度上消除原模型中的多重共线性。
4.岭回归方法。
二、序列相关问题/*Stata检查是否存在序列相关的方法:1.画图在做完回归之后,先生成残差项escatter e L.e2.BG检验estat bgodfrey(默认滞后阶数为1)3.Ljung-Box Q检验eg: reg y x1 x2 x3predict e,reswntestq e3.DW检验estat dwatson解决办法:1.Newey稳健性标准差newey y x,lag(p) (滞后阶数必选)2.可行广义最小二乘法(FGLS)prais y xprais y x,corc三、异方差问题Stata检查是否存在异方差的方法:1.看残差图【模型回归之后使用即可】rvfplot(残差与拟合值的散点图)rvpplot(残差与解释变量的的散点图)2.怀特(White,1980)检验【模型回归之后使用即可】estat imtest,white(怀特检验)whitetst(外源程序,需下载)3.BP(Breusch and Pagan,1979)检验【模型回归之后使用即可】estat hettest(默认设置使用拟合值y_hat)estat hettest(使用方程邮编的解释变量,而不是y_hat)estat hettest varlist(指定使用某些解释变量)解决办法:1.WLS加权最小二乘法reg y x1 x2 x3 [aw=1/var]eg: reg y x1 x2 x3predict e1,resg e2=e1^2g lne2=log(e2)reg lne2 y,nocpredict lne2fg e2f=exp(lne2f)reg y x1 x2 x3 [aw=1/e2f]2.White(1980)eg: reg y x1 x2 x3,robust3. wls0命令。
计量经济学基础线性回归与OLS估计线性回归是计量经济学中重要的经济分析工具之一,它对观测数据的统计关系进行建模。
OLS(Ordinary Least Squares)估计是一种常见的线性回归参数估计方法,它通过最小化观测数据的残差平方和来获得参数的估计值。
一、线性回归模型线性回归模型基于以下假设:存在一个线性关系,将自变量X的线性组合与因变量Y联系起来。
该模型可以表示为:Y = β0 + β1X1 + β2X2 + … + βkXk + ε其中,Y是因变量,X1、X2、…、Xk是自变量,β0、β1、β2、…、βk是待估计的参数,ε是误差项。
二、最小二乘法OLS估计根据最小二乘法的原理,通过最小化残差平方和来获得参数的估计值。
残差定义为观测值与模型估计值之间的差异,残差平方和则是所有残差平方的总和。
最小二乘估计的目标是找到最优的参数估计值,使得残差平方和最小。
为了实现这一目标,我们需要计算出各个参数的最优估计值。
具体计算方法如下:1. 计算回归系数的估计值回归系数的估计值可以通过以下公式计算:β̂j = Σ(xi - x)(yi - ȳ) / Σ(xi - x)²其中,β̂j是第j个回归系数的估计值,xi是第i个自变量的观测值,x是自变量的均值,yi是因变量的观测值,ȳ是因变量的均值。
2. 计算截距项的估计值截距项的估计值可以通过以下公式计算:β̂0 = ȳ - β̂1x1 - β̂2x2 - … - β̂k x k其中,β̂0是截距项的估计值。
三、OLS估计的性质OLS估计具有以下几个重要性质:1. 无偏性在满足线性回归模型的假设下,OLS估计是无偏的,即估计值的期望等于真实参数值。
2. 有效性在满足线性回归模型的假设下,OLS估计是最佳线性无偏估计,其方差最小。
3. 一致性当样本容量趋向于无穷大时,OLS估计是一致的,即估计值趋近于真实参数值。
四、OLS估计的假设OLS估计依赖于一些重要的假设:1. 线性关系假设线性回归模型假设因变量与自变量之间存在线性关系。
Stata实证稳健标准误回归模型一、前言在经济学和统计学研究中,回归分析是一种常用的方法,用于研究变量之间的关系。
然而,在进行回归分析时,我们常常会面对一些问题,比如数据的异方差性(heteroskedasticity)和数据的多重共线性(multicollinearity)等。
为了解决这些问题,研究者们引入了稳健标准误的概念,其中Stata实证稳健标准误回归模型就是其中之一。
二、Stata实证稳健标准误回归模型的定义Stata实证稳健标准误回归模型是一种在回归分析中应用的统计方法,它的主要特点是对数据的异方差性和多重共线性进行了有效的处理,从而得到了更为准确和稳健的结果。
在Stata中,可以通过使用特定的命令和选项来进行实证稳健标准误回归模型的估计和检验。
三、Stata实证稳健标准误回归模型的优点1. 解决异方差性和多重共线性:Stata实证稳健标准误回归模型通过对数据进行有效的修正,可以有效解决数据的异方差性和多重共线性问题,从而得到更为准确和可靠的结果。
2. 提高回归模型的稳健性:Stata实证稳健标准误回归模型可以使回归模型更为稳健,减少外生干扰的影响,提高模型的预测能力。
3. 适用范围广泛:Stata实证稳健标准误回归模型适用于各种类型的数据和研究领域,包括经济学、金融学、社会学等。
四、Stata实证稳健标准误回归模型的应用步骤1. 数据准备:首先需要准备好需要进行回归分析的数据,包括自变量和因变量等。
2. 设置Stata选项:在进行回归分析前,需要设置Stata的选项,使用特定的命令和选项来进行实证稳健标准误回归模型的估计和检验。
3. 进行回归分析:通过Stata软件进行回归分析,得到模型的参数估计、拟合优度等统计指标。
4. 检验模型假设:对回归模型的参数估计结果进行检验,包括异方差性和多重共线性的检验。
5. 解释回归结果:对回归结果进行解释和分析,得出结论并进行相关的推断和预测。
五、Stata实证稳健标准误回归模型的实例分析为了更好地说明Stata实证稳健标准误回归模型的应用,我们以某实证研究为例进行具体的分析。
stata基础回归命令Stata基础回归命令回归分析是统计学中常用的一种分析方法,用于研究变量之间的关系。
Stata是一种流行的统计软件,提供了丰富的回归分析功能。
本文将介绍Stata中的基础回归命令,并以实例演示其使用方法。
一、简单线性回归命令简单线性回归是回归分析中最简单的一种形式,用于研究两个变量之间的线性关系。
在Stata中,可以使用regress命令进行简单线性回归分析。
例如,我们有一个数据集,包含了变量Y和变量X,我们想要研究Y和X之间的关系。
我们可以使用以下命令进行简单线性回归分析:regress Y X其中,Y是因变量,X是自变量。
执行该命令后,Stata会输出回归结果,包括回归系数、标准误差、t值、p值等信息。
二、多元线性回归命令多元线性回归是回归分析中常用的一种形式,用于研究多个自变量对因变量的影响。
在Stata中,可以使用regress命令进行多元线性回归分析。
例如,我们有一个数据集,包含了因变量Y和自变量X1、X2、X3,我们想要研究这些自变量对Y的影响。
我们可以使用以下命令进行多元线性回归分析:regress Y X1 X2 X3执行该命令后,Stata会输出回归结果,包括各个自变量的回归系数、标准误差、t值、p值等信息。
三、加入控制变量的回归命令在实际研究中,我们常常需要控制其他变量的影响,以准确评估自变量对因变量的影响。
在Stata中,可以使用regress命令加入控制变量。
例如,我们有一个数据集,包含了因变量Y、自变量X和控制变量Z,我们想要研究X对Y的影响,并控制Z的影响。
我们可以使用以下命令进行回归分析:regress Y X Z执行该命令后,Stata会输出回归结果,包括X的回归系数、标准误差、t值、p值等信息。
四、回归诊断命令回归分析不仅包括了回归系数的估计,还需要对回归模型进行诊断,以评估模型的拟合优度和假设的满足程度。
在Stata中,可以使用一系列命令进行回归诊断。
Stata面板数据回归分析的步骤和方法哎哟,说起Stata面板数据回归分析,我这心里就直发痒。
我这人就是喜欢琢磨这些个数字,特别是这面板数据,看着就亲切。
来来来,咱们就坐在这,我给你掰扯掰扯这回归分析的步骤和方法。
首先啊,你得准备数据。
这数据啊,得是面板数据,就是横着竖着都是数据。
你得把数据导进Stata里头,看着那一排排数字,心里就得有谱,知道这数据从哪儿来,将来要干啥用。
然后啊,咱们先得把数据整理一下。
Stata里有那么多命令,咱们得用上“xtset”这个命令,告诉Stata这是面板数据。
然后呢,就得看看数据有没有问题,比如有没有缺失值啊,有没有异常值啊。
这就像咱们做人,也得讲究个整洁,别邋里邋遢的。
接下来啊,咱们得确定模型。
面板数据回归模型有好几种,比如说固定效应模型、随机效应模型,还有混合效应模型。
你得根据实际情况来选择。
就像做菜,得看你要做什么菜,是做炒菜还是炖菜。
选好了模型,那就得建模型了。
Stata里有“xtreg”这个命令,专门干这个活。
你把数据输入进去,再指定你的模型,Stata就帮你算出来了。
就像咱们孩子写作业,咱们给他点拨点拨,他就写得有模有样了。
算完模型,就得检验。
这就像咱们看完电影,得聊聊感想。
检验模型,就是看这个模型有没有问题,比如有没有多重共线性啊,残差有没有自相关啊。
这就像咱们吃饭,得看看吃得饱不饱,营养均衡不均衡。
最后啊,你得解释结果。
这结果啊,得结合实际情况来说。
就像咱们买衣服,得看合不合身。
解释结果,就是要看这些数字背后的故事,看看这些数据能告诉我们什么。
哎呀,说起来这Stata面板数据回归分析,真是门学问。
得有耐心,得有细心,还得有恒心。
就像咱们种地,得用心浇灌,才能收获满满。
好啦,我这就唠叨这么多了。
你要是想学这玩意儿,得多看多练。
就像咱们学说话,得多说多练,才能说得溜。
来来来,咱们下次再聊聊其他的话题。