第七章 频响函数及相干分析

传递函数频响函数频响函数（Frequency Response Function，简称FRF）是指系统对输入信号频率变化的响应情况，通常描述为系统的输出幅度和相位随输入频率变化的函数。

频响函数可用于研究系统的稳定性、动态响应和频率特性等。

频响函数一般表示为H(ω)，其中ω表示角频率。

频响函数可以分解为幅度响应H(ω)和相位响应φ(ω)两部分，即H(ω)=，H(ω)，e^(jφ(ω))。

其中，H(ω)，表示幅度响应，是输入信号经过系统后的输出信号的幅度相对于输入信号的幅度的比值，单位为分贝（dB）。

相位响应φ(ω)表示输出信号与输入信号之间的相位差。

频响函数的重要性在于可以帮助我们了解系统对不同频率输入信号的响应情况。

通过分析频响函数，我们可以判断系统是否能够适应所需的频率范围，以及在不同频率下的增益和相位变化。

在工程实际中，我们经常使用频响函数进行系统设计和分析。

下面就来介绍一些常用的传递函数和它们的频响函数表达式：1. 一阶惯性环节的传递函数为H(ω) = K/(jωT+1)，其中K为增益，T为时间常数。

对应的频响函数为，H(ω)，= K/√(1+(ωT)^2)和φ(ω) = -arctan(ωT)。

该传递函数常用于描述具有惯性的系统，如机械系统的动态响应。

2. 二阶系统的传递函数可以分为三类：欠阻尼、临界阻尼和过阻尼。

欠阻尼二阶系统的传递函数为H(ω) = K/((jω)^2+2ξωn(jω)+ωn^2)，其中K为增益，ξ为阻尼比，ωn为自然频率。

对应的频响函数为，H(ω)，= K/√((1-(ω/ωn)^2)^2+(2ξω/ωn)^2)和φ(ω) = -arctan((2ξω/ωn)/(1-(ω/ωn)^2))。

欠阻尼系统常用于描述振动系统，如机械臂的振动响应。

3. 在控制系统中，常用的传递函数包括比例控制器、积分控制器和微分控制器等。

比例控制器的传递函数为H(ω) = Kp，其中Kp为比例增益。

第七章频响函数及相干分析在信号处理领域中，频响函数及相干分析是非常重要的概念和工具。

频响函数是描述信号在频域上响应特性的函数，而相干分析则是用来研究信号之间的相关性和相关性随频率的变化规律。

1.频响函数频响函数是描述信号在频域上的响应特性的函数。

它可以是一个复数函数，表示信号在不同频率上的幅度和相位变化，也可以是一个实数函数，只表示信号的幅度变化。

常见的频响函数包括：-幅度响应函数：表示信号在不同频率上的幅度变化。

常用的表达方式有dB值和增益值。

在实际应用中，我们通常更关注信号的幅度响应，因为它反映了信号在传输过程中是否发生了衰减或放大。

-相位响应函数：表示信号在不同频率上的相位变化。

相位响应通常用角度表示，取值范围为-180°到180°，其表示不同频率上信号的相对延迟。

频响函数是非常重要的，因为它能帮助我们了解信号在不同频率上的响应特性，对信号的传输、放大以及滤波等处理过程有着重要的指导作用。

2.相干分析相干分析是用来研究信号之间的相关性和相关性随频率的变化规律的方法。

在信号处理中，我们经常需要了解不同信号之间的相互关系，相干分析就是用来帮助我们进行相关性的分析和判断。

相干分析可以帮助我们了解信号之间的相干性质，即它们在时间上的相关性以及在频率上的相关性。

通过相干分析，我们可以定量地描述不同信号之间的相关程度，并判断它们之间是否存在一定的关联关系。

相干分析常用的工具包括：-自相关函数：用于衡量信号在不同时间点上的自相关性。

自相关函数的值表示信号在不同时间点上与自身的相关程度。

-互相关函数：用于衡量两个信号之间的相关性。

互相关函数的值表示不同信号之间的相关程度。

-相干函数：用于衡量两个信号之间的相干性。

相干函数是互相关函数的归一化形式，其取值范围为0到1通过相干分析，我们可以深入了解信号之间的相关性，并对信号之间的相关关系进行量化和度量。

这对于信号处理领域的许多应用如通信、信号传输以及信号分析等都有着非常重要的意义。

计算频响函数和相干函数频响函数是指一些系统对于输入信号的不同频率成分的增益或衰减情况。

相干函数则是描述两个信号在时间上的相关性。

1.频响函数频响函数是描述系统对信号不同频率成分的响应情况的重要指标。

通过对信号的频谱进行分析，我们可以得到系统对不同频率的增益或衰减情况。

频响函数可以表示为H(f)，其中f表示频率。

频响函数通常用复数表示，具有幅度和相位两个部分。

幅度是指信号在通过系统时的增益或衰减情况。

通常以分贝（dB）为单位进行表示。

若系统的频响函数为H(f)，则幅度响应可以表示为，H(f)。

相位是指信号在通过系统时的相位变化情况。

相位响应可以表示为∠H(f)。

频响函数描述了系统对不同频率成分的影响，对于系统的建模和分析具有重要作用。

利用频响函数，我们可以预测系统对不同频率输入信号的输出情况，从而更好地设计和调节系统。

2.相干函数相干函数是描述两个信号在时间上的相关性的度量指标。

如果两个信号在一些时刻上有相同的变化趋势，我们可以认为它们是相关的；如果两个信号在一些时刻上有相反的变化趋势，我们可以认为它们是不相关的。

相干函数可以表示为C(t)，其中t表示时间延迟。

相干函数通常用复数表示，具有幅度和相位两个部分。

幅度是指两个信号之间的相关程度，通常以0到1之间的值进行表示。

如果两个信号完全相关，幅度为1；如果两个信号完全不相关，幅度为0。

相位是指两个信号之间的相对时间延迟。

如果两个信号在一些时刻上同时达到峰值，则相位为0；如果两个信号在一些时刻上一个达到峰值，另一个达到谷值，则相位为180度。

相干函数可以帮助我们了解两个信号之间的相关性。

在信号处理和通信系统中，相干函数是重要的性能评估指标，对于信号的传输和处理具有指导意义。

总结：频响函数描述了系统对不同频率信号的增益或衰减情况，是系统建模和分析的重要工具。

相干函数描述了两个信号在时间上的相关性，是信号处理和通信系统中的重要性能指标。

通过频响函数和相干函数的分析，我们可以更好地理解和优化系统的性能，提高信号的传输质量和处理效果。

[频响]频响分析方法总结(总1页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--频响分析，或者叫稳态动力学分析在abaqus中包括以下三种方法：直接稳态动力学分析（direct solution steady state dynamic analysis）模态稳态动力学分析（mode based steady state dynamic analysis）子空间稳态动力学分析（subspace projection steady state dynamic analysis）1）直接稳态动力学优点：在直接稳态动力学分析中，系统的稳态谐波响应是通过对模型的原始方程直接积分计算出来的。

如果分析的对象存在非对称刚度、包含模态阻尼以外的其他阻尼或者必须考虑粘弹性材料特性（频变特性），则不能提取特征模态的情况下，可以应用直接法进行稳态响应的计算和分析。

缺点：进行直接稳态动力学分析不需要提取系统的特征模态，而是在每个频率点对整个模型进行复杂的积分运算。

因此，对于具有大阻尼和频变特性的模型，应用直接法比模态分析方法精确，但是耗时较多。

2）模态稳态动力学分析模态稳态动力学分析方法是基于模态叠加法求解系统的稳态响应。

因此，在求解稳态响应之前必须先提取无阻尼系统的特征模态，也就是在说必须在step steady state dynamics,modal前加一步step frequency。

另外，必须确定需要保留的特征模态，以确保能够精确描述系统的动力学特性，也就是说如果是进行0-1000hz的分析，step frequency的number of eigenvalues requested选定的阶数的模态频率必须大于1000hz，简单的作法是这里选all……，下面的maximum……填入1000。

模态稳态动力学分析的特点：相较于直接法和子空间法分析速度快，耗时最少，计算精度低于直接法和子空间法，不适合于分析具有大阻尼特性的模型，不适合于分析具有粘弹性材料（频变特性）的模型。

频响特性曲线_模态测试之频响函数在进⾏模态测试时，核⼼就是测试结构输⼊点到相应点的频响函数，最终通过各种算法从频响函数中提取我们所关注的信息(频率、阻尼、振型...)。

本⽂我们就详细探讨⼀下有关频响函数的问题。

1、什么是频响函数(FRF)频响函数定义为结构的输出响应和输⼊激励⼒之⽐。

将测试的时域数据转换到频率的数据后，数据会显⽰为复数形式(实部和虚部、幅值和相位)，测量的多条频响函数为了⽅便统计，通常以矩阵形式表⽰。

下标可以⽅便地确定某个FRF输⼊-输出的位置，频响函数中第⼀个下标表⽰输出响应位置，第⼆个下标表⽰输⼊激励位置，下标k表⽰阶数。

所以H ij表⽰由‘j’点输⼊引起‘i’点响应的频响函数。

FRF元素的分⼦中包含留数信息，与模态振型直接相关；分母包含极点信息，与频率和阻尼相关。

因此，从频响函数矩阵可以得到系统全部的模态信息。

将分⼦留数信息展开可得式中右侧⽅程，可以得出以下结论：l 通过⽅程中分⼦信息我们可以发现：留数的值与输⼊位置的模态振型值相关，不同输⼊-输出位置的留数值是不同的，即振型值不同，也就是说留数值(振型)具有局部性，在做⼤型模态试验时需要多布置响应点来拾取局部振型，从⽽把振型更好的表达出来。

l 通过⽅程中分母信息我们可以发现：分母中包含极点信息是保持不变，即极点信息(频率阻尼)不依赖于输⼊输出的位置。

理论上讲，在避开节点的情况下⼀个测量位置即可测量出所有的模态频率。

2、什么是频响函数具有哪些性质l 频响函数是系统的固有特性，与系统本⾝有关，与激励、响应等外界因素没有关系。

l 频响函数具有互易性，即Hij=Hji，也就是说，‘j’点单位激励⼒在‘i’点引起的响应等于‘i’点单位激励⼒在‘j’点引起的响应，说明频响函数矩阵是对称的。

l 频响函数是复值函数，因⽽可以⽤幅值与相位或者实部与虚部表⽰，因此频响函数具有幅频、相频和实频、虚频等多种表现形式。

当幅频曲线和相频曲线同时显⽰时，称为伯德图。

名词解释1量纲和谐：一个完整的物理方程中，各项的量纲必须相同，因此方程才能用加减，并用等号联系起来，该性质即量纲和谐。

P92.2频响函数：系统的频率响应函数（简称频响函数）是系统的响应与激励的复振幅之比，它是激励频率w（或f）的复函数P1813自功率谱：单位频带的功率随频率变化的情况，称之为X（t）的自功率谱密度函数，简称自功率谱或自谱。

P1724相干函数：常相干函数用gxy2(f)表示，其定义是如果相干函数为零,表示输出信号与输入信号不相干，那么，当相干函数为1时，表示输出信号与输入信号完全相干。

若相干函数在0~1之间，则表明有如下三种可能：(1）测试中有外界噪声干扰；(2）输出y(t)是输入x(t)和其它输入的综合输出；(3）联系x(t)和y(t)的线性系统是非线性的。

5桩身截面波阻抗：Z=ρ.A.C是桩身材料密度、截面积、和桩身一维弹性纵波速的乘积，称为桩身截面阻抗。

P2776相似准数：相似准数π把相似系统中的各物理量联系起来，说明他们之间的关系，故又称“模型律”。

P907传递函数：系统的传递函数可以定义为输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。

如果把振动系统的激振力f（t）看作输入量，把振动的位移响应x（t）看作输出量，则振动系统的传递函数定义为H（s）=X（s）/F（s）P2198频率混淆：波形采样定理一般通过模数转换电路（A/D）来完成，采样率高，采样时间间隔小，如果缩短记录的时间长度，则可能产生较大的分析误差，采样率过低，即采样间隔过大，则离散的时间序列可能不足以反映原来信号的波形特征，频率分析会出现混淆现象P209 9正弦扫描激励：在扫描过程中，振动台的激励频率随着时间不断地变化，从而结构响应中的频率成份也随着时间而不断地变化，即结构响应信号是非平稳的。

这样，各种适用于非平稳信号分析的时频分析方法更加适合于正弦扫描振动试验结构响应分析。

P231 10:传感器的频率响应：在理想情况下，当所测振动的频率变化时，传感器的灵敏度应该不改变，但无论是传感器的机械系统还是机电转换系统都有一个频率响应问题，即灵敏度K随所测频率不同而有所变化，这个变化的规律就是传感器的频率响应。

频响分析是一种用来计算结构在稳态振动激励下的响应。

比如旋转的机器，不平衡的旋转的轮胎，或者直升机的机翼。

例如：旋转的机器，旋转的速度不同，频率不同；同时速度不同，力的幅值也不同，既力的幅值虽频率变化，频响分析的作用就是求出机器在不同的转速的状态下的响应。

在频响分析中，激励是频率的函数，在特定的频率下力已知。

激励力可以是载荷或者强迫振动（位移、速度或者加速度）。

力是时间的正弦函数F=A sin(ѡt+ф)
所有频响分析的激励都是这个形式，其中，A为幅值，是频率的函数；ф为初相位。

频响分析我们需要定义的就是这两个。

频响分析中使用复数描述力和响应。

位移的复数
力、速度、加速度等量的描述同上。

欧拉函数：e iѡt=cosѡt+i sinѡt
Natran中激励力的定义
RLOAD1 P(f)=A[C(f)+iD(f)]e i(θ−2πfτ)
RLOAD2 P(f)=AB(f)e i[ф(f)+θ−2πfτ]
比如，RLOAD1 A=1 C（f）=1 D(f)=0 τ=θ=0 那么就定义了一个幅值为1，不随频率而变
的激励力，F=sinѡt。

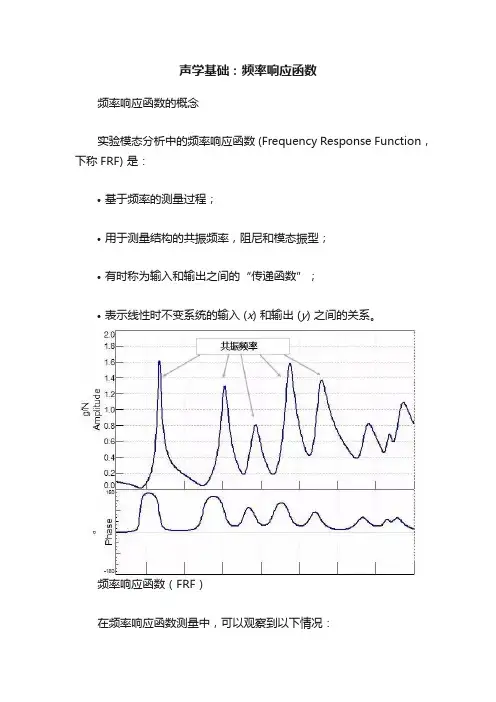
声学基础：频率响应函数频率响应函数的概念实验模态分析中的频率响应函数 (Frequency Response Function，下称FRF) 是：•基于频率的测量过程；•用于测量结构的共振频率，阻尼和模态振型；•有时称为输入和输出之间的“传递函数”；•表示线性时不变系统的输入 (x) 和输出 (y) 之间的关系。

频率响应函数（FRF）在频率响应函数测量中，可以观察到以下情况：•共振：峰值表示被测结构的固有频率；•阻尼：阻尼与峰的宽度成比例。

峰值越宽，阻尼越大；•模式振型：获取到结构上的公共参考的多个FRF的幅度和相位用于确定模式振型。

实验模态分析中频率响应函数许多类型的输入激励和响应输出可用于计算实验FRF，下面举一些例子：•声学系统：Q（体积加速度）输入和声压输出 (Pa)；•机械系统：输入为力，输出为加速度，速度或者位移；•上述两者的混合系统。

对于机械结构的实验模态分析，通常输入是力，输出是加速度，速度或位移。

输入及测量可以通过：•力锤•激振器输出响应可以通过如下方式测量：•加速度计：测量振动；•激光测振仪：测量物体表面速度。

一般来说，输入力的频谱(X)应该是平坦的，即均匀激励所有频率。

当查看响应(Y)时，响应中的峰值表示被测结构的自然/共振频率。

如下图所示。

因为FRF响应被“归一化”到输入，所以得到的FRF函数中的峰值是测试对象的共振频率。

FRF中的数字信号处理术语在命名法中，FRF通常由单个大写字母H表示。

输入为X 且输出为Y。

H，X和Y都是函数与频率的关系。

FRF是输入(x)和输出(y)的互功率谱(Sxy)除以输入的自功率谱(Sxx)。

自功率谱Sxx 是输入频谱与其自身的复共轭，它成为一个全实数函数，不包含相位。

互功率谱Sxy是输出频谱和输入频谱的复共轭，包含幅度和相位。

评估RFR的质量01计算Coherence相干性是函数与频率的关系，表示输出多少是由FRF中的输入引起的。

它可以作为FRF质量的指标，它能够评估FRF从测量到重复相同测量的一致性。

涉及到快速正弦扫描.百度文库“在模态试验时，频率响应函数的估计有三种估算形式，它们分别为： 第一估算式 1()()()fx ff G H G ωωω=第二估算式 2()()()xx xf G H G ωωω=第三估算式 2()()()xx a ff G H G ωωω=上面三个式子中的具体函数分别代表自谱和互谱函数。

还有一种计算方法，就是直接采用傅里叶变换转换到频率后，响应和输出相比。

在没有噪声污染的理想情况下，这三种估算形式是等价的。

实际上试验信号总会伴随噪声的存在，因此三种估算形式一般会有差异。

当只有响应信号受到噪声污染时，第一估算式为频响函数的真估计，第二、第三估算式均为频响函数的过估计；当只有激励信号受到噪声污染时，第二估算式为频响函数的真估计，第一、第三估算式均为频响函数的欠估计；激励和响应信号都受到噪声污染时，第一估算式为频响函数的欠估计，第二估算式为频响函数的过估计，第三估算式接近频响函数的真估计。

由三种情况可以看出，系统的频率响应函数是介于第一估算式和第二估算式之间，即12()()()H H H ωωω≤≤目前，高精度动态信号分析仪能同时给出三种估算式，则它们可以相互校核。

一般来说，在共振频率附近，响应信号强，激励信号弱，而弱信号的信噪比总是偏低，所以第二估算式比第一估算式更接近真值；而在反共振频率附近，响应信号较弱。

激励信号较强，第一估算式比第二估算式更接近真值。

现有一些分析仪一般只给出第一估算式，为了保证频响函数测量的可靠性，应同时测量相干函数。

相干函数()γω无论输入信号还是输出信号受到噪声污染时，它的值均小于1而大于零，即212()0()1()H H ωγωω≤=≤ 相干函数是描述系统输入与输出相关性的一个函数，如果测量的相干函数值偏小，说明我们测量的响应信号不完全是由激励引起的，可能还存在其它的激励或干扰，这时应分析干扰的来源；若测量的相干函数值接近1，则说明系统响应完全是由激励引起的。

传递函数频响函数频响函数是描述系统对输入信号中不同频率成分的响应情况的函数。

它可以用来分析信号在系统中的变化，从而对系统的性能进行评估和优化。

在信号处理和控制系统中，频响函数（也称为传递函数）是一个复数函数，它描述了输入信号在系统中通过后的变化。

通常，频响函数由两个部分组成：振幅响应和相位响应。

振幅响应表示系统对输入信号幅度的变化。

它描述了系统对不同频率成分的增益或衰减程度。

振幅响应通常使用幅度比表达，即输出信号的幅度与输入信号幅度之比。

振幅响应可以告诉我们系统在不同频率下对信号进行的放大或衰减程度。

例如，在音频系统中，我们可以使用频响函数来分析音频信号在不同频率下的放大或衰减程度，从而评估系统的音质。

相位响应表示系统对输入信号相位的变化。

它描述了系统对不同频率成分的相位偏移情况。

相位响应通常使用角度差表示，即输出信号的相位与输入信号相位之间的差值。

相位响应可以告诉我们系统对信号的相对时间延迟或提前程度。

在控制系统中，我们可以使用频响函数来分析系统对输入信号的相位变化，从而评估系统的稳定性和响应速度。

频响函数可以通过多种方式表示和分析。

一种常见的表示方式是极坐标表示，其中振幅响应和相位响应分别以幅度和角度的形式表示。

另一种常见的表示方式是复数表示，其中频响函数被表示为一个复数，其实部表示振幅响应，虚部表示相位响应。

频响函数的性质和特点对于系统设计和分析非常重要。

例如，频响函数可以用来评估系统在不同频率下的幅频特性和相频特性，从而确定系统的带宽和响应速度。

频响函数还可以用来设计滤波器，根据所需的频率响应特性，选择合适的滤波器类型和参数。

此外，频响函数还可以用来评估系统对噪声的抑制能力，对系统的稳定性和抗干扰性进行分析。

为了分析和处理频响函数，我们可以使用信号处理和控制理论中的一些基本工具和技术。

例如，傅里叶变换可以将时域信号转换为频域信号，从而分析信号的频率成分。

拉普拉斯变换可以将系统的微分方程转换为频域函数，从而分析系统的频响函数。

计算频响函数和相⼲函数频响函数（FRF）频率响应函数表征了测试系统对给定频率下的稳态输出与输⼊的关系。

这个关系具体是指输出、输⼊幅值之⽐与输⼊频率的函数关系，和输出、输⼊相位差与输⼊频率的函数关系。

这两个关系称为测试系统的频率特性。

频率响应函数⼀般是⼀个复数。

频率响应函数直观地反映了测试系统对各个不同频率正弦输⼊信号的响应特性。

通过频率响应函数可以画出反映测试系统动态特性的各种图形，简明直观。

此外，很多⼯程中的实际系统很难确切地建⽴其数学模型，更不易确定其模型中的参数，因此要完整地列出其微分⽅程式并⾮易事。

所以，⼯程上常通过实验⽅法，对系统施加激励，测量其响应，根据输⼊、输出关系可以确⽴对系统动态特性的认识。

因⽽频率响应函数有着重要的实际意义。

和传递函数之间的关系在系统传递函数已经知道的情况下，若系统是稳定的，令中的实部为零，即令代⼊，可以得到系统的频率响应函数。

若在时刻将输⼊信号接⼈定常线性系统，令代⼊拉普拉斯变换中，实际上是将拉普拉斯变换变成傅⾥叶变换。

⼜由于系统的初始条件为零，因此系统的频率响应函数就成为输出、输⼊的傅⾥叶变换之⽐，即上式告诉我们，在测得输出和输⼊后，由其傅⾥叶变换可求得频率响应函数。

需要注意的是，频率响应函数是描述系统的简谐输⼊和其稳态输出的关系，在测量系统频率响应函数时，必须在系统响应达到稳态阶段时才能测量。

传递函数是在复数域中来描述和考察系统的特性的，⽐在时域中⽤微分⽅程来描述和考察系统特性有许多优点。

但是⼯程中的许多系统却极难建⽴其微分⽅程式和传递函数，⽽且传递函数的物理概念也很难理解。

频率响应函数是在频率域中描述和考察系统特性的。

与传递函数相⽐较，频率响应函数的物理概念明确，也易通过实验来建⽴；利⽤它和传递函数的关系，由它极易求出传递函数。

因此频率响应函数是实验研究系统的重要⼯具。

意义根据定常线性系统的频率保持性，系统在简谐信号的激励下，所产⽣的稳态输出也是简谐信号）。

[转载]频响函数与机械阻抗等⼏个概念（备忘）原⽂地址：频响函数与机械阻抗等⼏个概念（备忘）作者：唔使晒命运动微分⽅程：mx_pp+cx_p+kx=P(t)=P_0*exp(i*omega*t)⼀、阻抗和导纳机械阻抗定义为：简谐激振时复数形式的输⼊与输出之⽐。

位移阻抗：Z_x_omega=P(t)/x(t)速度阻抗：Z_x_p_omega=P(t)/x_p(t)加速度阻抗：Z_x_pp_omega=P(t)/x_pp(t)机械阻抗的倒数称为机械导纳，⼯程上把位移阻抗和位移导纳⼜分别称为动刚度和动柔度。

这两个东西仅取决于系统本⾝的动⼒特性，都是复数，每个都同时反映了系统的幅频响应特性和相频响应特性。

⼆、频率响应函数机械阻抗的倒数还可以称为复频响应函数或频率响应函数。

记为H(omega):H(omega)=x(t)/P(t) % 记得都是复数形式的输出输⼊⽐，且为简谐激励条件。

以激励频率与固有频率之⽐lumda或者相对阻尼系数kesi为参变量，把H(omega,)绘制于复平⾯上时得到的曲线为Nyquist plot，即奈奎斯特图：⼆、传递函数与复频响应函数a、系统的传递函数定义为0初始条件下系统受任意激励时，输出的拉⽒变换与输⼊的拉⽒变换的⽐。

另外，单位脉冲响应是传递函数的拉⽒逆变换。

b、系统受任意激励时，复频响应函数定义为输出的傅⽒变换与输⼊的傅⽒变换之⽐X(f)/F(f)c、系统受简谐激励时，复频响应函数定义为复数形式的输出与输⼊之⽐。

三、已知时域输⼊输出信号，怎么得到频响函数由⼆可知，可以直接对输出输⼊做傅⽒变换后⽤输出⽐输⼊得到频响函数，但是分母可能有0值。

从⽽有对定义的X(f)/F(f)，分⼦分母同时乘以F(f)的共轭或者X(f)的共轭：a，输出输⼊互功率谱函数Gxf= X(f)*(F(f)的共轭) 除以输⼊⾃功率谱 Gff 得到b，输出⾃谱Gxx 除以输出输⼊互谱Gfx=F(f)*(X(f)的共轭 ) 得到。

人体频响函数的测量和分析人体频响函数是指在声源与接收器之间传播的声波经过人体部件的折射、反射和吸收后，在人体外部的平面上的反射声的总响应的振幅与频率的关系，是用来描述人体对不同频率的声波敏感性的一个重要指标。

由于它包含了人体对环境声音的阻抗，它对于评估个体对听力损伤、对听觉危害的耐受度等非常重要。

首先，在测量人体频响函数之前，我们需要准备测量设备、实验场地和测量物体。

测量设备包括激励源和原动机以及被动探头，激励源可以通过嘈杂模拟波或超声源来模拟连续的振动或驱动人体的声波，而原动机应当能够将激励源的电源转换成能够表达具体声频的振动。

被动探头用于收集测试物体反射声，它应当具有高灵敏度、低噪声抑制，以及可以测量宽频段的响应。

实验场地应当设置在一个半封闭房间中，无任何噪声和反射源，并且室内的噪声应该在16~20dB之间。

测量物体为人体，受试者应当坐在室内，着普通衣服，平视激励源。

其次，在测量人体频响函数时，需要确定的主要参数包括激励源的声压级、探头距离测试物体的距离、探头及测试物体之间的角度、探头接收面的尺寸以及测试物体的响应动态特性。

首先，确定声压级，即在确定测试物体本身的能量标准后，以获得足够的信号/噪声比，考虑测试区域的噪声级，为激励源设定合适的声压级；其次，确定探头及测试物体之间的距离和角度，在测试物体有反射模型可供计算时，可以计算出最佳位置，并根据实际情况确定探头位置；确定探头接收面的尺寸，用于测量物体的反射声面积；确定测试物体的响应动态特性，即要求受试者在测试台上保持安静，不要全身活动，嘴部及头部尽可能处于静止状态。

最后，在测量完成以后，我们可以使用声学波形分析软件，对测量的人体频响函数进行更进一步的处理分析。

其中，有一个经典的声学参数，即听觉相干遮蔽指数（ICRA），可以综合的衡量人体的空间响应特性。

ICRA可用于评估个体的听力损伤，以及耐受度对听觉危害的程度。

综上所述，人体频响函数测量是一种重要的声学实验，可以对人体对环境声音的阻抗进行评估，从而对个体对听力损伤、对听觉危害的耐受度等进行评估，具有十分重要的意义。