【解析版】2019数学北师大选修2-1精练：第二章 空间向量与立体几何 2.5.1-2.5.2

§2 空间向量的运算第1课时空间向量的加、减法及数乘运算课后训练案巩固提升A组1.在正方体ABCD-A1B1C1D1中,向量表达式化简后的结果是()A. B. C. D.解析;+()=.答案;A2.设a,b是两个不共线的向量,λ,μ∈R,若λa+μb=0,则()A.a=b=0B.λ=μ=0C.λ=0,b=0D.μ=0,a=0解析;∵a,b是两个不共线的向量,∴a≠0,b≠0,∴只有B正确.答案;B3.设空间四点O,A,B,P满足+t,其中0<t<1,则有()A.点P在线段AB上B.点P在线段AB的延长线上C.点P在线段BA的延长线上D.点P不一定在直线AB上解析;∵0<t<1,∴点P在线段AB上.答案;A4.已知正方体ABCD-A1B1C1D1的中心为O,有下列结论;①是一对相反向量;②是一对相反向量;③是一对相反向量;④是一对相反向量.其中正确的有()A.1个B.2个C.3个D.4个解析;∵O为正方体的中心,∴=-=-,故=-(),同理可得=-(),故=-(),∴①③正确;∵,∴是两个相等的向量,∴②不正确;∵=-,∴=-(),∴④正确.答案;C5.如图,已知正方体ABCD-A'B'C'D',点E是A'C'的中点,点F是AE的三等分点,且AF=EF,则=() A.B.C.D.解析;由条件AF=EF,知EF=2AF,∴AE=AF+EF=3AF,∴)=)=.答案;D6.在四面体A-BCD中,E,F分别是AB,CD的中点,则的关系是(填平行、相等或相反). 解析;设G是AC的中点,则),∴2,∴∥().故填平行.答案;平行7.若非零向量e1,e2不共线,则使e1+e2与e1+e2共线的值为.解析;若e1+e2与e1+e2共线,则存在实数λ,使e1+e2=λ(e1+e2),又e1,e2不共线,所以所以答案;1或-18.导学号90074020如图,在平行六面体ABCD-A1B1C1D1中,=2.设=a,=b,=c,试用a,b,c表示.解如图,连接AN,则)=)-)=c+(b-c)-(a+b)=-a+b+c.B组1.如图,在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且=α+β,则()A.α=,β=-1B.α=-,β=1C.α=1,β=-D.α=-1,β=解析;因为+()+)=,所以α=,β=-1.答案;A2.已知空间向量满足||=||+||,则()A. B.=-C.同向D.同向解析;由||=||+||=||+||,知C点在线段AB上,否则与三角形两边之和大于第三边矛盾, 所以同向.答案;D3.如图,已知四面体O-ABC中,M,N分别为OA,BC的中点,点G在线段MN上,且=2.若=+y+,则+y+=()A.1B.0C. D.解析;,所以=,y=,=,所以+y+=.答案;C4.如图,在三棱锥A-BCD中,若△BCD是正三角形,E为其中心,则化简的结果为.解析;延长DE交BC于点F,连接AF,则F为BC的中点,,故=0.答案;05.如图,已知正四棱锥P-ABCD,点O是正方形ABCD的中心,Q是CD的中点.(1)若++y,求,y的值;(2)若=m+n,求m,n的值.解(1)因为)=,所以=y=-.(2)因为O为AC的中点,Q为CD的中点,所以=2=2,所以=2=2,所以=2-2,所以m=2,n=-2.6.导学号90074021如图,在空间四边形ABCD中,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且.求证;四边形EFGH是梯形.证明因为E,H分别是边AB,AD的中点,所以)=)=)=.所以,且||=|≠||.又因为点F不在EH上,所以四边形EFGH是梯形.。

- 1 - §5 夹角的计算5.1 直线间的夹角 5.2 平面间的夹角课后训练案巩固提升A 组1.已知两平面的法向量分别为m =(0,1,0),n =(0,1,1),则两平面的夹角为( ) A .45° B .135°C .45°或135°D .90°解析;本题考查利用平面的法向量求两平面夹角的方法.cos <m ,n >=,即<m ,n >=45°,∴两平面的夹角为45°.答案;A2.已知在正方体ABCD-A 1B 1C 1D 1中,E ,F 分别是棱BB 1,DC 的中点,则异面直线AE 与D 1F 的夹角为( ) A.B.C.D.解析;设正方体的棱长为2,建立如图所示的空间直角坐标系,则D 1(0,0,0),A (2,0,2),E (2,2,1),F (0,1,2).∴=(0,2,-1),=(0,1,2),∴=0,∴.答案;D 3.如图,在三棱锥S-ABC 中,侧面SAB 与侧面SAC 均为等边三角形,∠BAC=90°,O 为BC 的中点,则平面ASC 与平面BSC 的夹角的余弦值是()A.-B.C.-D.解法一取SC的中点M,连接AM,OM,OA,由题意知SO=OC,SA=AC,得OM⊥SC,AM⊥SC.所以∠OMA为平面ASC与平面BSC的夹角.由AO⊥BC,AO⊥SO,SO∩BC=O,得AO⊥平面SBC.所以AO⊥OM.又AM=SA,AO=SA,故sin∠AMO=,cos∠AMO=.故平面ASC与平面BSC的夹角的余弦值为.解法二连接OA,由题易知AO,BO,SO两两垂直,则以O为坐标原点,射线OB,OA,OS分别为轴、y轴、轴的正半轴,建立如图所示的空间直角坐标系O-y.取SC的中点M,连接AM,OM,设B(1,0,0),则C(-1,0,0),A(0,1,0),S(0,0,1).SC的中点M,所以=(-1,0,-1),所以=0,=0.故MO⊥SC,MA⊥SC,< >等于二面角A-SC-B的平面角.cos<>=,所以平面ASC与平面BSC的夹角的余弦值为.答案;B4.把正方形ABCD沿对角线AC翻折,使平面ACD⊥平面ABC,点E,F分别是AD,BC的中点,O是正方形的中心,则折起后,直线OE与OF的夹角的大小是()A. B. C. D.- 2 -解析;如图,建立空间直角坐标系,设正方形的边长为2.则F,E,∴,∴cos∠EOF=cos<>==-,设直线OE与OF的夹角为θ,则cos θ=|cos∠EOF|=,即θ=.故直线OE与OF的夹角为.答案;A5.在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=,则平面SCD和平面SAB夹角的余弦值是.解析;建立如图所示的空间直角坐标系,则A(0,0,0),D,C(1,1,0),S(0,0,1),平面SAB的一个法向量是.设n=(,y,)是平面SCD的法向量,则n⊥,n⊥,即n·=0,n·=0.又,∴+y=0,且-+=0,令=1,得n=.∴cos<,n>=.故平面SCD和平面SAB的夹角的余弦值为.- 3 -答案;6.正方体ABCD-A1B1C1D1中,B1D与BC1夹角的大小是,若E,F分别为AB,CC1的中点,则异面直线EF与A1C1夹角的大小是.解析;以点D为原点,建立如图所示的空间直角坐标系,设正方体的棱长为2,则易得D(0,0,0),B(2,2,0),B1(2,2,2),C1(0,2,2),A1(2,0,2),E(2,1,0),F(0,2,1),所以=(-2,0,2),=(-2,-2,-2).因为=0,所以B1D与BC1夹角的大小是90°.又=(-2,2,0),=(-2,1,1),设异面直线EF与A1C1夹角为θ,则cos θ=,所以θ=30°.答案;90°30°7.已知平行六面体ABCD-A1B1C1D1的所有棱长都是1,且∠A1AB=∠A1AD=∠BAD=,E,F分别为A1B1与BB1的中点,求异面直线BE与CF夹角的余弦值.解如图,设=a,=b,=c,则|a|=|b|=|c|=1,<a,b>=<b,c>=<a,c>=.∴a·b=b·c=a·c=.而=-a+c,=-b+c,∴||=,||=.∴=a·b-a·c-b·c+c2=.cos<>=.- 4 -∴异面直线BE与CF的夹角的余弦值为.8.导学号90074040如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.(1)求证;PC⊥AB;(2)求平面ABP与平面APC夹角的余弦值.(1)证明∵AC=BC,AP=BP,∴△APC≌△BPC.又PC⊥AC,∴PC⊥BC.∵AC∩BC=C,∴PC⊥平面ABC.∵AB⫋平面ABC,∴PC⊥AB.(2)解如图,以C为原点建立空间直角坐标系C-y,则C(0,0,0),A(0,2,0),B(2,0,0).设P(0,0,t).∵PB=AB=2,∴t=2,∴点P的坐标为(0,0,2).=(-2,2,0),=(-2,0,2),设平面ABP的法向量n=(,y,),则令=1,则n=(1,1,1).由题易知平面APC的法向量m=(1,0,0),cos n,m=.∴平面ABP与平面APC的夹角的余弦值为.B组- 5 -- 6 -1.在正方体ABCD-A 1B 1C 1D 1中,M 是AB 的中点,则sin <>的值等于( )A .B .C .D .解析;如图,以D 为原点建立空间直角坐标系.设棱长为1,则D (0,0,0),B 1(1,1,1),C (0,1,0),M,∴=(1,1,1),.∴cos <>=.∴sin <>=.答案;B2.如图,已知E ,F 分别是棱长为1的正方体ABCD-A 1B 1C 1D 1的棱BC ,CC 1的中点,则截面AEFD 1与底面ABCD 所成的夹角的正弦值为( )A .B .C .D .解析;以D 为坐标原点,以DA ,DC ,DD 1所在直线分别为轴、y 轴、轴建立空间直角坐标系,如图所示,- 7 - 则A (1,0,0),E,D 1(0,0,1),∴=(-1,0,1),.设平面AEFD 1的法向量为n =(,y ,),则∴=2y=.取y=1,则n =(2,1,2).又平面ABCD 的一个法向量为u =(0,0,1),∴cos <n ,u >=,∴sin <n ,u >=.答案;C 3.导学号90074041如图,在三棱柱ABC-A 1B 1C 1中,侧棱AA 1⊥底面ABC ,且∠BCA=90°,点D 1,F 1分别是A 1B 1,A 1C 1的中点,若BC=CA=CC 1,则BD 1与AF 1所成角的余弦值是( )A .B .C .D .解析;设向量=a ,=b ,=c ,|a |=|b |=|c |=1,根据题意,得a ·b =b ·c =c ·a =0.又a -b +c ,=-a +c ,∴||2=,∴||=,同理,||=.又,∴cos <>=,故选B .答案;B4.已知正方形ABCD 所在平面与正方形ABEF 所在平面成60°的夹角,则异面直线AD 与BF 所成角θ的余弦值是 . 解析;建立如图所示的空间直角坐标系,设AB=1,则A(0,0,0),D,F(1,0,0),B(0,1,0),∴=(1,-1,0),∴cos θ=cos<>= .答案;5.如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.求;(1)异面直线A1B与C1D所成角的余弦值;(2)平面ADC1与平面ABA1夹角的正弦值.解(1)以A为坐标原点,建立如图所示的空间直角坐标系A-y,则B(2,0,0),D(1,1,0),A1(0,0,4),C1(0,2,4),所以=(2,0,-4),=(1,-1,-4).因为cos<>=,所以异面直线A1B与C1D所成角的余弦值为.(2)设平面ADC1的法向量为n1=(,y,),因为=(1,1,0),=(0,2,4),所以取=1,得=2,y=-2,所以n1=(2,-2,1)是平面ADC1的一个法向量.取平面ABA1的一个法向量为n2=(0,1,0),设平面ADC1与平面ABA1夹角的大小为θ.由cos θ=,得sin θ=.因此平面ADC1与平面ABA1夹角的正弦值为.- 8 -6.如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2,AB=1,点N是BC的中点,点M在CC1上.设平面DA1N与平面DMN的夹角为θ.(1)当θ=90°时,求AM的长;(2)当cos θ=时,求CM的长.解以D为原点,建立如图所示的空间直角坐标系D-y.设CM=t(0≤t≤2),则D(0,0,0),A(1,0,0),A1(1,0,2),N,M(0,1,t),所以=(0,1,t),=(1,0,2).设平面DMN的一个法向量为n1=(1,y1,1),则n1·=0,n1·=0,即1+2y1=0,y1+t1=0.令1=1,则y1=-t,1=2t,所以n1=(2t,-t,1)是平面DMN的一个法向量.设平面A1DN的一个法向量为n2=(2,y2,2),则n2·=0,n2·=0,即2+22=0,2+2y2=0.令2=1,则2=-2,y2=1,所以n2=(-2,1,1)是平面A1DN的一个法向量.(1)因为θ=90°,所以n1·n2=-5t+1=0,解得t=.从而M.所以|AM|=.(2)因为|n1|=,|n2|=,所以cos<n1,n2>=.因为<n1,n2>=θ或π-θ,所以,解得t=0或t=.根据图形可知t=,从而CM的长为.- 9 -。

5.3直线与平面的夹角课后训练案巩固提升1.下列有关角的说法正确的是()A.异面直线所成的角的范围是B.两平面的夹角可以是钝角C.斜线和平面所成角的范围是D.直线与平面的夹角的取值范围是解析:异面直线所成的角的范围是,A错;两平面的夹角的范围是,B错;斜线与平面所成角就是斜线与平面的夹角,规定斜线和平面所成角的范围是,C错;而直线与平面的夹角的取值范围是,D对.答案:D2.已知在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于()A.B.C.D.解析:以D为坐标原点,建立空间直角坐标系,如图.设AA1=2AB=2,则D(0,0,0),C(0,1,0),B(1,1,0),C1(0,1,2),则=(0,1,0),=(1,1,0),=(0,1,2).设平面BDC1的法向量为n=(x,y,z),则n⊥,n⊥,所以有令y=-2,得平面BDC1的一个法向量为n=(2,-2,1).设CD与平面BDC1所成的角为θ,则sin θ=|cos<n,>|=.答案:A3.在三棱柱ABC-A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C夹角的大小是()A. B. C. D.解析:如图,取BC的中点E,连接DE,AE,AD,依题意知三棱柱为正三棱柱,易得AE⊥平面BB1C1C,故∠ADE为AD与平面BB1C1C的夹角.设各棱长为1,则AE=,DE=,所以tan∠ADE=,所以∠ADE=,故选C.答案:C4.如图,在四棱锥P-ABCD中,PD⊥底面ABCD,四边形ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面ABCD所成的角θ满足()A.θ=B.cos θ=C.tan θ=D.sin θ=解析:建立如图所示的空间直角坐标系,则P(0,0,1),A(1,0,0),B(1,1,0),C(0,1,0),所以G.又平面ABCD的一个法向量为n=(0,0,1),则cos<,n>==-,所以PG与平面ABCD所成角的余弦值为.答案:B5.若平面α的一个法向量为n=(4,1,1),直线l的方向向量为a=(-2,-3,3),则l与α夹角的余弦值为.解析:∵cos<a,n>=,∴l与α夹角的余弦值为.答案:6.如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD的夹角为,则平面FBE与平面DBE夹角的余弦值是.解析:因为DA,DC,DE两两垂直,所以建立空间直角坐标系D-xyz,如图所示.因为BE与平面ABCD的夹角为,即∠DBE=,所以.由AD=3可知DE=3,AF=,则A(3,0,0),F(3,0,),E(0,0,3),B(3,3,0),C(0,3,0).所以=(0,-3,),=(3,0,-2).设平面BEF的法向量为n=(x,y,z),则令z=,则n=(4,2,).由题意知AC⊥平面BDE,所以为平面BDE的法向量,=(3,-3,0).所以cos<n,>=.故由题意知平面FBE与平面DBE夹角的余弦值为.答案:7.如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2,SA=SB=.(1)求证:SA⊥BC;(2)求直线SD与平面SAB夹角的正弦值.(提示:用向量法求解)(1)证明如图,作SO⊥BC,垂足为O,连接AO.由侧面SBC⊥底面ABCD,得SO⊥平面ABCD.因为SA=SB,所以AO=BO.又∠ABC=45°,故△AOB为等腰直角三角形,且AO⊥OB.如图,以O为坐标原点,OA为x轴正向,OB为y轴正向,OS为z轴正向,建立空间直角坐标系O-xyz,则A(,0,0),B(0,,0),C(0,-,0),S(0,0,1),所以=(,0,-1),=(0,2,0).所以=0.所以SA⊥BC.(2)解如上图,取AB的中点E.连接SE,取SE的中点G,连接OG,则.所以=0,=0,即OG与平面SAB内两条相交直线SE,AB垂直,所以OG⊥平面SAB.将的夹角记为α,SD与平面SAB的夹角记为β,则α与β互余.因为D(,-2,0),所以=(-,2,1),所以cos α=,所以sin β=.所以直线SD与平面SAB夹角的正弦值为.8.导学号90074044如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.(1)求证:BD⊥平面PAC;(2)若PA=AB,求PB与平面PAC所成角的余弦值;(3)若PA=4,求平面PBC与平面PDC所成角的余弦值.解(1)因为底面ABCD是菱形,所以BD⊥AC.又PA⊥平面ABCD,所以BD⊥PA.又PA∩AC=A,所以BD⊥平面PAC.(2)设BD∩AC=O,连接PO,由(1)可知∠BPO即为PB与平面PAC所成的角.因为PA=AB=2,所以PB=2.又∠BAD=60°,所以OB=BD=1,所以cos∠BPO=,所以PB与平面PAC所成角的余弦值为.(3)以BD与AC的交点O为坐标原点,OB为x轴,OC为y轴,过点O且垂直于平面ABCD的直线为z轴,建立如图所示的空间直角坐标系.由已知可得,AO=OC=,OD=OB=1,所以P(0,-,4),B(1,0,0),C(0,,0),D(-1,0,0),=(0,2,-4),=(-1,,0),=(-1,-,0).设平面PBC的法向量为n1=(x1,y1,z1),平面PDC的法向量为n2=(x2,y2,z2),由可得令x1=,可得n1=.同理,由可得n2=,所以cos<n1,n2>==-,所以平面PBC与平面PDC 所成角的余弦值为.。

§4用向量讨论垂直与平行课后训练案巩固提升A组1、已知a，b，c分别为直线a，b，c的方向向量，且a=λb( λ≠0 )，b·c=0，则a与c的位置关系是( )A、垂直B、平行C、相交D、异面详细解析:由a=λb( λ≠0 )，知a∥b、由b·c=0，知b⊥c，所以a⊥c、故选A、正确答案:A2、已知A( 1，0，0 )，B( 0，1，0 )，C( 0，0，1 )，则平面ABC的一个单位法向量是( )A、B、C、D、详细解析:=( -1，1，0 )，=( -1，0，1 )，=( 0，-1，1 )、设平面ABC的一个单位法向量为u=( x，y，z )，则u·=0，u·=0，可得x，y，z间的关系，且x2+y2+z2=1，再求出x，y，z的值、正确答案:D3、若平面α的法向量为u=( 1，-3，-1 )，平面β的法向量为v=( 8，2，2 )，则( )A、α∥βB、α与β相交C、α⊥βD、不确定详细解析:∵平面α的法向量为u=( 1，-3，-1 )，平面β的法向量为v=( 8，2，2 )，∴u·v=( 1，-3，-1 )·( 8，2，2 )=8-6-2=0、∴u⊥v，∴α⊥β、正确答案:C4、给出下列命题:①若n1，n2分别是平面α，β的法向量，则n1∥n2⇔α∥β;②若n1，n2分别是平面α，β的法向量，则α∥β⇔n1·n2=0;③若n是平面α的法向量，且向量a与平面α共面，则a·n=0;④若两个平面的法向量不垂直，则这两个平面一定不垂直、其中正确命题的个数是( )A、1B、2C、3D、4详细解析:①②不正确、正确答案:B5、导学号90074037如图，在平行六面体ABCD-A1B1C1D1中，M，P，Q分别为棱AB，CD，BC的中点，若平行六面体的各棱长均相等，则①A1M∥D1P;②A1M∥B1Q;③A1M∥平面DCC1D1;④A1M∥平面D1PQB1、以上结论正确的是、( 填序号)详细解析:∵，∴A1M∥D1P、又∵D1P⫋平面D1PQB1，∴A1M∥平面D1PQB1、又D1P⫋平面DCC1D1，∴A1M∥平面DCC1D1、∵D1B1与PQ平行不相等，∴B1Q与D1P不平行、∴A1M与B1Q不平行、正确答案:①③④6、已知=( 1，5，-2 )，=( 3，1，z )，=( x-1，y，-3 )、若，且BP⊥平面ABC，则实数x，y，z的值分别为、详细解析:∵=( 1，5，-2 )，=( 3，1，z )，，∴( 1，5，-2 )·( 3，1，z )=0，即3+5-2z=0，∴z=4、①又∵=( x-1，y，-3 )，⊥平面ABC，∴=0，即( x-1，y，-3 )·( 1，5，-2 )=0，x-1+5y+6=0、②=0，即( x-1，y，-3 )·( 3，1，4 )=0，3x-3+y-12=0、③由①②③得x=，y=-，z=4、正确答案:，-，47、如图，PA⊥平面ABCD，四边形ABCD为正方形，E是CD的中点，F是AD上一点，当BF⊥PE时，AF∶FD的值为、详细解析:建立如图所示的空间直角坐标系，设正方形边长为1，PA=a、则B( 1，0，0 )，E，P( 0，0，a )、设点F的坐标为( 0，y，0 )，则=( -1，y，0 )，、∵BF⊥PE，∴=0，解得y=，则点F的坐标为，∴F为AD的中点，∴AF∶FD=1、正确答案:18、如图，在直三棱柱ABC-A1B1C1中，∠ABC=90°，BC=2，CC1=4，点E在线段BB1上，且EB1=1，D，F，G分别为CC1，C1B1，C1A1的中点、求证:平面EGF∥平面ABD、证明如图所示，由条件知BA，BC，BB1两两互相垂直，以B为坐标原点，BA，BC，BB1所在直线分别为x 轴、y轴、z轴建立空间直角坐标系、由条件知B( 0，0，0 )，D( 0，2，2 )，B1( 0，0，4 )，E( 0，0，3 )，F( 0，1，4 )，设BA=a，则A( a，0，0 )，G、所以=( a，0，0 )，=( 0，2，2 )，=( 0，2，-2 )，=( 0，1，1 )、( 方法一)因为=0，=0+4-4=0，所以B1D⊥BA，B1D⊥BD、因为BA∩BD=B，所以B1D⊥平面ABD、又=0+2-2=0，=0+2-2=0、所以B1D⊥EG，B1D⊥EF、又EG∩EF=E，所以B1D⊥平面EFG，可知平面EGF∥平面ABD、( 方法二)设平面EGF的法向量为n1=( x1，y1，z1 )，则令y1=1，则n1=( 0，1，-1 )、设平面ABD的法向量为n2=( x2，y2，z2 )，则即令y2=1，则n2=( 0，1，-1 )、所以n1=n2，所以平面EGF∥平面ABD、9、如图，正三棱柱ABC-A1B1C1的所有棱长都为2，D为CC1的中点、求证:AB1⊥平面A1BD、证明如图所示，取BC的中点O，连接AO、因为△ABC为正三角形，所以AO⊥BC、因为在正三棱柱ABC-A1B1C1中，平面ABC⊥平面BCC1B1，所以AO⊥平面BCC1B1、取B1C1的中点O1，以O为原点，以为x轴、y轴、z轴建立空间直角坐标系，则B( 1，0，0 )，D( -1，1，0 )，A1( 0，2，)，A( 0，0，)，B1( 1，2，0 )、设平面A1BD的法向量为n=( x，y，z )，=( -1，2，)，=( -2，1，0 )、因为n⊥，n⊥，故令x=1，则y=2，z=-，故n=( 1，2，-)为平面A1BD的一个法向量，而=( 1，2，-)，所以=n，所以∥n，故AB1⊥平面A1BD、B组1、设平面α的一个法向量为( 1，2，-2 )，平面β的一个法向量为( -2，-4，k )，若α∥β，则k=( )A、2B、-4C、4D、-2详细解析:∵α∥β，∴存在实数λ，使( 1，2，-2 )=λ( -2，-4，k )，∴k=4、正确答案:C2、如图，AB是☉O的直径，VA垂直☉O所在的平面，点C是圆周上不同于A，B的任意一点，M，N分别为VA，VC的中点，则下列结论正确的是( )A、MN∥ABB、MN与BC所成的角为45°C、OC⊥平面VACD、平面VAC⊥平面VBC详细解析:因为M，N分别为VA，VC的中点，所以MN∥AC、因为AB∩AC=A，所以A选项不正确、因为AC⊥BC，所以MN与BC所成的角为90°，B选项不正确、又因为OC不垂直于AC，所以选项C不正确、因为VA垂直☉O所在的平面，依题意可得平面VAC⊥平面VBC、正确答案:D3、如图，定点A和B都在平面内，定点P∉α，PB⊥α，C是α内异于A和B的动点，且PC⊥AC，那么C在平面α内的轨迹是( )A、一条线段，但要去掉两个点B、一个圆，但要去掉两个点C、一个椭圆，但要去掉两个点D、半圆，但要去掉两个点详细解析:连接BC( 图略)，根据题意BC为PC在平面α内的射影、∵PC⊥AC，根据三垂线定理的逆定理知AC⊥BC，∴点C在以AB为直径的圆上、又C是不同于点A和B的动点，因此应去掉端点A和B、正确答案:B4、如图，在长方体ABCD-A1B1C1D1中，AA1=AD=1，E为CD的中点、若在棱AA1上取一点P，使得DP∥平面B1AE，此时AP的长为、详细解析:以A为原点，的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系( 如图所示)、设AB=a，则A( 0，0，0 )，D( 0，1，0 )，D1( 0，1，1 )，E，B1( a，0，1 )，故=( 0，1，1 )，=( a，0，1 )，、再设P( 0，0，z0 )，使得DP∥平面B1AE、此时=( 0，-1，z0 )、又设平面B1AE的法向量为n=( x，y，z )，则取x=1，得n=、要使DP∥平面B1AE，只要n⊥，有-az0=0，解得z0=、又DP⊈平面B1AE，∴存在点P，满足DP∥平面B1AE，此时AP=、正确答案:5、如图，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC，EF∥AC，AB=，CE=EF=1、求证:( 1 )AF∥平面BDE;( 2 )CF⊥平面BDE、证明( 1 )设AC与BD交于点G、因为EF∥AG，且EF=1，AG=AC=1，所以四边形AGEF为平行四边形，所以AF∥EG、因为EG⫋平面BDE，AF⊈平面BDE，所以AF∥平面BDE、( 2 )因为正方形ABCD和四边形ACEF所在的平面互相垂直，且CE⊥AC，所以CE⊥平面ABCD、如图，以C为原点，建立空间直角坐标系C-xyz，则C( 0，0，0 )，A( ，0 )，B( 0，，0 )，D( ，0，0 )，E( 0，0，1 )，F、所以=( 0，-，1 )，=( -，0，1 )、所以=0-1+1=0，=-1+0+1=0、所以CF⊥BE，CF⊥DE、又BE∩DE=E，所以CF⊥平面BDE、6、导学号90074038如图，在三棱锥P-ABC中，PA⊥平面ABC，AB⊥AC、( 1 )求证:AC⊥PB;( 2 )设O，D分别为AC，AP的中点，点G为△OAB内一点，且满足)，求证:DG∥平面PBC、证明( 1 )因为PA⊥平面ABC，AC⫋平面ABC，所以PA⊥AC、又因为AB⊥AC，且PA∩AB=A，所以AC⊥平面PAB、又因为PB⫋平面PAB，所以AC⊥PB、( 2 )证法一:因为PA⊥平面ABC，所以PA⊥AB，PA⊥AC、又因为AB⊥AC，所以建立如图所示的空间直角坐标系A-xyz、设AC=2a，AB=b，PA=2c，则A( 0，0，0 )，B( 0，b，0 )，C( 2a，0，0 )，P( 0，0，2c )，D( 0，0，c )，O( a，0，0 )，又因为)，所以G、于是=( 2a，-b，0 )，=( 0，b，-2c )、设平面PBC的一个法向量n=( x0，y0，z0 )，则有不妨设z0=1，则有y0=，x0=，所以n=、因为n·+1·( -c )=0，所以n⊥、又因为DG⊈平面PBC，所以DG∥平面PBC、证法二:取AB中点E，连接OE，则)、由已知)可得，则点G在OE上、连接AG并延长交CB于点F，连接PF、因为O，E分别为AC，AB的中点，所以OE∥BC，即G为AF的中点、又因为D为线段PA的中点，所以DG∥PF、又DG⊈平面PBC，PF⫋平面PBC，所以DG∥平面PBC、。

第二章空间向量与立体几何§1从平面向量到空间向量课后训练案巩固提升1.下面几个命题;①向量的模是一个正实数;②所有的单位向量相等;③所有的零向量相等;④一条直线的方向向量是相等的.其中错误的命题个数为()A.4B.3C.2D.1解析;0的模为0,故①错;所有单位向量的模相等,但方向不一定相同,故②错,③对;一条直线的方向向量不唯一,故④错.答案;B2.在四边形ABCD中,若,且||=||,则四边形ABCD为()A.菱形B.矩形C.正方形D.不确定解析;若,则AB=DC,且AB∥DC,所以四边形ABCD为平行四边形.又||=||,即AC=BD, 所以四边形ABCD为矩形.答案;B3.把空间所有单位向量归结到一个共同的始点,则这些向量的终点所构成的图形是()A.一个圆B.两个孤立的点C.一个球面D.一个平面解析;半径为1的球面上所有点到球心的距离为1.答案;C4.在正三棱锥A-BCD中,E,F分别为棱AB,CD的中点,设<>=α,<>=β,则α+β=()A. B. C. D.解析;如图,取BC的中点G,连接EG,FG,则EG∥AC,FG∥BD,故∠FEG=α,∠EFG=β.∵三棱锥A-BCD是正三棱锥,∴AC⊥BD,∴EG⊥FG,即∠EGF=.∴α+β=∠FEG+∠EFG=.答案;D 5.导学号90074018下列命题;①两个相反向量必是共线向量;②温度含有零上温度和零下温度,所以温度是向量;③已知空间四边形ABCD ,则由四条线段AB ,BC ,CD ,DA 分别确定的四个向量之和为零向量; ④不相等的两个空间向量的模必不相等.其中,真命题的序号为 . 答案;①6.如图,在正方体ABCD-A 1B 1C 1D 1中,E ,F ,G ,H 分别是AB ,AD ,BC ,CC 1的中点,则<>= .解析;连接DB ,BC 1,DC 1.∵ABCD-A 1B 1C 1D 1为正方体,∴△BDC 1为等边三角形.∵E ,F ,G ,H 分别是AB ,AD ,BC ,CC 1的中点, ∴EF ∥BD ,GH ∥BC 1. ∴<>=<>=.答案;7.如图,已知ABCD-A1B1C1D1为平行六面体,若以此平行六面体的顶点为向量的始点、终点,求;(1)与相等的向量;(2)的相反向量;(3)与平行的向量.解如图,连接AD1,CD1.(1)与相等的向量为.(2)的相反向量为.(3)与平行的向量为.8.如图,在正方体ABCD-A'B'C'D'中,求;(1)<>,<>,<>;(2)<>,<>.解(1)∵ABCD-A'B'C'D'为正方体,∴AB∥A'B',AD⊥D'C',AB∥C'D'.∴<>=0,<>=,<>=π.(2)∵在正方体ABCD-A'B'C'D'中AD∥BC,∴<>=<>=.连接AC,则△ACD'为等边三角形,∴<>=.9.如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,且PD=CD,E,F分别是PC,PB的中点.(1)试求以F为起点的直线DE的一个方向向量;(2)试求以F为起点的平面PBC的一个法向量.解(1)如图,取AD的中点M,连接MF,EF,∵E,F分别是PC,PB的中点,∴EF BC.又BC AD,∴EF AD,∴EF DM,∴四边形DEFM是平行四边形,∴MF∥DE,∴是以F为起点的直线DE的一个方向向量.(2)∵PD⊥平面ABCD,∴PD⊥BC.又BC⊥CD,且PD∩DC=D,∴BC⊥平面PCD.∵DE⫋平面PCD,∴DE⊥BC.又PD=CD,E为PC的中点,∴DE⊥PC.又BC∩PC=C,∴DE⊥平面PBC,∴是平面PBC的一个法向量,由(1),可知,∴就是以F为起点的平面PBC的一个法向量.。

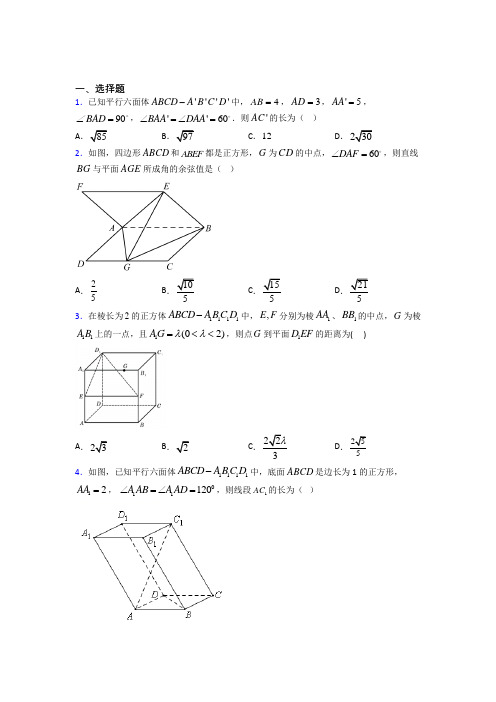
一、选择题1．已知平行六面体''''ABCD A B C D -中，4AB =，3AD =，'5AA =，90BAD ∠=，''60BAA DAA ∠=∠=．则'AC 的长为（ ）A ．85B ．97C ．12D ．230 2．如图，四边形ABCD 和ABEF 都是正方形，G 为CD 的中点，60DAF ∠=，则直线BG 与平面AGE 所成角的余弦值是（ ）A ．25B ．105C ．155D ．2153．在棱长为2的正方体1111ABCD A BC D -中，,E F 分别为棱1AA 、1BB 的中点，G 为棱11A B 上的一点，且1(02)AG λλ=<<，则点G 到平面1D EF 的距离为( )A ．23B ．2C ．223λD ．2554．如图，已知平行六面体1111ABCD A BC D -中，底面ABCD 是边长为1的正方形，12AA =， 011120A AB A AD ∠=∠=，则线段1AC 的长为（ ）A ．2B ．1C ．2D ．35．已知正方体1111ABCD A BC D -,M 为11A B 的中点，则异面直线A M 与1BC 所成角的余弦值为（ ）A ．105B ．1010C ．32D ．626．如图是由16个边长为1的菱形构成的图形，菱形中的锐角为,3π=,,a AB b CD =则=a b ⋅A ．5-B ．1-C ．3-D ．6-7．在空间直角坐标系Oxyz 中,已知(2,0,0)(2,2,0),(0,2,0),(1,1,2)A B C D .若123,,S S S 分别是三棱锥D ABC -在坐标平面上的正投影图形的面积，则（ ） A ．123S S S ==B ．21=S S 且23S S ≠C ．31S S =且32S S ≠D ．32S S =且31S S ≠8．圆锥的轴截面SAB 是边长为2的等边三角形，O 为底面的中心，M 为SO 的中点，动点P 在圆锥底面内（包括圆周）若,AM MP ⊥则点P 形成的轨迹的长度为( ) A ．76 B ．75 C ．72 D ．749．如图，在棱长为2的正方体1111ABCD A BC D -中，点E F 、分别是棱AB 、BC 的中点，则点1C 到平面1B EF 的距离等于（ ）A ．23B ．223C ．33D ．4310．如图，四棱锥P ABCD -的底面是边长为2的正方形， Q 为BC 的中点，PQ ⊥面ABCD ，且2PQ =，动点N 在以D 为球心半径为1的球面上运动，点M 在面 ABCD内运动，且PM 5=，则MN 长度的最小值为（ ）A ．352-B ．23-C ．25-+D ．332- 11．如图，棱长为1的正方体1111ABCD A BC D -，O 是底面1111D C B A 的中心，则O 到平面11ABC D 的距离是（ ）A ．12B ．24C ．22D 312．在平面直角坐标系中，()2,3A -、()32B -，，沿x 轴将坐标平面折成60︒的二面角，则AB 的长为（ ）A 2B ．211C ．32D ．42二、填空题13．在空间四边形ABCD 中，连接AC 、BD ,若BCD 是正三角形，且E 为其中心，则1322AB BC DE AD +--的化简结果为________． 14．已知三棱柱ABC ﹣A 1B 1C 1中，AA 1⊥面ABC ，AB ⊥AC ，且AA 1=AB=AC ，则异面直线AB 1与BC 1所成角为_____．15．已知平面向量()21,3m =+a 与()2,m =b 是共线向量且0⋅<a b ,则=b __. 16．已知四边形ABCD 为平行四边形，且A (4,1,3)，B (2，－5,1)，C (3,7，－5)，则顶点D 的坐标为________．17．如图所示，在正四棱柱1111ABCD A BC D -中，12AA =，1AB BC ==，动点P 、Q 分别在线段1C D 、AC 上，则线段PQ 长度的最小值是______．18．如图，空间四边形OABC 中，,M N 分别是对边,OA BC 的中点，点G 在线段MN 上，分MN 所成的定比为2，OG xOA yOB zOC =++，则,,x y z 的值分别为_____．19．在空间直角坐标系O xyz -中，点(1,2,3)A -到原点的距离为__________．20．三棱锥V-ABC 的底面ABC 与侧面VAB 都是边长为a 的正三角形，则棱VC 的长度的取值范围是_________.三、解答题21．在①()()DE CF DE CF +⊥-，②17||2DE =，③0cos ,1EF DB <<这三个条件中任选一个，补充在下面的横线中，并完成问题.问题：如图，在正方体1111ABCD A BC D -中，以D 为坐标原点，建立空间直角坐标系D xyz -.已知点1D 的坐标为()0,0,2，E 为棱11D C 上的动点，F 为棱11B C 上的动点，___________，试问是否存在点E ，F 满足1EF AC ⊥？若存在，求AE BF ⋅的值；若不存在，请说明理由.注：如果选择多个条件分别解答，按第一个解答计分.22．如图.四棱柱ABCD-A 1B 1C 1D 1的底面是直角梯形，BC ∥AD ，AB AD ，AD=2BC=2，四边形ABB 1A 1和ADD 1A 1均为正方形.（1）证明；平面ABB 1A 1平面ABCD ；（2）求二面角B 1 CD-A 的余弦值.23．如图，在四棱锥S ABCD -中，SA ⊥平面ABCD ，//AD BC ，AD AB ⊥，4AB AS ==，3AD =，6BC =，E 为SB 的中点．（1）求证：//AE 平面SCD ．（2）求二面角B AE C --的余弦值．24．如图，四棱锥P ABCD -的底面ABCD 是边长为2的菱形，60BAD ∠=，已知2,6PB PD PA ===，E 为PA 的中点．（1）求证PC BD ⊥；（2）求直线PC 与平面 PBD 所成角的正弦值．（3）求二面角B PC E --的余弦值．25．如图，平面ABCD ⊥平面ABEF ，其中四边形ABCD 为正方形，四边形ABEF 为直角梯形，1//902AB AF BE AF BE BAF ==∠=︒，，，M 为线段CE 上一点，//MF 平面ABCD ．（1）确定点M 的位置，并证明你的结论；（2）求直线DF 与平面BFM 所成角的正弦值．26．如图，四棱锥中P ABCD -中，底面ABCD 是直角梯形，//AB CD ，60DAB ∠=︒，2AB AD CD ==，侧面PAD ⊥底面ABCD ，且PAD △为等腰直角三角形，90APD ∠=︒．（Ⅰ）求证：AD PB ⊥；（Ⅱ）求平面PAD 与平面PBC 所成锐二面角的余弦值．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】用空间向量基本定理表示出AC '，然后平方后转化为数量积的运算求得．【详解】记a AB =，b AD =，c AA '=，则43cos900a b ⋅=⨯⨯︒=，同理152b c ⋅=，10a c ⋅=，由空间向量加法法则得AC a b c '=++， ∴22222()222AC a b c a b c a b b c a c '=++=+++⋅+⋅+⋅222154352210852=+++⨯+⨯=， ∴85AC '=AC '=．故选：A ．【点睛】方法点睛：本题考查求空间线段长，解题方法是空间向量法，即选取基底，用基底表示出向量，然后利用向量模的平方等于向量的平方转化为向量的数量积进行计算．2．C解析：C【分析】 以A 为原点，以AD 、AB 的方向分别为x 、y 轴的正方向，过A 作垂直平面ABCD 的直线作z 轴建立空间直角坐标系，设2AB =，利用空间向量法可求得直线BG 与平面AGE 所成角的正弦值，再利用同角三角函数的基本关系可求得结果.【详解】以A 为原点，以AD 、AB 的方向分别为x 、y 轴的正方向，过A 作垂直平面ABCD 的直线作z 轴，建立如图所示的空间直角坐标系A xyz -．设2AB =，得()0,0,0A 、()2,1,0G 、()0,2,0B 、(1,3E ，则()2,1,0AG =，(3AE =，()2,1,0BG =-，设平面AGE 的法向量为(),,n x y z =， 则20230n AG x y n AE x y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，取1x =，则2y =-，3z = 所以，平面AGE 的一个法向量为(1,2,3n =-， 从而10cos ,225n BGn BG n BG ⋅<>===⨯⋅， 故直线BG 与平面AGE 2101515⎛⎫-= ⎪ ⎪⎝⎭. 故选：C.【点睛】方法点睛：计算线面角，一般有如下几种方法：（1）利用面面垂直的性质定理，得到线面垂直，进而确定线面角的垂足，明确斜线在平面内的射影，即可确定线面角；（2）在构成线面角的直角三角形中，可利用等体积法求解垂线段的长度h ，从而不必作出线面角，则线面角θ满足sin h lθ=（l 为斜线段长），进而可求得线面角； （3）建立空间直角坐标系，利用向量法求解，设a 为直线l 的方向向量，n 为平面的法向量，则线面角θ的正弦值为sin cos ,a n θ=<>.3．D解析：D【分析】以D 为原点，DA 为x 轴、DC 为y 轴、1DD 为z 轴，建立空间直角坐标系，利用向量法能求出点G 到平面1D EF 的距离 .【详解】以D 为原点，DA 为x 轴、DC 为y 轴、1DD 为z 轴，建立空间直角坐标系， 则()()()()12,,2,0,0,2,2,0,1,2,2,1G D E F λ，()()()12,0,1,0,2,0,0,,1ED EF EG λ=-==，设平面1D EF 的法向量(),,n x y z =，则12020n ED x z n EF y ⎧⋅=-+=⎨⋅==⎩，取1x =，得()1,0,2n =，∴点G 到平面1D EF 的距离为 2255EG nd n ⋅===，故选D. 【点睛】本题主要考查利用空间向量求点到平面的距离，是中档题. 空间向量解答立体几何问题的一般步骤是：（1）观察图形，建立恰当的空间直角坐标系；（2）写出相应点的坐标，求出相应直线的方向向量；（3）设出相应平面的法向量，利用两直线垂直数量积为零列出方程组求出法向量；（4）将空间位置关系转化为向量关系；（5）根据定理结论求出相应的角和距离. 4．A解析：A【分析】由11AC AB BC CC =++，两边平方，利用数量积的运算法则及数量积公式能求出21AC 的值，从而可得结果.【详解】平行六面体1111ABCD A BC D -中，底面ABCD 是边长为1的正方形，1112,120AA A AB A AD =∠=∠=， 11AC AB BC CC ∴=++，()2211AC AB BC CC ∴=++222111222AB BC CC AB CC BC CC AB BC =+++⋅+⋅+⋅ 114212cos120212cos12002=+++⨯⨯⨯+⨯⨯⨯+=， ∴线段1AC 的长为12AC = A.【点睛】本题主要考查利用空间向量求线段的长，考查向量数量积的运算法则，属于中档题.向量数量积的运算主要掌握两点：一是数量积的基本公式cos a b a b θ⋅=；二是向量的平方等于向量模的平方22a a =. 5．A解析：A【分析】建立空间直角坐标系，求出向量AM 与1BC 的向量坐标，利用数量积求出异面直线A M 与1B C 所成角的余弦值.【详解】 以D 为坐标原点，建立空间直角坐标系，如图所示：设正方体的棱长为1，则(1,0,0)A ，1(1,0,1)A ，(1,1,0)B ，1(1,1,1)B ，(0,1,0)C ∵M 为11A B 的中点 ∴1(1,,1)2M ∴1(0,,1)2AM =，52AM =；1(1,0,1)B C =--，12B C =. ∴异面直线A M 与1B C 所成角的余弦值为111110cos ,10AM B C AM B C AM B C⋅===⋅ 故选A.【点睛】本题主要考查异面直线所成的角的定义和求法，找出两异面直线所成的角∠AEM （或其补角），是解题的关键．如果异面直线所成的角不容易找，则可以通过建立空间直角坐标系，利用空间向量来求解．6．B解析：B【解析】设菱形中横向单位向量为,m 纵向单位向量为n ，则111,1122m n m n ==⋅=⨯⨯=，2a AB m n ==+，32b CD m n ==-+，()()232a b m n m n ⋅=+-+=223443421m n m n -+-⋅=-+-=-，故选B. 7．D解析：D 【分析】试题分析：结合其空间立体图形易知，112222=⨯⨯=S ，2312222S S ==⨯⨯=，所以23S S =且13S S ≠，故选D ．考点：空间直角坐标系及点的坐标的确定，正投影图形的概念，三角形面积公式． 8．C 解析：C【分析】建立空间直角坐标系，写出点的坐标，设出动点的坐标，利用向量的坐标公式求出向量坐标，利用向量垂直的充要条件列出方程求出动点P 的轨迹方程，得到P 的轨迹是底面圆的弦，利用勾股定理求出弦长．【详解】建立空间直角坐标系．设A （0，﹣1，0），B （0，1，0），S （0，03M （0，0，3P （x ，y ，0）． 于是有AM =（0，13MP =（x ，y ，3 由于AM ⊥MP ，所以（0，13•（x ，y ，30， 即y 34=，此为P 点形成的轨迹方程，其在底面圆盘内的长度为2371()4-=．故选C ．【点睛】本题考查通过建立坐标系，将求轨迹问题转化为求轨迹方程、考查向量的数量积公式、向量垂直的充要条件、圆的弦长的求法．属中档题9．D解析：D【分析】建立空间直角坐标系，找到平面1B EF 的法向量，利用向量法求点到平面的距离求解即可.【详解】以1D 为坐标原点，分别以11D A ，11D C ，1D D 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系，则1(2,2,0)B ，1(0,2,0)C ，(2,1,2)E ，(1,2,2)F .设平面1B EF 的法向量为(,,)n x y z =，1(0,1,2)B E =-1(1,0,2)B F =-则1100n B E n B F ⎧⋅=⎪⎨⋅=⎪⎩，即2020y z x z -+=⎧⎨-+=⎩ 令1z =，得(2,2,1)n =.又11(2,0,0)BC =-，∴点1C 到平面1B EF 的距离1122|||2200|43||221n B C h n ⋅-⨯++===++， 故选：D .【点睛】 本题用向量法求点到平面的距离，我们也可以用等体积法求点到平面的距离，当然也可以找到这个垂线段，然后放在直角三角形中去求.10．C解析：C【分析】若要使MN 最短，点N 必须落在平面ABCD 内，且一定在DN 的连线上，此时应满足,,,D N M Q 四点共线，通过几何关系即可求解【详解】如图，当点N 落在平面ABCD 内，且,,,D N M Q 四点共线时，MN 距离应该最小，由PM 5=1MQ =，即点M 在以Q 为圆心，半径为1的圆上，由几何关系求得5DQ ，1DN MQ ==，故552NM DN MQ -=故答案选：C【点睛】本题考查由几何体上的动点问题求解两动点间距离的最小值，属于中档题11．B解析：B【分析】如图建立空间直角坐标系，可证明1A D ⊥平面11ABC D ，故平面11ABC D 的一个法向量为：1DA ，利用点到平面距离的向量公式即得解. 【详解】如图建立空间直角坐标系，则：1111(,,1),(0,0,1),(1,0,0),(1,1,0),(0,1,1)22O D A B C 111(,,0)22OD ∴=-- 由于AB ⊥平面111,ADD A AD ⊂平面11ADD A1AB A D ∴⊥，又11AD A D ⊥，1AB AD1A D ∴⊥平面11ABC D故平面11ABC D 的一个法向量为：1(1,0,1)DA = O ∴到平面11ABC D 的距离为： 1111||22||2OD DA d DA ⋅===故选：B【点睛】本题考查了点到平面距离的向量表示，考查了学生空间想象，概念理解，数学运算的能力，属于中档题.12．D解析：D 【分析】作AC x ⊥轴于C ，BD x ⊥轴于D ，则AB AC CD DB =++，两边平方后代入数量积即可求得2||AB ，则AB 的长可求．【详解】如图，()2,3A -，()3,2B -，作AC x ⊥轴于C ，BD x ⊥轴于D ，则()2,0C -，()3,0D ，3AC ∴=，5CD =，2DB =，沿x 轴把坐标平面折成60︒的二面角，CA ∴<，60DB >=︒，且0AC CD CD DB ⋅=⋅=，222||()AB AB AC CD DB ∴==++ 222222AC CD DB AC CD CD DB AC DB =+++⋅+⋅+⋅19254232322⎛⎫=+++⨯⨯⨯-= ⎪⎝⎭． 42AB ∴=即AB 的长为42故选：D ．【点睛】本题主要考查了空间角，向量知识的运用，考查学生的计算能力，属于中档题． 二、填空题13．【分析】由题意结合重心的性质和平面向量的三角形法则整理计算即可求得最终结果【详解】如图取BC 的中点F 连结DF 则∴【点睛】本题主要考查空间向量的运算法则及其应用意在考查学生的转化能力和计算求解能力 解析：0【分析】由题意结合重心的性质和平面向量的三角形法则整理计算即可求得最终结果.【详解】如图，取BC 的中点F ，连结DF ，则23DF DE =， ∴1322AB BC DE AD +--AB BF DF DA =+-+AF FD DA =++0=.【点睛】本题主要考查空间向量的运算法则及其应用，意在考查学生的转化能力和计算求解能力. 14．【解析】连结A1B ∵AA1⊥面ABC 平面A1B1C1∥面ABC ∴AA1⊥平面A1B1C1∵A1C1⊂平面A1B1C1∴AA1⊥A1C1∵△ABC 与△A1B1C1是全等三角形AB ⊥AC ∴A1B1⊥A1 解析：2π 【解析】连结A 1B ，∵AA 1⊥面ABC ，平面A 1B 1C 1∥面ABC ，∴AA 1⊥平面A 1B 1C 1，∵A 1C 1⊂平面A 1B 1C 1，∴AA 1⊥A 1C 1，∵△ABC 与△A 1B 1C 1是全等三角形，AB ⊥AC ，∴A 1B 1⊥A 1C 1，∵A 1B 1∩AA 1=A 1，∴A 1C 1⊥平面AA 1B 1B ，又∵AB 1⊂平面AA 1B 1B ，∴A 1C 1⊥AB 1，∵矩形AA 1B 1B 中，AA 1=AB ，∴四边形AA 1B 1B 为正方形，可得A 1B ⊥AB 1，∵A 1B∩A 1C 1=A 1，∴AB 1⊥平面A 1BC 1，结合BC 1⊂平面A 1BC 1，可得AB 1⊥BC 1，即异面直线AB 1与BC 1所成角为2π． 故答案为2π．15．【解析】∵向量与是共线向量∴∴或∵∴即∴则∴故答案为解析：22【解析】∵向量(21,3)a m =+与(2,)b m =是共线向量∴(21)6m m +=∴32m =或2m =- ∵0a b ⋅<∴(21)230m m +⨯+<，即27m <-∴2m =-，则(2,2)b =-∴22(b =+=故答案为16．【解析】由平行四边形中对角线互相平分的性质知AC 的中点即为BD 的中点AC 的中点设D(xyz)则∴x ＝5y ＝13z ＝－3故D(513－3)解析：(5,13,3)-【解析】由平行四边形中对角线互相平分的性质知，AC 的中点即为BD 的中点，AC 的中点7(,4,1)2O - ，设D (x ，y ，z )， 则7251,4,12222x y z +-++==-= ∴x ＝5，y ＝13，z ＝－3，故D (5,13，－3)．17．【分析】以点为坐标原点所在直线分别为轴建立空间直角坐标系利用空间向量法计算出异面直线的公垂线的长度即为所求【详解】由题意可知线段长度的最小值为异面直线的公垂线的长度如下图所示以点为坐标原点所在直线分解析：13【分析】以点D 为坐标原点，DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系，利用空间向量法计算出异面直线1C D 、AC 的公垂线的长度，即为所求.【详解】由题意可知，线段PQ 长度的最小值为异面直线1C D 、AC 的公垂线的长度.如下图所示，以点D 为坐标原点，DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系，则点()1,0,0A 、()0,1,0C 、()10,1,2C 、()0,0,0D ，所以，()1,1,0AC =-，()10,1,2=DC ，()1,0,0DA =，设向量(),,n x y z =满足n AC ⊥，1⊥n DC ，由题意可得1020n AC x y n DC y z ⎧⋅=-+=⎪⎨⋅=+=⎪⎩，解得2x y y z =⎧⎪⎨=-⎪⎩，取2y =，则2x =，1z =-， 可得()2,2,1n =-， 因此，min 23DA n PQ n ⋅==. 故答案为：23. 【点睛】 关键点点睛：解本题的关键在于将PQ 长度的最小值转化为异面直线AC 、1C D 的距离，实际上就是求出两条异面直线的公垂线的长度，利用空间向量法求出两条异面直线间的距离，首先要求出两条异面直线公垂线的一个方向向量的坐标，再利用距离公式求解即可. 18．【解析】∵∴∴故答案为解析：111,,633【解析】∵ O G OM MG =+，12OM OA =，2 ,3MG MN MN ON OM ==-，1 ()2ON OB OC =+，∴111 633OG OA OB OC =++，∴16x =，13y z ==，故答案为111,,63319．【解析】距离【解析】距离d ==20．【解析】分析：设的中点为连接由余弦定理可得利用三角函数的有界性可得结果详解：设的中点为连接则是二面角的平面角可得在三角形中由余弦定理可得即的取值范围是为故答案为点睛：本题主要考查空间两点的距离余弦定解析：)【解析】分析：设AB 的中点为D ，连接,,VD CD VC ，由余弦定理可得22233cos 22VC a a VDC =-∠，利用三角函数的有界性可得结果. 详解：设AB 的中点为D ，连接,,VD CD VC ，则VD VC == VDC ∠是二面角V AB C --的平面角，可得0,1cos 1VDC VDC π<∠<-<∠<，在三角形VDC 中由余弦定理可得，2222cos VC VDC ⎫⎫=+-∠⎪⎪⎪⎪⎝⎭⎝⎭ 2233cos 22a a VDC =-∠22030VC a VC <<⇒<<，即VC 的取值范围是()，为故答案为().点睛：本题主要考查空间两点的距离、余弦定理的应用，意在考查空间想象能力、数形结合思想的应用，属于中档题. 三、解答题21．答案见解析【分析】先利用已知条件写出点坐标，设(0,,2)(02),(,2,2)(02)E a a F b b ≤≤≤≤，进而得到1,,,EF A A F C E B 的坐标，利用空间向量数量积的坐标表示求出1,EF A AE BF C ⋅⋅；若选① ：利用空间向量数量积的坐标表示公式、空间向量垂直的性质即可求解；若选② ：利用空间向量模的坐标表示公式即可得出结果；若选③ ：利用空间向量夹角的性质进行求解即可.【详解】解：由题意，正方体1111ABCD A BC D -棱长为2，则1(2,0,0),(2,2,0),(2,0,2),(0,0,0),(0,2,0)A B A D C ，设(0,,2)(02),(,2,2)(02)E a a F b b ≤≤≤≤，则1(,2,0),(2,2,2),(2,,2),(2,0,2)EF b a A AE a BF b C =-=--=-=-， 所以142(),82EF A a b AE C BF b ⋅=-+⋅=-.选择①：()()DE CF DE CF +⊥-，所以22()()0,DE CF DE CF DE CF +⋅-==，得a b =，若10EF AC ⋅=得42()0a b -+=， 则1a b ==，故存在点(0,1,2),(1,2,2)E F ，满足10EF AC ⋅=，826AE BF b ⋅=-=. 选择②：因为17||2DE =，=， 得12a =， 若10EF AC ⋅=， 即42()0a b -+=，得32b =. 故存在点130,,2,,2,222E F ⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭， 满足10EF AC ⋅=，825AE BF b ⋅=-=. 选择③：因为0cos ,1EF DB <〈〉<，所以EF 与DB 不共线，所以2b a ≠-，即2a b +≠，则142()0EF AC a b ⋅=-+≠，故不存在点,E F 满足10EF AC ⋅=. 【点睛】关键点睛：建立空间坐标系，利用空间向量数量积的坐标表示、空间向量垂直的性质、空间向量模的坐标表示公式以及空间向量夹角的性质是解决本题的关键.22．（1）详见解析；（2）66. 【分析】（1）根据四边形ABB 1A 1和ADD 1A 1均为正方形，得到11,AA AB AA AD ⊥⊥，再由线面垂直的判定定理证得1AA ⊥平面ABCD ，然后利用面面垂直的判定定理证明.（2）以A 为原点，以1,,AB AD AA 分别为x ,y ,z 轴，建立空间直角坐标系,求得平面1BCD 的一个法向量为(),,m x y z =，又平面CDA 的一个法向量为()0,0,1n =，然后由cos ,m n m n m n ⋅=⋅求解.【详解】 （1）因为四边形ABB 1A 1和ADD 1A 1均为正方形.所以11,,AA AB AA AD AB AD A ⊥⊥⋂=，所以1AA ⊥平面ABCD ；又因为1AA ⊂平面ABB 1A 1，所以平面ABB 1A 1平面ABCD ；（2）以A 为原点，以1,,AB AD AA 分别为x ,y ,z 轴，建立空间直角坐标系：则()()()()10,0,0,2,1,0,0,2,0,2,0,2A C D B ，所以()()12,1,0,0,1,2CD CB =-=-，设平面1BCD 的一个法向量为(),,m x y z =， 则100m CD m CB ⎧⋅=⎪⎨⋅=⎪⎩，即2020x y y z -+=⎧⎨-+=⎩， 令1,2,1x y z ===，则()1,2,1m =，又平面CDA 的一个法向量为()0,0,1n =，所以16cos ,66m nm n m n ⋅===⋅， 二面角B 1CD-A 的余弦值是66【点睛】 方法点睛：求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐角还是钝角．23．（1）证明见解析；（2）2211. 【分析】（1）取SC 的中点F ，连接,DF EF ，证明四边形ADFE 为平行四边形，可得//AE DF ，即可证//AE 平面SCD ；（2）建立如图所示空间直角坐标系，然后写出各点坐标，得平面ABE 的法向量为AD ，计算平面ACE 的法向量m ，利用数量积公式代入计算二面角的余弦值.【详解】（1）证明：取SC 的中点F ，连接,DF EF因为E 、F 为SB 、SC 的中点，所以//EF BC 且132EF BC ==，又因为//AD BC ，3AD =，6BC =，所以//EF AD 且EF AD =，所以四边形ADFE 为平行四边形，所以//AE DF ，又AE ⊄平面SCD ，DF ⊂平面SCD ，所以//AE 平面SCD ． （2）因为SA ⊥平面ABCD ，AD AB ⊥，所以建立如图所示空间直角坐标系， 则(0,0,0),(4,0,0),(4,6,0),(0,3,0),(2,0,2)A B C D E ，(2,0,2),(4,0,0),(4,6,0)AE AB AC ===，(0,3,0)AD = 由题意可知AD ⊥平面ABE ，设平面ACE 的法向量(,,)m x y z =所以00AC m AE m ⎧⋅=⎨⋅=⎩，则460220x y x z +=⎧⎨+=⎩，得(3,2,3)m =-- 设二面角B AE C --的平面角为θ， 所以622cos cos ,322AD m θAD m AD m ⋅-====⨯，所以二面角B AE C --的余弦值为2211.【点睛】本题考查了立体几何中的线面平行的判定和二面角的求解问题，意在考查学生的空间想象能力和逻辑推理能力；解答本题关键在于能利用直线与直线、直线与平面关系的相互转化，通过中位线平行证明线线平行，同时对于立体几何中角的计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解.24．（1）证明见解析（2）22（3）155 【分析】(1)由PB PD =可得出PO BD ⊥，再由菱形性质可得AC BD ⊥，即可证明BD ⊥平面POC ，可得PC BD ⊥；（2）先证明OP ⊥平面ABCD ，可以O 为原点，以OB ，OC ，OP 为坐标轴建立空间直角坐标系，利用向量法求线面角；（3）由（2）利用向量法求二面角的余弦值.【详解】（1）设,AC BD 交点为O ,连接PO ，ABCD 是边长为2的菱形，,AC BD O ∴⊥是,AC BD 的中点，,PD O B BD P P =∴⊥，又PO ⊂平面POC ,AC ⊂平面 POC ，PO AC O =，BD ∴⊥平面POC ，PC ⊂平面POC ，.C BD P ∴⊥（2）60,2,A D B D A A B ︒===∠ABD ∴是等边三角形，又AB PB PD ==PBD ∴是等边三角形， 3P OA O ∴== 222OP PA OA +∴=，OA OP ∴⊥又,OP OB OA OB O ⊥⋂=OP ∴⊥平面ABCD ，以O 为原点，以OB ，OC ，OP 为坐标轴建立空间直角坐标系如图:则(1,0,0),3,0),3)B C P ，(0,3,3PC ∴=-，而3,0)OC →=是平面 PBD 的一个法向量，设直线PC 与平面PBD 所成角为θ， 则||2sin 263|||||PC OC PC OC θ→→→→⋅===⋅ 所以直线PC 与平面PBD 所成角的正弦值为22. (3)由（2）知(3,0)BC →=-,(3,3PC =-设平面BPC 的法向量n (x,y,z)→=， 则.0.0n PC n BC ⎧=⎨=⎩,33030y z x y ⎧-=⎪∴⎨-+=⎪⎩, 令1y =，得3,1x z ==，所以(3,1,1)n →=，又BD ⊥平面EPC , (1,0,0)m ∴=是平面 EPC 的一个法向量，315cos ,||||515m n m n m n ⋅∴〈〉===⋅⋅， ∴二面角B PC E --的余弦值为155. 【点睛】关键点点睛：根据题目所给条件，利用平面几何知识证明OA OP ⊥，再根据OP OB ⊥，证明OP ⊥平面ABCD ，得以O 为原点，以OB ，OC ，OP 为坐标轴建立空间直角坐标系是解题的关键所在.25．（1）点M 在CE 的中点处，证明见解析；（2）32. 【分析】（1）首先观察图形的特征，确定点M 的位置，之后利用线面平行的判定定理证明即可； （2）建立空间直角坐标系，设出边长，写出点的坐标，利用向量法求得线面角的正弦值.【详解】（1）点M 在CE 的中点处，证明如下：取BC 中点P ，连接,BP AP ，根据题意，可知//,PM AF PM AF =，所以四边形AFMP 是平行四边形，所以//AP MF ，又因为FM ⊄平面ABCD ，AP ⊂平面ABCD ，所以//MF 平面ABCD ；（2）设1AF AB AD ===，如图建立空间直角坐标系，则有1(1,0,1),(1,1,0),(0,1,),(0,0,0)2D F M B ，所以(0,1,1)DF =-，1(1,1,0),(0,1,)2BF BM ==，设平面BFM 的法向量为(,,)n x y z =， 则有00n BF n BM ⎧⋅=⎨⋅=⎩，即0102x y y z +=⎧⎪⎨+=⎪⎩，取1y =，则有1,2x z =-=-， 所以平面BFM 的一个法向量为(1,1,2)n =--， 所以03cos ,26DF nDF n DF n ⋅+<>===⋅， 所以直线DF 与平面BFM 3 【点睛】 思路点睛：该题考查的是有关立体几何的问题，解题思路如下：（1）首先根据图形的特征，判断出点的位置，之后利用线面平行的判定定理证明即可； （2）在证明的过程中，注意线在面外和线在面内的条件；（3）建立空间直角坐标系，求得平面的法向量和直线的方向向量；（4）利用向量所成角的余弦值得到线面角的正弦值.26．（Ⅰ）证明见解析；（Ⅱ）3913. 【分析】（Ⅰ）取AD 的中点G ，连结PG 、GB 、BD ，根据PA PD =和ABD △是正三角形，证明AD ⊥平面PGB 即可.（Ⅱ）根据侧面PAD ⊥底面ABCD ，PG AD ⊥，易得直线GA 、GB 、GP 两两互相垂直，以G 为原点，直线GA 、GB 、GP 所在直线为x 轴、y 轴和z 轴建立空间直角坐标系G xyz -，求得平面PBC 的一个法向量()000,,n x y z =，再由平面PAD 的一个法向量1(0,3,0)n GB a ==，设平面PAD 与平面PBC 所成锐二面角为θ，由11cos ||n n n n θ⋅=⋅求解. 【详解】（Ⅰ）如图所示：取AD 的中点G ，连结PG 、GB 、BD ．PA PD =，PG AD ∴⊥AB AD =，且60DAB ∠=︒，ABD ∴是正三角形，BG AD ⊥，又PG BG G =，AD ∴⊥平面PGB ．AD PB ∴⊥（Ⅱ）∵侧面PAD ⊥底面ABCD ，又PG AD ⊥，PG ∴⊥底面ABCD ．PG BG ∴⊥．∴直线GA 、GB 、GP 两两互相垂直，故以G 为原点，直线GA 、GB 、GP 所在直线为x 轴、y 轴和z 轴建立如图所示的空间直角坐标系G xyz -．设PG a =，则可求得(0,0,)P a ，(,0,0)A a ，3,0)B a ，(,0,0)D a -，33,02C a ⎛⎫- ⎪ ⎪⎝⎭． 33,,02BC a ⎛⎫∴=- ⎪ ⎪⎝⎭．(0,3,)PB a a ∴=-． 设()000,,n x y z =是平面PBC 的一个法向量，则0n BC ⋅=且0n PB ⋅=．0000330,230.ax ay az ⎧-=⎪∴⎪-=⎩解得00003,3.x y z y ⎧=⎪⎨⎪=⎩ 取03y =(1,3,3)n =-．又∵平面PAD 的一个法向量13,0)n GB a ==，设平面PAD 与平面PBC 所成锐二面角为θ， 则1139cos ||1393n n n n aθ⋅===⋅++⋅ 所以平面PAD 与平面PBC 39 【点睛】 方法点睛：求二面角最常用的方法：1、几何法：二面角的大小用它的平面角来度量．平面角的作法常见的有①定义法；②垂面法．注意利用等腰、等边三角形的性质．向量法：分别求出二面角的两个面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐角还是钝角．。

第二章测评( 时间:120分钟满分:150分)一、选择题( 本大题共12个小题，每小题5分，共60分、在每小题给出的四个选项中，只有一项是符合题目要求的)1、在以下命题中，不正确的有( )①|a|-|b|=|a+b|是a，b共线的充要条件;②若a∥b，则存在唯一的实数λ，使a=λb;③若向量a，b，c构成空间的一个基底，则a+b，b+c，c+a构成空间的另一个基底;④|( a·b )c|=|a||b||c|、A、1个B、2个C、3个D、4个详细解析:只有③正确，故选C、正确答案:C2、如图，已知四面体ABCD，E，F，G，H分别为AB，BC，CD，AC的中点，则)=( )A、B、C、D、详细解析:∵)=)=，又∵，∴)=、正确答案:C3、已知A( 2，-4，-1 )，B( -1，5，1 )，C( 3，-4，1 )，D( 0，0，0 )，令a=，b=，则a+b=( )A、( 5，-9，2 )B、( -5，9，-2 )C、( 5，9，-2 )D、( 5，-9，-2 )详细解析:∵A( 2，-4，-1 )，B( -1，5，1 )，C( 3，-4，1 )，D( 0，0，0 )，∴a==( -1，0，-2 )，b==( -4，9，0 )，∴a+b=( -5，9，-2 )、正确答案:B4、已知O-ABC是四面体，G1是△ABC的重心，G是OG1上一点，且OG=3GG1，若=x+y+z，则( x，y，z )为( )A、B、C、D、详细解析:如图，连接AG1并延长交BC于点E，则E为BC的中点，∴)=-2)，-2)、∵=3=3( )，∴)=，故选A、正确答案:A5、设x>y>0>z，空间向量m=，n=，且x2+9z2=4y( x-y )，则m·n的最小值是( )A、2B、4C、2D、5详细解析:∵空间向量m=，n=，∴m·n=x2++9z2=4y( x-y )+≥2=4、当且仅当4y( x-y )=时取等号、则m·n的最小值是4、正确答案:B6、如图，正方体ABCD-A1B1C1D1中，点E，F分别在A1D，AC上，且A1E=A1D，AF=AC，则( )A、EF至多与A1D，AC之一垂直B、EF与A1D，AC都垂直C、EF与BD1相交D、EF与BD1异面详细解析:以D为坐标原点，分别以的方向为x轴、y轴、z轴的正方向建立空间直角坐标系D-xyz，设正方体的棱长为3，则A( 3，0，0 )，C( 0，3，0 )，D( 0，0，0 )，A1( 3，0，3 )，E( 1，0，1 )，F( 2，1，0 )，B( 3，3，0 )，D1( 0，0，3 )，∴=( -3，0，-3 )，=( -3，3，0 )，=( 1，1，-1 )，∴=0，=0，∴，∴A1D⊥EF，AC ⊥EF、又=( -3，-3，3 )，∴=-3，即BD1与EF平行、故选B、正确答案:B7、已知空间三点O( 0，0，0 )，A( -1，1，0 )，B( 0，1，1 )，在直线OA上有一点H满足BH ⊥OA，则点H的坐标为( )A、( -2，2，0 )B、( 2，-2，0 )C、D、详细解析:由=( -1，1，0 )，且点H在直线OA上，可设H( -λ，λ，0 )，则=( -λ，λ-1，-1 )、又BH⊥OA，∴=0，即( -λ，λ-1，-1 )·( -1，1，0 )=0，即λ+λ-1=0，解得λ=，∴H，故选C、正确答案:C8、如图，正四棱锥S-ABCD中，O为顶点在底面内的投影，P为侧棱SD的中点，且SO=OD，则直线BC与平面PAC的夹角是( )A、30°B、45°C、60°D、90°详细解析:如图，以O为坐标原点建立空间直角坐标系O-xyz、设OD=SO=OA=OB=OC=a，则A( a，0，0 )，B( 0，a，0 )，C( -a，0，0 )，P，则=( 2a，0，0 )，=( a，a，0 )，设平面PAC的一个法向量为n，可取n=( 0，1，1 )，则cos<，n>=，所以<，n>=60°，所以直线BC与平面PAC的夹角为90°-60°=30°、正确答案:A9、如图，正方体ABCD-A1B1C1D1的棱长为1，E是A1B1的中点，则点E到平面ABC1D1的距离是( )A、B、C、D、详细解析:建立如图所示的坐标系，∵正方体的棱长为1，∴A( 1，0，0 )，B( 1，1，0 )，C( 0，1，0 )，D( 0，0，0 )，C1( 0，1，1 )，D1( 0，0，1 )，E、设平面ABC1D1的法向量为n=( x，y，z )、∴n·=0，且n·=0，即( x，y，z )·( 0，1，0 )=0，且( x，y，z )·( -1，0，1 )=0、∴y=0，且-x+z=0，令x=1，则z=1，∴n=( 1，0，1 )、∴n0=、又，∴点E到平面ABC1D1的距离为|·n0|=、正确答案:B10、如图，在四面体P-ABC中，PC⊥平面ABC，AB=BC=CA=PC，则平面ABP与平面APC的夹角的余弦值为( )A、B、C、D、详细解析:取AC的中点D，连接BD，过D作DE∥PC，以DB，DC，DE所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系、由图知平面APC的法向量为、设AB=1，则D( 0，0，0 )，B，A，C，P，∴=( 0，-1，-1 )，、设平面PAB的法向量为n=( x，y，z )，则令y=3，∴n=( -，3，-3 )、∴cos<，n>==-，即平面ABP与平面APC的夹角的余弦值为、正确答案:C11、设a，b为非零向量，|b|=2|a|，两组向量x1，x2，x3，x4和y1，y2，y3，y4均由2个a和2个b排列而成，若x1·y1+x2·y2+x3·y3+x4·y4所有可能取值中的最小值为4|a|2，则a与b的夹角为( )A、B、C、D、0详细解析:设a与b的夹角为θ、x1·y1+x2·y2+x3·y3+x4·y4有以下三种可能:①2a·a+2b·b=2|a|2+2|b|2=10|a|2;②4a·b=4|a|·2|a|cos θ=8|a|2cos θ;③a·a+2a·b+b·b=|a|2+2|a||b|cos θ+|b|2=5|a|2+4|a|2cos θ、由此易知②最小，则8|a|2cos θ=4|a|2，解得cos θ=，∴θ=、正确答案:B12、导学号90074051已知平面α与平面β的夹角为60°，AB⫋α，AB⊥l，A为垂足，CD⫋β，C∈l，∠ACD=135°，则异面直线AB与CD所成角的余弦值为( )A、B、C、D、详细解析:如图，在平面α内过C作CE∥AB，则∠ECD为异面直线AB与CD所成的角或其补角，不妨取CE=1，过E作EO⊥β于O、在平面β内过O作OH⊥CD于H，连EH，则EH⊥CD、因为AB∥CE，AB⊥l，所以CE⊥l、又因为EO⊥平面β，所以CO⊥l，所以∠ECO=60°、而∠ACD=135°，CO⊥l，所以∠OCH=45°、在Rt△ECO中，CO=CE·cos∠ECO=1·cos 60°=、在Rt△COH中，CH=CO·cos∠OCH=·sin 45°=、在Rt△ECH中，cos∠ECH=、所以异面直线AB与CD所成角的余弦值为、故选B、正确答案:B二、填空题( 本大题共4个小题，每小题5分，共20分、把正确答案填在题中的横线上)13、已知l∥α，且l的方向向量为( 2，m，1 )，平面α的法向量为，则m=、详细解析:∵l∥α，∴l的方向向量与平面α的法向量垂直，即( 2，m，1 )·=0，∴2+m+2=0，∴m=-8、正确答案:-814、已知正方体ABCD-A'B'C'D'的棱长为1，设=a，=b，=c，则=、详细解析:如图，取CC'中点E，连接AC，AE、∵正方体ABCD-A'B'C'D'的棱长为1，=a，=b，=c，∴a+b+c=、∴=||=、正确答案:15、如图，PD垂直于正方形ABCD所在的平面，AB=2，E为PB的中点，cos =、以D 为原点，分别以DA，DC，DP所在直线为x轴、y轴、z轴建立直角坐标系，则点E的坐标为、详细解析:设DP=2a，则P( 0，0，2a )，B( 2，2，0 )，E( 1，1，a )，A( 2，0，0 )、∵=( 0，0，2a )，=( -1，1，a )，∴cos =，解得a=1、∴E( 1，1，1 )、正确答案:( 1，1，1 )16、如图，等边三角形ABC与正方形ABDE有一公共边AB，平面ABC与平面ABDE的夹角的余弦值为，M，N分别是AC，BC的中点，则EM，AN所成角的余弦值为、详细解析:如图所示，过点C作CO⊥平面ABDE，垂足为O，取AB的中点F，连接CF，OF，OA，OB，则∠CFO为二面角C-AB-D的平面角，∴cos∠CFO=、设AB=1，则CF=，OF=，OC=，∴O为正方形ABDE的中心、如图建立空间直角坐标系，则E，A，M，N，∴，∴cos<>=、正确答案:三、解答题( 本大题共6个小题，共70分、解答时应写出文字说明、证明过程或演算步骤)17、( 满分10分)已知空间三点A( 1，2，3 )，B( 2，-1，5 )，C( 3，2，-5 )、( 1 )求△ABC的面积;( 2 )求△ABC中AB边上的高、解( 1 )由已知，得=( 1，-3，2 )，=( 2，0，-8 )，∴||=，||==2，=1×2+( -3 )×0+2×( -8 )=-14，∴cos<>=，∴sin<>=、∴S△ABC=|·||·sin<>=×2=3、( 2 )设AB边上的高为CD，则||==3，即△ABC中AB边上的高为3、18、( 满分12分)如图，在长方体ABCD-A'B'C'D'中，AB=2，AD=1，AA'=1、证明直线BC'平行于平面D'AC，并求直线BC'到平面D'AC的距离、解如图，建立空间直角坐标系，可得有关点的坐标为A( 1，0，1 )，B( 1，2，1 )，C( 0，2，1 )，C'( 0，2，0 )，D'( 0，0，0 )、设平面D'AC的法向量n=( u，v，w )，则n⊥，n⊥、因为=( 1，0，1 )，=( 0，2，1 )，n·=0，n·=0，所以解得u=2v，w=-2v、取v=1，得平面D'AC的一个法向量n=( 2，1，-2 )、因为=( -1，0，-1 )，所以n·=0，所以n⊥、又BC'不在平面D'AC内，所以直线BC'与平面D'AC平行、由=( 1，0，0 )，得点B到平面D'AC的距离d=，所以直线BC'到平面D'AC的距离为、19、( 满分12分)如图，在三棱锥P-ABC中，PB⊥底面ABC，∠BCA=90°，PB=BC=CA=2，E为PC的中点，点F在PA上，且2PF=FA、( 1 )求证:BE⊥平面PAC;( 2 )求直线AB与平面BEF所成角的正弦值、解( 1 )∵PB⊥底面ABC，且AC⫋底面ABC，∴AC⊥PB、由∠BCA=90°，可得AC⊥CB、又PB∩CB=B，∴AC⊥平面PBC、∵BE⫋平面PBC，∴AC⊥BE、∵PB=BC，E为PC的中点，∴BE⊥PC、∵PC∩AC=C，∴BE⊥平面PAC、( 2 )以点B为坐标原点，BC所在直线为x轴，BP所在直线为z轴建立如图所示的空间直角坐标系，则B( 0，0，0 )，C( 2，0，0 )，A( 2，2，0 )，P( 0，0，2 )，E( 1，0，1 )，、设平面BEF的法向量为m=( x，y，z )，由m·=0，m·=0，得x+y+z=0，x+z=0、取x=1，则y=1，z=-1，m=( 1，1，-1 )为平面BEF的一个法向量、又=( -2，-2，0 )，∴cos<，m>==-，∴直线AB与平面BEF所成角的正弦值为、20、( 满分12分)如图，在四棱锥O-ABCD中，底面ABCD是边长为1的菱形，∠ABC=，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点、( 1 )求证:直线MN∥平面OCD;( 2 )求异面直线AB与MD夹角的大小;( 3 )求点B到平面OCD的距离、解作AP⊥CD于点P、如图，分别以AB，AP，AO所在直线为x轴、y轴、z轴建立空间直角坐标系、A( 0，0，0 )，B( 1，0，0 )，P，D，O( 0，0，2 )，M( 0，0，1 )，N、( 1 )证明:、设平面OCD的法向量为n=( x，y，z )，则n·=0，n·=0，即取z=，解得n=( 0，4，)、∵·n=·( 0，4，)=0，又MN⊈平面OCD，∴MN∥平面OCD、( 2 )设AB与MD的夹角为θ，∵=( 1，0，0 )，，∴cos θ=、∴θ=，即AB与MD的夹角的大小为、( 3 )点B到平面OCD的距离为d=，∴点B到平面OCD的距离为、21、( 满分12分)如图，在直三棱柱ABC-A1B1C1中，底面△ABC是直角三角形，AB=AC=1，AA1=2，点P是棱BB1上一点，满足=λ( 0≤λ≤1 )、( 1 )若λ=，求直线PC与平面A1BC所成角的正弦值;( 2 )若平面PA1C与平面A1BC的夹角的正弦值为，求λ的值、解以A为坐标原点，分别以AB，AC，AA1所在直线为x轴、y轴、z轴，建立空间直角坐标系Axyz、因为AB=AC=1，AA1=2，则A( 0，0，0 )，B( 1，0，0 )，C( 0，1，0 )，A1( 0，0，2 )，B1( 1，0，2 )，P( 1，0，2λ )、( 1 )由λ=得，=( 1，0，-2 )，=( 0，1，-2 )、设平面A1BC的法向量为n1=( x1，y1，z1 )，由不妨取z1=1，则x1=y1=2，从而平面A1BC的一个法向量为n1=( 2，2，1 )、设直线PC与平面A1BC所成的角为θ，则sin θ=|cos<，n1>|=，所以直线PC与平面A1BC所成的角的正弦值为、( 2 )设平面PA1C的法向量为n2=( x2，y2，z2 )，=( 1，0，2λ-2 )，由不妨取z2=1，则x2=2-2λ，y2=2，所以平面PA1C的法向量为n2=( 2-2λ，2，1 )、则cos<n1，n2>=、又因为二面角P-A1C-B的正弦值为，所以，化简得λ2+8λ-9=0，解得λ=1或λ=-9( 舍去)，故λ的值为1、22、导学号90074052( 满分12分)如图，在三棱台DEF-ABC中，AB=2DE，G，H分别为AC，BC的中点、( 1 )求证:BD∥平面FGH;( 2 )若CF⊥平面ABC，AB⊥BC，CF=DE，∠BAC=45°，求平面FGH与平面ACFD夹角的大小、( 1 )证法一连接DG，CD，设CD∩GF=O，连接OH、在三棱台DEF-ABC中，AB=2DE，G为AC的中点，可得DF∥GC，DF=GC，所以四边形DFCG为平行四边形、则O为CD的中点，又H为BC的中点，所以OH∥BD，又OH⫋平面FGH，BD⊈平面FGH，所以BD∥平面FGH、证法二在三棱台DEF-ABC中，由BC=2EF，H为BC的中点，可得BH∥EF，BH=EF，所以四边形BHFE为平行四边形、可得BE∥HF、在△ABC中，G为AC的中点，H为BC的中点，所以GH∥AB、又GH∩HF=H，所以平面FGH∥平面ABED、因为BD⫋平面ABED，所以BD∥平面FGH、( 2 )解法一设AB=2，则CF=1、在三棱台DEF-ABC中，G为AC的中点，由DF=AC=GC，可得四边形DGCF为平行四边形，因此DG∥FC、又FC⊥平面ABC，所以DG⊥平面ABC、在△ABC中，由AB⊥BC，∠BAC=45°，G是AC中点，所以AB=BC，GB⊥GC，因此GB，GC，GD两两垂直、以G为坐标原点，建立如图所示的空间直角坐标系G-xyz、所以G( 0，0，0 )，B( ，0，0 )，C( 0，，0 )，D( 0，0，1 )、可得H，F( 0，，1 )，故=( 0，，1 )、设n=( x，y，z )是平面FGH的一个法向量，则由可得可得平面FGH的一个法向量n=( 1，-1，)、因为是平面ACFD的一个法向量，=( ，0，0 )，所以cos<，n>=、所以平面FGH与平面ACFD夹角的大小为60°、解法二作HM⊥AC于点M，作MN⊥GF于点N，连接NH、由FC⊥平面ABC，得HM⊥FC，又FC∩AC=C，所以HM⊥平面ACFD、因此GF⊥NH，所以∠MNH即为所求的角、在△BGC中，MH∥BG，MH=BG=，由△GNM∽△GCF，可得，从而MN=、由HM⊥平面ACFD，MN⫋平面ACFD，得HM⊥MN，因此tan∠MNH=，所以∠MNH=60°、所以平面FGH与平面ACFD夹角的大小为60°、。

第2课时空间向量的数量积课后训练案巩固提升A组1.下列命题中正确的是()A.(a·b)2=a2·b2B.|a·b|≤|a||b|C.(a·b)·c=a·(b·c)D.若a⊥(b-c),则a·b=a·c=0解析;对于A项,左边=|a|2|b|2cos2<a,b>,右边=|a|2|b|2,∴左边≤右边,故A错误.对于C项,数量积不满足结合律,∴C错误.在D中,∵a·(b-c)=0,∴a·b-a·c=0,∴a·b=a·c,但a·b与a·c不一定等于零,故D错误.对于B项,∵a·b=|a||b|cos<a,b>,-1≤cos<a,b>≤1,∴|a·b|≤|a||b|,故B正确.答案;B2.如图,已知空间四边形每条边和对角线长都等于a,点E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于a2的是()A.2B.2C.2D.2解析;2=-a2,故A错;2=-a2,故B错;2=-a2,故D错;2=a2,故只有C正确.答案;C3.如图,已知PA⊥平面ABC,∠ABC=120°,PA=AB=BC=1,则PC等于()A. B.1C.2D.4解析;∵,∴+2=1+1+1+2×1×cos 60°=4, ∴||=2.答案;C4.已知a,b是两个非零向量,现给出以下命题;①a·b>0⇔<a,b>∈;②a·b=0⇔<a,b>=;③a·b<0⇔<a,b>∈;④|a·b|=|a||b|⇔<a,b>=π.其中正确的命题有()A.1个B.2个C.3个D.4个解析;利用向量数量积公式可对以上四个命题的真假作出判断.∵a,b为非零向量,∴|a|≠0,|b|≠0.又∵a·b=|a||b|cos<a,b>,且0≤<a,b>≤π,于是a·b>0⇔cos<a,b>>0⇔<a,b>∈;a·b=0⇔cos<a,b>=0⇔<a,b>=;a·b<0⇔cos<a,b><0⇔<a,b>∈.因此,命题①②③均为真命题.∵|a·b|=|a||b|⇔|cos<a,b>|=1⇔<a,b>=0或π,∴|a·b|=|a||b|⇔<a,b>=π不正确,即命题④为假命题.故选C.答案;C5.若|a|=|b|,且非零向量a,b不平行,则a+b与a-b所在直线所形成的角的大小是.解析;如图,作=a,=b,以为邻边作▱OACB,则=a+b,=a-b.又∵|a|=|b|,∴四边形OACB为菱形,∴,故a+b与a-b的夹角为.答案;6.导学号90074024已知|a+b|=2,|a-b|=3,且cos<a+b,a-b>=,则|a|=,|b|=.解析;由|a+b|=2,知a2+2a·b+b2=4.由|a-b|=3,知a2-2a·b+b2=9.故2a2+2b2=13,则|a|2+|b|2=.①由cos<a+b,a-b>=,得|a|2-|b|2=.②由①②,得|a|=2,|b|=.答案;27.已知a,b,c中每两个的夹角都是,且|a|=4,|b|=6,|c|=2,试计算|a+b+c|.解∵|a|=4,|b|=6,|c|=2,且<a,b>=<a,c>=<b,c>=,∴|a+b+c|2=(a+b+c)·(a+b+c)=|a|2+|b|2+|c|2+2a·b+2a·c+2b·c=|a|2+|b|2+|c|2+2|a||b|cos<a,b>+2|a||c|·cos<a,c>+2|b||c|cos<b,c>=42+62+22+4×6+4×2+6×2=100,∴|a+b+c|=10.8.如图,在四面体A-BCD中,AB=2,BC=3,BD=2,CD=3,∠ABD=30°,∠ABC=60°,求AB与CD的夹角的余弦值.解∵,∴=||·||·cos<>-||·||·cos< >=2×2×cos 150°-2×3×cos 120°=-6+3=-3,∴cos<>==-,∴AB与CD的夹角的余弦值为.9.如图,在正三棱柱ABC-A1B1C1中,若侧面对角线AB1⊥BC1,求证;A1C⊥AB1.证明由题意,设=a,=b,=c,|a|=|b|=m,|c|=n,则a·b=m2cos 60°=,a·c=b·c=0.∵AB1⊥BC1,且=-a+c,=b+c,∴=(-a+c)·(b+c) =-a·b+c2=n2-m2=0,即m2=2n2,∴=(-a+c)·()=(-a+c)·(-c-a+b)=a2-c2-a·b=m2-n2-m2=0,∴A1C⊥AB1.B组1.设a,b,c是任意的非零向量,且它们相互不共线,下列命题;①(a·b)·c-(c·a)·b=0;②|a|-|b|<|a-b|;③(b·a)·c-(a·c)·b不与c垂直;④(3a+2b)·(3a-2b)=9|a|2-4|b|2.其中正确的有()A.①②B.②③C.③④D.②④解析;根据向量的数量积运算,结合模及向量垂直的性质知①③不正确,②④正确.答案;D2.平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,∠BAD=90°,∠BAA1=∠DAA1=60°,则AC1的长为()A. B. C. D.解析;∵,∴||==.∵AB=1,AD=2,AA1=3,∠BAD=90°,∠BAA1=∠DAA1=60°,∴<>=90°,<>=<>=60°.∴||=.答案;B3.设A,B,C,D是空间不共面的四点,且满足=0,则△BCD为()A.钝角三角形B.锐角三角形C.直角三角形D.不确定解析;,∴cos<>=>0,∴<>为锐角,同理cos <>>0,∴∠BCD为锐角,cos<>>0,∴∠BDC为锐角,即△BCD为锐角三角形.答案;B4.如图,在正方体ABCD-A1B1C1D1中,O为AC与BD的交点,G为CC1的中点,用向量法证明;A1O⊥平面GBD.证明设=a,=b,=c,则a·b=0,b·c=0,a·c=0.而)=c+(a+b),=b-a,)+(a+b)-c,所以·(b-a)=c·(b-a)+(a+b)·(b-a)=c·b-c·a+(|b|2-|a|2)=(|b|2-|a|2)=0.所以.所以A1O⊥BD.同理可证,所以A1O⊥OG.又因为OG∩BD=O,且A1O⊈平面GBD,所以A1O⊥平面GBD.5.在平行六面体ABCD-A1B1C1D1中,∠A1AB=∠A1AD=∠BAD=60°,AA1=AB=AD=.(1)求||;(2)求证;AC1⊥平面A1BD;(3)求的夹角.(1)解令=a,=b,=c,则=a+b+c,∴||=|a+b+c|==(a2+b2+c2+2a·b+2b·c+2c·a=+2×+2×=3.(2)证明=a-c,∴=(a+b+c)·(a-c)=a2-a·c+b·a-b·c+c·a-c2=0.∴,又=b-c,同理,∴AC垂直于平面A1BD内的两条相交直线A1D,A1B,∴AC1⊥平面A1BD.1(3)解cos<>===-.∴的夹角为π-arccos.6.导学号90074025如图,正方形ABCD与正方形ABEF的边长均为1,且平面ABCD⊥平面ABEF,点M 在AC上移动,点N在BF上移动.若CM=BN=a(0<a<).(1)求MN的长度;(2)求当a为何值时,MN的长最小.解(1)由题意,得AC=,BF=,CM=BN=a,∴.∴==)+)=)-(-)=.∴||===(0<a<).(2)由(1),知当a=时,||有最小值为,即M,N分别为AC,BF的中点时,MN的长最小,且最小值为.。

§4 用向量讨论垂直与平行课后训练案巩固提升A组1.已知a,b,c分别为直线a,b,c的方向向量,且a=λb(λ≠0),b·c=0,则a与c的位置关系是()A.垂直B.平行C.相交D.异面解析;由a=λb(λ≠0),知a∥b.由b·c=0,知b⊥c,所以a⊥c.故选A.答案;A2.已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的一个单位法向量是()A. B.C. D.解析;=(-1,1,0),=(-1,0,1),=(0,-1,1).设平面ABC的一个单位法向量为u=(,y,),则u·=0,u·=0,可得,y,间的关系,且2+y2+2=1,再求出,y,的值.答案;D3.若平面α的法向量为u=(1,-3,-1),平面β的法向量为v=(8,2,2),则()A.α∥βB.α与β相交C.α⊥βD.不确定解析;∵平面α的法向量为u=(1,-3,-1),平面β的法向量为v=(8,2,2),∴u·v=(1,-3,-1)·(8,2,2)=8-6-2=0.∴u⊥v,∴α⊥β.答案;C4.给出下列命题;①若n1,n2分别是平面α,β的法向量,则n1∥n2⇔α∥β;②若n1,n2分别是平面α,β的法向量,则α∥β⇔n1·n2=0;③若n是平面α的法向量,且向量a与平面α共面,则a·n=0;④若两个平面的法向量不垂直,则这两个平面一定不垂直.其中正确命题的个数是()A.1B.2C.3D.4解析;①②不正确.答案;B5.导学号90074037如图,在平行六面体ABCD-A1B1C1D1中,M,P,Q分别为棱AB,CD,BC的中点,若平行六面体的各棱长均相等,则①A1M∥D1P;②A1M∥B1Q;③A1M∥平面DCC1D1;④A1M∥平面D1PQB1.以上结论正确的是.(填序号)解析;∵,∴A1M∥D1P.又∵D1P⫋平面D1PQB1,∴A1M∥平面D1PQB1.又D1P⫋平面DCC1D1,∴A1M∥平面DCC1D1.∵D1B1与PQ平行不相等,∴B1Q与D1P不平行.∴A1M与B1Q不平行.答案;①③④6.已知=(1,5,-2),=(3,1,),=(-1,y,-3).若,且BP⊥平面ABC,则实数,y,的值分别为.解析;∵=(1,5,-2),=(3,1,),,∴(1,5,-2)·(3,1,)=0,即3+5-2=0,∴=4.①又∵=(-1,y,-3),⊥平面ABC,∴=0,即(-1,y,-3)·(1,5,-2)=0,-1+5y+6=0.②=0,即(-1,y,-3)·(3,1,4)=0,3-3+y-12=0.③由①②③得=,y=-,=4.答案;,-,47.如图,PA⊥平面ABCD,四边形ABCD为正方形,E是CD的中点,F是AD上一点,当BF⊥PE时,AF∶FD的值为.解析;建立如图所示的空间直角坐标系,设正方形边长为1,PA=a.则B(1,0,0),E,P(0,0,a).设点F的坐标为(0,y,0),则=(-1,y,0),.∵BF⊥PE,∴=0,解得y=,则点F的坐标为,∴F为AD的中点,∴AF∶FD=1.答案;18.如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.求证;平面EGF∥平面ABD.证明如图所示,由条件知BA,BC,BB1两两互相垂直,以B为坐标原点,BA,BC,BB1所在直线分别为轴、y轴、轴建立空间直角坐标系.由条件知B(0,0,0),D(0,2,2),B1(0,0,4),E(0,0,3),F(0,1,4),设BA=a,则A(a,0,0),G.所以=(a,0,0),=(0,2,2),=(0,2,-2),=(0,1,1).(方法一)因为=0,=0+4-4=0,所以B1D⊥BA,B1D⊥BD.因为BA∩BD=B,所以B1D⊥平面ABD.又=0+2-2=0,=0+2-2=0.所以B1D⊥EG,B1D⊥EF.又EG∩EF=E,所以B1D⊥平面EFG,可知平面EGF∥平面ABD. (方法二)设平面EGF的法向量为n1=(1,y1,1),则令y1=1,则n1=(0,1,-1).设平面ABD的法向量为n2=(2,y2,2),则即令y2=1,则n2=(0,1,-1).所以n1=n2,所以平面EGF∥平面ABD.9.如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.求证;AB1⊥平面A1BD.证明如图所示,取BC的中点O,连接AO.因为△ABC为正三角形,所以AO⊥BC.因为在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,所以AO⊥平面BCC1B1.取B1C1的中点O1,以O为原点,以为轴、y轴、轴建立空间直角坐标系,则B(1,0,0),D(-1,1,0),A1(0,2, ),A(0,0,),B1(1,2,0).设平面A1BD的法向量为n=(,y,),=(-1,2,),=(-2,1,0).因为n⊥,n⊥,故令=1,则y=2,=-,故n=(1,2,-)为平面A1BD的一个法向量,而=(1,2,-),所以=n,所以∥n,故AB1⊥平面A1BD.B组1.设平面α的一个法向量为(1,2,-2),平面β的一个法向量为(-2,-4,),若α∥β,则=()A.2B.-4C.4D.-2解析;∵α∥β,∴存在实数λ,使(1,2,-2)=λ(-2,-4,),∴=4.答案;C2.如图,AB是☉O的直径,VA垂直☉O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点,则下列结论正确的是()A.MN∥ABB.MN与BC所成的角为45°C.OC⊥平面VACD.平面VAC⊥平面VBC解析;因为M,N分别为VA,VC的中点,所以MN∥AC.因为AB∩AC=A,所以A选项不正确.因为AC⊥BC,所以MN与BC所成的角为90°,B选项不正确.又因为OC不垂直于AC,所以选项C不正确.因为VA垂直☉O所在的平面,依题意可得平面VAC⊥平面VBC.答案;D3.如图,定点A和B都在平面内,定点P∉α,PB⊥α,C是α内异于A和B的动点,且PC⊥AC,那么C在平面α内的轨迹是()A.一条线段,但要去掉两个点B.一个圆,但要去掉两个点C.一个椭圆,但要去掉两个点D.半圆,但要去掉两个点解析;连接BC(图略),根据题意BC为PC在平面α内的射影.∵PC⊥AC,根据三垂线定理的逆定理知AC⊥BC,∴点C在以AB为直径的圆上.又C是不同于点A和B的动点,因此应去掉端点A和B.答案;B4.如图,在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD的中点.若在棱AA1上取一点P,使得DP∥平面B1AE,此时AP 的长为.解析;以A为原点,的方向分别为轴、y轴、轴的正方向建立空间直角坐标系(如图所示).设AB=a,则A(0,0,0),D(0,1,0),D1(0,1,1),E,B1(a,0,1),故=(0,1,1),=(a,0,1), .再设P(0,0,),使得DP∥平面B1AE.此时=(0,-1,0).又设平面B1AE的法向量为n=(,y,),则取=1,得n=.要使DP∥平面B1AE,只要n⊥,有-a0=0,解得0=.又DP⊈平面B1AE,AE,此时AP=.∴存在点P,满足DP∥平面B1答案;5.如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=,CE=EF=1.求证;(1)AF∥平面BDE;(2)CF⊥平面BDE.证明(1)设AC与BD交于点G.因为EF∥AG,且EF=1,AG=AC=1,所以四边形AGEF为平行四边形,所以AF∥EG.因为EG⫋平面BDE,AF⊈平面BDE,所以AF∥平面BDE.(2)因为正方形ABCD和四边形ACEF所在的平面互相垂直,且CE⊥AC,所以CE⊥平面ABCD.如图,以C为原点,建立空间直角坐标系C-y,则C(0,0,0),A(,0),B(0,,0),D(,0,0),E(0,0,1),F.所以=(0,-,1),=(-,0,1).所以=0-1+1=0,=-1+0+1=0.所以CF⊥BE,CF⊥DE.又BE∩DE=E,所以CF⊥平面BDE.6.导学号90074038如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC.(1)求证;AC⊥PB;(2)设O,D分别为AC,AP的中点,点G为△OAB内一点,且满足),求证;DG∥平面PBC.证明(1)因为PA⊥平面ABC,AC⫋平面ABC,所以PA⊥AC.又因为AB⊥AC,且PA∩AB=A,所以AC⊥平面PAB.又因为PB⫋平面PAB,所以AC⊥PB.(2)证法一;因为PA⊥平面ABC,所以PA⊥AB,PA⊥AC.又因为AB⊥AC,所以建立如图所示的空间直角坐标系A-y.设AC=2a,AB=b,PA=2c,则A(0,0,0),B(0,b,0),C(2a,0,0),P(0,0,2c),D(0,0,c),O(a,0,0),又因为),所以G.于是=(2a,-b,0),=(0,b,-2c).设平面PBC的一个法向量n=(0,y0,0),则有不妨设0=1,则有y0=,0=,所以n=.因为n·+1·(-c)=0,所以n⊥.又因为DG⊈平面PBC,所以DG∥平面PBC.证法二;取AB中点E,连接OE,则).由已知)可得, 则点G在OE上.连接AG并延长交CB于点F,连接PF.因为O,E分别为AC,AB的中点,所以OE∥BC,即G为AF的中点.又因为D为线段PA的中点,所以DG∥PF.又DG⊈平面PBC,PF⫋平面PBC,所以DG∥平面PBC.。

3.3空间向量运算的坐标表示课后训练案巩固提升A组1.已知a=(1,-5,6),b=(0,6,5),则a与b()A.垂直B.不垂直也不平行C.平行且同向D.平行且反向解析;0+(-5)×6+6×5=0,故a⊥b.答案;A2.下列各组向量中,不平行的是()A.a=(1,2,-2),b=(-2,-4,4)B.c=(1,0,0),d=(-3,0,0)C.e=(2,3,0),f=(0,0,0)D.g=(-2,3,5),h=(16,-24,40)解析;选项A中,b=-2a,所以a∥b;选项B中,d=-3c,所以c∥d;选项C中,0与任何向量平行.答案;D3.已知向量a=(1,3,3),b=(5,0,1),则|a-b|等于()A.7B.C.3D.解析;|a-b|=|(1,3,3)-(5,0,1)|=|(-4,3,2)|=.答案;B4.若向量a=(1,λ,2),b=(-2,1,1),a,b夹角的余弦值为,则λ=()A.1B.-1C.±1D.2解析;∵a=(1,λ,2),b=(-2,1,1),a,b夹角的余弦值为,又a·b=|a||b|·cos<a,b>, ∴-2+λ+2=.∴λ=±1.∵a·b=λ>0,∴λ=1.答案;A5.已知三个力F1=(1,2,1),F2=(-1,-2,3),F3=(2,2,-1),则这三个力的合力的坐标为()A.(2,2,3)B.(0,0,0)C. D.0解析;F1+F2+F3=(1,2,1)+(-1,-2,3)+(2,2,-1)=(2,2,3).答案;A6.已知点A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形解析;=(5,1,-7),=(2,-3,1).因为=2×5-3×1-7×1=0,所以.所以∠ACB=90°.又因为||=5,||=,即||≠||,所以△ABC为直角三角形.答案;C7.已知向量a=(4-2m,m-1,m-1)与b=(4,2-2m,2-2m)平行,则m的值等于.解析;当m=1时,a=(2,0,0),b=(4,0,0),显然满足a∥b;当m≠1时,则依a∥b则有=-,解得m=3.综上可知m=1或m=3.答案;1或38.导学号90074033若=(-4,6,-1),=(4,3,-2),|a|=1,且a⊥,a⊥,则a= .解析;设a=(,y,),则有解此方程组得答案;9.已知向量a=(1,-3,2),b=(-2,1,1),点A(-3,-1,4),B(-2,-2,2).(1)求|2a+b|.(2)在直线AB上是否存在一点E,使⊥b(O为原点)?若存在,求出点E坐标;若不存在,说明理由.解(1)∵2a+b=(2,-6,4)+(-2,1,1)=(0,-5,5),∴|2a+b|==5.(2)假设存在这样的点E,则+t=(-3,-1,4)+t(1,-1,-2)=(-3+t,-1-t,4-2t).若⊥b,则·b=0,即-2(-3+t)+(-1-t)+(4-2t)=0,解得t=,故存在点E,使⊥b,此时E点坐标为.10.已知a=(,4,1),b=(-2,y,-1),c=(3,-2,),a∥b,b⊥c,求;(1)a,b,c;(2)a+c与b+c所成角的余弦值.解(1)∵a∥b,∴,解得=2,y=-4,故a=(2,4,1),b=(-2,-4,-1).又b⊥c,∴b·c=0,即-6+8-=0,解得=2,故c=(3,-2,2).(2)由(1)可得a+c=(5,2,3),b+c=(1,-6,1),设向量a+c与b+c所成的角为θ,则cos θ==-.B组1.长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则向量所成角的余弦值为()A. B. C. D.解析;建立坐标系如图,则A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2).所以=(-1,0,2),=(-1,2,1),故cos<>=.所以向量所成角的余弦值为.答案;B2.已知向量a=(1,2,3),b=(,2+y-2,y),并且a,b同向,则,y的值分别为.解析;由题意知a∥b,所以,即把①代入②得2+-2=0,(+2)(-1)=0,解得=-2,或=1,当=-2时,y=-6;当=1时,y=3.当时,b=(-2,-4,-6)=-2a,两向量a,b反向,不符合题意,所以舍去.当时,b=(1,2,3)=a,a与b同向,所以答案;1,33.已知向量a=(0,-1,1),b=(2,2,1),计算;(1)|2a-b|;(2)cos a,b;(3)2a-b在a上的投影.解(1)∵a=(0,-1,1),b=(2,2,1),∴2a-b=2(0,-1,1)-(2,2,1)=(-2,-4,1),∴|2a-b|=.(2)∵a=(0,-1,1),b=(2,2,1),∴a·b=(0,-1,1)·(2,2,1)=-2+1=-1,|a|=,|b|==3,∴cos a,b==-.(3)∵(2a-b)·a=(-2,-4,1)·(0,-1,1)=5,∴2a-b在a上的投影为.4.已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5),求以为邻边的平行四边形面积.解∵A(0,2,3),B(-2,1,6),C(1,-1,5),∴=(-2,1,6)-(0,2,3)=(-2,-1,3),=(1,-1,5)-(0,2,3)=(1,-3,2).∴||=,||=,=(-2,-1,3)·(1,-3,2)=-2+3+6=7.∴cos<>=,∴sin<>=.以为邻边的平行四边形的面积S=||||sin<>=7.5.已知空间三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a=,b=.(1)若|c|=3,c∥,求c;(2)若a+b与a-2b互相垂直,求.解(1)∵=(-3,0,4)-(-1,1,2)=(-2,-1,2)且c∥,∴设c=λ=λ(-2,-1,2)=(-2λ,-λ,2λ).∴|c|==3|λ|=3.解得λ=±1,∴c=(-2,-1,2)或c=(2,1,-2).(2)∵a==(-1,1,2)-(-2,0,2)=(1,1,0),b==(-3,0,4)-(-2,0,2)=(-1,0,2),∴a+b=(1,1,0)+(-1,0,2)=(-1,,2),a-2b=(1,1,0)-2(-1,0,2)=(+2,,-4).∵(a+b)⊥(a-2b),∴(a+b)·(a-2b)=0,即(-1,,2)·(+2,,-4)=22+-10=0.解得=2或=-.6.导学号90074034在Rt△ABC中,AC=BC=1,∠BCA=90°.现将△ABC沿着与平面ABC的垂直的方向平移到△A1B1C1的位置,已知AA1=2,分别取A1B1,A1A的中点P,Q.(1)求的模;(2)求cos,cos,并比较 大小;(3)求证;AB1⊥C1P.解以C为原点,建立如图所示的空间直角坐标系,则由已知得C(0,0,0),A(1,0,0),B(0,1,0),C'(0,0,2),P,Q(1,0,1),B(0,1,2),A1(1,0,2),1则=(1,-1,1),=(0,1,2),=(1,-1,2),=(-1,1,2),.(1)||=.(2)∵=0-1+2=1,||=,||=,∴cos=.又∵=0-1+4=3,,||=,∴cos=.∵0<<1,∴ , .又y=cos 在内递减,∴>.(3)证明;∵=(-1,1,2)·=0,∴,即AB⊥C1P.1。