下载文档原格式
热分析动力学一、 基本方程对于常见的固相反应来说，其反应方程可以表示为)(C )(B )(A g s s +→ （1）其反应速度可以用两种不同形式的方程表示：微分形式 )(d d ααf k t= （2） 和积分形式t k G =)(α （3）式中：α――t 时物质A 已反应的分数；t ――时间；k ――反应速率常数；f (α)—反应机理函数的微分形式； G(α)――反应机理函数的积分形式。
由于f （α）和G （α）分别为机理函数的微分形式和积分形式，它们之间的关系为：ααααd /)]([d 1)('1)(G G f == （4）k 与反应温度T （绝对温度）之间的关系可用著名的Arrhenius 方程表示：)/exp(RT E A k -= （5）式中：A ――表观指前因子； E ――表观活化能； R ――通用气体常数。
方程（2）～（5）是在等温条件下出来的，将这些方程应用于非等温条件时，有如下关系式：t T T β0+= （6）即：β/=t d dT式中：T 0――DSC 曲线偏离基线的始点温度（K ）； β――加热速率（K ·min -1）。
于是可以分别得到：非均相体系在等温与非等温条件下的两个常用动力学方程式：)E/RT)f(A t d d αexp(/-=α (等温) （7）)/exp()(βd d RT E f AT -=αα (非等温) （8）动力学研究的目的就在于求解出能描述某反应的上述方程中的“动力学三因子” E 、A 和f(α)对于反应过程的DSC 曲线如图所示。
在DSC 分析中，α值等于H t /H 0，这里H t 为物质A ′在某时刻的反应热，相当于DSC 曲线下的部分面积，H 0为反应完成后物质A ′的总放热量，相当于DSC 曲线下的总面积。
二、 微分法2．1 Achar 、Brindley 和Sharp 法：对方程)/exp()(βd d RT E f AT -=αα进行变换得方程：)/exp(d d )(βRT E A Tf -=αα （9）对该两边直接取对数有：RTEA T f -=ln d d )(βln αα （10）由式（11）可以看出，方程两边成线性关系。
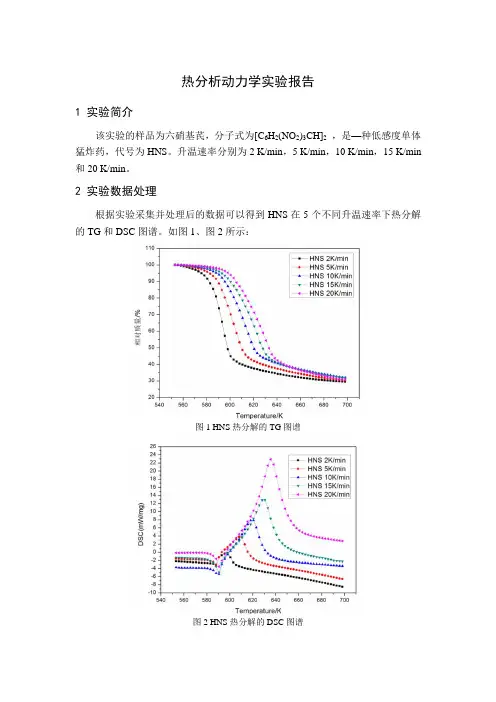
热分析动力学实验报告1 实验简介该实验的样品为六硝基芪，分子式为[C6H2(NO2)3CH]2，是—种低感度单体猛炸药，代号为HNS。
升温速率分别为2 K/min，5 K/min，10 K/min，15 K/min 和20 K/min。
2 实验数据处理根据实验采集并处理后的数据可以得到HNS在5个不同升温速率下热分解的TG和DSC图谱。
如图1、图2所示：图1 HNS热分解的TG图谱图2 HNS热分解的DSC图谱根据图1的TG 图谱，可得到5个升温速率下HNS 的相对失重量，起始温度和终止温度，具体如表1所示：表1 HNS 的TG 图谱解析表升温速率β 相对失重量/%起始温度/K 终止温度/K2 K/min 70.56 553.15 698.155 K/min 69.69 10 K/min 68.05 15 K/min 68.15 20 K/min 69.34根据图2中的DSC 图谱，可得到5个不同升温速率下HNS 热分解的峰值温度T p ，如表2所示：表2 峰值温度T p升温速率β 峰值温度T p /K2 K/min 598.15 5 K/min 608.15 10 K/min 620.65 15 K/min 630.65 20 K/min635.65根据实验采集并处理后的数据，可以得到HNS 分别在5个升温速率的条件下转化率随温度变化而变化的曲线，如图3所示：图3 HNS 转化率曲线根据图3的转化率曲线可以得到在不同升温速率下，转化率为10%，20%，30%，40%，50%，60%，70%，80%和90%对应的温度，如表3-表7所示：表3 升温速率为2 K/min转化率/% 10 20 30 40 50 60 70 80 90 温度/K579585589591593595598602626表4 升温速率为5 K/min转化率/% 10 20 30 40 50 60 70 80 90 温度/K586592596600603606609616641表5 升温速率为10 K/min转化率/% 10 20 30 40 50 60 70 80 90 温度/K592599604608612615619625650表6 升温速率为15 K/min转化率/% 10 20 30 40 50 60 70 80 90 温度/K596604610615619623626631650表7 升温速率为20 K/min转化率/% 10 20 30 40 50 60 70 80 90 温度/K6026096156206246286326376553 活化能计算3.1 Ozawa 法已知Ozawa 法的方程为lg lg(/()) 2.3050.4567/AE RG E RT βα=--将lg β与1/T 作图，然后经过线性拟合可得该拟合直线的斜率，如图4所示，得到的斜率值即为-0.4567E/R 的值。
热分析动力学一、 基本方程对于常见的固相反应来说，其反应方程可以表示为)(C )(B )(A g s s +→ （1）其反应速度可以用两种不同形式的方程表示：微分形式 )(d d ααf k t= （2） 和积分形式t k G =)(α （3）式中：α――t 时物质A 已反应的分数；t ――时间；k ――反应速率常数；f (α)—反应机理函数的微分形式； G(α)――反应机理函数的积分形式。
由于f （α）和G （α）分别为机理函数的微分形式和积分形式，它们之间的关系为：ααααd /)]([d 1)('1)(G G f == （4）k 与反应温度T （绝对温度）之间的关系可用著名的Arrhenius 方程表示：)/exp(RT E A k -= （5）式中：A ――表观指前因子； E ――表观活化能； R ――通用气体常数。
方程（2）～（5）是在等温条件下出来的，将这些方程应用于非等温条件时，有如下关系式：t T T β0+= （6）即：β/=t d dT式中：T 0――DSC 曲线偏离基线的始点温度（K ）； β――加热速率（K ·min -1）。
于是可以分别得到：非均相体系在等温与非等温条件下的两个常用动力学方程式：)E/RT)f(A t d d αexp(/-=α (等温) （7）)/exp()(βd d RT E f AT -=αα (非等温) （8）动力学研究的目的就在于求解出能描述某反应的上述方程中的“动力学三因子” E 、A 和f(α)对于反应过程的DSC 曲线如图所示。
在DSC 分析中，α值等于H t /H 0，这里H t 为物质A ′在某时刻的反应热，相当于DSC 曲线下的部分面积，H 0为反应完成后物质A ′的总放热量，相当于DSC 曲线下的总面积。
二、 微分法2．1 Achar 、Brindley 和Sharp 法：对方程)/exp()(βd d RT E f AT -=αα进行变换得方程：)/exp(d d )(βRT E A Tf -=αα （9）对该两边直接取对数有：RTEA T f -=ln d d )(βln αα （10）由式（11）可以看出，方程两边成线性关系。
热分析动力学汇总热分析动力学是指研究物质在升温或降温过程中的热物性变化规律及其与化学反应动力学之间的关系。
它通过测量热量或温度随时间的变化，结合热学或动力学理论，从而揭示了化学反应的机理和动力学参数。
本文将对热分析动力学的概念、基本原理、应用领域及研究方法等方面进行详细阐述。
一、热分析动力学的概念和基本原理热分析动力学的实验方法主要有热量计法、差示扫描量热法（DSC）和热重法（TG）。
其中，热量计法通过测量材料的热量变化，得到热分解反应的热效应曲线，从而确定反应的速率等动力学参数。
差示扫描量热法是比较常用的实验方法，它通过比较样品和参比样品的热量变化，得到样品的热效应曲线，从而确定热分解反应的动力学参数。
热重法是通过测量材料在升温或降温时的质量变化，得到热分解反应的质量曲线，从而探索反应的动力学参数。
二、热分析动力学的应用领域热分析动力学在材料科学、化学工程、药学和环境科学等领域都有重要应用。
在材料科学中，热分析动力学可以用于研究材料的热性质、热稳定性和热分解反应等方面，从而指导材料的合成和加工。
在化学工程中，热分析动力学可以用于优化工艺参数、预测反应过程和评估化学工艺的安全性。
在药学中，热分析动力学可以用于研究药物的热性质和稳定性，从而指导药物的贮存和运输。
在环境科学中，热分析动力学可以用于研究污染物在环境中的分解和转化过程，从而指导环境监测和治理。
三、热分析动力学的研究方法热分析动力学的研究方法包括实验方法和理论方法。
实验方法主要是通过实验测定材料的热效应曲线或质量曲线，从而确定反应的动力学参数。
理论方法主要是通过热学和动力学理论进行模拟和计算，以预测热效应曲线或质量曲线，从而确定反应的动力学参数。
在实验方法方面，热分析动力学主要使用差示扫描量热法和热重法。
差示扫描量热法通过比较样品和参比样品的热量变化，得到样品的热效应曲线，从而确定反应的速率等动力学参数。
热重法通过测量材料在升温或降温时的质量变化，得到热分解反应的质量曲线，从而探索反应的动力学参数。
固相反应动力学的研究方法固相反应动力学是一门研究固体物质内部反应速率的领域，它在材料科学、化学、地球科学等众多领域具有重要的应用价值。
本文将介绍几种常见的固相反应动力学研究方法，包括热分析法、差示扫描量热法、X射线衍射法和傅里叶变换红外光谱法。
1. 热分析法热分析法是一种常用的固相反应动力学研究方法，它通过对固体样品在一定温升速率下的质量或尺寸的变化进行定量测量，得到反应速率与温度的关系。
常见的热分析仪器包括差热分析仪（Differential Thermal Analysis，DTA）和热重分析仪（Thermogravimetric Analysis，TGA）。
通过对样品在不同温度下的变化情况进行分析，可以确定固相反应的反应特征和反应动力学参数。
2. 差示扫描量热法差示扫描量热法是一种通过测量样品与参比物在温度变化过程中的热量差异来研究固相反应动力学的方法。
它能够定量地测定样品的吸放热效应，并根据反应过程中的热量变化确定反应速率常数和反应机理。
差示扫描量热法具有高灵敏度、快速测量等优点，被广泛应用于固相反应动力学的研究。
3. X射线衍射法X射线衍射法是一种通过测量晶体或非晶体材料对入射X射线的散射强度来研究固相反应动力学的方法。
通过分析样品在反应过程中晶格结构的变化情况，可以得到反应过程的动力学信息。
X射线衍射法具有非破坏性、精确度高等优点，被广泛应用于材料的相变、合成等领域。
4. 傅里叶变换红外光谱法傅里叶变换红外光谱法是一种通过测量样品在红外辐射下的吸收光谱来研究固相反应动力学的方法。
通过分析样品在反应过程中红外吸收峰的强度和频率的变化，可以研究固相反应的进程和反应机理。
傅里叶变换红外光谱法具有快速、灵敏度高等优点，广泛应用于催化剂、能源材料等领域的研究。
总结：固相反应动力学的研究方法包括热分析法、差示扫描量热法、X射线衍射法和傅里叶变换红外光谱法。
这些方法在研究固体内部反应速率、反应机理等方面起着重要的作用，对于材料科学、化学和地球科学等领域的发展具有重要的意义。
热分析动力学在不同领域应用的研究热分析动力学是研究物质在加热过程中的结构变化、相变、化学反应和能量转化的一种技术手段。
它通过对物质在不同温度下吸收或释放的热量进行分析，来揭示物质的热力学和动力学性质。
这项技术在不同领域的应用非常广泛，下面将重点介绍其中几个领域的研究。
首先是材料科学领域。
热分析动力学可以用来研究材料的稳定性和热稳定性。
通过对材料在不同温度下的热分解行为进行监测和分析，可以确定材料的热稳定性，并且可以推导出材料的热分解动力学参数，如活化能、反应级数等。
这对于材料的设计和制备具有重要的指导意义。
热分析动力学也可以用来研究催化剂的性能。
催化剂是很多化学反应过程中的关键组成部分，了解催化剂的性质对于提高反应效率和选择性具有重要意义。
热分析动力学可以帮助我们揭示催化剂中催化活性材料的热稳定性、表面变化和活性中心的失活机制等，为催化剂的设计和优化提供了重要的依据。
热分析动力学还可以应用于生物医学研究。
生物分子、药物和制剂在不同温度下的热分解行为和相互作用可以通过热分析动力学来研究。
这对于药物的稳定性和药物释放的控制具有重要意义。
通过研究蛋白质和核酸的热解过程，可以了解它们的结构和功能。
这对于揭示生物大分子的折叠和解离机制具有重要的意义。
热分析动力学还可以应用于环境科学和能源领域。
在固体废物处理过程中，通过热分析动力学可以揭示废物的热解行为和生成物的析出机制，有助于寻找高效的废物处理方法。
热分析动力学还可以用来研究能源材料的热分解行为，为能源的存储和转换提供重要信息。
火灾学课程
热分析动力学
（Thermal Analysis Kinetics)
定义
¾热分析动力学:
用热分析技术研究某种物理变化或化学反应(以下统称反应)的动力学
热分析技术的定量化方法
热分析动力学的目的 理论上：探讨物理变化或化学反应
的机理（尤其是非均相、不等温）
生产上：提供反应器设计参数
应用上：建立过程进度、时间和温
度之间的关系，可用于预测材料的
使用寿命和产品的保质稳定期，评
估含能材料的危险性，从而提供储
存条件。
可估计造成环境污染物质
的分解情况…
发展历史
化学动力学
源于19世纪末－20世纪初
热分析动力学
始于20世纪30年代、盛于50年代（评估高分子材料在航空航天应用中的稳定性和
使用寿命研究的需要）
)
动力学模式(机理)函数
均相反应： f ( c）= ( 1 －c）n
非均相反应：根据控制反应速率的“瓶颈”
气体扩散
相界面反应
成核和生长
常见固态反应的机理函数（理想化）1. Acceleratory(The shape of a ~T curve) Symbol f(a)g(a)
n(α)1-1/n α 1/n
P
n
α lnα
E
1
2. Sigmoid
m(1−α)[−ln(1−α)]1−1/m[-ln(1-a)]1/m A
m
α(1−α) ln[α/(1−α)] B
1
(1/2)(1−α)[−ln(1−α)]−1 [−ln(1−α)]2 B
2
(1/3)(1−α)[−ln(1−α)]−2[−ln(1−α)]3 B
3
(1/4)(1−α)[−ln(1−α)]−3 [−ln(1−α)]4 B
4
3. Deceleratory
2(1−α)1/21−(1−α)1/2
R
2
3(1−α)2/31−(1−α)1/3
R
3
1/2α α2
D
1
[−ln(1−α)]−1(1−α)ln(1−α)+α D
2
D
(3/2)(1−α)2/3[1−(1−α)2/3]−1[1−(1−α)1/3]2 3
(3/2)[(1−α)−1/3−1]−11−2α/3−(1−α)2/3 D
4
D
(−3/2)(1−α)2/3[(1−α)1/3−1]−1[(1−α)1/3−1]2 5
D
(3/2)(1−α)4/3[(1−α)−1/3−1]−1 [(1−α)−1/3−1]2 6
F
* 1−α −1n(1−α) 1
(1－α) 21/(1－α) F
2
(1－α) 3/2(1/1−α) 2 F
3
2(1−α) 3/2(1−α) −1/2 F
(3/2)
(2/3)(1−α) 5/2(1−α) −3/2 F
(5/2)
*F1 is the same as A1
Sestak-Berggren empirical function(1971)
f (α ) = αm (1−α) n
2. 热分析动力学方法
按动力学方程形式：
微商法
积分法
按加热速率方式：
单个扫描速率法(single scanning method)
多重扫描速率法(multiple scanning method) (等转化率法，iso-conversional)
Kissinger-Akahira-Sunose equation
Anal. Chem., 29(1957)1702
作多重加热速率β下的测定，选择TA 曲线峰值对应的温度T p
由线性方程斜率——E ，然后由截矩——A 注：1. Kissinger(1956): 在最大速率处，适于n 级反应
2.Akahira-Sunose(1969): 指定α处亦可
3. Ozawa: 不限于n 级反应p
p
RT E E AR T /)/ln()/ln(2−=β非等温实验:特征点法
举例：CaCO3热解动力学分析
Friedman equation （model
free ）
J. Polym. Sci. Part C, 6(1964)183
作多重加热速率β下的测定，选择等α处斜率——E ；截矩——若则：斜率——E ; 截矩——A
RT E Af dT d /)](ln[)]/(ln[−=ααβn
f )1()(αα−=)
1ln(ln )](ln[αα−+=n A Af )]
(ln[αAf
温度积分的近似表达式
¾Doyle 近似式(J. Appl. Polym. Sci.,6(1962）639 )
¾
Schlomlich 展开级数（Doyle , Nature, 207(1965)290 )¾经验公式（Zsaco , J. Thermal Anal. 8(1975)593))
1()1()3)(2(2211[)1()(−+⋅⋅⋅−+⋅⋅⋅−++++−+=−n x n x x x x x e x p n x )2)(/()(−−≈−x d x e x p x )844/(162
+−=x x d x
x p 4567.0315.2)(lg −−≈)6020(≤≤x
2u u 2222(1)(1)u E RT e ART RT e u u E
E β−−−=−2[1]}RT E E RT −−
ADN的不等温热分解反应动力学参数
模式 E / kJ mol-1lnA/ min-1γP4 24.5 3.9 0.9783 P3 35.1 6.9 0.9813 P2 56.2 12.7 0.9837 P2/3 182.9 46.2 0.9862 D1 246.2 62.8 0.9865 F1 139.4 35.70.9928 A4 29.5 5.3 0.9903 A3 41.7 9.0 0.9913 A2 66.1 15.9 0.9921 D3 269.1 67.4 0.9928 R3 131.0 32.0 0.9924 R2 127.6 31.3 0.9910
Flynn-Wall-Ozawa equation （model free ）
Bull. Chem. Soc. Jpn.,38(1965)1881
取不同β下曲线的等α处之温度T
作lg β～1/T 图，由斜率——E
注：Ozawa (1965): 在最大转化速率处
Flynn-Wall (1966): 指定α处亦可
RT E Rg AE /4567.0315.2)
(lg lg −−=αβ
参考书籍
胡荣祖等. 《热分析动力学》(第二版) . 北京
科学出版社, 2008.。
