现金流量图
- 格式：doc
- 大小：1.65 MB
- 文档页数：65
下载文档原格式
合集下载
《现金流量图》课件
PART SIX
企业背景：某 制造型企业， 主要生产电子
产品
现金流量图： 展示了企业经 营活动现金流 量的变化情况
现金流量分析： 企业经营活动 现金流量呈上 升趋势，说明 企业经营状况
良好
建议：企业应 继续加强成本 控制，提高经 营效率，保持 现金流量的稳
定增长
企业背景：某大型制造企业 投资活动：新建生产线、研发新产品 现金流量：投资活动产生的现金流入和流出 分析结果：投资活动对现金流量的影响，以及企业的财务状况和经营状况
方案
投资决策：根 据现金流量图 预测项目的投 资回报率，决
定是否投资
风险管理：分 析现金流量图 的波动性，制 定风险应对措
施
企业经营决策：预测企业未来现金流量，评估投资项目可行性 财务分析：分析企业现金流量状况，评估企业偿债能力、盈利能力等 风险管理：预测企业现金流量风险，制定风险应对措施 投资决策：分析企业现金流量，评估投资项目风险和收益，制定投资决策
现金流量图的分类：经营活动现金流量、投资活动现金流量和筹资活动 现金流量
现金流量图的分析步骤：首先分析现金流入和现金流出，然后计算净现 金流量，最后分析现金流量的变化趋势
现金流量图的应用：用于评估企业的财务状况和经营业绩，预测企业的 未来发展前景，制定企业的投资决策和筹资决策。
现金流量表：反映企业一定时期内的现金流入、流出和结余情况 现金流量比率：衡量企业现金流量与负债、资产、收入等指标的关系 现金流量趋势分析：分析企业现金流量的变化趋势，预测未来现金流量 现金流量结构分析：分析企业现金流量的来源和用途，判断企业经营状况
确定时间轴：选择合适的时间单位，如年、月、日等
确定现金流量：包括收入、支出、投资、融资等
利用现金流量图计算借款利息
现金流量图是由横轴、箭线和杆线组成的。
横轴是时间轴，向右延伸表示时间延续，横轴线等分成若干间隔，通常时间单位是年。
时间轴上的点称为时点，表示该年年末。
与横轴相连的垂直箭线，代表流入或流出该系统的现金流量。
箭头向上为现金流入，向下为流出。
现金流入包括收到的借款的本金，现金流出包括支付的工程款、用于工程的材料款、工程人员的工资和借款的本金等。
与横轴相连的垂直杆线表示年末应计的利息金额，但不需支付现金。
例：MN 公司拟在厂区内建造一幢新厂房，有关资料如下：1〇2007年1月1日向银行专门借款5000万元，期限为3年，年利率为6%，每年l 月1日付息。
2〇除专门借款外，公司只有一笔一般借款，是2006年12月1日借入的长期借款6000万元，期限为5年，年利率为8%，每年12月1日付息。
3〇由于审批、办手续等原因，厂房于2007年4月1日才开始动工兴建。
2007年4月1日、2007年6月1日、2007年7月1日、2008年1月1日、2008年4月1日、2008年7月1日支付工程款2000万元、1000万元、3000万元、1000万元、500万元、500万元。
工程于2008年9月30日完工，达到预定可使用状态。
其中，由于施工质量问题工程于2007年9月1日~12月31日停工4个月。
4〇专门借款中未支出部分全部存入银行，假定月利率为0.25%。
假定全年按照360天算，每月按照30天算。
借款利息费用化、资本化和暂停资本化的现金流量图如下。
现利用现金流量图进行会计处理：1.2006年12月1日。
借：银行存款6000万元；贷：长期借款———一般借款6000万元。
2.2006年12月31日。
借：财务费用40万元；贷：应付利息40万元。
3.2007年1月1日。
借：银行存款5000万元；贷：长期借款———专门借款5000万元。
4.2007年12月1日。
借：应付利息480万元；贷：银行存款480万元。
5.2007年12月31日。
现金流量图和表练习
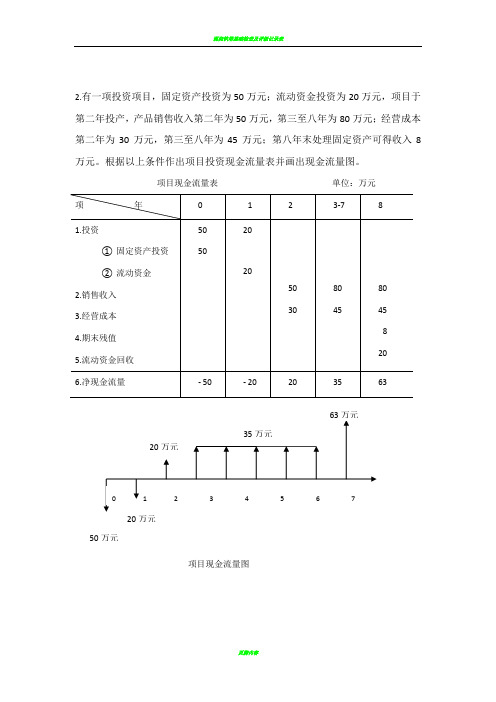
2.有一项投资项目，固定资产投资为50万元；流动资金投资为20万元，项目于第二年投产，产品销售收入第二年为50万元，第三至八年为80万元；经营成本第二年为30万元，第三至八年为45万元；第八年末处理固定资产可得收入8万元。
根据以上条件作出项目投资现金流量表并画出现金流量图。
项目现金流量表单位：万元
项目现金流量图
1.某项目第1年和第2年各有固定资产投资400万元，第2年投入流动资金300万元并当年达产，每年有销售收入580万元，生产总成本350万元，项目寿命期共10年，期末有固定资产残值50万元。
请作现金流量表，并画出现金流量图。
项目现金流量表单位：万元
700万元
项目现金流量图。
现金流量及现金流量图
现金流量及现金流量图
(一)现金流量
设备工程形成过程中存在着复杂的资金运动，这种不断运动的资金流就成为现金流量。
流入这个过程的资金称为现金流入，流出这个过程的资金称为现金流出。
现金流入用CI表示，现金流出用CO表示，同一时点现金流入与现金流出的差额叫净现金流量，用NCF表示
NCFt=（CI－CO）t
(二)现金流量图
把现金流量作为时间的函数，用一个二维的图形表示，叫现金流量图。
运用现金流量图，就可以全面、形象、直观地表达出设备工程形成过程中经济系统的资金运动状态。
现金流量图的做法如下：
①横轴表示时间轴，将横轴分为n等份，注意第n-1期终点和第n期的始点是重合的。
每一等分代表一个时间单位，可以是年、半年、季、月或天。
②与横轴垂直向下的箭头代表现金流出，与横轴垂直向上的箭头代表现金流入，箭头的长短与金额的大小成比例；
③代表现金流量的箭头与时间轴的焦点即表示该现金流量发生的时间。
由此可知，要正确绘制现金流量图，必须把握好现金流量的三要素，即现金流量的大小、方向、时间点。
现金流量图与立脚点有关，从借款人角度出发和从贷款人角度出发所绘现金流量图不同。
例5、把现金流量作为时间的函数，用一个二维的图形表示，叫现金流量图。
现金流量图的做法（）。
A．横轴表示时间轴，将横轴分为n等份
B．第n-1期终点和第n期的始点是不重合的
C．与横轴垂直向下的箭头代表现金流出，与横轴垂直向上的箭头代表现金流入
D．与横轴垂直箭头的长短与金额的大小成比例
E．现金流量图与立脚点有关
答案：A，C，D．E。
投资项目评估与管理第二章现金流量与资金的时间价值
b．实际利率 若将付息周期内的利息增值因素考虑在内， 所计算出来的利率称为实际利率。 实际年利率与名义年利率之间的关系可用下 式表示：
（2-11）
其中： —实际年利率 —名义年利率
m—年计息周期数。 下面推导式（2-11）。 设：投资一笔资金P，年计算周期数为m， 计息周期利率为r，则名义年利率i为：
建设 期
投产 期
……
稳产 期
回收处 理期
图2-5 新建项目的现金流量图
2.2 资金时间价值 2.2.1 资金时间价值的概念与意义
（1）资金时间价值的概念 资金的时间价值是指资金随着时间的推移而形 成的增值。 资金的时间价值可以从两方面来理解： 第一，将资金用作某项投资，由于资金的运动 ，可获得一定的收益或利润。 第二，如果放弃资金的使用权力，相当于付出 一定的代价。
根据图2-13，把等额系列现金流量视为n 个 一次支付的组合，利用一次支付终值公式（2-7 ）可推导出等额支付终值公式：
用
乘以上式，可得
由式（2-14）减式（2-13），得
经整理，得
（2-13） （2-14） （2-15）
式中 用符号
（2—16） 表示，称为等额支 付终值系数
[例2—5]若每年年末储备1000元，年利率为6%，连 续存五年后的本利和是多少？（excle表）
图2-9 年金A现金流量图
小结：
①大部分现金流量可以归结为上述三种现金流量 或者它们的组合。
②三种价值测度P、F、A之间可以相互换算。 ③在等值计算中，把将来某一时点或一系列时点 的现金流量按给定的利率换算为现在时点的等值现 金流量称为“贴现”或“折现” ；把现在时点或一系列 时点的现金流量按给定的利率计算所得的将来某时 点的等值现金流量称为“将来值”或“终值”。
（2-11）
其中： —实际年利率 —名义年利率
m—年计息周期数。 下面推导式（2-11）。 设：投资一笔资金P，年计算周期数为m， 计息周期利率为r，则名义年利率i为：
建设 期
投产 期
……
稳产 期
回收处 理期
图2-5 新建项目的现金流量图
2.2 资金时间价值 2.2.1 资金时间价值的概念与意义
（1）资金时间价值的概念 资金的时间价值是指资金随着时间的推移而形 成的增值。 资金的时间价值可以从两方面来理解： 第一，将资金用作某项投资，由于资金的运动 ，可获得一定的收益或利润。 第二，如果放弃资金的使用权力，相当于付出 一定的代价。
根据图2-13，把等额系列现金流量视为n 个 一次支付的组合，利用一次支付终值公式（2-7 ）可推导出等额支付终值公式：
用
乘以上式，可得
由式（2-14）减式（2-13），得
经整理，得
（2-13） （2-14） （2-15）
式中 用符号
（2—16） 表示，称为等额支 付终值系数
[例2—5]若每年年末储备1000元，年利率为6%，连 续存五年后的本利和是多少？（excle表）
图2-9 年金A现金流量图
小结：
①大部分现金流量可以归结为上述三种现金流量 或者它们的组合。
②三种价值测度P、F、A之间可以相互换算。 ③在等值计算中，把将来某一时点或一系列时点 的现金流量按给定的利率换算为现在时点的等值现 金流量称为“贴现”或“折现” ；把现在时点或一系列 时点的现金流量按给定的利率计算所得的将来某时 点的等值现金流量称为“将来值”或“终值”。
工程经济学【现金流量图】
某工程项目逐年支出、收入如下表所示，已知 基准贴现率i0=10%，求静态、动态投资回收期、 净现值、净年值、净现值指数和内部收益率。
项目 年 0 1 2
3
份
投资
100 800 100
经营费用
300
收入
350
4－7 8－12
450 485 700 700
32
思考题
年 净现 累计净现 净现金流 累计净现金 净现金 累计净现 份 金流 金流量 量现值 流量现值 流现值 金流现值
2000
2 1 ( 万 元 ) 0
N P V ( 1 4 % ) 2 0 0 0 3 0 0 ( P / F , 1 4 % , 1 ) 5 0 0 ( P / A , 1 4 % , 3 ) ( P / F , 1 4 % , 1 ) 1 2 0 0 ( P / F , 1 4 % , 5 ) 9 1 ( 万 元 ) 0
相同的计算期。
13
净现值函数曲线
NPV 1200
600
i*
0
i
10 20 30 40 50 60
(%)
-600
净现值函数曲线
14
思考题
NPV NPV 0 1 2 3 45
(i=10%) (i=20%) A -230 100 100 100 50 50 83.91 24.81 B -100 30 30 60 60 60 75.48 33.58
IRR
i1
NPV (i1) NPV (i1) | NPV (i2 )
|
(i2
i1)
12% 21 (14% 12%) 21 91
12.4% 20
思考题
某项工程方案的现金流量如下表所列，设其行业基准 收益率为15%。试用内部收益率法分析判断该方案是 否可行。
项目 年 0 1 2
3
份
投资
100 800 100
经营费用
300
收入
350
4－7 8－12
450 485 700 700
32
思考题
年 净现 累计净现 净现金流 累计净现金 净现金 累计净现 份 金流 金流量 量现值 流量现值 流现值 金流现值
2000
2 1 ( 万 元 ) 0
N P V ( 1 4 % ) 2 0 0 0 3 0 0 ( P / F , 1 4 % , 1 ) 5 0 0 ( P / A , 1 4 % , 3 ) ( P / F , 1 4 % , 1 ) 1 2 0 0 ( P / F , 1 4 % , 5 ) 9 1 ( 万 元 ) 0
相同的计算期。
13
净现值函数曲线
NPV 1200
600
i*
0
i
10 20 30 40 50 60
(%)
-600
净现值函数曲线
14
思考题
NPV NPV 0 1 2 3 45
(i=10%) (i=20%) A -230 100 100 100 50 50 83.91 24.81 B -100 30 30 60 60 60 75.48 33.58
IRR
i1
NPV (i1) NPV (i1) | NPV (i2 )
|
(i2
i1)
12% 21 (14% 12%) 21 91
12.4% 20
思考题
某项工程方案的现金流量如下表所列，设其行业基准 收益率为15%。试用内部收益率法分析判断该方案是 否可行。
现金流量图
现金流量图资金时间价值图解收益性物业的现金流单利计息与复利计息 （一）单利计息 （二）复利计息()n i P F n ⋅+=1i n P I n ⋅⋅=()n ni P F +=1()[]11-+=nn i P I名义利率与实际利率的关系式例：年利率12%，存款额1000元，期限1年，按季计息，则1后的本利和为多少？ 名义利率r=12%；周期利率=3%；每年计息周期数=4 关系式：名义利率=周期利率×每年计息周期数1.一次支付的现值系数和终值系数2、等额序列支付的现值系数和资金回收系数3、等额序列支付的终值系数和储存基金系数51.1125*1000*10001%)31()4%121(44===⎪⎭⎫ ⎝⎛+=++mm r P F 51.125100051.11251=-=-⎪⎭⎫ ⎝⎛+=-=P m r P P F I m()1111%)31(4-=-⎪⎭⎫ ⎝⎛+=-+=-=+m mm r P P m r P P P F i ()),,/(*1n i P F P i P F n=+=()),,/(*11)1(n i F P F F i F P i n n ==⎥⎦⎤⎢⎣⎡+=+-()()()⎥⎦⎤⎢⎣⎡+-=⎥⎦⎤⎢⎣⎡+-+=n n ni i A i i i A P 111111()()()11111-++=⎥⎦⎤⎢⎣⎡-++=n n n i Pi Pi i i i P A4、等差序列的现值系数和年费用系数5、等比序列的现值系数和年费用系数六、复利系数的应用［例3－l］已知某笔贷款的年利率为15%，借贷双方约定按季度计息，问该笔贷款的实际利率是多少？［例3－2］某投资者向银行贷款2000万元，期限为3年，年利率为8%，若该笔贷款的还款方式为期间按季度付息、到期后一次偿还本金，则开发商每次为该笔贷款支付的利息总额是多少？如果计算先期支付利息的时间价值，则贷款到期后开发商实际支付的利息又是多少？［例3－3］某写字楼投资项目在10年的持有期内各年净运营收益均为50万元，第10年末净转售收入为600万元，如果折现率为10%，求该写字楼投资项目的收益现值。
第五讲现金流量图绘制ppt课件
100
750 750 750 750 750 750
300 300
0
1234
5 67
8 9 10
200
500
年 单位：万元
1000
--
5.4 小结
现金流入
现金流出
1
现金流量的概念
净现金流量 现金流量的构成
现金流量的三要素
2 现金流量示方法
现金流量表 现金流量图
3 现金流量图的绘制
课后作业：完成任务单现金流量练习题。
统称）即指一项特定的经济系统在一定时期内 （年、半年、季等）现金流入或现金流出或流 入与流出数量的代数和。
--
5.1 现金流量的概念
现金流量是由
什么构成的呢？
现金流量三要素
现 投资
金 流
成本费用
量 销售收入
的 税金
量现素的 时点
金 三 大小 流要
方向
构 利润
成 残值、折旧等
--
5.2 现金流量的表示方法
--
5.3 现金流量图的绘制
例1：某工程项目预计初始投资1000万元，第2年开始投产后 每年销售收入抵销经营成本后为300万元，第5年追加投资 500万元，当年见效且每年销售收入抵销经营成本后为750万 元，该项目的经济寿命为10年，残值为100万元，试绘制该 项目的现金流量图。
分析：由题意可知，该项目整个寿命周期为10年。初始投资1000万元发 生在第一年的年初，第5年追加投资5 00万元（发生在年初）；其他费用 或收益均发生在年末，其现金流量如下图所示。
CONTENTS
第五讲现金流量及现金流量 图的绘制
5.1
现金流量的概念
5.2 现金流量的表示方法
750 750 750 750 750 750
300 300
0
1234
5 67
8 9 10
200
500
年 单位：万元
1000
--
5.4 小结
现金流入
现金流出
1
现金流量的概念
净现金流量 现金流量的构成
现金流量的三要素
2 现金流量示方法
现金流量表 现金流量图
3 现金流量图的绘制
课后作业：完成任务单现金流量练习题。
统称）即指一项特定的经济系统在一定时期内 （年、半年、季等）现金流入或现金流出或流 入与流出数量的代数和。
--
5.1 现金流量的概念
现金流量是由
什么构成的呢？
现金流量三要素
现 投资
金 流
成本费用
量 销售收入
的 税金
量现素的 时点
金 三 大小 流要
方向
构 利润
成 残值、折旧等
--
5.2 现金流量的表示方法
--
5.3 现金流量图的绘制
例1：某工程项目预计初始投资1000万元，第2年开始投产后 每年销售收入抵销经营成本后为300万元，第5年追加投资 500万元，当年见效且每年销售收入抵销经营成本后为750万 元，该项目的经济寿命为10年，残值为100万元，试绘制该 项目的现金流量图。
分析：由题意可知，该项目整个寿命周期为10年。初始投资1000万元发 生在第一年的年初，第5年追加投资5 00万元（发生在年初）；其他费用 或收益均发生在年末，其现金流量如下图所示。
CONTENTS
第五讲现金流量及现金流量 图的绘制
5.1
现金流量的概念
5.2 现金流量的表示方法
现金流量图cash flow diagram
现金流量图现金流量图（Cash flow diagram）目录[隐藏]• 1 什么是现金流量图• 2 现金流量图的要素• 3 现金流量图的画法• 4 案例分析o 4.1 案例一:现金流量图的例子o 4.2 案例二:现金流量图在教学中的应用[1]• 5 参考文献[编辑]什么是现金流量图现金流量图是一种反映经济系统资金运动状态的图式，即把经济系统的现金流量绘入一时间坐标图中，表示出各现金流入、流出与相应时间的对应关系。
运用现金流量图，就可全面、形象、直观地表达经济系统的资金运动状态。
现金流量图是描述现金流量作为时间函数的图形，它能表示资金在不同时间点流入与流出的情况。
它是经济分析的有效工具，其重要有如力学计算中的结构力学图。
[编辑]现金流量图的要素现金流量图包括三大要素：大小、流向、时间点。
其中：大小表示资金的数额；流向指项目的现金流入或流出；时间点是指现金流入或现金流出所发生的时间。
[编辑]现金流量图的画法1、横轴表示时间轴，将横轴分为n等份，注意第n-1期终点和第n期的始点是重合的。
每一等分代表一个时间单位，可以是年、半年、季、月或天。
2、与横轴垂直向下的箭头代表现金流出，与横轴垂直向上的箭头代表现金流入，箭头的长短与金额的大小成比例。
3、代表现金流量的箭头与时间轴的焦点即表示该现金流量发生的时间。
由此可知，要正确绘制现金流量图，必须把握好现金流量的三要素，即现金流量的大小、方向、时间点。
现金流量图与立脚点有关，从借款人角度出发和从贷款人角度出发所绘现金流量图不同。
[编辑]案例分析[编辑]案例一:现金流量图的例子说明：1、水平线是时间标度，时间的推移是自左向右，每一格代表一个时间单位（年、月、日）；时间长度称为期数。
2、垂直箭线表示现金流量：常见的向上——现金的流入，向下——现金的流出。
3、一般假定现金的支付都发生在每期期末。
4、现金流量图与立脚点有关。
注意：1、时间的连续性决定了坐标轴上的每一个时点既表示上一期期末也表示下一期期初，如第一年年末的时刻点同时也表示第二年年初。
工程经济学名词解释,简答
工程经济学名词解释,简答三、名词解释1.经济寿命：设备以全新状态投入使用开始到因继续使用不经济而提前更新所经历的时间，也就是一台设备从投入使用开始，到其年度费用最低的使用期限。
2.机会成本:由于资源的有限性，考虑了某种用途，就失去了其他被使用而创造价值的机会。
在所有这些其他可能被利用的机会中，把能获取最大价值作为项目方案使用这种资源的成本，称为机会成本。
3.等值：由于利息的存在而使不同时点上的不同金额的货币具有相同的经济价值，称为资金等值。
4.互斥方案：互斥方案即指采纳一组方案中的某一方案，必须放弃其他方案，即方案之间相互具有排他性。
5.现金流量：指一项特定的经济系统在一定时期内现金流入或现金流出或流入与流出数量的代数和。
一、名词解释1、现金流量图：一种反映经济系统资金运动状态的图式。
2、等值计算：不同时期、不同数额但其“价值等效”的资金计算。
3、名义利率：指计息周期利率乘以周期内的计息周期数所得的利率周期利率。
4、不确定性分析：考查各种因素变化时，对项目经济评价指标的影响。
5、资金成本：投资者在工程项目实施中，为筹集和使用资金而付出的代价。
6、影子价格：能够反映投入物和产出物真实经济价值，使资源得到合理配制的价格。
7、沉没成本：旧设备折旧后的账面价值与当前市场价值的差值。
8、价值工程：以最低的寿命周期成本，可靠地实现研究对象的必要功能，从而提高对象的价值。
9、项目后评价：对项目在建成投产并达到设计生产能力后的评价。
10、资金时间价值：资金随时间推移而增值，其增值的这部分资金就是原有资金的时间价值。
11、工程项目投资：某项工程从筹建开始到全部竣工投产为止所发生的全部资金投入。
12、终值：某计算期末资金的本利和。
13、净现值：反映投资方案在计算期内获利能力的动态评价指标。
14、盈亏平衡点：指一个项目盈利和亏损之间的转折点。
15、风险分析：对预期目标而言，经济主体遭受损失的不确定分析。
16、项目融资：以项目的资产、收益作抵押的融资。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
现金流量图现金流量图（Cash flow diagram）[编辑]什么是现金流量图现金流量图是一种反映经济系统资金运动状态的图式，即把经济系统的现金流量绘入一时间坐标图中，表示出各现金流入、流出与相应时间的对应关系。
运用现金流量图，就可全面、形象、直观地表达经济系统的资金运动状态。
现金流量图是描述现金流量作为时间函数的图形，它能表示资金在不同时间点流入与流出的情况。
它是经济分析的有效工具，其重要有如力学计算中的结构力学图。
[编辑]现金流量图的要素现金流量图包括三大要素：大小、流向、时间点。
其中：大小表示资金的数额；流向指项目的现金流入或流出；时间点是指现金流入或现金流出所发生的时间。
[编辑]现金流量图的画法1、横轴表示时间轴，将横轴分为n等份，注意第n-1期终点和第n期的始点是重合的。
每一等分代表一个时间单位，可以是年、半年、季、月或天。
2、与横轴垂直向下的箭头代表现金流出，与横轴垂直向上的箭头代表现金流入，箭头的长短与金额的大小成比例。
3、代表现金流量的箭头与时间轴的焦点即表示该现金流量发生的时间。
由此可知，要正确绘制现金流量图，必须把握好现金流量的三要素，即现金流量的大小、方向、时间点。
现金流量图与立脚点有关，从借款人角度出发和从贷款人角度出发所绘现金流量图不同。
[编辑]案例分析[编辑]案例一:现金流量图的例子说明：1、水平线是时间标度，时间的推移是自左向右，每一格代表一个时间单位（年、月、日）；时间长度称为期数。
2、垂直箭线表示现金流量：常见的向上——现金的流入，向下——现金的流出。
3、一般假定现金的支付都发生在每期期末。
4、现金流量图与立脚点有关。
注意：1、时间的连续性决定了坐标轴上的每一个时点既表示上一期期末也表示下一期期初，如第一年年末的时刻点同时也表示第二年年初。
2、立脚点不同，画法刚好相反。
3、净现金流量= 现金流入－现金流出4、现金流量只计算现金收支(包括现钞、转帐支票等凭证)，不计算项目内部的现金转移(如折旧等)。
应有明确的发生时点；必须实际发生（如应收或应付账款就不是现金流量）；不同的角度有不同的结果（如税收，从企业角度是现金流出；从国家角度都不是）。
[编辑]案例二:现金流量图在教学中的应用[1]一、现金流量图的画法现金流量图是一种反映经济系统资金运动状态的图式，即把经济系统的现金流量绘入一时间坐标图中，表示出各现金流入、流出与相应时间的对应关系。
运用现金流量图，就可全面、形象、直观地表达经济系统的资金运动状态。
它是在课程讲授和题目分析中使用，主要用于分析现金流量发生的时间点、大小、方向，确定其形式，并选择所使用的公式。
因为在需要分析现金流鼍的案例中，现金流量的时间点、大小和方向是最主要的三个因素，而且所涉及的因素和数据较多，有时候会涉及到纳税的计算、利息支出等，在分析中容易出现遗漏或错误。
而使用现金流量图更为直观，不容易遗漏数据。
具体画法如下：1.因为涉及到时间点的问题，我们在分析时，必须使用坐标图。
以横轴为时间轴，向右延伸表示时间的延续，根据题目中涉及的期间划分成若干个时间单位，轴上每一刻度表示一个时间单位，可取年、半年、季或月等，由左至右分别为起始日和终止日，时间单位分别标记为0、1、2……N，零表示时间序列的起点。
根据题目中的资金流动，分析每一笔资金流动的时点。
2.相对于时间坐标的垂直箭线代表不同时点的现金流量情况。
一般情况下，在横轴上方的箭线表示现金流入，即表示收益；在横轴下方的箭线表示现金流出，即表示费用。
3.箭头的长短表示现金的多少，在各箭线上方(或下方)注明现金流量的具体数值。
4.箭线与时间轴的交点即为现金流量发生的时间点，这对于分析现金流量的形式，选择使用公式有重要意义。
例如：某企业计划投资的一个项目，在第一年年末需要投资100万元，第二年年末需要投资150万，项目能在以后三年内每年年末产生100万的收入，如果资金成本为12％，试计算该项目是否值得投资?经过分析可以绘制出现金流量图如下图所示。
通过对这个现金流量图的分析，我们可以发现，两次现金流出的金额是不相等的，只能使用复利现值的公式分两步计算现金流出的现值。
而三次现金流入的金额是相等的，是一个递延年金的形式，期数为3，而递延期为2，就可以直接使用公式计算了。
总之，要正确绘制现金流量图，必须把握好现金流量的三要素，即：现金流量的大小(现金数额)、方向(现金流入或流出)和作用点(现金发生的时间点)。
二、现金流量图在教学中的应用1、一般应用在计算项目投资的时间价值时，现金流量的分析是最困难的，我们以一个简单的例题来说明现金流量图的使用。
当然在实际的工作或者考试中碰到的问题要复杂的多。
例：某个项目投资总额1000万元，分5年支付工程款，3年后开始投产，有效期限为5年。
投产开始时垫付流动资金200万元，结束时收回。
投产后每年可产生300万元的现金流入。
假设资金成本为10%，试用净现值法分析该项目是否可行?要计算这个题目，必须先分析现金流量，我们以现金流量图来进行分析。
为了更加清楚，我们用两个图形分别表示现金流出和现金流入。
该项目的现金流出情况如下图所示：上图可分解为A=200，n=5的普通年金和S=200，n=3的复利该项目的现金流人情况如下图所示：上图可分解为A=300，n=8，m=3的递延年金和5=200，n=8的复利。
通过这两个图形可以看出，现金流出量有两组数据需要计算：一个是A=200，n=5的普通年金现值，一个是S=200，n=3的复利现值；现金流入量也有两组数据需要计算：一个是A=300，n=8，m=3的递延年金现值。
一个是S=200，n=8的复利现值。
了解了这些就可以直接将数据代入相关的公式计算结果了。
2。
特殊用法在很多时候，分析项目的现金流量需要做一些变形，才能套用公式，可以大大减少计算量。
主要形式有预付年金和递延年金转化为普通年金，然后用普通年金的计算方法来计算。
在实际应用中，还有很多情况，需要根据题目的要求来具体分析，这里只用最基本的变形来说明。
(1)预付年金转化为普通年金预付年金是指在一定时期内，各期期初等额的系列收付款项。
它与后付年金的主要区别在于每期收付款项发生的时点不同，前者在期初，后者在期末。
因为后付年会在现实生活中更常见，所以通常又称之为普通年金。
财务管理教科书中一般均以普通年金作为教学的霞点，分别介绍其现值和终值的计算，并且在教科书中附普通年金终值系数表和普通年金现值系数表，以方便相应的终值和现值的计算。
而对于预付年会终值或现值的计算，一般是通过分析预付年金与普通年金之间的关系，利用普通年金终值系数或现值系数进行求解。
但是现有的教科书中对于预付年金与普通年金之问的关系的分析都比较晦涩，学生理解较困难。
而利用现金流量图可以使这种分析变得更直观，从而方便学生理解和记忆。
依据预付年金的定义，预付年金可以用下图表示：为了将预付年金转换为普通年金，可以将预付年金中每期发生的款项向后“平移“一期，根据复利终值的计算公式，平移后每期发生额均为原发生额乘以一年期终值系数，图示如下：很显然，上图正是一个标准的每期发生额为A(1+i)的n年期普通年金。
据此，预付年金的现值和终值计算公式可以表示为：预付年金现值PVAin=A x(1+i)×PVIFAin；预付年金终值FVAin=A×(1+i)×FVIFAin。
这样预付年金终值或现值的计算可以根据普通年金终值系数或普通年金现值系数计算出来，即只要给定贴现率和期数，利用普通年金终(现)值系数表就可以求出预付年金的终值或现值。
(2)递延年金转化为普通年金递延年金是指在最初若干期没有收付款项的情况下，随后若干期有等额的系列收付款项。
可以用下图表示：前m期没有收付款项，从m+l期期末开始收付款项，共发生n-m期。
递延年金也可以根据定义式进行计算，只是计算量大、非常复杂，但利用现金流量图将其转化为普通年金问题进行计算则较为简便。
比较递延年金与普通年金容易发现，在整个n期内，仅在前m期内未发生等额收付款项，在之后的n-m期内，是典刑的等额系列收付款项。
如果假设前rtl期也存在等额收付款项，则是一个n期的普通年金。
在计算现值的时候，可以先计算n期普通年金的现值，然后把不存在的前m期的普通年金现值减去，就得到了结果，计算量大大减少。
根据年金现值计算公式递延年金现值为：PVA in=A×(PVIFA-PVIFAim),直接可以通过查表得出结果。
同样可以推算递延年金的终值计算公式，从而使递延年金的终值计算转换成普通年金终值计算。
学生分析的过程大大简化，提高了计算速度和准确性。
审计风险决策模型[编辑]审计风险决策模型的演进[1]当今处于瞬息万变的市场经济中的各种经济组织无不关心会计信息的真实性和公允性。
而对会计信息主要载体的会计报表进行验证的审计组织，有的却因未能审查出被审计单位会计报表中存在的重大错报或漏报的问题并发表了不恰当意见而承担审计责任，构成审计风险，遭受不应有的损失，甚至被起诉。
多年以来，审计界的学者与专家对这个重要课题作了不懈的努力研究，企望通过构筑一定的审计风险模型来实现正确的审计决策，并已取得了行之有效的科研成果，使审计风险决策模型日臻完善。
目前具有代表的审计风险决策模型有以下两种模式。
(一)单级风险决策模型美国注册公共会计师协会(AICPA)在1981年发布的SAS39中，首先提出如下的审计风险决策模型：终极风险(US)=固有控制风险(IC)×分析性检查风险(AR)×帐项余额测试风险(1D)但这种模型并未全面、系统、完整地反映出控制风险和检查风险。
当AICPA很快认识其缺陷后，于1983年在其发表的SAS47中，提出一个新的比较完善的审计风险决策模型。
在这个模型中，审计风险是由终极风险、控制风险和检查风险四个要素组成的，这四个要素之间存在一定的函数关系，其数学表达式如下：审计风险(AR) =固有风险(LR)×控制风险(0R)×检查风险(DR)随后，一些学者陆续提出了其他形式的审计风险决策模型，但其基本内容与上述AICPA发表SAS47的模型相似就不再赘述，由于上述审计风险决策模型包括主要的风险要素，并标明其数量关系，具有广泛的适应性和可操作性，因而已被大多数审计组织及注册会计师所采用。
但也应看到这种审计风险决策模型的不足之处，在这个模型中，并未包括非统计抽样风险。
由于未能适当地考虑到非统计抽样风险对终极风险的影响，就在一定程度上降低了该种审计风险决策模型的实用价值。
(二)多级风险决策模型单级风险决策模型的先天不足，激励着人们进行更深入的探讨。
西奥多·J·莫克(Theodore．J．Mock)、弗丁斯柯及玛丽·T·华盛顿在“会计及审计中的风险评估”和“审计中的风险概念及风险评估”中，提出一个多级风险评价法(HRAA)。