模电中叠加定理的应用
- 格式:ppt
- 大小:57.00 KB
- 文档页数:2


电路叠加定理电路叠加定理是电路分析中常用的方法之一,它是基于线性电路原理的。
线性电路原理是指电路中的元件都是线性元件,即元件的电学性能不随电压、电流大小的变化而发生改变。
叠加定理是通过分解电路中的电压和电流源,分别计算每个源单独作用于电路的效果,最后将各个结果相加,得到整个电路的响应结果的方法。
电路叠加定理的描述:假设电路中有多个电压源和电流源,每个源单独作用于电路时所产生的电压或电流与其他源作用时产生的电压或电流之和等于所有电压或电流源分别单独作用于电路时产生的电压或电流之和。
叠加定理是建立在线性电路的假设上的,因此只适用于包含线性元件的电路。
此外,叠加定理只适用于计算某个节点的电压或某个支路的电流。
另外,在使用叠加定理时还有一些需要注意的事项:1. 所有源都需要在关闭状态下计算其他源的影响,否则计算结果可能不准确。
2. 考虑源的内阻和电路负载时不应使用叠加定理,因为内阻和负载会产生非线性效应。
3. 叠加定理只适用于计算线性电路中某个节点或支路的电压或电流,不能用于计算电路中的功率或电能等其他参数。
在使用叠加定理时,可以根据以下四个步骤进行分析:1. 保留一个源不变,将其他所有源都设为零。
2. 计算电路中的电流或电压响应。
3. 不断重复步骤1和2,直到所有源都计算过为止。
4. 将每个源的响应结果相加,得到整个电路的响应结果。
叠加定理的优点是可以分别分析电路中每个源的贡献,从而更清楚地了解电路中各元件之间的关系。
另外,叠加定理还可以帮助压缩电路分析的复杂度,节省计算时间和精力。
但是,使用叠加定理时需要进行多次计算,因此对于大型电路,其计算量可能会非常庞大。
电路叠加定理在电路分析中有着广泛的应用。
例如,在交流电路中,可以使用叠加定理对各个频率分量进行单独分析,然后将它们组合起来得到整个电路的响应结果。
此外,在直流电路中,可以使用叠加定理来计算各个电源对电路的影响,从而更好地理解电路中各元件之间的关系。

叠加定理适用范围一、引言叠加定理(Superposition Theorem)是电路分析中常用的一种方法,通过将电路分解为不同的独立电源进行分析,然后再将结果进行叠加得到最终的解。
这一定理在解决复杂电路问题时具有很大的优势,然而,叠加定理并非适用于所有电路。
本文将探讨叠加定理的适用范围,并提供一些例子来说明其中的限制和局限性。
二、叠加定理的基本原理叠加定理的基本原理可以概括为:在一个线性电路中,如果有多个独立电源作用于电路中,那么最终的电流或电压等可由各个单独电源所产生的效应叠加而成。
如果一个电路中有多个电源,我们可以把每个电源的作用看成是单独进行分析,最后将它们的效应相加得到整个电路的解。
三、叠加定理的适用范围尽管叠加定理对于解决复杂电路问题非常有用,但它并非适用于所有电路。
以下是叠加定理适用范围的一些主要方面:1.仅适用于线性电路:叠加定理只适用于线性电路,即电流与电压之间满足线性关系的电路。
对于非线性电路,叠加定理并不适用,因为非线性元件的电流-电压关系不满足叠加原理。
2.叠加定理不适用于功率和能量:叠加定理可以用于计算电路中特定节点的电压或电流,但它并不能直接计算功率和能量。
功率和能量通常需要通过其他方法进行分析和计算。
3.独立电源:叠加定理只适用于有多个独立电源的电路。
如果电路中的电源相互依赖或由其他因素控制,叠加定理将无法正确应用。
4.线性叠加:叠加定理适用于线性叠加的电路。
线性叠加是指电路响应与输入的线性组合成正比例。
如果电路的响应不满足线性叠加条件,叠加定理将无法得到正确的解。
五、例子和案例分析为了更好地理解叠加定理的适用范围,我们来看几个例子:1.并联电阻:假设有一个由两个电阻 R1 和 R2 并联组成的电路,并且电路中有一个电压源 V。
我们可以使用叠加定理来计算每个电阻上的电流。
关闭电压源 V,只保留 R1,并计算电流 I1。
关闭 R1,只保留 R2,并计算电流 I2。
将这两个电流相加得到总电流 I = I1 + I2。

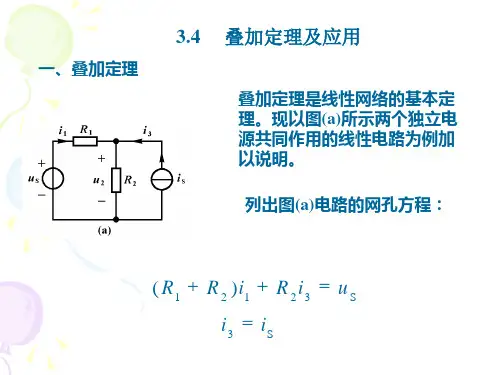
简述叠加原理的应用条件1. 引言在电路分析与设计中,叠加原理是一种重要的理论基础。
它提供了一种简化复杂线性电路分析的方法。
本文将简要介绍叠加原理的应用条件及其在电路分析中的应用。
2. 叠加原理概述叠加原理是基于线性电路的性质而建立的。
它指出,在一个线性电路中,各个电源或源的作用可以分别叠加,得到电源或源分别作用时的电流、电压或功率,并将它们相加得到整个电路的电流、电压或功率。
在叠加原理中,假设电路是线性的、无记忆的,并且各个电源或源之间没有相互影响。
3. 叠加原理的应用条件应用叠加原理进行电路分析需要满足以下条件:3.1 电路是线性的叠加原理仅适用于线性电路,即电阻、电感和电容符合线性关系。
非线性元件,如二极管和晶体管,不适用叠加原理。
3.2 电路是无记忆的无记忆性是指电路的响应仅取决于当前的电压和电流,而与过去的电压和电流无关。
只有电路满足无记忆性,叠加原理才能适用。
3.3 电路中各个电源或源之间没有相互影响叠加原理要求各个电源或源之间独立地叠加,即它们之间不会相互影响。
在实际电路中,电源和源之间的相互作用会导致非线性、记忆效应和相互耦合,因此叠加原理的应用需要排除这些因素的影响。
4. 叠加原理的应用叠加原理在电路分析中具有广泛的应用。
以下是一些常见的应用情况:4.1 电源分析叠加原理可以用于分析多个电源同时作用时电路中的电流和电压。
通过分别计算每个电源作用时的电流和电压,然后将它们叠加在一起,可以得到整个电路的电流和电压。
4.2 电阻网络分析在复杂的电阻网络中,叠加原理可以简化分析过程。
通过将每个电源或电压源分别作用于电阻网络,然后将它们的影响相加,可以求解整个电阻网络的电流和电压。
4.3 电容电路分析对于包含多个电容的电路,叠加原理可以用于计算各个电容的电压和电流。
分别考虑每个电压源作用时的电流和电压,然后将它们叠加在一起,可以得到整个电容电路的电流和电压。
4.4 电感电路分析对于包含多个电感的电路,叠加原理可以用于计算各个电感的电压和电流。
![3.5.3 应用叠加定理求解电路的步骤[共2页]](https://uimg.taocdn.com/ca110cfe647d27284a735177.webp)
电阻电路的一般分析方法 54 第3章其中,前一项就是E 1单独作用时(如图3-16(b )所示)在R 1支路产生的电流,即 2311122313
R R I E R R R R R R +'=++ 后一项就是2E 单独作用时(如图3-15(c )所示)在1R 支路产生的电流,即
312122313R I E R R R R R R ''=++ 同理 22
2333,I I I I I I ''''''=+=+ 又如图3-17所示,求解时,可以让电压源单独作用,再让电流源单独作用,然后再求和。
图3-17 电压源电流源单独作用
3.5.2 使用叠加定理应注意的一些问题
使用叠加定理时应注意以下问题。
(1)叠加定理只能用于线性电路。
(2)电压源作用电流源为零值,电流源作用电压源为零值。
(3)叠加求和时,注意电压和电流值的正、负。
(4)应用叠加原理时,每次只能有一种独立源作用。
3.5.3 应用叠加定理求解电路的步骤
(1)在原电路中标出所求量(总量)的参考方向。
(2)画出各电源单独作用时的电路,并标明各分量的参考方向。
(3)分别计算各分量。
(4)将各分量叠加,若分量与总量参考方向一致取正,否则取负。
(5)将各分量数值代入,计算结果。
【例3-11】 电路参数如图3-18所示,利用叠加定理求解。
图3-18 例3-11图。


叠加定理是电路理论中一个重要的分析工具,它允许我们通过将多个独立源的效应单独考虑并加总来求解复杂电路中的电压和电流。
以下是叠加定理的解释和注意事项:
叠加定理的解释:
叠加定理指出,在线性电路(即电路元件均为线性元件)中,任一节点或支路的电压或电流等于所有电源单独作用时在该节点或支路产生的电压或电流的代数和。
具体步骤如下:
1. 分析电路,确定各个独立电源。
2. 保留一个电源,将其他电源设为零值(理想电压源短路、理想电流源开路),计算出此时电路中所要求的电压或电流。
3. 将第二个电源开启,其他电源保持关闭状态,重复步骤2。
4. 对所有电源重复上述过程,并将结果相加得到最终答案。
叠加定理的注意事项:
1. 叠加定理只适用于线性电路。
如果电路中含有非线性元件(如二极管、晶体管等),则不能使用叠加定理。
1. 在使用叠加定理时,必须保证电路内部参数不变,例如电阻、电容、电感等元件的值。
3. 当需要计算的是功率时,叠加定理不适用,因为功率是电
流与电压的乘积,而它们分别是由不同电源产生的,无法直接进行叠加。
4. 在对电源进行“开”、“关”操作时,要特别注意电源类型(电压源还是电流源),以及如何正确处理这些源的开关状态。
5. 如果电路中有受控源(例如电压控制电压源VCVS、电流控制电压源CCVS等),当其他源被设定为零时,受控源可能会受到影响,因此在这种情况下,叠加定理可能不适用。
6. 使用叠加定理可以简化电路分析,但并不是所有的电路问题都可以用叠加定理解决,有时还需要结合其他电路分析方法,如戴维南定理、诺顿定理等。


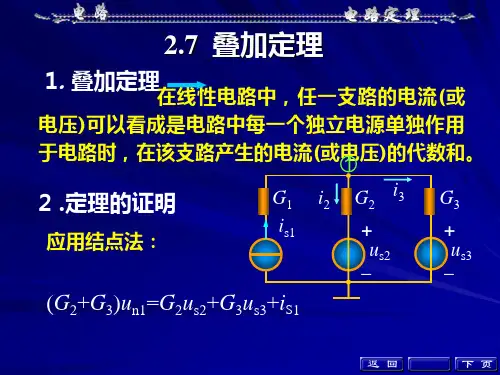
叠加定理叠加定理1.叠加定理的内容在线性电路中,任一支路的电流(或电压)都可以看成是电路中每一个独立电源单独作用于电路时,在该支路产生的电流(或电压)的代数和。
2.应用叠加定理分析1) 叠加定理只适用于线性电路。
这是因为线性电路中的电压和电流都与激励(独立源)呈一次函数关系。
2) 当一个独立电源单独作用时,其余独立电源都等于零(理想电压源短路,理想电流源开路)。
如图4.2所示。
=三个电源共同作用i s1单独作用+ +u s2单独作用us3单独作用图 4.23) 功率不能用叠加定理计算(因为功率为电压和电流的乘积,不是独立电源的一次函数)。
4) 应用叠加定理求电压和电流是代数量的叠加,要特别注意各代数量的符号。
即注意在各电源单独作用时计算的电压、电流参考方向是否一致,一致时相加,反之相减。
5) 含受控源(线性)的电路,在使用叠加定理时,受控源不要单独作用,而应把受控源作为一般元件始终保留在电路中,这是因为受控电压源的电压和受控电流源的电流受电路的结构和各元件的参数所约束。
6) 叠加的方式是任意的,可以一次使一个独立源单独作用,也可以一次使几个独立源同时作用,方式的选择取决于分析问题的方便。
3.叠加定理的应用例4-1 求图示电路的电压U.例4-1图解:应用叠加定理求解。
首先画出分电路图如下图所示当12V电压源作用时,应用分压原理有:当3A电流源作用时,应用分流公式得:则所求电压:例4-2计算图示电路的电压u 。
例4-2图解:应用叠加定理求解。
首先画出分电路图如下图所示当 3A 电流源作用时:其余电源作用时:则所求电压:本例说明:叠加方式是任意的,可以一次一个独立源单独作用,也可以一次几个独立源同时作用,取决于使分析计算简便。
例4-3计算图示电路的电压u 电流i 。
例4-3 图解:应用叠加定理求解。
首先画出分电路图如下图所示当 10V 电源作用时:解得:当5A电源作用时,由左边回路的KVL:解得:所以:注意:受控源始终保留在分电路中。
叠加定理的
叠加定理是一种重要的数学理论,它被广泛应用于许多学科领域,如信号处理、计算机网络和诸如此类的数学实验。
它是一种极其有用的理论,为应用提供了一种健全的方法。
叠加定理的基本概念是指,任意的两个信号叠加在一起后,最终的结果仍然是一个信号。
此外,根据叠加定理,在一定条件下,叠加后的信号可以通过噪声滤波器去除多余的噪声来改善信号的质量。
叠加定理是线性系统理论中的一个核心概念,它是用来描述系统信号经过叠加后的行为特征。
叠加定理有助于描述复杂系统中的简单行为,同时也有助于研究复杂系统的规律性。
叠加定理在信号处理中的应用有许多,例如调制解调器的设计、滤波器的设计、信号传输以及信号检测等等。
例如,在调制、解调器的设计中,需要考虑多载波信号的叠加原理,以确保多载波信号能够正确叠加。
此外,叠加定理还可以用于滤波器设计,例如对多载波信号的加权滤波器可以考虑到叠加定理,以确保多载波信号的正确加权。
在数字信号处理中,叠加定理还可以应用于空间域滤波器设计,广泛应用于机器视觉、图像处理、信号分析与处理等领域。
最后,叠加定理有助于更好地理解信号处理系统的动态特性,并且为信号处理系统的设计提供了一种灵活有效的方法。
总之,叠加定理是为许多学科领域提供了有效支持的重要理论,为研究人员提供了丰富的技术手段,极大地推动了科学技术的进步。