电工基础课件——第十讲 叠加定理及应用

电路中的叠加定理原理及应用电路中的叠加定理是一种重要的分析电路的方法，它基于电流和电压的线性性质，能够简化复杂的电路计算。

在本文中，将详细介绍电路中的叠加定理的原理及其应用。

一、叠加定理的原理叠加定理的原理基于电流和电压在线性电路中的叠加性质。

根据叠加定理，如果一个线性电路中有多个独立的电源，则可以将每个电源单独激活并计算其产生的电流或电压，然后将这些独立的结果叠加得到最终的电流或电压。

具体来说，在一个电路中有多个独立的电源时，首先将所有其他电源置零，只激活其中一个电源，计算得到该电源下的电流或电压。

然后，将当前电流或电压置零，激活下一个电源，再次计算得到新的电流或电压。

重复以上步骤，直到激活了所有电源并计算得到所有的电流或电压。

最后，将得到的各个电流或电压叠加在一起，即可得到最终的电流或电压。

这是因为线性电路的特性使得电流和电压具有叠加性质，可以将它们分别计算得到最后的结果。

二、叠加定理的应用叠加定理在电路分析中有广泛的应用。

以下将介绍它在不同情况下的具体应用。

1. 求解电流和电压通过叠加定理，可以更容易地求解电路中的电流和电压。

将每个电源单独激活并计算得到相应的电流或电压，然后将它们叠加在一起，即可得到最终的结果。

2. 计算功率叠加定理也可以用于计算电路中的功率。

根据功率公式P=VI，可以将每个电源单独激活并计算得到相应的功率，然后将它们叠加在一起，即可得到最终的功率。

3. 分析交流电路对于含有交流电源的电路，叠加定理同样适用。

只需将交流电源视为由正弦函数表示的电压源，按照同样的步骤进行计算。

这样可以更方便地求解交流电路中的电流、电压和功率。

4. 分析混合电路在存在混合电源（包括直流电压源和交流电压源）的电路中，叠加定理也可以成功应用。

根据叠加定理，可以分别计算出每个电源作用下的电流或电压，并将这些结果叠加在一起，得到最终的电流或电压。

5. 实际应用举例叠加定理在实际应用中非常有用。

例如，在设计电路时，如果需要知道某个元件的电流，可以将其他影响该元件的电源置零，只考虑该元件单独受到一个电源的影响，从而更容易计算得到准确的电流。

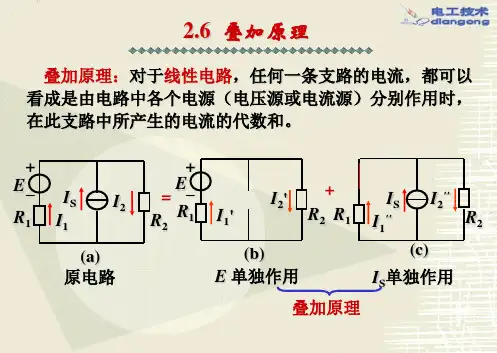
叠加定理的表述及应用叠加原理是线性电路的一个重要规律,内容是在线性电路中,任一支路的电流,{或电压}都是电路中各电源单独作用时在该支路中产生的电流{或电压}的代数和。

简单的说就是在一个电路里,一段支路的电压（电流）等于这个电路里每一个电源对这段支路的电压（电流）的总和。

叠加定理通常与等效电压（电流）源的方法一起用,求支路的电压（电流）：把电路里所有的电流源都等效成电压源,或者把电路里所有的电压源都等效成电流源,再用叠加定理求支路的电压或电流。

在使用叠加原理使用的条件和注意的是：1、叠加原理只适应求解线性电路的电压,电流。

对功率不适用。

2、每个独立电源单独作用时,其他独立电源不作用,电压源短接,电流源断开。

3、叠加时要注意电压,电流的参考方向，求和时要注意电压分量,和电流分量的正负。

叠加定理适用于线性电路。

叠加定理在电路分析中非常重要。

它可以用来将任何电路转换为诺顿等效电路或戴维南等效电路。

该定理适用于由独立源、受控源、无源器件（电阻器、电感、电容）和变压器组成的线性网络（时变或静态）。

应该注意的另一点是，叠加仅适用于电压和电流，而不适用于电功率。

换句话说，其他每个电源单独作用的功率之和并不是真正消耗的功率。

要计算电功率，我们应该先用叠加定理得到各线性元件的电压和电流，然后计算出倍增的电压和电流的总和。

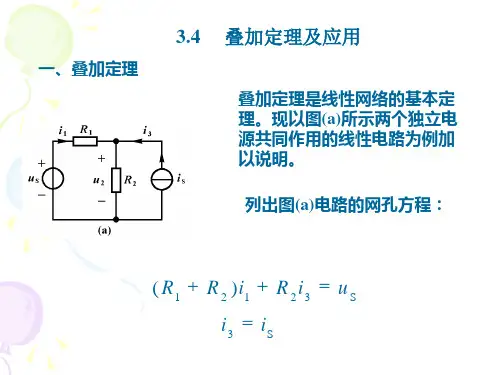
对于一个线性电路，有多个独立源共同作用时，各支路的电流（或电压）等于各个独立电源单独作用时，该路的电流（或电压）的代数和。

为了确定每个独立源的作用，所有的其他电源的必须进行“置零”操作：电压源短路（理想电压源的内部阻抗为零（短路））。

电流源开路（理想电流源的内部阻抗为无穷大（开路））。

二、应用三步曲（画标-计算-求和）1、画出电源独立作用时的分电路图，并标上待求量的参考方向；2、在分电路上求出各分量；3、将各分量求代数和得到总量，叠加时注意分量的参考方向。