下载文档原格式
用中档FPGA实现多相滤波器技术分类： 可编程器件 | 2009-06-24莱迪思半导体公司 Ron Warner引言在现代电子系统中，到处都可以看到数字信号处理（ DSP ）的应用，从MP3播放器、数码相机到手机。
DSP设计人员的工具箱的支柱之一是有限脉冲响应（ FIR ）滤波器。
FIR滤波器越长（有大量的抽头），滤波器的响应越好。
然而这里有折衷的情况，由于大量的抽头增加了对逻辑的需求、增加了计算的复杂性，增加了功耗，以及可能引起饱和/溢出。
多相技术可以用于实现滤波器，拥有与传统FIR滤波器可比的结果，而且使用了较少的逻辑、需要较少的计算资源、更低的功耗，并减少了可能的饱和/溢出。
可用如今新型的小规模、中档的FPGA，如LatticeECP3 来实现这些滤波器。
基本概念进入DSP世界可能会有些令人生畏，因此，让我们首先介绍一些简单的概念。
对于数字系统，如音频，视频和无线领域，形成信号的结果是与采样率相关的。
举例来说，以48 kHz（即每秒48000个样本）对专业音频信号进行采样。
相比之下，消费者的CD播放机则使用44.1 kHz的采样率。
多速率系统多速率系统使用多个采样速率。
在某些情况下，运行于某个速率的系统的一部分需要一个原来以另外某个速率采样的信号（转换专业音频到消费者的CD音频就是一个例子）。
在这种情况下，原始信号的速率必须根据需要增加或减少。
或者针对特定的用途，也可能以比实际需要更高的速率对原来的数据进行了采样。
因此，降低采样率，然后运行所得到的数据就可以大幅度降低数据吞吐量的要求，降低对存储器的要求，提高处理效率并降低功耗。
向下采样和抽取让我们首先考虑降低采样率的问题。
假设我们有一个信号，原来以我们称之为fHz的某一频率进行采样，如如图1所示。
图1 用f Hz采样率对原始信号采样现在假设我们要降低采样率至原来频率的1/4。
达到此目的一个方法来就是简单地扔掉每四个原始采样中的三个，如图2所示。
滤波器基本原理
滤波器是一种电子设备，用于改变信号的频率特性或解决信号中的干扰问题。
滤波器的基本原理是通过选择性地通过或阻断特定频率的信号来实现对信号的处理。
滤波器的工作原理可以通过频率响应来描述。
频率响应显示了滤波器对不同频率的信号的响应情况。
滤波器可以通过调整其频率响应来实现不同的滤波效果。
主要的滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
低通滤波器允许低于某个截止频率的信号通过，而阻断高于该频率的信号。
高通滤波器则相反，允许高于截止频率的信号通过。
滤波器的基本构成包括电容、电感、电阻等元件。
不同的滤波器类型使用不同的元件组合，并采用不同的电路连接方式来实现滤波效果。
滤波器的应用广泛，常见于通信系统、音频设备、图像处理等领域。
通过滤波器，我们可以对信号进行去噪、频率调整、数据提取等操作，使得信号更加符合我们的需求。
摘要软件雷达是现代雷达的重要发展方向。
其中数字化中频接收系统是关键技术之一。
本论文以某雷达数字化接收系统为背景，主要研究其中的关键技术——多相滤波器的原理及设计与仿真。
为了更好的理解，本文同时对数字滤波器作了简单的介绍，包括滤波器的定义、分类与实现方式。
对无线电中的两个最基础的概念内插与抽取也做了介绍。
对多相滤波器的原理进行了详细的说明，从公式推导上进行了理论实现的方法与可能。
讨论了多相滤波如何实现信道化。
最后介绍了数字滤波器的设计步骤并实现了多相滤波器的MATLAB仿真。
关键词：多相滤波器、软件无线电、数字滤波器。
AbstractSoftware radar is an important developing direction of modern radar. Which digital intermediate frequency receiving system is the key technical one. This paper taking a radar system for background, digital receiving main research key technology - multiphase the principle of filter and design and simulation. In order to better understanding of digital filter, the paper also makes brief introduction, including the definition, classification and filter implementation. The two most basic to radio the concept interpolation and extract presented also. The principle of multiphase filter for a detailed instructions from the formula, the method to realize the theory with possible. Discusses how to realize the multiphase filtering channelized. At last, the paper introduces the design procedures of the digital filter and realize the multiphase filter MATLAB simulation.Keywords: multiphase filter, software radio, digital filters摘要I第一章问题的提出IV第二章数字滤波器概论IV引言 (IV)2.1、数字滤波器的定义 (V)2.2、数字滤波器的实现方式 (V)2.3、数字滤波器的分类 (V)2.4实际滤波器的设计指标 (VI)第三章多相滤波器的理论原理VII引言 (VII)3.1整数倍抽取 (VII)3.2整数倍内插 (VII)3.3抽取内插器的实时处理结构——多相滤波结构 ........... V III3.4频域抽取 (IX)3.5用加权函数展宽输出滤波器 (XI)3.6改变输出采样速率 (XII)3.7多相滤波器实现信道化 ................................................... X III 第四章多相滤波器的MATLAB仿真XIV引言 (XIV)4.1数字滤波器设计的理论基础 (XIV)4.2FIR窗函数设计法 .............................................................. X V4.3多相滤波器的MATLAB仿真 (XVI)第五章总结XIX参考文献错误！未定义书签。
2013年4月信号抽取的多相形式实现一、理论基础理论情况下对信号进行多速率处理时，要在信号的抽取之前和信号的插值之后进行信号的限带滤波。
因为抽取是信号频谱扩展的过程、插值是信号频谱压缩的过程，若不进行限带滤波，则抽取后信号频谱在周期延拓扩展的过程中将会引起频谱的混叠造成信号的改变，使信号信息产生变化；同理，插值的过程没有限带时，也将会使我们不感兴趣的冗余信息压缩进信号的频谱中，造成信号携带信息的改变，使信号失真。
理论框图如下：内插器及其框图表示但这显然不是最优化的处理方法：因为多速率信号处理的核心目的之一就是在不改变信号携带信息的条件下降低信号的流速率，以减轻对信号处理器件的运算速度的压力，来最大化的提高系统效能。
可理论框图中：滤波器分别放置在抽取器之前和内插器之后。
而这两个位置恰恰是信号流速率相较另一侧更高的一端，显然这会加大硬件的处理负担。
由于这次实验是对抽取进行验证所以下文内容只讨论抽取的结构优化过程。
我们通过对限带滤波器h[n]的Z变换进行分析，结构变化可以发现H(z)可以转化为如下形式：()()nn H z h n z +∞-=-∞=∙∑()()()1M nkMk n Hz zh nMk z-+∞--==-∞=+∑∑()()()nnkk n n E z e n zh nM k z +∞+∞--=-∞=-∞==+∑∑()()1M k Mkk Hz z Ez --==∑再根据，抽取与滤波器之间的恒等变换，可以把抽取系统转化等效的多相形式表示如下：可见等效结构中：滤波器的运算是在对信号进行抽取之后的，这就显而易见的降低了原信号的信号流速率，使后续对信号处理过程的运算量大大的降低了。
这就体现出了多相滤波形式的一大优势，并且还可以根据后续处理的要求，采取不同的多相形式来提高系统的效率，节省了系统的内部资源。
2.实验过程上一节对多相滤波形式的优势及实用性进行了分析和阐述。
这一节将对其实现过程进行叙述。
基于分布式算法的FIR 平方根升余弦多相滤波器的仿真、设计与实现实验要求设计的实验原理过采样与滤波器的多相实现在通信系统中，不论是成型滤波器还是匹配滤波器都是对源信号进行过采样后的的信号进行滤波【1】。
图1、过采样和滤波示意图如图1所示，将想11()x n T 经I 倍过采样后得到22()up x n T ，再经过冲击响应为22()h n T 的FIRLPF 得到输出序列22()up y n T 。
22()up y n T 在时刻的值，是由下式来计算：（1）将带入（1）式有：（2）进一步定义，方程（2）变为：（3）由于22()up x n T 是11()x n T 经I 倍上采样得到的，即在每两个数据之间插入了I-1个0，因此，成立，所以方程（3）变为：（4）由方程（1）可看出，次滤波器是2M I 阶的，由于源序列是经过了I 倍过采样的信号，故可以化简为方程（4），由此可看出，对于任意一个时刻，实际上只用到了2M 个滤波器系数，当i 不同时，所用的滤波器系数不同，也就是将原来的一个2M I 阶滤波器分成了I 个2M 阶的滤波器来实现，这样降低了滤波器的阶数，从而减小了滤波延时，这种实现方式即称为滤波器的多相实现方式，其中称为第i 相子滤波器。
此处，对信号进行4被过采样，滤波器阶数为32，因此可将滤波器分为4相实现，每个子滤波器的阶数为8。
假设原滤波器系数为0131,......h h h ，则每一相的子滤波器系数，应时以下组合：它的实现框图如图2所示：图2、4倍过采样的滤波器多相实现结构图FIR 滤波器的分布式算法实现由前一部分可知，对一个I 过采样的信号进行滤波时，可以将滤波器拆为I 个低阶滤波器的组合来实现滤波过程这在一定程度上降低了运算量，减小了滤波延时；但是在FPGA 实现时对于滤波的卷积过程的实现一般并不是直接按照卷积的定义，每输入一个数据就去求一次卷积，这样运算的计算量仍然很大，基于此问题就提出了卷积过程的分布式实现算法。
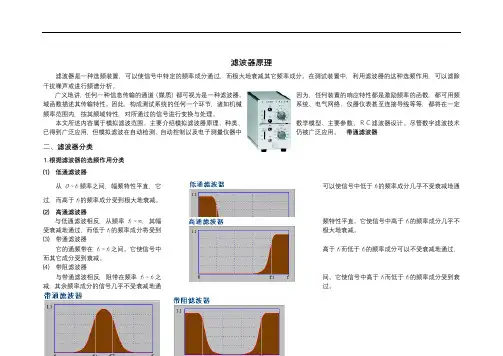
滤波器原理滤波器是一种选频装置，可以使信号中特定的频率成分通过，而极大地衰减其它频率成分。
在测试装置中，利用滤波器的这种选频作用，可以滤除干扰噪声或进行频谱分析。
广义地讲，任何一种信息传输的通道（媒质）都可视为是一种滤波器。
因为，任何装置的响应特性都是激励频率的函数，都可用频域函数描述其传输特性。
因此，构成测试系统的任何一个环节，诸如机械系统、电气网络、仪器仪表甚至连接导线等等，都将在一定频率范围内，按其频域特性，对所通过的信号进行变换与处理。
本文所述内容属于模拟滤波范围。
主要介绍模拟滤波器原理、种类、数学模型、主要参数、ＲＣ滤波器设计。
尽管数字滤波技术已得到广泛应用，但模拟滤波在自动检测、自动控制以及电子测量仪器中仍被广泛应用。
带通滤波器二、滤波器分类⒈根据滤波器的选频作用分类⑴低通滤波器从0～f2频率之间，幅频特性平直，它可以使信号中低于f2的频率成分几乎不受衰减地通过，而高于f2的频率成分受到极大地衰减。
⑵高通滤波器与低通滤波相反，从频率f1～∞，其幅频特性平直。
它使信号中高于f1的频率成分几乎不受衰减地通过，而低于f1的频率成分将受到极大地衰减。
⑶带通滤波器它的通频带在f1～f2之间。
它使信号中高于f1而低于f2的频率成分可以不受衰减地通过，而其它成分受到衰减。
⑷带阻滤波器与带通滤波相反，阻带在频率f1～f2之间。
它使信号中高于f1而低于f2的频率成分受到衰减，其余频率成分的信号几乎不受衰减地通过。
低通滤波器和高通滤波器是滤波器的两种最基本的形式，其它的滤波器都可以分解为这两种类型的滤波器，例如：低通滤波器与高通滤波器的串联为带通滤波器，低通滤波器与高通滤波器的并联为带阻滤波器。
低通滤波器与高通滤波器的串联低通滤波器与高通滤波器的并联⒉根据“最佳逼近特性”标准分类⑴巴特沃斯滤波器从幅频特性提出要求，而不考虑相频特性。
巴特沃斯滤波器具有最大平坦幅度特性，其幅频响应表达式为：⑵切比雪夫滤波器切贝雪夫滤波器也是从幅频特性方面提出逼近要求的，其幅频响应表达式为：ε是决定通带波纹大小的系数，波纹的产生是由于实际滤波网络中含有电抗元件；T n是第一类切贝雪夫多项式。
基于多相滤波结构的信道化及FPGA实现张诚;吴沁;贺浪【摘要】随着现代电子战中电磁环境的日益复杂,军用接收机需具备同时处理多个信道信号的能力,即具备全概率截获能力.信道化接收机可将一个复杂信号分成多个信道,从而方便后续处理.文中利用一种简化的结构验证了该种信道化方案的可行性,并节省了逻辑资源.【期刊名称】《电子科技》【年(卷),期】2014(027)003【总页数】4页(P102-105)【关键词】数字下变频;多相滤波;信道化【作者】张诚;吴沁;贺浪【作者单位】西安电子科技大学电子工程学院,陕西西安710071;西安电子科技大学电子工程学院,陕西西安710071;西安电子科技大学电子工程学院,陕西西安710071【正文语种】中文【中图分类】TN914在电子战中，传统上主要采用扫频式搜索接收机，但其截获概率受搜索速度的影响较为严重，且因其受到搜索速度与分辨率之间关系的制约，所以扫频式接收机对跳频信号的截获效果很不理想［1］。
信道化接收机是对某个频段的信号全概率接收的接收机，而基于多相结构的信道化接收机相对于传统意义上的信道化接收机对同一频段信号而言所需硬件资源更少，且更易于实现。
其相对传统的信道化接收机凭借其高效的多相结构，使其在多信道处理方面得到了广泛应用［2］，是接收机的发展趋势。
1 多相滤波结构的信道化原理1.1 信道的划分因实信号频谱具有对称特性，所以其频带划分较为特殊，这里只对［0，π］上的频谱进行信道划分［3］。
若划分K个信道，各信道的中心频率为ωk=kπ/K+π/2K，其中，k=0，1，…，K －1。
图1 实信号的信道排列形式由傅里叶变换可知，低通滤波器的频谱包括正负对称的两部分。
为使信道的划分如图1所示，需将滤波函数的频谱全部移到正半轴，这里对滤波器的频谱函数做如下变换此时反映到频域如图2所示，因此，采用复FIR滤波器对输入的实信号进行滤波。
图2 实信号与平移后的低通滤波器的频谱图1.2 基于多相结构滤波器的信道化原理信道化的主要过程为，先将每个信道乘以e－jωkn，对信号做频域的搬移［4］，再经过低通滤波器，滤除高频分量，并将频率均降到基带，做下变频［5］，最终进行抽取。
多相滤波器的设计多相滤波器是一种特殊类型的数字滤波器，它在滤波器的每个阶段都使用了不同的延时，从而使其具有相位非零的频率响应。
在信号处理的许多领域中，多相滤波器具有重要的应用，如通信系统、音频处理和图像处理等。
本文将介绍多相滤波器的设计方法和应用。
一、多相滤波器的基本原理多相滤波器的原理基于信号的采样和重建过程。
在数字信号处理中，信号首先经过采样器进行采样，然后通过低通滤波器进行滤波，再通过插值器进行重建。
在多相滤波器中，采样和重建滤波器通过相位差的变化，实现了对频率响应的调制。
多相滤波器通过引入不同的延迟路径，使得滤波器的频率响应在不同的相位上有所变化，从而实现了更强大的滤波性能。
二、多相滤波器的设计方法设计多相滤波器的方法通常包括两个步骤：滤波器设计和多相分解。
1.滤波器设计滤波器设计通常使用经典的滤波器设计方法，如巴特沃斯、切比雪夫和椭圆滤波器等。
选择合适的滤波器类型和参数，设计出满足特定要求的滤波器。
2.多相分解多相分解是将一个滤波器分解为多个子滤波器的过程。
多相分解可以通过多项式展开或快速离散余弦变换（DCT）等方法实现。
多相分解可以将一个滤波器变换为多个具有较小延迟的子滤波器，从而减少计算复杂度和存储需求。
多相分解的方法有很多种，如多项式分解、快速离散余弦变换、奇偶抽取法等。
三、多相滤波器的应用1.通信系统2.音频处理3.图像处理四、多相滤波器的优缺点1.多相滤波器具有更高的频率选择性和更好的滤波性能。
2.多相滤波器能够减少计算复杂度和存储需求。
3.多相滤波器可以实现非零的相位响应，从而更好地保留信号的相位信息。
然而，多相滤波器也存在一些缺点：1.多相滤波器的设计和实现较为复杂，需要考虑不同的延迟路径和相位差。
2.多相滤波器的性能受到设计参数的限制，需要选择合适的滤波器类型和参数。
综上所述，多相滤波器是一种在数字信号处理中广泛应用的滤波器，它通过引入多个延迟路径和相位差，实现了更好的滤波性能和相位响应。
多相滤波器原理多相滤波器是数字信号处理中常用的一种数字滤波器，其核心原理是将原始信号分解成不同的相位，通过频域滤波和加权后再进行重合成，从而达到滤波的目的。
本文将从多相滤波器的定义、性质、设计方法等多方面进行全面介绍。
一、多相滤波器的定义所谓多相滤波器，就是将一个传统的数字滤波器分解成不同的相位，然后再通过加权合成的方法，实现与原始滤波器相同的滤波效果。
在单相数字滤波器筛选的同一频率下，多相滤波器的性能更加优秀，尤其是对于高通和带阻滤波器的设计更为适用。
多相滤波器的关键是其级数，级数越高，相位数量越多，精度也就越高。
为了确保多相滤波器的稳定性和可控性，还需要对其级数进行严格的控制和设计。
1. 初态误差:在多相滤波器中，信号被分解成不同的相位，因此初态误差非常小。
这意味着，多相滤波器可以在不影响信号质量的前提下，实现更高的精度和稳定性。
2. 频率响应：多相滤波器的频率响应与传统数字滤波器的一样。
由于分解成了不同的相位，不同相位的频率响应会发生变化。
为了控制多相滤波器的频率响应，需要进一步对该滤波器进行优化和设计。
3. 相关性质：由于多相滤波器每个分支的滤波器都是一样的，因此不同相位的信号有很强的相关性。
这对于信号识别和提取等应用非常有用。
4. 敏感性：虽然多相滤波器的相位可以控制，但是在设计过程中，必须非常小心。
如果相位不精准，很容易导致滤波器的性能下降，影响整个系统的信息传输和处理能力。
多相滤波器的设计对于数字信号处理系统的性能有着非常重要的影响。
在设计过程中，必须仔细考虑多种因素，如相位数量、偏差、级数等等，以确保高效和稳定的性能。
1. 相位数量的选择：相位数量是多相滤波器设计中最重要的参数之一。
一般来说，相位数的选择取决于输入信号的采样频率和理论分辨率之间的比率。
如果相位数太小，则会限制滤波器的性能；相反，如果相位数太大，则会增加滤波器的复杂度。
2. 滤波器的级数：多相滤波器的级数越多，其精度和性能就越好，但是其计算量也会增加。
