光的衍射(二)

实验中常采用“缺级”的方法来克服重级现象。如420nm的第 三级谱线与630nm 的第二级谱线重叠，可用 d / a 2 的光栅 使其第二级谱线缺级，顺利地对420nm的光谱进行测量。也可 用滤色片将630nm的光滤掉（即吸收），来避免重级。
棱镜光谱是零级光谱。只有 一个级次，没有重级现象。
定义恰能分辨的两条谱线的平均波长 与 R 它们的波长差 之比为光栅的分辨本领 R
由光栅方程
P
( a b) sin k ( k 0,1,2) 加强
kf x a b
( k 0,1,2)
明纹
播放动画
播放动画
例：分光计作光栅实验，用波长 = 632.8 nm的激光照射光栅常数 d = 1/300 mm的光栅上，问最多能看到几条谱线。
解：在分光计上观 察谱线，最大衍射 角为 90°,
d
( a b) sin k
kmax ( a b) sin 90

o x

f
P

kmax
( a b) sin 90
3 . 5
3 1 10 9 300 632.8 10
-8
单缝衍射 轮廓线
4 8
-4
0
a b k m a k'
(m 1，3) 2，
m为整数时，光栅谱线中m、2m、3m等 处缺级。
I单
当 m=4 时 谱线中的第 –8、 – 4、4、 8级条纹缺级。
-2 -1
0 I 光栅衍射 光强曲线 1 2
单缝衍射 轮廓线
4 8
-8
-4
0
第五节 光栅光谱
X 射线的应用不仅开创了研究晶体结构的新领域， 而且用它可以作光谱分析，在科学研究和工程技 术上有着广泛的应用。 在医学和分子生物学领域也不断有新的突破。 1953年英国的威尔金斯、沃森和克里克利用 X 射线的结构分析得到了遗传基因脱氧核糖 核酸（DNA) 的双螺旋结构，荣获了1962 年 度诺贝尔生物和医学奖。

18
较大 符合
瑞利 判据
太小
小孔（直径D）对两个靠近的遥远的点光源的分辨 19
S1 *
D

0
I
* S2
最小分辨角 （angle of minimum resolution）：

1
1 . 22

D
分辨本领（resolving power）：
R 1


D 1 . 22
6
2、N=3
δ
-λ
3、N=4
0 0I
λ
δ
-λ
0
λ
I
N很大时,数目众多强度极弱 的次极大与极小混成一片, 淹没在杂散光的背景之中, 形成一片暗区，一般觉察不 δ 出它们的存在;各主极大成 为非常细的亮条纹。
三、光栅的衍射规律 1、可以证明：光栅衍射，是单缝衍射和多 光束干涉共同作用的结果。 各主极大受到单缝衍射的调制，衍射光强 大（小）的方向,主极大的光强也大（小）。
7
例：d 4a 情形
单缝衍射光强曲线 -2 -1
I
（参见书p181图4.12）
sin (/a)
多光束干涉光强曲线
0 I
1
2
-8
-4
0
I
4
sin 8 (/d)
光栅衍射光强曲线
单缝衍射 包络线
4 sin (/d)
8
-8
-4
0
8
19个明条纹
单缝衍射和多缝衍射干涉的对比 （d =10 a）
13
0
sin
五、光栅光谱
d sin k ( k 0 ,1 ,2 )
λ定, k |θ|
3级 2级 1级 0 1级

例:以氦放电管发出的光垂直照射到某 以氦放电管发出的光垂直照射到某 光栅上,测得波长 光栅上 测得波长λ1=0.668µm 的谱线的衍 射角为 ϕ =20°.如果在同样 ϕ 角处出现波 如果在同样 λ2=0.447µm的更高级次的谱线 的更高级次的谱线, 长 那么光栅常数最小是多少? 那么光栅常数最小是多少 解:由光栅公式得 由光栅公式得 sin ϕ = k1λ1 (a + b) = k2λ2 (a + b) k1λ1 = k2λ2 k2 k1 = λ1 λ2 = 0.668 0.447
§4
光栅衍射
一. 衍射对双缝干涉的影响 不考虑衍射时, 双缝干涉的光强分布图： 不考虑衍射时, 双缝干涉的光强分布图：
I I0
− 3λ − λ − λ λ 0 2d d 2d 2d
λ
d
3λ 2d
sin θ
设双缝的每个缝宽均为 a，在夫琅禾费衍 射下，每个缝的衍射图样位置是相重叠的。 射下，每个缝的衍射图样位置是相重叠的。
准直缝 晶体 X射线 射线 劳厄斑
* 穿透力强 * 波长较短的电磁波， 波长较短的电磁波， 范围在 0.001nm~10nm之间。 之间。 之间
·· · ·
证实了X射线的波动性
二. X射线在晶体上的衍射
同一晶面上相邻原子 D C 散射的光波的光程差 ϕ 1 零 AD-BC= 0， 它们 ， A B 相干加强。 相干加强。若要在该 P 2 N M 方向上不同晶面上原 d 3 子散射光相干加强， 子散射光相干加强， 则必须满足： 则必须满足： ∆ = NM + MP = kλ k = 1,2,3L 时各层面上的反射光相干加强， 即当 2d ⋅sin ϕ = kλ 时各层面上的反射光相干加强，形 成亮点， 级干涉主极大。该式称为布喇格公式 布喇格公式。 成亮点，称为 k 级干涉主极大。该式称为布喇格公式。 因为晶体有很多组平行晶面，晶面间的距离 d 各 因为晶体有很多组平行晶面， 不相同所以，劳厄斑是由空间分布的亮斑组成。 不相同所以，劳厄斑是由空间分布的亮斑组成。

讨论
中央明纹集中大部分能量， 明条纹级次越高亮度越弱。
二级明纹中心:
1 部分光线干涉相长 5

I
1 部分光线干涉相长 3
讨论条纹随 、 a 的变化
2 f 中央明纹 x a
一定
讨论 其余明纹 x f a
a 衍射显著 a 光强太弱
a

衍射不明显 a 直线传播
sin
d 缺级： k k a
(k 1,2)
（3）单缝衍射中央明纹区主极大条数
d d 2( ) 1 2 2( ) 1 a进整 a 进整
sin
小结
光栅衍射是N缝干涉和N个单缝衍射的总效果
I I0( sin
光强分布 式中：

sin N 2 ) ( ) sin

sin N 2 ) ( ) sin
2
单缝衍射因子
多(N)缝干涉因子
a sin
d sin
a:
缝宽
d : 光栅常数 a+b
: 衍射角
I I0(
sin

sin N 2 ) ( ) sin
2
同一缝中的子波相干影响亮度分布
sin
k , I
同学们好！
§14.3 光的衍射
复习： 单缝夫琅和费衍射
*明暗纹条件：
0
中央明纹中心
a sin ( 2k 1) 2

各级明纹中心 暗纹
k
k 1、 2、 3
注意： 注意
k 0
*条纹角宽度
sin
0
k
中央明纹中心

L

P
j
o
f
Q
3d d k 30 2 2

5.1 k 1.7
观察到k=0，±，-3， -5共5条明纹
光的衍射（二） 第十一章 光学 3．波长范围在450～650 nm之间的复色平行光垂直照 射在每厘米有5000条刻线的光栅上，屏幕放在透镜的 焦面处，屏上第二级光谱各色光在屏上所占范围的宽 度为35.1 cm．求透镜的焦距f． (1 nm=10-9 m) 解：光栅主极大 d sin k (k 0,1,2,) 1 k xk OQ f tan f tan[sin ( )] d 7
光栅主极大 d sin k
(k 0,1,2,) 1 k xk OQ f tan f tan[sin ( )] d
L
P
Q
a b

o
f
400107 x11 50 tan[sin ( )] 2.00cm 3 1.0 10 7 1 76010 x12 50 tan[sin ( )] 3.81cm 3 1.0 10
6
光的衍射（二）
第十一章 光学
5*．一平面透射多缝光栅，当用波长1=600nm的单 色平行光垂直入射时，在衍射角=30°的方向上可以看 到第2级主极大，并且在该处恰能分辨波长差=5×10-3 nm的两条谱线．当用波长2=400 nm的单色平行光垂直 入射时，在衍射角=30°的方向上却看不到本应出现的 第3级主极大．求光栅常数d和总缝数N，再求可能的缝 宽a。（不作要求） 解： 光栅主极大 d sin k (k 0,1,2,)
d sin j k (k 0,1,2,)
两光明纹重合处
d sin j k11 k22 440k1 660k2

~ i 2δ ~ ~ ik ( r1 + 2Δ ) E3 (θ ) = a0e sin cα = A0e sin cα
~ ~ i ( N -1) E N ( ) A0 e sin c
P点合振动的复振幅：
~ E (θ )
N 1

~ imδ A0 e s in cα
m 0
多缝衍射光强公式：
其中： ~ —衍射屏处复振幅及其它常量。 a0
e
ikrm
—第m个缝到P点的位相延迟。
sin c —单缝衍射因子，单缝在P 点引起的振动。
有：
~ ~ ~ ikr1 E1 (θ ) = a0 e sin cα = A0 sin cα
~ iδ ~ ~ ik ( r1 +Δ ) E2 (θ ) = a0 e sin cα = A0 e sin cα
sin
对多缝干涉因子
(
sin N sin
)
2
sin 0 sin N 2 当 时 ( ) 0 sin sin N 0

m' N
( m' 1, 2 N 1)
有干涉极小值。 两主极大间有N-1个极小值 。
对多缝干涉因子
(
sin N sin
)
r
r-OB
x
a
sin （P） I 0 I （ i

a (sin i sin i ) ）
2

a (sin i sin i)
① sini - sini’ = 0 时, I（Pi’）有极大值 即i ’ =i 时， I（Pi’）=Imax (反射定律成立时) ② sini - sini’ ≠ 0， 即 i ’ ≠i 时 只要满足 a>>λ， I（Pi’）≈ 0

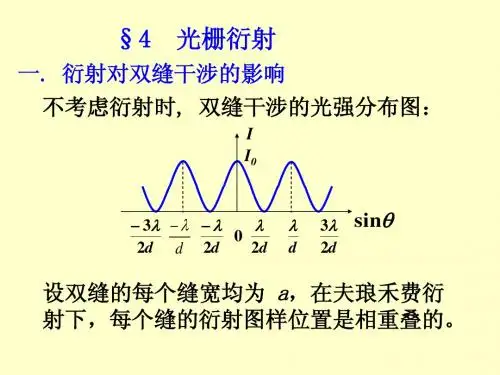
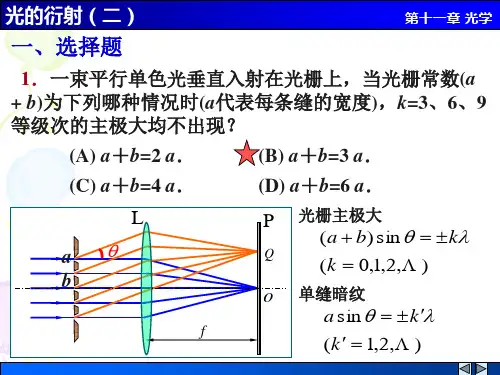
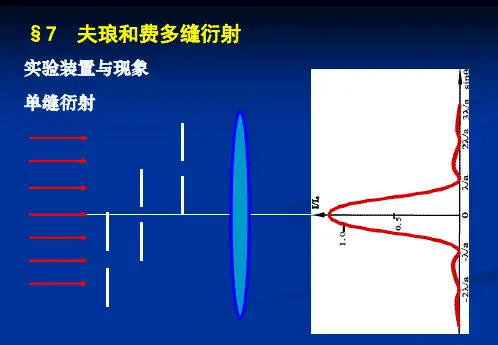
光的衍射(二)1.一束单色平面电磁波垂直投射在每厘米刻有4000条刻痕的衍射光栅上，若在与光栅法线夹30°角处找到第二级极大，则该电磁波长应为( D )(A)2.50×10-2m (B) 2.50×10-4m(C)6.25×10-5m (D) 6.25×10-7md=1/4000=2.5×10-4cm=2.5×10-6md sinφ=kλ→λ= d sinφ/k=2.5×10-6×0.5/2=6.25×10-7m2.若用衍射光栅准确测定一单色可见光的波长，在下列各种光栅常数的光栅中选用哪一种最好？( D )(A)1.0×10-1mm (B) 5.0×10-1mm(C)1.0×10-2mm (D) 1.0×10-3mm3.波长4000Å～7600Å的自然光照射光栅，其衍射谱的第二级和第三级重迭，则第二级光谱重迭部分的波长范围是：( C )(A)5067Å～7600Å (B)4000Å～5067Å(C)6000Å～7600Å (D)5067Å～6000Å4.若光栅的光栅常数d，缝宽a和入射光波长λ都保持不变，而使其缝数N增加，则光栅光谱的同级光谱线将变得更细、更亮。

5.用一束自然光垂直照射在每毫米有200条刻痕的光栅，则屏上的中夹明纹的颜色为白色；在衍射角为30°处，在可见光范围内哪几种波长的光得到加强606250Å、5000 Å、4167 Å。

解: ∵d sinϕ=kλ, k=0,则对任何λ都有sinϕ=0,所有波长的中央明纹相重叠, ∴中央明纹的颜色为白色由d sinϕ=kλ得λ=d sinϕ/k=(1/400k)mm,∵4×10-4mm≤λ≤7.6×10-4mm ,即4×10-4≤1/400k≤7.6×10-4得3.3≤k≤6.25,k只能取整数,∴k = 4, 5, 6λ=6.25×10-4mm, 5×10-4mm, 4.16710-4mm6.若光栅常数为(a+b)，缝宽为a，则满足a sinφ=±k'λd sinφ=±kλ条件时会出现缺级，要使3n(n=1，2，3……)级数缺级，则必须b=2a。

10
(2) ∵
ab k , a k
k3
( a b)k 6 a 8.0 10 k( m) k
取 k 1 得
amin 8.0 106 ( m )
P.49.2.一单色光垂直照射宽为a的单缝，缝后放一 焦距为f的薄凸透镜，屏置于焦平面上，若屏上第 一级衍射明纹的宽度为△x，则入射光波长为( A ) (A)a△x/f (B)△x/af (C)f△x/a (D)a/f△x
例、波长为6000Å的单色光垂直入射在一光栅上，第 二级明纹出现在sin2=0.2处，第4级为第一个缺级。 求：(1)光栅常数。(2)狭缝可能的最小宽度是多少？ (3)按上述选定的a、b值，实际上能观察到的全部明 纹数是多少？ λ = 6000 Å k=2 解: (1)
kλ d sin k , d 6 μm sin φ sinφ2=0.2 d d ( 2 ) k k k 4, 则 a k 4 a d 得 amin 1.5 m 取k 1 4 b d amin 4.5m
sin
图2 单缝衍射
sin
图3
双缝衍射 （调制）
sin
d
b a

S
L1

光栅
P0
P
L2
x
f
幕
3. 光栅衍射（N为任意）
光栅每个缝形成各自的单缝衍射图样。
光栅缝与缝之间形成的多缝干涉图样。
光栅衍射条纹是单缝衍射与多缝干涉的总效果。
（1） 光栅方程
d
b a

a
P0
δ
S
L1

光栅
x
d

P
L2
∴ x2 f tan 2 f 2 0.5 0.01 0.005(m)

a+b 2 × 10
λ
θ 1= ± 140 28′
第三级明纹k=3 第三级明纹
3λ 3 × 500 × 10 9 sin θ 3 = ± =± = ±0.75 6 a+b 2 × 10
θ 3= ± 480 35′
2 × 10 6 = =4 9 500 × 10 即最多能看到第4级明条 即最多能看到第 级明条 纹,考虑缺级 (a+b)/a=(a+a)/a=2. . 级明纹不出现, 第2,4级明纹不出现, , 级明纹不出现 从而实际出现的只有级, 从而实际出现的只有级, 因而只能看到5条明纹 条明纹. 因而只能看到 条明纹.
2,光栅衍射的实验装置与衍射图样
反射光栅
屏幕上对应于光直线传播的成像位置上出现中央明纹; 屏幕上对应于光直线传播的成像位置上出现中央明纹; 屏幕上对应于光直线传播的成像位置上出现中央明纹 在中央明纹两侧出现一系列明暗相间的条纹,两明条纹分 在中央明纹两侧出现一系列明暗相间的条纹, 在中央明纹两侧出现一系列明暗相间的条纹 得很开,明条纹的亮度随着与中央的距离增大而减弱; 得很开,明条纹的亮度随着与中央的距离增大而减弱; 明条纹的宽度随狭缝的增多而变细. 明条纹的宽度随狭缝的增多而变细. 明条纹的宽度随狭缝的增多而变细
θ=
代入数据,得: 代入数据,
1.5 × 4 × 10 3 S= = 8.9 × 10 3 m 1.22 × 5500 × 10 10
rD S= 1.22λ
r θ = θ 0 = 1.22 = D S
λ
S
§17-4 衍射光栅 -
引言:对于单缝: 引言:对于单缝: 若缝宽大,条纹亮,但条纹间距小, 若缝宽大,条纹亮,但条纹间距小,不易分辨 若缝宽小,条纹间距大,但条纹暗, 若缝宽小,条纹间距大,但条纹暗,也不易分辨 因而利用单缝衍射不能精确地进行测量. 因而利用单缝衍射不能精确地进行测量. 问题:能否得到亮度大,分得开,宽度窄的明条纹? 问题:能否得到亮度大,分得开,宽度窄的明条纹? 结论:利用衍射光栅所形成的衍射图样——光栅光谱 结论:利用衍射光栅所形成的衍射图样 光栅光谱 应用: 应用: 精确地测量光的波长; 精确地测量光的波长; 是重要的光学元件,广泛应用于物理,化学,天文, 是重要的光学元件,广泛应用于物理,化学,天文, 地质等基础学科和近代生产技术的许多部门. 地质等基础学科和近代生产技术的许多部门.

极小:5 次明纹 次明纹:4 极小
三、单缝衍射对多缝干涉图样的调制 单缝衍射对多缝干涉图样的调制
E
0
每条缝的单缝衍射图样相同且重 它对多缝干涉图样进行调制。 叠，它对多缝干涉图样进行调制。
I I0
单缝衍射
−2
多缝干涉
−1
0
1
2
− 6 − 5 − 4 − 3 − 2 −1 0 1 2 3 4 5 6
k = ±1,±2 ⋯
I
5λ 3λ − − 2a 2a
−λ a
I0
3λ 5λ 2 a 2a
λ
a
sin θ
§12-9 圆孔的夫琅和费衍射 12光学仪器的分辨率 一、圆孔的夫朗和费衍射
爱里斑 E
S
中央光斑称为爱里斑，光强占84% 中央光斑称为爱里斑，光强占84% .
θ1
d
f
E
第一级暗环半径对应的衍射角θ 第一级暗环半径对应的衍射角θ1满足
说明
A
P
x
θ C
θ
a
B
f
E
条纹在屏幕上的位置 x = f tgθ ≈ fθ
讨论： 讨论： (1)中央明纹：两个第 (1)中央明纹 中央明纹： 一级暗纹中心间的 明纹
θ1
E
半角宽
2 fλ 线宽度 ∆x0 = 2 f tg θ ≈ 2 fθ = a
∆θ 0 = θ1≈ sin θ1=
λ
a
(2)其它相邻明(暗)纹的间距是中央亮纹 (2)其它相邻明 其它相邻 纹的间距是中央亮纹 宽度的一半
解： (1)对双缝干涉第k级明纹有 (1)对双缝干涉第 对双缝干涉第k
d sin θ = ± kλ
第k级明纹在屏上的位置

Augustin-Jean
Fresnel 1788～1827
学生实验
用游标卡尺两测脚间的狹缝观看日光灯
练习：观察实验回答下列问题
1.在观察光的衍射现象的实验中,通过紧
靠眼睛的卡尺测脚形成的狭缝,观看远处
的日光灯管或线状白炽灯丝(灯管或灯丝
都要平行于狭缝),可以看到
A.黑白相间的直条纹
【C】
B.黑白相间的弧形条纹
取一个不透光的屏，
激
像
在它的中间装上一个
光
屏
宽度可以调节的狭缝，
束
用平行的单色光照射，
调节狭 缝宽窄
在缝后适当距离处放 一个像屏 ．
光的衍射
一、光的衍射
1、光的衍射： 光离开直线路径绕过障碍物传到阴
影里去的现象叫做光的衍射现象。 2、明显衍射的条件
障碍物或狭缝的尺寸比波长小或者跟 波长相差不多
3、物理意义： 光的衍射现象证明光是一种波
不同缝宽的单缝衍射
不同色光的单缝衍射
2、单缝衍射规律
(1)、波长一定时，单缝窄的中央条纹宽，各条 纹间距大．
(2)、单缝不变时，光波波长的（红光）中央 亮纹越宽，条纹间隔越大．
(3)、白光的单缝衍射条纹为中央亮，两侧为 彩色条纹，且外侧呈红色，靠近光源的内侧为 紫色．
3、干涉条纹与衍射条纹的区别
3.如图所示是用游标卡尺两测脚间的狭
缝观察日光灯光源时所看到的四个现象.
当游标卡尺两测脚间的狭缝宽度从
0.8mm逐渐变小时,所看到的四个图像的
顺序是
. abcd
二、单缝衍射
1、单色光单缝衍射条纹的特征 A、中央亮纹宽而亮． B、两侧条纹具有对称性，亮纹较窄、较暗．

光的衍射（二）1 用含有波长1λ、2λ的复色光作光栅衍射实验，先后两次实验用了A 、B 两块光栅常数d 相同、总刻痕数B A N N ≠的光栅，测得两组一级光谱(如图所示)，则［ ］。

A ．21;λλ><B A N NB ．21;λλ>>B A N NC ．21;λλ<<B A N ND ．21;λλ<>B A N N答：［D ］解：由光栅方程λθm d =sin ，同一级光栅衍射光谱，波长越大，衍射角越大，由图21λλ<。

由光栅的色分辨本领mN d R ==λλ，同一级光栅衍射光谱，光栅总刻痕数越多，光栅色分辨本领越高，能分辨的波长差越小，由图B A N N >。

2．某确定波长的光垂直入射一光栅，屏幕上只能看到0级和l 级主极大，要想在屏幕上观察到更高级次的衍射主极大，应该［］。

A ．减小光栅与观察屏之间的距离B ．增大光栅与观察屏之间的距离C ．换一个光栅常数较小的光栅D ．换一个光栅常数较大的光栅答：［D ］解：由光栅方程λθm d =sin 可知，屏幕上2级以上衍射主极大，是因为2级衍射角已经大于090。

为了减小2级以上衍射主极大的衍射角，靠改变光栅与观察屏之间的距离无济于事，在波长确定的情况下，只能换一个光栅常数较大的光栅。

3．波长为nm 500的单色光以030的倾角入射到光栅上，已知光栅常数m d μ1.2=、透光 缝宽m a μ7.0=，求：所有能看到的谱线级次。

解：斜入射光栅方程为 λθθm d =-)sin (sin 0所以，各级衍射角满足0sin /sin θλθ+=d m由于能够在屏幕上观察到的衍射主极大的衍射角必须满足009090+<<-θ因此，能够在屏幕上观察到的衍射主极大的级次必须满足15.02100500sin /0<+=+md m θλ 由此，解得 3.6;1.2-><-+m m所以，能够在屏幕上观察到的衍射主极大的级次最高为6;2-==-+m m又因－3和－6缺级，所以能看见2、1、0、－1、－2、－4、－5等7条谱线。

6
1 102 (a b) 2 10 6 m 5000
0 6 0
(a b) sin K 2 10 sin30 10 m 10000A K
K 1 K 2
10 6 m 10000 A
5000 A 3333 A
小结 1、光栅衍射条纹的特点： 光栅的衍射条纹是单缝衍射与多光束干涉的总效 果 。 k 0,1,2 2、光栅公式： （a b) sin k 3、缺级现象：
a si n k ' (a b) si n k
Hale Waihona Puke （a b) sin k
1）当k=0时， o，对应于中央 明纹，它位于透镜的主焦点p0上；
(k 0,1,2 )
(4)
光栅公式

（a b)
p
2） k=1，2…分别为第一、二…级明 纹，正负号表示各级明纹在中央明纹 两侧对称分布。
p0
对光栅公式的几点说明 ：

2
, ( k 1,2 )
2、中央明纹宽度的计算：
x 2

a
f
引言
光栅是由大量等宽等间距的平行狭缝所组成的光学元件。一般情况下用 来产生分光色散现象，也可用来测未知光的波长。它分为两类：
透射光栅——用于透射光衍射； 反射光栅——用于反射光衍射。
四、衍射光栅
b
a
（a b) 光栅常数
k 知，波长越长，衍射角越大。因 (a b)
此，白光通过光栅后，各种单色光将产生各自分开的条纹而形成光栅的衍射光 谱。中央明纹因各色光总汇合，仍为白色，其他各级明纹都形成由紫（靠近中 央明纹）到红（远离中央明纹）的彩色光谱带。

§5 X射线的衍射
一. X 射线的产生 X射线 λ : 10-1102Å
X射线管
-
K
A
+
X射线 射线
劳厄（Laue）实验（1912） 劳厄（Laue）实验（1912） 证实了X射线的波动性
准直缝 晶体 X射线 射线 劳厄斑
·· · ·
二. X射线在晶体上的衍射
1 晶面 • d
• • • •
Φ • •A dsinΦ • • •
N=4 单缝衍射 d = 4a 轮廓线 8 sinθ (λ /d )
-8
-4
0
4
(3) d、a 对条纹的影响
四. 光栅光谱, 光栅的色散本领、分辨本领 光栅光谱, 光栅的色散本领、 如果有几种单色光同时投射在光栅上， 如果有几种单色光同时投射在光栅上， 在屏上将出现光栅光谱。 在屏上将出现光栅光谱。
• • • • • •
•
德拜相
劳厄相
[ 例1 ] 用每厘米有5000条的光栅，观察钠光谱线 用每厘米有5000条的光栅 条的光栅，
λ = 5893 Å
问：1. 光线垂直入射时；2. 光线以30度角 光线垂直入射时； 光线以30 30度角 倾斜入射时，最多能看到几级条纹？ 倾斜入射时，最多能看到几级条纹？ 解： 1、由光栅方程： 由光栅方程：
屏 0 x
δ = AB + BC = d sin φ + d sin θ
光栅方程： 光栅方程：
d (sin φ + sin θ ) = kλ
λ
< d (1 + sin φ )
k=
d (sin φ + sin θ )
λ
= 5.09

讨论
(b b')sin k (k 0,1,2,)
光强分布
I
3 2 0
条纹最高级数
s in k


k
b b'
2
π,
2
(b b')sin
3
k

kmax

b b'

光栅中狭缝条数越多，明纹越亮.
亮纹的光强
I N 2 I0 （ N：狭缝数，
一 圆孔衍射
HP
L 艾里 斑
L
D
P


d
f
d
d ：艾里斑直径
d 2 1.22
f
D
二 瑞利判据
0.8I0
对于两个强度相等的不相干的点光源（物点），一个点光源的衍射图样的主 极大刚好和另一点光源衍射图样的第一极小相重合，这时两个点光源（或物点） 恰为这一光学仪器所分辨.
三 光学仪器的分辨本领
(b b') 913nm
10 每厘米大约有 条刻痕 4
1885年伦琴发现，受高速电子撞击的金属会发射一种穿透性很强的射线称Ｘ射 线．
X 射线 (0.04 ~ 10nm)
冷却水
K<
E1
P
E2
铅板
照
单晶片的衍射
像 底
1912年劳厄实验
片
单晶片
劳厄斑点
1913年英国布拉格父子提出了一种解释Ｘ射线衍射的方法，给出了定量结果， 并于1915年荣获物理学诺贝尔奖．
光栅的衍射条纹是衍 射和干涉的总效果
相邻两缝间的光程差：
Δ (b b')sin
明纹位置

θ与θ0在法线同侧时，上式取+号
θ与θ0在法线异侧时，上式取-号
光栅平面
思考： 3、白光入射时的光栅光谱如何？
光盘的凹槽形成一个衍射光栅，在白光下能观察到 入射光被分离成彩色光谱。
怎样用科学严谨的方法分析其中的物理规律？
▲
光栅光谱：
波长不同的同级谱线的集合称为光栅光谱。
光栅的主极大满足光栅方程
d sin k
Only is there diffraction 只考虑单缝衍射:
I -2 -1 1 2
Only is there interference 只考虑多光束干涉： I
There are diffraction and interference 干涉衍射均考虑： I -2
缺 级 缺 级
2 4 5
-5 -4
光栅平面图 许多等宽度、等距离的狭缝排列起来形成的光学元件。
L
衍射角
P

Q
o
f
三、实验装置
L1
d
G
L2

P
s
P0
将单缝衍射屏
换成
相互平行 等宽度 b 不透光部分 a 缝数 N
缝距 d
ab
的多缝衍射屏即可。
问题1：与单缝衍射比较，会出现那些新的实验现象？
N 3 单缝主极大中出现新的 极大和极小
法 线
0

d sin j ( j 0, 1, 2, 3)
★ 入射光与光栅面法线夹角为
d sin 0 d sin
光栅平面
θ0，衍射光与光栅面法线夹角为 θ时， 光栅方程取下列形式：
0

d sin sin 0 j

缝数 N = 4 时光栅衍射的光强分布图
次极大
k=-6
k=-4 k=-2 k=0 k=2 k=4 k=6 k=-1 k=3 k=-5 k=1 k=5 k=-3
缝数 N = 4 时光栅衍射的光强分布图
极小值
k=-6
k=-4 k=-2 k=0 k=2 k=4 k=6 k=-1 k=3 k=-5 k=1 k=5 k=-3
三 衍射光谱
d sin k
(k 0,1,2,)
入射光为白光时， k不同，按波长分开形成光谱. 不同，
I
sin
b b'
0
一级光谱
三级光谱 二级光谱
一级光谱 二级光谱
三级光谱
I
sin


d
0
一级光谱
三级光谱 二级光谱
白光的二级光谱有部分与三级重叠，求重叠范围
暗纹条件
主极大
n d sin （k ) 是暗条纹（极小）的公式 N （n 1,2, N 1) 两个主极大之间有N-1个极小
I
两个极小之间是次极大，光强非常弱可以忽略。
3 d
2 d
d
0

d
2 d
3 d
sin
这是未考虑单缝衍射效果的，5条缝光栅的光强度分布。
0

d
2 d
3 d
sin
d sin k1
光栅k1级主极大
a sin k2
每条单缝的k2暗纹
当光的衍射角为某个值时，K1、K2恰好都是整数， 此衍射角对应处的k1级主极大缺级。
d 即： k1 k 2 （k2 1， 2, a
3,