【配套K12】广东省惠州市2019年高考数学复习 5.3 解三角形 解三角形练习 文
- 格式:doc
- 大小:112.00 KB
- 文档页数:4

核心考点解读—解三角形正眩定理及其应用(II)余眩定理及其应用(II)三角形面积公式的应用(II)解三角形的实际应用(II)1.涉及本单元的选择题、填空题一般利用正弦定理、余弦定理及三角形的面积公式,考查三角形边、角、而积等的相关计算,同时注重与三角函数的图象与性质、基木不等式等的综合.2.从考查难度來看,本单元试题的难度中等,主要考查正弦定理、余弦定理及三角形的面积公式的应用,高考屮主要以三角形的方式来呈现,解决三角形中相关边、角的问题.3.从考查热点来看,正弦定理、余弦定理及三角形的面积公式的应用是高考命题的热点,要能够熟练应用公式进行三角形的边、角求值,三角形形状的判断及面积的相关计算等.注意三角形本身具有的性质的应用.1.正弦定理及其应用(1)」一=丄=」一= 2/?表示三角形屮对边与对角正弦值的比值关sin A sin B sin C系及与其外接圆的直径之间的等量关系.(2)能够利用正弦定理进行边、角计算:已知两角和一边求其他的边、角;已知两边和一对角求其他的边、角等,此时要根据“大边对大角"的性质注意三角形解的问题.⑶注意利用正弦定理实现边、角的互化,如-a = b-可转化为4t sin A = sin 等,转化过程中要注意平衡,^a2 = 2b -不可转化为“sin? A = 2sinB”.2.余弦定理及其应用(1)6Z2=Z?2+C2-2/?CCOS A表示三角形中三边与任意角之间的等量关系.(2)能够利用余弦定理进行边、角计算:已知三边求角;已知两边和一夹角求对边;已知两边和一对角求其他的边、角等•此时利用余弦定理可以通过解方程清楚了解三角形的解的问题.3.三角形的而积公式及其应用⑴三角形的面积公式:S = -absmC = -bcsinA =丄eosinB,利用三2 2 2角形的两边及一夹角求面积.(2)注意三角形的面积公式与正眩定理、余弦定理之间的联系4 .解三角形的应用通过正弦定理、余弦定理及三角形的面积公式所建立起来的边、角的等 量关系,不仅要能够求解三角形的边与角,还要能够求解三角形的面积 问题,考查二角形的形状问题,利用公式、定理转化,建立等边二角形、 等腰三角形、直角三角形等的判定条件,确定三角形的形状.5 .解三角形的实际应用解三角形的实际应用主要是实际问题屮的测量问题,如测量角度问题, 仰角、俯角、方位角、视角等;测量距离问题;测量高度问题等.此类问 题的关键在于通过构造三角形,应用正弦定理、余弦定理进行求解测量.6.解三角形与其他知识的综合(1) 解三角形的应用中要注意与基本不等式的结合,以此考查三角形中有关边、角的范围问题.利用正弦定理、余弦定理与二角形的面积公式,建立 女之间的等量关系与不等关系,通过基本不等式考查 相关范围问题.(2) 注意与三角函数的图象与性质的综合考查,将两者结合起來,既考查解 三角形问题,也注重对三角函数的化简、计算及考杳相关性质等.丰殛1亘;^21. (2017高考新课标I,理17) ZXABC 的内角A, B, C 的对边分别为G , b, c,己知△ABC 的面积为—^一3 sin A(1) 求 sin Bsin C;(2) 若 6cos Bcos C=1, a 二3,求/\ABC 的周长.2. (2017高考新课标II,理17) AABC 的内角A,B,C 的对边分别为a,b,c ,已知sin (A +C) = 8sin 2 y ・(1) 求 cosB ;(2) 若d + c = 6, AABC 的面积为2,求b .3.(2017 新课标 III,理 17) AABC 的内角 4, B, C 的对边分别为 a, b, C.已知 sin A 4-^3 cos A = 0,a=2y/l,b=2.(1)求 c ; (2)设D 为BC 边上一点,且AD 丄4C,求△ABD 的而积.4 5 4. (2016高考新课标II,理13) £\ABC 的内角A, B, C 的对边分别为a, b, c,若cos A=— , cos C-—, a- \,513则 b= ______ .理17)错误!未找到引用源。

2019-2020年高考数学一轮总复习第五章平面向量解三角形 5.3解三角形专用题组理新人教B版考点一正弦、余弦定理答案 A 由正弦定理得sin B(sin Acos C+sin Ccos A)=sin B,即sin Bsin(A+C)=sin B,因为sin B≠0,所以sin B=,所以∠B=或π,又因为a>b,故∠B=,选 A.19.(xx陕西,7,5分)设△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos B=asin A,则△ABC的形状为( )A.锐角三角形B.直角三角形C.钝角三角形D.不确定答案 B 由正弦定理得sin Bcos C+sin Ccos B=sin2A,得sin(B+C)=sin2A,∴sin A=1,即A=.故选 B.20.(xx福建,12,4分)若锐角△ABC的面积为10,且AB=5,AC=8,则BC等于.答案7解析设内角A,B,C所对的边分别为a,b,c.由已知及bcsin A=10得sin A=,因为A为锐角,所以A=60°,cos A=.由余弦定理得a2=b2+c2-2bccos A=25+64-2×40×=49,故a=7,即BC=7. 评析本题考查了三角形的面积和解三角形,利用三角形的面积求出cos A是求解关键. 21.(xx浙江,16,4分)在△ABC中,∠C=90°,M是BC的中点.若sin∠BAM=,则sin∠BAC=.答案解析令∠BAM=β,∠BAC=α,故|CM|=|AM|sin(α-β),∵M为BC的中点,∴|BM|=|AM|sin(α-β).在△AMB中,由正弦定理知:=,即=,∵sin β=,∴cos β=,∴=cos α·=sin αcos α-cos2α,整理得1=2sin αcos α-cos2α,解得tan α=,故sin α=.评析本题考查解三角形,正弦定理的应用和三角函数求值问题.考查学生的图形观察能力和数据处理能力.如何利用M是BC中点是解答本题的关键.22.(xx湖北,11,5分)设△ABC的内角A,B,C所对的边分别为a,b,c.若(a+b-c)(a+b+c)=ab,则角C= .答案解析由已知得a2+b2-c2=-ab,∴cos C==-,∴C=.评析本题考查余弦定理,考查学生的运算求解能力.23.(xx重庆,13,5分)设△ABC的内角A,B,C的对边分别为a,b,c,且cos A=,cos B=,b=3,则c= .答案解析∵A,B,C为三角形内角且cos A=,cos B=,∴sin A=,sin B=.sin C=sin[π-(A+B)]=sin(A+B)=sin Acos B+cos Asin B=×+×=.由正弦定理=,得c=b×=3×=.评析本题考查同角三角函数关系及正弦定理.24.(xx北京,15,13分)在△ABC中,a=3,b=2,∠B=2∠A.(1)求cos A的值;(2)求c的值.解析(1)因为a=3,b=2,∠B=2∠A,所以在△ABC中,由正弦定理得=.所以=.故cos A=.(2)由(1)知cos A=,所以sin A==.又因为∠B=2∠A,所以cos B=2cos2A-1=.所以sin B==.在△ABC中,sin C=sin(A+B)=sin Acos B+cos Asin B=.所以c==5.评析本题考查正弦定理及三角恒等变换,主要考查学生运算技巧和运算求解能力,二倍角公式和诱导公式的熟练应用是解决本题的关键.考点二解三角形及其综合应用16.(xx重庆,10,5分)已知△ABC的内角A,B,C满足sin 2A+sin(A-B+C)=sin(C-A-B)+,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,则下列不等式一定成立的是( )A.bc(b+c)>8B.ab(a+b)>16C.6≤abc≤12D.12≤abc≤24答案 A 设△ABC的外接圆半径为R,由三角形内角和定理知A+C=π-B,A+B=π-C.于是sin 2A+sin(A-B+C)=sin(C-A-B)+?sin 2A+sin 2B=-sin 2C+?sin 2A+sin 2B+sin 2C=?2sin(A+B)cos(A-B)+2sin Ccos C=?2sin C·[cos(A-B)-cos(A+B)]=?4sin Asin Bsin C=?sin Asin Bsin C=.则S=absin C=2R2·sin Asin Bsin C=R2∈[1,2],∴R∈[2,2],∴abc=8R3sin Asin Bsin C=R3∈[8,16 ],知C、D均不正确.bc(b+c)>bc·a=R3≥8,∴A正确.事实上,注意到a、b、c 的无序性,并且16>8,若B成立,则A必然成立,排除B.故选A.17.(xx浙江,16,14分)在△ABC中,内角A,B,C所对的边分别是a,b,c.已知A=,b2-a2=c2.(1)求tan C的值;(2)若△ABC的面积为3,求b的值.解析(1)由b2-a2=c2及正弦定理得sin2B-=sin2C,所以-cos 2B=sin2C.又由A=,即B+C=π,得-cos 2B=sin 2C=2sin Ccos C,解得tan C=2.(2)由tan C=2,C∈(0,π)得sin C=,cos C=.又因为sin B=sin(A+C)=sin,所以sin B=.由正弦定理得c=b,又因为A=,bcsin A=3,所以bc=6,故b=3.评析本题主要考查三角函数及其变换、正弦定理等基础知识,同时考查运算求解能力. 18.(xx陕西,17,12分)△ABC的内角A,B,C所对的边分别为a,b,c.向量m=(a,b)与n=(cos A,sin B)平行.(1)求A;(2)若a=,b=2,求△ABC的面积.解析(1)因为m∥n,所以asin B-bcos A=0,由正弦定理,得sin Asin B-sin Bcos A=0,又sin B≠0,从而tan A=,由于0<A<π,所以A=.(2)解法一:由a2=b2+c2-2bccos A及a=,b=2,A=,得7=4+c2-2c,即c2-2c-3=0,因为c>0,所以c=3.故△ABC的面积为bcsin A=.解法二:由正弦定理,得=,从而sin B=,又由a>b,知A>B,所以cos B=.故sin C=sin(A+B)=sin=sin Bcos+cos Bsin=.所以△ABC的面积为absin C=.19.(xx四川,19,12分)如图,A,B,C,D为平面四边形ABCD的四个内角.(1)证明:tan=;(2)若A+C=180°,AB=6,BC=3,CD=4,AD=5,求tan+tan+tan+tan的值.解析(1)tan===.(2)由A+C=180°,得C=180°-A,D=180°-B.由(1),有tan+tan+tan+tan=+++=+.连结BD.在△ABD中,有BD2=AB2+AD2-2AB·ADcos A,在△BCD中,有BD2=BC2+CD2-2BC·CDcos C,所以AB2+AD2-2AB·ADcos A=BC2+CD2+2BC·CDcos A.则cos A===.于是sin A===.连结AC.同理可得cos B===,于是sin B===.所以,tan+tan+tan+tan=+=+=.评析本题主要考查二倍角公式、诱导公式、余弦定理、简单的三角恒等变换等基础知识,考查运算求解能力、推理论证能力,考查函数与方程、化归与转化等数学思想.20.(xx北京,15,13分)如图,在△ABC中,∠B=,AB=8,点D在BC边上,且CD=2,cos∠ADC=.(1)求sin∠BAD;(2)求BD,AC的长.解析(1)在△ADC中,因为cos∠ADC=,所以sin∠ADC=.所以sin∠BAD=sin(∠ADC-∠B)=sin∠ADCcos B-cos∠ADCsin B=×-×=.(2)在△ABD中,由正弦定理得BD===3.在△ABC中,由余弦定理得AC2=AB2+BC2-2AB·BC·cos B=82+52-2×8×5×=49.所以AC=7.评析本题考查了三角恒等变换,及利用正、余弦定理解三角形;考查分析推理、运算求解能力.21.(xx陕西,16,12分)△ABC的内角A,B,C所对的边分别为a,b,c.(1)若a,b,c成等差数列,证明:sin A+sin C=2sin(A+C);(2)若a,b,c成等比数列,求cos B的最小值.解析(1)证明:∵a,b,c成等差数列,∴a+c=2b.由正弦定理得sin A+sin C=2sin B.∵sin B=sin[π-(A+C)]=sin(A+C),∴sin A+sin C=2sin(A+C).(2)∵a,b,c成等比数列,∴b2=ac.由余弦定理得cos B==≥=,当且仅当a=c时等号成立.∴cos B的最小值为.评析本题考查了等差、等比数列,正、余弦定理,基本不等式等知识;考查运算求解能力.22.(xx安徽,16,12分)设△ABC的内角A,B,C所对边的长分别是a,b,c,且b=3,c=1,A=2B.(1)求a的值;(2)求sin的值.解析(1)因为A=2B,所以sin A=sin 2B=2sin Bcos B.由正、余弦定理得a=2b·.因为b=3,c=1,所以a2=12,a=2.(2)由余弦定理得cos A===-.由于0<A<π,所以sin A===.故sin=sin Acos+cos Asin=×+×=.评析本题考查正、余弦定理,三角变换等知识,属容易题.23.(xx浙江,18,14分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a≠b,c=,cos2A-cos2B=sin Acos A-sin Bcos B.(1)求角C的大小;(2)若sin A=,求△ABC的面积.解析(1)由题意得-=sin 2A-sin 2B,即sin 2A-cos 2A=sin 2B-cos 2B,sin=sin.由a≠b,得A≠B,又A+B∈(0,π),得2A-+2B-=π,即A+B=,所以C=.(2)由c=,sin A=,=,得a=,由a<c,得A<C.从而cos A=,故sin B=sin(A+C)=sin Acos C+cos Asin C=,所以,△ABC的面积为S=acsin B=.评析本题主要考查诱导公式、二倍角公式、正弦定理、三角形面积公式等基础知识,同时考查运算求解能力.24.(xx四川,17,12分)在△ABC中,角A,B,C的对边分别为a,b,c,且2cos2cos B-sin(A-B)sinB+cos(A+C)=-.(2)若a=4,b=5,求向量在方向上的投影.解析(1)由2cos2cos B-sin(A-B)sin B+cos(A+C)=-,得[cos(A-B)+1]cos B-sin(A-B)sinB-cos B=-,即cos(A-B)cos B-sin(A-B)sin B=-.则cos(A-B+B)=-,即cos A=-.(2)由cos A=-,0<A<π,得sin A=,由正弦定理,有=,所以sin B==.由题意知a>b,则A>B,故B=.根据余弦定理,有(4)2=52+c2-2×5c×,解得c=1或c=-7(舍去).故向量在方向上的投影为||cos B=.评析本题主要考查两角和的余弦公式、二倍角公式、正弦定理、余弦定理、同角三角函数的关系等基础知识,考查运算求解能力,考查化归与转化等数学思想.25.(xx安徽,16,12分)在△ABC中,∠A=,AB=6,AC=3,点D在BC边上,AD=BD,求AD的长.解析设△ABC的内角A,B,C所对边的长分别是a,b,c,由余弦定理得a2=b2+c2-2bccos∠BAC=(3)2+62-2×3×6×cos=18+36-(-36)=90,所以a=3.又由正弦定理得sin B===,由题设知0<B<,所以cos B===.在△ABD中,由正弦定理得AD====.26.(xx湖南,17,12分)设△ABC的内角A,B,C的对边分别为a,b,c,a=btan A,且B为钝角.(1)证明:B-A=;(2)求sin A+sin C的取值范围.解析(1)由a=btan A及正弦定理,得==,所以sin B=cos A,即sin B=sin.又B为钝角,因此+A∈,故B=+A,即B-A=.(2)由(1)知,C=π-(A+B)=π-=-2A>0,所以A∈.于是sin A+sin C=sin A+sin=sin A+cos 2A=-2sin2A+sin A+1=-2+.因为0<A<,所以0<sin A<,因此<-2+≤.由此可知sin A+sin C的取值范围是.评析本题以解三角形为背景,考查三角恒等变形及三角函数的图象与性质,对考生思维的严谨性有较高要求.27.(xx江西,16,12分)在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A-sinA)cos B=0.(2)若a+c=1,求b的取值范围.解析(1)由已知得-cos(A+B)+cos Acos B-sin Acos B=0,即有sin Asin B-sin Acos B=0,因为sin A≠0,所以sin B-cos B=0,又cos B≠0,所以tan B=,又0<B<π,所以B=.(2)由余弦定理,有b2=a2+c2-2accos B.因为a+c=1,cos B=,所以b2=3+.又0<a<1,于是有≤b2<1,即有≤b<1.28.(xx课标全国Ⅰ,17,12分)如图,在△ABC中,∠ABC=90°,AB=,BC=1,P为△ABC内一点,∠BPC=90°.(1)若PB=,求PA;(2)若∠APB=150°,求tan∠PBA.解析(1)由已知得,∠PBC=60°,所以∠PBA=30°.在△PBA中,由余弦定理得PA2=3+-2××cos 30°=.故PA=.(2)设∠PBA=α,由已知得PB=sin α.在△PBA中,由正弦定理得=,化简得cos α=4sin α.所以tan α=,即tan∠PBA=.评析本题考查了利用正弦定理和余弦定理解三角形,考查了运算求解能力和分析、解决问题的能力.题目新颖且有一定的难度,通过PB把△PBC和△PAB联系起来利用正弦定理是解题关键.29.(xx江西,17,12分)在△ABC中,角A,B,C的对边分别为a,b,c.已知A=,bsin-csin=a.(1)求证:B-C=;(2)若a=,求△ABC的面积.解析(1)证明:由bsin-csin=a,应用正弦定理,得sin Bsin-sin Csin=sin A,sin B-sin Csin B+cos B=,整理得sin Bcos C-cos Bsin C=1,即sin(B-C)=1,由于0<B,C<π,从而B-C=.(2)B+C=π-A=,因此B=,C=.由a=,A=,得b==2sin,c==2sin,所以△ABC的面积S=bcsin A=sin·sin=cos·sin=.评析本题主要考查解三角形的基本知识,运用正弦定理、三角恒等变换及三角形的面积公式进行求解,考查了推理运算能力及应用意识.。

三角函数后考卷(四)时间 40分钟考试范围:三角函数(解三角形除外) 满分:70分班级_________ 姓名_________ 成绩_________ 一、选择题(每小题5分)1.sin585的值为( )A ..已知角α的终边经过点(4,3)-,则cos α=( )A .45 B .35 C .35- D .45-3. 已知α为第二象限角,3sin 5α=,则sin 2α=( )A .2524-B .2512-C .2512D .25244. 设函数()sin(2)cos(2)44f x x x ππ=+++,则( )A .()y f x =在(0,)2π单调递增,其图象关于直线4x π=对称B .()y f x =在(0,)2π单调递增,其图象关于直线2x π=对称 C .()y f x =在(0,)2π单调递减,其图象关于直线4x π=对称D .()y f x =在(0,)2π单调递减,其图象关于直线2x π=对称二、填空题(每小题5分)5. 设函数()cos (0)f x x ωω=>,将()y f x =的图像向右平移3π个单位长度后,所得的图像与原图像重合,则ω的最小值等于________ 6. 若函数()sin ([0,2])3x f x ϕϕπ+=∈是偶函数,则=ϕ_________. 7.已知322sin =α,则____)4(cos 2=+πα 8. 设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=______ 三、解答题(每题15分) 11.已知tan 2α=.()1求tan 4πα⎛⎫+⎪⎝⎭的值;()2求2sin 2sin sin cos cos 21ααααα+--的值.12.已知函数()2cos (sin cos )f x x x x =+.(1)求5()4f π的值; (2)求函数()f x 的最小正周期及单调递增区间.答案: 1-4 ADAD 5. 6 6. 23π 7. 61 8. 552- 9.(1)-3 (2)1 10.(1)2(2) 最小正周期π,单调递增区间为Z k k k ∈⎥⎦⎤⎢⎣⎡++-,8,83ππππ。

三角恒等变换与平面向量后考卷一、选择题1、已知平面向量)2,1(=,),2(m -=,且//,则=+32 ( ).A )4,2(-- .B )6,3(-- .C )8,4(-- .D )10,5(--21=2=,且⊥-)(,则与b 的夹角为 ( ).A6π .B 3π.C 32π .D 65π3、平面上有四个互异点D C B A ,,,,已知0))(2(=--+AC AB DA DC DB ,则ABC ∆的形状是 ( ).A 直角三角形 .B 等腰三角形 .C 等腰直角三角形 .D 不能确定4、在ABC ∆中,角C B A ,,所对的边分别是c b a ,,,若324=++c b a ,则=B cos ( ).A 2411-.B 2411 .C 3629 .D 3629- 5、函数ax ax ax y 2cos cos sin 5+=(0>a )的最小正周期为π,则=a ( ).A 1 .B 2 .C 3 .D 46、已知向量,,满足1==,21-=⋅b a ,︒>=--<60,,则的最大值等于 ( ).A 2 .B 3 .C 2 .D 1二、填空题712===a ,则_______2=a8、若已知),2(ππα∈,55)4sin(=+πα,则______sin =α 9、在锐角三角形ABC ∆中,B A x sin sin =,B A y cos cos =,则y x ,的大小关系是____ 10、在ABC ∆中,B A B A tan tan 33tan tan =++,则_______tan =C班级__________ 姓名_______________ 得分_________选择填空题答案填入下表三、解答题11、在ABC ∆中,︒=60B ,3=AC ,求BC AB 2-的取值范围。
解:12、在平面直角坐标系中,O 为坐标原点,已知向量),(cos ),0,1(),1,2(t B A a θ=,// (1=,求向量的坐标; (2)求22cos sin t y +--=θθ的最小值三角恒等变换与平面向量后考卷答案选择填空题答案填入下表11、在ABC ∆中,︒=60B ,3=AC ,求BC AB 2-的取值范围。

2019届高考数学总复习分类试卷三角函数、解三角形、平面向量(时间:120分钟总分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知sin(88°+θ)=23,则cos(178°+θ)=()A.23B.-23C.√53D.-√532.设P是△ABC所在平面内的一点,且CP⃗⃗⃗⃗ =2PA⃗⃗⃗⃗ ,则△PAB与△PBC的面积的比值是( )A.13B.12C.23D.343.在△ABC中,内角A,B,C所对的边分别是a,b,c.已知bsin A=3csin B,a=3,cos B=23,则b=( ) A.14 B.6 C.√14 D.√64.函数f(x)=cos(x+π4)-cos(x-π4)是( )A.周期为π的偶函数B.周期为2π的偶函数C.周期为π的奇函数D.周期为2π的奇函数5.函数y=2sin(π6-2x)(x∈[-π,0])的单调递增区间是( )A.[-π,-5π6] B.[-π3,0] C.[-2π3,-π6] D.[-π3,-π6]6.已知函数y=sin ωx(ω>0)在区间[0,π2]上为增函数,且图象关于点(3π,0)对称,则ω的取值集合为( )A.{13,23,1} B.{16,13} C.{13,23} D.{16,23}7.若把函数y=sin(ωx-π6)的图象向左平移π3个单位,所得到的图象与函数y=cos ωx的图象重合,则ω的一个可能取值是( )A.2B.32C.23D.128.在△ABC中,A=π3,AB=2,AC=3,CM⃗⃗⃗⃗⃗ =2MB⃗⃗⃗⃗⃗⃗ ,则AM⃗⃗⃗⃗⃗ ·BC⃗⃗⃗⃗ =( )A.-113B.-43C.43D.1139.在△ABC中,内角A,B,C所对的边分别是a,b,c.若c2=(a-b)2+6,C=π3,则△ABC的面积是( )A.3B.9√32C.3√32D.3√310.在△ABC中,内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且2S=(a+b)2-c2,则tan C 等于( )A.34B.43C.-43D.-3411.已知△ABC是边长为1的等边三角形,则(AB⃗⃗⃗⃗⃗ -2BC⃗⃗⃗⃗ )·(3BC⃗⃗⃗⃗ +4CA⃗⃗⃗⃗ )=( )A.-132B.-112C.-6-√32D.-6+√3212.将函数f(x)=2sin(ωx-π3)(ω>0)的图象向左平移π3ω个单位,得到函数y=g(x)的图象.若y=g(x)在[0,π4]上为增函数,则ω的最大值为( )A.1B.2C.3D.41 2 3 4 5 6 7 8 9 10 11 12 得分二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中的横线上)13.若单位向量e1,e2的夹角为π3,向量a=e1+λe2(λ∈R),且|a|=√32,则λ=.14.△ABC中,角A,B,C所对的边分别为a,b,c,△ABC的面积为S,若4√3S=(a+b)2-c2,则角C的大小为.15.已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<π2),y=f(x)的部分图象如图,则f(π24)= .16.在平面四边形ABCD中,若AB=1,BC=2,∠B=60°,∠C=45°,∠D=120°,则AD= .三、解答题(本大题共6小题,共70分,解答时写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)已知函数f(x)=√3sin 2ωx+cos4ωx-sin4ωx+1(其中0<ω<1),若点(-π6,1)是函数f(x)图象的一个对称中心.(1)求f(x)的解析式,并求距y轴最近的一条对称轴的方程;(2)先列表,再作出函数f(x)在区间[-π,π]上的图象.18.(本小题满分12分)已知函数f(x)=2√3sin(x+π4)·cos(x+π4)+sin 2x+a的最大值为1.(1)求函数f(x)的单调递增区间;(2)将函数f(x)的图象向左平移π6个单位,得到函数g(x)的图象,若方程g(x)=m在x∈[0,π2]上有解,求实数m的取值范围.19.(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,a+1a=4cos C,b=1.(1)若A=90°,求△ABC的面积;(2)若△ABC的面积为√32,求a,c.20.(本小题满分12分)设△ABC的内角A,B,C的对边分别为a,b,c,满足2asin A=(2sin B-√3sinC)b+(2sin C-√3sin B)c.(1)求角A的大小;(2)若a=2,b=2√3,求△ABC的面积.21.(本小题满分12分)已知函数f(x)=2cos(2x+2π3)+√3sin 2x.(1)求函数f(x)的最小正周期和最大值;(2)设△ABC的三个内角分别是A,B,C,若f(C2)=-12,且AC=1,BC=3,求sin A的值.22.(本小题满分12分)已知函数f(x)=2√3sin xcos x-3sin 2x-cos 2x+2. (1)当x ∈[0,π2]时,求f(x)的值域;(2)若△ABC 的内角A,B,C 的对边分别为a,b,c,且满足ba =√3,sin(2A+C)sinA=2+2cos(A+C),求f(B)的值.三角函数、解三角形、平面向量一、选择题1.B ∵sin(88°+θ)=23,∴cos(178°+θ)=cos(90°+88°+θ)=-sin(88°+θ)=-23.2.B ∵CP ⃗⃗⃗⃗ =2PA ⃗⃗⃗⃗⃗ ,∴|CP ⃗⃗⃗⃗⃗ ||PA ⃗⃗⃗⃗⃗ |=2,又△PAB 边PA 上的高与△PBC 边PC 上的高相等,∴S △PAB S△PBC=|PA ⃗⃗⃗⃗⃗||CP ⃗⃗⃗⃗⃗ |=12. 3.D 在△ABC 中,由asinA =bsinB,可得bsin A=asin B,又bsin A=3csin B,所以a=3c,又a=3,故c=1.由b 2=a 2+c 2-2accos B,cos B=23,可得b=√6.故选D.4.D f(x)=cos (x +π4)-cos (x -π4)=-√2sin x,所以函数f(x)是周期为2π的奇函数. 5.C 因为y=2sin (π6-2x)=-2sin (2x -π6),所以函数y=2sin (π6-2x)的单调递增区间就是函数y=sin (2x -π6)的单调递减区间.由π2+2kπ≤2x-π6≤3π2+2kπ(k∈Z ),解得π3+kπ≤x ≤5π6+kπ(k∈Z ),即函数y=2sin (π6-2x)的单调递增区间为[π3+kπ,5π6+kπ](k ∈Z ),又x ∈[-π,0],所以k=-1,故函数y=2sin (π6-2x)(x ∈[-π,0])的单调递增区间为[-2π3,-π6].6.A 由题意知{π2ω≥π2,3ωπ=kπ,k ∈Z,即{0<ω≤1,ω=k 3,k ∈Z,则ω=13或ω=23或ω=1.7.A 把函数y=sin (ωx -π6)的图象向左平移π3个单位得函数y=sin [ω(x +π3)-π6]=sin [ωx +(π3ω-π6)]的图象,由题意,得π3ω-π6=2kπ+π2(k ∈Z ),所以ω=6k+2(k∈Z ),所以ω的一个可能取值是2,故选A.8.C 因为AM ⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ +CM ⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ +23CB ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ +23(AB ⃗⃗⃗⃗⃗ -AC ⃗⃗⃗⃗⃗ )=13AC ⃗⃗⃗⃗⃗ +23AB ⃗⃗⃗⃗⃗ ,所以AM ⃗⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =(13AC ⃗⃗⃗⃗⃗ +23AB ⃗⃗⃗⃗⃗ )·(AC ⃗⃗⃗⃗⃗ -AB ⃗⃗⃗⃗⃗ )=13×32-23×22+13AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =13+13×3×2cos π3=43,故选C. 9.C c 2=(a-b)2+6,即c 2=a 2+b 2-2ab+6①.∵C=π3,∴由余弦定理得c 2=a 2+b 2-ab②,由①和②得ab=6,∴S △ABC =12absin C=12×6×√32=3√32,故选C.10.C 由2S=(a+b)2-c 2得2×12absin C=a 2+b 2-c 2+2ab,得absin C=2abcos C+2ab,sin C-2cos C=2,∴sin 2C+4cos 2C-4sin Ccos C=4, ∴tan 2C -4tanC+4tan 2C+1=4,∴tan C=-43或0(舍去),故选C.11.B (AB ⃗⃗⃗⃗⃗ -2BC ⃗⃗⃗⃗⃗ )·(3BC ⃗⃗⃗⃗⃗ +4CA ⃗⃗⃗⃗⃗ )=3AB ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ -6BC ⃗⃗⃗⃗⃗ 2+4AB ⃗⃗⃗⃗⃗ ·CA ⃗⃗⃗⃗⃗ -8BC ⃗⃗⃗⃗⃗ ·CA ⃗⃗⃗⃗⃗ =3|AB ⃗⃗⃗⃗⃗ |·|BC⃗⃗⃗⃗⃗ |cos 120°-6|BC ⃗⃗⃗⃗⃗ |2+4|AB ⃗⃗⃗⃗⃗ |·|CA ⃗⃗⃗⃗⃗ |cos 120°-8|BC ⃗⃗⃗⃗⃗ |·|CA ⃗⃗⃗⃗⃗ |cos 120°=3×1×1×(-12)-6×12+4×1×1×(-12)-8×1×1×(-12)=-32-6-2+4=-112,故选B. 12.B 将函数f(x)=2sin (ωx -π3)(ω>0)的图象向左平移π3ω个单位,得g(x)=2sin ω(x +π3ω)-π3=2sin (ωx +π3-π3)=2sin ωx 的图象,当x ∈[0,π4]时,ωx∈[0,ωπ4],要使y=g(x)在[0,π4]上为增函数,需满足ωπ4≤π2,即ω≤2,故ω的最大值为2.二、填空题 13.答案 -12解析 由题意可得e 1·e 2=12,|a |2=(e 1+λe 2)2=1+2λ×12+λ2=34,化简得λ2+λ+14=0,解得λ=-12. 14.答案π3解析 由4√3S=a 2+b 2-c 2+2ab 可得,2√3absin C=2abcos C+2ab,即√3sin C-cos C =2sin (C -π6)=1,sin (C -π6)=12,由题意知0<C<π,∴-π6<C-π6<56π,∴C -π6=π6,解得C=π3. 15.答案 √3解析 由题图可知:T=2(3π8-π8)=π2, ∴ω=2,∴2×π8+φ=kπ+π2,k ∈Z ,又|φ|<π2, ∴φ=π4.又f(0)=1,∴Atan π4=1, 得A=1,∴f(x)=tan (2x +π4),∴f (π24)=tan (π12+π4)=tan π3=√3. 16.答案√6-√22解析 连接AC.在△ABC 中,AC 2=BA 2+BC 2-2BA ·BC ·cos 60°=3,所以AC=√3,又AC 2+BA 2=4=BC 2,所以△ABC 是直角三角形,且∠BAC=90°.在四边形ABCD 中,∠BAD=360°-(60°+45°+120°)=135°,因此∠CAD=∠BAD-∠BAC=45°,所以∠ACD=180°-∠CAD-∠D=15°.在△ACD 中,由ADsin ∠ACD =ACsin ∠D,即ADsin15°=√3sin120°,得AD=√3sin15°sin120°=√3×(√6-√2)4×√3=√6-√22. 三、解答题17.解析 (1)f(x)=√3sin 2ωx+(cos 2ωx -sin 2ωx)(cos 2ωx+sin 2ωx)+1=√3sin 2ωx+cos 2ωx+1 =2sin (2ωx +π6)+1.∵点(-π6,1)是函数f(x)图象的一个对称中心,∴-ωπ3+π6=kπ,k∈Z ,∴ω=-3k+12,k ∈Z . ∵0<ω<1,∴ω=12,∴f(x)=2sin (x +π6)+1.由x+π6=kπ+π2,k ∈Z ,得x=kπ+π3,k ∈Z ,令k=0,得距y 轴最近的一条对称轴方程为x=π3.(2)由(1)知, f(x)=2sin (x +π6)+1,当x ∈[-π,π]时,列表如下:x+π6-5π6-π2π2π 7π6 x-π -2π3 -π6π3 5π6 π f(x) 0 -1 13 1则函数f(x)在区间[-π,π]上的图象如图所示.18.解析 (1)f(x)=√3sin (2x +π2)+sin 2x+a=√3cos 2x+sin 2x+a=2sin (2x +π3)+a,由题意知2+a=1,解得a=-1. 由-π2+2kπ≤2x+π3≤π2+2kπ,k∈Z , 解得-5π12+kπ≤x ≤π12+kπ,k∈Z ,∴函数f(x)的单调递增区间是[-5π12+kπ,π12+kπ],k ∈Z .(2)∵将函数f(x)的图象向左平移π6个单位,得到函数g(x)的图象,∴g(x)=f (x +π6)=2sin [2(x +π6)+π3]-1=2sin (2x +2π3)-1,当x ∈[0,π2]时,2x+2π3∈[2π3,5π3],当2x+2π3=2π3时,sin (2x +2π3)=√32,g(x)取最大值√3-1; 当2x+2π3=3π2时,sin (2x +2π3)=-1,g(x)取最小值-3.∴-3≤m ≤√3-1. 19.解析 (1)∵b=1, ∴a+1a =4cos C=4×a 2+b 2-c 22ab=2(a 2+1−c 2)a,∴2c 2=a 2+1.又A=90°,∴a 2=b 2+c 2=c 2+1, ∴2c 2=a 2+1=c 2+2,解得c=√2, ∴S △ABC =12bcsin A=12bc=12×1×√2=√22.(2)∵S △ABC =12absin C=12asin C=√32, ∴sin C=√3a ,∵a+1a=4cos C,∴[14(a +1a)]2+(√3a)2=1, 化简得(a 2-7)2=0,∴a=√7, ∴cos C=2√77. 由余弦定理得c 2=a 2+b 2-2ab ·cos C =7+1-2×√7×1×2√77=4,从而c=2.20.解析 (1)由已知及正弦定理可得2a 2=(2b-√3c)b+(2c-√3b)c,整理得b 2+c 2-a 2=√3bc,所以cos A =√32. 又A ∈(0,π),故A=π6. (2)由a sinA=b sinB ,a=2,b=2√3,A=π6, 得sin B=√32. 又B ∈(0,5π6),故B=π3或2π3. 若B=π3,则C=π2,于是S △ABC =12ab=2√3; 若B=2π3,则C=π6,于是S △ABC =12absin C=√3. 21.解析 (1)f(x)=2cos (2x +2π3)+√3sin 2x=-cos 2x,∴函数f(x)的最小正周期T=π,函数f(x)的最大值为1. (2)由(1)知f(x)=-cos 2x, ∴f (C2)=-cos C=-12,可得cos C=12. ∵C∈(0,π),∴sin C=√32. 由余弦定理可得,AB 2=AC 2+BC 2-2AC ·BC ·cos C=1+9-2×1×3×12=7, ∴AB=√7.第 11 页 共 11 页 ∴由正弦定理可得,sin A=BC ·sinC AB =3×√32√7=3√2114. 22.解析 (1)f(x)=2√3sin xcos x-3sin 2x-cos 2x+2 =√3sin 2x-2sin 2x+1=√3sin 2x+cos 2x=2sin (2x +π6).∵x∈[0,π2],∴2x+π6∈[π6,7π6], ∴sin (2x +π6)∈[-12,1],∴f(x)在x ∈[0,π2]上的值域是[-1,2]. (2)由题意可知sin[A+(A+C)]=2sin A+2sin Acos(A+C),即sin Acos(A+C)+cos Asin(A+C)=2sin A+2sin Acos(A+C), 化简可得sin C=2sin A,由正弦定理可得c=2a,∵b=√3a,∴cos B=a 2+c 2-b 22ac =a 2+4a 2-3a 22a ·2a =12, ∵0<B<π,∴B=π3.∴f(B)=2sin (2×π3+π6)=1.。
2019年高考数学小题精练+B 卷及解析:专题(09)解三角形及解析 专题(09)解三角形1.已知△ABC 的内角A 满足sin2A =,则sin A +cos A =( )A .B . -C .D . -【答案】A2.设△ABC 的内角A ,B ,C 所对的边长分别为a ,b ,c ,若bcos C+ccos B=2acos A ,则A=( ) A .6πB .3πC .4πD .3π或23π【答案】B【解析】∵bcos C+ccos B=2acos A ,∴由正弦定理可得:sin B cos C+sin C cos B=2sin A cos A , 可得:sin (B+C )=sin A=2sin A cos A , ∵A ∈(0,π),sin A≠0, ∴cos A=12, ∴可得A=3π. 故选:B .3.在ABC ∆中,角A B C 、、 所对边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为( )A .B .C . 12D . 12- 【答案】C【解析】()22212c a b =+,由余弦定理得,222221cos 242a b c a b C ab ab +-+==≥当且仅当a b =时取“=”, cos C ∴的最小值为12,选C .4.在ABC ∆中,角,,A B C 所对边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为( )A .B .C . 12D . 12- 【答案】C【解析】试题分析:因为2222a b c +=,所以由余弦定理可知,.故选C .考点:余弦定理. 5.在△ABC 中, 其面积,则BC 长为( )A .B . 75C . 51D . 49【答案】D6.在△ABC 中,b cos A =a cos B ,则三角形的形状为( )A . 直角三角形B . 锐角三角形C . 等腰三角形D . 等边三角形 【答案】C 【解析】 ,,则,则,三角形为等腰三角形,选C . 7.在△ABC 中,,则等于( )A . 1B . 2C .D . 3 【答案】B【解析】根据正弦定理, ,,,则,则,,选B .8.在△ABC 中,若则A=( )A .B .C .D .【答案】B 【解析】,,,,则,选B . 9.在锐角中,已知,则的取值范围为( )A .B .C .D .【答案】A10.在ABC ∆中,角A,B,C 所对的边分别是c b a ,,,2222c b a =+,则角C 的取值范围是( ) A .⎥⎦⎤ ⎝⎛30π, B .⎪⎭⎫ ⎝⎛30π,C .⎥⎦⎤ ⎝⎛60π,D .⎪⎭⎫ ⎝⎛60π,【答案】A考点:余弦定理;基本不等式求最值.11.如图,ABC ∆中,D 是边BC 上的点,且,2,2AC CD AC AB AD ===,则sin B等于( )A B C D 【答案】C考点:正余弦定理的综合应用.【思路点晴】本题主要考查的是解三角形以及正余弦定理的应用,属于中档题目.题目先根据AD AC 32=设出x AD 2=,从而AB CD AC ,,均可用x 来表示,达到变量的统一,因此只需列出等式求出x 的值即可.先由余弦定理求出ADC ∠cos ,接下来由ADB ∠和ADC ∠互补,得出其正弦值相等,再从ADB ∆中使用正弦定理,从而求出sin B .12.在ABC ∆中,已知10103cos ,21tan ==B A ,若ABC ∆最长边为10,则最短边长为( ) A .2 B .3 C .5D .22【答案】A 【解析】试题分析:由021tan >=A ,得51sin ,52cos ==A A ,由010103cos >=B ,得101sin =B ,于是021sin sin cos cos )cos(cos <-=+-=+-=B A B A B A C ,即C ∠为最大角,故有10=c ,最短边为b ,于是由正弦定理CcB b sin sin =,求得2=b . 考点:解三角形. 【思路点晴】由于021tan >=A ,010103cos >=B ,所以角A 和角B 都是锐角.利用同角三角函数关系,分别求出51sin ,52cos ==A A ,101sin =B ,利用三角形的内角和定理,结合两角和的余弦公式,可求得cos 0C <,所以C 为最大角,且10=c ,由于sin sin A B >所以B 为最小的角,b 边为最小的边,再利用正弦定理可以求出b 的值.专题09 解三角形1.设△ABC 的内角A ,B ,C 所对的边长分别为a ,b ,c ,若bcos C+ccos B=2acos A ,则A=( ) A .6πB .3πC .4πD .3π或23π【答案】B2.在ABC ∆中,角A B C 、、 所对边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为( )A .. C . 12 D . 12- 【答案】C【解析】()22212c a b =+,由余弦定理得, 222221cos 242a b c a b C ab ab +-+==≥当且仅当a b =时取“=”, cos C ∴的最小值为12,选C .3.在ABC ∆中,内角A , B , C 所对的边分别是a , b , c ,已知85b c =, 2C B =,则cos C =( ) A .725 B . 725- C . 725± D . 2425【答案】A【解析】试题分析:据正弦定理结合已知可得,整理得55sin sin cos 8422C C C = sin2C =,故,由二倍角公式得.考点:正弦定理及二倍角公式.【思路点晴】本题中用到了正弦定理实现三角形中边与角的互化,同角三角函数间的基本关系及二倍角公式,如,这要求学生对基本公式要熟练掌握解三角形时常借助于正弦定理,余弦定理,实现边与角的互相转化.4.在ABC∆中, 60,A a=︒=sinAa b csinB sinC++++=()A.B..D.【答案】C点睛:由正弦定理及已知可得sinA,sinB,sinC,则sin sin sina b cA B C++==++5.在ABC∆中,cos cosa Ab B=,则ABC∆的形状为()A.等腰三角形 B.直角三角形 C.等腰或直角三角形 D.等腰直角三角形【答案】C【解析】在ABC∆中,cos cosa Ab B=,∴由正弦定理2sin sina bRA B==,得2sin,2sin,sin cos sin cosa R Ab R B A A B B==∴=,112222sin A sin B∴=,22,22sin A sin B A B ∴=∴=或22A B π=-, A B ∴=或2A B π+=, ABC ∴∆为等腰或直角三角形,故选C .6.在△ABC 中,AB =7,AC =6,M 是BC 的中点,AM =4,则BC 等于( ) A .B .C .D .【答案】B点睛:解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向. 第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化. 第三步:求结果. 7.在△ABC 中,sin A =34,a =10,则边长c 的取值范围是( ) A . 15,2⎛⎫+∞⎪⎝⎭ B . (10,+∞) C. (0,10) D . 400,3⎛⎤⎥⎝⎦【答案】D【解析】由正弦定理得sin 104040sin sin 0,3sin 334a C c C C A ⎛⎤===∈ ⎥⎝⎦ ,选D . 8.已知ABC ∆ 是锐角三角形,若2A B = ,则ab的取值范围是( ) A .B .)2 C .( D . ()1,2【答案】A【解析】由题意得,在ABC ∆中,由正弦定理可得sin sin a Ab B=,又因为2A B = ,所以 2cos a B b = ,又因为锐角三角形,所以ππ20,,π30,22B C B ⎛⎫⎛⎫∈=-∈ ⎪ ⎪⎝⎭⎝⎭所以ππ,2cos 64B B <<∈故选A .9.设ABC ∆的内角,,A B C 的对边分为,,a b c , 1,sin 62b C A π===.若D 是BC 的中点,则AD = ( )A .74 B . C . 14 D . 12【答案】B点睛:解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向. 第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化. 第三步:求结果.10.ABC ∆中,若)sin sin cos C A A B =+,则( )A .3B π=B .2b a c =+C .ABC ∆是直角三角形D .222a b c =+或2B A C =+ 【答案】D 【解析】考点:解三角形.11.在ABC ∆中,内角,,A B C 的对边分别是,,a b c ,若2c a =,1sin sin sin 2b B a A a C -=,则sin B 为( )A B .34CD .13【答案】A【解析】考点:1、正弦定理及余弦定理;2、同角三角函数之间的关系. 12.在ABC △中,a b c ,,分别是角A B C ,,的对边,且cos cos 2B bC a c=-+,则B ∠=________.【答案】23π【解析】试题分析:由正弦定理得cos cos 2B bC a c=-+CA Bsin sin 2sin +-=,化简得A B C B sin cos 2)sin(-=+,即21cos -=B ,所以在ABC ∆中,B ∠=23π. 考点:正弦定理、三角恒等变换.。
同角三角函数基本关系式及诱导公式后考卷考试时间:40分钟班级__________ 姓名_____________ 学号___________ 得分__________ 一、选择题(每小题5分) 1. tan 8π3的值为( )A.33 B .-33C. 3 D .- 3 2.设α是第二象限角,P (x,4)为其终边上的一点,且cos α=15x ,则tan α=( )A.43B.34 C .-34 D .-43 3. 已知sin α是方程5x 2-7x -6=0的根,且α是第三象限角,则sin ⎝ ⎛⎭⎪⎫-α-3π2cos ⎝ ⎛⎭⎪⎫3π2-αtan 2π-αcos ⎝ ⎛⎭⎪⎫π2-αsin ⎝ ⎛⎭⎪⎫π2+α=( )A.916B .-916C .-34D.344. 已知α为第二象限角,则cos α1+tan 2α+sin α1+1tan 2α的值为( ). A .-2 B .2 C .0 D .35. 已知sin x cos x =38,且x ∈⎝ ⎛⎭⎪⎫π4,π2,则cos x -sin x =________. A .13- B .12-C .13D .1- 二、填空题(每小题5分) 6、若tan 2α=,则22sin 21sin 4cos ααα++= .7、已知3(,)22ππα∈,sin()πα+=,则tan α=______.8. 已知sin(2π+θ)tan(π+θ)tan(3π-θ)cos(π2-θ)tan(-π-θ)=1,则3sin 2θ+3sin θcos θ+2cos 2θ的值是_____ 9. 已知3sin()35x π-=,则5c o s ()6x π-= ______.10、已知f (x )=a sin(πx +α)+b cos(πx -β),其中α、β、a 、b 均为非零实数,若f (2 010)三、解答题 (每题20分)11、已知角α的终边在第二象限,且与单位圆交于点)415,(m P . (1)求实数m 的值; (2)求1)23sin()sin()2sin(+--+-απαππα的值.12、已知sin(3π+θ)=13,求π+θcos θπ-θ-1]+θ-2πsin ⎝⎛⎭⎪⎫θ-3π2θ-π-sin ⎝ ⎛⎭⎪⎫3π2+θ的值.1、【答案】D 【解析】 tan8π3=tan ⎝⎛⎭⎪⎫2π+2π3=tan 2π3=- 3. 2【答案】D 【解析】 ∵α是第二象限角,∴cos α=15x <0,即x <0.又cos α=15x =xx 2+16,解得x =-3,∴tan α=4x =-43.3【答案】B 【解析】 ∵方程5x 2-7x -6=0的根为x 1=2,x 2=-35,由题知sin α=-35,∴cos α=-45,tan α=34,∴原式=cos α-sin α2αsin αcos α=-tan 2α=-916.4【答案】C5【答案】B【解析】 ∵x ∈⎝ ⎛⎭⎪⎫π4,π2,∴sin x >cos x ,即cos x -sin x <0,∴(cos x -s in x )2=1-2sin x cos x=14,∴cos x -sin x =-12. 6、7、【解析】由sin()πα+=得sin (,)32πααπ=∴∈,所以1cos ,tan 3αα==-=- 8、9【解析】∵3sin()sin[()]cos()32665x x x ππππ-=-+=+=,∴53cos()cos[()]cos()6665x x x ππππ-=-+=-+=- 10、【解析】由诱导公式知f (2 010)=a sin α+b cos β=-1,∴f (2 011)=a sin(π+α)+b cos(π-β)=-(a sin α+b cos β)=1.11、12、【解析】 ∵sin(3π+θ)=-sin θ=13,∴sin θ=-13.∴原式= -cos θcos θ-cos θ-+cos θcos θ-cos θ+cos θ=11+cos θ+cos θ-cos 2θ+cos θ=11+cos θ+11-cos θ =21-cos 2θ=2sin 2θ=2⎝ ⎛⎭⎪⎫-132=18.。
解三角形 先考题一、选择题1、已知△ABC 中,a =10,b = A =45°,则B 等于 ( )A 60°B 120°C 30°D 60°或1202、在ABC ∆中,已知2,33,150===c a B ,则b 等于( )A 7B 6C 5 D3、在△ABC 中,已知b =40,c =20,C =60°,则三角形的解的情况( )A .有一解B .有两解C .无解D .有解但解的个数不确定4、钝角ABC ∆的面积是12,1,AB BC ==则AC =( ).5A .B .2C .1D5、如图所示,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为75°,30°,此时气球的高度是60 m ,则河流的宽度BC 等于( )A .240(3-1)mB .180(2-1)mC .120(3-1)mD .30(3+1)m6、在△ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,若角A ,B ,C 依次成等差数列且a =1, b =3,则S △ABC 等于( )A . 2B . 3C .32D .2 二、填空题7、在ABC ∆中,已知 120,32,2===C c b ,则ABC ∆的面积 8、在ABC ∆中,3:2:1::=C B A ,则三边之比=c b a ::9、在ABC ∆中,若a 、b 、c 成等比数列,且2c a =,则cos B = .10、在ABC ∆中,若cos cos a A b B ⋅=⋅,则这个三角形形状是__________ 三角形11、在ABC ∆中,若2b a =,B =A +60,则A =_________.三、解答题12、在ABC ∆中,D 是BC 上的点,AD 平分`BAC ∠,ABD S ∆=2ACD S ∆。
(Ⅰ)求CB ∠∠sin sin ; (Ⅱ) 若AD =1,DC =22求BD 和AC 的长.14、如图,在△ABC 中,∠ABC =90°,AB= 3 ,BC=1,P 为△ABC 内一点,∠BPC =90°(1)若12PB =,求PA ; (2)若∠150APB =°,求tan PBA ∠A BC P答案:1-6 DACBCC 7.3 6.2:3:1 9.43 10.等腰或直角三角形 11.︒3012(1)21 ;(2)1=b 13(1)23;(2)43。
5.3 解三角形问题
一、解三角形,即已知三角形的六个量(三条边、三个角)中的三个量,求另外三个量。
二、在ABC ∆中,求解三角形
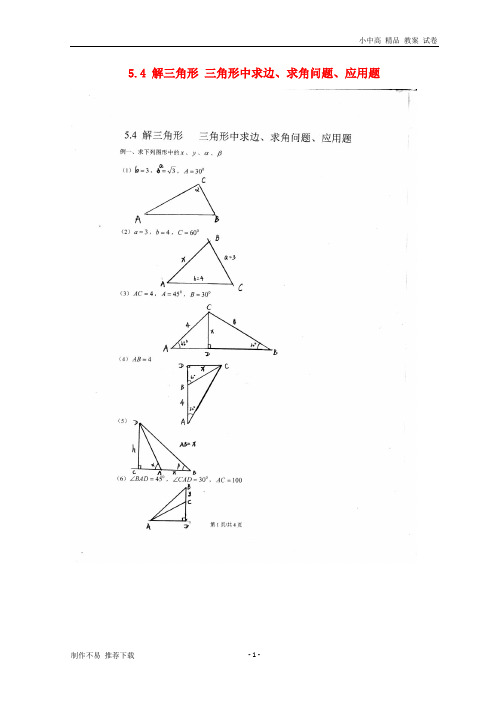
1、45a b A =
==︒, 2、8,60,75a B C ==︒=︒
3、6,30,b A a ==︒=
4、6,30,3b A a ==︒=
5、6,30,2b A a ==︒=
6、6,30,6b A a ==︒=
7、6,60,b A a ==︒= 8、6,30,b C a ==︒=
9、15,10,9===c b a
10、08,60,75a B C ==︒=,求ABC ∆德尔外接圆面积、ABC ∆的面积
例3、在锐角ABC ∆中, ,,a b c 分别是ABC ∆的对边,cos A B =
=,(1)求cos()A B +的值,
(2)若4,a =求ABC ∆的面积
练习:(选作) (1)在ABC ∆中,45,30,10A C c =︒=︒=,解三角形。
(已知两角和任意一边)
(2)在ABC ∆中,1,30a b A ===︒。
解三角形(已知两边及一边的对角)
(3)在ABC ∆中,12,150.a c B ===︒求b (已知两边及两边的夹角)
(4)在ABC ∆中,a b c ===
(5)在ABC ∆中,若7,3,8,a b c ===,(1)求ABC S ∆,(2)求AC 边上的高(面积公式)
11、在ABC ∆中,13tan ,tan 45A B =
=,(1)求角C 的大小,(2)若AB ,求BC 边的长
参考答案:
1、125,3ππ==
C B ,226+=c 或 12,32ππ==C B ,226-=c 2、4π=
A , 64=b ,344+=c 3、34,2,3===
c C B ππ 或32,3,32===c C B ππ 4、33,3
,2===c C B ππ
5、无解
6、36,32,3===
c C B ππ 7、12,2,6===c C B ππ
或6
5π=B (舍去)
8、6=c ,6π=B ,3
2π=
C 9、7561cos =A ,4511cos -=C ,135103cos =B 10、π32=圆S ,3824+=∆ABC S
例3、(1)2
2)cos(-=+B A (2)6=S 练习(1) )26(5,210,10+
===b a c 练习(2)2,2,3===c C B π
π
或1,6
,32===c C B ππ 练习(3)2012=b
练习(4)3π
=A ,4π
=B ,12
5π=C 练习(5) (1)36=S (2)34=h
11、(1)4
3π=C (2)2=BC。