基于宏程序的复杂非圆曲线编程方法研究冯艳宏

基于MACRO的非圆二次旋转曲线轮廓的数控加工研究李润;陈兆兴【摘要】针对常规手工编程中难以加工非圆二次旋转曲线的问题,对华中数控系统中典型的非圆二次函数公式曲线轮廓的车削加工进行研究。

首先根据加工轮廓确定中心在坐标原点,且不倾斜的曲线方程,在solidworks软件中创建表达式,应用规律曲线参数模块绘制出曲线图形;然后将表达式中的方程进行坐标旋转及平移转换,绘制出与加工图纸一致的曲线轮廓;最后采用分析归纳法得出二次旋转曲线的宏程序模块,并给出该宏程序在旋转双曲线和椭圆曲面零件加工中的编程应用。

实践表明,该宏程序对数控编程基础人员灵活应用非圆二次旋转曲线轮廓的编程方法与技巧有实际的指导意义。

%It is difficult to process Non-round conic hyperbola curve in conventional manual programming,now,studying turning of Non-round conic hyperbola outliner on HNC-21T numerical control system.First,acts according to the processing outline determination center in the origin of coordinates,founds the expression of non-incline equation of a cure by the solidworks software,and draws up the curvilinear figure based on the application rule curve parameter module,then carries on the expression in equation coordinates revolving and the translation transforms,draws up with the processing blueprint consistent curve outline,the general macro of Non-round conic hyperbolic is obtained in analysis and induction,and is applicated in Revolving hyperbolic curve processing parts.Processing practices prove： it is significant to improve programming methods and techniques for the certain person who has the basis of NC programming.【期刊名称】《兰州石化职业技术学院学报》【年(卷),期】2011(011)003【总页数】4页(P16-19)【关键词】宏程序;非圆二次曲线;数控程序;旋转椭圆;旋转双曲线【作者】李润;陈兆兴【作者单位】兰州石化职业技术学院机械工程系,甘肃兰州730060;山东特种设备检验研究院,山东济南250101【正文语种】中文【中图分类】TG659随着数控技术的不断进步，数控车床加工各类复杂形面也日渐增多。

采用数控宏程序解决非圆曲线类零件的加工阳夏冰【摘要】@@%本文针对非圆曲线加工精度和效率不高的问题,采用数控编程并结合编制的宏程序加工,可以有效地解决这类问题,实践表明,采用此方法加工非圆曲线类的零件,不但降低了工作量和劳动强度,而且还提高了加工精度和效率.【期刊名称】《制造业自动化》【年(卷),期】2012(034)018【总页数】3页(P44-46)【关键词】非圆曲线;数控;宏程序【作者】阳夏冰【作者单位】武汉城市职业学院,武汉430064【正文语种】中文【中图分类】TG6590 引言在普通加工中，加工非圆曲线类零件通常采用制作样板或靠模，然后利用仿形机床加工，但在小批量生产中，制作样板或靠模效益不高，在加工中受到仿形机床的仿形精度影响，加工精度也受到影响；在数控加工中，数控系统只有直线和圆弧插补功能，要对椭圆、双曲线和抛物线等非圆曲线进行加工，数控系统无法直接实现插补，需要通过一定的数学处理。

数学处理的方法是，用直线段或圆弧段去逼近非圆曲线，逼近线段与被加工曲线的交点称为节点，各几何要素之间的连接点称为基点。

如图1所示，OE是一段椭圆，在OE之间插入节点A、B、C、D，相邻两点之间在Z方向的距离相等，均为a。

节点数目的多少或a的大小，决定了椭圆加工的精度和程序的长度。

采用直线段OA、AB、BC、CD、DE去逼近椭圆，关键是求出节点O、A、B、C、D、E的坐标。

若只采用现有的数控程序编程加工，节点的计算比较复杂，且节点数量较多，手工计算无法实现，因此必须借助宏程序的转移和循环指令处理。

求得各节点后，就可按相邻两节点间的直线来编写加工程序。

1 宏程序宏程序类似于高级语言的程序，程序员可以使用变量进行算术运算、逻辑运算和函数的混合运算，此外还可以使用循环语句、分支语句和子程序调用语句对刀具路径进行控制，利于编制各种复杂的零件加工程序减少乃至免除手工编程时进行繁琐的数值计算，以及精简程序量，使程序应用更加灵活、方便。

宏程序在非圆曲线类零件车削加工中的应用黄启红【摘要】文章分析了宏程序功能的突出特点、编程思路及常用编程格式,并以HNC-21/22T系统数控车床为例,对含抛物线及椭圆轮廓的非圆曲线类数控车削零件,如何用宏程序来加工的设计思路、工艺参数、结构流程图及程序编制等进行了具体分析.在数控车削加工中,宏程序使用变量、算术、逻辑运算及循环语句等方法,能够编制传统数控编程无法实现的非圆曲线类零件的加工,其变量编程方式增加了应用对象的灵活性,使宏程序具有通用性,大大增强了数控机床的使用功能.【期刊名称】《制造业自动化》【年(卷),期】2011(033)009【总页数】3页(P49-51)【关键词】宏程序;非圆曲线;数控车削加工【作者】黄启红【作者单位】岳阳职业技术学院机电工程系,岳阳,414000【正文语种】中文【中图分类】TH161在数控车削加工中，有时会遇到一些非圆曲线类零件的加工，这类零件若采用软件自动编程，则生成程序占用内存较大、程序修改困难且受设备和条件的限制，若采用传统的CNC手工编程，则数控系统提供的直线插补和圆弧插补功能无法直接满足用户的要求。

但是，如果利用数控系统提供的用户宏程序功能，可以很好的解决这些形状或尺寸有规律的非圆曲线类零件的加工。

现代数控系统都为用户配备了强有力的类似高级语言的宏程序功能，用户可以使用变量进行算术运算、逻辑运算和函数的混合运算。

宏程序提供了循环语句、分支语句和子程序调用语句等功能，用以编制非圆曲线等各类复杂零件的加工程序并可精简程序量，减少甚至免除手工编程时繁琐的数值计算。

用户宏程序是带变量的手工编程，是手工编程的精髓。

其程序具有简洁精悍，逻辑严密；很好的易读性和易修改性，通用性强，编程效率高；程序内存量小，比执行CAD/CAM软件生成的程序更加快捷，反应更加迅速，能弥补自动编程的不足等特点。

宏程序加工非圆曲线轮廓的基本编程思路是用数段直线逼近轮廓线。

具体而言，就是设想先将某段非圆弧曲线细分成若干微小线段，然后在每一小段线段上做直线或圆弧插补，来近似表示这一段非圆弧曲线。

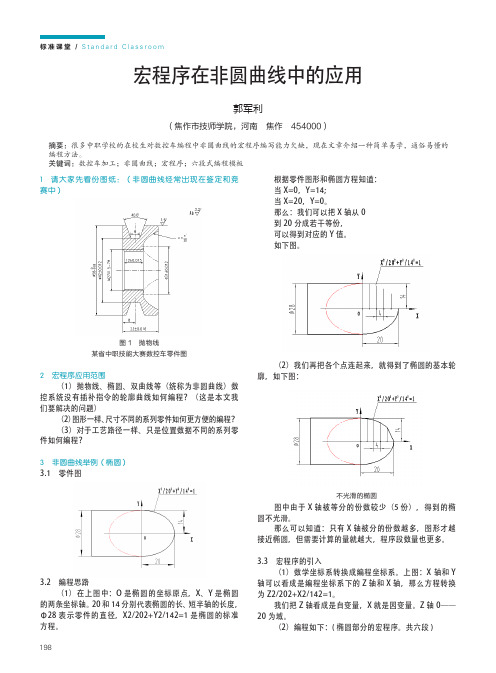
标准课堂/S t a n d a r d C l a s s r o o m198（焦作市技师学院，河南　焦作　454000）摘要：很多中职学校的在校生对数控车编程中非圆曲线的宏程序编写能力欠缺，现在文章介绍一种简单易学，通俗易懂的编程方法。

关键词：数控车加工；非圆曲线；宏程序；六段式编程模板1　请大家先看份图纸：（非圆曲线经常出现在鉴定和竞赛中）图1 抛物线某省中职技能大赛数控车零件图2 宏程序应用范围（1）抛物线、椭圆、双曲线等（统称为非圆曲线）数控系统没有插补指令的轮廓曲线如何编程？（这是本文我们要解决的问题）（2）图形一样、尺寸不同的系列零件如何更方便的编程？（3）对于工艺路径一样、只是位置数据不同的系列零件如何编程？3 非圆曲线举例（椭圆）3.1 零件图3.2 编程思路（1）在上图中：O是椭圆的坐标原点，X、Y是椭圆的两条坐标轴。

20和14分别代表椭圆的长、短半轴的长度，Φ28表示零件的直径，X2/202+Y2/142=1是椭圆的标准方程。

根据零件图形和椭圆方程知道：当X=0，Y=14;当X=20，Y=0。

那么：我们可以把X轴从0到20分成若干等份，可以得到对应的Y值。

如下图。

（2）我们再把各个点连起来，就得到了椭圆的基本轮廓，如下图：不光滑的椭圆图中由于X轴被等分的份数较少（5份），得到的椭圆不光滑。

那么可以知道：只有X轴被分的份数越多，图形才越接近椭圆，但需要计算的量就越大，程序段数量也更多。

3.3 宏程序的引入（1）数学坐标系转换成编程坐标系。

上图：X 轴和Y 轴可以看成是编程坐标系下的Z轴和X轴，那么方程转换为 Z2/202+X2/142=1。

我们把Z轴看成是自变量，X就是因变量。

Z轴0——20为域。

（2）编程如下：(椭圆部分的宏程序。

共六段)郭军利宏程序在非圆曲线中的应用S t a n d a r d C l a s s r o o m /标准课堂199…#1=20.（Z 向初始值，椭圆的加工起点在数学坐标系中的Z 值WHILE[#1GE0]DO1（椭圆的加工终点在数学坐标系中的Z 值）#2=14./20.×SQRT[400.-#1×#1]（椭圆标准方程）G1X[#2×2.]Z[#1-20.]（数学坐标原点到编程原点的Z 向距离）#1=#1-0.1（步距的大小决定椭圆的精度） END1（结束）…4 六段式编程验证（抛物线图形）我们用椭圆编程实例中的六段编程格式编写图一中抛物线图形的程序如下：…#1=10.WHILE[#1GE0]DO1#2=SQRT[10.×#1]G1X[2.×#2+31.]Z[#1-10.]F0.1#1=#1-0.1END1…（经过仿真加工证明六段式编程是可行的，图略）5 归纳根据椭圆举例和抛物线练习，宏程序可以归纳为：六段式模板#1=？WHILE[#1GE ？]DO1#2=非圆曲线方程G1X[？±2.×#2]Z[#1－？]#1=#1-0.1END16 结论（1）编写非圆曲线宏程序完全可以采用 六段式编程模板（格式简单，不易出错，具有通用性）。

宏程序在编制非圆曲线类零件程序中的应用日期: 2009-11-10 18:51:38 浏览: 10 来源: 学海网收集整理作者: 佚名摘要：文章以在华中数控NHC-21Ｔ型数控车系统上编制椭圆加工程序为例,介绍了采用宏程序编程法在编制非圆曲线类零件程序时的分析方法及思路。

关键词：宏程序椭圆循环变量引言在用宏程序加工非圆曲线类零件时，一般思路是先把工件坐标原点偏置到该类零件的对称中心上，然后采用直线逼近（也叫拟合）法，即在Z向或X向分段，以一个适合的步距，并把Z或X作为自变量，X作为Z或Z作为X的函数来进行处理。

为了适应不同类型的非圆曲线（即不同长短轴的椭圆，不同实、虚轴的双曲线，不同对称轴和不同焦点的抛物线），不同起始点和不同的步距，我们可以编制一个只用变量不用具体数据的通用宏程序，然后在主程序中呼出该宏程序的用户宏指令段内为上述变量赋值。

这样，对于不同的非圆曲线、不同的起始点和不同的步距，不必修改程序，而只需要修改主程序中用户宏指令段内的赋值数据即可。

由于思考方法大致相同，本文只对椭圆的精加工通用程序和适用程序的应用进行介绍。

一、椭圆类精加工通用程序分析图（一）所示为带有椭圆过渡的零件，假设椭圆短半轴为a,长半轴为b;我们可使用变量为此类零件编出精加工通用宏程序。

1）分析：椭圆的一般方程: ，我们把Z作为自变量，X作为Z的函数则：在第一、二象限内可转换为：在第三、四象限内可转换为：用变量来表达上式为：#23=#0*SQRT[1－[#25*#25]/[#1*#1]]#23=－#0*SQRT[1－[#25*#25]/[#1*#1]]图（一）椭圆过渡类零件图2）根据前面所述的一般思路，可画如图（二）所示的椭圆宏程序结构流程图：图（二）椭圆精加工宏程序结构流程图3）通用程序示例我们以工件右端面与轴心线的交点作为坐标原点来建立工件坐标系，如图（一）所示，程序中所用到的局部变量含义如下：#23=e；e为椭圆轮廓的起始点工件X坐标值#25=d；d为椭圆轮廓的轴起始点工件Z坐标值#0=a；a为X向椭圆半轴长度#1=b；b为Z向椭圆半轴长度#2=c；c为椭圆轮廓终点工件Z坐标值#3=f；f为Z轴递变量#4=g；g为Z轴偏移量，在数值上与d相等#5=h；h为切削速度主程序：%01 ;程序号N1 T0101N2 M03 S600N3 M98 P02 A a B b C c D f E g F h X e Z d ；调用车削椭圆曲线类零件的用户宏程序，并为变量呼出相应值N4 G00 X100 Z100 ；回到换刀点N5 M30；程序结束并返回程序开头%02；宏程序名N1 G00 X[#23] Z1 ；快速定位N2 WHILE #25 GE #2 ；判断是否走到椭圆Z轴终点N3 #23=#0*SQRT[1－[#25*#25]/[#1*#1]]；（计算椭圆上任一点X坐标值）N4 G01 X[2*#23] Z[#25-#4] F[#5]；将工件坐标系原点偏移到椭圆对称中心，并直线插补椭圆N5 #25=#25-#3 ；Z轴步距递减N6 ENDW；返回循环体N7 M99；子程序结束并返回主程序二、椭圆适用程序解析以上为椭圆精加工通用程序，但是我们在实际加工过程中，往往不仅仅只涉及精加工，可能还有较多加工余量需要我们处理。

非圆曲线轮廓数控车削标准化过程设计作者：刘丰来源：《外语学法教法研究》2014年第11期【摘要】本文基于宏程序的运用，提出了一种标准化过程用于非圆曲线的数控车削加工。

读者可通过固定化的格式：曲线函数分析、加工类型选择、宏程序模板填空三个步骤，编辑出适应于实际生产加工的函数曲线加工程序。

由于笔者能力有限，该过程并不十分完善，但这一过程体系比较开放，读者可在其中任何环节作补充修改。

希望本文的构思能得到大家的批评指正，使得该标准化过程在实际生产中得到推广运用。

【关键词】数控车削函数曲线标准化过程宏程序【中图分类号】G640 【文献标识码】A 【文章编号】2095-3089（2014）11-0021-02＼一、前言数控车削加工现在已在生产领域中被广泛应用，其轮廓控制的加工方式使得曲线轮廓的加工变得简单而准确。

但除圆以外的曲线目前都只能用宏程序来实现，而宏程序的编写对于普通的操作者来说都比较困难，若没有一定的编写经验积累很难写出合理的宏程序。

本文设想提出一种标准化过程，操作者可通过简单的判断、选择和计算，按流程步骤操作，最终就能得到适应于实际生产加工的函数曲线加工程序。

该过程应具有普遍实用性，能够适应多种函数曲线以及曲线轮廓在不同象限的情况。

下面我将通过标准化过程提出和实例分析两个部分来讲述本文设计内容。

二、非圆曲线轮廓数控车削标准化过程本文所设计的标准化过程主要分三个部分，分别是标准化流程、常用曲线函数分析表和宏程序模板。

其中标准化流程是主线，具有较好数学基础（函数部分）和宏程序基础知识的读者可直接根据该流程完成加工程序。

若读者数学基础较差，则可参照常用函数分析表完成函数分析和数据采集。

最后宏程序模板可以为不懂宏程序的读者提供方便，读者只需做好模板中的填空便能完成加工程序。

三部分相互关系如图一所示。

图一（一）非圆曲线的数控车削标准化流程如图二所示，标准化流程分为函数曲线分析准备和宏程序模板分类两部分。

函数曲线分析准备是根据零件轮廓曲线进行分析，完成作三个方面的准备工作：1、得出曲线方程表达式；2、得出工件原点与函数原点的坐标差值（注：x方向按半径差值计算）；3、计算出曲线轮廓起点和终点的函数坐标。

宏程序编制非圆弧曲线的编程模块刘小清【摘要】宏程序的模块化可大大简化程序,提高手工编程的效率,拓展数控机床手工编程应用范围,提高机床的使用性能.将相关的参数填写在格式模块对应的位置,就可以编制非圆弧二次曲线的程序.【期刊名称】《鄂州大学学报》【年(卷),期】2011(018)002【总页数】4页(P23-26)【关键词】宏程序;编程;模块化【作者】刘小清【作者单位】鄂州职业大学,机械系,湖北,鄂州,436000【正文语种】中文【中图分类】TP311;TH164目前市场上的数控加工系统一般只具有直线插补和圆弧插补功能，这就限制了数控机床的加工范围。

随着各种复杂的零件应用越来越普及，非圆弧二次曲线的编程就成为每个数控编程人员必须掌握的基本技能。

加工非圆弧二次曲线的方法有两种：一种是利用系统的强大的计算功能及宏功能来编程，另一种是利用各种编程软件进行自动编程。

宏程序对初学者来说难于理解，但有一种模块化的格式，无论你是否懂宏程序，只要记住这些模块，将相关的参数填写在对应的位置，就可以编制任何非圆弧二次曲线的程序了。

一般数控系统都为用户配备了强有力的类似于高级的宏程序功能，用户可以使用变量进行算术运算（+、-、*、/）、逻辑运算（AND、OR、NOT）和函数运算（SIN、COS等），宏程序还提供了循环语句、判断语句、分支语句和子程序调用语句。

可以利用宏程序来编制复杂的零件加工程序，减少乃至免除手工编程时进行繁琐的数字计算，以简化程序量。

简单地说，宏程序是一种具有计算能力和决策能力的数控程序，宏程序具有如下的特点：[1]例如：（1）G01X[#3+8] 表达式#3+8（2）G01X4F[#1] 变量#1（3）G01Y[50*SIN[30]] 函数运算50×SIN30°例如：（1）IF#3GE9 选择执行命令……ENDIF（2）WHILE#1LT#4*5 条件循环命令……ENDW（1）宏程序引入了变量和表达式，还有函数功能，具有实时动态计算能力，可以加工非圆弧曲线，如抛物线、椭圆、双曲线、三角函数曲线等；（2）宏程序可以完成图形一样、尺寸不同的系列零件加工；（3）宏程序可以完成工艺路径一样、位置不同的系列零件加工；（4）宏程序具有一定的决策能力，能根据条件选择性地执行某些部分；（5）使用宏程序能极大地简化编程，精简程序，适合于复杂零件的加工编程。