下载文档原格式
第四章 流体的有旋流动和无旋流动在上一章中我们阐述了流体流动的一些基本概念，导出了流体流动的连续性方程、欧拉运动方程、伯努利方程和动量方程等，为解决工程实际问题奠定了一定的理论基础。
本章将进一步讨论流体的有旋流动和无旋流动。
第一节 流体微团运动的分析我们知道，刚体的运动一般可以分解为移动和转动两部分。
但流体与刚体不同，流体受力便会发生运动状态的变化，即流体具有流动性，极易变形。
因此，流体微团在运动过程中不但会发生移动和转动，而且还会发生变形运动。
所以，在一般情况下流体微团的运动可以分解为移动、转动和变形运动三部分。
变形运动又分为线变形运动和角变形运动两种情况。
下面我们分别讨论这几种运动情况。
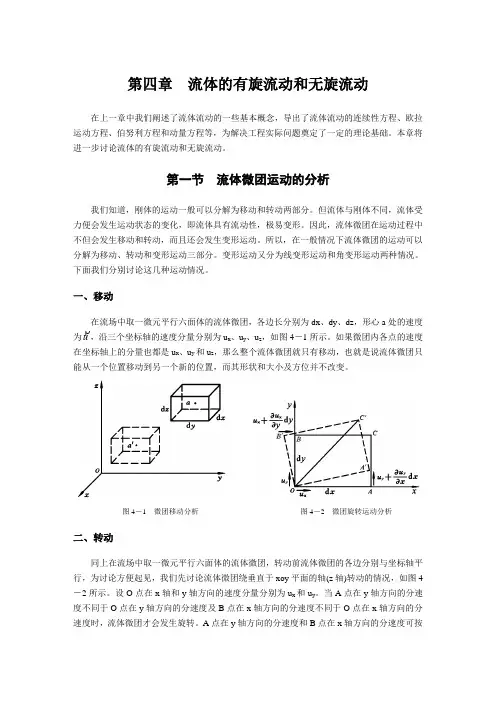
一、移动在流场中取一微元平行六面体的流体微团，各边长分别为dx 、dy 、dz ，形心a 处的速度为u，沿三个坐标轴的速度分量分别为u x 、u y 、u z ，如图4－1所示。
如果微团内各点的速度在坐标轴上的分量也都是u x 、u y 和u z ，那么整个流体微团就只有移动，也就是说流体微团只能从一个位置移动到另一个新的位置，而其形状和大小及方位并不改变。
图4－1 微团移动分析4－2 微团旋转运动分析二、转动同上在流场中取一微元平行六面体的流体微团，转动前流体微团的各边分别与坐标轴平行，为讨论方便起见，我们先讨论流体微团绕垂直于xoy 平面的轴(z 轴)转动的情况，如图4－2所示。
设O 点在x 轴和y 轴方向的速度分量分别为u x 和u y 。
当A 点在y 轴方向的分速度不同于O 点在y 轴方向的分速度及B 点在x 轴方向的分速度不同于O 点在x 轴方向的分速度时，流体微团才会发生旋转。
A 点在y 轴方向的分速度和B 点在x 轴方向的分速度可按泰勒级数展开，并略去高阶无穷小量而得到，它们分别为x xu u d y y ∂∂+和y yu u d xx ∂∂+，它们相对于O 点的对应分速度(相对于O 点的线速度)分别为x xu d y ∂∂和y yu d x∂∂，所以它们相对于O 点的角速度(逆时针方向旋转为正)应为A 点上xu x x xu ∂∂=∂∂y y d /dB 点上 yuy y y u ∂∂-=∂∂-x x d /d 而对于微团中其它各点绕z 轴转动的角速度(如C 点等)则是由该点y 向的分速度在x 轴方向的变化量和x 向的分速度在y 轴方向的变化量共同产生的。
