成都市2008-2009学年八年级上期调研考试数学试卷(含答案)

成都市2008～2009学年度上期期末调研考试高一物理A卷非选择题与B卷试卷分析成都市十八中学杨波展阅成都市2008～2009学年度上期期末调研考试高一物理A卷非选择题与B卷部分，试题立意高，设问巧，语言简洁、流畅，灵活而不落俗套，新颖而不离基础，强调能力而不脱离实际，有一定的难度，在整张卷中具有较好的区分度，给人一股清新的感觉。

A卷非选择题11道题、共58分；B卷8道题，其中选择题5道共20分，非选择题3道共30分。

一、试卷分析1、试题重视对基础知识和基本技能的考查试题以考查基础知识为主，知识点多，覆盖面广，１6个题中内容涉及高一物理上期的主干知识，重点考查了双基，注重对学科基础知识、重点知识、主体知识的考核，检验学生是否真正理解和掌握这些基本概念和规律的实质。

很多题目略做变化，就成了一道质量教高的新题，特别是B卷第6题的设计体现了出卷人独到的设计能力，考查了学生利用所学知识解决实际问题的能力。

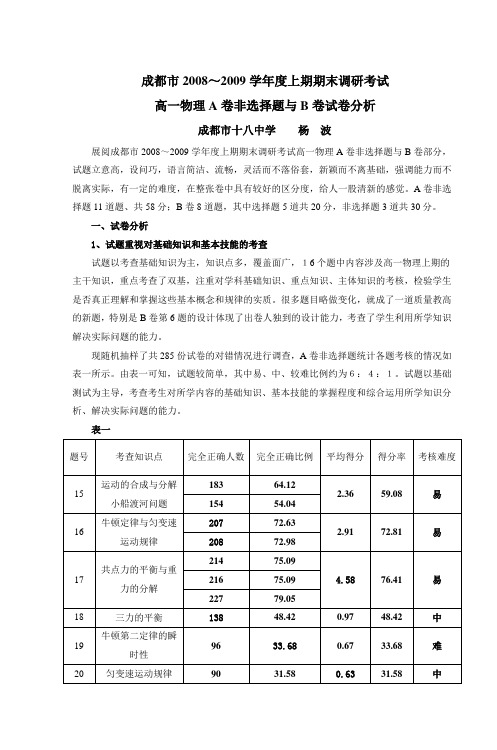
现随机抽样了共285份试卷的对错情况进行调查，A卷非选择题统计各题考核的情况如表一所示。

由表一可知，试题较简单，其中易、中、较难比例约为６：４：１。

试题以基础测试为主导，考查考生对所学内容的基础知识、基本技能的掌握程度和综合运用所学知识分析、解决实际问题的能力。

表一①学生对基本知识和基本技能的掌握基本到位。

如填空题第15、16、17，实验题第23题第1、2、4空，计算题第24、25题。

②学生对实际运用类型的问题办法不多。

如填空题第9题与B卷第6题。

主要原因是学生死记硬背公式，不了解知识的物理意义，从而硬套公式，当物理情景不是熟悉情意时就无所适从。

③游标卡尺的读数问题是许多学生的老大难问题。

要处理好这个难点，一是要在让学生掌握游标卡尺的原理，从根本上解决问题，二是要让学生在实践中运用游标卡尺去测量常见物理的长度，从而加深印象，三是使用一些简单方法让学生记意深刻，如游标卡尺的精度为游标刻度的倒数，如使用精度检查读数是否准确，特别是最后一位为零时是否省略。

成都市2007-2008学年度上期末八年级数学试题本试卷分A 、B 卷。

A 卷100分，B 卷50分，共150分。

一、选择题（本题共有10个小题，每小题3分，共30分）在每小题给出的四个选项中，只有一项是正确的，把正确的序号填在题后的括号内。

1．下列实数中是无理数的是（ ） （A ）38.0 （B ）π （C ）4 （D ） 722-2．在平面直角坐标系中，点A （1，－3）在（ ）（A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限 3．－8的立方根是（ ）（A ）2± （B ）2 （C ） －2 （D ）24 4．下列四组数据中，不能．．作为直角三角形的三边长是（ ） （A ）3，4，6 （B ）7，24，25 （C ）6，8，10 （D ）9，12，15 5．下列各组数值是二元一次方程43=-y x 的解的是（ ）（A ）⎩⎨⎧-==11y x （B ）⎩⎨⎧==12y x （C ）⎩⎨⎧-=-=21y x （D ）⎩⎨⎧-==14y x6．已知一个多边形的内角各为720°，则这个多边形为（ ） （A ）三角形 （B ）四边形 （C ）五边形 （D ）六边形7经理决定本周进货时多进一些红色的，可用来解释这一现象的统计知识是（ ）（A ）平均数 （B ）中位数 （C ）众数 （ D ）平均数与中位数 8．如果03)4(2=-+-+y x y x ，那么y x -2的值为（ ） （A ）－3 （B ）3 （C ）－1 （D ）19．在平面直角坐标系中，已知一次函数b kx y +=则下列结论正的是（ ）（A ）k >0,b >0 （B ）k >0, b <0 （C ）k <0, b >0 （D ）k <0, b 10．下列说法正确的是（ ）（A ）矩形的对角线互相垂直 （B ）等腰梯形的对角线相等（C ）有两个角为直角的四边形是矩形 （D ）对角线互相垂直的四边形是菱形 二、填空题：（每小题4分，共16分）11．9的平方根是 。

FEDCBA2008－2009学年八年级第一学期数学期中考试调研试题一、选择题（请将正确答案填在下面相应的表1 2 3 4 5 6 7 8 9 10 11 12一、选择题（共12小题，每小题3分，共36分） 1．下列银行标志中是轴对称图形的个数有（ ）A ．2个B ．3个C ．4个D ．5个2．下列说法中正确的是（ ）A ．36的平方根是6B ．16的平方根是±2C ．8的立方根是－2D ．4的算术平方根是－2 3．a 是一个无理数，且满足3＜a ＜4，则a 可能是（ ）A ．2-B 21C ．πD ．38-4．如图，△ACE ≌△DBF ，若AD ＝8，BC ＝2，则AB 的长度等于（ ）A ．6B ．4C ．3D ．25．已知点P 1（a －1，5）和P 2（2，b －1）关于x 轴对称，则（a ＋b ）2009的值为（ ） A ．0 B ．－1 C ．1 D ．（－3）20096、△ABC 的两边的长分别为353 ） A ．33 B ．43 C ．53 D ．3 7．下列四个条件，可以确定△ABC 与△A 1B 1C 1全等的是( )A ．BC ＝B 1C 1，AC ＝A 1C 1，∠A ＝∠A 1 B ．AB ＝A 1B 1，∠C ＝∠C 1=900C ． AC ＝A 1C 1，∠A ＝∠A 1，∠B ＝∠B 1 ；D ．∠A ＝∠A 1，∠B ＝∠B 1，∠C ＝∠C 1题号 1-1213-16 17-20 21-23 24-25 总分 分数 3612 27 23 22 120 得分21A BCDEDCBAEDCBASR QP CBA8．如图：△ABC 中，D 为BC 上一点，△ACD 的周长为12cm ，DE 是线段AB 的垂直平分线，AE ＝5cm ，则△ABC 的周长是（ ）A ．17cmB ．22cmC ．29cmD ．32cm 9．如图，直径为1个单位长度的圆从原点沿数轴向右滚动一周， 圆上一点由原点到达点A ， 下列说法正确的是（ ）A ．点A 所表示的是π.B ．数轴上只有一个无理数π.C ．数轴上只有无理数没有有理数.D ．数轴上的有理数比无理数要多一些.10．如图所示，△ABC 中，D 为BC 上一点，且AB ＝AC ＝BD ．则图中∠1与∠2的关系是( )A ．∠1＝2∠2B ．∠1＋∠2＝180°C ．∠1＋3∠2＝180°D ．3∠1－∠2＝180°11．四边形ABCD 中， AC 和BD 交于点E ，若AC 平分∠DAB ，且AB ＝AE ， AC ＝AD ，有以下四个命题： ①AC ⊥BD ；②BC ＝DE ； ③∠DBC ＝21∠DAB ；④AB ＝BE ＝AE 。

成都市八年级上数学期末调研试题 一、选择题 1. 16的值等于（ A ）A ．4B ．－4C ．±4D ．±22.下列四个点中，在正比例函数x y 52-=的图象上的点是（ D ） A ．（2，5）B ．（5，2）C ．（2，－5）D ．（5，―2）3.估算324+的值是（ C ）A ．在5与6之间B ．在6与7之间C ．在7与8之间D ．在8与9之间4.下列算式中错误的是（ C ）A ．8.064.0-=-B ．4.196.1±=±C ．53259±= D ．238273-=-5. 下列说法中正确的是（ C ）A ．带根号的数是无理数B ．无理数不能在数轴上表示出来C ．无理数是无限小数D ．无限小数是无理数6.如图，一根垂直于地面的旗杆在离地面5m 处撕裂折断，旗杆顶部落在离旗杆底部12m 处，旗杆折断之前的高度是（ D ）A ．5mB ． 12mC ．13mD ．18m 7. 已知一个两位数，十位上的数字x 比个位上的数字y 大1，若颠倒个位与十位数字的位置，得到新数比原数小9，求这个两位数列出的方程组正确的是（D ） A．⎩⎨⎧=+++=-9)()(1x y y x y x B ．⎩⎨⎧++=++=9101x y y x y x C ．⎩⎨⎧++=+=+910101x y y x y x D ．⎩⎨⎧++=++=910101x y y x y x8. 点A （3，y 1，），B （－2，y 2）都在直线32+-=x y 上，则y 1与y 2的大小关系是（ B ） A ．y 1＞y 2B ．y 2＞y 1C ．y 1＝y 2D ．不能确定9.为了让人们感受丢弃废旧电池对环境造成的影响，某班环保小组的6名同学记录了自己家中一个月内丢弃废电池的数量，结果如下（单位：个）：7,5,6,4,8,6，如果该班有45名学生，那么根据提供的数据估计该月全班同学各家总共丢弃废旧电池的数量约为（ ）A .180B .225C .270D .31510．如图，点O 是矩形ABCD 的对称中心，E 是AB 边上的点，沿CE 折叠后， 点B 恰好与点O 重合，若BC=3，则折痕CE= A ．2 3 B ．332 C ．3 D ．6二、填空题11. 计算：5312-⨯ ．12. 写出一个解是⎩⎨⎧==21y x 的二元一次方程组 ． 13．一次函数y ＝x ＋1的图象与y ＝－2x －5的图象的交点坐标是__________．14．已知2x －3y ＝1，用含x 的代数式表示y ，则y ＝______，当x ＝0时，y ＝______.（6）ABCD EO （第10题图）15.已知函数b kx y +=的图象不经过第三象限则k 0，b 0． 三、解答题(共52分）16.（1）计算7002871-+ )23)(23()132(2-++- （3）解方程组⎩⎨⎧-=-=-547965y x y x17.某校教师为了对学生零花钱的使用进行教育指导，对全班50名学生每人一周内的零花钱数额进行了调查统计，并绘制了下表 零花钱数额/元5 10 15 20 学生人数1015205（1）求出这50名学生每人一周内的零花钱数额的平均数、众数和中位数（2）你认为（1）中的哪个数据代表这50名学生每人一周零花钱数额的一般水平较为合适？简要说明理由.（1）平均数是12元（2分） 众数是15元（1分） 中位数是12.5元（1分）（2）用众数代表这50名学生一周零花钱数额的一般水平较为合适，因为15元出现次数最多，所以能代表一周零花钱的一般水平（2分）18. （本题10分） 折叠矩形ABCD 的一边AD ，使点D 落在BC 边的F 点处，若AB=8cm ，BC=10cm ，求EC 的长.、19．某景点的门票价格规定如下表 购票人数 1—50人 51—100人 100人以上 每人门票价12元10元8元某校八年（1）（2）两班共102人去游览该景点，其中（1）班不足50人，（2）班多于50人，如果两班都以班为单位分别购票，则一共付款1118元 （1）两班各有多少名学生？（2）如果你是学校负责人，你将如何购票？你的购票方法可节省多少钱？20（1）设一班学生x 名，二班学生y 名根据题意⎩⎨⎧=+=+1181012102y x y x （5分）解得⎩⎨⎧==5349y x （2分）答 （1分）（2）两班合并一起购团体票1118－102×8＝302 （2分） ∴可节省302元20. 我国是世界上严重缺水的国家之一，为了增强居民的节水意识，某自来水公司对居民用水采取以户为单位分段计费办法收费；即每月用水10吨以内（包括10吨）的用户，每吨水收费a 元，每月用水超过10吨的部分，按每吨b 元（b ＞a ）收费，设一户居民月用水x （吨），应收水费y （元），y 与x 之间的函数关系如图所示. （1）分段写出y 与x 的函数关系式.（2）某户居民上月用水8吨，应收水费多少元？（3）已知居民甲上月比居民乙多用水4吨，两家一共交水费46元，求他们上月分别用水多少吨？故两家用水均超过10吨（1分）设甲、乙两户上月用水分别为m 、n 吨 则⎩⎨⎧=-+-=-4652524n m n m （3分）一/填空题21.若点A 在第二象限，且A 点到x 轴的距离为3，到y 轴的距离为4，则点A 的坐标为 ． 22.．若直线y ＝ax ＋7经过一次函数y ＝4－3x 和y ＝2x －1的交点，则a 的值是______．23.如图，已知A 地在B 地正南方3千米处，甲、乙两人同时分别从A 、B 两地向正北方向匀速直行，他们与A 地的距离S （千米）与所行时间t （小时）之间的函数关系图象如右图所示的AC 和BD 给出，当他们行走3小时后，他们之间的距离为 千米．24.、在直角坐标系中，正方形1111A B C O 、2221A B C C 、…、n n n n-1A B C C 按如图所示的方式放置，其中点123A A A 、、、…、n A 均在一次函数y kx b =+的图象上，点123C 、C 、C 、…、n C 均在x 轴上．若点1B 的坐标为（1，1），点2B 的坐标为（3，2），则点n A 的坐标为_______________25.．（5分）（2013•凉山州）如图，在平面直角坐标系中，矩形OABC 的顶点A 、C 的坐标分别为（10，0），（0，4），点D 是OA 的中点，点P 在BC 上运动，当△ODP 是腰长为5的等腰三角形时，点P 的坐标为 （2，4）或（3，4）或（8，4） ．26、（9分）已知雅美服装厂现有A种布料70米，B种布料52米，•现计划用这两种布料生产M、N两种型号的时装共80套．已知做一套M型号的时装需用A种布料1.•1米，B种布料0.4米，可获利50元；做一套N型号的时装需用A种布料0.6米，B种布料0.•9米，可获利45元．设生产M型号的时装套数为x，用这批布料生产两种型号的时装所获得的总利润为y元．①求y（元）与x（套）的函数关系式，并求出自变量的取值范围；②当M型号的时装为多少套时，能使该厂所获利润最大？最大利润是多？27、如图（1），一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．，与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，（1）如图（2），当EF与AB相交于点M GFFN满足的数量关系，并证明你的猜想；（2）若三角尺GEF旋转到如图（3）所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．28、如图，直线y=kx-1与x轴、y轴分别交与B、C两点，12 OBOC．(1)求B点的坐标和k的值；(2)若点A（x，y）是第一象限内的直线y=kx-1上的一个动点，当点A运动过程中，试写出△AOB的面积S与x的函数关系式；(3)在（2）的条件下，探索：①当点A运动到什么位置时，△AOB的面积是1/4；②在①成立的情况下，x 轴上是否存在一点P，使△POA是等腰三角形，若存在，请直接写出满足条件的所有P点的坐标；若不存在，请说明理由．[。

2008–2009（上）期末考试八年级数学试卷参考答案一、1.A 2.D 3.B 4.B 5.A 6.C 7.C 8.A二、9.0，1 10.30 11.-2 12.（-7，-4）13.y=180-2x 14.2 15.略 16.100a+10b 17.58,5518.10三、19.原式=()2-12+-1+1 (2分)=2-1+-1+1 （4分）=1+ （6分）20.①整理得8x+3y=-13 ……③（1分）③+①×3得：14x=-19 x=- (3分)把x=-代入①得y=- (5分) 即x=-、y=- (6分)21.s=100-60t(0≤t≤) (3分) 图象看情况扣分（6分）22. ① 70.5 (2分) ②70 . 80 (6分)23.∵∠AEB=900 AB=BC=2BE ∴∠EAB=300∴∠B=600 (1分) ∴∠C=1200 (2分)又∵∠ABD=∠B=300 (3分) ∴AC=AB=6 AC=12 (5分) BD=6 BD=12 （6分）四、24. ①∵L2与y=2x+2平行∴K=2 （1分）又∵L2过（4，7）∴b=-1 (2分)②所围三角形的底长1+3=4，高是4 （5分）∴面积=×4×4=8 （7分）25.（略）不要求严格推理。

26.设……（1分）得（5分）解得（6分）答：（7分）五、27. ①当a≥4时无面积（1分）②当2≤a＜4时直线y=-x+a与正方形CD交点E（2，-2+a ）直线y=-x+a与直线y=x交点F（，）真的不掉线吗？？、？？？？？？？？？？？？∴EC=2-（-2+a ）=4-a △CEF的高为2- ∴S△=··（4-a）=（4-a）（3分）当0≤a＜2时直线y=-x+a与直线y=x交点F’（，）此时S△=×2×2-··a=2-a2 （5分）2008–2009（上）期末考试八年级英语试卷参考答案及评分标准Ⅰ．共20分，每小题1分。

-2009学年四川省成都市八年级（上）期末数学试卷一、选择题（共10小题，每小题3分，满分30分）1、（2008•广州）将图按顺时针方向旋转90°后得到的是（）A、B、C、D、考点：生活中的旋转现象。

专题：操作型。

分析：根据旋转的意义，找出图中眼，眉毛，嘴5个关键处按顺时针方向旋转90°后的形状即可选择答案．解答：解：根据旋转的意义，图片按顺时针方向旋转90度，即正立状态转为顺时针的横向状态，从而可确定为A图，故选A．点评：本题考查了图形的旋转变化，学生主要要看清是顺时针还是逆时针旋转，旋转多少度，难度不大，但易错．2、下列运算正确的是（）A、B、|﹣3|=3C、D、考点：实数的运算。

专题：计算题。

分析：A、根据算术平方根的定义即可判定；B、根据绝对值的定义即可判定；C、根据算术平方根的定义即可判定；D、根据立方根的定义即可判定．解答：解：A、C、=2，故选项错误；B、|﹣3|=3，故选项正确；D、9不能开三次方，故选项错误．故选B．点评：此题主要考查了实数的运算，注意，正数的算术平方根是正数．3、（2006•佛山）内角和与外角和相等的多边形一定是（）A、八边形B、六边形C、五边形D、四边形考点：多边形内角与外角。

分析：多边形的内角和与边数相关，随着边数的不同而不同，而外角和是固定的360°，从而可代入公式求解．解答：解：多边形外角和=360°，根据题意，得（n﹣2）•180°=360°，解得n=4．故选D．点评：此题比较简单，只要结合多边形的内角和公式与外角和的关系来寻求等量关系，构建方程即可求解．4、在平面直角坐标系中，位于第二象限的点是（）A、（﹣2，﹣3）B、（2，4）C、（﹣2，3）D、（2，3）考点：点的坐标。

分析：第二象限的点的横坐标小于0，纵坐标大于0．解答：解：根据第二象限的点的坐标的特征：横坐标符号为负，纵坐标符号为正，各选项中只有C（﹣2，3）符合，故选C．点评：本题主要考查了平面直角坐标系中各象限的点的坐标的符号特点，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．5、下列几组数据能作为直角三角形的三边长的是（）A、2，3，4B、5，3，4C、4，6，9D、5，11，13考点：勾股定理的逆定理。

成都市2009-2010学年度上期期末调研考试八年级数学班级 姓名： 学号： 得分：A 卷（100分）一、选择题（每小题3分，共30分）1、已知点A(3，a ）在x 轴上，则a 等于（ ）（A ）-1 （B ）1 （C ）0 （D ）±1 2、下列各数中是无理数的是（ ）（A ）23（B ）9 （C ）327 （D ）1+π 3、下列函数中，y 随x 增大而减小的是（ ）（A ）1-=x y （B ） 32+-=x y （C ）12-=x y （D ）121+=x y 4、下列各组数中，是勾股数的为（ ）（A ）1，2，3， （B ）4，5，6， （C ）3，4，5， （D ）7，8，9， 5、如图，△AOB 中，∠B=25°，将△AOB 绕点Ｏ顺时针旋转 60°，得到△A ´OB ´，边A ´B ´与边OB 交于点C （A ´不在 OB 上），则∠A ´CO 的度数为（ ） （A ）85° （B ）75° （C ） 95° （D ）105°6、我国在近几年奥运会上所获金牌数（单位：枚）统计如下： 则这组数据的众数与中位数分别是（ ）（A ） 32，32 （B ）32，16 （C ）16，16 （D ）16，32 7、下列命题中正确的是（ ）（A ）平行边形是轴对称图形 （B ）等腰三角形是中心对称图形 （C ）菱形的对角线相等（D ）对角线相等的平行四边形是矩形。

8、如图，∠1，∠2，∠3，∠4是五边形ABCDE 的外角， 且∠1=∠2=∠3=∠4=75°，则∠AED 的度数是（ ）（A ）120° （B ）110° （C ）115° （D ）100° 9、已知⎩⎨⎧-==k y kx 32是二元一次方程142=-y x 的解，则k 的值是（ ）（A ）2 （B ）-2 （C ）3 （D ）-310、汽车开始行驶时，油箱内有油40升，如果每小时耗油5升，则油箱内的余油量Q （升）与行驶时间（t 小时）之间的函数关系的图象是（ ）A BO A ´ B ´C第5题1 2 34 5A BCD E二、填空题（每小题4分，共16分）11、化简：(1)、()=-22 ；（2）、3125= 。

2008—2009学年度第一学期期末考试初 二 年 级 数 学 试 卷<满分100分 完卷时间90分钟） 命题人：李冬青 审核人：丁新华1. 在327，131313.0，5，2-中，无理数的个数为< ） A ．1 B ．2 C ．3 D ．42. 下列一次函数中y 的值随着x 值的增大而减小的是< ） A ．43-=x y B ．38-=x y C ．x y 1.02+-= D ．4--=x y3.以下列各组数为三角形的边长，能构成直角三角形的是< ） A. 8，12，17； B. 1，2，3； C. 6，8，10； D. 5，12，93n9HmSCmUm4.已知正比例函数y=kx<k ≠0）的函数值y 随x 的增大而增大，则一次函数y=x+k 的图象大致是< ）3n9HmSCmUm5.下列图案是中心对称而不是轴对称的图案的个数是< ）H W S ZA. 1B. 2C. 3D. 46.为筹备班级的新年联欢会，班长对全班学生爱吃哪几种水果作了民意调查．那么最终买什么水果，下面的调查数据中最值得关注的是< ）3n9HmSCmUmA.中位数B.平均数C.众数D.加权平均数7.若532+y x b a 与x y b a 2425-是同类项．则< ） A.⎩⎨⎧==2,1y x B.⎩⎨⎧-==1,2y x C.⎩⎨⎧==2,0y x D.⎩⎨⎧==1,3y x8.甲、乙两人相距42km ，若相向而行，2h 相遇；若同向而行，乙14h 才能追上甲.则甲、乙两人每小时各走< ）3n9HmSCmUm A. 12km, 9km B. 11km, 10km C. 10km, 11km D. 9km, 12km3n9HmSCmUm 9. 下列说法中错误的是< ）A. 四个角相等的四边形是矩形B.对角线互相垂直的矩形是正方形C.对角线相等的菱形是正方形D.四条边相等的四边形是正方形10.如图中的图象<折线ABCDE ）描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离s<千M ）和行驶时间t<小时）之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千M ；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为380千M/时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有< ）3n9HmSCmUm A. 1个 B. 2个 C. 3个 D. 4个 二、填空题<每题3分，共30分）11. 9的算术平方根是______, 27的立方根是__________.12.如图，数轴上点A 表示的数是 .13. 菱形的两条对角线长为6和8，则菱形的面积是 . 14. 若⎩⎨⎧=-=12y x 是方程2x+3my=1的一个解，则m= .15. B<0，－4）在直线b x y +-=图象上，则b ＝ .16. 一次函数y=-x+2的图象与两条坐标轴所围成的三角形的面积为 .17. 一个多边形的内角和等于1080°，那么这个多边形为 边形.18. 如图，在梯形ABCD 中，AD ∥BC ，过D 作DE ∥AB 交BC 于点E ，若AD=6cm ，ΔDCE 的周长为21cm ，那么梯形的周长为 cm. 3n9HmSCmUm19. 已知A (a,2>与B (-3,2>关于y 轴对称，则a =____ .20.如图，正三角形ABO 以O 为旋转中心，旋转120而得到的图形是 .三、解答题AD21.计算：<每题5分，共10分）<1）23652045⨯-+ <2）()()22126262⎪⎭⎫ ⎝⎛---+22.解下列方程组：<每题5分，共10分）<1）⎩⎨⎧+==+31423y x y x <2）⎩⎨⎧=-+=-+0519203637y x y x23.如图，在离旗杆15M 的E 处，用测角仪测得杆顶的 45=∠BCA ，已知测角仪高CE=1M ，求旗杆的高AD. <共5分）3n9HmSCmUmEC24.某校招聘一名教师，对三名应聘者进行了三项素质测试，下面是绩分别赋予权2、3、4，三人中谁将被录用？(共5分>3n9HmSCmUm 25.如图 ，在△ABC 中，D 、E 分别是AB 、AC 边的中点，F 是DE 延长线上的点，且EF=DE ，请找出图中的平行四边形，并说明理由。

成都市2008-2009学年度八年级上期期末调研考试数学试题注意事项： 1．本试卷分为A 、B 两卷。

A 卷100分，B 卷50分，全卷总分150分。

考试时间120分钟。

2．若使用机读卡，在答题前，考生务必将自己的姓名、考号、考试科目涂写在机读卡的相应位置上，并用钢笔或圆珠笔将试卷密封线内的项目填写清楚；在答A 卷选择题时，当每小题选出答案后，用2B 铅笔将机读卡上对应的答案标号涂黑；其余试题用钢笔或圆珠笔直接写在试卷的相应位置上。

3．若不使用机读卡，答题前，考生务必用钢笔或圆珠笔将试卷密封线内的项目填写清楚；答题时用钢笔或圆珠笔直接将答案写在试卷的相应位置上。

A 卷（共100分） 第Ⅰ卷(选择题，共30分)一、选择题（本题共有10个小题，每小题3分，共30分）在每小题给出的四个选项中，只 有一项是正确的，把正确的序号填在题后的括号内。

1.将右边的图案按顺时针方向旋转90º后可以得到的图案是( )（A ） （B ） （C ） （D ） 2.下列运算正确的是( ) (A)24-= (B)33=- (C)24±= (D)393=3.内角和与外角和相等的多边形是( )(A)三角形 (B) 四边形 (C) 五边形 (D) 六边形 4.在平面直角坐标系中,位于第二象限的点是( ) (A) (－2，－3) (B) (2, －4) (C) ( －2,3) (D) (2,3) 5.下面几组数据能作为直角三角形三边的是( )(A) 2，3，4 (B) 5，3，4 (C)4，6，9 (D)5，12，14 6.已知⎩⎨⎧-==11y x 是方程032=--my x 的一个解,那么m 的值是( )(A) 1 (B) 3 (C) －3 (D) －17.下列图形既量轴对称又是中心对称的图形是( )(A) 正三角形 (B) 平行四边形 (C) 等腰梯形 (D) 正方形 8.在平面直角坐标系中,直线k b kx y (+=<0,b >0)不经过 ( ) (A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限9.如图,将张矩形纸片对折后再对折,然后沿着图中的虚线剪下,得到①、②两部分,将②展开的得到的平面图形是( )(A) 矩形 (B) 平行四边形 (C) 梯形 (D) 菱形10.如图,在平面直角坐标系中,平行四边形ABCD 的顶点A 、B 、D 的坐标分别为（0,0）、（5,0）、（2,3）, 则顶点C 的坐标是( )(A) (3,7) (B) (5,3) (C) (7,3) (D) (8,2) 二、填空题：（每小题4分，共16分） 11.若022=+-y x ，则=+y x .12.若菱形的两条对角线长分别为6cm 、8cm ，则其周长为 cm .13.对于一次函数52-=x y ,如果21x x <,那么1y 2y (填“>” 、“=” “<”). 14.如图是用形状、大小完全相同的等腰梯形密铺成的图案的一部分, 则该图案中等腰梯形的较大内角的度数为 度.三、(第15题每小题6分,第16题6分,共18分) 15.解下列各题:(1)解方程组: ⎩⎨⎧=-=+115332y x y x(2)化简:）（）（12212141180-+---π.16.如果523++-b a b a 为b a 3-的算术平方根,1221---b a a 为21a -的立方根,求b a 32-的平方根.① ②ACE BF DCDBE A四、（每小题8分，共16分）17.如图,在△ABC 中,已知D 是BC 边上的一点,连接AD,取AD 的中点E,过点A 作BC 的平行线与CE 的延长线交于点F,连接DF .(1)求证:AF=DC.(2)若AD=CF,试判断四边形AFDC 是什么样的四边形?并证明你的结论.18.某长途汽车站规定,乘客可以免费携带一定质量的行李,若超过该质量则需购买行李票,且行李费y (元)与行李质量x (千克)间的一次函数关系式为)0(5≠-=k kx y .现知贝贝带了60千克的行李,交了行李费5元.(1)若京京带了84千克的行李,则该交行李费多少元?(2)旅客最多可免费携带多少千克的行李?五、(每小题10分，共20分)19.如图,已知AD 是△ABC 的中线,∠ADC=45º,把△ABC 沿AD 对折,点C 落在点E 的位置,连接BE,若BC=6cm .(1)求BE 的长;(2)当AD=4cm 时,求四边形BDAE 的面积.20.如图,在平面直角坐标系xOy 中,已知直线2321+-=x y 与x 轴、y 轴分别交于点A和点B,直线)0(2≠+=k b kx y 经过点C(1,0)且与线段AB 交于点P ,并把△ABO 分成两部分.(1)求△ABO 的面积.(2)若△ABO 被直线CP 分成的两部分的面积相等,求点P 的坐标及直线CP 的函数表达式.B 卷(50分)一、填空题：（每小题4分，共20分） 21.若某数的平方根为3+a 和152-a ,则a = . 22.如图,在平面直角坐标系中, △ABC 的顶点坐标分别 为A(3,6)、B(1,3)、C(4,2).如果将△ABC 绕点C 顺时针 旋转90º,得到C B A '''∆,那么点A 的对应点A '的坐标 为 . 23.当53+=x 时,代数式1062+-x x 的值为 .24.在四边形ABCD 中,对角线AC 、BD 交于点O ，从①AB=CD ；②AB ∥CD ；③OA=OC ；④OB=OD ；⑤AC=BD ；⑥∠ABC=90º这六个条件中，可选取三个推出四边形ABCD 是矩形，如①②⑤→四边形ABCD 是矩形.请再写出符合要求的两个: ; .25.若直线p x y +=3与直线q x y +-=2的图象交x 轴于同一点,则p 、q 之间的关系式为 . 二、（共8分）26.某校八年级一班20名女生某次体育测试的成绩统计表如下:(1)备用图（2）在(1)的条件下,设20名学生本次测试成绩的众数是a ,中位数为b ,求5ba -的值.三、（共10分）27.如图①,在Rt △ABC 中,已知∠A=90º,AB=AC,G 、F 分别是AB 、AC 上两点，且GF ∥BC ，AF=2，BG=4.(1)求梯形BCFG 的面积.(2)有一梯形DEFG 与梯形BCFG 重合,固定△ABC,将梯形DEFG 向右运动,直到点D 与点C 重合为止,如图②.①若某时段运动后形成的四边形G G BD '中,DG ⊥G B ',求运动路程BD 的长,并求此时2B G '的值.②设运动中BD 的长度为x ,试用含x 的代数式表示出梯形DEFG 与Rt △ABC 重合部分的面积.AG FB(D)C(E)图①A GFB DC EG 'F ' 图②四、（共12分）28.如图,在平面直角坐标系xOy 中,已知直线PA 是一次函数y=x+m (m>0)的图象,直线PB 是一次函数n n x y (3+-=>m )的图象,点P 是两直线的交点,点A 、B 、C 、Q 分别是两条直线与坐标轴的交点。

ADB EC F2008—2009第一学期期末考试八年级数学试题（卷）题 号 一 二 三 总 分 得 分说明：本试题（卷）共6页，满分120分，考试时间90分钟一、填空题（每小题2分，共20分） 1．计算：25的平方根是 。

2．计算：=÷⋅6323)(x x x 。

3．计算：=÷+-x x x x 3)3129(23 。

4．若三角形三边分别为1+x ，2+x ，3+x ，当x ＝ 是，此三角形是直角三角形。

5．正方形是轴对称图形，它共有 条对称轴。

6．要使一个矩形成为正方形，则需增加的条件是 （填上一个条件即可） 7．已知： ABCD 中，ABC ∠的平分线交AD 于E ，且AE ＝2， DE ＝1 的周长 。

8．如图，△ABC 是等腰直角三角形，AD ⊥BD 于D ，△ABD可以看做由△ACD 绕D 点逆时针旋转得到的，旋转的角度是 。

9．如图所示，△DEF 是由△ABC 经过平移得到的，︒=∠30A ，︒=∠45B ，则=∠F 。

10．梯形ABCD 中，AD ∥BC ，AD ＝3，AB ＝4，BC ＝5，则腰 CD 的取值范围是 。

A B C D 二、选择题（每小题只有一个选项符合题意，请将你认为正确的选项字母填入下表相题 号 1 2 3 4 5 6 7 8 9 10 选 项1．下列各题计算正确的是 A 、632632x x x =⋅ B 、923)(a a = C 、9336)2(a a -=-D 、n n b 226)(=-2．下列各式中，运算结果等于42-x 的是A 、)2)(2(-+x xB 、)2)(2(----x xC 、)2)(2(x x -+D 、)2)(2(+--x x3．如图，将图中的正方形图案绕中心旋转180°后，得到的图案是4．下列图形中，不是中心对称图形的是A 、矩形B 、等腰三角形C 、平行四边形D 、线段 5．等腰三角形的腰长为10，底边长为12，则这个等腰三角形的面积为 A 、60B 、50C 、48D 、306．下列说法中不正确的是 A 、全等三角形的周长相等 B 、全等三角形的面积相等 C 、全等三角形能重合D 、全等三角形一定是等边三角形 7．用两块对称的含︒30角的三角形拼成形状不同的平行四边形，最多可以拼成A 、1个B 、2个C 、3个D 、4个8．下列性质中，菱形具有的是A 、四个角都是直角B 、对角线相等且互相平分C 、对角线垂直且互相平分D 、对角线垂直且相等 9．正方形具有面菱形不具有的性质是 A 、四条边相等B 、对角线互相平分C 、对角线平分一组对角D 、对角线相等 10．矩形、菱形、正方形都具有的性质是 A 、对角线相等B 、对角线平分一组对角C 、对角线互相平分D 、对角线互相垂直三、解答题（共70分）1．（12分）分解因式（或利用分解因式计算） （1）22363ay axy ax +-（2）114351156522⨯-⨯2．（8分）如图所示，AC 是矩形ABCD 的对角线，DAC BAC ∠=∠2，求BAC ∠和DAC ∠的度数。