20120402 清明假期文科数学作业
- 格式:doc
- 大小:508.50 KB
- 文档页数:9


人教版七下清明节数学作业班级____________姓名____________成绩___________1、选择题:(本大题共10个小题,每小题4分,共40分)1.式子有意义,则满足的条件是()A.B.C.D.为一切实数2.已知是方程kx+2y=﹣5的解,则k的值为()A.3 B.4 C.5 D.﹣53. 已知,OA⊥OC,且∠AOB:∠AO C=2:3,则∠BOC的度数为()A.30° B.150° C.30°或150° D.90°4.如图,小强告诉小华图中A、B两点的坐标分别为(﹣3,3)、(3,3),小华一下就说出了C在同一坐标系下的坐标()A.(﹣1,5) B.(﹣5,1) C.(5,﹣1) D.(1,﹣5)5.下列各式中正确的是()A.=±4 B.C.= -3 D.6. 如图,直线a、b被直线c所截,a∥b,∠1=∠2,若∠4=63°,则∠3等于()A.63° B.60° C.54° D.45°第6题图第4题图7.在2,﹣,π,0,,2.1010,3.14,﹣,0.1212212221…(相邻两个1之间2的个数逐次加1)这些数中,是无理数的个数是()A.1 B.2 C.3 D.48.已知a、b满足方程组,则3a+b的值为()A.8 B.4 C.﹣4 D.﹣89.下列说法:(1)是无理数;(2)的整数部分是5;(3)如果一个数的立方根是这个数本身,那么这个数是—1或0;(4)若,则x=4;(5)若则a+b=0;那么正确的个数有()A.1个 B.2个 C.3个 D.4个10.已知点P(2a,1﹣3a)在第二象限,且点P到x轴的距离与到y轴的距离之和为6,则a的值为()A.﹣1 B.1 C.5 D.311. 哥哥与弟弟的年龄和是18岁,弟弟对哥哥说:“当我的年龄是你现在年龄的时候,你就是18岁”.如果现在弟弟的年龄是x岁,哥哥的年龄是y岁,下列方程组正确的是()A.B.C.D.12.如图,△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的,若△ABC的面积为20 cm2,则四边形A1DCC1的面积为()A.10 cm2 B.12 cm2 C.15cm2 D.17 cm2第12题图第14题图2、填空题:(本大题共8个小题,每小题4分,共32分)13.把“同位角相等”改为“如果,那么”的形式是 .14.如图,AC⊥BC,且BC=5,AC=12,AB=13,则点A到BC的距离是______,点B到点A的距离是_________.15.计算:=____________.16.二元一次方程的正整数解有__________个.17将平面直角坐标系平移,使原点O移至点A(3,﹣2),这时在新坐标系中原来点O的坐标是___________.18.小明解方程组的解为,由于不小心,滴上了两滴墨水,刚好遮住了两数■和★,请你帮她找回这两个数,■=,★=.19.如果的平方根等于±3,那么a= .20. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0)→(2,0)→(2,1)→(3,2)→(3,1)→(3,0)…,如果(1,0)是第一个点,那么第50个点的坐标是____________.第20题图三、解答题:(第21题12分,第22题8分,共20分),解答题应写出计算过程或推理步骤.21.解方程组:(1)(用代入法)(2)(用加减法)(3)22. 若,求的平方根和立方根.四、解答题(23题8分,24、25、26每题10分,27题12分,共50分)解答题应写出计算过程或推理步骤.23. 如图,已知:EB∥DC,∠A=∠ADE,你认为∠C和∠E相等吗?说明理由.24.如图所示,在平面直角坐标系中,△ABC的三个顶点分别为A(4,4)、B、C.(1)请在该平面直角坐标系中画出△ABC向右平移6个单位,向下平移4个单位后的△DEF,并直接写出D、E、F的坐标.(2) 求△DEF的面积.25.先阅读材料,然后解方程组:材料:解方程组:解:由①得x+1=6y③把③代入②得×6y﹣y=11,得y=1把y=1代入③,得x+1=6,∴x=5∴方程组的解为.上述方法为“整体代入法”,请用上述方法解下列方程组:.26.已知:A(0,1),B(2,0),C(4,3)(1)求△ABC的面积;(2)设点P在坐标轴上,且△ABP是△ABC的面积的2倍,求点P的坐标.27. 已知:BC∥OA,∠B=∠A=100°,试回答下列问题:(1)在图①中,试说明:OB∥AC;(4分)(2)如图②,若点E、F在BC上,且∠FOC=∠AOC,OE平分∠BOF.则∠EOC 的度数是_______;(2分)(3)在(2)的条件下,若左右平行移动AC,如图③,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;(4分)(4)在(3)的条件下,当∠OEB=∠OCA时,则∠OCA的度数是________.(2分)。

初三数学假期作业1.把方程(x +3)(x -2)=4化为一般形式为 ,其中二次项系数为 ,常数项是 .2.若关于x 的方程x 2-3x +m =0有一根为0,则m = .3.[]222(_____)(_____)3y y y -+=+. x 2+x ab + =( )2 4.若(x+5)2=4,则x= , (x-a) 2=b(b ≥0)的解为 把方程x 2-6x+5=0化成(x+m) 2=k 的形式,则m= ,k=5.若代数式x 2-7x +13的值为31,则x = .6x = .7.关于x 的代数式x 2+(m +2)x +(4m -7)中,当m = 时,代数式为完全平方式. 8.下列命题正确的是( )A .方程ax 2+bx +c =0是一元二次方程B .方程x 2-5x =0的常数项为0C .方程2279x x -=+是一元二次方程D .方程2141x x+=是整式方程9.下列方程中,是关于x 的一元二次方程的是( )A .2110x x -+= B21x = C .x 2-x =x (x +2) D .ax 2+x -1=0(a ≠0) 10.用配方法解方程22103x x -+=,正确的解法是( )A .21839x ⎛⎫-= ⎪⎝⎭,133x =±B .21839x ⎛⎫-=- ⎪⎝⎭,无实根C .22539x ⎛⎫-= ⎪⎝⎭,x =D .22539x ⎛⎫-=- ⎪⎝⎭,无实根11.要使分式2544x x x -+-的值为0,x 应等于( )A .1B .4或1C .4D .-4或-112.关于x 的方程(a 2-a -2)x 2+ax +b =0是一元二次方程的条件是( ) A .a ≠-2且a =1 B .a ≠2 C .a ≠2且a ≠-1 D .a =-113.在一幅长80cm ,宽50cm 的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如题1,如果要使整幅挂图的面积是5 400cm 2,设金色纸边的宽为x cm ,那么x 满足的方程是( )A .x 2+130x -1 400=0B .x 2+65x -350=0C .x 2-130x -1 400=0D .x 2-65x -350=0 14.已知关于x 的一元二次方程(m -1)x 2+x +m 2+2m -3=0的一个根为0,则m 的值为( )A.1B.-3C.1和-3D.不等于1的任何数15.已知2y 2+y -2的值为3,则4y 2+2y +1值为( )A .10 B.11 C.10或11 D.3或1 16.用适当的方法解方程:(1)(5x +3)2-4=0; (2)2x 2-4x +1=0; (3))4(5)4(2+=+x x(4)x x 4)1(2=+ (5)31022=-x x (6)2(3x -2)=(2-3x )(x +1)17.用配方法证明:(1)4x 2-12x+10的值恒大于0 (2)-2y 2+2y-1的值恒大于018.已知a ,b0b =,解关于x 的方程:(a +2)x 2+b 2=a -1.19.已知等腰三角形的底边长为8,腰长是方程x 2-9x +20=0的一个根,求这个三角形的面积.。

清明节数学作业:(策略:先复习课本再做市资料)
复习课本《等腰三角形》部分在课本九(上)第一章,需理解和记忆的东西较琐碎,请大家先把课本2页---39页中涉及的:等腰三角形(含等边三角形)的性质、判定;角的平分线和线段的垂直平分线的性质、判定、作图。
(课本P8反证法及小明举例,P13例2,P15第5T,P18几个概念,P34做一做,P38例题。
推荐)
《平行四边形》部分在课本九(上)第三章,大家复习课本后,以吃透教材证明(三)再次回顾。
(课本P86做一做,P89--90定理证明;P91例1;P98例2。
推荐)做市资料:
84页-----89页考点----等腰三角形;
97页----101页考点----平行四边形;
60页---78页考点------统计、概率。
2012年4月1日。

清明节数学作业一、填空:1.(1)207读作()(2)八百零三写作:________________(3)375是由()个百()个十和()个一组成的.(4)九百六十一写作:_______________(5)从996往后接着数5个数是()、()、()、()、().(6)最大的三位数是(),最小的四位数比最大的三位数多().2.在()里填上合适的数.5431=5000+400+30+1286=()+()+()7560=()+()+()2048=()+()+()8009=()+()3070=()+()3.80里面有()个十.190里面有()个十.4.填空.(1)10个一百是(),10个一千是().十万里面有()个一万,一千里面有()个十.(2)从右边起百位是第()位,右边起的第五位是()位,千位是第()位.(3)8008这个数从右边起第一位上的8表示8个(),第四位上的8表示8个().(4)892是()位数,最高位是()位,10000是()位数,最高位是()位.5.读写出下面各数.4050()6009()二千零六写作()五千八百七十二写作()5个百和8个十是()1个千、2个百、3个十和4个一是()六个一、八个千是()一个万是()6.用2、7、0 三张数字卡片,可以排出()个不同的三位数,把它们写出来是______和______.其中最大的数是_______,最小的数是______.7 、用5、0、3、9组成一个最大的四位数是(),最小的四位数是().8 、按顺序,找规律填数.102、____、100、____、____97、____.190、____、____、160、____、____、____、120、____、____5000、____、6000、____、7000、____、____、____、____、95009、一个数从右起第三位是()位,第五位是()位。
10、4603是()位数,最高位是()位,其中4在()位,表示()个()。
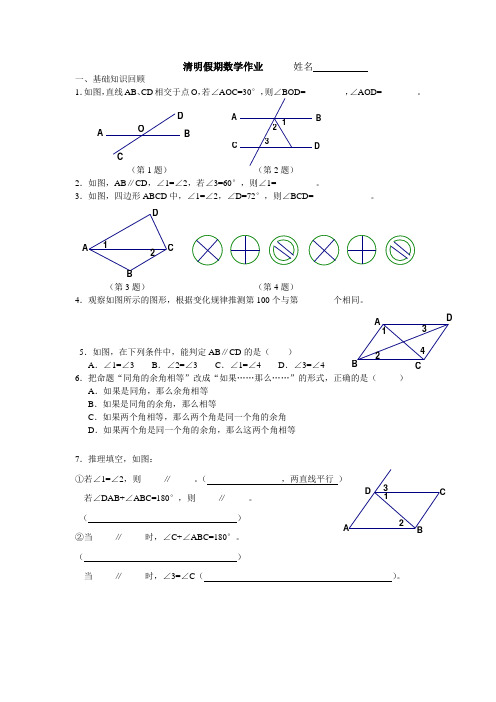
O D C BA 321DC B A 21D C BA4321D CB A 321DBA清明假期数学作业 姓名一、基础知识回顾 1.如图,直线AB 、CD 相交于点O ,若∠AOC=30°,则∠BOD=_________,∠AOD=________。
(第1题) (第2题)2.如图,AB ∥CD ,∠1=∠2,若∠3=60°,则∠1=_________。
3.如图,四边形ABCD 中,∠1=∠2,∠D=72°,则∠BCD=_____________。
(第3题) (第4题)4.观察如图所示的图形,根据变化规律推测第100个与第________个相同。
5.如图,在下列条件中,能判定AB ∥CD 的是( ) A .∠1=∠3 B .∠2=∠3 C .∠1=∠4 D .∠3=∠4 6.把命题“同角的余角相等”改成“如果……那么……”的形式,正确的是( )A .如果是同角,那么余角相等B .如果是同角的余角,那么相等C .如果两个角相等,那么两个角是同一个角的余角D .如果两个角是同一个角的余角,那么这两个角相等7.推理填空,如图:①若∠1=∠2,则_____∥_____。
( ,两直线平行 ) 若∠DAB+∠ABC=180°,则_____∥_____。
( )②当_____∥_____时,∠C+∠ABC=180°。
( )当_____∥_____时,∠3=∠C ( )。
D CEBAF4321ED CB A8.如图,AC 平分∠DAE ,∠DAE=120°,∠B=60°,说明:AC ∥BE.9.如图,B 在线段AC 上,E 在线段DF 上,且∠1=∠2,∠C=∠D 。
说明: AB ∥DF 。
10.41的平方根是 ( ) A 、161 B 、81 C 、21 D 、21±11.下列等式正确的是( )A .43169±= B .11-=- C .393-=- D .31312=⎪⎭⎫⎝⎛- 12.下列各式中无意义的是 ( ) A 、7- B 、7 C 、7- D 、()27--13 ).A .±4B .4C .±2D .214.求下列各式中的x(1)4x 2 = 16 (2)()912=-x (3) ()823=-x。
2012届大连一中高三年级文科假期作业(一)数学试卷一、选择题 (共12 小题,每小题 5分) 1. 已知:a>b>c,且a+b+c=0,则( )A .ab>bcB .ac>bcC .ab>acD .a │b │>c │b │2. 下表是x 与y 之间的一组数据,则y 关于x 的回归直线必过( )A .点(2,2)B .点(1.5,2) C.点(1,2) D.点(1.5,4) 3. 数列﹛a n ﹜的前n 项和 S n =n 2a n (n ≥2) .而a 1=1,通过计算a 2,a 3,a 4,猜想a n =( ) A .2(n+1)2 B .2n(n+1)C .22n -1D .22n-14. 平面内原有k 条直线,它们的交点个数记ƒ(k),则增加一条直线ι后,它们的交点个数最多为 ( )A .ƒ(k)+1B .ƒ(k)+kC .ƒ(k)+k+1D .k ·ƒ(k)5. ()()()等于则可导在设xx x f x x f ,x x f x 3lim0000--+→ ( )A 、()02x f 'B 、()0x f 'C 、()03x f 'D 、()04x f '6. 复数32322323i ii i+--=-+ ( ) A 、0 B 、2 C 、-2i D 、2i7. “y x ≠”是“y x sin sin ≠”的( )条件A 、充分不必要B 、必要不充分C 、充要D 、既不充分又不必要8. 命题:“若0),,(,022==∈=+b a R b a b a 则”的逆否命题是 ( )A 、若0),,(022≠+∈≠≠b a R b a b a 则 B 、若0),,(022≠+∈≠=b a R b a b a 则 C 、若0),,(0022≠+∈≠≠b a R b a b a 则且 D 、若0),,(0022≠+∈≠≠b a R b a b a 则或9. 曲线54223++-=x x x y 在1=x 处的切线方程是 ( )A 、053=++y xB 、053=-+y xC 、053=--y xD 、053=+-y x10. 设)(x f '是函数)(x f 的导函数,)(x f y '=的图象如图所示,则)(x f y =的图象最有可能的是 ( )11. 已知函数2sin y x x =,则y '= ( )A 、2sin x xB 、 2cos x xC 、22sin cos x x x x +D 、22cos sin x x x x +12. 设函数)()0(1)6sin()(x f x x f '>-+=的导数ωπω的最大值为3,则f (x )的图象的一条对称轴的方程是 ( )、6π=x C 、3π=xD 、2π=x二、填空题 (共5 小题,每小题 20 分)13. 已知m>0,n>0,向量()()111a m b n ==-,,,,且a //b,则12m n+的最小值是 .14. 以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间]4,0[对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间]4,0[上(除两个端点外)的点,在第二次操作完成后,恰好被拉到与4重合的点所对应的坐标是 ;原闭区间]4,0[上(除两个端点外)的点,在第n 次操作完成后(1≥n ),恰好被拉到与4重合的点所对应的坐标为 .15. 已知抛物线px y 22=)0(>p ,过点)0,2(p M 的直线与抛物线相交于A ,B ,=⋅OB OA16. 已知非零向量,a b ,||2||a b =,若关于x 的方程20x a x a b ++⋅=有实根,则a 与b的夹角的最小值为三、解答题17. 已知抛物线y x 42=的焦点为B A F ,,是抛物线上的两动点,且).0(>=λλ过A 、B 两点分别作抛物线的切线,设其交点为M.(Ⅰ)证明AB FM ⋅为定值;(Ⅱ)设△ABM 的面积为S ,写出)(λf S =的表达式,并求S 的最小值.18. 已知数列{a n }满足a 1=1,a 1+n =2a n +1(n ∈N *)(Ⅰ)求数列{a n }的通项公式;(Ⅱ)若数列{b n }满足4k1-14k2-1…4k-1=(a n +1)km (n ∈N *),证明:{b n }是等差数列; (Ⅲ)证明:231213221na a a a a a n n n <<++⋯++-(n ∈N *).19. 已知椭圆12222=+b y a x (0>>b a )的两个焦点分别为)0)(0,(),0,(21>-c c F c F ,过点)0,(2ca E 的直线与椭圆相交于点A,B 两点,且||2||,//2121B F A F B F A F = (Ⅰ求椭圆的离心率 (Ⅱ)直线AB 的斜率;(Ⅲ)设点C 与点A 关于坐标原点对称,直线B F 2上有一点H(m,n)(0≠m )在C AF 1∆的外接圆上,求mn的值。
清明节假期作业高二下数学(文)一、选择题:本大题共12个小题,每小题5分,共60分. 1.已知R 是实数集,集合 ,,则( )A .B .C .D .2.已知是虚数单位,若(为虚数单位)所对应的点位于复平面内的( ) A .第一象限B .第二象限C .第三象限D .第四象限3.已知命题:;命题:函数有一个零点,则下列命题为真命题的是( )A .B .C .D .4.有一段演绎推理是这样的“有些有理数是真分数,整数是有理数,则整数是真分数”结论显然是错误的,是因为( )A .大前提错误B .小前提错误C .推理形式错误D .非以上错误5.已知双曲线的左、右焦点分别为,,右焦点与抛物线的焦点相同,离心率为,若双曲线左支上有一点到右焦点距离为,为的中点,为坐标原点,则等于( )A .B .C .D .6.运行如下程序框图,分别输入,则输出的和为( )A .B .C .D . 7.用反证法证明某命题时,对结论:“自然数a ,b ,c 中恰有一个偶数”正确的反设为( ) A .a ,b ,c 中至少有两个偶数 B .a ,b ,c 中至少有两个偶数或都是奇数 C .a ,b ,c 都是奇数 D .a ,b ,c 都是偶数{}21216x A x +=≥{|(1)(3)0}B x x x =--<A B =R()()1,2[]1,2()1,33(1,)2i 32i 2ii i 12iz ++=+-i p 000,sin cos 3x x x ∃∈+=R q ()121()2x f x x =-p q ∧p q ∨q ⌝()p q ∧⌝22221x y a b-=1F 2F 2F 2y =5e =M 2F 18N 2MF O NO 2312417245,3t t ==-s 2017-20172016-20168.观察(x 2)′=2x ,(x 4)′=4x 3,(cos x )′=-sin x ,由归纳推理可得:若定义在R 上的函数f (x )满足f (-x )=f (x ),记g (x )为f (x )的导函数,则g (-x )等于( ) A .f (x )B .-f (x )C .g (x )D .-g (x )9.在等比数列中,,若满足,则的最小值是( ) A .B .2C .D . 10.在中,内角的对边分别为,,若且,则的面积为( ) A . B .C .D . 11.如图所示,F 1,F 2是双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左,右焦点,过F 2的直线与双曲线C 交于A ,B 两点.若△ABF 1为等边三角形,则双曲线的离心率为( ) A.13 B.7 C. 5 D.212.已知f (x )=|x 2-1|+x 2+kx ,若关于x 的方程f (x )=0在(0,2)上有两个不相等的实根,则k 的取值范围是( )A .(-1,0)B .(-72,+∞)C .(-∞,-72)△(-1,+∞)D .(-72,-1)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知x ,y 的取值如表所示:若y 与x 呈线性相关,且线性回归方程为y ^=b ^x +72,则b ^=________.x 2 3 4 y54614.在△ABC 中,A =2π3,a =3c ,则bc=________.15.变量满足约束条件,则目标函数的最小值为,若时,恒成立,则实数的取值范围是____________.16.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的一条渐近线为2x +y =0,一个焦点为(5,0),则a =__;b =__.{}n a 5461,422a a a =+=,m n a a 14m n a a a =14m n+3273256ABC △C B A ,,c b a ,,3C π=()()6,,,6c a b a b c =--=-+m n ∥m n ABC △393223333 x y ,20201x y x y y +-≥⎧⎪--≤⎨⎪≥⎩3z x y =+m 11a -≤≤2()20x a m x m a +-+->x三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知b +c =2a cos B . (1)证明:A =2B ;(2)若△ABC 的面积S =a 24,求角A 的大小.18.在各项均为正数的等比数列{a n }中,a 1=2,且a 3,3a 2,a 4成等差数列. (1)求等比数列{a n }的通项公式;(2)若数列{b n }满足b n =(n +2)log 2a n ,求数列{1b n }的前n 项和T n .19.(本小题满分12分)随着手机使用的不断普及,现在全国各地的中小学生携带手机进入校园已经成为了普遍的现象,也引起了一系列的问题。
介父从州今凶分市天水学校鲍沟二零二零—二零二壹七年级数学下学期清明节假期作业试题第1-2章练习题一、选择题1.以下运算正确的选项是〔〕A.B.C.D.2.要使多项式〔x2+px+2〕〔x﹣q〕不含关于x的二次项,那么p与q的关系是〔〕A.相等B.互为相反数C.互为倒数D.乘积为﹣13.以下等式中,正确的有〔〕.①;②;③;④.A.个B.个C.个D.个4.,,那么〔〕.A.B.C.D.5.计算的结果是〔〕A.B.C.D.以上都不对6.+所得的结果是〔〕A.B.C.D.7.假设x2+mxy+4y2是完全平方式,那么常数m的值为〔〕A.4 B.﹣4C.±4D.以上结果都不对8.如下列图,,,,那么的度数是〔〕.A.B.C.D.9.如下列图,在灌溉农田时,要把河(直线l表示一条河)中的水引到农田P处,设计了四条路线PA,PB,PC,PD(其中PB⊥l),你选择哪条路线挖渠才能使渠道最短()A.PA B.PB C.PC D.PD10.如图,用两个相同的三角板按照如下列图的方式作平行线,能解释其中道理的是( )A.同位角相等,两直线平行B.内错角相等,两直线平行C.同旁内角互补,两直线平行D.以上都不对11.如图,BE平分∠ABC,DE∥BC,图中相等的角共有〔〕A.3对B.4对C.5对D.6对12.如图,AB∥CD,假设EM平分∠BEF,FM平分∠EFD,EN平分∠AEF,那么与∠BEM互余的角有( ).A.6个B.5个C.4个D.3个二、填空题13.3x=4,那么3x+2=_____.14.假设x m=16,x n=2,x≠0,那么x m+n=_____.15.下面的计算是否正确?假设有错误,应该怎样改正?〔1〕a5•a5=2a5_____;〔2〕x3+x3=x6_____;〔3〕m2•m3=m6_____;〔4〕c•c3=c3_____;〔5〕〔﹣y〕2•y4=﹣y6_____;〔6〕〔﹣a〕3•a2=﹣a5_____.16.:那么=___________.17.如图,把一块含有的直角三角形的两个顶点放在直尺的对边上. 如果,那么的度数是________.18.将如图1的长方形ABCD纸片沿EF折叠得到图2,折叠后DE与BF相交于点P. 如果∠EPF=70°,那么∠PEF的度数为_________ .19.如图,,垂足为,过作.假设,那么__________.20.如下列图,,分别交、于、两点,是的延长线.假设,,那么__________.三、解答题21.计算:〔1〕〔2a〕3•b4÷12a3b2〔2〕〔x+3y〕2+〔2x+y〕〔x﹣y〕22.先化简,再求值:(1) (x+1)(x-1)+x2(1-x)+x3,其中x=2;(2) a(a-3b)+(a+b)2-a(a-b),其中a=1,b=-.23.,求代数式的值.24.如图,点为上的点,为上的点,,,求证:.证明:∵〔〕,,〔〕,∴〔等量代换〕.∴____________________〔〕.∴〔〕.∵〔〕,∴__________〔〕.∴〔〕.25.:如图,,,.求证:.26.如图,∠1+∠2=180°,∠B=∠E,试猜想AB与CE之间有怎样的位置关系?并说明理由。
智才艺州攀枝花市创界学校七年级数学清明作业一、选择题:1、假设一个角的补角是150°,那么这个角的度数是〔〕A.30°B.60°C.90°D.120°2、如图,直线a、b被直线c所截,a∥b,∠1=130°,那么∠2=〔〕A.130°B.50°C.40°D.60°3、以下说法错误的选项是()A.内错角相等,两直线平行.B.两直线平行,同旁内角互补.C.相等的角是对顶角.D.等角的补角相等.4、以下列图中∠1和∠2是同位角的是〔〕A.⑴、⑵、⑶,B.⑵、⑶、⑷,C.⑶、⑷、⑸,D.⑴、⑵、⑸5、:如图,∠1=∠2,那么有()∥CD∥DFC.AB∥CD且AE∥DFD.以上都不对6、如图,直线AB与CD交于点O,OE⊥AB于O,图∠1与∠2的关系是()A.对顶角B.互余C.互补D相等7、如图,DH∥EG∥BC,且DC∥EF,那么图中和∠1相等的角的个数是〔〕A.2,B.4,C.5,D.68、如图,AB//CD,BC//DE,那么∠B+∠D的值是〔〕A.90°B.150°C.180°D.以上都不对B DE 13A CF2 9、如图,直线AB 与CD 相交于点O ,OB 平分∠DOE.假设∠DOE =60º, 那么∠AOE 的度数是〔〕A.90°B.150°C.180°D.不能确定 二、填空10、用尺规作图时,用画直线、射线和直线,用画弧或者圆。
11、黎教师家在小星家的北偏东68度,那么小星家在黎教师家的南偏西度。
12、如图①,假设∠=∠,可得AD ∥BC ,你的根据是。
13、如图②,∠1=82º,∠2=98º,∠3=80º,那么∠4=度。
14、如图③,直线AB ,CD ,EF 相交于点O ,AB ⊥CD ,OG 平分∠AOE ,∠FOD=28º,那么∠BOE=度,∠AOG=度。
20120402 假期文科数学作业参考公式:独立性检测中,随机变量()()()()22()n ad bc k a b c d a c b d -=++++分类变量X 与Y 有关系的可信度表:()2P K k ≥ … 0.050.025 0.010 0.005 0.001 k…3.8415.0246.6357.87910.8281.在复平面内,复数1i iz =-(i 是虚数单位)对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限2.甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和方差如下表所示:从这四个人中选择一人参加奥运会射击项目比赛,最佳人选是 A .甲 B . 乙 C . 丙 D .丁3.一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60, 得到一组新数据,则所得新数据的平均数和方差分别是 ( )A .57.2, 3.6B .57.2, 56.4C .62.8, 63.6D .62.8, 3.6 4.已知条件 :12p x +>,条件 2:56q x x ->,则 p ⌝是 q ⌝的:A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 5.下列四种说法中,错误..的个数是( ) ①.命题“2,320x R x x ∀∈--≥均有”的否定是:“2,320x R x x ∃∈--≤使得” ②.“命题q p ∨为真”是“命题q p ∧为真”的必要不充分条件; ③.“若b a bm am <<则,22”的逆命题为真; ④.{}0,1A =的子集有3个 A .0个 B .1个 C .2 个 D .3个 6.定义3x y x y ⊗=-, 则()h h h ⊗⊗等于A .h -B .0C .hD .3h 7.若两个分类变量x 和y 的列联表为:则认为“x 与y 之间有关系”犯错误的概率不高于( )A BC D 1C 1B 1A 1 A .0.1%B .99.9%C .97.5%D .0.25% 8.已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率等于 .9.当(1,2)x ∈时,不等式240x mx ++<恒成立,则m 的取值范围是 。
10.如图,PAB 、PCD 是圆的两条割线,已知PA =6,AB =2,PC =21CD .则PD =________.11.如图,点,,A B C 是圆O 上的点, 且04,45AB AC B =∠=,则圆O 的面积等于 .12.已知整数对的序列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4), ,则第80个数对是 。
13.记关于x 的不等式01<+-x a x 的解集为P ,不等式|x -1|≤1的解集为Q .(1)若a = 3,求P ; (2)若Q ⊆P ,求正数a 的取值范围.14.(本小题满分12分)如图所示,直棱柱1111ABC D A B C D -中,底面A B C D 是直角梯形,90B A D A D C ∠=∠=︒,222AB AD C D ===.(1)求证:A C ⊥平面11BB C C ; (2)在A 1B 1上是否存一点P ,使得D P 与平面1A C B 平行?证明你的结论.A15.(本小题满分14分)已知椭圆(222:13x yE a a+=>的离心率12e =. 直线x t =(0t >)与曲线E 交于不同的两点,M N ,以线段M N 为直径作圆C ,圆心为C . (1)求椭圆E 的方程;(2)若圆C 与y 轴相交于不同的两点,A B ,求A B C ∆的面积的最大值.16. (本小题满分14分)设函数f(x)=tx2+2t2x+t-1(x∈R,t>0).(1)求f(x)的最小值h(t);(2)若h(t) < -2t + m对t∈(0,2)恒成立,求实数m的取值范围.20120402 假期文科数学作业参考公式:独立性检测中,随机变量()()()()22()n ad bc k a b c d a c b d -=++++分类变量X 与Y 有关系的可信度表:()2P K k ≥ … 0.050.025 0.010 0.005 0.001 k…3.8415.0246.6357.87910.8281.在复平面内,复数1i iz =-(i 是虚数单位)对应的点位于( )CA .第一象限B .第二象限C .第三象限D .第四象限2.甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和方差如下表所示:从这四个人中选择一人参加奥运会射击项目比赛,最佳人选是 A .甲 B . 乙 C . 丙 D .丁3.一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60, 得到一组新数据,则所得新数据的平均数和方差分别是 ( )DA .57.2, 3.6B .57.2, 56.4C .62.8, 63.6D .62.8, 3.6 4.已知条件 :12p x +>,条件 2:56q x x ->,则 p ⌝是 q ⌝的:AA .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 5.下列四种说法中,错误..的个数是( )D ①.命题“2,320x R x x ∀∈--≥均有”的否定是:“2,320x R x x ∃∈--≤使得” ②.“命题q p ∨为真”是“命题q p ∧为真”的必要不充分条件; ③.“若b a bm am <<则,22”的逆命题为真; ④.{}0,1A =的子集有3个 A .0个 B .1个 C .2 个 D .3个 6.定义3x y x y ⊗=-, 则()h h h ⊗⊗等于A .h -B .0C .hD .3h 7.若两个分类变量x 和y 的列联表为:则认为“x 与y 之间有关系”犯错误的概率不高于( )CA BC DD 1C 1B 1A 1 A .0.1%B .99.9%C .97.5%D .0.25% 8.已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率等于 .239.当(1,2)x ∈时,不等式240x mx ++<恒成立,则m 的取值范围是 。
(]5,--∞10.如图,PAB 、PCD 是圆的两条割线,已知PA =6,AB =2,PC =21CD .则PD =________.1211.如图,点,,A B C 是圆O 上的点, 且04,45AB AC B =∠=,则圆O 的面积等于 .π812.已知整数对的序列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4), ,则第80个数对是 。
13.记关于x 的不等式01<+-x a x 的解集为P ,不等式|x -1|≤1的解集为Q .(1)若a=3,求P ; (2)若Q ⊆P ,求正数a 的取值范围. 解:(1)由301x x -<+,得{}13P x x =-<<.-----------5分(2){}{}1102Q x x x x =-=≤≤≤.由0a >,得{}1P x x a =-<<,又Q P ⊆,所以2a >, 即a 的取值范围是(2)+∞,.-----------12分14.(本小题满分12分)如图所示,直棱柱1111ABC D A B C D -中,底面A B C D 是直角梯形,90B A D A D C ∠=∠=︒,222AB AD C D ===.(1)求证:A C ⊥平面11BB C C ; (2)在A 1B 1上是否存一点P ,使得D P 与平面1A C B 平行?证明你的结论.A BDD 1C 1B 1A 1(1)证明:直棱柱1111A B C D A B C D -中,1B B ⊥平面A B C D ,1BB AC ∴⊥ …2分又 90B A D A D C ∠=∠=︒,222AB AD C D ===∴45,AC C AB BC BC AC =∠=︒∴=∴⊥ ………………5分又1BB BC B = ∴ A C ⊥平面11BB C C . ……………6分(2)存在点P ,P 为11A B 的中点可满足要求. ………………7分 证明:由P 为11A B 的中点,有1//PB AB ,且112P B A B =………………8分又∵11//,,//2C D A B C D A B C D P B =∴,且1C D PB =,∴1C D PB 为平行四边形, 1//D P C B ∴ ………………10分又1C B ⊂面1A C B ,D P ⊄面1A C B ,∴//D P 面1A C B ………………12分 15.(本小题满分14分)已知椭圆(222:13x yE a a+=>的离心率12e =. 直线x t =(0t >)与曲线E 交于不同的两点,M N ,以线段M N 为直径作圆C ,圆心为C . (1)求椭圆E 的方程;(2)若圆C 与y 轴相交于不同的两点,A B ,求A B C ∆的面积的最大值.(1)解:∵椭圆(222:13x yE a a+=>的离心率12e =,∴12a=. …… 2分解得2a =.∴ 椭圆E 的方程为22143xy+=. …… 4分(2)解法1:依题意,圆心为(,0)(02)C t t <<.由22,1,43x t x y=⎧⎪⎨+=⎪⎩ 得221234t y -=. ∴ 圆C的半径为2r =. …… 6分∵圆C与y轴相交于不同的两点,A B,且圆心C到y轴的距离d t=,∴2t<<,即07t<<.∴弦长||A B===……8分∴A B C∆的面积12S=⋅…… 9分)=)2212712t+-≤7=.…… 12分=7t=时,等号成立.∴A B C∆7…… 14分解法2:依题意,圆心为(,0)(02)C t t<<.由22,1,43x tx y=⎧⎪⎨+=⎪⎩得221234ty-=.∴圆C的半径为2r=.…… 6分∴圆C的方程为222123()4tx t y--+=.∵圆C与y轴相交于不同的两点,A B,且圆心C到y轴的距离d t=,∴2t<<,即07t<<.在圆C的方程222123()4tx t y--+=中,令0x=,得2y=±,∴弦长||AB=…… 8分∴A B C∆的面积12S=⋅…… 9分)=)2212712t+-≤7=.…… 12分=7t=时,等号成立.∴A B C∆7.…… 14分16. (本小题满分14分)设函数f(x)=tx2+2t2x+t-1(x∈R,t>0).(1)求f(x)的最小值h(t);(2)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.解:(1)23()()1(0)f x t x t t t x t=+-+-∈>R,,∴当x t=-时,()f x取最小值3()1f t t t-=-+-,即3()1h t t t=-+-. ------------5分(2)令3()()(2)31g t h t t m t t m=--+=-+--,由2()330g t t'=-+=得1t=,1t=-(不合题意,舍去).------------7分当t变化时()g t',()g t的变化情况如下表:分()g t∴在(02),内有最大值(1)1g m=-.------------12分()2h t t m<-+在(02),内恒成立等价于()0g t<在(02),内恒成立,即等价于10m-<, ---13分所以m的取值范围为1m>. ---14分。