2014年干一镇初级中学数学竞赛及优录培训11

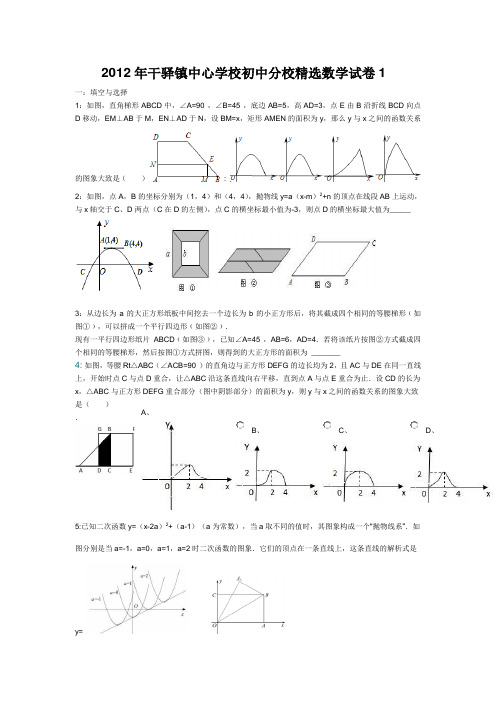
2012年干驿镇中心学校初中分校精选数学试卷1一：填空与选择1：如图，直角梯形ABCD 中，∠A=90°，∠B=45°，底边AB=5，高AD=3，点E 由B 沿折线BCD 向点D 移动，EM ⊥AB 于M ，EN ⊥AD 于N ，设BM=x ，矩形AMEN 的面积为y ，那么y 与x 之间的函数关系的图象大致是（ ）:2：如图，点A ，B 的坐标分别为（1，4）和（4，4），抛物线y=a （x-m ）2+n 的顶点在线段AB 上运动，与x 轴交于C 、D 两点（C 在D 的左侧），点C 的横坐标最小值为-3，则点D 的横坐标最大值为_____3：从边长为a 的大正方形纸板中间挖去一个边长为b 的小正方形后，将其截成四个相同的等腰梯形﹙如图①﹚，可以拼成一个平行四边形﹙如图②﹚．现有一平行四边形纸片ABCD ﹙如图③﹚，已知∠A=45°，AB=6，AD=4．若将该纸片按图②方式截成四个相同的等腰梯形，然后按图①方式拼图，则得到的大正方形的面积为 _______4: 如图，等腰Rt △ABC（∠ACB=90°）的直角边与正方形DEFG 的边长均为2，且AC 与DE 在同一直线上，开始时点C 与点D 重合，让△ABC 沿这条直线向右平移，直到点A 与点E 重合为止．设CD 的长为x ，△ABC 与正方形DEFG 重合部分（图中阴影部分）的面积为y ，则y 与x之间的函数关系的图象大致是（ ）．5:已知二次函数y=（x-2a ）2+（a-1）（a 为常数），当a取不同的值时，其图象构成一个“抛物线系”．如图分别是当a=-1，a=0，a=1，a=2时二次函数的图象．它们的顶点在一条直线上，这条直线的解析式是y=A 、B 、C 、D 、6:如图，在平面直角坐标系中，将矩形OABC沿OB对折，使点A落在A1处，A点坐标为（，0），C点坐标为（0，1），则A1点的坐标为（）．2：如图，二次函数（m＜4）的图象与x轴相交于点A、B两点．（1）求点A、B的坐标（可用含字母m的代数式表示）；（2）如果这个二次函数的图象与反比例函数的图象相交于点C，且∠BAC的正弦值为，求这个二次函数的解析式．3:（1）将抛物线y1=2x2向右平移2个单位，得到抛物线y2的图象，则y2=（2）如图，P是抛物线y2对称轴上的一个动点，直线x=t平行于y轴，分别与直线y=x、抛物线y2交于点A、B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，求满足条件的t的值，则t=4:王强在一次高尔夫球的练习中，在某处击球，其飞行路线满足抛物线y=- x2+ x，其中y（m）是球的飞行高度，x（m）是球飞出的水平距离，结果球离球洞的水平距离还有2m．（1）请写出抛物线的开口方向，顶点坐标，对称轴．（2）请求出球飞行的最大水平距离．（3）若王强再一次从此处击球，要想让球飞行的最大高度不变且球刚好进洞，则球飞行路线应满足怎样的抛物线，求出其解析式．5:如图，把一张长12cm，宽10cm的矩形硬纸板的四周各剪去一个同样大小的正方形，再折合成一个无盖的长方体盒子（纸板的厚度忽略不计）．（1）要使长方体盒子的底面积为48cm2，那么剪去的正方形的边长为多少？（2）你感到折合而成的长方体盒子的侧面积会不会有更大的情况？如果有，请你求出最大值和此时剪去的正方形的边长；如果没有，请你说明理由．6:某商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件．后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件．（1）求商场经营该商品原来一天可获利润多少元？（2）设后来该商品每件降价x元，商场一天可获利润y元．①若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？②求出y与x之间的函数关系式，并通过画该函数图象的草图，观察其图象的变化趋势，结合题意写出当x取何值时，商场获利润不少于2160元．7: 施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米．现以O点为原点，OM所在直线为x轴建立直角坐标系（如图1所示）．（1）求出这条抛物线的函数解析式，并写出自变量x的取值范围；（2）隧道下的公路是双向行车道（正中间是一条宽1米的隔离带），其中的一条行车道能否行驶宽2.5米、高5米的特种车辆？请通过计算说明；（3）施工队计划在隧道门口搭建一个矩形“脚手架”CDAB，使A、D点在抛物线上．B、C点在地面OM线上（如图2所示）．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少，请你帮施工队计算一下．8:如图，梯形ABCD中，AD∥BC，∠BAD=90°，AD=1，E为AB的中点，AC是ED的垂直平分线．（1）求证DB=DC；（2）在图（2）的线段AB上找出一点P，使PC+PD的值最小，标出点P的位置，保留画图痕迹，并求出PB的值．9: 抛物线y=x2+（m-3）x-m+2的图象交x轴正半轴于点A，交x轴负半轴于点B，交y轴于点C．（1）求m的取值范围；（2）若△ABC恰为等腰三角形，求m．10:如图，矩形ABCD，M为CD中点，点E在线段MC上运动，GH垂直平分AE，垂足为O，分别交于AD、BC于点G、H，AB=3，BC=4．（1）求AE：GH；（2）设CE=x，四边形AHEG的面积为y，求y关于x的函数关系式；当y取最大值时，判断四边形AHEG 的形状，并说明理由．11: 如图，在平面直角坐标系中，抛物线A（-1，0），B（3，0），C（0，-1）三点．（1）求该抛物线的表达式；（2）点Q在y轴上，点P在抛物线上，要使Q、P、A、B为顶点的四边形是平行四边形，求所有满足条件点P的坐标．12: 如图，在直角坐标系xOy中，正方形OCBA的顶点A，C分别在y轴，x轴上，点B坐标为（6，6），抛物线y=ax2+bx+c经过点A，B两点，且3a-b=-1．（1）求a，b，c的值；（2）如果动点E，F同时分别从点A，点B出发，分别沿A→B，B→C运动，速度都是每秒1个单位长度，当点E到达终点B时，点E，F随之停止运动，设运动时间为t秒，△EBF的面积为S．①试求出S与t之间的函数关系式，并求出S的最大值；②当S取得最大值时，在抛物线上是否存在点R，使得以E，B，R，F为顶点的四边形是平行四边形？如果存在，求出点R的坐标；如果不存在，请说明理由．13: 在△ABC中，AC=BC，∠ACB=90°，点D为AC的中点．（1）如图1，E为线段DC上任意一点，将线段DE绕点D逆时针旋转90°得到线段DF，连接CF，过点F作FH⊥FC，交直线AB于点H．判断FH与FC的数量关系并加以证明；（2）如图2，若E为线段DC的延长线上任意一点，（1）中的其他条件不变，你在（1）中得出的结论是否发生改变，直接写出你的结论，不必证明．14:如图，△OAB是边长为2的等边三角形，过点A的直线+m与x轴交于点E．（1）求点E的坐标；（2）求过A、O、E三点的抛物线解析式；（3）若点P是（2）中求出的抛物线AE段上一动点（不与A、E重合），设四边形OAPE的面积为S，求S的最大值．。

2014年全国初中数学竞赛试题参考答案及评分标准一、选择题（共10小题，每小题6分，满分60分.） 1.已知x 、y 、z 满足2x =3y-x =5z+x ，则5x-yy+2z的值为（ ）（A ）1 （B ）13 （C ）-13 （D ）12【答】B ．解：设 2x =3y-x =5z+x =1k 则x=2k ，y-z=3k ，z+x=5k ，即x=2k ，y=6k ，z=3k 。

所以5x-y y+2z =5·2k-6k 6k+6k =13，故选B.2.已知等腰三角形的周长为12，则腰长a 的取值范围是（ ）（A ）a ＞3 （B ）a ＜6 （C ）3＜a ＜6 （D ）4＜a ＜7 【答】C.解：腰长为a ，则底长为12-2a ，由2a ＞12-2a 及12-2a ＞0可得3＜a ＜6 故选C. 3.设 21x x 、 是一元二次方程032=-+x x的两根，则 1942231+-x x 等于（ ）（A ）-4 （B ）8 （C ）6 （D ）0 【答】D.解：将21x x 、代入方程，将目标整式降次，利用两根之和求解.4．如果a b ，为给定的实数，且1a b <<，那么1121a a b a b ++++，， ，这四个数据的平均数与中位数之差的绝对值是（ ） （A ）1 （B ）214a - （C ）12 （D ）14【答】D.解：由题设知，1112a a b a b <+<++<+，所以这四个数据的平均数为1(1)(1)(2)34244a ab a b a b+++++++++=， 中位数为 (1)(1)44224a ab a b++++++=， 于是 4423421444a b a b ++++-=. 故选D.5. 如图，正方形A BCD 和EFGC 中，正方形EFGC 的边长为a ，用a 的代数式表示阴影部分△AEG 的面积为（ ）（A ）232a （B ）223a （C ）212a （D ）2a【答】C ．6.若△ABC 的三条边a,b,c 满足关系式a 4+b 2c 2- a 2c 2-b 4=0，则△ABC 的形状是（ ） （A ）等腰三角形 （B ）等边三角形（C ）直角三角形 （D ）等腰三角形或直角三角形 【答】D.解法一：原方程左边变形为 （a 4-b 4）+（b 2c 2-a 2c 2）=0， （a 2+b 2）（a 2-b 2）+（b 2-a 2+）c 2=0，∴（a 2-b 2）（a 2+b 2-c 2）=0， ∴a=b 或c 2=a 2+b 2.∴△ABC 为等腰三角形或直角三角形. 解法二：应用配方法a 4+b 2c 2- a 2c 2-b 4=0， （a 4-a 2c 2）-（-b 2c 2+b 4）=0 （a 2-22c ）2 -（22c -b 2）2=0 ∴（a 2-b 2）（a 2+b 2-c 2）=0， ∴a 2-b 2=0,或a 2+b 2-c 2=0. ∴a=b 或c 2=a 2+b 2. ∴△ABC 为等腰三角形或直角三角形. 故选D.7．一批志愿者组成了一个“爱心团队”，以募集爱心基金.第一个月他们就募集到资金1万元，随着影响的扩大，第n (n ≥2)个月他们募集到的资金都将会比上个月增加20%，则当该月所募集到的资金首次突破10万元时(参考数据: 51.22.5≈，61.2 3.0≈，71.2 3.6≈)，相应的n 的值为（ ）（A ）11 （B ）12 （C ）13 （D ）14 【答】D.8．如图：点D 是△ABC 的边BC 上一点，若∠CAD = ∠DAB = 60°，AC = 3 ，AB = 6，则AD 的长度是（ ）（A ）2 （B ）2.5 （C ）3 （D ）3.5 【答】A.解：如图，作BE ⊥AC 交CA 的延长线于E ，在Rt △ABE 中， ∠BAE= 60° ∴∠ABE= 30° ∴AE=21AB = 3 由勾股定理得BE =33∴21BCA s △AC ·BE =329 ∵∠CAD = ∠DAB = 60°同理得△ADC 和△ABD 中AD 边上的高分别是323和33 ∴=CD A s △343AD ,=B DA s △323AD 又CD A s △+B DA s △=BC A s △ ∴343AD + 323AD =329 ∴AD = 2 故选A9.若m=20132+20132×20142+20142，则m ( )（A ）是完全平方数，还是奇数 （B ）是完全平方数，还是偶数 （C ）不是完全平方数，但是奇数 （D ）不是完全平方数，但是偶数 【答】A.解 ：原式=20132-2×2013×2014+20142+2×2013×2014+20132×20142=(2013-2014)2+2×2013×2014+(2013×2014)2=1+2×2013×2014+(2013×2014)2=(2013×2014+1)2所以(2013×2014+1)2是一个完全平方数，末尾数字是9，所以也是奇数. 故选A. 10、设非零实数a ，b ，c 满足2302340a b c a b c ++=⎧⎨++=⎩，，则222ab bc caa b c ++++的值为（ ） （A ）12-（B ）0 （C ）12（D ）1 【答】A.解：由已知得(234)(23)0a b c a b c a b c ++=++-++=，故 2()0a b c ++=．于是 2221()2ab bc ca a b c ++=-++， 所以22212ab bc ca a b c ++=-++．故选A.二、填空题（共5小题，每小题6分，满分30分）11.已知整数1234a a a a ⋅⋅⋅，，，，满足下列条件：10a =，21|1|a a =-+，32|2|a a =-+，43|3|a a =-+，…，依次类推，则2012a 的值为 ．【答】1006-12.如图，四边形ABCD 中，AB ＝BC ，∠ABC ＝∠CDA ＝90°， BE ⊥AD 于点E ，且四边形ABCD 的面积为8，则BE ＝ ．【答】解：.如图，可以通过旋转变换将△ABE 绕点B 逆时针旋转90°，得到△CBF.证明出四边形BFDE 是正方形,且它的面积是8，则边长是或者过点B 作BF ⊥BE ，交DC 延长线于F. 证明△ABE ≌△CBF ，其余思路同上。

2012年全国初中数学竞赛（河南赛区）预赛试卷　一、选择题（共6小题，每小题6分，共36分.以下每道小题均给出了代号为A，B，C，D的四个选项，其中有且只有一个选项是正确的.请将正确选项的代号字母填入题后的括号里，不填、多填或错填都得0分）1．（6分）在1，3，6，9四个数中，完全平方数、奇数、质数的个数分别是（ ）　A ．2，3，1B．2，2，1C．1，2，1D．2，3，22．（6分）已知一次函数y=（m+1）x+（m﹣1）的图象经过一、二、三象限，则下列判断正确的是（ ）　A ．m＞﹣1B．m＜﹣1C．m＞1D．m＜13．（6分）如图，在⊙O中，，给出下列三个结论：（1）DC=AB；（2）AO⊥BD；（3）当∠BDC=30°时，∠DAB=80°．其中正确的个数是（ ）　A．0B．1C．2D．34．（6分）有4张全新的扑克牌，其中黑桃、红桃各2张，它们的背面都一样，将它们洗匀后，背面朝上放到桌面上，从中任意摸出2张牌，摸出的花色不一样的概率是（ ）　A．B．C．D．5．（6分）在平面直角坐标系中，点A的坐标是（1，0），点B的坐标是（﹣3，﹣3），点C是y轴上一动点，要使△ABC为等腰三角形，则符合要求的点C的位置共有（ ）　A．2个B．3个C．4个D．5个6．（6分）已知二次函数y=2x2+bx+1（b为常数），当b取不同的值时，其图象构成一个“抛物线系”，图中的实线型抛物线分别是b取三个不同的值时二次函数的图象，它们的顶点在一条抛物线上（图中虚线型抛物线），这条抛物线的解析式是（ ）、管路敷设技术不规范问题，而且可保障各类管路习题到位。

在管路敷设过程中弯曲半径标高等，要求技术交底。

管线敷设技术中包含线槽、管架等多项方、电气课件中调试对全部高中资料试卷电气设备，在安装过程中以及安装结行空载与带负荷下高中资料试卷调控试验；对设备进行调整使其在正常工况下高中资料试卷调试方案，编写重要设备高中资料试卷试验方案以及系统启动程规定，制定设备调试高中资料试卷方案。

2014年建设兵团一中小学升初中招生数学试卷（90分钟，100分）一、填空：1、114，1.3，1.13%，1.313，请将这四个数按大小排列（）2、五分之四，分子或分母同时加上一个相同的数，得到四分之五，求这个数？（）3、12支足球队比赛，每两个队赛一场，要赛多少场？（）4、有一列数，按照下列规律排列：1，22，333，4444，55555，666666，这列数的第34个数是（）5、用同样大小的黑色棋子按如图所示的规律摆放，第五个图形有多少黑色棋子？（），第10个图形有（）颗黑色棋子．第n个图形有（）颗黑色棋子二、选择：1、在含有30%的盐水中，加入6克盐14克水，这时盐水的百分比是（）A等于30%B小于30%C大于30%D无法确定2、已知A>B>C（）A BA＜1B 1A>1B C C A>C B D无法确定3、用3，4或7去除都余2的数中，最小的是（）A82B8486D884、在一条线段中间另有6个点，则这8个点可以组成（）条线段A21B28C36D485、盒子里人8个黄球，5个红球，至少摸（）次一定会摸到红球。

A8B5C9D66、从甲堆货物中取出19给乙堆，这时两堆货物质量相等，原来甲乙两堆的质量比是（）A7：9B9：8C9：7D9：6三解答题1、已知四边形ABCD是正方形，边长为5厘米，三角形的ECF的面积比三角形ADF大5平方厘米，求CE的长度？2、红星村挖了一口井，井口的外沿周长3.14米，想给它配上一个井盖，井盖的面积是多少？如果沿着井边铺3.5米宽的石子地，每车小石子能铺12平方米，那么至少要运几车？3、已知长方形的周长是40厘米，如果把它的长和宽都增加5厘米，那么它的面积就增加了多少平方厘米？四、应用题1、加工一批零件，甲单独做需要10天，乙单独需要15天，丙单独做需要20天，现在三人合作，但单因有事停工几天，结果6天才将任务完成，单停工几天？2、商店有甲乙两件物品，标价都是240元，卖出甲商品赚了百分之10，卖出乙商品亏了百分之10，如果两种物品都卖出，那么商店是赚了还是亏了？赚了或亏了都是多少元？3、甲乙丙三个工程队完成某项工程的天数和日工资如下表：工程队单独完成工程所需要的天数每日工资（万元）甲1018乙1512丙208请你选择两个工程队合作这项工程，如果工期很紧，想尽快完工，应选择哪两个队合作？几天可以完工？完工后，两队各得多少工资？4、某工程队铺一段铁路，原计划每天铺3.2千米，实际每天比原计划多铺14，实际铺完这段铁路用了12天，原计划用多少天铺完？5、小明早上从家步行去学校，走完一半路程时，爸爸发现小明的数学书丢在家里，随即骑车去给小明送书，追上时，小明还有310的路程没走完，小时随即上了爸爸的车，由爸爸送往学校，这时小明比独自步行提早5分钟到校，小明从家到学校全部步行需要多少时间？。

2014年城北中学七年级数学竞赛试卷一 满分100分，考试时间90分钟 一、选择题（共10小题，每小题4分，满分40分．）1．若实数a 、b 、c 在数轴上对应点的位置如图所示, 则|c |-|b -a |+|b +c |等于 ( ) A ． -a B .-a +2b C .-a -2c D .a -2b 2．从 -3, -2, -1, 4, 5中任取2个数相乘, 所得积中的最大值记为a ，最小值记为b ，则 a b 的值为（ ）． A ．34- B ．21- C ．31 D ．320 3.适合81272=-++a a 的整数a 的值的个数有（ ） A ．5 B ．4 C ．3 D ．2 4.王老伯在集市上先买回5只羊，平均每只a 元，稍后又买回3只羊，平均每只b 元，后 来他以每只2b a +的价格把羊全部卖掉了，结果发现赔了钱，赔钱的原因是（ ） A ．b a > B ．b a < C ．b a = D ．与a 、b 的大小无关 5.已知一列有规律的数：2，3，5，9，17，33，…，其中第10个数是 ( ) A ．512 B ．513 C ．1024 D ．1025 6.如果有2014名学生排成一列，按1、2、3、4、3、2、1、2、3、4、3、2、1……的规律 报数，那么第2014名学生所报的数是（ ） A ．1 B ．2 C ．3 D ．4 7.设n ﹗表示从1连续乘到n,如：1！=1， 2！=1×2， 3！=1×2×3，…， 100！=1×2×3…×100，那么1！+2！+3！+…+100！的个位数字是( • ) A ．1 B ．2 C ．3 D ．4 8．如图，长方形ABCD 恰好可分成7个形状大小相同的小长方，如果小长方形的面积是3，则长方形ABCD 的周长是 ( )A ．7B ．9C ．19D ．219．上午九点钟的时候,时针与分针成直角,•那么下一次时针与分针成直角的时间是…………… ( ) A ．9时30分 B ．10时5分 C ．10时5511分 D ．9时32811分 10．若k 是正整数，1768117<<k ，且768k 可表示为nm 11+（m 、n 均为正整数）的形式，则k 的最大值是 ( ). 县区 学校 坐位号 姓名 A D B C （第6题图）A ．526B ．576C ． 640D ．760二、填空题（有9小题，自主选择其中8道题完成，每小题5分，满分40分）11．定义b a ab b a ++=⊗,若273=⊗x ，则x 的值是__ ___.12．定义：(,)(,)f a b b a =，(,)(,)g m n m n =--. 例如(2,3)(3,2)f =，(1,4)(1,4)g --=，则((5,6))g f -= .13．若a ,b,c 都是质数，其中a 最小，且a +b+c=44，ab+3=c ，则a b+c=________.14．小明开车从江山去杭州旅游，在高速公路和非高速公路上的行驶速度分别是120千米/时和60千米/时.若小明驶完全程用了6小时，其中在高速公路上行驶的路程是在非高速公路上行驶的路程的6倍，则全程长____________千米.15．已知0≠abc ，若||4||3||2c c b b a a m ⨯⨯=，则__________122=++m m . 16．按一定规律排列的一串数：112312345123,,,,,,,,,,,, (133355555777)------中，第98个数是______________ 17．定义一种对正整数n 的“F ”运算：①当n 为奇数时，结果为3n ＋5；②当n 为偶数时，结果为k n2（其中k 是使k n 2为奇数的正整数），并且运算重复进行．例如，取n ＝26，则：若n ＝49，则第449次“F 运算”的结果是_____________．18．为确保信息安全，信息需加密传输，发送方由明文→密文（加密）；接 收方由密文→明文（解密）.已知加密规则为：明文a ，b ，c ，d 对应密文，b a +2，c b 23+，d c 52+，d 3.当接收方收到密文10，16，29，15时，解密得到明文a ，b ，c ，d ，则=+++d c b a .19．有依次排列的3个数：3，5，9，对任相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，2，5，4，9，这称为第一次操作；做第二次同样的操作后也可产生一个新数串：3，-1，2，3，5，-1，4，5，9，继续依次操作下去. 问：第100次操作以后所产生的那个新数串的所有数之和是多少 . 26 13 44 11 第一次 F ② 第二次 F ① 第三次 F ② …三、解答题（共2题，满分20分）20．（本题10分）两个同样的圆柱形水池A和B，深度都是1.2米，1号抽水机18分钟可1将A池注满，2号抽水机24分钟可将A池的满池水注入B池，现在，若A池中储有6池水，B池没有水，同进打开1号，2号抽水机，当A池水深0.6米时，同时关闭两个抽水机，求此时B池的水深.21．（本题10分）阅读下面一段材料：计算1＋5＋52＋53……＋599＋5100观察发现，上式从第二项起，每项都是它前面一项的5倍，如果将上式各项都乘以5，所得新算式中除个别项外，其余与原式中的项相同，于是两式相减将使差易于计算。

龙潭中心校2014年九年级数学上竞赛试题说明：本试卷考试时间90分钟，满分100分。

一、选择题：（每小题5分，共40分）1. 下列四个图形中，既是轴对称图形又是中心对称图形的是（ ）．A ．B ．C ．D ．2. 一元二次方程210x -=的根是 （ ）A. 1x =B. 1x =-C. 121,1x x ==-D. 0x =3、已知关于x 的方程240x x a ++=有两个实数根12,x x ，且1227x x -=，则a 的值为（ ）A 、-3B 、-4C 、-5D 、-6 4、已知,,a b c 在数轴上的位置如图，代数式22()a a b c a b c -++-++的值是（ ）A 、2c a -B 、C 、D 、a5、若a b c A b c a c a b===+++，则A 的取值是（ ）A 、-1B 、12 C 、1 D 、12或 -1 6、若长方形的长增加了%p 以后，为了使长方形面积保持不变，则这个长方形的宽应该减少（ ）A 、%pB 、100%100p p + C 、%1pp+ D 、(1)%p -7、已知x 是实数，则1x x x πππ--+-+的值是（ ）b a 0 cA 、11π-B 、11π+C 、11π- D 、无法确定8、已知方程组{42=-=+by ax by ax 的解为{21==x y 则23a b -的值为（ ）A 、4B 、6C 、-6D 、-49、已知点(,)P x y 在函数21y x x=+-的图像上，则点P 应在平面直角坐标系中的（ ）A 、第一象限B 、第二象限C 、第三象限D 、第四象限10、在△ABC 中，已知BD 和CE 分别是两边上的中线，并且,4,6BD CE BD CE ⊥==，那么△ABC 面积等于（ ）A 、12B 、14C 、16D 、18二、填空题(每题4分，共20分)1、直线y kx b =+经过(2,1),(1,2)A B --两点，则不等式122x kx b >+>-的解集为__________________。

2013年秋学期临泽四中七年级数学竞赛试卷一、选择题（每小题3分，共30分）1、下列说法中，正确的是（ ）A 、没有最大的正数，但有最大的负数。

B 、有绝对值最小的数，没有绝对值最大的数。

C 、有理数包括正有理数和负有理数。

D 、相反数是本身的数是正数。

2、正四面体的顶点数和棱数分别是（ ）A 、3，4B 、3，6C 、4，4D 、4，63、设a 是最小的自然数，b 是最大的负整数，c 是绝对值最小的有理数，a ，b ，c 三个数的和为（ ）A 、-1B 、0C 、1D 、不存在4、对于任何有理数a ，下列各式中一定为负数的是（ ）A 、-（-3+a ）B 、-aC 、-|a+1|D 、-|a|-15. 适合81272=-++a a 的整数a 的值的个数有 ………………（ ）A ．5B ．4C ．3D ．26. 已知一列有规律的数：2，3，5，9，17，33，…，其中第10个数是…………( )A ．512B ．513C ．1024D ．10257. 碳纳米管的硬度与金刚石相当，却拥有良好的柔韧性，可以拉伸，我国某物理所研究组已研制出直径为0.5纳米的碳纳米管，1纳米=0.000000001米，则0.5纳米用科学记数法表示为（ ）A 、0.5×10-9米B 、5×10-8米C 、5×10-9米D 、5×10-10米8. 已知（a+3）2+|b-2|=0，则a b 的值是（ ）A 、-6B 、6C 、-9D 、99. 用代数式表示“比m 的平方的3倍大1的数“是（ ）A 、m 2+1B 、3m 2+1C 、3（m+1）2D 、（3m+1）210. 在下列的语句中，正确的有（ ）（1）- 23a 2b 3与 12a 3b 2是同类项；（2） (-12)2x 2yz 与-zx 2y 是同类项；（3）-1与 15是同类项； （4）字母相同的项是同类项．A 、1个B 、2个C 、3个D 、4个二、填空题（每小题3分，30分）11．一箱某种零件上标注的直径尺寸是20mm{， 若某个零件的直径为19.97 mm ，则该零件 标准．（填“符合”或“不符合”）．12. 定义b a ab b a ++=⊗,若273=⊗x ，则x 的值是__ ___. 0.05mm-0.04mm+13.-m）n=14.m的绝对值为2，则15.画一条直线，可将平面分成2个部分，画2条直线，最多可将平面分成4个部分，那么，画6条直线最多可将平面分成_______个部分．16.旅游商店出售两件纪念品，每件120元，其中一件赚20%，而另一件亏20%，那么这家商店出售这样两件纪念品是，那么（填赚了或亏了多少元）17. 已知有理数a、b、c在数轴上的位置如图所示，则0。

初中数学竞赛培训题（初中二年级）希望杯”第十四届”2:236:2:621: C A D B．如果两个三角形的两条边和其中一边上的高对应相等，那么这两个三角形中，第三条边所对的12一．选择题（以下每题的四个先项中，只有一个是正确的，请将表示正确答案的英文字母填在每题D互补或相等 C 互余后面的括号里）） A 相等 B 不相等角关系是（2a?2001?a?a?20022001a?）的值等于（1．已知实数a ，那么满足：2003DA 2000B 2001C 20022x?y?的实数对（x，y）共有（2．若x，y 均为整数，则满足）对。

9D 7 B 5 C A 322223243yyxy?2xyx??6x?y?2xy?10x61y?x?3．若）的值等于（，则1?3D C 1 0 A B 0030?C90??ABC?ABC?BC+DE，，则，D为AB13．如图1，在Rt上一点，若BD=a中，??231?b)??aba(a?a?b?ab?bA A为正整数，设，b是一个质数，则，4．已知a5a3a D C 2.5a 的值等于（）A 2a B ）a+b的值等于（?AEF?C4 D A 1 B 2 C 3 的大小是（，那么2，在菱形ABCD中，作一个正），又AE=AB14．如图220000x?25?y135120100130）的解有（x5．若，y是非负数，那么满足方程 D B C AAB∥DCAC?BC?B C 4组D 3组组 A 1组 B 2 的大小等于（．如图3，在梯形ABCD中，则,AD=BC=DC，）150000 60 D C 50 B A 30 45 1??23?63?x2?xy??x点，若PAN与MC交于、中，M，N分别是ADDC 边的中点，，在矩形16．如图4ABCD_ ，那么（是实数，．已知6x x3?0NBC?MCB??）+33，那么的大小是（0 0 0 78 D A 33 B 66 C 45 0?y0?0y?yy?0 D CB A222xx???4xx?12??x?x496?)( ，．7If 1<x<2 thenamount tox2?x2??3x D A 1 B C??2?2?x?x)x8．已知是任意实数，那么(0 小于0 不大于0 一定等于A B C D 不小于c?ba?cb?ac?bacb?a??????），为三角形的三边长，，，a若9．bc（应等于则化简c2?2b4a C B 0 A 2a+2b+2c D）三年中利润最高是是某商场近如图5，3年的资金投放与利润统计示意图，由图形可知，（．）．下列命题的逆命题中是真命题的是（10 17 C 年年A 2000 如果两个有理数相等，它们的绝对值也相等 B 全等三角形的对应角相等 A B 2001 D 年2002 无法比较对顶角相等C D 两直线平行，内错角相等）．如果一个正三角形与一个正六边形的面积相等，那么它们的周长比是（11．）18．某地一昼夜中整点时刻的气温统计如下表：那么20022C温度（） 5 4 2 4 6 8 6 10 13 17 15 13 10 111322?x?xx?0x?1x?3? =_______．已知=_______，。