当前位置：文档之家 › 20080423高一数学(1.1.2弧度制)

20080423高一数学(1.1.2弧度制)

  • 格式：ppt
  • 大小：191.00 KB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

1.1.2 弧度制[概述PPT课件

1.1.2 弧度制[概述PPT课件

3.弧度制与角度制之间如何换算？ 利用：
角度制与弧度制的换算公式：
[例1]把下列各角化为弧度
（1）30°（2）-45°（3）6730
解：∵
6730
67
1 2
∴
6730
π 180
rad
67
1 2
3πrad 8
例2 角度与弧度互化
(1)22 30'
(4)
12
(2)-210
(5)- 4
3
(3)1200
You Know, The More Powerful You Will Be
谢谢大家
荣幸这一路，与你同行
It'S An Honor To Walk With You All The Way
演讲人：XXXXXX 时 间：XX年XX月XX日
2rad
A
r
Oo
AOB=1rad
AOC=2rad
1弧度：α
L r
?
我们把等于半径长的圆弧所对的圆心角
叫做1弧度的角．
完成下列填空：若圆的半径为 r；弧长为 L．
当L取下列值时写出对应的 圆心角
(1)L r
α _1_r__a__d;
(2)L 2.5r α2_._源自_r__a_d;(3)L πr α __r__a_d_;
(4)L 2πr α2___r__a_d;
思考：若角α是一个负 角；它的弧度数如何表示？
若L 4πr;α 0则：
L 4r 4
rr
|α|
L r
结论：正角的弧度数是 正数；
负角的弧度数是一个负 数；
零角的弧度数是0。
2.周角是多少度？多少弧度？平角呢？ 直角呢？

1.1.2弧度制(必修一-数学-优秀课件)

1.1.2弧度制(必修一-数学-优秀课件)
用“弧度” 做单位来度量角的制度，叫做弧度制 。
第5页，共23页。
弧度数的计算公式可以用弧长与其半径的比 值来表示，那么一个角的弧度数与所在的圆 的半径之间存在一定的联系么？若存在，请 阐述是什么关系？若不存在，说明理由。
结论：当圆心角一定时，它所对的弧长与半径的比
值是一定的，与所在圆的半径大小无关。
例7. 已知一半径为R的扇形，它的周长等于所在
圆的周长，那么扇形的中心角是多少弧度？合多少 度？扇形的面积是多少？
解：周长=2πR=2R+l，所以l=2(π－1)R. 所以扇形的中心角是2(π－1) rad.
合( 360( 1) ) º
扇形面积是 ( 1)R2
第21页，共23页。
小 结 1.圆心角α所对弧长与半径的比是一个仅
（4）以弧度和度为单位的角，都是一个与半径无
关的定值。
第8页，共23页。
二、弧度与角度的换算
思考： 1.若弧是一个整圆，其圆心角的弧度数是多少？
2.若弧是一个半圆，其圆心角的弧度数是多少？
若l=2 π r,则∠AOB= 若l=π r, 则∠AOB=
360°= 2π 弧度 180°= π 弧度
l r
设弧AB的长为: l
若 l =r,则∠AOB=
l r
=1弧度
B l=r
若 l=2r,则∠AOB=
l r
=2 rad
Or A
若 l=3r,则∠AOB=
l
r
= 3 rad
第3页，共23页。
思考：若圆心角∠AOB表示一个顺时针方向旋 转的角，且它所对的弧的长为3r,则∠AOB的弧
度数的绝对值是？弧度数是？
第12页，共23页。
例3：请用弧度制表示下列角度所在区间。 锐角：{θ|0°＜θ＜90°} 直角： {θ|θ=90°} 钝角： {θ|90°＜θ＜180°} 平角： {θ|θ=180°} 0°到90°的角：{θ|0°≤θ<90°} 小于90°角：{θ|θ＜90°}

高一数学 弧度制

高一数学 弧度制

57.30
例1、把 67º30 化成弧度。 （1）精确值
[பைடு நூலகம்结]
（1）仅出现度的，可
以直接乘
rad
180
（2）精确到0.001的近似值
约简即可；出现分秒的
解：
（1）6730
(67
1 2
)
180
rad
(67
1 2
)
应先化为度，然后再换 算。 （2）用弧度作单位时， 常常把弧度数写成多少
3 rad
180
2
（3）将 l R
代入 s
1 R2
2
得
S
1 lR 2
例4：利用计算器比较 sin1.5 和 sin 85 的大小。
解：由计算器 MODE MODE 2
sin 1.5 = 0.997494986
MODE MODE 1
sin 85 。，，， = 0.996194698
所以 sin1.5 > sin 85
B
1º
A
弧度制
1、什么叫弧度制？
以弧度作为单位来度量角的单位制，叫做弧度制。
2、1弧度的角是怎样规定的？
把长度等于半径长的弧所对的圆心角叫做1弧度（radian）的角。
3、弧度制的单位是什么？
演示课件
用符号rad表示，读作弧度。 （可以省略）
4、怎样计算弧度数，角度和弧度间如何转化？
AB的长 OB旋转
3 2
2
对应关系
角的集合与实数集R之间可以建立一种一一对应的关系
任意角的集合 正角 零角
实数集R 正实数 0
例如； 弧度的角
6
2 弧度的角
正数 6
负数 2

1.1.2弧度制 课件

1.1.2弧度制 课件
半径为R,
l 2R = 10 根据题意: 1 lR = 4 2 由①得 l = 10 2R ,
2 R 5R 4 = 0 代入②得
①
②ห้องสมุดไป่ตู้
解得 R1 =1,R 2 =4
l 当R=1时,l=8cm时, = = 8 2 R l 1 = = 当R=4时,l=2cm时, R 2 1 ∴所求扇形的圆心角的弧度数为 2
6
30
4、若2 rad的圆心角所对的弧长是4cm，则这个 圆心角所在扇形的面积为_________ 4cm2
练习7：当扇形的中心角为600，半径为10cm， 求扇形的弧长及该弧所在的弓形面积 3 600=π/3 L=10π/3 S = 50( )cm2
3 2
8.已知扇形的周长为20 cm，当扇形的中心角 为多大时，它有最大面积，最大面积是多少?
弧度制 ： 定义： 我们把长度等于半径长的弧所对的 圆心角叫做1弧度的角，即用弧度制度量时， 这样的圆心角等于1rad。 单位符号 ：rad B
l =r O
读作弧度 C
l = 2r
2 rad O r
o
1rad r
A
A
o
AOB=1rad
AOC=2rad
(1)正角的弧度数是正数，负角的弧度数是负数， 零角的弧度数是0
舍去
1、已知扇形周长为6cm，面积为2cm2，则扇形 圆心角的弧度数为 C A 、1 B 、4 C 、1 或4 D 、2 或4 2、当圆心角α=-216o，弧长l =7πcm时，其半径 35 r=________ cm 40 所对圆弧的长为___________
2 3、在半径为 的圆中，圆心角为周角的 的角 3
180 =

1.1.2弧度制

1.1.2弧度制

1.定义：把长度等于半径长的弧所对的圆 心角叫做1弧度的角. l | a |= 用符号rad表示。
r r
r
其中 : 1、l是以角 作为圆心角时所对弧的长，r是半径； 2、正角的弧度数是一个正数，负角的弧度数是 一个负数，零角的弧度数是0； 2 r 3、圆心角 为周角时，l 2 r，则 2 r r 4、圆心角 为半角时，l r，则 r
退出
§1.1.2 弧度制
温故 知新1 角的分类 知新2 知新3 知识应用 小结 作业
180 rad

360 2 rad








退出
§1.1.2 弧度制
温故 知新1 知新2 关系换算 知新3 知识应用 小结 作业
360 2 rad

180 rad
y 0
x
5 4
退出
§1.1.2 弧度制
温故 知新1 弧度制 知新2 知新3 知识应用 小结 作业
弧度制的作用：
1、求弧长：
l l r r
l = ar 1 2 S = ar 2
2、求扇形的面积：
S扇 S圆 2 1 2 2 r r 2 2
1 1 r r lr 2 2
l = 2p r S = pr
2
退出
§1.1.2 弧度制
温故 知新1 知新2 知新3 知识应用 小结 作业
例：已知4弧度的圆心角所对的弦长为2， 那么这个圆心角所对的弧长是 ？
O C A 分析：l r r ? 解：过O作弦的垂线OC，所以 建立直角三角形 1 B
角为2弧度，对边为1 r= 1 sin2

课件6：1.1.2 弧度制

课件6：1.1.2 弧度制
答案：4 cm2
(2)已知一半径为 R 的扇形，它的周长等于所在圆的周长，那么扇形的 圆心角是多少弧度？面积是多少？
解：设扇形的弧长为 l， 由题意得 2πR＝2R＋l，所以 l＝2(π－1)R， 所以扇形的圆心角是Rl ＝2(π－1)， 扇形的面积是12Rl＝(π－1)R2.
谢谢观看！
解：如图，330°角的终边与－30°角的终边相同，
将－30°化为弧度，即－π6，而 75°＝75×1π80＝51π2，
∴终边落在阴影部分内(不包括边界)的角的集合为
θ|
2kπ－π6＜θ＜2kπ＋51π2，k∈Z.
题型三 扇形的弧长及面积公式
例 3 (1)若圆的半径变为原来的 2 倍，弧长也变为原来的 2 倍，则( )
题型二 用弧度制表示角的集合
例 2 已知角 α＝2 005°. (1)将 α 改写成 β＋2kπ(k∈Z，0≤β＜2π)的形式，并指出 α 是第几象限的角； (2)在[－5π，0)内找出与 α 终边相同的角．
解：(1)2
005°＝2
π 005×180
rad＝40316π
rad＝5×2π＋4316π
答案：(1)D (2)2
(3)如图所示，扇形 AOB 的面积是 4 cm2，它的周长是 10 cm，求扇形的 圆心角 α 的弧度数及弦 AB 的长．
解：设弧 AB 的长为 l(cm)，扇形半径为 r(cm)， 由题意得l12＋lr＝2r＝ 4，10，解得rl＝＝24，或rl＝＝81，(舍)， 故 α＝24＝12(弧度)，AB＝2×4sin 14＝8sin 14(cm)．
变式训练 3 (1)已知扇形的周长为 8 cm，圆心角为 2， 则扇形的面积为________．
解析：设扇形的半径为 r cm，弧长为 l cm，由圆心角为 2 rad， 依据弧长公式可得 l＝2r，从而扇形的周长为 l＋2r＝4r＝8， 解得 r＝2，则 l＝4. 故扇形的面积 S＝12rl＝12×2×4＝4 (cm2)．

课件1：1.1.2 弧度制


把长度等于半 周角的1/360叫做1
单位规 径长的弧所对 度的角。
定
的圆心角叫做1
弧度的角。
换算关
系
360 2rad
180 rad
基本关系
1

rad 0.01745rad
180
180
1rad
57.30 5718

导出关系
弧度制与角度制的互化技巧
=
180 8

.
把
8
5
化成度。
解：1rad=
180
(
)

8 8 180

(
)
5
5

288Βιβλιοθήκη 度与角度的互化过程中，要掌握其中的原理和方法，必要时可以借助一些特殊角
来判断，会转换到别的地方。
题型三
将3.14 rad 换算成角度(用度数表示，
精确到0.001).
解:∵1=(180/π)0
弧度的角，用符号rad表示，读作弧度。这种
用弧度作为单位度量角的单位制叫做弧度制。
要点阐释
一般地，正角的弧度数是一个正数，负角的
弧度数是一个负数，零角的弧度数是0，如果
半径为r的圆的圆心角a所对弧的长为l，那么，
角a的弧度数的绝对值是 | a | = l / r
典例剖析
题型一
1．下列说法中，错误的说法是 (
180π°进行转化．
题型二
（1) 把112º30′化成弧度(精确到0.001)；
（2）把112º30′化成弧度（用π表示）。
解： （1）112º30′=112.5º，

1
0.0175

1.1.2弧 度 制名师课件


s 1 r2 1 lr
2
2
例1：把67 30化成弧度
解：
67
30


67
1 2

67 30 rad 67 1 3 rad
180
28
1


180
(rad)
Hale Waihona Puke 1(rad)
180

例2：把 4 rad化成角度。
5
解：4 rad 4 180 144
法二:(利用弧度与角度之间的互换关系)
rad (180 ) , n 180


l n r r (180 ) r 180 180
l r
(2)扇形面积公式 方法一：
s n r2 (角度制）
360
由弧长的计算公式（或弧度与角度的运算关系）
正角 零角 负角
任意角的集合
正实数 零 负实数
实数集合
4.角度制与弧度制的换算
用“弧度”与“度”去度量每一个角时， 除了零角以外，所得到的量数都是不同的， 但它们既然是度量同一个角的结果，二者就 可以相互换算．
若弧是一个整圆，它的圆心角是周角， 其弧度数是2π ，而在角度制里它是3600.
因此 3600 =2π (一般情况下弧度 单位yad可以省略不写)
3、若是第二象限角，那么 和
22
都不是第几象限角（ B ）
A.一 B.二 C.三 D.四
4、下列各对角中，终边相同的是( C )
A. 3 和2k 3（k Z） B. 和 22
2
2
55
C. 7 和11
D. 20 和122

高中数学课件-1.1.2弧度制


练:已知扇形的周长为8cm，当它的半径和 圆心角各取什么值时，扇型的面积最大？ 求出最大面积。
任意角的集合 正角 零角
实数集R 正实数 0
例如； 弧度的角 6
2弧度的角
正数 6
负数 2
负角
负实数
每一个角都有唯一的一个实数（这个角的弧度数或度数）与它对应；
反之，每一个实数也都有唯一的一个角（弧度数或度数等于这个实 数的角）与它对应。
五、小结：
弧度制
角度制
度量单位
弧度(10进制)
度(60进制,1=60,1′=60)
[总结]
2 rad 360
rad 180
1rad
180
57.30 5718
（1）仅出现“弧度”，
可以直接乘 (180)
化简即可
例2、把 3 rad ,-2.1 rad 化成度。
5
解： 3 rad 3 (180)108
5
5
2.1rad
2.1 (180)
120.33
三、课堂练习：
课堂练习
1、下列诸命题中，正确的是（ C ）
A、１弧度是１度的圆心角所对的弧 B、１弧度是长度为半径的弧 C、１弧度是长度等于半径长的弧所对的圆心角 D、１弧度是１度的弧与１度的角之和
二、角度与弧度的换算： [总结]
1、把角度换成弧度：
l r
（1）仅出现“度”，
360 2 rad
180 rad
1.1.2弧 度 制
1、1º的角是怎样规定的？
O• 规定周角的1/360叫做1度的角。
2、什么叫角度制？
用度作单位来度量角的单位制叫做角度制。
3、角度制的单位是什么？ “度”（即“ º”） 不能省略

高中数学课件--必修四1.1.2 弧度制


0° 360°
x
几何法
如图
如图
1.1.2
弧度制
弧度制定义
我们把长度等于半径长的弧所对的圆心角叫 做 1弧度的角， 即用弧度制度量时，这样的 圆心角等于1 rad. 若弧 AB 的长等于半径 r , 则∠AOB= 1 rad.
若弧 AB 的长等于 2r , 则∠AOB= 2 rad.
问题 1 ：若弧是一个半圆，则其圆心角的弧度数是多 少？若弧是一个整圆呢？
2 当 k 2n( n Z ) 时 ，
180°
y
90°
0°
O
360°
x
n 360 n 360 45 ， n Z 2 故 是第一象限的角 . 2 当 k 2n 1( n Z ) 时 ， n 360 180 n 360 225 ， n Z 2 故 是第三象限的角 . 2 综上可知： 是第一或第三象限的角 .
4 r AOB 4 . r
注意: 用角度制和弧度制来度量零角，单位不同， 但量数相同（都是0）； 用角度制和弧度制度量任一非零角，单位不同，量数 也不同.
角度制与弧度制的换算
若弧是一个整圆，它的圆心角是周角， 其弧度数是2π，而在角度制里它是360°，
因此 360 2 rad ，
例3.利用弧度制证明扇形弧长公式：l =R; 面积公式 :
1 S lR ，其中 l是扇形的弧长 ， R是圆的半径 .( 0) 2
圆心角为 1 rad 的扇形面积为 证明：
R
又 弧长为 l 的扇形的圆心角是 l O l rad R 1 2 l 1 扇形的面积 S R lR . 2 R 2 说明：扇形面积公式还可以表示为 S 1 | | R 2 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

l=
360
n
思考3 如图, 思考3:如图,把长度等于半径长的圆弧 所对的圆心角叫做1弧度的角,记作1rad 1rad, 所对的圆心角叫做1弧度的角,记作1rad, 读作1弧度. 那么, 读作1弧度. 那么,1弧度圆心角的大小 与所在圆的半径的大小是否有关? 与所在圆的半径的大小是否有关?为什 么? r
思考5 已知一个扇形所在圆的半径为R 思考5:已知一个扇形所在圆的半径为R, 弧长为l,圆心角为α 弧长为 ,圆心角为α( 0 < a < 2p )那么 扇形的面积如何计算? 扇形的面积如何计算?
1 1 2 l S = lR = aR = 2 2 2a
2
思考6:在弧度制下,与角α终边相同的 思考6 在弧度制下,与角α 角如何表示? 角如何表示? 终边在坐标轴上的角如何 表示? 表示? β = α + 2kπ (k ∈Z) 终边x轴上: 终边x轴上: kπ (k ∈Z) π 终边y轴上: 终边y轴上: + kπ (k ∈Z) 2
0
p 6
p 4
p 3
p 2
2p 3
3p 4
5p 6
p
3p 2
2p
今后用弧度制表示角时,"弧度"二字 今后用弧度制表示角时, 弧度" rad"通常略去不写 通常略去不写, 或"rad 通常略去不写,而只写该角所 对应的弧度数. α=2表示 表示α 2rad的角 的角. 对应的弧度数.如α=2表示α是2rad的角. 思考4 在弧度制下, 思考4:在弧度制下,角的集合与实数集 之间可以建立一个一一对应关系, R之间可以建立一个一一对应关系,这个 对应关系是如何理解的? 对应关系是如何理解的?
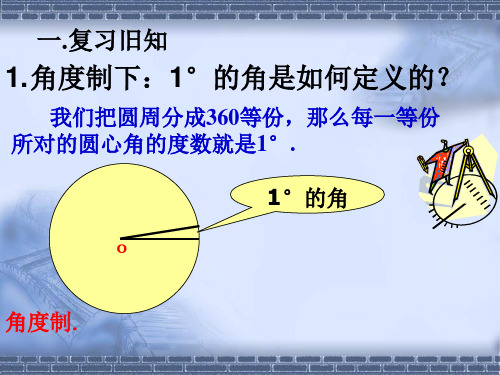
探究1 探究1:弧度的概念 思考1 在平面几何中, 思考1:在平面几何中,1°的角是怎样 定义的? 定义的? 将圆周分成360等份, 将圆周分成360等份,每一段圆弧所 360等份 对的圆心角就是1 的角. 对的圆心角就是1°的角. 思考2 在半径为r的圆中,圆心角n 思考2:在半径为r的圆中,圆心角n°所 对的圆弧长如何计算? 对的圆弧长如何计算? 2πr
3.与 是什么? 是什么? S={β|β=α+ 360 360° S={β|β=α+k360°,k∈Z} 4.长度可以用米,厘米,英尺, 4.长度可以用米,厘米,英尺,码等 长度可以用米 不同的单位度量, 不同的单位度量,物体的重量可以用千 磅等不同的单位度量. 克,磅等不同的单位度量.不同的单位制 能给解决问题带来方便, 能给解决问题带来方便,以度为单位度 量角的大小是一种常用方法, 量角的大小是一种常用方法,为了进一 步研究的需要, 步研究的需要,我们还需建立一个度量 角的单位制. 角的单位制.
小结作业 1.用度为单位来度量角的单位制叫做 用度为单位来度量角的单位制叫做角 1.用度为单位来度量角的单位制叫做角 度制, 度制,用弧度为单位来度量角的单位制 叫做弧度制 弧度制. 叫做弧度制 2.度与弧度的换算关系,由180°= π 度与弧度的换算关系, 180° rad进行转化,以后我们一般用弧度为 rad进行转化, 进行转化 单位度量角. 单位度量角. 3.利用弧度制, 3.利用弧度制,使得弧长公式和扇形的 利用弧度制 面积公式得以简化, 面积公式得以简化,这体现了弧度制优 点.
l= 2p r n 360
A
B r 1rad O
思考4 约定:正角的弧度数为正数, 思考4:约定:正角的弧度数为正数,负 角的弧度数为负数, 角的弧度数为负数,零角的弧度数 2r A 0.如果将半径为 如果将半径为r 为0.如果将半径为r圆的一条 r 半径OA OA, 半径OA,绕圆心顺时针旋转到 O B OB,若弧AB长为2r 那么∠ AB长为2r, OB,若弧AB长为2r,那么∠AOB 的大小为多少弧度? 的大小为多少弧度? -2rad. 思考5 如果半径为r的圆的圆心角α 思考5:如果半径为r的圆的圆心角α所 对的弧长为l,那么, 对的弧长为 ,那么,角α的弧度数的绝 对值如何计算? 对值如何计算? l
§3
弧度制
问题提出
1.角是由平面内一条射线绕其端点从 1.角是由平面内一条射线绕其端点从 一个位置旋转到另一个位置所组成的图 其中正角,负角, 形,其中正角,负角,零角分别是怎样 规定的? 规定的? 2.在直角坐标系内讨论角, 2.在直角坐标系内讨论角,象限角是 在直角坐标系内讨论角 什么概念? 什么概念?
知识迁移 按照下列要求, 67°30′化成 例1 按照下列要求,把67°30′化成 弧度: 弧度: 精确值; (1)精确值; 精确到0.001的近似值. 0.001的近似值 (2)精确到0.001的近似值.
3 67 30= p rad 1.178 rad 8
0
已知扇形的圆心角为72 72° 例2 (1) 已知扇形的圆心角为72°, 半径等于20cm 求扇形的弧长和面积; 20cm, 半径等于20cm,求扇形的弧长和面积; 已知扇形的周长为10cm 10cm, (2)已知扇形的周长为10cm,面积为 求扇形的圆心角的弧度数. 4cm2,求扇形的圆心角的弧度数.
作业: 作业:
习题1.1 A组 P10 习题1.1 A组: 6,7,8,9,10.
�
α=
r
思考6 半径为r的圆的圆心与原点重合, 思考6:半径为r的圆的圆心与原点重合, 角的始边与x轴的非负半轴重合, 角的始边与x轴的非负半轴重合,交圆于 终边与圆交于点B 下表中∠AOB的 点A,终边与圆交于点B,下表中∠AOB的 弧度数分别是多少? 弧度数分别是多少?
pr 弧AB的长 AB的长 OB旋转的方向 OB旋转的方向 逆时 针 ∠AOB的弧度 ∠AOB的弧度 数
2pr r 逆时 顺时 针 针
2r 顺时 针
3pr 顺时 针
p
2p
-1
-2 - 3p
探究( ):度与弧度的换算 探究(二):度与弧度的换算 思考1 思考1:一个圆周角以度为单位度量是多 少度?以弧度为单位度量是多少弧度? 少度?以弧度为单位度量是多少弧度? 由此可得度与弧度有怎样的换算关系? 由此可得度与弧度有怎样的换算关系? 180°=p rad. 180° 思考2 根据上述关系, 思考2:根据上述关系,1°等于多少弧 1rad等于多少度 等于多少度? 度?1rad等于多少度?
180 0 180 0 0 1rad = ≈ 57.30 = 57 18′ π 1 =
0
π
rad ≈ 0.01745rad
思考3 根据度与弧度的换算关系, 思考3:根据度与弧度的换算关系,下表 中各特殊角对应的弧度数分别是多少? 中各特殊角对应的弧度数分别是多少?
度 00 弧 度 300 450 600 900 1200 1350 1500 1800 2700 3600