三河市2010-2011数学第一次模拟考试九年级参考答案

反比例函数基础练习题一一、选择题1.（衢山初中2011年中考一模）如图，直线和双曲线（）交于A 、B 两点，P 是线段AB 上的点（不与A 、B 重合），过点A 、B 、P 分别向x 轴作垂线，垂足分别为C 、D 、E ，连接OA 、OB 、OP ，设△AOC 的面积为、△BOD 的面积为、△POE 的面积为，则 ( )A ．B ．C ．D ．2.（2011年北京四中三模）若点（-5，y 1）、(-3,y 2)、(3,y 3)都在反比例函数y= -3x 的图像上，则（ ）A ．y 1＞y 2＞y 3B ．y 2＞y 1＞y 3C ．y 3＞y 1＞y 2D ．y 1＞y 3＞y 2 3.（2011年北京四中五模）已知反比例函数xy k=的图象在一、三象限，则直线k k +=x y 的图象经过（ ）.A 、一、二、三象限B 、二、三、四象限C 、一、三、四象限D 、一、二、四象限 4．（淮安市启明外国语学校2010－2011学年度第二学期初三数学期中试卷）已知反比例函数y ＝－2x ，下列结论不正确．．．的是（ ） A ．图象经过点（－2，1） B ．图象在第二、四象限 C ．当x ＜0时，y 随着x 的增大而增大 D ．当x ＞－1时， y ＞25.（2011年浙江省杭州市城南初级中学中考数学模拟试题）如图，矩形ABCD 的对角线BD 经过坐标原点，矩形的边分别平行于坐标轴，点C 在反比例函数ky x=的图象上.若点A 的坐标为（－2，－2），则k 的值为（ ） A ．-2 B ．2 C ．3 D ．4 6．（2011年上海市卢湾区初中毕业数学模拟试题）如图，某反比例函数的图像过点M （2-，1），则此反比例函数表达式为（ ） A ．2y x =B ．2y x =-C ．12y x= D ．12y x =-.第1题图l ky x=0k >1S 2S 3S 123S S S <<123S S S >>123S S S =>123S S S =<x-21y O第6题图第5题7．（2011年北京四中模拟26）已知k ＞0 ，那么函数y=kx的图象大致是 （ ）8．(2011山西阳泉盂县月考)在反比例函数y=xm21-的图象上有两点A （x 1,y 1）,B (x 2,y 2),当x 1＜0＜x 2时，有y 1＜y 2, 则m 的取值范围是（ ） A. m ＜0 B. m ＞0 C. m ＜21 D. m ＞219．（2011年北京四中中考模拟19）在同一直角坐标系中，函数y=kx+k ，与y=xk-（k 0≠）的图像大致为（ ）10. （2011年黄冈市浠水县中考调研试题）如图,某个反比例函数的图象经过点(－1,1),则它的解析式为（ ）A .)0(1>=x x y B .)0(1>-=x x y C .)0(1<=x x y D .)0(1<-=x xy 11. （2011年北京四中中考全真模拟17）在函数21-=x y 中，自变量x 的取值范围是（ ）A. x ≥2B. x>2C. x ≤2D. x<212.(北京四中模拟)已知三点11(,)x y 、22(,)x y 、33(,)x y 均在双曲线4y x=上，且1230x x x <<<，则下列各式正确的是（ ）A.123y y y <<B.213y y y <<C.312y y y <<D.321y y y <<13.（2011杭州模拟）探索二次函数2x y =和反比例函数xy 1=交点个数为 ( ) A ．1个 B ．2个 C ．3个 D ．0个 14.（2011杭州模拟25）双曲线x 10y =与x6y =在第一象限内的图象依次是M 和N ，设点P 在图像M 上，PC 垂直于X 轴于点C 交图象N 于点A 。

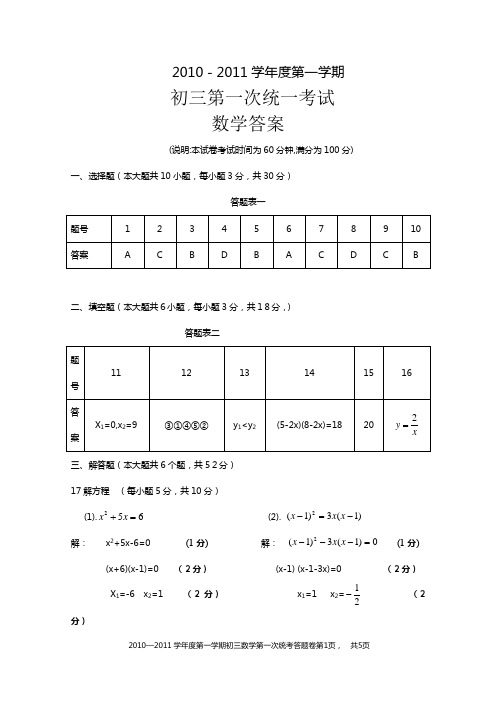
2010－2011学年度第一学期初三第一次统一考试数学答案(说明:本试卷考试时间为60分钟,满分为100分)一、选择题（本大题共10小题，每小题3分，共30分）答题表一二、填空题（本大题共６小题，每小题3分，共1８分，） 答题表二三、解答题（本大题共6个题，共5２分） 17解方程 （每小题5分，共10分）(1).652=+x x (2). )1(3)1(2-=-x x x解： x 2+5x-6=0 (1分) 解： 0)1(3)1(2=---x x x (1分)(x+6)(x-1)=0 （2分） (x-1) (x-1-3x)=0 （2分） X 1=-6 x 2=1 （2分） x 1=1 x 2=21-（2分） 18.（7分）解：（1）画图准确即得 3分CBMN D（图25-1）1 2Q（2）由（1）得：5DE ,DE 10(m)36==得（4分） 19.（7分）证明：连结BD 交AC 与O 点 （1分） ∵□ABCD∴AO=CO,BO=DO (2分) 又∵AP=CQ ∴AP+AO=CQ+CO即 PO=QO （2分） ∴四边形PBQD 是平行四边形 （2分） （其他方法酌情给分）20.解：设每套房降价x 万元时，每天获利1200万元 （40-x ）(20+2x)=1200 （3分） X 2-30x+200=0 (x-10)(x-20)=0X 1=10 x 2=20 （2分）因为一套房降价≤100×1500÷1000=15（万元），所以x=20不合题意，舍去 （1分） 答：每套房降价10万元时每天获利1200万元 （1分）21[解] （1）证明：∵四边形ABCD 是菱形∴AB = AD ，∠1 =∠2 （2分）又∵AN = AN∴△ABN ≌ △ADN （2分）（2）解：∵∠ABC =90°，∴菱形ABCD 是正方形（1分） ∴∠CAD =45°.下面分三种情形：Ⅰ）若ND =NA ，则∠ADN =∠NAD =45°.此时，点M 恰好与点B 重合，得x =6 （1分） Ⅱ）若DN =DA ，则∠DNA =∠DAN =45°.此时，点M 恰好与点C 重合，得x =12；（1分） Ⅲ）若AN =AD =6，则∠1=∠2，由AD ∥BC ，得∠1=∠4，又∠2=∠3， ∴∠3=∠4，从而CM =CN ， 易求AC =62，∴CM =CN =AC －AN=62－6， （1分） 故x = 12－CM =12－（62－6）=18－62 （1分）综上所述：当x = 6或12 或18－62时，△ADN 是等腰三角形 （1分） 22.（1）解：∵xmy =过点A （1,4） ∴m=4 （2分） ∴反比例函数解析式为：xy 4= （1分） （2）∵B(a,b)在xy 4=上 ∴ab=4 (1分) S △ABD =21BD(AC-OD) ∴4)4(21=-a a 解得：a=3 （1分）∴b=34（1分） B(3, 34) （1分）（3）解：设直线AB 为y=kx+b⎪⎩⎪⎨⎧=+=+3434b k b k 解得：k=34- b=316直线AB 为y=-34-x+316(1分 )直线AB 与x 轴的交点为E(0, 316)OE=316 (1分 )S △AOB =S △BOE -S △AOE =21OE ·BD-21OE ·OC=21×316×3-21×316×1=316 (2分 )其他方法按步骤给分。

三河市2010－2011学年度第一学期期末考试九年级数学参考答案一、选择题（本大题共12个小题，每小题2分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确答案的选项填入下表中）二、填空题（本大题共6个小题，每小题3分，共18分．把答案写在题中横线上） 13、x ≥1 14、50° 15、113 16、2 17、2 18、252或12.5 三、解答题（本大题共8个小题，共78分．解答应写出文字说明、证明过程或演算步骤）19．（本小题满分8分） 解：由题意得：05)1()1(2=-⨯-+-m …………………………………2分解得m =-4………………………………………4分当m =-4时，方程为0542=--x x ………………………………………6分 解得：x 1=-1 x 2=5所以方程的另一根x 2=5………………………………………8分 20．（本小题满分8分）解：设正方形观光休息亭的边长为x 米. ………………………………………1分依题意，有(1002)(502) 3 600.x x --=………………………………………4分 整理，得2753500.x x -+=………………………………………5分 解得12570.x x ==，………………………………………6分7050x =>Q 不合题意，舍去， 5.x ∴=………………………………7分答：矩形花园各角处的正方形观点休息亭的边长为5米. ………………………8分21．（本小题满分9分） （1） 证明：∵ △ABC 是等边三角形，∴ ∠BAC ＝∠ACB ＝60°．∠ACF ＝120°．………………………………3分 ∵ CE 是外角平分线， ∴ ∠ACE ＝60°．∴ ∠BAC ＝∠ACE ． ………………………………5分 又∵ ∠ADB ＝∠CDE ，∴ △ABD ∽△CED ． ………………………………7分 （2）由（1）△ABD ∽△CED 得，AB ADEC CD==2………………………………8分 ∵AB ＝6∴EC=3………………………………9分 22．（本小题满分9分） 解：（1）设二次函数的解析式为2y ax bx c =++………………………………1分 ∵二次函数的图象经过点 ()()()033025--，，，，，，得： ∴ 3930425c a b c a b c =⎧⎪-+=⎨⎪++=-⎩…………………………………………………………4分解得：1a =-，2b =-，3c =，……………………………………………………5分 ∴二次函数的解析式为223y x x =--+………………………………………………6分 （2）∵2(2)2(2)34433---⨯-+=-++=∴点(23)P -，在这个二次函数的图象上 ················································································· 7分∵2230x x --+= ∴1231x x =-=，∴与x 轴的交点为(30)-，、(10)， ·························································································· 8分 14362PAB S =⨯⨯=△ ············································································································· 9分23．（本小题满分10分） 解: （1）法一：·············································· 4分 ············································ 6分P (和为奇数)=126=21. ···································································································· 8分 （2）公平.理由为：P (和为偶数)=126=21 ∵P (和为奇数)= P (和为偶数) ∴该方法公平 ························································································································ 10分 24．（本小题满分10分） （1）100+-=x m …………………………………3分 不写范围或写成（0≤x ≤100）或（50≤x ≤100）不扣分 （2）函数解析式为y ＝－x 2＋150x －5000……………………7分 （3）∵x ＝－)1(2150-⨯＝75………………………………9分在50＜x ＜75元时，每天的销售利润随着x 的增大而增大………10分 25．（本小题满分12分）解：（1）DE Q 垂直平分AC ， 90DEC ∴∠=°．DC DEC ∴为△外接圆的直径.DC ∴的中点O 即为圆心. …………………………2分连接.OE又知BE O 是⊙的切线，90EBO BOE ∴∠+∠=°．………………………………4分在Rt ABC △中，E 是斜边AC 的中点， BE EC ∴=． EBC C ∴∠=∠. 又2BOE C ∠=∠Q , 290C C ∴∠+∠=°.30C ∴∠=°.………………………………………………………………6分（2）在Rt ABC △中，AC =B （第26题图）（2））A D E F GC122EC AC ∴==…………………………………………………8分 90ABC DEC ∠=∠=Q °D C ABCE ∴∽△△．……………………………………10分A CBCD CE C∴=……………………………………11分 54DC ∴=. D E C ∴△外接圆的半径为58. ……………………………………………12分26．（本小题满分12分）解：（1）当正方形DEFG 的边GF 在BC 上时，如图（1），过点A 作BC 边上的高AM ，交DE 于N ，垂足为M .∵S △ABC =48，BC =12，∴AM =8.∵DE ∥BC ，△ADE ∽△ABC , ………2分∴AMANBC DE =，而AN=AM －MN=AM －DE ，∴8812DEDE -=. ……………………4分 解之得8.4=DE .∴当正方形DEFG 的边GF 在BC 上时，正方形DEFG 的边长为4.8.…6分 （2）分两种情况：①当正方形DEFG 在△ABC 的内部时，如图（2），△ABC与正方形DEFG 重叠部分的面积为正方形DEFG 的面积，∵DE =x ，∴2x y =，此时x 的范围是x <0≤4.8…7分 ②当正方形DEFG 的一部分在△ABC 的外部时，如图（2），设DG 与BC 交于点Q ，EF 与BC 交于点P ， △ABC 的高AM 交DE 于N ，∵DE =x ，DE ∥BC ，∴△ADE ∽△ABC , …………8分 即AMANBC DE =，而AN =AM －MN =AM －EP , （第26题图(1)）A D E C N∴8812EP x -=，解得x EP 328-=.………9分 所以)328(x x y -=, 即x x y 8322+-=.………10分由题意，x >4.8，x <12,所以128.4<<x .因此△ABC 与正方形DEFG 重叠部分的面积为⎪⎩⎪⎨⎧<<+-=)128.4(83222x x x x y …………………………………11分 当x <0≤4.8时，△ABC 与正方形DEFG 重叠部分的面积的最大值为4.82=23.04当128.4<<x 时，因为x x y 8322+-=，所以当6)32(28=-⨯-=x 时，△ABC 与正方形DEFG 重叠部分的面积的最大值为24)32(480)32(42=-⨯-⨯-⨯.因为24>23.04，所以△ABC 与正方形DEFG 重叠部分的面积的最大值为24. …………………12分M B （第26题图(3)）AD EF GCNP Q (0< x ≤4.8)。

分式一、 选择题 A 组1、（2011年北京四中模拟26） 若分式31xx -有意义，则x 应满足 （ ） A ．x =0 B ．x ≠0 C ．x =1 D ．x ≠1答案：D3、（淮安市启明外国语学校2010－2011学年度第二学期初三数学期中试卷）化简 m 2－1m ÷m+1m的结果是（ ）A ．m －1B ．mC ．1mD ．1m －1答案：A4、（2010－2011学年度河北省三河市九年级数学第一次教学质量检测试题）化简22424422x x xx x x x ⎛⎫--+÷ ⎪-++-⎝⎭，其结果是（ ） A ．82x -- B ．82x - C ．82x -+ D ．82x + 答案：D5、（2011年浙江杭州七模）在函数21-=x y 中，自变量x 的取值范围是（ ） A ．2-≠x B ．2≠xC ．x ≤2D ．x ≥2答案：BB 组1、（2011浙江慈吉 模拟）已知分式xx -+21, 当x 取a 时, 该分式的值为0; 当x 取b 时, 分式无意义; 则ab 的值等于（ ） A. 2- B. 21C. 1D. 2 答案：B2、（2011年三门峡实验中学3月模拟）要使式子a ＋2a有意义，a 的取值范围是（ ） A 、a ≠0 B 、a ＞－2且a ≠0 C 、a ＞－2或a ≠0 D 、a ≥－2且a ≠0 答案：D3、（2011杭州上城区一模）下列判断中，你认为正确的是（ ）A ．0的倒数是0 B.2π是分数 12答案：C4、（安徽芜湖2011模拟）化简29333a a a a a ⎛⎫++÷⎪--⎝⎭的结果为 （ ） A ．aB ．a -C ．()23a +D ．1答案: A5、（浙江杭州金山学校2011模拟）（原创）函数14y x =-中自变量x 的取值范围是（ ▲ ）A ．x ≤3B ．x ＝4C ． x ＜3且x≠4D ．x≤3且x ≠4 答案：A6、（2011深圳市全真中考模拟一）化简24()22a a a a a a---+ 的结果是 (A)一4 (B)4 (C)2a (13) 2a +4 答案：A7、（2011年北京四中33模）若分式1632--x x 的值为0,则x 的值为（ ） A ．4B. －4C. ±4D. 3答案D二、 填空题A 组1、（2011年北京四中三模）若x 为12-的倒数，则633622-++÷---x x x x x x 的值为 .答案：12、（2011年北京四中四模）化简112-+x x 得___ __. 答案：11-x 4．（2011年江苏连云港）若一个分式含有字母m 2，且当5m =时，它的值为2，则这个分式可以是 ． （写出一个．．即可） 答案250m（不唯一）； B 组1、（2011浙江慈吉 模拟）化简: mm m -+-2242=______________. 答案：2--m2、（2011 天一实验学校 二模）在函数15y x =-中，自变量x 的取值范围是 ． 答案： x ≠5__3、（2011北京四中模拟）化简：23224x x xx x x 骣÷ç-?÷ç÷ç桫++-答案：24x -4、（2011深圳市三模）函数函数12-+=x x y 中自变量x 的取值范围是 ；答案： 2-≥x 且1≠x ；5、（浙江杭州靖江2011模拟）函数y=)2(1--x x 的自变量x 的取值范围是_____________。

直角三角形与勾股定理练习题含参考答案（第3 题）直角三角形与勾股定理练习题含参考答案选择题1、(浙江杭州模拟14)如图折叠直角三角形纸片的直角，使点 C 落在斜边AB 上的点 E 处.已知AB= ,∠B=30°,则DE的长是(). A.6B.4C. D.2答案：B 2.（湖北崇阳县城关中学模拟）直角三角形两直角边和为7，面积为6，则斜边长为（）A.5B.C.7D.答案：A3 ．（年杭州市上城区一模）梯形ABCD 中AB ∥ CD ，∠ ADC +∠ BCD =90°，以AD 、AB 、BC 为斜边向形外作等腰直角三角形，其面积分别是S 1 、S2 、S3 ，且S 1 + S 3 =4 S 2 ，则CD =（）A.2.5 ABB.3 ABC.3.5 ABD.4 AB 答案：B4．（年浙江省杭州市模2）直角三角形两直角边和为7，面3 83 4 3 积为6，则斜边长为（）A.5B.C.7D.答案：A填空题1、（年北京四中三模）如图是一个艺术窗的一部分，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大正方形的边长为5cm，则正方形A、B、C、D 的面积和是．答案：25cm22．（2010－学年度河北省三河市九年级数学第一次教学质量检测试题）如图是两个全等的三角形纸片，其三边长之比为3：4：5，按图中方法分别将其对折，使折痕（图中虚线）过其中的一个顶点，且使该顶点所在两边重合，记折叠后不重叠部分面积分别为S A ，S B ，已知S A +S B =13，则纸片的面积是. B A C D答案：36 3、(浙江杭州模拟15)如图，将含30°角的直角三角尺ABC绕点B 顺时针旋转150°后得到△EBD，连结CD.若AB=4cm.则△BCD 的面积为．答案：4．(年宁夏银川)将一副三角尺如图所示叠放在一起，若=14cm ，则阴影部分的面积_________cm2 ．答案：5.(浙江省杭州市8 模)如图1，是我国古代著名的“赵爽弦图”的示意图，它是由四全等的直角三角形围成的，若AC =6，BC =5，将四个直角三角形中边长为6 的直角边分别向外延长一倍，得到图 2 所示的“数学风车”，则这个风车的外围周长是__________；23cmAB249第2 题图S AS B第4 题图A C E D B F 30°45°图2 A B C 图1 A B C(第5 题图)答案:76 6、（年浙江杭州二模）如图是小明设计用手电来测量某古城墙高度的示意图，点P 处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD 的顶端C 处，已知AB⊥BD，CD⊥BD，且测得AB=1.2 米，BP=1.8 米，PD=12 米，那么该古城墙的高度是米. 答案：87、（年浙江杭州八模）如图，小明在A 时测得某树的影长为3米，B 时又测得该树的影长为12 米，若两次日照的光线互相垂直，则树的高度为_____米. . 答案：6AB PDC第6 题图（第7 题）A 时B 时图2 A BC 图1 A B C第8 题图8、（年浙江杭州八模）如图1，是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC =6，BC=5，将四个直角三角形中边长为6 的直角边分别向外延长一倍，得到图2 所示的“数学风车”，则这个风车的外围周长是__________；答案：76 9 9 .(浙江省杭州市党山镇中年中考数学模拟试卷)如图，将边长为的等边△ ABC 折叠，折痕为DE ，点B 与点F 重合，EF 和DF 分别交于点M 、N ，DF AB ，垂足为D ，AD＝1，则重叠部分的面积为. 答案：B B 组1．（年杭州三月月考）将一副三角板按如图1 位置摆放,使得两块三角板的直角边AC 和MD 重合.已知AB = AC =8cm,将△ MED 绕点 A ( M )逆时针旋转60°后(图2),两个三角形重叠（阴影）部分的面积是▲cm2答案：3 3AC 3 934 4+3 16 48__A图2图1A(M)__BA(M)(第1 题)2．（年重庆江津区七校联考一模）一元二次方程的两根恰好是一直角三角形的两边长，则该直角三角形的面积为。

2010年初中毕业学业考试第一次模拟考试试卷数 学亲爱的同学：1、祝贺你完成了初中阶段的学习，现在是展示你的学习成果之时，你可以尽情地发挥，仔细、仔细、再仔细！祝你成功！2、本试卷共六道大题, 满分120分,考试时量120分钟。

一、精心选一选，旗开得胜 (本大题共10个小题, 每小题3分，满分30分. 每小题给出的四个选项中，只有一项是符合题设要求的，请把你认为符合题目要求的选项填在下表中相应的题号下)1.20101的倒数是Ａ．2010 B ．2010- C ．20101 D ．20101-2. 温家宝总理在政府工作报告中指出，2009年在国际金融危机的强烈冲击下，我国国内生产总值仍达到33.5万亿元，比上年增长8.7%．33.5万亿元这个数据用科学记数法表示为 A ．33.5×109元B ．33.5×1012元C ．3.35×1012元 D ．3.35×1013元3.一个不等式的解集为12x -<≤，那么在数轴上表示正确的是4. 反比例函数1y x=的图象位于A ．第一、二象限B ．第一、三象限C ．第二、四象限D ．第三、四象限1- 02ABC D1- 021- 021- 025. 如图1，直线a ∥b ，直线c 与a 、b 相交，∠1 ＝70°，则∠2 等于 A ．70°B ．20°C ．110°D ．50°6. 下列命题中，正确的是A ．矩形的对角线相互垂直 图1B ．菱形的对角线相等C ．平行四边形是轴对称图形D ．等腰梯形的对角线相等7. 如图2，若用半径为9，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的 底面半径是A ．1.5B ．2C ．3D ．68. 如图3，把一张长方形纸片对折，折痕为AB ，以AB 的中点O 为顶点把平角∠AOB 三等分，沿平角的三等分线折叠，将折叠的图形剪出一个以O 为顶点的等腰三角形，那么剪出的平面图形一定是A ．正三角形B ．正方形C ．正五边形D ．正六边形图39. 二次函数2(1)2y x =--的图象上最低点的坐标是A ．(-1，-2)B ．(1，-2)C ．(-1，2)D ．(1，2) 10. 下列说法中，正确的是（ ）A ．“明天降雨的概率是80％”，表示明天有80％的时间降雨B ．“抛一枚硬币正面朝上的概率是0.5”，表示每抛硬币2次就有1次出现正面朝上C ．“彩票中奖的概率是1%”，表示买100张彩票一定有1张会中奖D ．在同一年出生的367名学生中，至少有两人的生日是同一天120°图2A BOO二、细心填一填，一锤定音(本大题共8个小题, 每小题4分, 满分32分)11. 计算：)6(2-⨯= ．12.一筐苹果总重x 千克，筐本身重2千克，若将苹果平均分成5份，则每份重 千克. 13.不等式组40320x x ->⎧⎨+>⎩的解集是 .14．函数xx y -=3的自变量x 的取值范围是_____________.15．如图4，点C 是线段AB 上的点，点D 是线段BC 的中点，若AB ＝10，AC ＝6 ，则CD ＝______________．图4 16．图5中圆与圆之间不同的位置关系有____________种．17．如图6，在梯形A B C D 中，D C A B ∥，D A C B =．若104A B D C ==，，tan 2A =，则这个梯形的面积是__________．18．在一个不透明的口袋中装有若干个只有颜色不同的球，如果已知袋中只有4个红球，且摸出红球的概率为31，那么袋中的球共有_________ 个．图）A C D BABCD图6图5三、用心做一做，慧眼识金(本大题共3个小题，第19小题7分，第20、21小题各8分，满分23分)19.化简：22221()11x x x x x x -+-÷+-20. 如图7，九年级某班同学要测量校园内旗杆的高度，在地面的C 点处用测角器测得旗杆顶A点的仰角∠AFE ＝60º，再沿直线CB 后退8m 到D 点，在D 点又用测角器测得旗杆顶A 点的仰角∠AGE ＝45º；已知测角器的高度为1.6m ，求旗杆AB 的高度(3≈1.73，结果保留一位小数)．图721. 小王某月手机话费的各项费用统计情况如图8所示图表，请你根据图表信息完成下列各题：图8 (1) 该月小王手机话费共多少元？(2）扇形统计图中，表示短信费的扇形圆心角为多少度？(3) 请将表格补充完整；(4) 请将条形统计图补充完整．能费话费话费费月功能费四、综合用一用，马到成功（本题满分8分)22．为了拉动内需，全省启动“家电下乡”活动。

动点与折叠专题 （1动点）例1、如图（后图备用），在梯形ABCD 中，AD //BC ，E 是BC 的中点，AD =5，BC =12，CD =24，∠C =45°，点P 是BC 边上一动点，设PB 的长为x ．（1）当x 的值为____________时，以点P 、A 、D 、E 为顶点的四边形为直角梯形； （2）当x 的值为____________时，以点P 、A 、D 、E 为顶点的四边形为平行四边形；；（3）点P 在BC 边上运动的过程中，以P 、A 、D 、E 为顶点的四边形能否构成菱形？试说明理由．PEABCDEABCD例2. 如图，ABC △中，点O 是边AC 上一个动点，过O 作直线MN BC ∥，设MN 交BCA ∠的平分线于点E ，交BCA ∠的外角平分线于点F ．（1）探究：线段OE 与OF 的数量关系并加以证明；（2）当点O 在边AC 上运动时，四边形BCFE 会是菱形吗？若是，请证明，若不是，则说明理由； （3）当点O 运动到何处，且ABC △满足什么条件时，四边形AECF 是正方形？AFN DC BM EO例3、在直角坐标系中，O 是原点，A 、B 、C 三点的坐标分别为A （18，0），B （18，8），C （6，8），四边形OABC 是梯形，点P 、Q 同时从原点出发，分别做匀速运动，其中点P 沿OA 向终点A 运动，速度为每秒2个单位，点Q 沿OC 、CB 向终点B 运动，速度为每秒3个单位，当这两点有一点到达自己的终点则另一点也停止运动，设从出发起，运动了t 秒， ①求直线OC 的解析式。

②试写出点Q 的坐标，并写出此时t 的取值范围。

③从运动开始，梯形被直线PQ 分割后的图形中是否存在平行四边形，若存在，求出t 的值，若不存在，请说明理由。

④t 为何值时，直线PQ 把梯形OCBA 分成面积为1︰7的两部分？例4．已知在正△ABC 中，AB =4，点M 是射线AB 上的任意一点（点M 与点A 、B 不重合），点N 在边BC 的延长线上，且AM = CN ．联结MN ，交直线AC 于点D ．设AM = x ，CD = y ． （1）如图，当点M 在边AB 上时，求y 关于x 的函数解析式，并写出自变量x 的取值范围． （2）当点M 在边AB 上，且四边形BCDM 的面积等于△DCN 面积的4倍时，求x 的值．（3）过点M 作ME ⊥AC ，垂足为点E ．当点M 在射线AB 上移动时，线段DE 的长是否会改变？请证明你的结论．ABC M ND例5、已知：如图，在菱形ABCD 中，AB =4，∠B =60°，点P 是射线BC 上的一个动点， ∠PAQ =60°，交射线CD 于点Q ，设点P 到点B 的距离为x ，PQ =y ． （1）求证：△APQ 是等边三角形；（2）求y 关于x 的函数解析式，并写出它的定义域；（3）如果PD ⊥AQ ，求BP 的值．例6、在梯形ABCD 中，AD //BC ，AB=CD=AD =5cm ，BC =11cm ，点P 从点D 出发沿DA 边以每秒1cm 的速度移动，点Q 从点B 出发，沿BC 边以每秒2cm 的速度移动（当点P 到达点A 时，点P 与点Q 同时停止移动），假设点P 移动的时间为x （秒），四边形ABQP 的面积为y （平方厘米）。

2011年九年级第一次模拟考试数学试题参考答案及评分说明说明：1．各校在阅卷过程中，如考生还有其它正确解法，可参照评分标准按步骤酌情给分．2．坚持每题评阅到底的原则，当考生的解答在某一步出现错误，影响了后继部分时，如果该步以后的解答未改变这一题的内容和难度，可视影响的程度决定后面部分的给分，但不得超过后继部分应给分数的一半；如果这一步后面的解答有较严重的错误，就不给分．3．解答右端所注分数，表示正确做到这一步应得的累加分数．只给整数分数．一、选择题（每小题2分，共24分）二、填空题（每小题3分，共18分）13．－1/3；14．5； 15．1/3； 16．x=5，y=1； 17．4л；18．243三、解答题（共78分）19．解：去分母：方程两边都乘以x(x+3)得：x+3=5 x…………………………………………………………………………4分移项合并得：4x=3 ……………………………………………………………………5分系数化1得：x=3/4 ……………………………………………………………………6分经检验：x=3/4 是原方程的根，………………………………………………………7分所以原方程的根是x=3/4.………………………………………………………………8分20．解：（1）先将等腰Rt△ABC向上平移4个单位，再向右平移6个单位后，可使点A平移到点O的位置. ……………………………………………………………………………2分图（略）……………………………………………………………………………3分（2）∵△ABC是等腰直角三角形，∴∠BAC=45°………………………………………………………………………4分又∵⊙O的半径为2 ，∴S扇形=（45л×22）/360 …………………………………………………………5分 =1/2л……………………………………………………………………………6分（3）图（略）………………………………………………………………………………8分21．解：（1）“3点朝上”的频率为：1/10 ………………………………………………………1分“5点朝上”的频率为：1/3；………………………………………………………2分（2）小明的说法不正确，因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大，只有当试验的次数足够大时，该事件发生的频率稳定在事件发生的概率附近.小强的说法也不正确，因为事件发生具有随机性，故“6点朝上”的次数不一定是100次. …………………………………………………………………………………………6分（3）开始……………8分 ∴P=1/3…………………………………………………………………………………………9分22．解：（1）将A （1，4）代入函数k y x 中，k =4，所以y =4/x ………………………1分 （2）∵S △ABD =1/2BD ·AE =1/2m （4－n ） =4，……………………………………………2分 B （m ，n ）在函数y =4/x 的图象上，所以mn =4， ………………………………3分 ∴m =3，n =4/3 ， ………………………………………………………………………4分即：点B （3，4/3）………………………………………………………………………5分（3）设直线AB 的解析式为：y =kx +b∵直线AB 经过A （1，4），B （3，4/3）∴ ………………………………………………………………………6分 解得：k =－4/3，b =16/3……………………………………………………………………7分 ∴直线AB 的解析式为：y =－4/3x +13/6…………………………………………………8分（4）10/3 ……………………………………………………………………………………9分23.解：（1）路线1：l 12=AC 2=25+π2； ……………………………………………………………1分路线2：l 22=（AB +BC ）2=49． ………………………………………………………2分 ∵l 12＜l 22，∴l 1＜l 2（填＞或＜）， ………………………………………………………3分 ∴选择路线1较短． ………………………………………………………………………4分（2）l 12=AC 2=AB 2+ 2=h 2+（πr ）2， …………………………………………………5分 l 22=（AB+BC ）2=（h+2r ）2， …………………………………………………………6分 l 12－l 22=h 2+（πr ）2－（h +2r ）2=r （π2r －4r －4h ）=r [（π2－4）r －4h ]；r 恒大于0，只需看后面的式子即可．……………………………………………………7分 当 时，l 12=l 22； 当r ＞ 时，l 12＞l 22； 当r ＜ 时，l 12＜l 22．……10分24．（1）同意． ………………………………………………………………………………1分 连接EF ， …………………………………………………………………………………2分 ∵∠EGF =∠D =90°，EG =AE =ED ，EF =EF ．∴Rt △EGF ≌Rt △EDF …………………………………………………………………3分 ∴GF =DF …………………………………………………………………………………4分 1 2 3 4 5 61 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 61 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 k +b =43k +b =4/3（2）由（1）知，GF =DF ．设DF = x ，BC =y ，则有GF = x ，AD =y ．∵DC =2DF ，∴CF =x ，DC = AB = BG =2x ，∴BF =BG +GF =3x ． …………………………………………………………………………5分 在Rt △BCF 中，BC 2+CF 2=BF 2 ，即y 2+x 2=(3x )2 ．…………………………………………6分.2AD y y AB x∴=∴== …………………………………………………………7分 （3）由（1）知，GF DF =．设DF x BC y ==，，则有.GF x AD y ==，DC n DF = ·，DC AB BG nx ∴===．(1)1CF n x BF BG GF n x ∴=-=+=+，（）． …………………………………………8分 在Rt BCF △中，222BC CF BF +=，即222[1][(1)]y n x n x +-=+（）． …………9分AD y yAB nx n ∴=∴==⎝． ……………………………………………10分 25．解: (1)在△ACD 是中，∵∠OAC =60°，OC =CA ，∴△ACO 是等边三角形， ……………………………………………………………1分 ∴∠AOC =60°， ……………………………………………………………………2分（2）∵CP 与⊙O 相切，OC 是半径，∴CP ⊥OC ， …………………………………………………………………………3分 ∴∠P =90°－∠AOC =30°， ………………………………………………………4分 ∴PO =2CD =8， ……………………………………………………………………5分（3）由等积三角形的判定方法知，需先确定M 的运动位置，再求弧长，①当点M 运动到点C 关于直径AB 的对称点M 1时，连结AM 1，OM 1，易得S △M 1AO = S △CAO ，∠AOM 1=60°， ……………………6分 ∴弧AM 1=4/3л ……………………………………………………………………7分 ②当点M 运动到点C 关于圆心O 的对称点M 2时，连结AM 2，OM 2，易得S △M 2AO = S △CAO ，∠AOM 2=120°， …………………8分 ∴弧AM 2=8/3л ………………………………………………………………………9分 ③当点M 运动到点C 关于直径AB 的对称点M 13时，连结AM 3，OM 3，易得S △M 3AO = S △CAO ，∠BOM 3=60°， ……………………10分 ∴弧AM 2M 3=16/3л …………………………………………………………………11分 所以，动点M 经过的弧长为：4/3л，8/3л，16/3л. ……………………………………12分26．解：（1）∵y =ax 2＋x ＋c 的图象经过A （－2，0），C （0，3）.∴c =3，a =－1/4∴所求解析式为：y =－1/4x 2＋x ＋3 …………………………………………1分（2）（6，0） …………………………………………………………………………2分（3）在Rt △AOC 中，∵AO =2，OC =3∴AC=根号13 ………………………………………………………………………………3分① 当P1A=AC时（P1在x轴的负半轴），P1（－2－根号13）；…………………4分②当P2A=AC时（P2在x轴的正半轴），P2（根号13－2）；……………………5分③当P3C=AC时（P3在x轴的正半轴），P3（2，0）；……………………………6分④当P4C=P4A时（P4在x轴的正半轴），在Rt△P4OC中，设P4O=x，则(x+2)2=x2+32解得：x=5/4∴P4（5/4，0）；………………………………………………………………………7分(4) 如图,设Q点坐标为(x，y) ，因为点Q在y=－1/4x2＋x＋3 上，即：Q点坐标为(x，－1/4x2＋x＋3)…………………………………………………8分连接OQ，S四边形ABQC= S△AOC+ S△OQC+ S△OBQ=3+3/2x+3(－1/4x2＋x＋3)=－3/4x2＋3/2x＋12…………………………∵a＜0，∴S四边形ABQC最大值=75/4，……………………11分Q点坐标为（3，15/4）…………………………12分。

ABCD EHF 三河市2010年学科抽测活动初赛试题九年级数学参考答案一、选择题（本大题共6个小题，每小题2分，共12分．在每小题给出的四个选项中，二、填空题（本大题共5个小题，每小题5分，共25分．把答案写在题中横线上）1、())22(21122+=-+n n n 2、0 3、π2 4、7 5、40︒ 6、1三、解答题1、（本小题满分8分）解：原式＝3x 2＋x －3x －1－x 2－2x －1…………………………（3分）＝2x 2－4x －2…………………………（5分）当x 2－2x ＝1时，原式＝2(x 2－2x)－2＝2×1－2＝0…………………………（8分）2、解：如图，分别过点D E 、作DF BC ⊥于点F ，EH BC ⊥于点H ． ∴EH DF ∥，90DFB DFC EHB EHC ∠=∠=∠=∠=︒．又90A ∠=︒，AD BC ∥， 90ABC ∴∠=︒ .∴四边形ABFD 是矩形． ∵AB=4,AD=22BF AD ∴==，4DF AB ==． ························ 2分 在Rt DFC △中，45C ∠=，∴∠FDC=45°∴∠FDC=∠C4FC DF ∴==． ···························································································································· 4分 又∵DE=EC ，EH DF ∥122EH DF ∴==． ························································································································ 6分2HC EH ∴==． 2FH ∴=．4BH ∴=． ······································································································································· 8分在Rt EBH △中，BE ∴== ············································································10分 说明：本题答案不唯一，其他解法，只要正确，请参照本评分标准给分。