下载文档原格式
第三节酶催化反应的动力学复习题问：略新授：Ⅰ酶反应动力学的概念：研究酶促反应速度及其影响因素（哪些因素影响、如何影响）称酶促反应动力学。
Ⅱ酶反应动力学的影响因素：酶浓度、底物浓度、pH、温度、抑制剂及激活剂等。
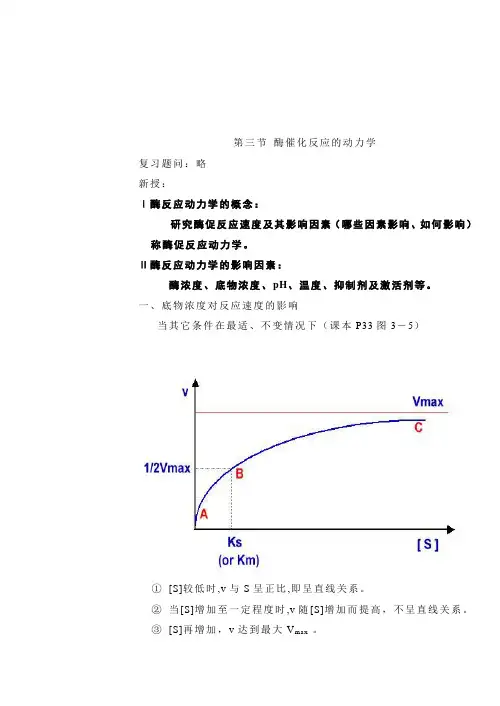
一、底物浓度对反应速度的影响当其它条件在最适、不变情况下（课本P33图3－5）①[S]较低时,v与S呈正比,即呈直线关系。
②当[S]增加至一定程度时,v随[S]增加而提高，不呈直线关系。
③[S]再增加，v达到最大V ma x 。
（一）米－曼氏方程式：⒈概念：酶促反应速度与底物浓度关系的数学方程式。
⒉方程式：说明：⑴Vmax为最大反应速度，［S］为底物浓度，K M为米氏常数⑵v是在不同［S］时的反应速度⑶当底物浓度很低时，V＝Vmax *［S］／K M，反应速度与底物成正比；反之，v≌Vmax ，反应速度达最大；再增加底物浓度，反应速度不受影响。
⒊K M概念：反应速度达到最大反应速度一半时的作用物浓度。
述：K M是酶的特征性常数，表示酶与作用物的亲和力大小。
K M越大，酶与作用物的亲和力越小。
同工酶的K M不同。
⒋米氏方程应用⑴酶的鉴定——根据K M相同与否判定是否同一个酶⑵酶的纯化——根据K M稳定与否判定酶是否被纯化⑶计算欲使反应速度达到某一特定反应速度时的合理[S]（二）Km的意义⒈K M值等于酶促反应速度达到Vmax一半时的作用物浓度⒉K M值可反映酶对底物的亲和力，两者呈反比⒊K M值是酶的特征性常数之一，只与酶的结构、底物和反应环境（如温度、pH、离子强度）有关，与酶浓度无关。
二、酶浓度对反应速度的影响（课本P33图3－6）述：在酶促反应系统中，当[S]足够大时，v∝[E] 。
三、温度对反应速度的影响⒈两者联系：温度对酶促反应的具有双重影响。
升高温度可加快酶促反应速度，同时也增加酶变性的机会。
述：温度升高到60℃以上时，大多数酶开始变性；80℃时，多数酶的变性已不可逆。
⒉最适温度⑴概念：酶催化活性最大时的环境温度述：人体组织中酶的最适温度一般在37－40℃⑵影响因素：反应时间⑶相互关系①酶可以在较短的时间内耐受较高的温度；相反，延长反应时间，最适温度变降低。
米氏方程动力学曲线嘿，朋友们，今天咱们来聊聊米氏方程动力学曲线，那可真是个有趣的小玩意儿，就像一场生物化学世界里的奇妙舞蹈。
你看啊，米氏方程就像一把神奇的钥匙，试图打开酶促反应速度这个神秘大门。
它的方程是v = Vmax[S] / (Km + [S])，这里面的v就像是一个小馋猫，它对底物浓度[S]那可是充满了渴望，就盼着能多吃点底物，好让反应速度快快跑起来呢。
这个动力学曲线啊，一开始的时候就像个刚睡醒的小懒虫，反应速度v 慢慢悠悠地往上爬。
底物浓度[S]就像是给小懒虫的小零食，开始的时候少得可怜，小懒虫只能有一搭没一搭地动一动，反应速度增加得那叫一个慢，就像蜗牛在爬玻璃墙。
当底物浓度[S]慢慢增加，达到一定程度的时候，就像小懒虫突然看到了一堆美食，那兴奋劲儿就别提了。
反应速度v开始蹭蹭地往上涨，就像火箭发射一样，这个阶段就像是曲线的加速期，小馋猫v看到越来越多的底物[S]，吃得不亦乐乎，反应速度也越来越快。
但是呢，这小馋猫也有吃饱的时候，就算底物浓度[S]再怎么增加，就像美食多得像小山一样，反应速度v也不会无限制地涨下去了。
这时候就到了曲线的平台期，v就像个吃饱喝足的大肚汉，懒洋洋地不想再动了，它已经达到了最大反应速度Vmax，不管再塞多少底物进去，它也就那么个速度了，就像一辆汽车已经踩到底油门，再怎么踩也快不了啦。
Km这个常数啊，就像是小馋猫的一个小脾气。
如果Km小，就说明小馋猫对底物特别亲近，很容易就和底物结合，反应速度也容易起来，就像两个人一见钟情，一点就着。
要是Km大呢，就像是小馋猫比较挑剔，底物得费好大劲儿才能让小馋猫有反应，就像追一个特别难追的对象似的。
这个米氏方程动力学曲线啊，还像一场音乐会。
底物浓度[S]是乐谱，反应速度v是演奏的旋律。
开始的时候乐谱简单，旋律也简单缓慢。
随着乐谱变得复杂，旋律也变得激昂起来，最后到了高潮，就一直维持在那个美妙的高音上，也就是Vmax啦。
再想象一下，这个曲线就像一个人爬山。
酶促反应动力学目的：酶催化反应的速度及各种因素对反应速度的影响1.米氏方程的推导米氏学说是1913年Michaelis和Menton建立的，认为反应分为两步，先生成酶-底物复合物（中间产物），再分解形成产物，释放出游离酶。
经过Briggs和Haldane的补充与发展，得到了现在的米氏方程。
对于上面的反应，首先有三点假设：第一，底物大过量，即[S]》[E]。
第二，在反应初期，产物浓度极小，忽略逆反应即k-2=0；第三，稳态假设，即随着反应的进行，复合物的形成速度逐渐降低，分解加快，在某一时刻达到平衡，复合物的浓度为常数，这种状态称为“稳态”。
体系达到稳态后，底物的消耗和产物的生成速度都是常数，且相等。
经测定，酶加入体系后，在几毫秒之内即可达到稳态，所以我们测定的初速度通常是稳态速度。
在产物积累较多之前，体系一直保持稳态，所以反应速度v=k2[ES]。
根据稳态假设，有k1[E][S]=(k-1+k2)[ES]，即[ES]=k1[E][S]/(k-1+k2)。
定义(k-1+k2)/k1=Km，因为[E]=[E]0-[ES]，故[ES]= [E]0[S]/(Km+[S])。
代入速度方程，得到v= k2[E]0[S]/(Km+[S])。
因为当[ES]=[E]0时速度最大，所以Vm=k2[E]0。
代入，得到下列米氏方程：2.米氏常数的意义米氏常数的物理意义是反应速度达到最大反应速度一半时的底物浓度。
其酶学意义在于，它是酶的特征常数，只与酶的性质有关，与酶浓度无关。
不同的酶其Km不同，同种酶对不同底物也不同。
在k2极小时1/Km可近似表示酶与底物的亲和力，1/Km越大，亲和力越大。
在酶的多种底物中，Km最小的底物叫做该酶的天然底物。
3.米氏常数的测定从酶的v-[s]图上可以得到Vm，再从1/2Vm处读出[s]，即为Km。
但实际上只能无限接近Vm，却无法达到。
为得到准确的米氏常数，可以把米氏方程加以变形，使它相当于线性方程，通过作图得到准确的米氏常数。
米氏动力学
米氏动力学（Meyerian Dynamics）是著名的心理学家John Meyer
提出的一种心理机制，他认为，在人们对新情况和变化做出反应时，
会产生三大基本动力：接纳、拒绝和延迟。
这三种动力使我们看待变
化事物的方式，也决定了我们对变化的态度和反应。
米氏动力学的主要概念是，做出正确的反应并不仅仅取决于事实
的认知和外部环境，而且也取决于内在动机、情感因素以及受影响的“感性因素”。
根据米氏动力学，我们会有三种不同的反应：接纳变化、拒绝变化、忽略变化。
接纳变化：人们接纳变化时，意味着他们把变化当作机遇来对待，乐于尝试新的可能性。
他们可能会激发出新的想法和行为来响应变化，对充满可能性的未来充满信心，并有积极的行动来实现它。
拒绝变化：有时，我们的反应会停留在拒绝变化的水平上，即坚
持原来的行业或者决定，而不进行更深入的思考和行动。
在拒绝前，
我们通常会把全部精力集中在重新确定自己内心深处的价值观和价值
体系上，希望找寻出对待变化的立场。
忽略变化：有时，我们可能会选择忽略变化。
忽略变化的重要性
是把变化的影响低估，或者直接将之忽略，贴以“慢慢来”的态度，
希望时间能够慢慢地影响变化并使之消失。
米氏动力学是John Meyer提出的一种心理服务动力学框架，通过它，我们可以深入探究人们对变化的态度和反应，更好地理解和改善
人们的心理反应，以实现全面健康的心理服务。
米氏酶动力学米氏酶动力学是指酶在催化反应中随底物浓度的变化而发生的反应速率变化规律，是酶学领域中的重要研究方向之一。
米氏酶动力学研究不仅对深入了解酶催化机理、生物化学过程具有重要意义，也对疾病治疗、药物设计等具有应用价值。
米氏酶动力学理论的提出米氏酶动力学理论基于酶催化能力的基本假设，酶与底物结合形成酶底物复合物，在催化反应过程中逐渐转化为酶产物复合物。
1940年，英国生物化学家米氏（L. H. Michaelis）和加拿大生物化学家门登（M. L. Menten）首次提出了酶催化反应的动力学方程，被称为米氏-门登方程，是酶动力学研究的基础。
米氏-门登方程描述了酶催化反应速率（v）与底物浓度（[S]）之间的关系，具有如下形式：v = V_max [S] / (K_M + [S])，其中V_max为酶最大催化速率，K_M为米氏常数，描述酶与底物复合物的解离常数。
米氏酶动力学的研究方法研究米氏酶动力学的主要方法有单酶动力学实验、酶速率常数的测定、酶底物复合物的性质研究等。
单酶动力学实验是研究酶单个分子的反应速率，通过光学或荧光显微镜观察酶底物复合物的形成、解离过程及反应速率，可获取单个酶在不同底物浓度下的酶速率常数，进而推导出米氏常数和最大反应速率。
酶速率常数的测定主要包括毛细管电泳、色谱法等，通过测定底物浓度与反应速率之间的关系，计算出米氏常数和最大反应速率。
酶底物复合物的性质研究可通过核磁共振、质谱等技术研究酶底物复合物的结构、性质。
米氏酶动力学的应用米氏酶动力学的研究应用广泛，主要应用于酶催化反应机制的研究、药物研发、生物传感器的设计等领域。
酶催化反应机制的研究是米氏酶动力学的主要应用之一。
通过研究酶底物复合物的性质、反应活化能、中间产物等，深入了解酶催化反应的机制和过程。
药物研发中，米氏酶动力学常用于评估药物的效价、毒性等指标，合理优化药物剂量和给药方案。
生物传感器是一种能够检测和转换生物或生化反应信号的器官，是目前生物医学诊断和生物分析中的重要工具。
