第十章 多元统计分析方法
- 格式:ppt
- 大小:355.50 KB
- 文档页数:59



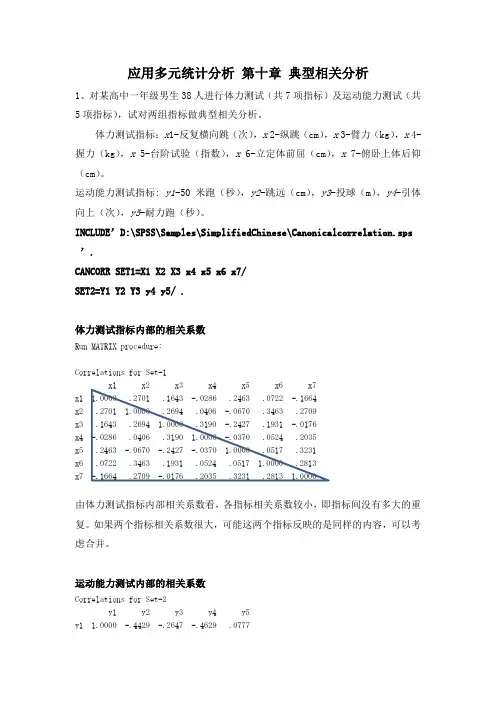
应用多元统计分析第十章典型相关分析1、对某高中一年级男生38人进行体力测试(共7项指标)及运动能力测试(共5项指标),试对两组指标做典型相关分析。
体力测试指标:x1-反复横向跳(次),x2-纵跳(cm),x3-臂力(kg),x4-握力(kg),x 5-台阶试验(指数),x 6-立定体前屈(cm),x 7-俯卧上体后仰(cm)。
运动能力测试指标: y1-50米跑(秒),y2-跳远(cm),y3-投球(m),y4-引体向上(次),y5-耐力跑(秒)。
INCLUDE’D:\SPSS\Samples\SimplifiedChinese\Canonicalcorrelation.sps ’.CANCORR SET1=X1 X2 X3 x4 x5 x6 x7/SET2=Y1 Y2 Y3 y4 y5/ .体力测试指标内部的相关系数Run MATRIX procedure:Correlations for Set-1x1 1.0000 .2701 .1643 -.0286 .2463 .0722 -.1664x2 .2701 1.0000 .2694 .0406 -.0670 .3463 .2709x3 .1643 .2694 1.0000 .3190 -.2427 .1931 -.0176x4 -.0286 .0406 .3190 1.0000 -.0370 .0524 .2035x5 .2463 -.0670 -.2427 -.0370 1.0000 .0517 .3231x6 .0722 .3463 .1931 .0524 .0517 1.0000 .2813x7 -.1664 .2709 -.0176 .2035 .3231 .2813 1.0000由体力测试指标内部相关系数看,各指标相关系数较小,即指标间没有多大的重复。
如果两个指标相关系数很大,可能这两个指标反映的是同样的内容,可以考虑合并。
运动能力测试内部的相关系数Correlations for Set-2y1 y2 y3 y4 y5y1 1.0000 -.4429 -.2647 -.4629 .0777y2 -.4429 1.0000 .4989 .6067 -.4744y3 -.2647 .4989 1.0000 .3562 -.5285y4 -.4629 .6067 .3562 1.0000 -.4369y5 .0777 -.4744 -.5285 -.4369 1.0000运动能力测试指标间的相关系数也较小,不过y2(跳远)和y4(引体向上)之间的相关系数较大,达到0.6067两组指标间的相关系数Correlations Between Set-1 and Set-2y1 y2 y3 y4 y5x1 -.4005 .3609 .4116 .2797 -.4709x2 -.3900 .5584 .3977 .4511 -.0488x3 -.3026 .5590 .5538 .3215 -.4802x4 -.2834 .2711 -.0414 .2470 -.1007x5 -.4295 -.1843 -.0116 .1415 -.0132x6 -.0800 .2596 .3310 .2359 -.2939x7 -.2568 .1501 .0388 .0841 .1923上表输出的是体力与远动能力之间的相关系数,从二者的直接相关系数来看,只有x2(纵跳)和y2(跳远)之间的关联程度较大(0.5584),而其他体力与远动能力指标间的直接关联不大,更可能是综合的影响。

多元统计分析⽅法多元统计分析概述⽬录⼀、引⾔ (3)⼆、多元统计分析⽅法的研究对象和主要内容 (3)1.多元统计分析⽅法的研究对象 (3)2.多元统计分析⽅法的主要内容 (3)三、各种多元统计分析⽅法 (3)1.回归分析 (3)2.判别分析 (6)3.聚类分析 (8)4.主成分分析 (10)5.因⼦分析 (10)6. 对应分析⽅法 (11)7. 典型相关分析 (11)四、多元统计分析⽅法的⼀般步骤 (12)五、多元统计分析⽅法在各个⾃然领域中的应⽤ (12)六、总结 (13)参考⽂献 (14)谢辞 (15)⼀、引⾔统计分布是⽤来刻画随机变量特征及规律的重要⼿段,是进⾏统计分布的基础和提⾼。
多元统计分析⽅法则是建⽴在多元统计分布基础上的⼀类处理多元统计数据⽅法的总称,是统计学中的具有丰富理论成果和众多应⽤⽅法的重要分⽀。
在本⽂中,我们将对多元统计分析⽅法做⼀个⼤体的描述,并通过⼀部分实例来进⼀步了解多元统计分析⽅法的具体实现过程。
⼆、多元统计分析⽅法的研究对象和主要内容(⼀)多元统计分析⽅法的研究对象由于⼤量实际问题都涉及到多个变量,这些变量⼜是随机变量,所以要讨论多个随机变量的统计规律性。
多元统计分析就是讨论多个随机变量理论和统计⽅法的总称。
其内容包括⼀元统计学中某些⽅法的直接推⼴,也包括多个随即便量特有的⼀些问题,多元统计分析是⼀类范围很⼴的理论和⽅法。
现实⽣活中,受多个随机变量共同作⽤和影响的现象⼤量存在。
统计分析中,有两种⽅法可同时对多个随机变量的观测数据进⾏有效的分析和研究。
⼀种⽅法是把多个随机变量分开分析,⼀次处理⼀个随机变量,分别进⾏研究。
但是,这样处理忽略了变量之间可能存在的相关性,因此,⼀般丢失的信息太多,分析的结果不能客观全⾯的反映整个问题,⽽且往往也不容易取得好的研究结论。
另⼀种⽅法是同时对多个随机变量进⾏研究分析,此即多元统计⽅法。
通过对多个随即便量观测数据的分析,来研究随机变量总的特征、规律以及随机变量之间的相互关系。



河南省考研数理统计复习资料多元统计分析方法河南省考研数理统计复习资料-多元统计分析方法多元统计分析方法是数理统计学领域的重要内容,它旨在通过分析多个变量之间的关系,揭示数据中的模式和结构。
在河南省考研数理统计复习中,熟悉和掌握多元统计方法是必不可少的。
本文将对河南省考研数理统计复习资料中的多元统计分析方法进行详细介绍。
一、多元统计分析方法概述多元统计分析方法是一种通过同时考虑多个变量来揭示数据中潜在结构和关系的统计学方法。
它包括多元方差分析、主成分分析、因子分析、判别分析、聚类分析等多个具体分析方法。
这些方法都有其独特的特点和适用领域。
在河南省考研数理统计复习中,多元统计分析方法通常用于处理多个统计变量的问题。
例如,在社会调查中,我们可能对多个指标(如年龄、教育程度、收入等)进行分析,以了解它们之间的关联或分类情况。
而多元统计分析方法可以帮助我们揭示这种关系和结构。
二、多元方差分析多元方差分析是一种用于比较多个样本或处理之间差异的统计方法。
它通常用于探索多个自变量对一个或多个因变量的影响。
在河南省考研数理统计复习中,多元方差分析是非常重要的内容。
多元方差分析包括两个主要方面:多元方差分析的假设检验和多元方差分析的效应量度。
前者用于判断不同处理之间是否存在差异,而后者则用于衡量这种差异的大小。
这两个方面的结合可以帮助我们理解数据中不同变量之间的关系。
三、主成分分析主成分分析是一种减少变量维度的方法,它可以将高维度的数据转化为低维度的数据。
在河南省考研数理统计复习中,主成分分析常常用于降维和探索数据结构。
主成分分析的核心思想是找出数据中最重要的成分,并将其作为新的变量。
通过保留数据中的主要信息,主成分分析可以大大简化数据的分析和解释。
在应用中,我们可以根据主成分的解释方差比例和加载系数来解释数据中的结构和关系。
四、因子分析因子分析是一种通过探索共同变化的数据结构来解释多个变量之间关系的方法。
在河南省考研数理统计复习中,因子分析常常用于分析问卷调查等涉及多个变量的数据。


一、什么是多元统计分析❖多元统计分析是运用数理统计的方法来研究多变量(多指标)问题的理论和方法,是一元统计学的推广。
❖多元统计分析是研究多个随机变量之间相互依赖关系以及内在统计规律的一门统计学科。
二、多元统计分析的内容和方法❖1、简化数据结构(降维问题)将具有错综复杂关系的多个变量综合成数量较少且互不相关的变量,使研究问题得到简化但损失的信息又不太多。
(1)主成分分析(2)因子分析(3)对应分析等❖2、分类与判别(归类问题)对所考察的变量按相似程度进行分类。
(1)聚类分析:根据分析样本的各研究变量,将性质相似的样本归为一类的方法。
(2)判别分析:判别样本应属何种类型的统计方法。
例5:根据信息基础设施的发展状况,对世界20个国家和地区进行分类。
考察指标有6个:1、X1:每千居民拥有固定电话数目2、X2:每千人拥有移动电话数目3、X3:高峰时期每三分钟国际电话的成本4、X4:每千人拥有电脑的数目5、X5:每千人中电脑使用率6、X6:每千人中开通互联网的人数❖3、变量间的相互联系一是:分析一个或几个变量的变化是否依赖另一些变量的变化。
(回归分析)二是:两组变量间的相互关系(典型相关分析)❖4、多元数据的统计推断点估计参数估计区间估计统 u检验计参数 t检验推 F检验断假设相关与回归检验卡方检验非参秩和检验秩相关检验❖1、假设检验的基本原理小概率事件原理❖ 小概率思想是指小概率事件(P<0.01或P<0.05等)在一次试验中基本上不会发生。
反证法思想是先提出假设(检验假设H0),再用适当的统计方法确定假设成立的可能性大小,如可能性小,则认为假设不成立;反之,则认为假设成立。
❖ 2、假设检验的步骤 (1)提出一个原假设和备择假设❖ 例如:要对妇女的平均身高进行检验,可以先假设妇女身高的均值等于 160 cm (u=160cm )。
这种原假设也称为零假设( null hypothesis ),记为 H 0 。

多元统计分析方法多元统计分析是指同时考虑多个自变量与一个因变量之间关系的统计方法。
它可以帮助我们更全面深入地分析、理解和解释数据,揭示出变量之间的相互关系和影响,并基于这些关系提供对因变量的预测和解释。
以下将介绍多元统计分析的常见方法。
一、回归分析回归分析是通过建立一个数学模型,研究自变量与因变量之间的关系。
它可以帮助我们确定自变量对因变量的影响程度和方向,并进行预测和解释。
回归分析包括简单线性回归、多元线性回归、逐步回归、Logistic回归等方法。
1.简单线性回归分析:研究一个自变量对因变量的影响。
2.多元线性回归分析:研究多个自变量对因变量的共同影响。
3.逐步回归分析:逐步选择和删除自变量,建立较为准确的回归模型。
4. Logistic回归分析:适用于因变量为二分类变量的情况,研究自变量对因变量的影响。
二、方差分析方差分析用于比较两个或多个组别之间的平均差异是否显著。
它可以帮助我们了解不同组别之间的差异和相关因素。
1.单因素方差分析:比较一个自变量对因变量的影响。
2.双因素方差分析:比较两个自变量对因变量的影响,同时考虑两个自变量以及它们之间的交互作用。
3.多因素方差分析:比较多个自变量对因变量的影响,并可以考虑它们的交互作用。
三、协方差分析协方差分析是一种特殊的方差分析方法,用于比较两个或多个组别之间的平均差异,并控制其他因素对该差异的影响。
它可以帮助我们研究特定因素对组别间差异的贡献程度。
四、主成分分析主成分分析是一种降维方法,用于将原始的高维数据降低到更低维度的数据。
它可以帮助我们发现数据中的主要组成部分,提高数据的解释性和处理效率。
五、因子分析因子分析是一种降维方法,用于发现数据中的潜在变量并对其进行解释。
它可以帮助我们理解数据背后隐藏的结构和关系。
六、聚类分析聚类分析是一种无监督学习方法,将样本分为不同的组别或类别。
它可以帮助我们发现数据内在的结构和相似性。
七、判别分析判别分析是一种有监督学习方法,用于将样本分为两个或多个已知类别。