zz-多元统计分析方法(含答案)

《多元统计分析》思考题答案记得老师课堂上说过考试内容不会超出这九道思考题，如下九道题题目中有错误的或不清楚的地方，欢迎大家指出、更改、补充。

1、 简述信度分析答题提示：要答可靠度概念，可靠度度量，克朗巴哈α系数、拆半系数、单项与总体相关系数、稀释相关系数等（至少要答四个系数，至少要给出两个指标的公式）答：信度（Reliability ）即可靠性，它是指采用同样的方法对同一对象重复测量时所得结果的一致性程度。

信度指标多以相关系数表示，大致可分为三类：稳定系数（跨时间的一致性），等值系数（跨形式的一致性）和内在一致性系数（跨项目的一致性）。

信度分析的方法主要有以下四种：1)、重测信度法这一方法是用同样的问卷对同一组被调查者间隔一定时间重复施测，计算两次施测结果的相关系数。

重测信度属于稳定系数。

重测信度法特别适用于事实式问卷，如果没有突发事件导致被调查者的态度、意见突变，这种方法也适用于态度、意见式问卷。

由于重测信度法需要对同一样本试测两次，被调查者容易受到各种事件、活动和他人的影响，而且间隔时间长短也有一定限制，因此在实施中有一定困难。

2)、复本信度法复本信度法是让同一组被调查者一次填答两份问卷复本，计算两个复本的相关系数。

复本信度属于等值系数。

复本信度法要求两个复本除表述方式不同外，在内容、格式、难度和对应题项的提问方向等方面要完全一致，而在实际调查中，很难使调查问卷达到这种要求，因此采用这种方法者较少。

3)、折半信度法折半信度法是将调查项目分为两半，计算两半得分的相关系数，进而估计整个量表的信度。

折半信度属于内在一致性系数，测量的是两半题项得分间的一致性。

这种方法一般不适用于事实式问卷（如年龄与性别无法相比），常用于态度、意见式问卷的信度分析。

在问卷调查中，态度测量最常见的形式是5级李克特（Likert ）量表。

进行折半信度分析时，如果量表中含有反意题项，应先将反意题项的得分作逆向处理，以保证各题项得分方向的一致性，然后将全部题项按奇偶或前后分为尽可能相等的两半，计算二者的相关系数。

第五章聚类分析5.1 判别分析和聚类分析有何区别？答：即根据一定的判别准则,判定一个样本归属于哪一类。

具体而言,设有n 个样本,对每个样本测得p 项指标〔变量的数据,已知每个样本属于k 个类别〔或总体中的某一类,通过找出一个最优的划分,使得不同类别的样本尽可能地区别开,并判别该样本属于哪个总体。

聚类分析是分析如何对样品〔或变量进行量化分类的问题。

在聚类之前,我们并不知道总体,而是通过一次次的聚类,使相近的样品〔或变量聚合形成总体。

通俗来讲,判别分析是在已知有多少类及是什么类的情况下进行分类,而聚类分析是在不知道类的情况下进行分类。

5.2 试述系统聚类的基本思想。

答：系统聚类的基本思想是：距离相近的样品〔或变量先聚成类,距离相远的后聚成类,过程一直进行下去,每个样品〔或变量总能聚到合适的类中。

5.3 对样品和变量进行聚类分析时,所构造的统计量分别是什么？简要说明为什么这样构造？ 答：对样品进行聚类分析时,用距离来测定样品之间的相似程度。

因为我们把n 个样本看作p 维空间的n 个点。

点之间的距离即可代表样品间的相似度。

常用的距离为 〔一闵可夫斯基距离：1/1()()pq qij ik jk k d q X X ==-∑q 取不同值,分为 〔1绝对距离〔1q = 〔2欧氏距离〔2q =〔3切比雪夫距离〔q =∞ 〔二马氏距离 〔三兰氏距离对变量的相似性,我们更多地要了解变量的变化趋势或变化方向,因此用相关性进行衡量。

将变量看作p 维空间的向量,一般用 〔一夹角余弦 〔二相关系数5.4 在进行系统聚类时,不同类间距离计算方法有何区别？选择距离公式应遵循哪些原则？ 答：设d ij 表示样品X i 与X j 之间距离,用D ij 表示类G i 与G j 之间的距离。

〔1. 最短距离法 〔2最长距离法 〔3中间距离法 其中 〔4重心法 〔5类平均法 〔6可变类平均法 其中β是可变的且β <1〔7可变法 22221()2kr kp kq pq D D D D ββ-=++其中β是可变的且β <1 〔8离差平方和法2222(1)()p q kr kp kq pq r rn n D D D D n n ββ=-++通常选择距离公式应注意遵循以下的基本原则：〔1要考虑所选择的距离公式在实际应用中有明确的意义。

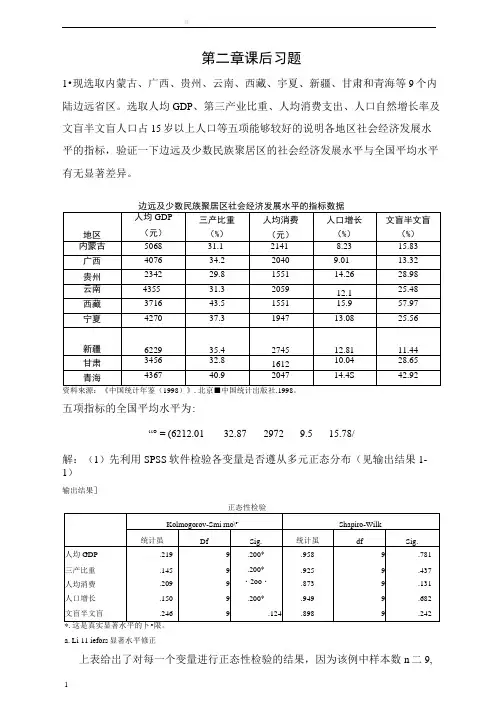
年第二章课后习题1•现选取内蒙古、广西、贵州、云南、西藏、宇夏、新疆、甘肃和青海等9个内陆边远省区。

选取人均GDP、第三产业比重、人均消费支出、人口自然增长率及文盲半文盲人口占15岁以上人口等五项能够较好的说明各地区社会经济发展水平的指标，验证一下边远及少数民族聚居区的社会经济发展水平与全国平均水平有无显著差异。

五项指标的全国平均水平为:“° = (6212.01 32.87 2972 9.5 15.78/解：（1）先利用SPSS软件检验各变量是否遵从多元正态分布（见输出结果1-1）输出结果］a. Li 11 iefors显著水平修正上表给岀了对每一个变量进行正态性检验的结果，因为该例中样本数n二9,所以此处选用Shapiro-Wilk统计量。

则Sig.值分别为0. 781、0. 437、0. 131、0.682、0.242均大于显著性水平，由此可以知道,人均GDP、三产比重、人均消费、人口增长、文盲半文盲这五个变量组成的向量均服从正态分布，即我们认为这五个指标可以较好对各地区社会经济发展水平做出近似的度量。

（2）提出原假设及备选假设Hi :（3）做出统讣判断，最后对统讣判断作出具体的解释SPSS的GLM模块可以完成多元正态分布有关均值与方差的检验。

依次点选Analyze —>General Linear Mode^ IMultivariate ..................... 进入Multivariate 对话框，将人均GDP、第三产业比重、人均消费支出、人口自然增长率及文盲半文盲人口占15岁以上人口等这五项指标选入Dependent列表框，将分类指标选入Fixed Factor （s）框，点击OK运行，则可以得到如下结果（见输出结果1-2）。

输出结果1-2a.设计：截距+分类b.精确统计虽少年易学老难成,上面第一张表是样本数据分别来自边远及少数民族聚居区社会经济发展水平、全国的个数。

多元统计分析习题与答案多元统计分析是一种在社会科学研究中广泛应用的方法，它通过同时考虑多个变量之间的关系，帮助研究者更全面地理解和解释现象。

在本文中，我将分享一些多元统计分析的习题和答案，希望能够帮助读者更好地掌握这一方法。

习题一：相关分析假设你正在研究一个学生的学习成绩和他们每天花在学习上的时间之间的关系。

你收集了100个学生的数据，学习成绩用分数表示，学习时间用小时表示。

以下是你的数据：学习成绩（X）：75, 80, 85, 90, 95, 70, 65, 60, 55, 50学习时间（Y）：5, 6, 7, 8, 9, 4, 3, 2, 1, 0请计算学习成绩和学习时间之间的相关系数，并解释其含义。

答案一：首先，我们需要计算学习成绩和学习时间之间的协方差和标准差。

根据公式，协方差可以通过以下公式计算：协方差= Σ((X - X平均) * (Y - Y平均)) / (n - 1)其中，X和Y分别表示学习成绩和学习时间，X平均和Y平均表示它们的平均值，n表示样本数量。

标准差可以通过以下公式计算：标准差= √(Σ(X - X平均)² / (n - 1))根据以上公式，我们可以得出学习成绩和学习时间之间的协方差为-22.5，标准差分别为18.03和2.87。

然后，我们可以通过以下公式计算相关系数：相关系数 = 协方差 / (X标准差 * Y标准差)根据以上公式，我们可以得出相关系数为-0.93。

由于相关系数接近于-1，可以得出结论：学习成绩和学习时间之间存在强烈的负相关关系，即学习时间越长，学习成绩越低。

习题二：多元线性回归假设你正在研究一个人的身高（X1）、体重（X2）和年龄（X3）对其收入（Y）的影响。

你收集了50个人的数据，以下是你的数据：身高（X1）：160, 165, 170, 175, 180, 185, 190, 195, 200, 205体重（X2）：50, 55, 60, 65, 70, 75, 80, 85, 90, 95年龄（X3）：20, 25, 30, 35, 40, 45, 50, 55, 60, 65收入（Y）：5000, 5500, 6000, 6500, 7000, 7500, 8000, 8500, 9000, 9500请利用多元线性回归分析，建立一个预测人的收入的模型，并解释模型的结果。

2.1.试叙述多元联合分布和边际分布之间的关系。

解：多元联合分布讨论多个随机变量联合到一起的概率分布状况，12(,,)p X X X X '=L 的联合分布密度函数是一个p 维的函数，而边际分布讨论是12(,,)p X X X X '=L 的子向量的概率分布，其概率密度函数的维数小于p 。

2.2设二维随机向量12()X X '服从二元正态分布，写出其联合分布。

解：设12()X X '的均值向量为()12μμ'=μ，协方差矩阵为21122212σσσσ⎛⎫ ⎪⎝⎭，则其联合分布密度函数为1/21222112112222122121()exp ()()2f σσσσσσσσ--⎧⎫⎛⎫⎛⎫⎪⎪'=---⎨⎬ ⎪⎪⎝⎭⎝⎭⎪⎪⎩⎭x x μx μ。

2.3已知随机向量12()X X '的联合密度函数为121212222[()()()()2()()](,)()()d c x a b a x c x a x c f x x b a d c --+-----=--其中1ax b ≤≤，2c x d ≤≤。

求（1）随机变量1X 和2X 的边缘密度函数、均值和方差； （2）随机变量1X 和2X 的协方差和相关系数；（3）判断1X 和2X 是否相互独立。

（1）解：随机变量1X 和2X 的边缘密度函数、均值和方差；112121222[()()()()2()()]()()()dx cd c x a b a x c x a x c f x dx b a d c --+-----=--⎰12212222222()()2[()()2()()]()()()()dd c c d c x a x b a x c x a x c dx b a d c b a d c -------=+----⎰ 121222202()()2[()2()]()()()()dd c c d c x a x b a t x a t dt b a d c b a d c ------=+----⎰ 2212122222()()[()2()]1()()()()d cdc d c x a x b a t x a t b a d c b a d c b a------=+=----- 所以 由于1X 服从均匀分布，则均值为2b a+，方差为()212b a -。

多元统计分析习题答案多元统计分析习题答案多元统计分析是一种应用广泛的统计方法，用于研究多个变量之间的关系。

在实际应用中，我们常常会遇到一些多元统计分析的习题，通过解答这些习题可以更好地理解和掌握多元统计分析的方法和技巧。

下面我将为大家提供一些多元统计分析习题的答案，希望对大家的学习有所帮助。

1. 在一个实验中，研究者想要探究三种不同的肥料对植物生长的影响。

他们随机选取了30个样本，将它们分为三组，分别施加不同的肥料。

最后测量了每个样本的植物高度、叶片数量和花朵数量。

请问该如何分析这个实验的数据？答案：这是一个多元方差分析（MANOVA）问题。

由于我们有三个不同的肥料处理组，每个组有三个观测变量（植物高度、叶片数量和花朵数量），所以我们可以使用MANOVA来分析这个实验的数据。

MANOVA可以同时考虑多个因变量之间的差异，并判断这些差异是否显著。

2. 一个公司想要了解员工的满意度与工资、工作时长以及晋升机会之间的关系。

他们随机选取了100个员工，并收集了他们的满意度得分、工资水平、工作时长和晋升机会的数据。

请问该如何分析这个问题的数据？答案：这是一个多元回归分析问题。

我们可以使用多元回归分析来探究员工的满意度与工资、工作时长以及晋升机会之间的关系。

满意度得分可以作为因变量，而工资水平、工作时长和晋升机会可以作为自变量。

通过多元回归分析，我们可以得出各个自变量对于因变量的影响程度以及它们之间的相互关系。

3. 一家餐厅想要了解顾客满意度与菜品质量、服务质量和价格之间的关系。

他们随机选取了200个顾客，并要求他们对菜品质量、服务质量和价格进行评分。

请问该如何分析这个问题的数据？答案：这是一个主成分分析问题。

我们可以使用主成分分析来降维和提取数据中的主要信息。

首先，我们将菜品质量、服务质量和价格作为变量进行主成分分析，得到几个主成分。

然后，我们可以根据这些主成分的得分来评估顾客的满意度。

主成分分析可以帮助我们理解哪些因素对于顾客满意度的贡献最大。

多元统计1-5章习题答案多元统计学是一门研究多个变量之间关系的学科，它涉及到统计学中的各种方法和技术。

在多元统计学的学习过程中，习题是非常重要的一部分，通过解答习题可以加深对知识的理解和掌握。

本文将回答多元统计学1-5章的一些习题，帮助读者更好地学习和应用多元统计学。

第一章是多元统计学的基本概念和原理，其中包括多元数据的描述和总体参数的估计。

在这一章的习题中，常见的问题是关于均值、方差和协方差的计算。

通过计算这些统计量，可以了解数据的分布和变异程度。

同时，还有一些关于总体参数估计的问题，如最大似然估计和矩估计。

这些问题可以帮助读者理解参数估计的原理和方法。

第二章是关于多元正态分布的内容，其中包括多元正态分布的性质和参数估计。

在这一章的习题中，常见的问题是关于多元正态分布的性质和特点。

例如，如何计算多元正态分布的密度函数和累积分布函数，以及如何利用多元正态分布进行假设检验和置信区间估计。

这些问题可以帮助读者理解多元正态分布的基本概念和应用。

第三章是关于多元方差分析的内容，其中包括单因素多元方差分析和多因素多元方差分析。

在这一章的习题中，常见的问题是如何进行多元方差分析和解释结果。

例如，如何计算多元方差分析的F统计量和p值，以及如何进行多重比较和效应大小的计算。

这些问题可以帮助读者理解多元方差分析的原理和应用。

第四章是关于多元线性回归的内容，其中包括多元线性回归模型和参数估计。

在这一章的习题中，常见的问题是如何建立多元线性回归模型和解释结果。

例如，如何进行多元线性回归的参数估计和假设检验，以及如何进行模型选择和解释变量的重要性。

这些问题可以帮助读者理解多元线性回归的基本原理和应用。

第五章是关于主成分分析和因子分析的内容，其中包括主成分分析和因子分析的原理和应用。

在这一章的习题中，常见的问题是如何进行主成分分析和因子分析，并解释结果。

例如，如何计算主成分和因子的贡献率和累积贡献率，以及如何解释主成分和因子的含义。

〔T 0 a x 1 ．多元分析研究的是多个随机变量及其相互关系的统计总体。

2 ．多元统计中常用的统计量有：样本均值、样本方差、样本协方差和样本相关系数。

3 ．协方差和相关系数仅仅是变量间离散程度的 一种度量， 并不能刻画变量间可能存在的关联程度。

4 ．人们通过各种实践，发现变量之间的相互关系可以分成相关和不相关两种类型。

5 ．总离差平方和可以分解为回归离差平方和和 剩余离差平方和两个部分， 各自的自由度为 p和 n-p-1 ，其中回归离差平方和在总离差平方和中所占比重越大，则线性回归效果越显著。

7 ．偏相关系数是指多元回归分析中，当其他变量固定后，给定的两个变量之间的的相关系数。

8 ．Spss 中回归方程的建模方法有一元线形回 归、多元线形回归、 岭回归、 多对多线形回归等。

9 ．主成分分析是通过适当的变量替换，使新变 量成为原变量的综合变量， 并寻求相关性的一种方法。

10 ．主成分分析的基本思想是： 设法 将 原来 众多 具 有一 定 相 关 性 （ 比 如 P 个 指 标 ）， 重新 组 合 成 一 组 新 的 互 相 无 关 的 综 合 指 标 来 代 替原 来 的 指 标 。

11 ．主成分的协方差矩阵为对角矩阵。

12 ．主成分表达式的系数向量是相关系数矩阵的特征向量。

13 ．原始变量协方差矩阵的特征根的统计含义是原始数据的相关系数。

14 ．原始数据经过标准化处理，转化为均值为 0 ，方差为 1 的标准值，且其协方差矩阵与相关系数矩阵相等。

15 ．样本主成分的总方差等于1 。

16 ．变量按相关程度为，在相关性很强程度下， 主成分分析的效果较好。

17 ．在经济指标综合评价中，应用主成分分析法，则评价函数中的权数为方差贡献度。

19 ．因子分析是把每个原始变量分解为两部分 因素， 一部分是公共因子， 另一部分为特殊因子。

20 ．变量共同度是指因子载荷矩阵中第 i 行元素的平方和。

21 ． 公 共 因子 方差 与 特 殊因 子 方差 之 和为 1 。

第1章 多元正态分布1、在数据处理时，为什么通常要进行标准化处理？数据的标准化是将数据按比例缩放，使之落入一个小的特定区间。

在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

其中最典型的就是0-1标准化和Z 标准化。

2、欧氏距离与马氏距离的优缺点是什么？欧氏距离也称欧几里得度量、欧几里得度量，是一个通常采用的距离定义，它是在m 维空间中两个点之间的真实距离。

在二维和三维空间中的欧氏距离的就是两点之间的距离。

缺点：就大部分统计问题而言，欧氏距离是不能令人满意的。

每个坐标对欧氏距离的贡献是同等的。

当坐标表示测量值时，它们往往带有大小不等的随机波动，在这种情况下，合理的方法是对坐标加权，使变化较大的坐标比变化较小的坐标有较小的权系数，这就产生了各种距离。

当各个分量为不同性质的量时，“距离”的大小与指标的单位有关。

它将样品的不同属性之间的差别等同看待，这一点有时不能满足实际要求。

没有考虑到总体变异对距离远近的影响。

马氏距离表示数据的协方差距离。

为两个服从同一分布并且其协方差矩阵为Σ的随机变量与的差异程度:如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。

优点：它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关。

由标准化数据和中心化数据计算出的二点之间的马氏距离相同。

马氏距离还可以排除变量之间的相关性的干扰。

缺点：夸大了变化微小的变量的作用。

受协方差矩阵不稳定的影响，马氏距离并不总是能顺利计算出。

3、当变量X1和X2方向上的变差相等，且与互相独立时，采用欧氏距离与统计距离是否一致？统计距离区别于欧式距离，此距离要依赖样本的方差和协方差，能够体现各变量在变差大小上的不同，以及优势存在的相关性，还要求距离与各变量所用的单位无关。

如果各变量之间相互独立,即观测变量的协方差矩阵是对角矩阵, 则马氏距离就退化为用各个观测指标的标准差的倒数作为权数的加权欧氏距离。

(完整版)多元统计分析试题及答案试题：1. 试解释多元统计分析的含义及其与单变量和双变量统计分析的区别。

2. 简述卡方检验方法及适用场景。

3. 请解释回归分析中的回归系数及其p值的含义及作用，简单说明如何进行回归模型的选择和评估。

4. 试解释主成分分析的原理及目的，如何进行主成分分析及如何解释因子载荷矩阵。

5. 请列举和简要解释聚类分析和判别分析的适用场景，并说明两种方法的区别。

答案：1. 多元统计分析是一种将多个变量进行综合分析的方法。

与单变量和双变量统计分析不同的是，多元统计分析可以处理多个自变量和因变量的组合关系，从而探究它们之间的综合关系。

该方法通常适用于探究多种变量在某个问题中的关系、探究影响某一结果变量的因素、探究各个变量相互作用的影响等。

2. 卡方检验是根据样本数据与期望值的差异来判断观察值与理论预期是否相符，以此来验证假设是否成立的方法。

它通常用于对某个现象进行分类的相关度检验。

适用场景包括：样本的数量大于等于40，且至少有一个期望值小于5；变量为分类变量，且分类类别数不超过10个。

卡方检验的原理是将观察值和期望值进行比较，并计算卡方值，然后根据卡方值与自由度的乘积查找p值，从而得出结论。

3. 回归系数是回归方程中自变量与因变量之间的关系，在线性回归中，回归系数表示每一个自变量单位变化与因变量单位变化的关系。

p值是评估回归系数是否具有显著性的指标。

回归模型的选择有两种方法：一种是逐步回归分析，根据不同的准则进行多个回归模型的比较，选择最优的模型；另一种是正则化回归，通过加入惩罚项来保证回归模型具有良好的泛化性能。

回归模型的评估有多种方法，包括：残差分析、R方值、方差齐性检验、变量的共线性检验等。

4. 主成分分析是一种将多维数据降维处理的方法，它的目的是通过数据的变换，将多个变量转化为一些综合指标，这些指标是原始变量的线性组合。

主成分分析的步骤包括：数据标准化、计算协方差矩阵或相关系数矩阵、计算特征值和特征向量、选取主成分。

多元统计分析课后习题答案多元统计分析课后习题答案在学习多元统计分析时，课后习题是巩固所学知识的重要环节。

通过解答习题，我们可以进一步理解和应用统计学的概念和方法。

下面将给出一些多元统计分析课后习题的答案，希望能对大家的学习有所帮助。

1. 在多元统计分析中，什么是协方差矩阵？如何计算协方差矩阵？答：协方差矩阵是用来衡量多个随机变量之间的线性关系的矩阵。

它是一个对称矩阵，对角线上的元素是各个变量的方差，非对角线上的元素是两个变量之间的协方差。

计算协方差矩阵的方法是，首先计算每个变量的平均值，然后计算每个变量与其他变量的协方差。

最后将这些协方差按照矩阵的形式排列，即得到协方差矩阵。

2. 什么是主成分分析？主成分分析的步骤是什么？答：主成分分析是一种用于降维的统计方法，它可以将多个相关变量转化为一组无关的主成分。

主成分分析的目标是找到能够解释原始变量大部分方差的少数几个主成分。

主成分分析的步骤如下：(1) 标准化数据：将原始数据进行标准化处理，使得每个变量的均值为0，标准差为1。

(2) 计算协方差矩阵：根据标准化后的数据计算协方差矩阵。

(3) 计算特征值和特征向量：求解协方差矩阵的特征值和特征向量。

(4) 选择主成分：根据特征值的大小选择主成分，通常选择特征值较大的前几个主成分。

(5) 构造主成分：将选择的主成分与原始数据进行线性组合，得到新的主成分。

3. 什么是判别分析？判别分析的步骤是什么？答：判别分析是一种用于分类的统计方法，它通过寻找最佳的分类边界，将样本分为不同的类别。

判别分析的目标是找到能够最大程度地区分不同类别的线性组合。

判别分析的步骤如下：(1) 收集样本数据：首先收集包含已知类别的样本数据。

(2) 计算类均值向量：根据样本数据计算每个类别的均值向量。

(3) 计算类内离散度矩阵：根据样本数据计算每个类别的类内离散度矩阵。

(4) 计算类间离散度矩阵：根据样本数据计算类间离散度矩阵。

(5) 计算投影向量：根据类内离散度矩阵和类间离散度矩阵计算投影向量。