32代数式的值

3.4 代数式的值
第1课时求代数式的值
（-2）+2 输出38
（1）按照上面的程序，请计算X=3，X=6时的输出值.
（2）任意取X的两个值，请完成上面的求值过程，并与同学相互检查求值过程和结果是否正确.
师生活动：教师引导学生思考，感受代数式的值的变化与字母的取值的变化之间的联系，同桌之间核对答案.
【归纳总结】
用数值代替代数式中的字母，按照代数式中给出的运算程序计算出的结果，叫作代数式的值.这个过程叫作求代数式的值.
3.学以致用，应用新知
【例1】根据下面a,b的值,求代数式a-b
a
的值:
(1)a=2,b=-6;(2)a=-10,b=4.
解:(1)当a=2,b=-6时,
a-b
a = 2-- 6
2
=2+3=5.
(2)当a=-10,b=4时,
a- b
a =-10-4
- 10
=-10+2
5
=-48
5
.
【例2】如图所示,已知长方体的高为h,底面是边长为a的正方形.当h=3,a=2时,分别求其体积V和表面积S.
解:因为V=a2h,S=2a2+4ah,
所以当a=2,h=3时,
V=a2h=22×3=12,
S=2a2+4ah=2×22+4×2×3=32.
4.随堂训练，巩固新知
1.当x=1时,代数式4-3x的值是()。

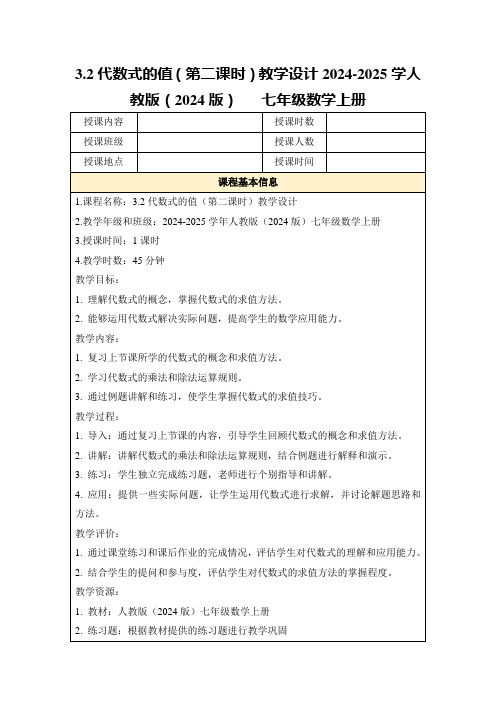
3.2代数式学习目标1.了解代数式、单项式、单项式的系数和次数、多项式、多项式的次数、整式的概念.2.用代数式表示简单问题的数量关系，解释一些简单代数式的实际背景或几何意义.3.通过具体例子感受“同一个代数式可以表示不同的实际意义“，”理解符号所代表的数量关系“，初步感受模型思想.考点考频1.列代数式。

（必考点）2.识别单项式、多项式、整式。

（常考点）3.确定一个单项式的系数、次数.（常考点）4.确定一个多项式的项、次数.（常考点）知识点1代数式的概念（重点；掌握）1.代数式的概念用基本的运算符号把数或表示数的字母连接而成的式子叫做代数式.单独一个数或一个字母也是代数式.2.代数式的书写注意点（1）乘法书写注意点:①字母与字母相乘时，乘号通常不写或简写“·”；②数字与字母（或式子）相乘时，要把数字写在字母（或式子）的前面；③数与数相乘时乘号不能省略.（2）除法书写注意点:一般按照分数的写法书写，即被除数作为分子，除数作为分母. （3）单位书写注意点:①结果是乘除关系的，直接在后面写单位；②结果是加减关系的，先把式子用括号括起来，再在括号后面写单位.（4）添括号注意点:①表示与数的运算顺序一致的运算，列代数式时不添加括号；②表示与数的运算顺序不一致的运算，列代数式时要添加括号.例1（1）下列各式:9，x + y，5x，s = a2.其中，代数式的个数为（）A.1B.2C.3D.4（2）下列各式:①113x；②2·3；③20%x；④a b ÷c；⑤m2+n26；⑥x5千克.其中，不符合代数式书写要求的有（）A.5个B.4个C.3个D.2个练习1（1）下列各式中，是代数式的为（）①2πr，②m+n2，③a + b = 4，①x1< 0，⑤S = πr2，⑥ab + cdA.①②③④⑤⑥B.①②⑤⑥C.③④⑤D.①②⑥（2）下列符合代数式书写要求的是（）A.m ÷nB.213x C.14ab3D.a·10%1.（1）D（2）C知识点2列代数式（重难点；掌握）列代数式就是把实际问题中的数量关系用数学式子表示出来，其本质就是将文字语言转化为数学语言.例2用代数式表示:（1）m的3倍与n的和.（2）x与y的倒数的差（y≠0）.（3）a，b两数和的平方减去它们差的平方.练习2设某数为m，那么代数式2m2+12表示（）A.某数的2倍的平方加上1除以2B.某数的2倍加上1的一半C.某数与1和的2倍除以2D.某数的平方的2倍与1的和的一半2.D知识点3单项式及其相关测念概念（重点；掌握）1.单项式数字与字母的积所组成的代数式叫做单项式.单独一个数或一个字母也是单项式.[注意]单项式中的运算只能是乘法或乘方，不能含有加、减、除运算，分母中不含字母，如代数式（x+1）2不是单项式；字母不能出现在分母里，如 4a不是单项式.2.单项式的系数与次数单项式中的数字因数叫做单项式的系数.单项式中各个字母的指数的和叫做单项式的次数.[注意]判断单项式的系数:π是常数，可以作为系数；一个单项式的系数是1或1时，“1”通常省略不写，如“ 1” × “ab”写成“ ab”；若系数是带分数，要化成假分数. 例3下列说法正确的个数是（）①单项式a的系数为0，次数为0；②ab−12是单项式；③xyz的系数为1，次数是1；④π是单项式，而2不是单项式.A.0B.1C.2D.3 练习3（2020•扬州江都区期末）单项式3x^22的系数是（）A.−32B.3 C.−12D.323.A练习4下面说法正确的是（）A. 5的倒数是15B. 0是最小的非负数C.1x是单项式D.单项式43πab2的系数和次数分别为−43和44.B[提示:A.5的倒数是15，故此选项错误:B.最小的非负数是0.正确:C.1x不是单项式，故此选项错误；D.单项式43πab2的系数和次数分别为43π和3.故此选项错误.]知识点4多项式及其相关概念（重点；掌握）1.多项式几个单项式的和叫做多项式.[特别提醒]判断多项式:有加减号；分母中不含有字母. 2.多项式的项多项式里含有几项，就把这个多项式叫做几项式. 多项式的每一项都包括它前面的符号. 3.多项式的次数多项式中，次数最高的项的次数叫做这个多项式的次数，不含字母的项叫常数项. 例4x 2y−16是（ ）A .二次二项式B .二次三项式C .三次二项式D .单项式练习5下列说法正确的是（ ） A .3a 5的项是3a ，5B .2x 2y + xy 2 + x 2是二次三项式C . 1x 是单项式D . a +b2 和x 2 + 2xy + y 2都是多项式5.D [提示:A .3a 5的项是3a ， 5，故此选项错误:B .2x 2y + x y 2 + x 2是三次三项式，故此选项错误；C . 1 x 不是单项式，故此选项错误:D . a +b2 和x 2 + 2xy + y 2都是多项式.正确.]知识点5整式（重点；掌握）1.单项式和多项试统称整式.2.代数式包括整式、整式是单项式与多项式的统称.如 1xy ，x + 2y 都是代数式，但其中只有 x4 ，x + 2y 是整式.而 1x 的分母中含有字母，不是整式.例5（2020·哈尔滨南岗区校级期中）下列式子:x 2 + 5， 1， 3x + 2，π 5x x 2 + 1x +1，5x ，其中整式有（ ） A .3个B .4个C .5个D .6个练习6（2020·上海徐汇区校级月考）①12；②1x+3；③x−15；④a中，整式有_________ （只需填入相应的序号）.6.①③④——题型总结——题型1用代数式表示多位数例1一个三位数，百位数字为x，十位数字比百位数字大2，个位数字比百位数字的2倍小3，用代数式表示这个三位数为（）A.x（x + 2）（2x3）B.100x + 10（x2）+ 2x 3C.100x + 10（x + 2）+ 2x 3D.100x + 10（x2）+ 2x + 3练习1把一个两位数m放在一个三位数n的前面，组成一个五位数，这个五位数可表示为 .1000 m + n题型2列代数式例2（2020·徐州邳州市期中）某商品原价为a元，因销量下滑，经营者连续两次降价，每次降价10%，后因供不应求，又一次提价20%，则现在这种商品的价格是（）A.1.08a元B.0.88a元C.0.972a元D.0.968a元练习2某校计划组织七年级师生去绍兴鲁迅故居研学.若学校租用可载乘客30人的客车x辆，则有15人无法乘坐；若租用可载乘客45人的客车，则可少租用2辆，且最后一辆车还没坐满.那么乘坐最后一辆可载乘客45人的客车的人数是 _________（用含x的代数式表示）.30x + 15 45（x3）题型3阐述代数式的意义例3下列赋于4 m实际意义的叙述中不正确的是（）A.若葡萄的价格是4元/千克，则4 m表示买m千克葡萄的金额B.若m表示一个正方形的边长，则4 m表示这个正方形的周长C.将一个小木块放在水平桌面上，若4表示小木块与桌面的接触面积，m表示桌面受到的压强，则4 m表示小木块对桌面的压力D.若一个两位数中的十位数字为4，个位数字为m，则4 m表示这个两位数练习3请你用实例解释下列代数式的意义.（1）4 + 3；（2）3a；（3）(1 2 )33.解:答案不唯一.（1） 4 + 3表示气温从4℃上升3℃的温度.（2）3a表示一辆车以akm/h的速度行驶3小后的路程.（3）表示棱长为12的正方体的体积.题型4求单项式与多项式中字母的值例4如果（a+1）2x2y n1是关于x，y的五次单项式，那么a，n应满足的条件是_________ .练习4（2020·苏州高新区期末）多项式− 13 x|m|+(m4)x + 7是关于x的四次三项式，则m的值是( )A.4B. 2C. 4D.4或 4 C题型5探究单项式中的规律例5观察下列单项式:x，3x2，5x3，7x4，…，37x19，39x^20……写出第n个单项式.为了解决这个问题，特提供下面解题思路:（1）这组单项式的系数的符号规律是 _______ ，系数的绝对值规律是 ________ ；（2）这组单项式的次数的规律是 _________ ；（3）根据上面的归纳，可以猜想第n个单项式是 ______（只能填写一个代数式）；（4）请你根据猜想，写出第2018个、第2019个单项式，它们分别是_________ .练习5观察下列单项式:x，2x2，4x3，8x4，16x5…根据你发现的规律写出第10个单项式为 _________ ，第n个单项式为 _________ .29x10 （1）n + 12n1）x n题型6多项式中的“不含”问题例6已知（a2）x2 + （b + 1）xy x + y7是关于x，y的多项式，如果该多项式不含二次项，求3a + 8b的值.练习6多项式（2b + a）xy3x + y7是关于x，y的多项式，若该多项式不含二次项，求4b + 2a的值.6.解:由题意知2b + a = 0，则4b + 2a = 2（2b + a）= 0.——能力培优训练——能力通关1.下列代数式的写法，正确的是（）A.“负x的平方”记作x2B.“y与113的积”记作y13C.“x的3倍”记作x3D.“2a除以3b的商”记作2a3b1.D2.多项式2x3 + 4y25的二次项的系数与常数项的和等于（）A.1B.9C.9D. 12.D[提示:因为二次项的系数为4，常数项为5，所以4 5 = 1.]3.（2020·南通市海安期末）二次三项式2x23x1的二次项系数、一次项系数、常数项分别是（）A.2，3，1B.2，3，1C.2，3，1D.2，3，13.A4.多项式2x2y x3+ 1是 ______ 次 ______ 项式.4.三三5.用代数式表示:（1）某班共有x名学生，其中男生人数占45%，则女生人数为 _________ .（2）a的立方的2倍与1的和为 _________ .（3）m与n两数差的平方减去它们平方的和: _________ .5.（1）0.55x (2)2a31 (3)(mn)2(m2+n2)6.一个三位数，百位数字是a，十位数字和个位数字组成的两位数是b，用式子表示这个三位数是 _________ .6.100a + b7.已知多项式3x2y2 + 1 + r3y3x41是五次四项式.且单项式3x2y2的次数与该多项式的次数相同.（1）求m，n的值:（2）把这个多项式按x的升幂排列.7.解:（1）因为3x2y（m+1）+ x3y3x41是五次四项式，所以2 + m + 1 = 5，解得m = 2，因为单项式3x2n y^2 m的次数与该多项式的次数相同，所以2n + 2 m = 5，即2n + 2 2 = 5.解得n = 5 2.（2）把这个多项式按x的升幂排列为 1 3x233 + x3y3x4.巅峰训练8.（2020·杭州萧山区期中）一组按规律排列的单项式:a2，3a4，5a6，7a8，…，则第n（n为正整数）个式子表示最恰当的是（）A.±（2n1）a2nB.±（2n + 1）a2nC.（1）n（2n1）a2nD.（1）n（2n + 1）a2n8.C9.（2020·哈尔滨平房区模拟）甲、乙两个商家对标价相同的同一件商品进行价格调整，甲的方案是:先提价8%，再降价8%；乙的方案是:先降价8%，再提价8%；则甲、乙两个商家对这件商品的最终定价（）A.甲比乙多B.乙比甲多C.甲、乙一样多D.无法确定9.C素养提升10.（2020·南京玄武区期中）为响应国家节能减排的号召，鼓励人们节约用电，保护能源，某市实施用电“阶梯价格”收费制度.收费标准如下表:已知小刚家上半年的用电情况如下表（以200千瓦时为标准，超出200千瓦时记为正、低于200千瓦时记为负）:根据上述数据、解答下列问题:（1）小刚家用电量最多的是 _________ 月份，实际用电量为 _________ 千瓦时:（2）小刚家一月份应缴纳电费 _________ 元；（3）若小刚家七月份用电量为x千瓦时，求小刚家七月份应缴纳的电费（用含x的代数式表示）.10.（1）五236[提示:由表格可知五月份用电量最多，实际用电量为200 + 36 = 236（千瓦时）.]（2）85[提示:小刚家一月份用电:200 + （50）= 150（千瓦时），小刚家一月份应缴纳电费:0.5 × 50 + （150 50）× 0.6 = 25 + 60 = 85（元）.] （3）解:当0 < x≤50时，电费为0.5x元:当50 < x≤200时，电费为0.5 × 50 + （x50）× 0.6 = 25 + 0.6x30 = 0.6x5（元）；当x > 200时，电费为0.5 × 50 + 0.6 × 150 + （x200）× 0.8 = 25 + 90 + 0.8x160 = 0.8x45（元）.11.现代营养学家用身体质量指数来判断人体的健康状况.这个指数等于人体体重（千克）除以人体身高（米）的平方所得的商.一个健康人的身体质量指数在20~25之间；身体质量指数低于18，属于不健康的瘦；身体质量指数高于30，属于不健康的胖.（1）若一个人的体重为w（千克），身高为h（米），求他的身体质量指数p （即用含w，h的式子表示p）；（2）小张的身高是1.75米，体重是68千克，请你判断小张的身体是否健康.11.解:（1）由题意可得p = w h2.（2）w=68,h=1.75时，p = wh2≈ 22.2.因为20 < 22.2 < 25.所以小张的身体健康.。

发现学习、自主、合作、探究
知识与技能：掌握代数式的值的概念，能解释代数式的值的实际意义.会求代数式的值，进一步理解代数式的应用.
过程与方法：经历观察、猜想，验证等数学活动过程，初步体会到数学中抽象概况的思维方法.在代数式求值过程中，培养准确运算的能力.
情感态度价值观：通过求代数式的值，对问题进行探索猜想，进一步体会由具体到抽象、有特殊到一般和由一般到特殊的过程，发展合理推理能力.
重点：深入体会列代数式和代数式的值的实际意义，当所含字母取某一定值时，能够求出代数式的值.
难点：从特例入手，发现规律，推导出题目中的数量关系.体会特殊与一般相互转化在实际问题重点意义.。

3.2代数式的值 教学任务分析教学流程安排课前安排教学过程设计问题与情境师生行为设计意图活动1问题1 试一试有四个同学做传数游戏A 任意报一个数给B ，B 把这个数加1传给C ，C 把听到的数平方后传给D ，D 把听到的数减1报出答案.请裁判D 的答案是否正确.问题2 你是怎样快速判断出D 的答案是否正确的？问题3（1）代数式（x+1）2-1的值与什么有关？是否确定？（2）你认为什么是代数式的值？活动2问题1.例1：当a=2,b=-1,c=-3时,求下列代数式的值.（1）b2-4ac(2)a2+b2+c2+2ab+2bc+2ac(3)(a+b+c)2问题2.教材96页练习1、2活动3问题1观察例1中的（2）、（3）两题的结果，你有何想法？问题2再取一组数值试一试，看看结果如何，并在小组内交流你的结论.活动4问题1例2某企业去年的年产值为a 亿元，今年比去年增长了10%.请你预测一教师提出问题1．学生分组进行传数、裁判. 教师提出问题2．学生思考、回答、交流.．教师提出问题3．学生思考、交流、回答问题，自我建构平方根的定义．教师应关注学生的：（1）抽象概括能力；（2）对代数式的值的解释；（3）部分同学的参与水平．教师出示例1学生自由练习，互相纠正错误，确定好的解题格式与方法，有利于调动学生的积极性，促进学生能力的提高. 在活动2中，教师关注学生：（1）书写规范；（2）准确计算． 教师提出问题1．学生思考、回答、验证、总结. 在活动3中教师要关注学生：（1）是否愿意与同伴交流各自的想法；（2）动手实践问题1中数学游戏有挑战性，易激发学生的学习兴趣． 问题2的目的在于引导学生将游戏与代数式 （x+1）2-1的值联系起来. 学生通过大胆的猜想、多次取值、验证，发现规律，激活了学生的思维，提高计算推理的能力.学生经历操作、确认等数学活动过程，发展了合情推理能力.学生巩固、提高、发展。