答:它的体积是448立方厘米。
2、一根长方体木料,长5米,横截面的面积是
0.06平方米。这根木料的体积是多少?
长
根据V=Sh,可以这样计算:
5 米
0.06×5=0.3(立方米)
答:它的体积是0.3立方米。
22
0.06平方米
3、一块长方体铝块,体积是1200平方厘 米,横截面面积是80平方厘米,这块铝块的 长是多少厘米? 1200÷80=15(厘米)
2、 一种正方体铁皮水箱长0.8米,这个水箱能装水多少升? (铁皮的厚度略去不计)
解1:
0.8×0.8×0.8=0.512(立方米) 0.512立方米=512立方分米=512升
答:这个水箱能装水512升。
解2: 0.8米=8分米 8×8×8=512(立方分米)
512立方分米=512升
答:这个水箱能装水512升。
因为它们都含有同样多的体积单位------12个1厘米 3
体积都相同,而长、 宽、高不同。
10
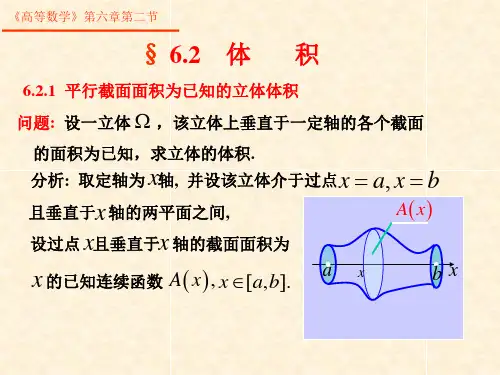
观察:右图这个长方体,长、宽、高的数,
除了表示出长、宽、高的长度外,还表示什么?
表示长的数,除了表示4厘米长外,还表示出一 排摆了4个1厘米的正方体.
表示宽的数,除了表示3厘米宽外,还表示出 摆了3排.
表示高的数,除了表示2厘米高外,还表示出 摆了2层.
高级单位
低级单位
低级单位的数÷进率
一块长方形的钢板长2.2米,宽1.5米,厚0.01米。 它的体积是多少立方分米?
解法(一)2.2×1.5×0.01=0.033(立方米) 0.033立方米=33(立方分米)
答:这块钢板的体积是33立方分米。
解法(二) 2.2米=22分米
1.5米=15分米