简谐运动的图像和公式

简谐运动的公式和定义1公式：$x=A/sin（ωT+φ）$2公式中的参数：（1）式中，$x$是振动粒子相对于平衡位置的位移，t是振动时间。

（2）A是距振动粒子平衡位置的最大距离，即振幅。

（3）ω称为简谐运动的圆频率，也代表简谐运动的振动速度。

三。

定义：如果作用在质点上的力与质点离开平衡位置的位移成正比，且始终指向平衡位置，则质点的运动为简谐运动。

4特征：（1）简谐运动是最基本、最简单的振动。

（2）简谐运动的位移按正弦规律随时间变化，因此它不是匀速变速运动，而是在变力作用下的变加速度运动。

5特征：（1）力特性：恢复力$f=-KX$，$f$（或$a$）与$x$的大小成正比，方向相反。

（2）运动特性：接近平衡位置时，$a、F、x$减小，$V$增大；远离平衡位置时，$a、F、x$增大，$V$减小。

（3）能量特性：振幅越大，能量越大。

在运动过程中，动能和势能相互转化，系统的机械能守恒。

（4）周期性特征：质点的位移、回复力、加速度和速度随时间呈周期性变化，变化周期为简谐运动周期，动能和势能也随时间呈周期性变化，变化周期为$-fracT2$。

（5）对称特征：在平衡位置的两个对称点，加速度、速度、动能、势能相等，相对平衡位置的位移相等。

6平衡位置：物体在振动过程中恢复力为零的位置。

7恢复力的定义：使物体恢复到平衡位置的力。

8恢复力方向：始终指向平衡位置。

9恢复力的来源：属于效应力。

它可以是某个力，几个力的合力或某个力的分力。

2、简谐运动的例子关于简谐运动和简谐运动中物体的完全振动的意义，下面的说法是正确的____A、当位移减小时，加速度减小，速度增大B、位移方向总是与加速度方向相反，与速度方向相同C、动能或势能首先恢复到原来大小的过程D、速度和加速度第一次同时恢复到原来的大小和方向的过程E、当物体的运动方向指向平衡位置时，速度方向与位移方向相反；当物体偏离平衡位置时，速度方向与位移方向相同答案：阿德分析：当位移减小时，恢复力减小，加速度减小，物体移动到平衡位置，速度增大，a正确；恢复力与位移方向相反，加速度与位移方向相反，但速度和位移方向可以相同，也可以相反；当物体的运动方向指向平衡位置时，速度方向与位移方向相反；位置偏离平衡位置时，速度方向与位移方向相同，所以B是错误的，E是正确的；在一次完全振动中，动能和势能可以多次恢复到原来的尺寸，所以C是错误的；在第一次完全振动中，速度和加速度同时恢复到原来的尺寸和方向的过程是完全振动，所以D是正确的。

第3节简谐运动的图像和公式1.简谐运动图像是一条正弦(或余弦)曲线，描述了质点做简谐运动时位移x 随时间t 的变化规律，并不是质点运动的轨迹。

2．由简谐运动图像可以直接得出物体振动的振幅、周期、某时刻的位移及振动方向。

3．简谐运动的表达式为x ＝A sin(2πTt ＋φ)或x ＝A sin(2πft＋φ)，其中A 为质点振幅、(2πTt ＋φ)为相位，φ为初相位。

1．建立坐标系以横轴表示做简谐运动的物体的时间t ，纵轴表示做简谐运动的物体运动过程中相对平衡位置的位移x 。

2．图像的特点一条正弦(或余弦)曲线，如图所示。

3．图像意义表示物体做简谐运动时位移随时间的变化规律。

4．应用由简谐运动的图像可找出物体振动的周期和振幅。

[跟随名师·解疑难]1．图像的含义表示某一做简谐运动的质点在各个时刻的位移，不是振动质点的运动轨迹。

2．由图像可以获取哪些信息？ (1)可直接读取振幅、周期。

(2)任意时刻质点的位移的大小和方向。

如图甲所示，质点在t 1、t 2时刻的位移分别为x 1和－x 2。

甲 乙(3)任意时刻质点的振动方向：看下一时刻质点的位置，如图乙中a 点，下一时刻离平衡位置更远，故a 此刻向上振动。

(4)任意时刻质点的速度、加速度、位移的变化情况及大小比较：看下一时刻质点的位置，判断是远离还是靠近平衡位置，若远离平衡位置，则速度越来越小，加速度、位移越来越大，若靠近平衡位置，则速度越来越大，加速度、位移越来越小。

如图乙中b 点，从正位移向着平衡位置运动，则速度 为负且增大，位移、加速度正在减小；c 点从负位移远离平衡位置运动，则速度为负且减小，位移、加速度正在增大。

[学后自检]┄┄┄┄┄┄┄┄┄┄┄┄┄┄(小试身手)如图所示为某质点做简谐运动的图像，则质点在前6 s 内通过的路程为________ cm ，在6～8 s 内的平均速度大小为________ cm/s ，方向________。

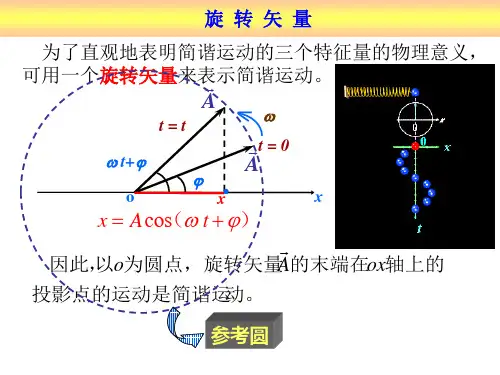
简谐运动知识点汇总第一节 简谐运动一、弹簧振子1、定义：我们把小球（物块）和弹簧组成的系统统称为弹簧振子。

2、理想化条件：忽略摩擦力等各种阻力、小球看成质点、忽略弹簧质量、弹簧始终在弹性限度内3、平衡位置：振子在振动方向上合理为零的点，速度最大，振动位移、回复力、回复加速度为零4、振动位移：由平衡位置指向振子位置的有向线段。

5、振动图像（x -t 图像）图像信息：① 横坐标 —— 时间（周期）② 纵坐标 —— 位移和路程③ 斜率 —— 速度④ 平衡位置 —— 位移为0，速度最大⑤ 最大位移处 —— 位移最大，速度为0二、简谐运动1、定义：如果物体的位移与时间的关系遵从正弦函数的规律，即它的振动图像（x -t 图像）是一条正弦曲线)sin(ϕω+=t A x ，这样的振动是一种简谐运动。

简谐运动是最基本的振动2、对称性： 关于平衡位置对称的两点位移大小相等，方向相反速度大小相等，方向可同可反时间对称第二节 简谐运动的描述一、振幅1、定义：振动物体离开平衡位置的最大距离，叫做振动的振幅，常用字母A 表示、是个标量。

2、说明：振子振动范围的大小是振幅的两倍----2A;振幅的大小直接反映了振子振动能量(E=EK+EP)的高低，振子质量一定时，振幅越大，振动系统能量越大。

二、周期频率三、圆频率：是一个与周期成反比，与频率成正比的量，叫作简谐运动的“圆频率”。

它也表示简谐运动的快慢f T ππω22== 四、相位、初相第三节 简谐运动的回复力和能量一、回复力1、定义：指向平衡位置使振子回到平衡位置的力2、特点：（1）回复力是效果力，由性质力充当，可以是一个力，可以是一个力的分力，可以是几个力的合力（2）回复力一定指向平衡位置且与位移方向相反3、公式F=-KX4、简谐运动定义2: 如果质点所受的力与它偏离平衡位置的位移大小成正比，即 F =-k x ，质点的运动就是简谐运动.第四节 单摆一、单摆：1、定义：细线一端固定在悬点，另一端系一个小球，如果细线的质量与小球相比可以忽略；球的直径与线的长度相比也可以忽略，这样的装置就叫做单摆2、特点（1）摆球：体积小，质量大可视为质点；（2）摆线：细长，不可伸长，质量忽略；（3）不计一切阻力（4）单摆是理想化模型（5）摆角一般小于5°3、回复力x L mg F -=回4、周期公式gl T π2=（注意等效摆长和等效重力加速度的换算）4、说明：单摆在平衡位置合力不为零（合力等于向心力），回复力为零第六节 受迫振动 共振一、固有振动和固有频率1、定义：振动系统在没有外力干预下的振动称为固有振动，也称自由振动，其频率称为固有频率。

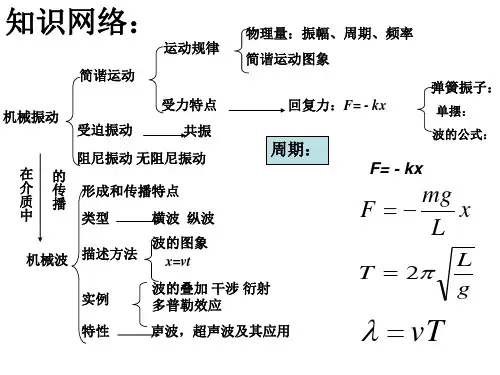
简谐运动的规律和图像一、简谐运动的基本规律1.简谐运动的特征2.注意：（1）弹簧振子（或单摆）在一个周期内的路程一定是4A，半个周期内路程一定是2A，四分之一周期内的路程不一定是A。

（2）弹簧振子周期和频率由振动系统本身的因素决定（振子的质量m和弹簧的劲度系数k ），与振幅无关。

二、简谐运动的图像1．简谐运动的数学表达式：x＝A sin(ωt＋φ)2．根据简谐运动图象可获取的信息(1)振幅A、周期T(或频率f)和初相位φ(如图所示)．(2)某时刻振动质点离开平衡位置的位移．(3)某时刻质点速度的大小和方向：曲线上各点切线的斜率的大小和正负分别表示各时刻质点的速度的大小和速度的方向，速度的方向也可根据下一时刻物体的位移的变化来确定．(4)某时刻质点的回复力、加速度的方向：回复力总是指向平衡位置，回复力和加速度的方向相同，在图象上总是指向t轴．(5)某段时间内质点的位移、回复力、加速度、速度、动能和势能的变化情况．3．简谐运动图象问题的两种分析方法法一图象－运动结合法解此类题时，首先要理解x －t 图象的意义，其次要把x －t 图象与质点的实际振动过程联系起来．图象上的一个点表示振动中的一个状态(位置、振动方向等)，图象上的一段曲线对应振动的一个过程，关键是判断好平衡位置、最大位移及振动方向．法二 直观结论法简谐运动的图象表示振动质点的位移随时间变化的规律，即位移－时间的函数关系图象，不是物体的运动轨迹．三、针对练习1、一个小物块拴在一个轻弹簧上，并将弹簧和小物块竖直悬挂处于静止状态，以此时小物块所处位置为坐标原点O ，以竖直向下为正方向建立Ox 轴，如图所示。

先将小物块竖直向上托起使弹簧处于原长，然后将小物块由静止释放并开始计时，经过s 10π，小物块向下运动20cm 第一次到达最低点，已知小物块在竖直方向做简谐运动，重力加速度210m /s g =，忽略小物块受到的阻力，下列说法正确的是（ ）A ．小物块的振动方程为0.1sin 102x t π⎛⎫=+ ⎪⎝⎭（m ） B ．小物块的最大加速度为2gC 2m /sD ．小物块在0～1330s π的时间内所经过的路程为85cm2、（多选）某弹簧振子在水平方向上做简谐运动，其位移x 随时间变化的关系式为x ＝A sin ωt ，如图所示，则( )A ．弹簧在第1 s 末与第5 s 末的长度相同B ．简谐运动的频率为18Hz C ．第3 s 末，弹簧振子的位移大小为22A D ．第3 s 末至第5 s 末，弹簧振子的速度方向不变3、（多选）如图甲所示，悬挂在竖直方向上的弹簧振子，在C 、D 两点之间做简谐运动，O 点为平衡位置。