(1)理解任意角的概念; (2) 建立直角坐标系讨论任意角,判断 象限角,掌握终边相同角的集合的书写; (3) 掌握象限角的集合和非象限角的 集合的书写; (4)掌握区域角的集合的书写.
一、角的概念:
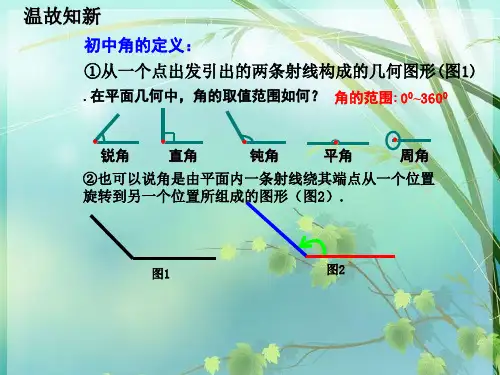
初中定义:从一点出发的两条射线组成
的几何图形叫做角。角的范围:[0,360)
顶
边
点
边
一、角的概念:
{ | 0 k • 360 90 k • 360 , k Z}
第二象限角的集合:
{ | 90 k • 360 180 k • 360 , k Z}
第三象限角的集合:
{ |180 k • 360 270 k • 360 , k Z}
第四象限角的集合:
{ | 270 k • 360 360 k • 360 , k Z}
例1:写出与-950º角终边相同的角的集合S, 并把S中在0º~360º间的角写出来:
S { | 950 k • 360 , k Z} 950 3 360 130,
为第二象限角
终边在坐标轴上角的取值
y 90 +k×360
180 +k×360 O
x 0 +k×360 或360+k×360
观察: 390,330,它们的终边
y
-3300 3900OΒιβλιοθήκη 与30角的终边有什么关系?
300 x
3900=300+3600 =300+1 x 3600
-3300=300-3600 =300-1 x 3600
300=
=300+0 x 3600
与300终边相同的角的一般形式为:
300+k·3600,k ∈ Z
270 +k×360