电力系统不对称短路计算..

电力系统不对称故障分析与计算及其程序设计电力系统是现代社会不可或缺的组成部分。

在电力系统中，不对称故障是一种严重的故障，其影响可以导致电力系统的瘫痪。

因此，不对称故障分析与计算非常重要，是电力系统维护的基础工作之一。

本文将重点讨论电力系统不对称故障分析与计算及其程序设计。

1. 不对称故障的概念不对称故障是指在电力系统中，一侧电源与另一侧负载不对称导致的故障。

不对称故障通常包括短路故障和开路故障两种情况。

短路故障是指两个相之间或者相与地之间的短路，导致电路异常加热、设备损坏、电压降低等问题。

开路故障是指电路中出现的缺失和断路，导致电流无法正常流动，使电力系统无法正常运行。

2. 不对称故障分析与计算在出现不对称故障时，需要进行分析和计算。

基本的不对称故障分析和计算包括以下内容：（1）不对称故障电流的计算。

不对称故障电流是指出现不对称故障时电路中的电流。

不同类型的故障电流计算方法不同，需要根据具体情况进行计算。

不对称故障电流的计算非常关键，可以为后续的故障处理提供依据。

（2）故障影响分析。

不对称故障会对电力系统产生不同程度的影响，包括电压降低、设备故障、负荷损失等。

需要进行故障影响分析，为后续处理提供依据。

（3）电力系统稳态分析。

在不对称故障发生时，需要进行电力系统的稳态分析，分析电力系统受故障干扰后的运行情况，为后续处理提供可靠的指导。

3. 不对称故障计算程序设计对于电力系统不对称故障计算，可以设计相应的计算程序，以提高计算效率和准确性。

根据不同的故障情况和计算需求，可以设计不同的计算程序。

一般而言，不对称故障计算程序应包括以下部分：（1）输入信息。

输入信息主要包括电路图、电力系统参数、故障类型等。

输入信息的准确性对计算结果具有重要的影响。

（2）故障电流计算。

根据输入的电路图和电力系统参数，计算不对称故障电流。

不对称故障电流是不对称故障计算的基础。

（3）故障影响分析。

根据不对称故障电流，计算电力系统电压降低、设备故障等影响，预测故障对电力系统的影响程度。

电力系统不对称故障的分析计算1. 引言电力系统是现代社会中不可或缺的根底设施之一。

然而，由于各种原因，电力系统可能会发生不对称故障，导致电力系统的正常运行受到严重影响甚至导致短路事故。

因此，对电力系统不对称故障进行分析和计算是非常重要的。

本文将分析电力系统不对称故障的原因、特点以及进行相应计算的方法，并使用Markdown文本格式进行输出。

2. 不对称故障的原因和特点不对称故障是指电力系统中出现相序不对称的故障。

其主要原因包括：单相接地故障、双相接地故障以及两相短路故障等。

不对称故障的特点如下：1.电流和电压的相位不同：在不对称故障中，电流和电压的相位不同，通常表现为电流和电压波形的不对称。

2.非对称系统功率：由于不对称故障，电力系统中的功率将变得非对称。

正常情况下，三相电流和电压的功率应该平衡，但在不对称故障中，这种平衡被破坏。

3.对称分量的存在：在不对称故障中，由于相序的不同，电流和电压中会存在对称正序分量、对称负序分量和零序分量。

3. 不对称故障的分析计算方法对于不对称故障的分析计算，一般可以采用以下步骤：3.1 系统参数获取首先，需要获取电力系统的各项参数，包括发电机、变压器、线路和负载的参数等。

这些参数将用于后续的计算。

3.2 故障状态建模根据故障的类型和位置，对故障状态进行建模。

常见的故障状态包括单相接地故障、双相接地故障和两相短路故障等。

3.3 网络方程建立基于故障状态的建模，可以建立电力系统的节点方程或潮流方程。

通过求解节点方程或潮流方程，可以得到电流和电压的分布情况。

3.4 不对称故障计算根据网络方程的求解结果，可以计算不对称故障中电流、电压和功率的各项指标，包括正序分量电流、负序分量电流、零序电流等。

3.5 故障保护和控制根据不对称故障的计算结果，可以对故障保护和控制系统进行设计和优化。

通过故障保护和控制系统的响应，可以及时检测和隔离故障，保证电力系统的平安运行。

4. 结论电力系统不对称故障的分析计算是确保电力系统平安运行的重要步骤。

不对称短路的分析和计算Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】目录摘要电力系统的安全、稳定、经济运行无疑是历代电力工作者所致力追求的，但是从电力系统建立之初至今电力系统就一直伴随着故障的发生而且电力系统的故障类型多样。

在电力系统运行过程中，时常会发生故障，且大多是短路故障。

短路通常分为三相短路、单相接地短路、两相短路和两相接地短路。

其中三相短路为对称短路，后三者为不对称短路。

电力运行经验指出单相接地短路占大多数，因此分析与计算不对称短路具有非常重要意义。

求解不对称短路，首先应该计算各原件的序参数和画出等值电路。

然后制定各序网络。

根据不同的故障类型，确定出以相分量表示的边界条件，进而列出以序分量表示的边界条件，按边界条件将三个序网联合成复合网，由复合网求出故障处各序电流和电压，进而合成三相电流电压。

关键词: 不对称短路计算、对称分量法、节点导纳矩阵1电力系统短路故障的基本概念短路故障的概述在电力系统运行过程中，时常发生故障，其中大多数是短路故障。

所谓短路：是指电力系统正常运行情况以外的相与相之间或相与地（或中性线）之间的连接。

除中性点外，相与相或相与地之间都是绝缘的。

电力系统短路可分为三相短路，单相接地短路。

两相短路和两相接地短路等。

三相短路的三相回路依旧是对称的，故称为不对称短路。

其他的几种短路的三相回路均不对称，故称为不对称短路。

电力系统运行经念表明，单相短路占大多数，上述短路均是指在同一地点短路，实际上也可能在不同地点同时发生短路，例如两相在不同地点接地短路。

依照短路发生的地点和持续时间不同，它的后果可能使用户的供电情况部分地或全部地发生故障。

当在有由多发电厂组成的电力系统发生端来了时，其后果更为严重，由于短路造成电网电压的大幅度下降，可能导致并行运行的发电机失去同步，或者导致电网枢纽点电压崩溃，所有这些可能引起电力系统瓦解而造成大面积的停电事故，这是最危险的后果。

第5 章电力系统不对称短路的计算分析5.1 基本认识5.2 元件的序阻抗及系统序网络的拟制及化简5.3 不对称短路时短路点电流和电压的分析及计算前言：1. 不对称短路时短路点的电流和电压出现不对称，短路点电流和电压的计算关键是求出其中一相的各序电流、电压分量。

2. 各序电流、电压分量分量的计算方法：解析法——解方程：上述 5.1 中三序网的基本式+三个补充方程（据不同类短路型的边界条件列出。

——繁，不用有两种复合序网法——将三个序网适当连接———组成复合序网法，求各序电流、电压（该法易记，方便，故广泛用——实际上是由解析法推导出的）3. 何谓“复合序网’——将三个序网适当连接，体现 a 相各序电流、电压关系的网络图。

4. 设对短路点各序网络图以简化到最简单的形式（见下图）——且表达形式有三种正序网E jX1 I a1E jX 1Ia1(n) f ++Ua1X1Ua1__G表达1 表达2 表达3 jX jX2 2I Ia 2a2+(n)f+Ua2Ua 2X2__表达1 表达2 表达3零序网jX jXIIa0a0+(n)f+Ua0Ua 0X_—表达1 表达2 表达3一、复合序网图及相量图（一）单相接地(1)f （如下图所示）a—E+aa 相——故障相，特殊相—E b +bc 相——非故障相—E c +I I b I ca分析：边界条件：I (1)b I (1)cU (1) a 0据对称分量法, 得：I1 1(1) (1) (1) 2 (1) (1) (1)a (I aI a I ) I I I1 3a b c a a23(1)a0——即三序电流相等U (1) (1) (1)a U U Ua1 a2 (1)a0三序电流、电压可用下图5-30 体现，称为复合序网。

E jX1Ia1+Ua1_jX2Ia2+Ua 2jXIa0+Ua 0图5-30 f (1) 复合序网注：(1) 复合序网，体现了三序电流、电压的关系I (1) (1) (1)a I I1 a2a0U (1) (1) (1)a U U1 a2a0(2) 由复合序网, 可直接写出短路点 f (1) 点的各序电流、电压IE(1) (1)aa I I1 ( ) a2j X X X1 2 3(1)a0U (1) (1) (1) (1)a E jI X (U U1 a a1 a2 a01 )(1) (1) U a20 jI a X2 2(1) (1)U a00 jI a X0（3）短路点故障相电流( 31) (1) (1) (1) (1)I a I I I I ——即为正序电流a1 a 2 a0 a1(1)I 的3 倍a1(1) (1) o2. 相量图（设I a I 0 )1 a1注：（1）由相量图可见，短路点:(1) 故障相电压U 0a I (1) 3a I(1)a1非故障相电压(1) (1) 但相位差(1) (1) 0OIb IU b U , 120c c （2）作相量图方法A 先作各相各序分量B 再作各相U、I 相量（二）两相短路( 2)f （如下图所示）b,cbc 相——故障相—E a +a 相——非故障相，特殊相—E +b—E+cI I b I ca分析：边界条件：I (2) a 0I (2)b I ( 2) cU ( 2)b U ( 2)c 0据对称分量法, 得：(2) (2)I a U （无零序网）0, 0 0a0I (2) (2)a I1 a2U (2) ( 2)a U1 a2三序电流、电压可用下图5-31 体现，称为复合序网。

电力系统不对称故障的分析计算电力系统不对称故障是指系统中发生了一相接地、两相短路或者两相间接地短路等故障情况。

这些故障会引起系统中电流、电压的不对称变化，给电力设备和系统带来了严重的影响和损坏。

因此，对于电力系统不对称故障的分析计算具有重要的理论和实际意义。

首先，在进行不对称故障分析计算之前，需要了解电力系统的基本参数和特性。

电力系统由发电机、变电站、输电线路和用户负载等组成，其中电力设备的参数包括电阻、电抗和电导等。

在进行计算时，需要收集和记录各个电力设备的参数。

然后，可以进行电力系统的不对称故障计算。

根据不同类型的故障情况，可以采用不同的计算方法和理论模型。

一般来说，对于发生了一相接地故障的情况，可以采用等值法来计算。

即将一相接地作为一个等效阻抗连接到系统中，然后进行系统的节点分析和电流计算。

对于发生了两相短路或者两相间接地短路的情况，可以采用对称分量法进行计算。

即将系统中的电流、电压分解为正序、负序和零序三个部分，然后分别计算其大小和方向，并根据这些结果来判断系统中的故障情况和对电力设备的影响程度。

不对称故障分析计算的输出结果主要包括故障电流、故障电压和故障功率等。

这些结果可以用来评估系统中电力设备的可靠性和安全性，并为对故障设备的维修和更换提供参考依据。

此外，还可以利用这些结果进行系统的保护和自动化控制设计，以提高电力系统的性能和可操作性。

总之，电力系统不对称故障的分析计算是电力系统研究和运行中的重要内容。

通过对故障情况的分析和计算，可以更好地了解和解决系统中的故障问题，提高系统的可靠性和稳定性，保障电力供应的安全和稳定。

第八章 电力系统不对称故障的分析计算主要内容提示：电力系统中发生的故障分为两类：短路和断路故障。

短路故障包括：单相接地短路、两相短路、三相短路和两相接地短路；断路故障包括：一相断线和两相断线。

除三相短路外，均属于不对称故障，系统中发生不对称故障时，网络中将出现三相不对称的电压和电流，三相电路变成不对称电路。

直接解这种不对称电路相当复杂，这里引用120对称分量法，把不对称的三相电路转换成对称的电路，使解决电力系统中各种不对称故障的计算问题较为方便。

本章主要内容包括：对称分量法，电力系统中主要元件的各序参数及各种不对称故障的分析与计算。

§8—1 对称分量法及其应用利用120对称分量法可将一组不对称的三相量分解为三组对称的三序分量（正序分量、负序分量、零序分量）之和。

设c b a F F F ∙∙∙为三相系统中任意一组不对称的三相量、可分解为三组对称的三序分量如下：()()()()()()()()()021021021c c c c b b b b a a a a F F F F F F F F F F F F ∙∙∙∙∙∙∙∙∙∙∙∙++=++=++= 三组序分量如图8-1所示。

正序分量： ()1a F ∙、()1b F ∙、()1c F ∙三相的正序分量大小相等，彼此相位互差120°，与系统正常对称运行方式下的相序相同，达到最大值的顺序a →b →c ，在电机内部产生正转磁场，这就是正序分量。

此正序分量为一平衡的三相系统，因此有：()()()111c b a F F F ∙∙∙++=0。

负序分量：()2a F ∙、()2b F ∙、()2c F ∙三相的负序分量大小相等，彼此相位互差120°，与系图 8-1 三序分量Fc(0) ·零序F b(0) ·F a(0) ·120°120° 120° 正序F b(1)·F a(1)·F c(1) ·ω120°120°120°负序 F a(2)·F c(2)·F b(2)·ω统正常对称运行方式下的相序相反，达到最大值的顺序a →c →b ，在电机内部产生反转磁场，这就是负序分量。

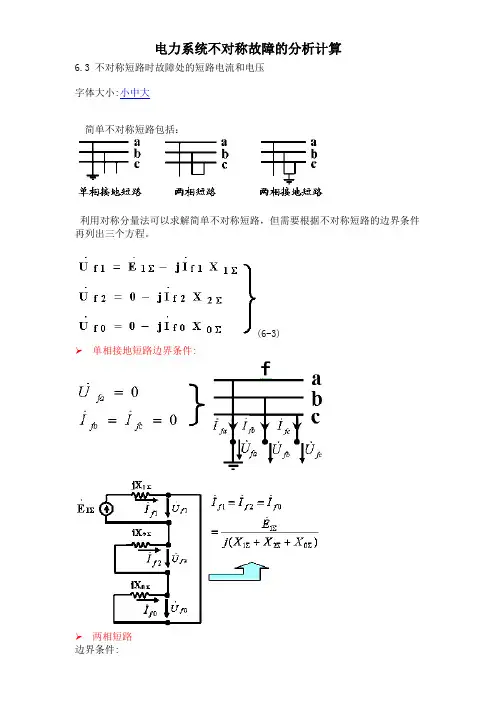
电力系统不对称故障的分析计算6.3 不对称短路时故障处的短路电流和电压字体大小:小中大简单不对称短路包括：利用对称分量法可以求解简单不对称短路，但需要根据不对称短路的边界条件再列出三个方程。

(6-3)➢单相接地短路边界条件:➢两相短路边界条件:复合序网：➢两相接地短路边界条件:复合序网：6.3.1 单相接地短路边界条件:由式6-1直接可以得到（略去了a相的下标a）：由式6-2可以得到：所以（略去了a相的下标a）：(6-4)将式6-3和式6-4联立求解，则(6-5)根据式6-4可以得到单相接地短路的复合序网。

复合序网—根据边界条件所确定的短路点各序量之间的关系，将各序网络连接起来所形成的网络。

显然，由复合序网也可以直接得到式6-5。

此外：再利用式6-1，可以得到短路点的故障相电流：短路点的非故障相电压：一般X1∑≈X2∑，因此，如果X0∑＜X1∑，则单相短路电流大于同一地点的三相短路电流；反之，则单相短路电流小于三相短路电流。

[例6-2] 在图示电力系统中，变压器T2高压侧发生a相接地短路，不计负荷作用，试计算短路瞬间故障点的短路电流。

解：取功率基准值SB=120MVA ，各级电压基准值U B =U av =115、37、10.5kV 。

计算各元件的电抗标幺值，并做出正序、负序和零序等值电路。

X G1=X G2=0.14X L1=105×0.4×120/1152=0.381=X L2 X L0=3×0.381=1.143X T1_1=10.5/100×120/120=0.105=X T1_2=X T1_0 X T2_1=10.5/100×120/60=0.21=X T2_2=X T2_0化简正序、负序和零序等值电路，并做出单相接地短路的复合序网。

X 1∑=X G1+X T1_1+X L1=0.626=X 2∑短路点的故障相电流：短路电流有效值：6.3.2 两相短路边界条件:复合序网：由复合序网可以得到：再利用式6-1可以得到短路点的故障相电流：如果，则：短路点的各相对地电压：6.3.3 两相接地短路边界条件:复合序网：由复合序网可以得到：再利用式6-1可以得到短路点的故障相电流：短路点的非故障相电压：6.3.4 正序等效定则及其应用三种不对称短路时，正序电流分别为:单相接地短路两相短路两相接地短路因此，三种不对称短路时，正序电流可以归纳为:正序等效定则—简单不对称短路故障的短路点正序电流分量，与在短路点每一相中加入附加电抗后发生的三相短路时的电流相等。

摘要随着电力事业的快速发展，电力电子新技术得到了广泛应用；出于技术、经济等方面的考虑，500kV及以上的超高压输电线路普遍不换位，再加上大量非线性元件的应用，电力系统的不对称问题日益严重。

因此电力系统不对称故障分析与计算显得尤为重要。

基于对称分量法的基本理论，对称分量法采取的具体方法之一是解析法，即把该网络分解为正，负，零序三个对称序网，这三组对称序分量可分别按对称的三相电路分解。

计算机程序法。

通过计算机形成三个序网的节点导纳矩阵，然后利用高斯消去法通过相应公式对他们进行数据运算，即可求得故障端点的等值阻抗。

最后根据故障类型选取相关公式计算故障处各序电流，电压，进而合成三相电流电压。

进行了参数不对称电网故障计算方法的研究。

通过引计算机算法，系统介绍电网参数不对称的计算机算法方法。

根据断相故障和短路故障的特点，通过在故障点引入计算机算法，，给出了各种断相故障和短路故障的仿真计算。

此方法以将故障电网分为对称网络和不网络两部分，在程序法则下建立起不对称电网故障计算统一模型，根据线性电路的基本理论，并借助于相序参数变换技术完成故障计算。

关键词：参数不对称电网故障计算1 短路故障的概述在电力系统运行过程中，时常发生故障，其中大多数是短路故障。

所谓短路：是指电力系统正常运行情况以外的相与相之间或相与地（或中性线）之间的连接。

除中性点外，相与相或相与地之间都是绝缘的。

电力系统短路可分为三相短路，单相接地短路。

两相短路和两相接地短路等。

三相短路的三相回路依旧是对称的，故称为不对称短路。

其他的几种短路的三相回路均不对称，故称为不对称短路。

电力系统运行经念表明，单相短路占大多数，上述短路均是指在同一地点短路，实际上也可能在不同地点同时发生短路，例如两相在不同地点接地短路。

依照短路发生的地点和持续时间不同，它的后果可能使用户的供电情况部分地或全部地发生故障。

当在有由多发电厂组成的电力系统发生端来了时，其后果更为严重，由于短路造成电网电压的大幅度下降，可能导致并行运行的发电机失去同步，或者导致电网枢纽点电压崩溃，所有这些可能引起电力系统瓦解而造成大面积的停电事故，这是最危险的后果。

电力系统不对称故障分析与计算及其程序设计电力系统不对称故障是指系统中至少有一个相数不相等的故障，其中至少一个相与其他相之间的短路发生。

此类故障会产生较大的电流和较高的瞬态电压，对电力设备带来严重的损坏，并可能引发系统崩溃。

因此，对电力系统不对称故障进行准确的分析与计算，并进行相应的程序设计具有重要意义。

首先，对于电力系统的不对称故障分析，需要进行故障类型及位置的识别。

常见的不对称故障类型包括对地短路故障、对线短路故障和对相短路故障。

针对不同类型的故障，需要使用不同的分析方法和计算模型来进行准确的故障分析和计算。

对于不对称故障的计算，主要包括短路电流计算和瞬态电压计算两个方面。

短路电流计算是为了确定故障点附近电力设备的额定电流和相对短路电流，以便评估系统的稳定性，并为保护装置的选择提供参考。

瞬态电压计算是为了确定故障点附近的电力设备所受到的瞬态电压，以评估设备的耐受能力和选择适当的绝缘等级。

针对电力系统不对称故障的分析与计算，可以采用数值计算方法和仿真软件进行。

数值计算方法包括传统的对称分量法、复数隔离法和序列分解法等。

这些方法可以通过求解线性方程组和迭代计算等手段，得到故障前后系统的电压、电流等参数。

而仿真软件，如PSCAD、EMTP-RV等，能够通过建立系统拓扑模型和设备参数，模拟不对称故障并进行动态仿真分析，实现系统参数的精确计算和分析。

为了更好地进行电力系统不对称故障的分析与计算，需要进行相应的程序设计。

程序设计的关键是实现数值计算方法和仿真软件的算法流程，并配以友好的用户界面和可视化展示。

常用的程序设计语言包括C++、MATLAB等，通过编写相关的算法和模块，实现故障分析与计算的自动化和高效化。

程序设计的目标是提高计算速度和精度，减少人工操作的难度和错误。

总之，电力系统不对称故障的分析与计算是保障电力系统安全稳定运行的关键环节。

通过准确的分析与计算，可以评估系统的稳定性和设备的耐受能力，为保护装置的选择和系统运行的优化提供参考。