2020高考数学(文)一轮复习专题突破训练《解答题组合练A》

2020年领军高考数学一轮复习(文理通用)集合与常用逻辑用语章节验收测试卷A卷姓名班级准考证号1．设全集，集合，则( )A．[－1,0) B．(0,5] C．[－1,0] D．[0,5]【答案】C【解析】由题，解得集合集合故[－1,0]故选C2．设集合，则（）A．B．C．D．【答案】A【解析】因为，所以，选A. 3．已知集合，则下图中阴影部分所表示的集合为（）A．B．C．D．【答案】B【解析】阴影部分对应的集合为A∩∁R B，，则∁R B＝{x|﹣1＜x＜1}，则A∩∁R B＝{0}，故选：B．4．已知集合，则（）A．B．C．D．【答案】C【解析】故选C项.5．设集合，则（）A．B．C．D．【答案】A【解析】由解得，故，所以，故选A. 6．已知全集，集合，则（）A．B．C．D．【答案】A【解析】集合中：，集合中：故选A项.7．集合，若，则由实数组成的集合为（）A．B．C．D．【答案】D【解析】∵集合A＝{-1，2}，B＝{x|ax﹣2＝0}，B⊆A，∴B＝∅或B＝{-1}或B＝{2}∴a＝0，1，-2故选：D．8．已知集合，则满足的集合的个数为（）A．B．C．1D．【答案】A【解析】由可知集合中一定有元素2，所以符合要求的集合，共4种情况，所以选A项. 9．已知集合，则（）A．B．C．D．【答案】B【解析】∵，∴，∴．故选B．10．若命题p：，则该命题的否定是（）A．B．C．D．【答案】D【解析】解：由特称命题的否定可知：命题p的否定是“，故选：D．11．下列说法正确的是A．若命题p，都是真命题，则命题“”为真命题B．命题“若，则”的否命题为“若”C．“”是“”的必要不充分条件D．命题“”的否定是“”【答案】D【解析】由于为真命题，故为假命题，所以为假命题，故A选项错误.原命题的否命题是“若”，故B选项错误.当时，，为充分条件，故C选项判断错误.根据全称命题的否定是特称命题的知识可以判断D选项正确，故选D.12．下列三个命题：①命题，则；②命题，命题，则成立的充分不必要条件；③在等比数列中，若，则；其中真命题的个数为( )A．B．C．D．【答案】A【解析】①命题，则，所以该命题是假命题；②命题：0≤x≤1，命题：x＜1，则成立的非充分非必要条件，所以该命题是假命题；③在等比数列中，若，则，但是等比数列的奇数项都是同号的，所以要舍去-4,所以.所以该命题是假命题.故选:A13．设命题在定义域上为减函数；命题为奇函数，则下列命题中真命题是( ) A．B．C．D．【答案】B【解析】f（x）在定义域上不满足减函数的定义，如时，即时，故命题p是假命题，sin x为奇函数，故命题q是真命题，则（￢p）∧q为真命题，其余为假命题，故选：B．14．命题的否定是A．B．C．D．【答案】C【解析】全称命题的否定为特称命题，命题的否定是，故选：C．15．已知平面平面，则的A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】A【解析】由题意知，平面平面，当时，利用面面垂直的性质定理，可得成立，反之当时，此时不一定是垂直的，所以的充分不必要条件，故选A.16．已知集合．若，则实数a的值为____．【答案】4【解析】∵，∴a=4故答案为417．已知集合，则______．【答案】【解析】，则，故答案为：．18．已知集合，则________．【答案】{0，1}【解析】因为，所以．故答案为：．19．已知集合，则=______.【答案】【解析】由题得故答案为：20．已知集合，且，则实数的值是_________. 【答案】5【解析】，集合，可得，所以，故答案为5 .。

高考数学一轮复习排列与组合专题练习及答案高考数学一轮复习排列与组合专题练习及答案一、填空题1.市内某公共汽车站有6个候车位(成一排)，现有3名乘客随便坐在某个座位上候车，则恰好有2个连续空座位的候车方式的种数是________.[解析] 由于题目要求的是奇数，那么对于此三位数可以分成两种情况：奇偶奇，偶奇奇.如果是第一种奇偶奇的情况，可以从个位开始分析(3种选择)，之后十位(2种选择)，最后百位(2种选择)，共322=12种;如果是第二种偶奇奇的情况，个位(3种情况)，十位(2种情况)，百位(不能是0,1种情况)，共321=6种，因此总共12+6=18种情况.[答案] 182.若从1,2,3，，9这9个整数中同时取4个不同的数，其和为偶数，则不同的取法共有________种.[解析] 满足题设的取法可分为三类：一是四个奇数相加，其和为偶数，在5个奇数1,3,5,7,9中，任意取4个，有C=5(种);二是两个奇数加两个偶数其和为偶数，在5个奇数中任取2个，再在4个偶数2,4,6,8中任取2个，有CC=60(种);三是四个偶数相加，其和为偶数，4个偶数的取法有1种，所以满足条件的`取法共有5+60+1=66(种).[答案] 663.(2014福州调研)若一个三位数的十位数字比个位数字和百位数字都大，称这个数为伞数.现从1,2,3,4,5,6这六个数字中取3个数，组成无重复数字的三位数，其中伞数有________个.[解析] 分类讨论：若十位数为6时，有A=20(个);若十位数为5时，有A=12(个);若十位数为4时，有A=6(个);若十位数为3时，有A=2(个).因此一共有40个.[答案] 404.一个平面内的8个点，若只有4个点共圆，其余任何4点不共圆，那么这8个点最多确定的圆的个数为________.[解析] 从8个点中任选3个点有选法C种，因为有4点共圆所以减去C种再加1种，共有圆C-C+1=53个.[答案] 535.某同学有同样的画册2本，同样的集邮册3本，从中取出4本赠送给4位朋友，每位朋友1本，则不同的赠送方法共有________种.[解析] 分两种情况：选2本画册，2本集邮册送给4位朋友有C=6(种)方法;选1本画册，3本集邮册送给4位朋友有C=4(种)方法，不同的赠送方法共有6+4=10(种).[答案] 106.用数字1,2,3,4,5,6六个数字组成一个六位数，要求数字1,2都不与数字3相邻，且该数字能被5整除，则这样的五位数有________个.[解析] 由题可知，数字5一定在个位上，先排数字4和6，排法有2种，再往排好的数字4和6形成的3个空位中插入数字1和3，插法有6种，最后再插入数字2，插法有3种，根据分步乘法计数原理，可得这样的六位数有263=36个.[答案] 367.现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张，从中任取3张，要求这3张卡片不能是同一种颜色，且红色卡片至多1张，不同取法有________种.[解析] 第一类，含有1张红色卡片，共有不同的取法CC=264(种);第二类，不含有红色卡片，共有不同的取法C-3C=220-12=208(种).由分类计数原理知不同的取法有264+208=472(种).[答案] 4728.在1,2,3,4,5这五个数字组成的没有重复数字的三位数中，各位数字之和为偶数的三位数共有________个.[解析] 在1,2,3,4,5这五个数字中有3个奇数，2个偶数，要求三位数各位数字之和为偶数，则两个奇数一个偶数，符合条件的三位数共有CCA=36(个).[答案] 36二、解答题9.从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组，则骨科、脑外科和内科医生都至少有1人的选派方法种数是多少?(用数字作答).[解] 分三类：选1名骨科医生，则有C(CC+CC+CC)=360(种);选2名骨科医生，则有C(CC+CC)=210(种);选3名骨科医生，则有CCC=20(种).骨科、脑外科和内科医生都至少有1人的选派方法种数是360+210+20=590种.10.四个不同的小球放入编号为1,2,3,4的四个盒子中.(1)若每个盒子放一球，则有多少种不同的放法?(2)恰有一个空盒的放法共有多少种?[解] (1)每个盒子放一球，共有A=24(种)不同的放法;(2)法一先选后排，分三步完成.第一步：四个盒子中选一只为空盒，有4种选法;第二步：选两球为一个元素，有C种选法;第三步：三个元素放入三个盒中，有A种放法.故共有4CA=144(种)放法.法二先分组后排列，看作分配问题.第一步：在四个盒子中选三个，有C种选法;第二步：将四个球分成2,1,1三组，有C种放法;第三步：将三组分到选定的三个盒子中，有A种放法.故共有CCA=144种放法.。

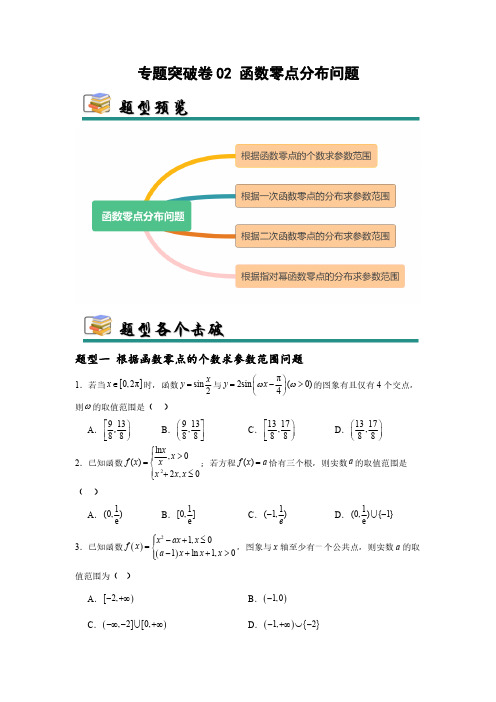
专题突破卷02 函数零点分布问题题型一 根据函数零点的个数求参数范围问题1．若当[]0,2πx Î时，函数sin 2x y =与π2sin (0)4y x w w æö=->ç÷èø的图象有且仅有4个交点，则w 的取值范围是（ ）A ．91388éö÷êëø,B ．913,88æùçúèûC ．1317,88éö÷êëøD ．1317,88æöç÷èø2．已知函数2ln ,0()2,0xx f x x x x x ì>ï=íï+£î；若方程()f x a =恰有三个根，则实数a 的取值范围是（ ）A ．1(0,)e B ．1[0,e C ．1(1,)e -D ．1(0,{1}e-U 3．已知函数()()21,01ln 1,0x ax x f x a x x x ì-+£ï=í-++>ïî，图象与x 轴至少有一个公共点，则实数a 的取值范围为（ ）A ．[)2,-+¥B ．()1,0-C ．(][),20,-¥-+¥U D ．(){}1,2-+¥È-4．()2ln x f x x=，()()()21g x f x mf x éù=--ëû，若()g x 在其定义域上有且仅有两个零点，则m 的取值范围是（ ）A ．21,e æö++¥ç÷èøB ．2e e 2,e 22e æö--ç÷èøC ．2e ,e 2æö-¥-ç÷èøD ．ee 1,122æö-+ç÷èø5．已知函数()432,0,ln ,0,x x x x f x x x x ì+-<=í>î若关于x 的方程()0f x m x -=有两个不同的实根，则实数m 的取值范围是（ ）A ．(],0-¥B ．[]0,1C ．(){},01¥-ÈD ．(]{},01-¥U 6．已知函数()223sin 1,sin 0sin 1,sin 0x x f x x x ì-³=í-<î且()0,2πx Î，若方程()1f x a =+与方程()1f x a =-共有6个不同的实数根，则实数a 的取值范围为（ ）A ．12,63æöç÷èøB ．12,33æöç÷èøC ．()0,1D ．1,16æöç÷èø7．定义在R 上的偶函数()f x 满足()()11f x f x +=-，且当[]0,1x Î时，()1e xf x =-，若关于x 的方程()()()10f x m x m =+<恰有5个实数解，则实数m 的取值范围为（ ）A ．()0,e 1-B ．1e 1e ,56--æöç÷èøC ．e 1e 1,86--æöç÷èøD ．1e 1e ,46--æöç÷èø8．已知函数()2()3e xf x x =-，若方程()f x a =有三个实数解，则实数a 的取值范围为（ ）A ．360,e æöç÷èøB ．(2e,0)-C ．362e,e æö-ç÷èøD ．32,6e e æö-ç÷èø9．已知函数()ln f x a x x =-有两个零点，则（ ）A ．0a £B ．0ea <<C ．ea ³D ．ea >10．若不等式ln 0a x x -³有且仅有三个整数解，则实数a 的取值范围是（ ）A ．25,ln 2ln5éö÷êëøB ．25,ln 2ln5æùçúèûC ．35,ln 3ln5éö÷êëøD ．35,ln 3ln 5æùçúèû11．设()321f x x ax bx =++-.函数()y f x =在1x =处取得极大值3，则以下说法中正确的数量为（ ）个.①320a b +=；②对任意的1m <，曲线()y f x =在点()(),m f m 处的切线一定与曲线()y f x =有两个公共点；③若关于x 的方程()f x k =有三个不同的根123,,x x x ，且这三个根构成等差数列，则1k =.A ．0B ．1C ．2D ．312．设函数()()2e1ln 2ax f x a x x -=+---有2个零点，则实数a 的取值范围是（ ）A ．(),e ¥-B ．10,e æöç÷èøC ．1,e e æöç÷èøD ．()0,e 13．若函数()()22e e 4e e 2x x x xf x b --=+-++（b 是常数）有且只有一个零点，则b 的值为（ ）A ．2B ．3C ．4D ．514．若函数121,02()πsin(π6xx x f x x x w ìæö--£ïç÷ïèø=íï-<<ïî有4个零点，则正数w 的取值范围是（ ）A ．1319,66éö÷êëøB ．1319,66æùçúèûC ．1925,66éö÷êëøD ．1925,66æùçúèû15．若函数()2341f x ax x =-+-在区间()1,1-内恰有一个零点，则实数a 的取值范围为（ ）A ．5,13æö-ç÷èøB ．54,33éù-êúëûC ．54,133éùìü-íýêúëûîþU D ．24,133éùìü-íýêúëûîþU 题型二 根据一次函数零点的分布求参数范围问题16．若函数f （x ）＝3ax ＋1－2a 在区间（－1，1）内存在一个零点，则a 的取值范围是（ ）A ．1,5æö+¥ç÷èøB ．11,5æö-ç÷èøC ．（－∞，－1）D ．（－∞，－1）∪1,5æö+¥ç÷èø17．若方程2222|1|0x ax a x -+++-=在区间()0,3内有两个不等实根，则实数a 的取值范围为（ ）A ．192,5æöç÷èøB．19(,3)15æö-¥-ç÷èøUC ．19(,115æö-¥+ç÷èøU D ．1915æöç÷èø18．当||1x £时，函数21y ax a =++的值有正也有负，则实数a 的取值范围是（ ）A ．1,3éö-+¥÷êëøB ．(,1]-¥-C ．11,3æö--ç÷èøD ．11,3æù--çúèû19．已知函数()312f x ax a =--在区间(1,1)-上存在零点，则（ ）A ．115a <<B ．15a >C ．15a <-或1a >D ．15a <-20．已知函数f （x ）=3ax -1-2a 在区间（-1，1）上存在零点，则（ ）A ．1a <或15a >B ．15a >C ．15a <-或1a >D ．15a <-21．若函数1y ax =+在(0,1)内恰有一解，则实数a 的取值范围是（ ）A ．1a >-B ．1a <-C ．1a >D ．1a <22．已知函数()312f x ax a =--在区间()1,1-上存在零点，则实数a 的取值范围是A ．1(,1),5æö-¥-È+¥ç÷èøB ．1,5æö+¥ç÷èøC ．1,(1,)5æö-¥-È+¥ç÷èøD ．1,5æö-¥-ç÷èø23．已知直线:3l y x =与函数3,1,(), 1.x x x f x ax a x ì-£=í->î的图像交于三点，其横坐标分别是1x ，2x ，3x .若1230x x x ++<恒成立，则实数a 的取值范围是A ．3a >B ．04a <£C ．36a <£D ．6a >24．已知函数2|log ,0(),21,0x x f x x x ìï=í+-£ïî若函数()1y f x m =-+有四个零点,零点从小到大依次为,,,,a b c d 则a b cd ++的值为( )A ．2B ．2-C ．3-D ．325．已知函数2()21f x mx x =--在区间(2,2)-恰有一个零点，则m 的取值范围是( )A ．31,88éù-êúëûB ．31,88æö-ç÷èøC ．31,88éö-÷êëøD ．13,88æù-çúèû26．已知()213,(0)(1)f x ax a f f =-+<且在()1,2内存在零点，则实数a 的取值范围是( )A ．(11,53)B ． 11(,64C ．11(,75D ．11(,)8627．已知函数()()221,03,(0)ax x x f x ax x ì++£=í->î有3个零点，则实数a 的取值范围是（ ）A ．1a <B ．01a <<C ．1a ³D ．0a >28．“4a <-”是“函数()3f x ax =+在区间[]1,1-上存在零点”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件29．设函数2()3f x x ax a =-++，()2g x ax a =-，若0R x $Î，使得0()0f x <和0()0g x <同时成立，则a 的取值范围为A ．(7,)+¥B ．(6,)(,2)+¥È-¥-C ．(,2)-¥-D ．(7,)(,2)+¥È-¥-30．“函数在区间上存在零点”是“”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件题型三 根据二次函数零点的分布求参数范围问题31．若函数()()2ln 0b cf x a x ac x x =++¹有且仅有极大值，则（ ）A ．0a >B ．0ab >C ．280b ac +>D ．0c <32．二次函数2,(,y ax bx c a b c =++是常数，且0)a ¹的自变量x 与函数值y 的部分对应值如下表：x…-1012…y…m 22n…且当32x =时，对应的函数值0y <．下列说法正确的有（ ）A ．0abc >B ．1009mn >C ．关于x 的方程20ax bx c ++=一定有一正、一负两个实数根，且负实数根在12-和0之间D ．()112,P t y +和()222,P t y -在该二次函数的图象上，则当实数12t <时，12y y >33．已知函数()()ln 1f x a x ax a =-+ÎR ，()()2312g x f x x =+-，则下列说法正确的是（ ）A ．当1a =时，()0f x £在定义域上恒成立B ．若经过原点的直线与函数()f x 的图像相切于点()()3,3f ，则1ln31a =-C ．若函数()g x 在区间3,42éùêúëû单调递减时，则a 的取值范围为[)16,¥+D ．若函数()g x 有两个极值点为()1212,x x x x ¹，则a 的取值范围为(),12¥-34．已知1x ，2x 是关于x 的方程2220()x ax a -+=ÎR 的两个不相等的实数根，则下列说法正确的有（ ）A ．若12112+=x x ，则2a =B ．若121x x <<，则32a >C ．若π02a b <<<，且1tan x a =，2tan x b =，则a b +为锐角D ．若1x ，2x 均小于2，则(3,2a öÎ-¥÷øU 35．已知函数()23,021,0x x x x f x x -ì-£=í->î，若关于x 的方程()()()221630f x a f x a +-×-=有4个不同的实根，则实数a 可能的取值有（ ）A ．112-B ．38-C ．14-D ．18-36．已知函数()222,0log ,0x x x f x x x ì--£ï=í>ïî，且()()234230f x af x a -++=有5个零点，则a 的可能取值有（ ）A ．1B ．32-C ．3-D ．5-37．已知函数()()2222,41log 1,14x x f x x x +ì--££-ï=í+-<£ïî，若函数()()21f x mf x --恰有5个零点，则m的值可以是（ ）A ．0B ．1C ．32D ．238．已知函数()()()()2221,0,22log ,0x x f x g x f x mf x x x ì+£ï==-+í>ïî，下列说法正确的是（ ）A ．若()y f x a =-有两个零点，则2a >B ．()y f x =只有一个零点1x =C ．若()y f x a =-有两个零点()1212,x x x x ¹，则121=x x D ．若()g x 有四个零点，则32m >.39．已知函数()e xxf x =，且关于x 的方程()()20f x mf x m ++=éùëû有3个不等实数根，则下列说法正确的是（ ）A ．当0x >时，()0f x >B ．()f x 在()1,+¥上单调递减C ．m 的取值范围是1,02æö-ç÷èøD ．m 的取值范围是21,0e e æö-ç÷+èø40．设函数()2e ,0313,022x x f x x x x ì£ï=í-++>ïî，函数()()()222g x f x bf x b =-+-，则下列说法正确的是（ ）A ．当1b =时，函数()g x 有3个零点B ．当4140b =时，函数()g x 有5个零点C ．若函数()g x 有2个零点，则2b <-或625b <<D ．若函数()g x 有6个零点，则112b <<41．已知函数()224,021,0x x x x f x x -ì+<=í-³î，若关于x 的方程()()244230f x a f x a -×++=有5个不同的实根，则实数a 的取值可以为（ ）A ．32-B ．43-C ．54-D ．76-42．已知函数()()21,0,0x ax x f x f x x ì++³ï=í--<ïî，有4个零点()12341234,,,x x x x x x x x <<<，则（ ）A ．实数a 的取值范围是(),2¥--B ．函数()f x 的图象关于原点对称C ．12342x x x x =D ．1234357x x x x +++的取值范围是()8,¥+43．已知函数()21243,0log ,0x x x f x x x ì---£ï=í>ïî，若方程()()2[]10f x mf x ++=恰有6个不相等的实数根，则实数m 的值可能是（ ）A ．53B ．73C ．103D ．11344．在下列命题中，正确的是（ ）A ．已知命题p ：“0x "³，都有tan x x ³，则命题p 的否定：“0x $<，都有tan x x <”B ．若函数()f x 满足()()2sin f x f x x +-=，则π162f æö=ç÷èøC ．“方程210x ax -+=有两个不相等的正实数根”的充要条件是“2a >”D ．若函数()1e 1x af x =-+是定义在区间[]2,a b -上的奇函数，则2b =45．已知函数()f x 的定义域为D ，且[,]a b D Í，若函数()f x 在[],x a b Î的值域为[],ka kb ，则称[],a b 为()f x 的“k 倍美好区间”.特别地，当1k =时，称[],a b 为()f x 的“完美区间”，则（）A ．函数21()2f x x x =-+存在“3倍美好区间”B ．函数1()3f x x=-+不存在“完美区间”C．若函数()f x m =-“完美区间”，则1,04m æùÎ-çúèûD ．若函数||1()||m x f x x -=存在“完美区间”，则(2,)m Î+¥题型四 根据指对幂函数零点的分布求参数范围问题46．已知函数()f x 的定义域为R ，且()10f ¹，若()()()f x y f x f y xy +-=-，则（ ）A ．()01f =B ．()23log 32f f æö>ç÷èøC ．方程()21xf x =-有唯一的实数解D ．函数()y xf x =有最小值47．已知函数()()ln ,12,1x a x x f x f x x +³ì=í-<î存在n 个零点12,,,,N n x x x n *×××Î，则（ ）A ．n 为偶数B ．e 1a -££-C ．122n x x x +++=L D ．1224n x x x ×××<L 48．已知实数,,x y z满足：22log xz ==，则下列不等式中可能成立的是（ ）A ．y x z <<B ．x y z <<C ．y z x<<D ．x z y<<49．已知函数()()()22124,1log 1,1x x f x x x +ì£-ï=í+>-ïî，若函数()y f x m =-有三个零点1x 、2x 、3x ，且123x x x <<，则（ ）A ．14m <£B ．3151162x -<£-C ．函数()1f x +的增区间为[]2,1--D．2212log x x ++8+50．已知函数()14,0lg 1,0x x f x xx x ì++<ï=íï+>î，若方程()f x a =有4个不同实根()12341234,,,x x x x x x x x <<<，则（ ）A ．2a >B ．411110x x ->C ．341100x x =D ．221211214x x <+<51．已知1x ，2x 为函数()()32024log 3xf x x -=--的两个零点，则下列结论中正确的有（ ）A ．()()12440x x --<B ．()()120331x x <--<C ．()()12331x x -->D ．若12x x <，则1213320242024x x --<52．已知函数221,0()log ,0x kx x f x x x ì-+£=í>î，下列关于函数[()]1y f f x =+的零点个数的说法中，正确的是（ ）A ．当1k >，有1个零点B ．当1k >时，有3个零点C ．当0k <时，有9个零点D ．当4k =-时，有7个零点53．记函数1,0()lg ,0x x f x x x ì+£=í>î，若123()()()f x f x f x ==（1x ，2x ，3x 互不相等），则123x x x ++的值可以是（ ）A ．2-B ．6C ．8D ．954．已知函数()1231,0,log ,0,x x f x x x +ì-£ï=í>ïî1x ，2x ，3x ，4x 是函数()()g x f x m =-的4个零点，且1234x x x x <<<，则（ ）A ．m 的取值范围是(]0,2B ．122333x x+=C ．344x x +的最小值是4D ．1234332x x x x ++55．已知函数()121x f x -=-，若关于x 的方程()()f f x m =有6个不相等的实根，则实数m的值可能为（ ）A ．14B ．13C ．12D56．已知函数()()()1101xf x x x x =--×>，()()()1lg 1g x x x x x =--×>的零点分别为12,x x ，则（ ）A ．1210x x ×<B ．12lg x x =C ．12111x x +=D ．124x x +>57．已知函数()222,0log ,0x x x f x x x ì--£ï=í>ïî，若1234x x x x <<<，且()()()()1234f x f x f x f x k ====，则下列结论正确的是（ ）A ．121x x +=-B ．341x x =C ．412x <<D ．01k <<58．已知函数()21,144,1x x f x x x x ì-<ï=í+-³ïî，若存在实数m 使得方程()f x m =有四个互不相等的实数根()12343124,,,x x x x x x x x >>>，则下列叙述中正确的有（ ）A ．140x x +<B ．124x x ×=C ．()3f m<D ．()32f x x +有最小值59．已知函数()2ln ,041,0x x f x x x x ì>=í--+£î，若关于x 的方程()()22210f x af x a -+-=有()k k ÎN 个不等的实根1x 、2x 、L 、k x 且12k x x x <<<L ，则下列判断正确的是（ ）A ．当0a =时，5k =B ．当2k =时，a 的范围为(),1-¥-C ．当8k =时，14673x x x x ++=-D ．当7k =时，a 的范围为()1,260．已知函数()()()lg2lg512xf x =+-，实数a 、()b a b <是函数()y f x m =-的两个零点，则下列结论正确的有（ ）A ．1m >B ．01m <<C ．222a b +=D．0a b +<1．函数()ln 1f x x =-的零点是（ ）A ．eB ．1eC ．10D ．1102．已知函数()()()()221,log 111x x xf x xg x x x x x =->=->--的零点分别为,a b ，则11a b +的值是（ ）A ．1B ．2C ．3D ．43．已知正数a b c ，，满足e ln e ln 1a c a b b c ===，则a b c ，，的大小关系为（ ）A ．c<a<bB ．c b a<<C ．a b c<<D ．a c b<<4．已知a 是方程e 40x x +-=的实根，则下列各数为正数的是（ ）A ．22a a -B ．e 2a -C ．ln aD ．23a a -5．下列命题为真命题的是（ ）A ．若22ac bc >，则a b>B ．函数()1f x +的定义域为[]0,1，则()3xf 的定义域为[]3,9C ．若幂函数()f x 的图像过点13,27A æöç÷èø，则()3f x x-=D ．函数()3ln f x x x=-的零点所在区间可以是()1,26．关于函数()π2sin 213f x x æö=-+ç÷èø，下列结论正确的是（ ）A ．π,06æöç÷èø是()f x 的一个对称中心B ．函数()f x 在π0,6æöç÷èø上单调递增C ．函数()f x 图像可由函数()2cos21g x x =+的图像向右平移5π12个单位得到D ．若方程()20f x m -=在区间π12π,2éùêúëû上有两个不相等的实根，则2,6m éùÎëû7．对于函数()3e x xf x =，下列说法正确的是（ ）A ．()f x 有最小值但没有最大值B ．对于任意的(),0x Î-¥，恒有()0f x <C ．()f x 仅有一个零点D ．()f x 有两个极值点8．已知函数224,0()log ,0x x x f x x x ì--£ï=í>ïî，若1234x x x x <<<，且()()()()1234f x f x f x f x ===，则下列结论正确的是（ ） A ．124x x +=-B ．341x x ×=C ．414x <<D ．123402x x x x <£9．（多选）已知函数()()22,02ln 11,0x x t x f x x x ì-+£ï=í+->ïî，若函数(())y f f x =恰好有4个不同的零点，则实数t 的取值可以是（ ）A ．-3B ．-2C ．0D ．210．已知函数3()34,[0,2]f x x x x =-+Î，则下列选项中正确的是（ ）A ．()f x 的值域为[]2,6B ．()f x 在1x =处取得极小值为2C ．()f x 在[]0,2上是增函数D ．若方程()f x a =有2个不同的根，则[2,4]a Î11．已知函数()1e ,01ln ,04x x x f x x x +ì-£ï=í->ïî，下列选项中正确的是（ ）A ．()f x 在(),1-¥-上单调递增，在()1,0-上单调递减B ．()f x 有极大值C ．()f x 无最小值D ．若函数()()()()2[]24h x f x af x a =-+ÎR 恰有6个零点，则实数a 的取值范围是5,2æö+¥ç÷èø12．方程()230x m x m +-+=有两个实根，则实数m 的取值范围是．13．若函数()cos2sin f x x m x =-在π,π6æöç÷èø上有2个零点，则m 的取值范围是.14．若关于x 的方程sin cos x x k -=无解，则实数k 的取值范围是.15．已知函数()22x f x x =+-，()2log 2g x x x =+-，()32h x x x =+-的零点分别为a ，b ，c ，则a b c ++=．若1x 满足22=5x x +，2x 满足222log (1)5x x +-=，则12=x x + .16．设函数 22,0()lg ,0x x x f x x x ì+£ï=í>ïî若关于x 的方程22()(12)()0f x m f x m m +-+-=有5个不的取值范围是．17．已知函数()44,4x f x f x x £<=-³ïî，若对于正数()*n k n ÎN ，直线n y k x =与函数()f x 的图像恰好有21n +个不同的交点，则22212n k k k +++=L．18．若函数 ()22ln 1f x ax x =--有两个零点，则a 的取值范围为 .19．已知函数()|ln |f x x b =+，关于以下四个结论：①函数()f x 的值域为[,)b +¥；②当a b >时，方程()f x a =有两个不等实根；③当0b =，0a >时，设方程()f x a =的两个根为1x ，2x ，则12x x +为定值；④当0b =，0a >时，设方程(1)f x a +=的两个根为1x ，2x ，则12120x x x x ++=．则所有正确结论的序号为 ．20．已知函数2)()(e x f x x ax =-.(1)若曲线()y f x =在=1x -处的切线与y 轴垂直，求()y f x =的极值.(2)若()f x 在(0,)+¥只有一个零点，求a .。

考点规范练13函数模型及其应用一、基础巩固1.在我国大西北,某地区荒漠化土地面积每年平均比上一年增长10.4%,专家预测经过x年可能增长到原来的y倍,则函数y=f(x)的图象大致为()y=(1+10.4%)x,函数是底数大于1的指数函数,故选D.2.某电视新产品投放市场后第一个月销售100台,第二个月销售200台,第三个月销售400台,第四个月销售790台,则下列函数模型中能较好地反映销量y与投放市场的月数x之间关系的是()A.y=100xB.y=50x2-50x+100C.y=50×2xD.y=100log2x+100,应为指数型函数模型.3.已知某矩形广场的面积为4万平方米,则其周长至少为()A.800米B.900米C.1 000米D.1 200米x米,则宽为米.故其周长为l=2≥800,当且仅当x=200时取等号.4.在如图所示的锐角三角形空地中,欲建一个面积不小于300 m2的内接矩形花园(阴影部分),则其边长x(单位:m)的取值范围是()A.[15,20]B.[12,25]C.[10,30]D.[20,30]y m,则由三角形相似知,,∴y=40-x.∵xy≥300,∴x(40-x)≥300, ∴x2-40x+300≤0,∴10≤x≤30.5.某产品的总成本y(单位:万元)与产量x(单位:台)之间的函数关系是y=3 000+20x-0.1x2(0<x<240,x∈N*),若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总成本)的最低产量是() A.100台 B. 120台 C.150台 D.180台f(x)万元,则f(x)=25x-(3 000+20x-0.1x2)=0.1x2+5x-3 000(0<x<240,x∈N*).令f(x)≥0,得x≥150,故生产者不亏本时的最低产量是150台.6.某房地产公司计划出租70套相同的公寓房.当每套房月租金定为3 000元时,这70套公寓能全租出去;当月租金每增加50元时(设月租金均为50元的整数倍),就会多一套房子租不出去.设租出的每套房子每月需要公司花费100元的日常维修等费用(设租不出去的房子不需要花这些费用).要使公司获得最大利润,每套公寓月租金应定为()A.3 000元B.3 300元C.3 500元D.4 000元,设利润为y元,租金定为(3 000+50x)元(0≤x≤70,x∈N),则y=(3 000+50x)(70-x)-100(70-x)=(2 900+50x)(70-x)=50(58+x)(70-x)≤50=204 800,当且仅当58+x=70-x,即x=6时,等号成立,故每月租金定为3 000+300=3 300(元)时,公司获得最大利润,故选B.7.某位股民购进某只股票,在接下来的交易时间内,他的这只股票先经历了n次涨停 (每次上涨10%),又经历了n次跌停(每次下跌10%),则该股民这只股票的盈亏情况(不考虑其他费用)为()A.略有盈利B.略有亏损C.没有盈利也没有亏损D.无法判断盈亏情况a元,则经历n次涨停后的价格为a(1+10%)n=a×1.1n元,经历n次跌停后的价格为a×1.1n×(1-10%)n=a×1.1n×0.9n=a×(1.1×0.9)n=0.99n·a<a,故该股民这只股票略有亏损.8.根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080,则下列各数中与最接近的是()(参考数据:lg 3≈0.48)A.1033B.1053C.1073D.1093=x=,两边取对数,得lg x=lg=lg 3361-lg 1080=361lg 3-80≈93.28,所以x≈1093.28,即与最接近的是1093.故选D.9.一个人以6 m/s的速度去追赶停在交通灯前的汽车,当他离汽车25 m时交通灯由红变绿,汽车开始变速直线行驶(汽车与人前进方向相同),汽车在时间t内的路程为s=t2 m,则此人()A.可在7 s内追上汽车B.可在9 s内追上汽车C.不能追上汽车,但期间最近距离为14 mD.不能追上汽车,但期间最近距离为7 ms=t2,车与人的间距d=(s+25)-6t=t2-6t+25= (t-6)2+7.当t=6时,d取得最小值7.结合选项可知选D.10.(2018山东泰安联考)已知甲、乙两种商品在过去一段时间内的价格走势如图所示.假设某商人持有资金120万元,他可以在t1至t4的任意时刻买卖这两种商品,且买卖能够立即成交(其他费用忽略不计).如果他在t4时刻卖出所有商品,那么他将获得的最大利润是()A.40万元B.60万元C.120万元D.140万元6元时该商人全部买入甲商品,可以买120÷6=20(万份),在t2时刻全部卖出,此时获利20×2=40(万元),乙4元时该商人全部买入乙商品,可以买(120+40)÷4=40(万份),在t4时刻全部卖出,此时获利40×2=80(万元),共获利40+80=120(万元),故选C.11.设某公司原有员工100人从事产品A的生产,平均每人每年创造产值t万元(t为正常数).公司决定从原有员工中分流x(0<x<100,x∈N*)人去进行新开发的产品B的生产.分流后,继续从事产品A生产的员工平均每人每年创造产值在原有的基础上增长了1.2x%.若要保证产品A的年产值不减少,则最多能分流的人数是.,分流前每年创造的产值为100t(万元),分流x人后,每年创造的产值为(100-x)(1+1.2x%)t,则解得0<x≤.因为x∈N*,所以x的最大值为16.二、能力提升12.“好酒也怕巷子深”,许多著名品牌是通过广告宣传进入消费者视线的.已知某品牌商品靠广告销售的收入R与广告费A之间满足关系R=a(a为常数),广告效应为D=R-A.那么精明的商人为了取得最大广告效应,投入的广告费应为.(用常数a表示)2t=(t≥0),则A=t2,∴D=a-A=at-t2=-a2,∴当t=a,即A=a2时,D取得最大值.13.某食品的保鲜时间y(单位:h)与储藏温度x(单位:℃)满足函数关系y=e kx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0 ℃的保鲜时间是192 h,在22 ℃的保鲜时间是48 h,则该食品在33 ℃的保鲜时间是()A.16 hB.20 hC.24 hD.28 h,得(0,192)和(22,48)是函数y=e kx+b图象上的两个点,所以由②得,48=e22k·e b,③把①代入③得e22k=,即(e11k)2=,所以e11k=.所以当储藏温度为33 ℃时,保鲜时间y==(e11k)3·e b=×192=24(h).14.为了在“十一”黄金周期间降价搞促销,某超市对顾客实行购物优惠活动,规定一次购物付款总额:①若不超过200元,则不予优惠;②若超过200元,但不超过500元,则按标价给予9折优惠;③若超过500元,则其中500元按第②条给予优惠,超过500元的部分给予7折优惠.辛云和她母亲两次去购物,分别付款168元和423元,假设他们一次性购买上述同样的商品,则应付款额为..6元,价值为x元的商品和实际付款额f(x)之间的函数关系式为f(x)=当f(x)=168时,由168÷0.9≈187<200,故此时x=168;当f(x)=423时,由423÷0.9=470∈(200,500],故此时x=470.故两次共购得价值为470+168=638元的商品.又500×0.9+(638-500)×0.7=546.6元,即若一次性购买上述商品,应付款额为546.6元.15.2017年10月9日—10月13日为天猫亲子理想生活季.天猫某商家为了庆祝该节日,于2017年10月1日起特意推行亲子款十二生肖纪念章.通过市场调查,得到该纪念章每枚的市场价y(单位:元)与上市时间x(单位:天)的数据如下:(1)根据上表数据,为描述亲子款十二生肖纪念章的市场价y与上市时间x的变化关系,从下列函数中选取一个最佳的函数模型是.①y=ax+b;②y=ax2+bx+c;③y=log a x.(2)利用你选取的函数,求亲子款十二生肖纪念章的市场价最低时的上市时间及最低价格.(3)设你选取的函数为y=f(x),若对任意实数k,方程f(x)=kx+2m+120恒有两个相异实数根,求m的取值范围.由于市场价y随上市时间x的增大而先减小后增大,而模型①③均为单调函数,不符合题意,故选择二次函数模型②.(2)由表中数据可知解得∴函数模型为y=x2-10x+126=(x-20)2+26.∴当市场价最低时的上市时间为20天,最低价格为26元.(3)∵f(x)=x2-10x+126=kx+2m+120,∴x2-(10+k)x+6-2m=0恒有两个相异实数根,∴Δ=(10+k)2-(6-2m)>0恒成立,即-2m<k2+20k+94.∵k2+20k+94=(k+10)2-6≥-6,∴-2m<-6,∴m>3.故m的取值范围是(3,+∞).三、高考预测16.如图,正方形ABCD的顶点A,B,顶点C,D位于第一象限,直线l:x=t(0≤t≤)将正方形ABCD分成两部分,记位于直线l左侧阴影部分的面积为f(t),则函数s=f(t)的图象大致是()分段画出函数的图象可得图象如选项C所示,故选C.。

答案：C f f的重心，则|FA|+ |FB|+ |FC|的值为() C . 3T T T 3 111 3332,则 |FA|+ |FB|+ |FC|=（X 1 + 刁+ （X 2 + 2）+ X 3 + ? =（X 1 + X 2 + X 3）+ " = " + 寸 3•选 C. 答案：C4. （2018沈阳质量监测）已知抛物线x 2= 4y 的焦点为F ，准线为I , P 为抛物线上一点，过 P 作PA 丄I 于点A ，当/ AFO = 30°0为坐标原点）时，|PF|= _________ .解析：设I 与y 轴的交点为 B ,在Rt △ABF 中，/AFB = 30° |BF|= 2，所以|AB| = 爭，设2 3 2 1 4课时规范练A 组基础对点练21. （2018沈阳质量监测）抛物线y = 4ax （a 丰0）的焦点坐标是（） A . (0, a) B . (a,0) C. 0,D. £，0 解析: 2 2 1 将y = 4ax （a z 0）化为标准方程得 x =扃丫@工0）,所以焦点坐标为0，花，所以选 C. 答案: 2. （2018 •宁五校联考）已知AB 是抛物线y 2 = 2x 的一条焦点弦，RB|= 4,则AB 中点C 的 横坐标是（ ） 1 B.1c ・3 D*5 解析：设 A (X 1, y 1), B(x 2, y 2),则 |AB|= X 1+ X 2+ p = 4，又 p = 1，所以 X 1 + X 2= 3，所以点 C 的横坐标是 X 1+ X 2 2 3 2.3. （2018邯郸质检）设F 为抛物线y 2= 2x 的焦点, A 、B 、C 为抛物线上三点，若F ABC解析：依题意，设点A （x 1, y"、B （X 2, y 2)、C(X 3, y 3),又焦点F 1, 0 , 1 X 1 + X 2 + X 3= 3X 2 =P（x0, y0），则X0= ± 3，代入x = 4y 中，得y = 3,从而|PF|=|FA| = y°+ 1 = 3.答案：45.已知抛物线C的方程为y2= 2px(p>0), O M的方程为x2+ y2+ 8x + 12 = 0,如果抛物线C 的准线与O M相切，那么p的值为_____________________ .解析：将O M的方程化为标准方程：(x+ 4)2+ y2= 4,圆心坐标为(一4,0)，半径r = 2,又抛物线的准线方程为x=- |,^|4-P|= 2,解得p = 12或4.答案：12或46•如图，过抛物线y2= 2px(p> 0)的焦点F的直线l依次交抛物线及其准线于点A, B, C,若|BC|= 2|BF|,且|AF|= 3，则抛物线的方程是________________ .解析：分别过点A、B作准线的垂线AE、BD，分别交准线于点E、D(图略)，则|BF|=|BD|, •••|BC|= 2|BF|,「.|BC|= 2|BD|,「./BCD = 30 ° 又|AE|= AF|= 3,「.AC|= 6，即点F 是AC 的3 2中点，根据题意得p= 2 ,•••抛物线的方程是y2= 3x.答案：y2= 3x7. 已知抛物线y2= 4px(p>0)的焦点为F，圆W：(x+ p)2+ y2= p2的圆心到过点F的直线l的距离为p.(1)求直线l的斜率；⑵若直线l与抛物线交于A、B两点，△ WAB的面积为8，求抛物线的方程.解析：⑴易知抛物线y2= 4px(p>0)的焦点为F(p,0)，依题意直线I的斜率存在且不为0,设直线l的方程为x= my+ p,因为W( —p,0),|—p—p| 厂\[3所以点W到直线l的距离为------------- =p，解得m= ±, 3，所以直线l的斜率为士才.V1 + (-mf 3⑵由(1)知直线I的方程为x= ±. 3y+ p，由于两条直线关于x轴对称，不妨取x= . 3y+ p,x =^3y+ p, 2厂2联立2消去x得y —4.3py—4p = 0,y = 4px,设A(X1, y1), B(X2, y2)，则y1 + y2= 4 . 3p, y1y2= —4p2,所以|AB= ,‘1+ 3 2• 4 3p 2+ 4X 4p2= 16p,1因为A WAB的面积为8,所以^p X 16p= 8,得p= 1,所以抛物线的方程为 y 2 = 4x.8. 已知抛物线 C i : x 2= 2py(p >0), O 是坐标原点，点A , B 为抛物线C i 上异于O 点的两点， 以OA 为直径的圆C 2过点B.(1) 若A( — 2,i)，求p 的值以及圆C 2的方程；(2) 求圆C 2的面积S 的最小值(用 p 表示).解析：⑴VA( — 2,1)在抛物线C i 上, A4= 2p , p = 2.又圆C 2的圆心为 —1 , 1 ,半径为号勺=•••x 2= x 2 + 詈 + 8p 2>2 i6p 4+ 8p 2= i6p 2，当且仅当 x 2=詈，即 x 2 = 4p 2 时取等号.2 2X i i 4 2 2 22又|OA| = X i + 4^= 4^(x 1 + 4p X 1)，注意到 X i > i6P , 2 /.|OA|2> 4p2(i62p 4+ 4p 2 i6p 2)= 80p 2.而 S = n^4A_ , A S> 20 p 2,即S 的最小值为20 p 2，当且仅当x 2= 4p 2时取得.B 组能力提升练i . (20i8唐山统考)已知抛物线y 2= 2px(p > 0),过点C(— 2,0)的直线I 交抛物线于A 、B 两点, 坐标原点为O , OA OB = i2.(1) 求抛物线的方程；(2) 当以AB 为直径的圆与y 轴相切时，求直线I 的方程.解析：⑴设I : x = my — 2，代入y 2= 2px ,2得 y — 2pmy + 4p = 0.(*)舟，•圆C 2的方程为(X + i)2+2 2 (2)记 A(x i , |p), B(x 2, 2p) •则 OB =(X 2, \1722 -P AB = (x 2— x i , 2 2 X 2— X i2p )• 由 OB AB = 0 知, X 2(X 2 — X i )+2 2 2X 2 X 2 — X i4P 2= 0. • X 2^ 0，且 X i X2,.°.X 2+ X i X 2=— 4p2,.°.X i = X 2 + 24p_) X 2丿 "=5 2 = 4.设 A(x i , y i ), B(X 2, y 2),则 y i + y 2= 2pm , y i y 2 = 4p ，则 因为 OA OB = i2,所以 x i X 2 + y i y 2= i2,即 4+ 4p = i2,2 2 y i y 2 X i X 2= ’ 2 = 4. 4p得p = 2，抛物线的方程为 y 2= 4x.2⑵(1)中(*)式可化为y - 4my + 8 = 0, y i + y 2= 4m , y i y 2= 8.设AB 的中点为M ,2则 |AB|= 2X M = x i + X 2= m(y i + y 2)— 4 = 4m — 4,①又|AB|= 1 + m 2|y 1 — y 2|= 1 + m 2 16m 2— 32，②2 2 2 2由①②得(1 + m)(16m — 32) = (4m — 4),解得 m 2= 3, m = + 3.x + . 3y + 2 = 0 或 X — . 3y + 2 = 0.y 2= mx + 1(m >0, X > 0)和半圆X 2+ y 2= r 2(x w 0)所组成的曲线称为r 2 2 2 2••• “黄金抛物线 C ”的方程为y = x + 1(X >0)和X + y = 1(X < 0).⑵假设存在这样的直线I ，使得QP 平分/AQB ，显然直线I 的斜率存在且不为2 2 1— 2k ,消去y ，得 k X + (2k — 1)X = 0,「.X B = ~k ?, k --k BQ = ,1 — 2ky = kx + 1联立X 2+ y 2= 1 ,消去y ,所以，直线I 的方程为2•如图，由部分抛物线:“黄金抛物线C ”，若 黄金抛物线 C ”经过点(3,2)和—舟, a -H-. (1)求“黄金抛物线 C ” 的方程;⑵设P(0,1)和Q(0, — 1),过点P 作直线I 与“黄金抛物线 C ”相交于A , P , B 三点，问是否存在这样的直线I ，使得QP 平分/ AQB ?若存在，求出直 线I 的方程；若不存在，说明理由.解析：(1) 黄金抛物线C ”过点(3,2)和设直线I : y = kx + 1,联立* y = kx + 12 ‘ y = x +1 1 — k y B = k ，即 B 1 — 2k 1 — k〒,〒,1 2, =1,4 = 3m + 1 ,「.m = 1.2 2得(k + 1)x + 2kx = 0, 2k.••X A =— ~2 , y B = ~2,k + 1 k + 1•.QP 平分Z AQB , • k AQ + k BQ = 0, •盘-=°,解得 k =-1 ±2, 由图形可得k =— 1 — .2应舍去，• k =2 — 1,•••存在直线 I : y = ( .2 — 1)x + 1,使得QP 平分Z AQB. •'•k AQ = 1k，1 - k 2。

集合的概念与运算1．(2018·全国卷Ⅰ)已知集合A＝{0,2}，B＝{－2，－1,0,1,2}，则A∩B＝(A)A．{0,2} B．{1,2}C．{0} D．{－2，－1,0,1,2}A∩B＝{0,2}∩{－2，－1,0,1,2}＝{0,2}．2．(2016·山东卷)设集合U＝{1,2,3,4,5,6}，A＝{1,3,5}，B＝{3,4,5}，则∁U(A∪B)＝(A)A．{2,6} B．{3,6}C．{1,3,4,5} D．{1,2,4,6}因为A＝{1,3,5}，B＝{3,4,5}，所以A∪B＝{1,3,4,5}．又U＝{1,2,3,4,5,6}，所以∁U(A∪B)＝{2,6}．3．(2018·武汉调研测试)已知集合M＝{x|x2＝1}，N＝{x|ax＝1}，若N M，则实数a 的取值集合为(D)A．{1} B．{－1,1}C．{1,0} D．{1，－1,0}M＝{x|x2＝1}＝{－1,1}，又N M，N＝{x|ax＝1}，则N＝{－1}，{1}，∅满足条件，所以a＝1，－1,0，即实数a的取值集合为{1，－1,0}．4．(2018·佛山一模)已知全集U＝R，集合A＝{0,1,2,3,4}，B＝{x|x2－2x＞0}，则图中阴影部分表示的集合为(A)A．{0,1,2} B．{1,2}C．{3,4} D．{0,3,4}因为B＝{x|x2－2x＞0}＝{x|x＞2或x＜0}，所以∁U B＝{x|0≤x≤2}，所以图中阴影部分表示的集合为A ∩(∁U B )＝{0,1,2}．5．设集合A ＝{1,2,3}，B ＝{4,5}，M ＝{x |x ＝a ＋b ，a ∈A ，b ∈B }，则集合M 中的元素个数为(B)A ．3B ．4C ．5D ．6M ＝{5,6,7,8}，所以M 中的元素个数为4.6．(2017·江苏卷)已知集合A ＝{1,2}，B ＝{a ，a 2＋3}．若A ∩B ＝{1}，则实数a 的值为 1 .因为A ∩B ＝{1}，A ＝{1,2}，所以1∈B 且2∉B .若a ＝1，则a 2＋3＝4，符合题意． 又a 2＋3≥3≠1，故a ＝1.7．已知集合A ＝{y |y ＝1x}，B ＝{y |y ＝x 2}，则A ∩B ＝ (0，＋∞) .A ＝{y |y ＝1x}＝(－∞，0)∪(0，＋∞)，B ＝{y |y ＝x 2}＝[0，＋∞)，所以A ∩B ＝(0，＋∞)．8．设集合A ＝{x |x 2－3x －4<0}，则A ∩Z ＝ {0,1,2,3} ，A ∩Z 的所有子集的个数为 16 .A ＝{x |x 2－3x －4<0}＝{x |－1<x <4}，所以A ∩Z ＝{0,1,2,3}，A ∩Z 的子集个数有24＝16个．9．(2017·山东卷)设集合M ＝{x ||x －1|<1}，N ＝{x |x <2}，则 M ∩N ＝(C) A ．(－1,1) B ．(－1,2) C ．(0,2) D ．(1,2)因为M ＝{x |0<x <2}，N ＝{x |x <2}，所以M ∩N ＝{x |0<x <2}∩{x |x <2}＝{x |0<x <2}．10．已知集合A ＝{x |y ＝lg(x －x 2)}，B ＝{x |x 2－cx <0，c >0}，若A ⊆B ，则实数c 的取值范围是(B)A ．(0,1]B ．[1，＋∞)C ．(0,1)D ．(1，＋∞)由x －x 2>0，得0<x <1，所以A ＝(0,1)，由x 2－cx <0，得0<x <c ，所以B ＝(0，c )， 因为A ⊆B ，所以c ≥1.11．已知M ＝{x |－2≤x ≤5}，N ＝{x |a ＋1≤x ≤2a －1}． (1)若a ＝3，则M ∪(∁R N )＝ R .(2)若N ⊆M ，则实数a 的取值范围为 (－∞，3] .(1)当a ＝3时，N ＝{x |4≤x ≤5}，所以∁R N ＝{x |x <4或x >5}． 所以M ∪(∁R N )＝R .(2)①当2a －1<a ＋1，即a <2时，N ＝∅， 此时满足N ⊆M .②当2a －1≥a ＋1，即a ≥2时，N ≠∅，由N ⊆M ，得⎩⎪⎨⎪⎧a ＋1≥－2，2a －1≤5，所以2≤a ≤3.综上，实数a 的取值范围为(－∞，3]．12．(2018·黄石月考)某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为 12 人．设全集U 为某班30人，集合A 为喜爱篮球运动的15人，集合B 为喜爱乒乓球运动的10人，如图．设两者都喜欢的人数为x 人，则只喜爱篮球的有(15－x )人，只喜爱乒乓球的有(10－x )人，由此可得(15－x )＋(10－x )＋x ＋8＝30，解得x ＝3.所以15－x ＝12，即所求人数为12人．命题及其关系、充分条件与必要条件1．(2018·深圳市第二次调研)设A ，B 是两个集合，则“x ∈A ”是“x ∈A ∩B ”的(B)A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件因为x ∈A ∩B ⇒x ∈A 且x ∈B ⇒x ∈A .但x ∈A ≠> x ∈A ∩B .所以“x ∈A ”是“x ∈A ∩B ”的必要不充分条件． 2．命题“若α＝π4，则tan α＝1”的逆否命题为(C)A ．若α≠π4，则tan α≠1 B．若α＝π4，则tan α≠1C ．若tan α≠1，则α≠π4D ．若tan α≠1，则α＝π4将条件和结论分别否定后作为结论和条件即得到逆否命题．3．(2018·天津卷)设x ∈R ，则“x 3>8”是“|x |>2”的(A) A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件由x 3>8⇒x >2⇒|x |>2，反之不成立，故“x 3>8”是“|x |>2”的充分而不必要条件．4．(2018·广东肇庆一模)原命题：设a ，b ，c ∈R ，若“a >b ”，则“ac 2>bc 2”，以及它的逆命题、否命题、逆否命题中，真命题共有(C)A ．0个B ．1个C ．2个D ．4个因为当c ＝0时，由a >b ≠> ac 2>bc 2，所以原命题为假，从而逆否命题为假．又ac 2>bc 2⇒a >b ，所以逆命题为真，从而否命题为真． 故真命题共有2个．5．(2018·湖北新联考四模)若“x >2m 2－3”是“－1<x <4”的必要不充分条件，则实数m 的取值范围是(D)A ．[－3,3]B ．(－∞，－3]∪[3，＋∞)C ．(－∞，－1]∪[1，＋∞) D．[－1,1]“x >2m 2－3”是“－1<x <4”的必要不充分条件，所以(－1,4) (2m 2－3，＋∞)，所以2m 2－3≤－1，解得－1≤m ≤1.6．命题“若a >b ，则2a>2b－1”的否命题为 若a ≤b ，则2a≤2b－1 .7．(2018·北京卷)能说明“若a ＞b ，则1a ＜1b”为假命题的一组a ，b 的值依次为 1，－1(答案不唯一) .只要保证a 为正b 为负即可满足要求．当a ＞0＞b 时，1a ＞0＞1b.只要取满足上述条件的a ，b 值即可，如a ＝1，b ＝－1(答案不唯一)．8．f (x )是R 上的增函数，且f (－1)＝－4，f (2)＝2，设P ＝{x |f (x ＋t )＋1<3}，Q ＝{x |f (x )<－4}，若“x ∈P ”是“x ∈Q ”的充分不必要条件，则实数t 的取值范围为 (3，＋∞) .依题意P ＝{x |f (x ＋t )＋1<3}＝{x |f (x ＋t )<2}＝{x |f (x ＋t )<f (2)}，Q ＝{x |f (x )<－4}＝{x |f (x )<f (－1)}， f (x )是R 上的增函数，所以P ＝{x |x <2－t }，Q ＝{x |x <－1}， 要使“x ∈P ”是“x ∈Q ”的充分不必要条件， 需2－t <－1，解得t >3，所以实数t 的取值范围是(3，＋∞)．9．(2016·天津卷)设x ＞0，y ∈R ，则“x ＞y ”是“x ＞|y |”的(C) A ．充要条件 B ．充分而不必要条件C ．必要而不充分条件D ．既不充分也不必要条件(1)分别判断x >y ⇒x >|y |与x >|y |⇒x >y 是否成立，从而得到答案．当x ＝1，y ＝－2时，x >y ，但x >|y |不成立； 若x >|y |，因为|y |≥y ，所以x >y .所以“x >y ”是“x >|y |”的必要而不充分条件．10．(2017·浙江卷)已知等差数列{a n }的公差为d ，前n 项和为S n ，则“d ＞0”是“S 4 ＋S 6＞2S 5”的(C)A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件(方法一)因为数列{a n }是公差为d 的等差数列， 所以S 4＝4a 1＋6d ，S 5＝5a 1＋10d ，S 6＝6a 1＋15d ， 所以S 4＋S 6＝10a 1＋21d,2S 5＝10a 1＋20d . 若d >0，则21d >20d,10a 1＋21d >10a 1＋20d ， 即S 4＋S 6>2S 5.若S 4＋S 6>2S 5，则10a 1＋21d >10a 1＋20d ，即21d >20d ， 所以d >0.所以“d >0”是“S 4＋S 6>2S 5”的充分必要条件． (方法二)因为S 4＋S 6>2S 5S 4＋S 4＋a 5＋a 6>2(S 4＋a 5a 6>a 5a 5＋d >a 5d >0，所以“d >0”是“S 4＋S 6>2S 5”的充分必要条件．11．(2018·武汉调研测试)在△ABC 中，角A ，B ，C 的对应边分别为a ，b ，c ，条件p ：a ≤b ＋c 2，条件q ：A ≤B ＋C 2，那么条件p 是条件q 成立的(A)A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件条件q ：A ≤B ＋C2A ≤π－A 2A ≤π3. 条件p ：a ≤b ＋c2⇒cos A ＝b 2＋c 2－a22bc≥b 2＋c 2－b ＋c222bc＝3b 2＋3c 2－2bc 8bc ≥12⇒0<A ≤π3.所以p ⇒q ，但q p .如∠A ＝60°，a ＝3，b ＝1，c ＝2，不能得到a ≤b ＋c2.所以p 是q 的充分而不必要条件．12．(2018·江西赣中南五校二模)“a >0”是“函数y ＝ax 2＋x ＋1在(0，＋∞)上单调递增”的 充分不必要 条件．当a >0时，y ＝a (x ＋12a )2＋1－14a ，在(－12a，＋∞)上单调递增，因此在(0，＋∞)上单调递增，故充分性成立．当a ＝0时，y ＝x ＋1，在R 上单调递增，因此在(0，＋∞)上单调递增．故必要性不成立．综上，“a >0”是“函数y ＝ax 2＋x ＋1在(0，＋∞)上单调递增”的充分不必要条件．简单的逻辑联结词、全称量词与存在量词1．若p 是真命题，q 是假命题，则(D) A ．p ∧q 是真命题 B ．p ∨q 是假命题 C ．﹁p 是真命题 D ．﹁q 是真命题由“且”命题一假则假，“或”命题一真则真，命题与命题的否定真假相反，得A 、B 、C 都是错误的，故选D.2．(2018·河北五校高三联考)已知命题p ：“a >b ”是“2a>2b”的充要条件；q ：∃x ∈R ，|x ＋1|≤x ，则(D)A ．﹁p ∨q 为真命题B ．p ∧q 为真命题C ．p ∧﹁q 为假命题D ．p ∨q 为真命题对于p ：因为a >b ⇒2a>2b，反之，2a>2b⇒a >b ，所以“a >b ”是“2a >2b”的充要条件，即p 是真命题．对于q ：|x ＋1|≤x ⇔⎩⎪⎨⎪⎧x ＋1≥0，x ＋1≤x 或⎩⎪⎨⎪⎧x ＋1<0，－x －1≤x .解得x ∈∅，即不等式无实数解，所以q 是假命题． 所以p ∨q 为真命题．3．命题“∃x 0∈(0，＋∞)，ln x 0＝x 0－1”的否定是(A) A ．∀x ∈(0，＋∞)，ln x ≠x －1 B ．∀x ∉(0，＋∞)，ln x ＝x －1 C ．∃x 0∈(0，＋∞)，ln x 0≠x 0－1 D ．∃x 0∉(0，＋∞)，ln x 0＝x 0－1修改原命题中的两个地方即可得其否定，∃改为∀，否定结论，即ln x ≠x －1，故选A.4．(2018·三亚校级期中)命题“对任意的x ∈R ，x 3－x 2＋1≤0”的否定是(C) A ．不存在x ∈R ，x 3－x 2＋1≤0 B ．存在x 0∈R ，x 30－x 20＋1≥0 C ．存在x 0∈R ，x 30－x 20＋1>0 D ．对任意的x ∈R ，x 3－x 2＋1>05．(2018·湖南省六校联考) 下列各组命题中，满足“p ∨q ”为真、“p ∧q ”为假、“﹁q ”为真的是(B)A ．p ：0＝∅；q ：0∈∅B ．p ：x >2是x >1成立的充分不必要条件；q ：∀x ∈{1，－1,0},2x ＋1>0C ．p ：a ＋b ≥2ab (a >0，b >0)；q ：不等式|x |>x 的解集是(－∞，0)D ．p ：y ＝1x在定义域内是增函数；q ：f (x )＝e x ＋e －x是偶函数由题意可知，满足“p ∨q ”为真、“p ∧q ”为假、“﹁q ”为真，可知p 为真、q为假．A 中，p 、q 都为假；B 中，p 为真，q 为假；C 中，p 、q 都为真；D 中，p 为假、q 为真．故选B.6．(2017·湖北武汉2月调研)命题“y ＝f (x )(x ∈M )是奇函数”的否定是(D) A ．∃x ∈M ，f (－x )＝－f (x ) B ．∀x ∈M ，f (－x )≠－f (x ) C ．∀x ∈M ，f (－x )＝－f (x ) D ．∃x ∈M ，f (－x )≠－f (x )命题“y ＝f (x )(x ∈M )是奇函数”的否定是∃x ∈M ，f (－x )≠－f (x )． 7．已知命题p ：“∃x 0∈R ，|x 0|＋x 20<0”，则﹁p 为 ∀x ∈R ，|x |＋x 2≥0 _. 8．若x ∈[0，π4]，tan x ≤m ”是真命题，则实数m 的最小值为 1 .由题意，原命题等价于tan x ≤m 在区间[0，π4]上恒成立，即y ＝tan x 在[0，π4]上的最大值小于或等于m ，又y ＝tan x 在[0，π4]上的最大值为1，所以m ≥1，即m 的最小值为1.9．(2018·湖南长郡中学联考)已知命题p ：∃x 0∈(－∞，0)，2x 0<3x 0，命题q ：∀x ∈(0，π2)，tan x >sin x ，则下列命题为真命题的个数是(B)①p ∨q ；②p ∨(﹁q )；③(﹁p )∧q ；④p ∧(﹁q )． A ．1个 B ．2个 C ．3个 D ．4个因为幂函数y ＝x α，当α<0时在(0，＋∞)上递减， 由x 0<0,2<3，得2x 0>3x 0，所以p 为假命题．因为对于x ∈(0，π2)，sin x <x <tan x ，所以q 为真命题．所以①为真，②为假，③为真，④为假． 即真命题的个数是2.10．(2018·兰州模拟)已知下列四个命题：p 1：若直线l 和平面α内的无数条直线垂直，则l ⊥α； p 2：若f (x )＝2x －2－x ，则x ∈R ，f (－x )＝－f (x )； p 3：若f (x )＝x ＋1x ＋1，则∃x 0∈(0，＋∞)，f (x 0)＝1；p 4：在△ABC 中，若A >B ，则sin A >sin B .其中真命题的个数是(B) A ．1 B ．2 C ．3 D ．4平面的斜线l 可以和平面内无数条平行直线垂直，p 1为假命题．因为f (－x )＝2－x－2x＝－f (x )，所以p 2为真命题． 因为f (x )＝x ＋1x ＋1＝x ＋1＋1x ＋1－1 ≥2x ＋1x ＋1－1＝1， 取等号的条件为x ＋1＝1x ＋1，得到x ＝－，＋∞)，所以当x ∈(0，＋∞)时，f (x )>1，不存在x 0∈(0，＋∞)，满足f (x 0)＝1，所以p 3为假命题．在△ABC 中，A >B ⇒a >b ⇒sin A >sin B ，所以p 4为真命题． 故p 2和p 4为真命题，真命题的个数为2.11．若命题“存在实数x ，使x 2＋ax ＋1<0”的否定为真命题，则实数a 的取值范围为 [－2,2] .(方法一)由题意，命题“对任意实数x ，都有x 2＋ax ＋1≥0”是真命题，故Δ＝a 2－4×1×1≤0，解得－2≤a ≤2.(方法二)若命题“存在实数x ，使x 2＋ax ＋1<0”是真命题， 则Δ＝a 2－4×1×1>0，解得a >2或a <－2.故所求的实数a 的取值范围是取其补集，即[－2,2]． 12．(2018·华南师大附中模拟)设有两个命题：p ：关于x 的不等式a x >1(a >0，且a ≠1)的解集是{x |x <0}；q ：函数y ＝lg(ax 2－x ＋a )的定义域为R .如果p ∨q 为真命题，p ∧q 为假命题，则实数a 的取值范围是 (0，12]∪(1，＋∞) .p ：“关于x 的不等式a x>1(a >0，且a ≠1)的解集是{x |x <0}”为真⇒0<a <1.q ：“函数y ＝lg(ax 2－x ＋a )的定义域为R ”为真⇒ax 2－x ＋a >0恒成立⇒⎩⎪⎨⎪⎧a >0，Δ<0⇒a >12.因为p ∨q 为真命题，p ∧q 为假命题，所以p ，q 一真一假．⎩⎪⎨⎪⎧ p 真，q 假⇒⎩⎪⎨⎪⎧ 0<a <1，a ≤12⇒0<a ≤12.⎩⎪⎨⎪⎧p 假，q 真⇒⎩⎪⎨⎪⎧a >1，a >12⇒a >1.所以实数a 的取值范围是(0，12]∪(1，＋∞)．函数及其表示1．函数y ＝x ·ln(1－x )的定义域为(B) A ．(0,1) B ．[0,1) C ．(0,1] D ．[0,1]由⎩⎪⎨⎪⎧x ≥0，1－x >0，解得0≤x <1.2．已知函数f (x )＝⎩⎪⎨⎪⎧x 2－x ， x ≤1，11－x， x >1， 则f [f (－2)]的值为(C)A.12B.15 C ．－15 D ．－12因为f (－2)＝(－2)2－(－2)＝6，所以f [f (－2)]＝f (6)＝11－6＝－15. 3．若函数f (x )的定义域为[0,2]，则函数g (x )＝f x x －1的定义域是(B)A ．[0,1]B ．[0,1)C ．[0,1)∪(1,4]D ．(0,1)因为f (x )的定义域为[0,2]，所以⎩⎪⎨⎪⎧0≤2x ≤2，x －1≠0，解得0≤x <1.4．(2018·黑龙江模拟) 设函数f (x )＝2x ＋3，g (x ＋2)＝f (x )，则g (x )的解析式为(C) A ．3x －1 B ．3x ＋1 C ．2x －1 D ．2x ＋1g (x ＋2)＝f (x )＝2x ＋3，即g (x ＋2)＝2x ＋3，令x ＋2＝t ，所以x ＝t －2， 所以2x ＋3＝2(t －2)＋3＝2t －1， 所以g (x )＝2x －1.5．已知函数f (x )在[－1,2]上的图象如下图所示，则函数f (x )的解析式为f (x )＝ ⎩⎪⎨⎪⎧x ＋1， －1≤x ≤0，－12x ， 0＜x ≤2 .由图可知，图象是由两条直线的一段构成，故可采用待定系数法求出其表示式．当－1≤x ≤0时，设y ＝k 1x ＋b 1，将(－1,0)，(0,1)代入得k 1＝1，b 1＝1，所以y ＝x ＋1， 当0<x ≤2时，设y ＝k 2x ＋b 2，将(0,0)，(2，－1)代入得k 2＝－12，b 2＝0，所以y ＝－12x .所以f (x )＝⎩⎪⎨⎪⎧x ＋1， －1≤x ≤0，－12x ， 0＜x ≤2.6．设函数f (x )＝⎩⎪⎨⎪⎧3x －b ，x <1，2x ， x >1，若f [f (56)]＝4，则b 等于 12.因为56<1，所以f (56)＝3×56－b ＝52－b .若52－b <1，即b >32时， f (52－b )＝3(52－b )－b ＝152－4b ＝4，解得b ＝78，不满足b >32，舍去；若52－b ≥1，即b ≤32时， f (52－b )＝2(52－b )＝5－2b ＝4，解得b ＝12，满足b ≤32.故b ＝12.7．已知f (x )＝⎩⎪⎨⎪⎧x ＋2， x ≤－1，x 2， －1<x <2，－2x ＋8， x ≥2.(1)求f (3)，f [f (－2)]，f (a )(a >0)的值；(2)画出f (x )的图象，并求出满足条件f (x )>3的x 的值．(1)因为3>2，所以f (3)＝－2×3＋8＝2.因为－2<－1，所以f (－2)＝2－ 2. 又－1<2－2<2，所以f [f (－2)]＝f (2－2)＝(2－2)2＝6－4 2. 又a >0，当0<a <2时，f (a )＝a 2； 当a ≥2时，f (a )＝－2a ＋8.综上所述，f (a )＝⎩⎪⎨⎪⎧a 2， 0<a <2，－2a ＋8， a ≥2.(2)f (x )的图象如图所示．当x ≤－1时，f (x )＝x ＋2≤1，此时无解；当－1<x <2时，由x 2＝3，解得x ＝±3， 因为x ＝－3<－1，故舍去；当x ≥2时，由－2x ＋8＝3，解得x ＝52.由图知，不等式f (x )>3的解为(3，52)．8．(2018·湖北武汉调研)已知函数f (x )满足f (1x )＋1xf (－x )＝2x (x ≠0)，则f (－2)＝(C)A ．－72 B.92C.72 D ．－92令x ＝2，可得f (12)＋12f (－2)＝4，①令x ＝－12，可得f (－2)－2f (12)＝－1，②联立①②解得f (－2)＝72.9．(2017·全国卷Ⅲ)设函数f (x )＝⎩⎪⎨⎪⎧x ＋1， x ≤0，2x， x >0，则满足f (x )＋f (x －12)>1的x的取值范围是 (－14，＋∞) .由题意知，可对不等式分x ≤0,0＜x ≤12，x ＞12三段讨论．当x ≤0时，原不等式为x ＋1＋x ＋12＞1，解得x ＞－14，所以－14＜x ≤0.当0＜x ≤12时，原不等式为2x＋x ＋12＞1，显然成立．当x ＞12时，原不等式为2x＋2x －12＞1，显然成立．综上可知，x 的取值范围是(－14，＋∞)．10．函数f (x )＝－a2x 2＋－a x ＋6.(1)若f (x )的定义域为R ，求实数a 的取值范围； (2)若f (x )的定义域为[－2,1]，求实数a 的值．(1)因为对于x ∈R ，(1－a 2)x 2＋3(1－a )x ＋6≥0恒成立，所以①当a ＝1时，原不等式变为6≥0，此时x ∈R . ②当a ＝－1时，原不等式变为6x ＋6≥0，此时x R .③若a ≠±1时，则⎩⎪⎨⎪⎧1－a 2>0，Δ≤0，所以⎩⎪⎨⎪⎧1－a 2>0，－a 2－－a2，解得－511≤a <1，所以实数a 的取值范围为[－511，1]． (2)因为f (x )的定义域为[－2,1]，所以不等式(1－a 2)x 2＋3(1－a )x ＋6≥0的解集为[－2,1]， 所以x ＝－2，x ＝1是方程(1－a 2)x 2＋3(1－a )x ＋6＝0的两根，所以⎩⎪⎨⎪⎧1－a 2<0，－2＋1＝－－a 1－a 2，－2×1＝61－a2，解得a ＝2.函数的值域与最值1．已知函数f (x )的值域为[－2,3]，则函数f (x －2)的值域为(D) A ．[－4,1] B ．[0,5]C ．[－4,1]∪[0,5]D ．[－2,3]函数y ＝f (x －2)的图象是由y ＝f (x )的图象向右平移2个单位而得到的，其值域不变．2．函数y ＝16－4x的值域是(C) A ．[0，＋∞) B．[0,4] C ．[0,4) D ．(0,4)因为16－4x≥0，且4x>0，所以0≤16－4x<16，所以0≤16－4x<4.3．已知函数f (x )＝e x－1，g (x )＝－x 2＋4x －3.若有f (a )＝g (b )，则b 的取值范围为(B)A ．[2－2，2＋2]B ．(2－2，2＋2)C ．[1,3]D ．(1,3)f (a )的值域为(－1，＋∞)，由－b 2＋4b －3>－1，解得2－2<b <2＋ 2.4．(2018·重庆期中)已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋x ＋a ，x <1，1－ln x ， x ≥1的值域为R ，则实数a 的取值范围是(C)A ．(－∞，－1]B ．[－1，＋∞)C ．(－∞，54]D ．[54，＋∞)当x ≥1时，f (x )＝1－ln x ≤1.由于函数f (x )＝⎩⎪⎨⎪⎧x 2＋x ＋a ，x <1，1－ln x ， x ≥1的值域为R ，且当x <1时，f (x )＝x 2＋x ＋a ≥a －12＋14＝a －14，所以a －14≤1，解得a ≤54.5．函数y ＝x 2x 2＋1(x ∈R )的值域为 [0,1) .y ＝x 2x 2＋1＝x 2＋1－1x 2＋1＝1－1x 2＋1.因为x 2＋1≥1，所以0<1x 2＋1≤1，所以0≤y <1. 6．若关于x 的不等式x 2－4x ≥m 对任意x ∈(0,1]恒成立，则m 的取值范围为 (－∞，－3] .只需要在x ∈(0,1]时，(x 2－4x )min ≥m 即可．而当x ＝1时，(x 2－4x )min ＝－3，所以m ≤－3. 7．求下列函数的值域： (1)y ＝x ＋1x －3； (2)y ＝2x ＋4x －1； (3)y ＝|x ＋1|＋x －2.(1)y ＝x －3＋4x －3＝1＋4x －3，因为4x －3≠0，所以y ≠1， 即所求函数的值域为(－∞，1)∪(1，＋∞)． (2)因为函数的定义域为{x |x ≥1}，又函数是增函数，所以函数的值域为[2，＋∞)． (3)y ＝|x ＋1|＋|x －2|＝⎩⎪⎨⎪⎧2x －1， x ≥2，3， －1≤x ＜2，1－2x ， x ＜－1.画出函数的图象，由图象观察可知，所求函数的值域为[3，＋∞)．8．已知函数y ＝1－x ＋x ＋3的最大值为M ，最小值为m ，则m M的值为(A) A.22B. 2 C ．2 2 D ．2由⎩⎪⎨⎪⎧1－x ≥0，x ＋3≥0，得定义域为[－3,1]，y ≥0，所以y 2＝4＋2x ＋－x ＝4＋2－x ＋2＋4，当x ＝－3或x ＝1，(y 2)min ＝4，所以y min ＝2； 当x ＝－1时，(y 2)max ＝8，所以y max ＝2 2. 即m ＝2，M ＝22，所以mM ＝22. 9．已知函数f (x )满足2f (x )－f (1x )＝3x2，则f (x )的最小值为 2 2 .由2f (x )－f (1x )＝3x2， ①令①式中的x 变为1x，可得2f (1x)－f (x )＝3x 2， ②由①②可解得f (x )＝2x2＋x 2，由于x 2>0，由基本不等式可得f (x )＝2x 2＋x 2≥22x2·x 2＝2 2.当x 2＝2时取等号，因此，其最小值为2 2. 10．已知函数f (x )＝1a －1x(a ＞0，x ＞0)．(1)若f (x )在[m ，n ]上的值域是[m ，n ]，求a 的取值范围，并求相应的m ，n 的值； (2)若f (x )≤2x 在(0，＋∞)上恒成立，求a 的取值范围．(1)因为f (x )＝1a －1x(a ＞0，x ＞0)，所以f (x )在(0，＋∞)上为增函数．那么当x ∈[m ，n ]时，y ∈[m ，n ]，所以⎩⎪⎨⎪⎧fm ＝m ，fn ＝n .即m ，n 是方程1a －1x＝x 相异的两实根，由1a －1x ＝x ，得x 2－1ax ＋1＝0，由题设知：⎩⎪⎨⎪⎧m ＋n ＝1a>0，m ·n ＝1＞0，Δ＝1a 2－4＞0.所以0＜a ＜12.此时，m ＝1－1－4a 22a ，n ＝1＋1－4a22a .(2)若1a －1x≤2x 在(0，＋∞)上恒成立．那么a ≥12x ＋1x恒成立．令g (x )＝12x ＋1x(x ＞0)．所以g (x )≤122x ·1x＝24. 故a ≥24.函数的单调性1．(2018·西城区期末)下列四个函数中，定义域为R 的单调递减函数是(D) A ．y ＝－x 2B ．y ＝log 0.5xC ．y ＝1xD ．y ＝(12)xy ＝－x 2在R 上没有单调性，排除A ；y ＝log 0.5x 的定义域不是R ，排除B ；y ＝1x的定义域不是R ，排除C ；y ＝(12)x的定义域为R ，且在R 上单调递减，故选D.2．已知函数f (x )＝|x ＋a |在(－∞，－1)上是单调函数，则a 的取值范围是(A) A ．(－∞，1] B ．(－∞，－1] C ．[－1，＋∞) D．[1，＋∞)因为函数f (x )在(－∞，－a )上是单调函数，所以－a ≥－1，解得a ≤1.3．已知f (x )是R 上的减函数，则满足f (|1x|)<f (1)的实数x 的取值范围是(C)A ．(－1,1)B ．(0,1)C ．(－1,0)∪(0,1)D ．(－∞，－1)∪(1，＋∞)因为f (x )是R 上的减函数，所以f (|1x |)<f1x|>1，所以0<|x |<1，所以x∈(－1,0)∪(0,1)．4．(2018·城关区期中)已知f (x )＝⎩⎪⎨⎪⎧a －x ＋4a ， x ＜1，log a x ， x ≥1是(－∞，＋∞)上的减函数，那么a 的取值范围是(C)A ．(0,1)B ．(0，13)C ．[17，13)D ．[17，1)因为f (x )＝log a x (x ≥1)是减函数，所以0＜a <1，且f (1)＝0.因为f (x )＝(3a －1)x ＋4a (x <1)为减函数， 所以3a －1<0，所以a <13，又因为f (x )＝⎩⎪⎨⎪⎧a －x ＋4a ，x ＜1，log a x ， x ≥1是(－∞，＋∞)上的减函数，所以f (x )在(－∞，1]上的最小值大于或等于f (x )在[1，＋∞)上的最大值．所以(3a －1)×1＋4a ≥0，所以a ≥17，故a ∈[17，13)．5．函数f (x )＝log 2(4x －x 2)的单调递减区间是 [2,4) .因为4x －x 2>0，所以0<x <4，又y ＝log 2t 为增函数，所求函数f (x )的递减区间为t ＝4x －x 2(0<x <4)的递减区间是[2,4)．6．已知函数f (x )为(0，＋∞)上的增函数，若f (a 2－a )>f (a ＋3)，则实数a 的取值范围为 (－3，－1)∪(3，＋∞) .由条件得⎩⎪⎨⎪⎧a 2－a >a ＋3，a 2－a >0，a ＋3>0，即⎩⎪⎨⎪⎧a 2－2a －3>0，a >1或a <0，a >－3.解得⎩⎪⎨⎪⎧a >3或a <－1，a >1或a <0，a >－3，所以a 的取值范围为(－3，－1)∪(3，＋∞)． 7．已知函数f (x )＝2x ＋1x ＋1.(1)判断f (x )在区间[1，＋∞)上的单调性，并用定义证明你的结论； (2)求该函数在区间[1,4]上的最大值与最小值．(1)函数f (x )在[1，＋∞)上是增函数，证明如下：任取x 1，x 2∈[1，＋∞)，且x 1<x 2，则f (x 1)－f (x 2)＝2x 1＋1x 1＋1－2x 2＋1x 2＋1＝x 1－x 2x 1＋x 2＋，因为x 1－x 2<0，(x 1＋1)(x 2＋1)>0， 所以f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)． 所以函数f (x )在[1，＋∞)上为增函数． (2)由(1)知， 函数f (x )在[1,4]上是增函数， 故f (x )max ＝f (4)＝95，f (x )min ＝f (1)＝32.8．(2017·山东卷)若函数e xf (x )(e ＝2.718 28…是自然对数的底数)在f (x )的定义域上单调递增，则称函数f (x )具有M 性质．下列函数中具有M 性质的是(A)A ．f (x )＝2－xB ．f (x )＝x 2C ．f (x )＝3－xD ．f (x )＝cos x(方法一)若f (x )具有性质M ，则[e x f (x )]′＝e x[f (x )＋f ′(x )]>0在f (x )的定义域上恒成立，即f (x )＋f ′(x )>0在f (x )的定义域上恒成立．对于选项A ，f (x )＋f ′(x )＝2－x－2－xln 2＝2－x(1－ln 2)>0，符合题意． 经验证，选项B ，C ，D 均不符合题意．故选A.(方法二)对于A ，e x f (x )＝(e 2)x ，因为e 2>1，所以e xf (x )为增函数．9．函数f (x )＝⎩⎪⎨⎪⎧1， x >0，0， x ＝0，－1， x <0，g (x )＝x 2·f (x －1)，则函数g (x )的递减区间是(B)A ．[0，＋∞)B ．[0,1)C ．(－∞，1)D ．(－1,1)由条件知g (x )＝⎩⎪⎨⎪⎧x 2， x >1，0， x ＝1，－x 2， x <1.如图所示，其递减区间是[0,1)．10．(2018·安徽皖江名校联考题改编)已知定义在(－2,2)上的函数f (x )满足(x 1－x 2)[f (x 1)－f (x 2)]>0，x 1≠x 2，且f (a 2－a )>f (2a －2)．(1)求实数a 的取值范围；(2)求函数g (x )＝log a (x 2－x －6)的单调区间．(1)因为定义在(－2,2)上的函数f (x )满足(x 1－x 2)[f (x 1)－f (x 2)]>0，x 1≠x 2，所以f (x )在(－2,2)上单调递增， 又f (a 2－a )>f (2a －2)， 所以⎩⎪⎨⎪⎧－2<a 2－a <2，－2<2a －2<2，2a －2<a 2－a ，即⎩⎪⎨⎪⎧－1<a <2，0<a <2，a <1或a >2.所以0<a <1.即a 的取值范围为(0,1)．(2)g (x )＝log a (x 2－x －6)可以看作由y ＝log a u 与u ＝x 2－x －6的复合函数． 由u ＝x 2－x －6>0，得x <－2或x >3.因为u ＝x 2－x －6在(－∞，－2)上是减函数，在(3，＋∞)上是增函数， 因为0<a <1，所以y ＝log a x 在(0，＋∞)上是减函数，所以y ＝log a (x 2－x －6)的单调递增区间为(－∞，－2)，单调递减区间为(3，＋∞)．函数的奇偶性与周期性1．(2017·北京卷)已知函数f (x )＝3x－(13)x ，则f (x )(B)A ．是偶函数，且在R 上是增函数B ．是奇函数，且在R 上是增函数C ．是偶函数，且在R 上是减函数D ．是奇函数，且在R 上是减函数因为函数f (x )的定义域为R ，f (－x )＝3－x －(13)－x ＝(13)x －3x ＝－f (x )，所以函数f (x )是奇函数．因为函数y ＝(13)x在R 上是减函数，所以函数y ＝－(13)x在R 上是增函数．又因为y ＝3x在R 上是增函数，所以函数f (x )＝3x－(13)x 在R 上是增函数．2．设函数f (x )，g (x )的定义域都为R ，且f (x )是奇函数，g (x )是偶函数，则下列结论正确的是(C)A ．f (x )g (x )是偶函数B ．|f (x )|g (x )是奇函数C ．f (x )|g (x )|是奇函数D ．|f (x )g (x )|是奇函数因为f (x )是奇函数，g (x )是偶函数，所以f (－x )＝－f (x )，g (－x )＝g (x )， 所以f (－x )g (－x )＝－f (x )g (x )， 所以f (x )g (x )为奇函数．|f (－x )|g (－x )＝|f (x )|g (x )， 所以|f (x )|g (x )为偶函数．f (－x )|g (－x )|＝－f (x )|g (x )|，所以f (x )|g (x )|为奇函数． |f (－x )g (－x )|＝|f (x )g (x )|， 所以|f (x )g (x )|为偶函数．3．(2018·华大新高考联盟教学质量测评)设f (x )是周期为4的奇函数，当0≤x ≤1时，f (x )＝x (1＋x )，则f (－92)＝(A)A ．－34B ．－14C.14D.34f (－92)＝f (－92＋4)＝f (－12)＝－f (12)＝－12(1＋12)＝－34.4．(2018·天津一模)已知偶函数f (x )对于任意x ∈R 都有f (x ＋1)＝－f (x )，且f (x )在区间[0,2]上是递增的，则f (－6.5)，f (－1)，f (0)的大小关系为(A)A ．f (0)<f (－6.5)<f (－1)B ．f (－6.5)<f (0)<f (－1)C ．f (－1)<f (－6.5)<f (0)D ．f (－1)<f (0)<f (－6.5)由f (x ＋1)＝－f (x )，得f (x ＋2)＝－f (x ＋1)＝f (x )， 故函数f (x )是周期为2的函数． 又f (x )为偶函数，所以f (－6.5)＝f (－0.5)＝f (0.5)，f (－1)＝f (1)， 因为f (x )在区间[0,2]上是递增的， 所以f (0)<f (0.5)<f (1)， 即f (0)<f (－6.5)<f (－1)．5．(2017·山东卷)已知f (x )是定义在R 上的偶函数，且f (x ＋4)＝f (x －2)．若当x ∈[－3,0]时，f (x )＝6－x，则f (919)＝ 6 .因为f (x ＋4)＝f (x －2)，所以f [(x ＋2)＋4]＝f [(x ＋2)－2]，即f (x ＋6)＝f (x )，所以f (x )是周期为6的周期函数， 所以f (919)＝f (153×6＋1)＝f (1)． 又f (x )是定义在R 上的偶函数， 所以f (1)＝f (－1)＝6，即f (919)＝6.6．已知奇函数f (x )在定义域[－10,10]上是减函数，且f (m －1)＋f (2m －1)>0，则实数m 的取值范围为 [－92，23) .由f (m －1)＋f (2m －1)>0f (m －1)>－f (2m －1)，因为f (x )为奇函数，所以－f (x )＝f (－x )， 所以f (m －1)>f (1－2m )， 又f (x )在[－10,10]上是减函数， 所以⎩⎪⎨⎪⎧－10≤m －1≤10，－10≤2m －1≤10，m －1<1－2m ，解得－92≤m <23.7．设f (x )是定义在R 上的奇函数，且对任意实数x 恒有f (x ＋2)＝－f (x )，当x ∈[0,2]时，f (x )＝2x －x 2.(1)求证：f (x )是周期函数；(2)当x ∈[2,4]时，求f (x )的解析式； (3)计算f (0)＋f (1)＋f (2)…＋f (2019)的值．(1)证明：因为f (x ＋2)＝－f (x )，所以f (x ＋4)＝－f (x ＋2)＝f (x )． 所以f (x )是周期为4的周期函数．(2)因为x ∈[2,4]，所以－x ∈[－4，－2]，所以4－x ∈[0,2]， 所以f (4－x )＝2(4－x )－(4－x )2＝－x 2＋6x －8， 又f (x )是周期为4的奇函数， 所以f (4－x )＝f (－x )＝－f (x )， 所以f (x )＝－f (4－x )，所以f (x )＝x 2－6x ＋8，x ∈[2,4]．(3)因为f (0)＝0，f (1)＝1，f (2)＝0，f (3)＝－1， 又f (x )是周期为4的周期函数，所以f (0)＋f (1)＋f (2)＋f (3)＝f (4)＋f (5)＋f (6)＋f (7)＝…＝f (2016)＋f (2017)＋f (2018)＋f (2019)＝0，所以f (0)＋f (1)＋f (2)…＋f (2019)＝0.8．(2016·山东卷)已知函数f (x )的定义域为R .当x <0时，f (x )＝x 3－1；当－1≤x ≤1时，f (－x )＝－f (x )；当x >12时，f (x ＋12)＝f (x －12)，则f (6)＝(D)A ．－2B ．－1C ．0D ．2由题意知，当x ＞12时，f (x ＋12)＝f (x －12)，则当x ＞0时，f (x ＋1)＝f (x )． 又当－1≤x ≤1时，f (－x )＝－f (x )， 所以f (6)＝f (1)＝－f (－1)． 又当x ＜0时，f (x )＝x 3－1，所以f (－1)＝－2，所以f (6)＝2.故选D.9．(2018·全国卷Ⅲ)已知函数f (x )＝ln(1＋x 2－x )＋1，f (a )＝4，则f (－a )＝ －2 .(方法一)令g (x )＝ln(1＋x 2－x )，则f (x )＝g (x )＋1，因为1＋x 2－x >|x |－x ≥0，所以g (x )的定义域为R ， 因为g (－x )＝ln(1＋x 2＋x )＝ln 11＋x 2－x＝－g (x )， 所以g (x )为奇函数，所以f (a )＝g (a )＋1＝4，所以g (a )＝3，所以f (－a )＝g (－a )＋1＝－g (a )＋1＝－3＋1＝－2.(方法二)因为f (x )＋f (－x )＝ln(1＋x 2－x )＋1＋ln(1＋x 2＋x )＋1＝ln(1＋x 2－x 2)＋2＝2，所以f (a )＋f (－a )＝2，所以f (－a )＝－2.10．已知函数f (x )是定义在R 上的奇函数，且当x ≥0时，f (x )＝－x 2＋ax . (1)若a ＝－2，求函数f (x )的解析式； (2)若函数f (x )为R 上的单调减函数，①求a 的取值范围；②若对任意实数m ，f (m －1)＋f (m 2＋t )<0恒成立，求实数t 的取值范围．(1)当x <0时，－x >0，又因为f (x )为奇函数，且a ＝－2， 所以当x <0时，f (x )＝－f (－x )＝x 2－2x ，所以f (x )＝⎩⎪⎨⎪⎧x 2－2x ， x <0，－x 2－2x ， x ≥0.(2)①当a ≤0时，对称轴x ＝a2≤0，所以f (x )＝－x 2＋ax 在[0，＋∞)上单调递减， 由于奇函数在关于原点对称的区间上单调性相同， 所以f (x )在(－∞，0)上单调递减，又在(－∞，0)上f (x )>0，在(0，＋∞)上f (x )<0， 所以当a ≤0时，f (x )为R 上的单调减函数．当a >0时，f (x )在(0，a 2)上单调递增，在(a2，＋∞)上单调递减，不合题意．所以函数f (x )为单调减函数时，a 的取值范围为(－∞，0]． ②因为f (m －1)＋f (m 2＋t )<0， 所以f (m －1)<－f (m 2＋t )，又因为f (x )是奇函数，所以f (m －1)<f (－t －m 2)， 因为f (x )为R 上的减函数， 所以m －1>－t －m 2恒成立，所以t >－m 2－m ＋1＝－(m ＋12)2＋54对任意实数m 恒成立，所以t >54.即t 的取值范围为(54，＋∞)．二次函数1．已知a >0，函数f (x )＝ax 2＋bx ＋c ，若x 0满足关于x 的方程2ax ＋b ＝0，则下列选项的命题中为假命题的是(C)A ．∃x ∈R ，f (x )≤f (x 0)B ．∃x ∈R ，f (x )≥f (x 0)C ．∀x ∈R ，f (x )≤f (x 0)D ．∀x ∈R ，f (x )≥f (x 0)函数f (x )的最小值是f (－b2a)＝f (x 0)，等价于x ∈R ，f (x )≥f (x 0)，所以C 错误．2．若函数y ＝x 2－3x －4的定义域为[0，m ]，值域为[－254，－4]，则m 的取值范围是(D)A ．[0,4]B ．[32，4]C ．[32，＋∞) D．[32，3]二次函数的对称轴为x ＝32，且f (32)＝－254，f (3)＝f (0)＝－4，结合图象可知m ∈[32，3]．3．(2018·双桥区校级月考)设abc >0，二次函数f (x )＝ax 2＋bx ＋c 的图象可能是(D)(方法一)对于A 选项，因为a <0，－b2a<0，所以b <0，又因为abc >0，所以c >0，由图知f (0)＝c <0，矛盾，故A 错．对于B 选项，因为a <0，－b2a>0，所以b >0，又因为abc >0，所以c <0，由图知f (0)＝c >0，矛盾，故B 错．对于C 选项，因为a >0，－b2a<0，所以b >0，又因为abc >0，所以c >0，由图知f (0)＝c <0，矛盾，故C 错．故排除A ，B ，C ，选D.(方法二)当a >0时，b ，c 同号，C ，D 两图中c <0，故b <0， 所以－b2a>0，选D.4．(2018·皖北联考)已知二次函数f (x )＝－x 2＋2ax ＋1－a 在x ∈[0,1]上有最大值2，则a 的值为(D)A ．2B ．－1或－3C ．2或－3D ．－1或2因为f (x )＝－(x －a )2＋a 2－a ＋1，所以f (x )的图象是开口向下，对称轴是x ＝a 的抛物线，(1)当a <0时，对称轴x ＝a 在区间[0,1]的左边，f (x )在[0,1]上单调递减， 所以f (x )max ＝f (0)＝1－a ＝2，解得a ＝－1. (2)当0≤a ≤1时，对称轴x ＝a ∈[0,1]，f (x )在[0，a ]上单调递增，在[a,1]上单调递减，所以f (x )max ＝f (a )＝a 2－a ＋1＝2，无解．(3)当a >1时，对称轴x ＝a 在区间[0,1]的右边，f (x )在[0,1]上单调递增， 所以f (x )max ＝f (1)＝a ＝2，有a ＝2. 综上可知，a ＝－1或a ＝2.5．若x ≥0，y ≥0，且x ＋2y ＝1，那么2x ＋3y 2的最小值为 34 .由x ≥0，y ≥0，且x ＋2y ＝1，得x ＝1－2y ≥0，所以0≤y ≤12，设t ＝2x ＋3y 2，把x ＝1－2y 代入，得t ＝2－4y ＋3y 2＝3(y －23)2＋23.因为t ＝f (y )在[0，12]上单调递减，所以当y ＝12时，t 取最小值，t min ＝34.6．设f (x )＝x 2－2ax ＋1.(1)若x ∈R 时恒有f (x )≥0，则a 的取值范围是 [－1,1] ；(2)若f (x )在[－1，＋∞)上递增，则a 的取值范围是 (－∞，－1] ； (3)若f (x )的递增区间是[1，＋∞)，则a 的值是 1 .(1)由Δ≤0，得4a 2－4≤0，所以a ∈[－1,1]．(2)a ≤－1.(3)由对称轴x ＝1知a ＝1.7．已知函数f (x )＝x 2－2ax ＋5(a >1)．(1)若f (x )的定义域和值域均是[1，a ]，求实数a 的值；(2)若f (x )在区间(－∞，2]上是减函数，且对任意的x 1，x 2∈[1，a ＋1]，总有|f (x 1)－f (x 2)|≤4，求实数a 的取值范围．(1)因为f (x )＝(x －a )2＋5－a 2(a >1)， 所以f (x )在[1，a ]上是减函数， 又定义域和值域均为[1，a ]，所以⎩⎪⎨⎪⎧f＝a ，fa ＝1，即⎩⎪⎨⎪⎧1－2a ＋5＝a ，a 2－2a 2＋5＝1，解得a ＝2.(2)因为f (x )在区间(－∞，2]上是减函数，所以a ≥2. 又x ＝a ∈[1，a ＋1]，且(a ＋1)－a ≤a －1， 所以f (x )max ＝f (1)＝6－2a ，f (x )min ＝f (a )＝5－a 2， 因为对任意的x 1，x 2∈[1，a ＋1]，总有|f (x 1)－f (x 2)|≤4， 因为f (x )max －f (x )min ≤4，得－1≤a ≤3.又a ≥2，所以2≤a ≤3. 故实数a 的取值范围为[2,3]．8．(2017·浙江卷)若函数f (x )＝x 2＋ax ＋b 在区间[0,1]上的最大值是M ，最小值是m ，则M －m (B)A ．与a 有关，且与b 有关B ．与a 有关，但与b 无关C ．与a 无关，且与b 无关D ．与a 无关，但与b 有关(方法一)设x 1，x 2分别是函数f (x )在[0,1]上的最小值点与最大值点，则m ＝x 21＋ax 1＋b ，M ＝x 22＋ax 2＋b .所以M －m ＝x 22－x 21＋a (x 2－x 1)，显然此值与a 有关，与b 无关．(方法二)由题意可知，函数f (x )的二次项系数为固定值，则二次函数图象的形状一定．随着b 的变动，相当于图象上下移动，若b 增大k 个单位，则最大值与最小值分别变为M ＋k ，m ＋k ，而(M ＋k )－(m ＋k )＝M －m ，故与b 无关．随着a 的变动，相当于图象左右移动，则M －m 的值在变化，故与a 有关．9．(2018·重庆模拟)已知函数f (x )＝x 2＋mx －1，若对于任意x ∈[m ，m ＋1]，都有f (x )<0成立，则实数m 的取值范围是 (－22，0) .作出二次函数f (x )的图象，对于任意x ∈[m ，m ＋1]，都有f (x )<0，则有⎩⎪⎨⎪⎧fm ，fm ＋，即⎩⎪⎨⎪⎧m 2＋m 2－1<0，m ＋2＋m m ＋－1<0，解得－22<m <0.10．已知f (x )＝ax 2－2x (0≤x ≤1)，求f (x )的最小值．(1)当a ＝0时，f (x )＝－2x 在[0,1]上递减，所以f (x )min ＝f (1)＝－2.(2)当a >0时，f (x )＝ax 2－2x ，图象开口向上，且对称轴为x ＝1a.①当1a≤1，即a ≥1时，f (x )＝ax 2－2x 图象的对称轴在[0,1]内，所以f (x )在[0，1a ]上递减，在[1a，1]上递增，所以f (x )min ＝f (1a )＝1a －2a ＝－1a.②当1a>1，即0<a <1时，f (x )＝ax 2－2x 图象的对称轴在[0,1]的右侧，所以f (x )在[0,1]上递减， 所以f (x )min ＝f (1)＝a －2.(3)当a <0时，f (x )＝ax 2－2x 的图象的开口向下，且对称轴x ＝1a<0，在y 轴的左侧，所以f (x )＝ax 2－2x 在[0,1]上递减， 所以f (x )min ＝f (1)＝a －2.综上所述，f (x )min ＝⎩⎪⎨⎪⎧a －2， a <1，－1a， a ≥1.指数与指数函数1. 若函数f (x )＝12x ＋1， 则该函数在(－∞，＋∞)上是(A)A ．单调递减无最小值B ．单调递减有最小值C ．单调递增无最大值D ．单调递增有最大值f (x )在R 上单调递减，又2x＋1>1，所以0<f (x )<1，无最大值也无最小值．2．若函数f (x )＝2x＋12x －a 是奇函数，则使f (x )>3成立的x 的取值范围为(C)A ．(－∞，－1)B ．(－1,0)C ．(0,1)D ．(1，＋∞)因为函数y ＝f (x )为奇函数，所以f (－x )＝－f (x )，即2－x＋12－x －a ＝－2x＋12x －a ，化简可得a ＝1， 则2x＋12x －1＞3，即2x＋12x －1－3＞0，即2x＋1－x－2x－1＞0，故不等式可化为2x－22x －1＜0，即1＜2x＜2，解得0＜x ＜1，故选C.3．函数y ＝|2x－1|在区间(k －1，k ＋1)内不单调，则k 的取值范围是(C) A ．(－1，＋∞) B．(－∞，1) C ．(－1,1) D ．(0,2)由于函数y ＝|2x－1|在(－∞，0)内单调递减，在(0，＋∞)内单调递增，而函数在区间(k －1，k ＋1)内不单调，所以有k －1<0<k ＋1，解得－1<k <1.4．已知函数f (x )＝|2x－1|，a <b <c ，且f (a )>f (c )>f (b )，则下列结论中，一定成立的是(D)A ．a <0，b <0，c <0B ．a <0，b ≥0，c >0C ．2－a<2c D ．2a ＋2c<2作出函数y ＝|2x－1|的图象，如下图．因为a <b <c ，且f (a )>f (c )>f (b )，结合图象知， 0<f (a )<1，a <0，c >0，所以0<2a<1. 所以f (a )＝|2a－1|＝1－2a<1，。

课后限时集训(五十三)(建议用时：60分钟)A组基础达标一、选择题1．从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a，b组成复数a＋b i，其中虚数的个数是( )A．30 B．42C．36 D．35C[因为a＋b i为虚数，所以b≠0，即b有6种取法，a有6种取法，由分步乘法计数原理知可以组成6×6＝36个虚数．]2．高三年级的三个班去甲、乙、丙、丁四个工厂参加社会实践，但去何工厂可自由选择，甲工厂必须有班级要去，则不同的分配方案有( )A．16种B．18种C．37种D．48种C[三个班去四个工厂不同的分配方案共43种，甲工厂没有班级去的分配方案共33种，因此满足条件的不同的分配方案共有43－33＝37种．故选C.]3．已知两条异面直线a，b上分别有5个点和8个点，则这13个点可以确定不同的平面个数为( )A．40 B．16C．13 D．10C[分两类情况：第1类，直线a分别与直线b上的8个点可以确定8个不同的平面；第2类，直线b分别与直线a上的5个点可以确定5个不同的平面．根据分类加法计数原理知，共可以确定8＋5＝13个不同的平面．]4.一个旅游景区的游览线路如图所示，某人从P点处进，Q点处出，沿图中线路游览A，B，C三个景点及沿途风景，则不重复(除交汇点O外)的游览线路有( )A．6种B．8种C．12种D．48种D[从点P处进入后，参观第一个景点时，有6个路口可以选择，从中任选一个，有C16种选法，参观完第一个景点，参观第二个景点时，有4个路口可以选择，从中任选一个，有C14种选法，参观完第二个景点，参观第三个景点时，有2个路口可以选择，从中任选一个，有C12种选法，则共有C16C14C12＝48(种)线路．故选D.]5．某地实行高考改革，考生除参加语文、数学、英语统一考试外，还需从物理、化学、生物、政治、历史、地理六科中选考三科．学生甲要想报考某高校的法学专业，就必须要从物理、政治、历史三科中至少选考一科，则学生甲的选考方法种数为( ) A．6 B．12C．18 D．19D[在物理、政治、历史中选一科的选法有C13C23＝9(种)；在物理、政治、历史中选两科的选法有C23C13＝9(种)；物理、政治、历史三科都选的选法有1种．所以学生甲的选考方法共有9＋9＋1＝19(种)，故选D.]6．(2018·南昌一模)某校毕业典礼上有6个节目，考虑整体效果，对节目演出顺序有如下要求：节目甲必须排在前三位，且节目丙、丁必须排在一起．则该校毕业典礼节目演出顺序的编排方案共有( )A．120种B．156种C．188种D．240种A[法一：记演出顺序为1～6号，对丙、丁的排序进行分类，丙、丁占1和2号，2和3号，3和4号，4和5号，5和6号，其排法种数分别为A22A33，A22A33，C12A22A33，C13A22A33，C13A22A33，故总编排方案有A22A33＋A22A33＋C12A22A33＋C13A22A33＋C13A22A33＝120(种)．法二：记演出顺序为1～6号，按甲的编排进行分类，①当甲在1号位置时，丙、丁相邻的情况有4种，则有C14A22A33＝48(种)；②当甲在2号位置时，丙、丁相邻的情况有3种，共有C13A22A33＝36(种)；③当甲在3号位置时，丙、丁相邻的情况有3种，共有C13A22A33＝36(种)．所以编排方案共有48＋36＋36＝120(种)．]7．(2019·长沙模拟)三对夫妻站成一排照相，则仅有一对夫妻相邻的站法总数是( ) A．72 B．144C．240 D．288D[第一类：选一对夫妻相邻捆绑，插入第二对夫妻中间，最后一对夫妻排在首尾，则有C13A22C12A22A22＝48.第二类：选一对夫妻相邻捆绑，插入形如BCbc(其中Aa，Bb，Cc为三对夫妻)中，共有C13A12C12A22A22C15＝240种．故共有48＋240＝288种排列方式．]二、填空题8．由数字2,0,1,9组成没有重复数字的四位偶数的个数为________．10[根据所组成的没有重复数字的四位偶数的个位是否为0进行分类计数：第一类，个位是0时，满足题意的四位偶数的个数为A33＝6；第二类，个位是2时，满足题意的四位偶数的个数为C12A22＝4.由分类加法计数原理得，满足题意的四位偶数的个数为6＋4＝10.]9．国家教育部为了发展贫困地区的教育，在全国重点师范大学免费培养教育专业师范生，毕业后要将他们分配到相应的地区去任教．现要将6名免费培养的教育专业师范毕业生平均分配到3所学校去任教，有________种不同的分配方法．90 [先把这6名毕业生平均分成3组，有C 26C 24C 22A 33种方法，再将这3组毕业生分配到3所学校，有A 33种方法，故将这6名毕业生平均分配到3所学校去任教，共有C 26C 24C 22A 33·A 33＝90(种)分配方法．]10．12个相同的小球放入编号为1,2,3,4的盒子中，要求每个盒子中的小球个数不少于其编号数，则不同的方法有________种．10 [先把每个盒子装上与其编号数相同的小球，还剩2个小球，2个小球装在4个盒子里需3个隔板，3个隔板看成3个元素，共5个元素，最后从5个元素里选出3个隔板就行了，共有C 35＝10种．]B 组 能力提升1．(2019·日照模拟)甲、乙、丙3人站到共有7级的台阶上，若每一级台阶最多站2人，同一级台阶上的人不区分站的位置，则不同的站法总数为( )A ．336B ．84C ．343D ．210 A [若3人站在不同的台阶上共有A 37种不同的站法；若3人中恰有2人同时在一个台阶上，则共有C 13A 27种不同的站法．故共有A 37＋C 13A 27＝336种不同的站法，选A.]2．把3男2女5名新生分配到甲、乙两个班，每个班分到的新生不少于2名，且甲班至少分配1名女生，则不同的分配方案种数为( )A ．16B ．20C ．26D ．40A [把5名新生分配到甲、乙两个班，每个班分到的新生不少于2名，有C 25A 22种分配方案，其中甲班都是男生的分配方案有(C 23＋1)种，则不同的分配方案种数为C 25A 22－(C 23＋1)＝16.故选A.]3.(2019·衡水模拟)已知一个公园的形状如图所示，现有3种不同的植物要种在此公园的A ，B ，C ，D ，E 这五个区域内，要求有公共边界的两块相邻区域种不同的植物，则不同的种法共有________种．18 [根据题意，分两步进行分析．第一步，对于A ，B ，C 区域，三个区域两两相邻，种的植物都不能相同，将3种不同的植物全排列，安排在A，B，C区域，有A33＝6(种)种法；第二步，对于D，E区域，若A，E区域种的植物相同，则D区域有1种种法，若A，E区域种的植物不同，则E区域有1种种法，D区域有2种种法，则D，E区域共有1＋2＝3(种)不同的种法．故不同的种法共有6×3＝18(种)．]4.如图，将一个四棱锥的每一个顶点染上一种颜色，并使同一条棱上的两顶点异色，如果只有5种颜色可供使用，则不同的染色方法种数是________．420[法一：由题设，四棱锥S­ABCD的顶点S，A，B所染的颜色互不相同，不同的染色方法共有5×4×3＝60(种)．当S，A，B染好时，不妨设其颜色分别为1,2,3，其余两种颜色为4,5，若C染2，则D 可染3或4或5，有3种不同的染色方法；若C染4，则D可染3或5，有2种不同的染色方法；若C染5，则D可染3或4，有2种不同的染色方法．所以当S，A，B染好时，C，D还有7种不同的染色方法，故不同染色方法有60×7＝420(种)．法二：以S，A，B，C，D的顺序分步染色．第一步，S点染色，有5种不同的方法．第二步，A点染色，与S在同一条棱上，有4种不同的方法．第三步，B点染色，与S，A分别在同一条棱上，有3种不同的方法．第四步，C点染色，也有3种不同的方法，但考虑到D点与S，A，C分别在同一条棱上，需要对A与C是否同色进行分类，当A与C同色时，D点有3种不同的染色方法；当A与C不同色时，因为C与S，B也不同色，所以C点有2种不同的染色方法，D点也有2种不同的染色方法．由分步乘法、分类加法计数原理，得不同的染色方法共有5×4×3×(1×3＋2×2)＝420(种)．法三：按所用颜色种数分类．第一类，5种颜色全用，共有A55种不同的染色方法；第二类，只用4种颜色，则必有某两个顶点同色(A与C或B与D)，共有2×A45种不同的染色方法；第三类，只用3种颜色，则A与C，B与D必定同色，共有A35种不同的染色方法．由分类加法计数原理，得不同的染色方法种数为A55＋2×A45＋A35＝420.]。

2020年高考文科数学一轮复习大题篇----数列题型一 等差数列、等比数列的交汇【例】记S n 为等比数列{a n }的前n 项和．已知S 2＝2，S 3＝－6.(1)求{a n }的通项公式；(2)求S n ，并判断S n ＋1，S n ，S n ＋2是否成等差数列．【解】 (1)设{a n }的公比为q .由题设可得⎩⎪⎨⎪⎧ a 11＋q ＝2，a 11＋q ＋q 2＝－6.解得q ＝－2，a 1＝－2.故{a n }的通项公式为a n ＝(－2)n .(2)由(1)可得S n ＝a 11－q n 1－q ＝－23＋(－1)n 2n ＋13. 由于S n ＋2＋S n ＋1＝－43＋(－1)n 2n ＋3－2n ＋23 ＝2⎣⎡⎦⎤－23＋－1n 2n ＋13＝2S n ， 故S n ＋1，S n ，S n ＋2成等差数列．【思维升华】 等差与等比数列的基本量之间的关系，利用方程思想和通项公式、前n 项和公式求解．求解时，应“瞄准目标”，灵活应用数列的有关性质，简化运算过程．【训练】已知公差不为0的等差数列{a n }的前n 项和为S n ，S 1＋1，S 3，S 4成等差数列，且a 1，a 2，a 5成等比数列．(1)求数列{a n }的通项公式；(2)若S 4，S 6，S n 成等比数列，求n 及此等比数列的公比．【解】 (1)设数列{a n }的公差为d ，由题意可知⎩⎪⎨⎪⎧ 2S 3＝S 1＋1＋S 4，a 22＝a 1a 5，d ≠0，整理得⎩⎪⎨⎪⎧ a 1＝1，d ＝2a 1，即⎩⎪⎨⎪⎧a 1＝1，d ＝2，∴a n ＝2n －1. (2)由(1)知a n ＝2n －1，∴S n ＝n 2，∴S 4＝16，S 6＝36，又S 4S n ＝S 26，∴n 2＝36216＝81，∴n ＝9，公比q ＝S 6S 4＝94. 题型二 新数列问题【例】对于数列{x n }，若对任意n ∈N ＋，都 有x n ＋2－x n ＋1>x n ＋1－x n 成立，则称数列{x n }为“增差数列”．设a n ＝t 3n ＋n 2－13n，若数列a 4，a 5，a 6，…，a n (n ≥4，n ∈N ＋)是“增差数列”，求实数t 的取值范围。

一、选择题1.用数字1，2，3，4，5组成的无重复数字的四位偶数的个数为()A.8B.24C.48D.120解析末位数字排法有A12种，其他位置排法有A34种，共有A12A34＝48(种). 答案 C2.不等式A x8<6×A x－28的解集为()A.{2，8}B.{2，6}C.{7，12}D.{8}解析8！（8－x）！<6×8！（10－x）！，∴x2－19x＋84<0，解得7<x<12.又x≤8，x－2≥0，∴7<x≤8，x∈N*，即x＝8.答案 D3.从6本不同的书中选出4本，分别发给4个同学，已知其中两本书不能发给甲同学，则不同分配方法有()A.180种B.220种C.240种D.260种解析因为其中两本书不能发给甲同学，所以甲只能从剩下的4本中分一本，然后再选3本分给3个同学，故有A14·A35＝240种.答案 C4.(一题多解)从4名男同学和3名女同学中选出3名参加某项活动，则男女生都有的选法种数是()A.18B.24C.30D.36解析法一选出的3人中有2名男同学1名女同学的方法有C24C13＝18种，选出的3人中有1名男同学2名女同学的方法有C14C23＝12种，故3名学生中男女生都有的选法有C24C13＋C14C23＝30种.法二从7名同学中任选3名的方法数，再除去所选3名同学全是男生或全是女生的方法数，即C37－C34－C33＝30.答案 C5.从1，3，5，7，9这五个数中，每次取出两个不同的数分别记为a，b，共可得到lg a－lg b的不同值的个数是()A.9B.10C.18D.20解析由于lg a－lg b＝lg ab(a＞0，b＞0)，∴lg ab有多少个不同的值，只需看ab不同值的个数.从1，3，5，7，9中任取两个作为ab有A25种，又13与39相同，31与93相同，∴lg a－lg b的不同值的个数有A25－2＝18.答案 C6.10名同学合影，站成了前排3人，后排7人，现摄影师要从后排7人中抽2人站前排，其他人的相对顺序不变，则不同调整方法的种数为()A.C27A55B.C27A22C.C27A25D.C27A35解析首先从后排的7人中抽2人，有C27种方法；再把2个人在5个位置中选2个位置进行排列有A25种.由分步乘法计数原理知不同调整方法种数是C27A25.答案 C7.(2019·济南模拟)有六人排成一排，其中甲只能在排头或排尾，乙、丙两人必须相邻，则满足要求的排法有()A.34种B.48种C.96种D.144种解析特殊元素优先安排，先让甲从头、尾中选取一个位置，有C12种选法，乙、丙相邻，有4种情况，乙、丙可以交换位置，有A22种情况，其余3人站剩余的3个位置，有A33种情况，由分步乘法计数原理知共有4C12A22A33＝96种.答案 C8.福州西湖公园花展期间，安排6位志愿者到4个展区提供服务，要求甲、乙两个展区各安排一个人，剩下两个展区各安排两个人，不同的安排方案共有() A.90种 B.180种 C.270种 D.360种解析 根据题意，分3步进行分析：①在6位志愿者中任选1个，安排到甲展区，有C 16＝6种情况；②在剩下的5个志愿者中任选1个，安排到乙展区，有C 15＝5种情况；③将剩下的4个志愿者平均分成2组，然后安排到剩下的2个展区，有C 24C 22A 22×A 22＝6种情况，则一共有6×5×6＝180种不同的安排方案. 答案 B二、填空题9.从6名同学中选派4人分别参加数学、物理、化学、生物四科知识竞赛，若其中甲、乙两名同学不能参加生物竞赛，则选派方案共有________种(用数字作答). 解析 特殊位置优先考虑，既然甲、乙都不能参加生物竞赛，则从另外4个人中选择一人参加，有C 14种方案；然后从剩下的5个人中选择3个人参加剩下3科，有A 35种方案.故共有C 14A 35＝4×60＝240种方案.答案 24010.已知1C m 5－1C m 6＝710C m 7，则m ＝________. 解析 由组合数公式化简整理得m 2－23m ＋42＝0解得m ＝2或m ＝21(舍去). 答案 211.在一展览会上，要展出5件艺术作品，其中不同书法作品2件、不同绘画作品2件、标志性建筑设计1件，在展台上将这5件作品排成一排，要求2件书法作品必须相邻，2件绘画作品不能相邻，则该次展出这5件作品不同的摆放方案共有________种(用数字作答).解析 将2件必须相邻的书法作品看作一个整体，同1件建筑设计展品全排列，再将2件不能相邻的绘画作品插空，故共有A 22A 22A 23＝24种不同的展出方案.答案 2412.(2019·烟台模拟)某班主任准备请2019届毕业生做报告，要从甲、乙等8人中选4人发言，要求甲、乙两人至少一人参加，若甲、乙同时参加，则他们发言中间需恰隔一人，那么不同的发言顺序共有________种(用数字作答).解析若甲、乙同时参加，有C22C26C12A22A22＝120种，若甲、乙有一人参与，有C12C36A44＝960种，从而总共的发言顺序有1 080种.答案 1 080能力提升题组(建议用时：15分钟)13.甲、乙、丙、丁四位同学高考之后计划去A，B，C三个不同社区进行帮扶活动，每人只能去一个社区，每个社区至少一人.其中甲必须去A社区，乙不去B 社区，则不同的安排方法种数为()A.8B.7C.6D.5解析根据题意，分2种情况：①乙和甲一起去A社区，此时将丙丁二人安排到B，C社区即可，有A22＝2种情况，②乙不去A社区，则乙必须去C社区，若丙丁都去B社区，有1种情况，若丙丁中有1人去B社区，则先在丙丁中选出1人，安排到B社区，剩下1人安排到A或C社区，有2×2＝4种情况，则不同的安排方法种数有2＋1＋4＝7.答案 B14.(2019·天津和平区一模)把8个相同的小球全部放入编号为1，2，3，4的四个盒中，则不同的放法种数为()A.35B.70C.165D.1 860解析根据题意，分4种情况讨论：①没有空盒，将8个相同的小球排成一列，排好后，各球之间共有7个空位，在7个空位中任选3个，插入隔板，将小球分成4组，顺次对应4个盒子，有C37＝35种放法；②有1个空盒，在4个盒中任选3个，放入小球，有C34＝4种选法，将8个相同的小球排成一列，排好后，各球之间共有7个空位，在7个空位中任选2个，插入隔板，将小球分成3组，顺次对应3个盒子，有C27＝21种分组方法，则有4×21＝84种放法；③有2个空盒，在4个盒中任选2个，放入小球，有C24＝6种选法，将8个相同的小球排成一列，排好后，各球之间共有7个空位，在7个空位中任选1个，插入隔板，将小球分成2组，顺次对应2个盒子，有C17＝7种分组方法，则有6×7＝42种方法；④有3个空盒，即将8个小球全部放进1个盒子，有4种放法.故一共有35＋84＋42＋4＝165种放法.答案 C15.(2019·江西八所重点中学模拟)摄像师要对已坐定一排照像的5位小朋友的座位顺序进行调整，要求其中恰有2人座位不调整，则不同的调整方案的种数为________(用数字作答).解析从5人中任选3人有C35种，将3人位置全部进行调整，有C12·C11·C11种.故有N＝C35·C12·C11·C11＝20种调整方案.答案2016.设集合A＝{(x1，x2，x3，x4，x5)|x i∈{－1，0，1}，i＝1，2，3，4，5}，那么集合A中满足条件“1≤|x1|＋|x2|＋|x3|＋|x4|＋|x5|≤3”的元素有________个(用数字作答).解析因为x i∈{－1，0，1}，i＝1，2，3，4，5，且1≤|x1|＋|x2|＋|x3|＋|x4|＋|x5|≤3，所以x i中至少两个为0，至多四个为0.①x i(i＝1，2，3，4，5)中4个0，1个为－1或1，A有2C15＝10个元素；②x i中3个0，2个为－1或1，A有C25×2×2＝40个元素；③x i中2个0，3个为－1或1，A有C35×2×2×2＝80个元素；从而，集合A中共有10＋40＋80＝130个元素.答案 130新高考创新预测17.(多填题)将甲、乙等5位同学分别保送到北京大学、上海交通大学、浙江大学三所大学就读，每所大学至少保送一人.(1)有________种不同的保送方法；(2)若甲不能被保送到北大，有________种不同的保送方法.解析 (1)5名学生可分成2，2，1和3，1，1两种形式，当5名学生分成2，2，1时，共有12C 25C 23A 33＝90种方法；当5名学生分成3，1，1时，共有C 35A 33＝60种方法.根据分类加法计数原理知共有90＋60＝150种保送方法.(2)先将五人分成三组，因为要求每组至少一人，所以可选择的只有2，2，1或3，1，1，所以有C 25C 23C 11A 22＋C 35C 12C 11A 22＝25(种)分组方法.因为甲不能被保送到北大，所以有甲的那组只有上海交大和浙大两个选择，剩下的两组无限制，一共有4种方法，所以不同的保送方案共有25×4＝100(种).答案 (1)150 (2)100。

排列与组合一、选择题（共12小题；共60分）1. 某同学逛书店，发现 3 本喜欢的书，决定至少买其中一本，则购买方案有 ( )A. 3 种B. 6 种C. 7 种D. 9 种2.A 76−A 65A 54=( )A. 12B. 24C. 30D. 363. 学校体育组新买 2 颗同样篮球，3 颗同样排球，从中取出 4 颗发放给高一 4 个班，每班 1 颗，则不同的发放方法共 ( )A. 4 种B. 20 种C. 18 种D. 10 种4. 把 4 个不同的黑球，4 个不同的红球排成一排，要求黑球、红球分别在一起，不同的排法种数是 ( )A. A 88B. A 44A 44C. A 44A 44A 22D. 以上都不对5. 已知圆上 9 个点，每两点连一线段，所有线段在圆内的交点最多可以有 ( )A. 36 个B. 72 个C. 63 个D. 126 个6. 把 3 封信投到 4 个信箱，所有可能的投法共有 ( )A. 24 种B. 4 种C. 43 种D. 34 种7. C 30+C 41+C 52+C 63+⋯+C 2017 的值为 ( )A. C213B. C203C. C204D. C2148. 有4位教师在同一年级的4个班中各教一个班的数学，在数学检测时要求每位教师不能在本班监考，则不同的监考方法有( )A. 8种B. 9种C. 10种D. 11种9. 3对夫妇去看电影，6个人坐成一排．若女性的邻座只能是其丈夫或其他女性，则坐法的种数为( )A. 54B. 60C. 66D. 7210. 从某学习小组的5名男生和4名女生中任意选取3名学生进行视力检测，其中至少要选到男生与女生各一名，则不同的选取种数为( )A. 35B. 70C. 80D. 14011. 6个停车位置，有3辆汽车需要停放，若要使3个空位连在一起，则停放的方法总数为( )A. A33B. A63C. A64D. A4412. 小明有4枚完全相同的硬币，每个硬币都分正反不同的两面．他想把这4枚硬币摆成一摞，且满足相邻2枚硬币的正面与正面不相对，不同的摆法有( )A. 4种B. 5种C. 6种D. 9种二、填空题（共5小题；共25分）13. 5位同学报名参加两个课外活动小组，每位同学限报其中一个小组，则不同的报名方法有种．2−n<7的解集为．14. 不等式A n−115. 有20个零件，其中16个一等品，4个二等品，若从20个零件中任意取3个，那么至少有1个一等品的不同取法有种．16. 解方程3A8x=4A9x−1，正整数x=．17. 如图所示，在连接正八边形的三个顶点而成的三角形中与正八边形有公共边的三角形有个．三、解答题（共5小题；共65分）18. 电视台在“欢乐在今宵”节目中拿出两个信箱，其中放着竞猜中成绩优秀的观众来信，甲箱中有30封，乙箱中有20封，现由主持人抽奖确定幸运之星和幸运观众，若先确定一名幸运之星，再从两箱中各确定一名幸运观众，有多少种不同结果?19. 在一次数学竞赛中，某学校有12人通过了初试，学校要从中选出5人去参加市级培训，在下列条件下，有多少种不同的选法?（1）任意选5人；（2）甲、乙、丙三人必须参加；（3）甲、乙、丙三人不能参加；（4）甲、乙、丙三人只能有1人参加；（5）甲、乙、丙三人至少1人参加．20. 一条铁路有n个车站，为适应客运需要，新增了m个车站，且知m>1，客运车票增加了62种，问原有多少个车站?现在有多少个车站?21. 空间有10个点，其中有5个点共面（除此之外再无4点共面），以每4个点为顶点作一个四面体，问一共可作多少个四面体?22. 同室4人各写一张贺年卡，先集中起来，然后每人从中拿一张别人送出的贺年卡，求4张贺年卡不同的分配方式有多少种?答案第一部分1. C2. D 【解析】A 76=7×6×A 54，A 65=6×A 54，所以 原式=36A 54A 54=36． 3. D 【解析】根据题意，分 2 种情况讨论，①，将 3 个排球、 1 个篮球分给 4 个班，在 4 个班中取出 3 个，分得排球剩余 1 个班分得篮球即可，则有 C 43=4 种情况，②，将 2 个排球、 2 个篮球分给 4 个班，在 4 个班中取出 2 个，分得排球剩余 2 个班分得篮球即可，则有 C 42=6 种情况，则共有 6+4=10 种发放方法．4. C5. D【解析】此题可化归为：圆上 9 个点可组成多少个四边形，每个四边形的对角线的交点即为所求，所以，交点有 C 94=126（个）．6. C 【解析】第 1 封信投到信箱中有 4 种投法；第 2 封信投到信箱中也有 4 种投法；第 3 封信投到信箱中也有 4 种投法．只要把这 3 封信投完，就做完了这件事情，由分步乘法计数原理可得共有 43 种方法．7. D【解析】原式=(C 40+C 41)+C 52+C 63+⋯+C 2017=(C 51+C 52)+C 63+⋯+C 2017=(C 62+C 63)+⋯+C 2017=C 2117=C 2121−17=C 214. 8. B 【解析】设四位监考教师分别为A ，B ，C ，D ，所教班分别为a ，b ，c ，d ，假设A 监考b ，则余下三人监考剩下的三个班，共有 3 种不同方法，同理A 监考c ，d 时，也分别有 3 种不同方法，由分类加法计数原理，共有 3+3+3=9（种）不同的监考方法．9. B 【解析】第一大类，若三个女的都相邻，又有四类，（男男女女女男，男女女女男男，男男男女女女，女女女男男男）有2A33+2A33⋅A21=36种，第二类，若其中两个女的相邻，又有三类（男女女男男女，女男男男女女，女女男男男女，女男男女女男）有4A33=24种，根据分类计数原理，得到36+24=60种．10. B【解析】从9人中，任取3人进行视力检测，分析可得，这是组合问题，共C93=84种情况．若选出的3人都为男生时，有C53=10种情况，选出的3人都为女生时，有C43=4种情况．根据排除法，可得符合题意的选法共有84−10−4=70种．11. D 【解析】3个空位连在一起作为1个元素与3辆汽车看成4个不同元素的全排列，故有A44种停放方法．12. B 【解析】没有限制条件的所有摆法一共有24=16种．正面与正面相对的情况有：①有两组正面相对，1种；②有一组正面相对，当正面与正面相对的硬币处于中间位置，有2×2=4种；当正面与正面相对的硬币处于顶部或底部时，有2×3=6种．所以，一共有24−1−4−6=5种．第二部分13. 32【解析】每位同学都有2种报名方法，因此，可分五步安排5名同学报名，由分步乘法计数原理，知总的报名方法共2×2×2×2×2=32（种）．14. {3,4}2−n<7，【解析】由不等式A n−1得(n−1)(n−2)−n<7，整理得n2−4n−5<0，解得−1<n<5，又因为n−1≥2且n∈N+，即n≥3且n∈N+，所以n=3或n=4，2−n<7的解集为{3,4}．故不等式A n−115. 1136【解析】方法一：将“至少有1个是一等品的不同取法”分三类：“恰有1个一等品”，“恰有2个一等品”，“恰有3个一等品”，由分类加法计数原理，知有C161C42+C162C41+C163=1136（种）．方法二：考虑其对立事件“3个都是二等品”，用间接法：C203−C43=1136（种）．16. 617. 40【解析】满足条件的有两类：第一类：与正八边形有两条公共边的三角形有m1=8（个）；第二类：与正八边形有一条公共边的三角形有m2=8×4=32（个），所以满足条件的三角形共有8+32=40（个）．第三部分18. 分两类：①幸运之星在甲箱中抽，有30×29×20=17400种．②幸运之星在乙箱中抽取，有20×19×30=11400种．共有不同结果17400+11400=28800种．19. （1）C125=792（种）不同的选法．（2） 甲、乙、丙三人必须参加，只需从另外的 9 人中选 2 人，共有 C 92=36（种）不同的选法．（3） 甲、乙、丙三人不能参加，只需从另外的 9 人中选 5 人，共有 C 95=126（种）不同的选法．（4） 甲、乙、丙三人只能有 1 人参加，分两步，先从甲、乙、丙中选 1 人，有 C 31=3（种）选法，再从另外的 9 人中选 4 人有 C 94 种选法，共有 C 31C 94=378（种）不同的选法．（5） 方法一（直接法）可分为三类：第一类：甲、乙、丙中有 1 人参加，共有 C 31C 94 种；第二类：甲、乙、丙中有 2 人参加，共有 C 32C 93 种；第三类：甲、乙、丙 3 人均参加，共有 C 33C 92 种．共有 C 31C 94+C 32C 93+C 33C 92=666（种）不同的选法．方法二（间接法）12 人中任意选 5 人共有 C 125 种，甲、乙、丙三人都不参加的有 C 95 种，所以，共有 C 125−C 95=666（种）不同的选法．20. 由题意可知，原有车票的种数是 A n 2 种，现有车票的种数是 A n+m 2 种，所以 A n+m 2−A n 2=62，即 (n +m )(n +m −1)−n (n −1)=62．所以 m (2n +m −1)=62=2×31，因为 m <2n +m −1，且 n ≥2，m,n ∈N +，所以 {m =2,2n +m −1=31,解得 m =2，n =15，故原有 15 个车站，现有 17 个车站．21. 不考虑任何限制，10 个点可得 C 104 个四面体．由于有 5 个点共面，这 5 个点中的任意 4 个点都不能构成四面体，共有 C 54 种情形．所以构成四面体的个数为 C 104−C 54=210−5=205．22. 解法1：设 4 人A 、B 、C 、D 写的贺年卡分别是a 、b 、c 、d ，当A 拿贺年卡b ，则B 可拿a 、c 、d 中的任何一个，即B 拿a ，C 拿d ，D 拿c 或B 拿c ，D 拿a ，C 拿d 或B 拿d ，C 拿a ，D 拿c ，所以A拿b时有3种不同的分配方式．同理，A拿c、d时也各有3种不同的分配方式．由加法原理，4张贺年卡共有3+3+3=9种分配方式．解法2：让4人A、B、C、D依次拿1张别人送出的贺年卡．如果A先拿有3种取法，此时写被A拿走的那张贺年卡的人也有3种不同的取法．接下来，剩下的两个人都各只有一种取法．由乘法原理，4张贺年卡不同的分配方式有3×3×1×1=9种．。