一元二次函数PPT教学课件
- 格式：ppt
- 大小：2.36 MB
- 文档页数：56
文档推荐
-
最新：人教版九年级上册数学第二十二章《二次函数》全章课件页数:150
-
二次函数全章课件演示文稿页数:50
-
二次函数全部PPT课件页数:400
-
二次函数全章课件页数:65
-
二次函数全章 ppt课件页数:64
-
《二次函数》PPT课件页数:25
下载文档原格式
合集下载
二次函数与一元二次方程二次函数优秀ppt课件
7.一元二次方程 3 x2+x－10=0的两个根是x1=－
2 ，x2=5/3，那么二次函数 y= 3 x2+x－10与x轴的交
点坐标是＿(-2＿，＿0＿) ＿(5＿/3，＿＿0).
8.已知抛物线y = ax2+bx+c的图象如图,则关 于x的方程ax2 + bx + c－3 = 0根的情况是（ A）
有 (2.5,0)， (-1,0)
归纳：一元二次方程ax2+bx+c=0的两个根为 x1,x2 ,则抛物线 y=ax2+bx+c与x轴的交点坐标 是(x1,0),(x2,0)
随堂练习
1.不与x轴相交的抛物线是（ D ）
A. y = 2x2 – 3
B. y=－2 x2 + 3
C. y= －x2 – 3x D. y=－2(x+1)2 －3
一般地，当y取定值时，二次函数为一元 二次方程。
如：y=5时，则5=ax2+bx+c就 是一个一元二次方程。
从以上可以看出,
已知二次函数y的值为m，求相应自变量x的 值，就是求相应一元二次方程的解.
例如,已知二次函数y=-X2+4x的值为3,求自变 量x的值. 就是求方程3=-X2+4x的解,
例如,解方程X2-4x+3=0 就是已知二次函数y=X2-4x+3的值为0,求自变量 x的值.
考虑下列问题:（2）球的飞行高度能否达到 20 m? 若能，需要多少时间?
20 m
2s
（2）当 h = 20 时， 20 t – 5 t 2 = 20 t 2 － 4 t ＋4 = 0 t1=t2=2 当球飞行 2s 时，它的高度为 20m .
2 ，x2=5/3，那么二次函数 y= 3 x2+x－10与x轴的交
点坐标是＿(-2＿，＿0＿) ＿(5＿/3，＿＿0).
8.已知抛物线y = ax2+bx+c的图象如图,则关 于x的方程ax2 + bx + c－3 = 0根的情况是（ A）
有 (2.5,0)， (-1,0)
归纳：一元二次方程ax2+bx+c=0的两个根为 x1,x2 ,则抛物线 y=ax2+bx+c与x轴的交点坐标 是(x1,0),(x2,0)
随堂练习
1.不与x轴相交的抛物线是（ D ）
A. y = 2x2 – 3
B. y=－2 x2 + 3
C. y= －x2 – 3x D. y=－2(x+1)2 －3
一般地，当y取定值时，二次函数为一元 二次方程。
如：y=5时，则5=ax2+bx+c就 是一个一元二次方程。
从以上可以看出,
已知二次函数y的值为m，求相应自变量x的 值，就是求相应一元二次方程的解.
例如,已知二次函数y=-X2+4x的值为3,求自变 量x的值. 就是求方程3=-X2+4x的解,
例如,解方程X2-4x+3=0 就是已知二次函数y=X2-4x+3的值为0,求自变量 x的值.
考虑下列问题:（2）球的飞行高度能否达到 20 m? 若能，需要多少时间?
20 m
2s
（2）当 h = 20 时， 20 t – 5 t 2 = 20 t 2 － 4 t ＋4 = 0 t1=t2=2 当球飞行 2s 时，它的高度为 20m .
一元二次函数ppt课件
a 0, b 0, c 0 ，
二次函数图象开口向上、对称轴 x
而选项中二次函数图象对称轴 x
错，不符合题意；
b
在区间[0，＋∞]上，函数值y随自变量x的增大而增大；
函数在x＝0处有最小值，记作ymin＝0．
当a＜0时，抛物线开口向下；
在区间（－∞，0]上，函数值y随自变量x的增大而增大；
在区间上[0，＋∞]，函数值y随自变量x的增大而减小；
函数在x＝0处有最大值，记作：ymax＝0
02
探索新知
思考
y＝ax2（a≠0）的图象与y＝－ax2（a≠0）的图象有什么内在关系？
1.二次项系数a决定了函数图象的开口方向及开口大小.
2.直线−
是一元二次函数图象的对称轴，所以a和b共同决定了抛物线对称轴的位置.
2
3.c的值决定了抛物线y＝ax2＋bx＋c(a≠0)与y轴交点的位置.
当x＝0时，y＝c，所以抛物线y＝ax2＋bx＋c(a≠0)与y轴有且只有一个交点(0,c)，故
一元二次函数y＝ax2＋bx＋c = ( + ) +
(a，b，c是常数，且a≠0)
2
4
函数
变化趋势
b
在区间 , 上，y随x的增大而减小，
2a
b
在区间 , 上，y随x的增大而增大
2a
b
在区间 , 上，y随x的增大而增大，
2a
在区间（－∞，0]上，函数值y随自变量x的增大而减小；
在区间[0，＋∞]上，函数值y随自变量x的增大而增大；
函数在x＝0处有最小值，记作ymin＝0．
y＝－2x2，抛物线开口向下；
二次函数图象开口向上、对称轴 x
而选项中二次函数图象对称轴 x
错，不符合题意；
b
在区间[0，＋∞]上，函数值y随自变量x的增大而增大；
函数在x＝0处有最小值，记作ymin＝0．
当a＜0时，抛物线开口向下；
在区间（－∞，0]上，函数值y随自变量x的增大而增大；
在区间上[0，＋∞]，函数值y随自变量x的增大而减小；
函数在x＝0处有最大值，记作：ymax＝0
02
探索新知
思考
y＝ax2（a≠0）的图象与y＝－ax2（a≠0）的图象有什么内在关系？
1.二次项系数a决定了函数图象的开口方向及开口大小.
2.直线−
是一元二次函数图象的对称轴，所以a和b共同决定了抛物线对称轴的位置.
2
3.c的值决定了抛物线y＝ax2＋bx＋c(a≠0)与y轴交点的位置.
当x＝0时，y＝c，所以抛物线y＝ax2＋bx＋c(a≠0)与y轴有且只有一个交点(0,c)，故
一元二次函数y＝ax2＋bx＋c = ( + ) +
(a，b，c是常数，且a≠0)
2
4
函数
变化趋势
b
在区间 , 上，y随x的增大而减小，
2a
b
在区间 , 上，y随x的增大而增大
2a
b
在区间 , 上，y随x的增大而增大，
2a
在区间（－∞，0]上，函数值y随自变量x的增大而减小；
在区间[0，＋∞]上，函数值y随自变量x的增大而增大；
函数在x＝0处有最小值，记作ymin＝0．
y＝－2x2，抛物线开口向下；
《基本不等式》一元二次函数、方程和不等式PPT教学课件(第一课时基本不等式)
1．下列不等式中，正确的是( )
A．a＋4a≥4
B．a2＋b2≥4ab
C． ab≥a＋2 b
D．x2＋x32≥2 3
解析：选 D.a＜0，则 a＋4a≥4 不成立，故 A 错；a＝1，b＝1，
a2＋b2＜4ab，故 B 错，a＝4，b＝16，则 ab＜a＋2 b，故 C 错；
由基本不等式可知 D 项正确．
2.2 基本不等式
第1课时 基本不等式
第二章 一元二次函数、方程和不等式
考点
学习目标
基本不等式
理解基本不等式的内容及 导出过程
利用基本不等式 能够运用基本不等式求函
求最值
数或代数式的最值
核心素养 逻辑推理 数学运算
第二章 一元二次函数、方程和不等式
问题导学 预习教材 P44－P46，并思考以下问题： 1．基本不等式的内容是什么？ 2．基本不等式成立的条件是什么？ 3．利用基本不等式求最值时，应注意哪些问题？
栏目 导引
第二章 一元二次函数、方程和不等式
■名师点拨 利用基本不等式求最值，必须按照“一正，二定，三相等”的 原则，即： ①一正：符合基本不等式a＋2 b≥ ab成立的前提条件，a＞0，b ＞0； ②二定：化不等式的一边为定值； ③三相等：必须存在取“＝”号的条件，即“＝”号成立． 以上三点缺一不可．
第二章 一元二次函数、方程和不等式
所以 y＝x＋x－4 2＝x－2＋x－4 2＋2
≥2 （x－2）·x－4 2＋2＝6，
当且仅当 x－2＝x－4 2， 即 x＝4 时，等号成立．
所以 y＝x＋x－4 2的最小值为 6.
栏目 导引
第二章 一元二次函数、方程和不等式
(2)因为 0<x<12， 所以 1－2x>0， 所以 y＝12x(1－2x)＝14×2x×(1－2x)≤142x＋12－2x2＝14×14＝ 116， 当且仅当 2x＝1－2x， 即当 x＝14时，ymax＝116.
【课件】必修1第二章《一元二次函数》
跟踪练习
已知函数f(x)=2x2-2ax+3在区间［-1,1］ 上有最小值,记作g(a). (1)求g(a)的函数表达式; (2)求g(a)的最大值.
已知f(x)=x2+ax+3-a，若当 x∈［-2,2］时，f(x)≥0恒成立，求a 的范围.
1.数形结合是讨论二次函数问题的基本方法.特别是 涉及二次方程、二次不等式的时候常常结合图形寻找思 路.
二、二次函数性质的应用
函数f(x)=2x2+mx-1在区间［-1,+∞)上递
增，则 f(-1)的取值范围
是
(-∞,-3］
.
【分析】 利用二次函数的对称轴解决问题.
三、二次函数在给定区间上的最值问题
（1） f ( x) x2; (2) f (x) x2 2x 1, x [0,3)
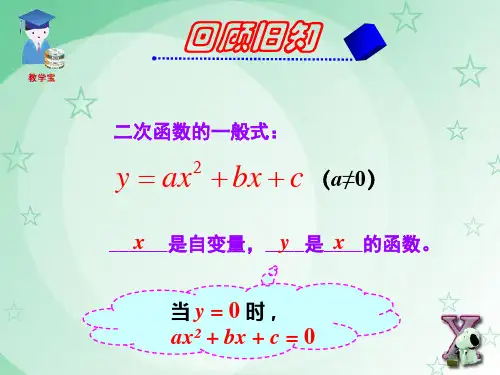
一元二次函数
1.二次函数
函数
y=ax2+bx+c(a≠0) 叫做二次函数,它的定
义域是 R .单调区间
.
2.y=ax2(a≠0)的性质和图象特征
(1)定义域是
R
.
(2)顶点坐标为
(0,0)
.
(3)偶函数,图象关于y轴对称,其对称轴为 x=0 .
(4)单调区间
.
3.二次函数的三种表示形式
一般式: y=ax2+bx+c(a≠0) .
x轴必有两个交点;
(2)设这个二次函数的图象与x轴交于点
A(x1,0),B(x2,0),且x1,x2的倒数和为
2 3
,求这个二
次函数的解析式.
已知二次函数f(x)=ax2+bx+c满足条件 f(2-x)=f(2+x),其图象的顶点为A,图象与x 轴的交点为B,C,其中B点的坐标为(-1,0) 且△ABC的面积为18,试确定这个二次函 数的解析式.
人教版高中数学必修一第二章一元二次函数方程和不等式全套PPT课件
[解析] ， ，又 , ，即 .又 ， ，即 ．故 ， ．
【变式探究】
已知 且 ，求 的取值范围．
[解析] 令 ， ，则 ， ．由 解得 ,又 ， ， ， ．
方法总结 不等式具有可加性（需同向）与可乘性（需同正），但不能相减或相除，应用时要充分利用所给条件进行适当变形来求范围，注意等价变形．
方法总结 应用基本不等式时，注意下列常见变形中等号成立的条件：
第二章 一元二次函数、方程和不等式
2.1 等式性质与不等式性质
学习目标
1.会用不等式（组）表示实际问题中的不等关系.（数学建模）
2.会运用作差法比较两个数或式子的大小.（数学运算）
3.梳理等式的性质，掌握不等式的性质，会用不等式的性质证明不等式或解决范围问题.（逻辑推理）
自主预习·悟新知
合作探究·提素养
（2）已知 ， .求证： ．
②
[解析] （1）对于①，若 ， ， ， ，则 ，①错误；对于②，对于正数 ， ， ，若 ，则 ，所以 ，所以 ，又 ，所以 ，②正确．综上，正确结论的序号是②．（2）因为 ，所以 .所以 ．又因为 ，所以 .所以 ，即 ，所以 ．
探究2 重要不等式
设 ， ，记 ， ， 分别为 ， 的算术平均数、几何平均数、调和平均数.古希腊数学家帕波斯于公元4世纪在其名著《数学汇编》中研究过 时， ， ， 的大小关系.
问题1：.你能探究 ， ， 的大小关系吗？
[答案] 能,因为 ， ， ，所以 ，即 ； ，即 .所以 .所以 ， ， 中最大的为 ，最小的为 .
问题1：.小明的说法正确吗？用什么性质判断小明的说法是否正确？
[答案] 不正确，用等式的性质.当 时， 一定成立，反过来，当 时，不能推出 ，如当 时， 成立， 不成立.故“ 是 成立的充要条件”是错误的.
【变式探究】
已知 且 ，求 的取值范围．
[解析] 令 ， ，则 ， ．由 解得 ,又 ， ， ， ．
方法总结 不等式具有可加性（需同向）与可乘性（需同正），但不能相减或相除，应用时要充分利用所给条件进行适当变形来求范围，注意等价变形．
方法总结 应用基本不等式时，注意下列常见变形中等号成立的条件：
第二章 一元二次函数、方程和不等式
2.1 等式性质与不等式性质
学习目标
1.会用不等式（组）表示实际问题中的不等关系.（数学建模）
2.会运用作差法比较两个数或式子的大小.（数学运算）
3.梳理等式的性质，掌握不等式的性质，会用不等式的性质证明不等式或解决范围问题.（逻辑推理）
自主预习·悟新知
合作探究·提素养
（2）已知 ， .求证： ．
②
[解析] （1）对于①，若 ， ， ， ，则 ，①错误；对于②，对于正数 ， ， ，若 ，则 ，所以 ，所以 ，又 ，所以 ，②正确．综上，正确结论的序号是②．（2）因为 ，所以 .所以 ．又因为 ，所以 .所以 ，即 ，所以 ．
探究2 重要不等式
设 ， ，记 ， ， 分别为 ， 的算术平均数、几何平均数、调和平均数.古希腊数学家帕波斯于公元4世纪在其名著《数学汇编》中研究过 时， ， ， 的大小关系.
问题1：.你能探究 ， ， 的大小关系吗？
[答案] 能,因为 ， ， ，所以 ，即 ； ，即 .所以 .所以 ， ， 中最大的为 ，最小的为 .
问题1：.小明的说法正确吗？用什么性质判断小明的说法是否正确？
[答案] 不正确，用等式的性质.当 时， 一定成立，反过来，当 时，不能推出 ，如当 时， 成立， 不成立.故“ 是 成立的充要条件”是错误的.
一元二次函数 ppt课件
－3
3
二次函数 y = x2的图象是一条曲线，它的 形状类似于投篮球时球在空中所经过的路线， 只是这条曲线开口向上，这条曲线叫做抛物 线 y = x2 ，
二次函数的图象都是抛物线。
一般地，二次函数 y = ax2 + bx + c（a≠0）的图象叫做抛物线y = ax2 + bx + c
思考：这个二次函数图象有什么特征？
y轴对称,y轴就
的值最小,最小值是0.
是它的对称轴.
8
6
4
对称轴与抛物 线的交点叫做
当x<0 (在对称轴的
2
抛物线的顶点.
左侧)时,y随着x的增大而
1
减小. -4
-3 -2
-1
0
1
2 当x3>0 (在4对称x轴的
-2
右侧)时, y随着x的增大而
增大.
在学中做—在做中学
(1)二次函数y=-x2的图象是什么形状？
y x2
当x<0 (在对称轴的 左侧)时,y随着x的增大而
减小.
当x>0 (在对称轴的 右侧)时, y随着x的增大而
增大.
当x=-2时，y4 当x=-1时，y=1
抛物线y=x2在x轴的 上方(除顶点外),顶点 是它的最低点,开口 向上,并且向上无限 伸展;当x=0时,函数y 的值最小,最小值是0.
7 2018
一元二次函数
1.在某一问题中，保持不变 的量叫常量，可以取不同数值 的 量，叫做变量.
2.函数：在同一变化过程中，有两个变量x和y，如果对于 x的每—个值，y都有__唯__一__确_定__的__值___与之对应，我们就把 y叫做x的函数，其中x叫做自变量.如果自变量x取a时，y 的值是b，就把b叫做x=a时的函数值.
1.4.1一元二次函数(课件)高一数学(北师大版2019)
导入课题 新知探究 典例剖析 课堂小结
思考交流：用待定系数法求一元二次函数的解析式
待定系数法
导入课题 新知探究 典例剖析 课堂小结
思考交流：利用函数图象的变换规律求一元二次函数的解析式
待定系数法
导入课题 次函数图象的变换规律 三、一元二次函数的性质
谢谢聆听！
北师大版（2019）高中数学必修第一册
第一章 预备知识 第4节 一元二次函数与
一元二次不等式
4.1 一元二次函数
导入课题 新知讲授 典例剖析 课堂小结
一元二次函数在高中也是很重要很常见的一种函数，因此，今天我们要更加深入地学习这个 函数——一元二次函数.
导入课题 新知探究 典例剖析 课堂小结
一、一元二次函数
1，一元二次函数是高中数 学十分重要的函数之一， 熟练地掌握一元二次函数 的性质和图像，可以为后 面我们学习其它类型的函 数打下坚实的基础 2，待定系数法，是高中数 学常用的求函数解析式的 思想方法之一. 2，数形结合法，是高中数 学常用的一种思想方法.
导入课题 新知探究 典例剖析 课堂小结
课后作业
导入课题 新知探究 典例剖析 课堂小结
二、一元二次函数图像的变换规律
一元二次函数图像的变换规律
导入课题 新知探究 典例剖析 课堂小结
三、一元二次函数的性质
教材P34例题
导入课题 新知探究 典例剖析 课堂小结
解：
教材P34练习
导入课题 新知探究 典例剖析 课堂小结
教材P34练习
导入课题 新知探究 典例剖析 课堂小结
新教材北师大版必修第一册 4.1一元二次函数 课件(46张)
2.参数“a,h,k”对y=a(x-h)2+k(a≠0)的图象的影响 (1)a的符号和绝对值大小分别决定了二次函数图象的开口方向和大小; (2)h决定了二次函数图象的对称轴的位置; (3)k决定了二次函数图象的顶点的高度.
【跟踪训练】
1.已知二次函数 y=x2-8x +c的图象的顶点在 x轴上,则c=
类型三 一元二次函数的最大值和最小值(数学运算)
角度1 求一元二次函数的最大值或最小值
【典例】求函数y= 1 x2-2x+4的最小值.
2
【思路导引】先配方变形,然后确定函数图象的开口方向和对称轴,最后求最小
值.
【解析】配方:y=
1 2
x2-2x+4=
1 (x 2)2 +2,此函数的图象是一条抛物线,开口
【拓展训练】 已知一元二次函数的图象经过点(1,0),(-5,0),且顶点纵坐标为 9 ,求这个函
2
数的解析式.
类型二 一元二次函数的函数值的变化趋势(逻辑推理) 【典例】试述一元二次函数y=3x2-6x-1函数值的变化趋势.
【解题策略】
一元二次函数y=ax2+bx+c(a≠0) 函数值的变化趋势
2
y=x2-mx+5的函数值y随x的增大而增大,所以 m ≤2,解得m≤4.
2
2.一元二次函数y=-x2+(m-1)x+m的图象与y轴交于(0,7)点. (1)求出m的值和此函数图象与x轴的交点坐标; (2)试述函数值的变化趋势.
【补偿训练】 试述一元二次函数y=4x2+16x+5函数值的变化趋势. 【解析】配方,得y=4x2+16x+5=4(x+2)2-11, 此函数的图象开口向上,对称轴是直线x=-2, 所以在区间 (－,－上2,]y随x的增大而减小; 在区间 [－2,上),y随x的增大而增大.
人教高中数学必修一A版《二次函数与一元二次方程、不等式》一元二次函数、方程和不等式PPT教学课件
返回至目录
典例精讲
角度2 参数影响二次项系数与对应方程根的大小
返回至目录
方法指导
含参一元二次不等式的解法
➢ 判定二次项系数是否为零，分别讨论； ➢ 在二次项系数不为零的条件下，讨论判别式与0的关系； ➢ 在有根的情况下进行因式分解或利用求根公式求出对应二次方程的根； ➢ 比较两根的大小，分别得到参数的范围，写出解集； ➢ 综上所述，按照参数的范围分别写出解集．
学习目标
➢ 掌握一元二次不等式在实际应用问题中的应用； ➢ 初步掌握解决实际问题的一般步骤.
返回至目录
典例精讲
题型 一元二次不等式的实际应用
返回至目录
典例精讲
返回至目录
典例精讲
返回至目录
变式训练
返回至目录
方法指导
一元二次不等式实际应用解题的方法： ➢ 选取合适的字母设题中的未知量； ➢ 由题中给出的不等关系，列出关于未知数的不等式（组）； ➢ 求解所列出的不等式（组）； ➢ 结合题目的实际意义下结论.
第二章 一元二次函数、方程和不等式
2.3 二次函数与一元二次方程、不等式 第3课时
学习目标 典例精讲 课堂小结 随堂检测
学习目标
➢ 会解含参一元二次不等式.（重难点）
返回至目录
题型1 含参一元二次不等式的解集
角度1 参数影响对应方程根的大小
典例精讲
返回至目录
典例精讲
返回至目录
典例精讲
角度2 参数影响二次项系数与对应方程根的大小
返回至目录
课堂小结
➢一个题型
一元二次不等式实际应用题 注意实际问题的具体范围
返回至目录
随堂检测
返回至目录
随堂检测
返回至目录
典例精讲
角度2 参数影响二次项系数与对应方程根的大小
返回至目录
方法指导
含参一元二次不等式的解法
➢ 判定二次项系数是否为零，分别讨论； ➢ 在二次项系数不为零的条件下，讨论判别式与0的关系； ➢ 在有根的情况下进行因式分解或利用求根公式求出对应二次方程的根； ➢ 比较两根的大小，分别得到参数的范围，写出解集； ➢ 综上所述，按照参数的范围分别写出解集．
学习目标
➢ 掌握一元二次不等式在实际应用问题中的应用； ➢ 初步掌握解决实际问题的一般步骤.
返回至目录
典例精讲
题型 一元二次不等式的实际应用
返回至目录
典例精讲
返回至目录
典例精讲
返回至目录
变式训练
返回至目录
方法指导
一元二次不等式实际应用解题的方法： ➢ 选取合适的字母设题中的未知量； ➢ 由题中给出的不等关系，列出关于未知数的不等式（组）； ➢ 求解所列出的不等式（组）； ➢ 结合题目的实际意义下结论.
第二章 一元二次函数、方程和不等式
2.3 二次函数与一元二次方程、不等式 第3课时
学习目标 典例精讲 课堂小结 随堂检测
学习目标
➢ 会解含参一元二次不等式.（重难点）
返回至目录
题型1 含参一元二次不等式的解集
角度1 参数影响对应方程根的大小
典例精讲
返回至目录
典例精讲
返回至目录
典例精讲
角度2 参数影响二次项系数与对应方程根的大小
返回至目录
课堂小结
➢一个题型
一元二次不等式实际应用题 注意实际问题的具体范围
返回至目录
随堂检测
返回至目录
随堂检测
返回至目录
一元二次函数ppt
例1）直线 y ax b 与x轴交于点（-3，0）， 则关于x的方程 ax b 的解为？ 0 2）一次函数 y kx b 的图像如图，
y
2
-2 0
x
则 kx b 0的解是？
请思考，一次函数与一次方程的关系
猜想: y ax2 bx c ( a 0) 的解是 ax2 bx c 0 的图像与x轴交点的 横坐标。
09级应数8班韩冰 主讲
教学策略
课后作业
巩固练习
教学过程
学习目标
1、会根据 y ax2 bx c ax2 bx c 0 的近似解。
( a 0)
的图像求
2、理解并掌握一元二次方程根的情况和抛 物线与x轴交点个数的关系
你知道高尔夫球吗？如图，以40m/s的速度将小球沿 与地面成40度角的方向击出。小球的飞行路线是一条抛 物线，若不计阻力，球飞行高度h与飞行时间t之间具有 关系式 h 20t 5t 2 你能计算出球飞行到落地需要的时长？
请问：这些信息在对应的函数图象中是如何展示的
呢？？？
2 2 例：请分别画出y x 4x 4和 y x 4 x 5 的图像。
y
y
5 4 1 0 0 2 x 2 x
对应的一元二次方程 Δ>0， 函数图像与x轴有一个交点
对应的一元二次方程 Δ<0， 函数图像与x轴无交点
2 二次函数 y ax bx c ( a 0) 的图像
知：方程的根与函数和X轴的横坐标交点相同。 故，猜想正确。即： 二次函数 y ax bx c ( a 0) 的图像与x轴的交点 横坐标为一元二次方程 ax2 bx c 0 的解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
-10
y=2x2+5x+3
160 140 120 100 80 60 40 20
0 -5 0 x 5
數列1 10
一元二次函數圖像和系數的關 係
✓ 右圖顯示的是函數
y =- 2x2-5x+3 的圖像
它和前述的y=2x2+5x+3 比較，有二個符號不一 -10 樣。
✓ 但這兩條曲條的拐點同 樣在 y-軸的左邊，可見
y=-2x2+5x+1
y=-2x2+5x-2
10
10
10
0
0
0
-10 -5 -10 0 5 10
-10 -5 -10 0 5 10
-10 -5 -10 0 5 10
-20
-20
-20
-30 y
-40
數列1
-30
y
-40
-30
數列1 y
-40
數列1
-50
-50
-50
-60
-60
-60
-70
-70
-70
攀禽类：啄木鸟、杜鹃、鹦鹉
4、哪种喙和脚适于在水中捞食水草？
游禽类：天鹅、野鸭、鸬鹚、鸳鸯、鸊鹈
5、哪种喙和脚适于在水中捕鱼？
涉禽类：丹顶鹤、白鹭、黑颧
6、哪种喙和脚适于扒土寻食？鸡、绿孔雀
项目 形态特点 生活习性 代表种
类群
鸣禽类
喙细而尖 足短而细 三趾向前 一趾向后
体态轻捷 善于鸣啭 巧于营巢
別， ，但曲線向上開口，
可見開口端是曲系數a
-10
的符號决定的，a 是正
數、向上，a 是負數、
y=2x2-5x+3 90 80 70 60 50 40 30 20 10 0 -5 x0 5
數列1 10
一元二次函數圖像和系數的關 係
▪ 右圖顯示的是函數 y = 2x2+5x+3 的圖像 它和前述的y =2x25x+3 比較，也只有 一符號的差別，但 y 這條曲條的拐點， 卻落在y-軸的左邊。
画眉
伯劳
伯劳
黄鹂
织 布 鸟
减少
鸟类类群 几维鸟
我国的珍贵鸟类： 丹顶鹤 、 绿孔雀、 朱鹮 、 褐马鸡 、
黄腹角雉为国家一级保护动物； 锦鸡 、 天鹅、 白鹇等为国家二级保护动物
游禽类
猛禽类
陆禽类
攀禽类
鸣禽类 涉禽类
a
b
c
d
e
f
小结： 1、鸟类的形态和结构特征与它们的
生活习性相适应。
2、鸟类是我们的朋友，我们应该保 护鸟类。
家燕 画眉 黄鹂 八哥
攀禽类
喙直而坚硬 足短而健壮 二趾向前 二趾向后
善于攀援 树木
啄木鸟 杜鹃 金丝燕 翠鸟
猛禽类
喙强大而呈钩状
足强大有力 性情凶猛 鸮（猫头鹰）
爪锐利而钩曲 在上空翱翔 雕 鸢
翼大善飞
掠食动物 隼
项目 形态特点 生活习性 代表种
类群
涉禽类
喙、颈、腿、 善于在浅水 脚趾都很长 中行走和啄
數列1
-40
y
數列1
-50
-50
-50
-60
-60
-60
-70
-70
-70
-80
-80
-80
-90 x
-90 x
-90 x
一元二次函數圖像和系數關係 的解說
Y=ax2+bx+c =a(x2+b/a x+c/a) =a[x2+2(b/2a)x+(b/2a)2 - (b/2a)2 +c/a] =a[(x+b/2a)2-(b/2a)2+c/a)] =a(x+b/2a)2+a[-(b/2a)2+c/a] =a(x+b/2a)2+a[-b2/4a2 +c/a] =a(x+b/2a)2 + a[-b2+4ac/4a2] =a(x+b/2a)2 – (b2-4ac)/4a
總結: 不管a 的符號是+或-, D = 0 有 一 交點, D>0 有二交點, D<0沒有交點
❖一元二次函數例子的解答(I)
36-x
y=-x2+36x
x
400
300
❖ Y = -x2+36x
200
✓ 怎樣的 x 才可以找到最大值
100
的Y?
y
0
❖ 右邊的圖表給了解答，它說
-10
0
10
20
30
40
取食物
鹭类 鹤类 鹳类
游禽类
喙大宽而扁平
足短
善于游泳
趾间有蹼
雁类、鸥类 鹅类、鸭类
陆禽类 喙短而坚硬
（鹑鸡类）后 强肢健中型而
善走、不善飞 适于挖土
趾端有钩爪
翼短小
褐马鸡 绿孔雀 白鹇 鸡
项目 形态特点 生活习性 代表种
类群
走禽类 翼退化，胸 善于奔跑， 鸵鸟
骨中没有龙 不会飞行。 鸸鹋
骨突，足趾 现存最大的 美洲鸵鸟
明在 x=18 cm 的時候，Y有最
-100
大值，也是拐點的坐標
-200
❖ 就是說：給予一定邊長矩形
-300
的條件下，正方形的面積最
x
大。
一元二次函數例子的解答(II)
Y = -x2+36x
36-x
x
一元二次函數普遍表達式
Y=ax2+bx+c==a(x+b/2a)2 – (b2-4ac)/4a
一元二次函數圖像和系數關係 的表解
y=ax*x+bx+c
a>0
a<0
拋物線開口向上
拋物線開口向下
b*b-4ac=D
b*b-4ac=D
D>0
D=0
D<0
D>0
D=0
D<0
拋物線與x-軸有二交點 拋物線與x-軸有一交點 拋物線與x-軸沒有交點 拋物線與x-軸有二交點 拋物線與x-軸有一交點 拋物線與x-軸沒有交點
生一個 y 的數值 a、b、 c 在這裡代表一些數值，稱為函數的系
數
一元二次函數圖像的普遍式樣
▪ 右圖顯示的是函數
y=-2x2-5x+3 20
y = -2x2-5x+3 的圖像 ▪ 所有的一元二次函數都 -10
有相似的圖像
▪ 這樣形式的圖像稱為抛 y 物線
▪ 每條抛物線都有一最高 或最低的點稱「拐點」
右圖顯示的是函數
y
y =- 2x2+5x+c 的圖像，
隨著 c 值 由 3 遞減至 –
7，曲線也在同一位置
由上向下滑動。
y=-2x2+5x+3 10 0 -5 -10 0 5 -20 -30 -40 -50 -60 -70 -80 x
10 數列1
一元二次函數圖像和系數的關 係
y=-2x2+5x+2
y
拐點是由系數 b/a決定
的:
b/a 是 +，拐點在y-軸左 邊
b/a 是-，拐點在y-軸右 邊
y=-2x2-5x+3
20
0
-5 -20 0
5
-40
-60
-80
-100
-120
-140 x
10 數列1
一元二次函數圖像和系數的關 係
曲線的左右移動决定於 a、b 的符號
曲線的上下移動决定於 a、b、c 的符號及數值 -10 的大小
-80
-80 x
-80 x
-90 x
一元二次函數圖像和系數的關 係
y=-2x2+5x-3
y=-2x2+5x-4
y=-2x2+5x-7
0
0
0
-10 -5 -10 0 5 10
-10 -5 -10 0 5 10
-10 -5 -10 0 5 10
-20
-20
-20
-30
-30
-30
-40 y
數列1 y
-40
解答可以在隨後有關一元二次 函數的解說中獲得
36-x x
一元二次函數的專有名辭
一元二次函數有著普遍的表達式 Y=ax2+bx+c
它表示了ｘ(自變量) 和ｙ(因變量) 的關係 在等式右邊只有一變量 x，所以稱為一元 X自乘的最高次數是二，所以稱為二次 函數的意思是每次選定一個 x 的數值，只會產
一元二次函數
Ｙ＝ａｘ２ ＋ ｂｘ ＋ ｃ
性質及應用
一若干?
解答 :
此長方形周長的一半是36cm， 設它的一邊長為x cm， 則另一 邊長為 (36-x) cm
此長方形的面積 y 和 x 的關係 可以表達成:
Y =x(36-x) =36x – x2
作出比較 a=-1，b=36，c=0，可見在 x=b/2a 時，即x=-36/2(-1)=18，Y有最大值
此結果與用圖解方法所獲得的答案相同
第三节 鸟类的生态类群
喙
脚
思考题： 1、哪种喙和脚适于捕食小动物？
猛禽类：鴞、鸢、雕
2、哪种喙和脚适于在树枝上捕虫？
鸣禽类：家燕、画眉、黄鹂
3、哪种喙和脚适于在树干上捕虫？
這是典型的一元二次函數例子
36-x x
一元二次函數的例子
周長為72 cm 的長方形，當面 積最大時，各邊長應為若干?
解答 :
此長方形的面積 y 和 x 的關係 既然已找到:
Y =x(36-x) =36x – x2= -x2+36x
y=2x2+5x+3
160 140 120 100 80 60 40 20
0 -5 0 x 5
數列1 10
一元二次函數圖像和系數的關 係
✓ 右圖顯示的是函數
y =- 2x2-5x+3 的圖像
它和前述的y=2x2+5x+3 比較，有二個符號不一 -10 樣。
✓ 但這兩條曲條的拐點同 樣在 y-軸的左邊，可見
y=-2x2+5x+1
y=-2x2+5x-2
10
10
10
0
0
0
-10 -5 -10 0 5 10
-10 -5 -10 0 5 10
-10 -5 -10 0 5 10
-20
-20
-20
-30 y
-40
數列1
-30
y
-40
-30
數列1 y
-40
數列1
-50
-50
-50
-60
-60
-60
-70
-70
-70
攀禽类：啄木鸟、杜鹃、鹦鹉
4、哪种喙和脚适于在水中捞食水草？
游禽类：天鹅、野鸭、鸬鹚、鸳鸯、鸊鹈
5、哪种喙和脚适于在水中捕鱼？
涉禽类：丹顶鹤、白鹭、黑颧
6、哪种喙和脚适于扒土寻食？鸡、绿孔雀
项目 形态特点 生活习性 代表种
类群
鸣禽类
喙细而尖 足短而细 三趾向前 一趾向后
体态轻捷 善于鸣啭 巧于营巢
別， ，但曲線向上開口，
可見開口端是曲系數a
-10
的符號决定的，a 是正
數、向上，a 是負數、
y=2x2-5x+3 90 80 70 60 50 40 30 20 10 0 -5 x0 5
數列1 10
一元二次函數圖像和系數的關 係
▪ 右圖顯示的是函數 y = 2x2+5x+3 的圖像 它和前述的y =2x25x+3 比較，也只有 一符號的差別，但 y 這條曲條的拐點， 卻落在y-軸的左邊。
画眉
伯劳
伯劳
黄鹂
织 布 鸟
减少
鸟类类群 几维鸟
我国的珍贵鸟类： 丹顶鹤 、 绿孔雀、 朱鹮 、 褐马鸡 、
黄腹角雉为国家一级保护动物； 锦鸡 、 天鹅、 白鹇等为国家二级保护动物
游禽类
猛禽类
陆禽类
攀禽类
鸣禽类 涉禽类
a
b
c
d
e
f
小结： 1、鸟类的形态和结构特征与它们的
生活习性相适应。
2、鸟类是我们的朋友，我们应该保 护鸟类。
家燕 画眉 黄鹂 八哥
攀禽类
喙直而坚硬 足短而健壮 二趾向前 二趾向后
善于攀援 树木
啄木鸟 杜鹃 金丝燕 翠鸟
猛禽类
喙强大而呈钩状
足强大有力 性情凶猛 鸮（猫头鹰）
爪锐利而钩曲 在上空翱翔 雕 鸢
翼大善飞
掠食动物 隼
项目 形态特点 生活习性 代表种
类群
涉禽类
喙、颈、腿、 善于在浅水 脚趾都很长 中行走和啄
數列1
-40
y
數列1
-50
-50
-50
-60
-60
-60
-70
-70
-70
-80
-80
-80
-90 x
-90 x
-90 x
一元二次函數圖像和系數關係 的解說
Y=ax2+bx+c =a(x2+b/a x+c/a) =a[x2+2(b/2a)x+(b/2a)2 - (b/2a)2 +c/a] =a[(x+b/2a)2-(b/2a)2+c/a)] =a(x+b/2a)2+a[-(b/2a)2+c/a] =a(x+b/2a)2+a[-b2/4a2 +c/a] =a(x+b/2a)2 + a[-b2+4ac/4a2] =a(x+b/2a)2 – (b2-4ac)/4a
總結: 不管a 的符號是+或-, D = 0 有 一 交點, D>0 有二交點, D<0沒有交點
❖一元二次函數例子的解答(I)
36-x
y=-x2+36x
x
400
300
❖ Y = -x2+36x
200
✓ 怎樣的 x 才可以找到最大值
100
的Y?
y
0
❖ 右邊的圖表給了解答，它說
-10
0
10
20
30
40
取食物
鹭类 鹤类 鹳类
游禽类
喙大宽而扁平
足短
善于游泳
趾间有蹼
雁类、鸥类 鹅类、鸭类
陆禽类 喙短而坚硬
（鹑鸡类）后 强肢健中型而
善走、不善飞 适于挖土
趾端有钩爪
翼短小
褐马鸡 绿孔雀 白鹇 鸡
项目 形态特点 生活习性 代表种
类群
走禽类 翼退化，胸 善于奔跑， 鸵鸟
骨中没有龙 不会飞行。 鸸鹋
骨突，足趾 现存最大的 美洲鸵鸟
明在 x=18 cm 的時候，Y有最
-100
大值，也是拐點的坐標
-200
❖ 就是說：給予一定邊長矩形
-300
的條件下，正方形的面積最
x
大。
一元二次函數例子的解答(II)
Y = -x2+36x
36-x
x
一元二次函數普遍表達式
Y=ax2+bx+c==a(x+b/2a)2 – (b2-4ac)/4a
一元二次函數圖像和系數關係 的表解
y=ax*x+bx+c
a>0
a<0
拋物線開口向上
拋物線開口向下
b*b-4ac=D
b*b-4ac=D
D>0
D=0
D<0
D>0
D=0
D<0
拋物線與x-軸有二交點 拋物線與x-軸有一交點 拋物線與x-軸沒有交點 拋物線與x-軸有二交點 拋物線與x-軸有一交點 拋物線與x-軸沒有交點
生一個 y 的數值 a、b、 c 在這裡代表一些數值，稱為函數的系
數
一元二次函數圖像的普遍式樣
▪ 右圖顯示的是函數
y=-2x2-5x+3 20
y = -2x2-5x+3 的圖像 ▪ 所有的一元二次函數都 -10
有相似的圖像
▪ 這樣形式的圖像稱為抛 y 物線
▪ 每條抛物線都有一最高 或最低的點稱「拐點」
右圖顯示的是函數
y
y =- 2x2+5x+c 的圖像，
隨著 c 值 由 3 遞減至 –
7，曲線也在同一位置
由上向下滑動。
y=-2x2+5x+3 10 0 -5 -10 0 5 -20 -30 -40 -50 -60 -70 -80 x
10 數列1
一元二次函數圖像和系數的關 係
y=-2x2+5x+2
y
拐點是由系數 b/a決定
的:
b/a 是 +，拐點在y-軸左 邊
b/a 是-，拐點在y-軸右 邊
y=-2x2-5x+3
20
0
-5 -20 0
5
-40
-60
-80
-100
-120
-140 x
10 數列1
一元二次函數圖像和系數的關 係
曲線的左右移動决定於 a、b 的符號
曲線的上下移動决定於 a、b、c 的符號及數值 -10 的大小
-80
-80 x
-80 x
-90 x
一元二次函數圖像和系數的關 係
y=-2x2+5x-3
y=-2x2+5x-4
y=-2x2+5x-7
0
0
0
-10 -5 -10 0 5 10
-10 -5 -10 0 5 10
-10 -5 -10 0 5 10
-20
-20
-20
-30
-30
-30
-40 y
數列1 y
-40
解答可以在隨後有關一元二次 函數的解說中獲得
36-x x
一元二次函數的專有名辭
一元二次函數有著普遍的表達式 Y=ax2+bx+c
它表示了ｘ(自變量) 和ｙ(因變量) 的關係 在等式右邊只有一變量 x，所以稱為一元 X自乘的最高次數是二，所以稱為二次 函數的意思是每次選定一個 x 的數值，只會產
一元二次函數
Ｙ＝ａｘ２ ＋ ｂｘ ＋ ｃ
性質及應用
一若干?
解答 :
此長方形周長的一半是36cm， 設它的一邊長為x cm， 則另一 邊長為 (36-x) cm
此長方形的面積 y 和 x 的關係 可以表達成:
Y =x(36-x) =36x – x2
作出比較 a=-1，b=36，c=0，可見在 x=b/2a 時，即x=-36/2(-1)=18，Y有最大值
此結果與用圖解方法所獲得的答案相同
第三节 鸟类的生态类群
喙
脚
思考题： 1、哪种喙和脚适于捕食小动物？
猛禽类：鴞、鸢、雕
2、哪种喙和脚适于在树枝上捕虫？
鸣禽类：家燕、画眉、黄鹂
3、哪种喙和脚适于在树干上捕虫？
這是典型的一元二次函數例子
36-x x
一元二次函數的例子
周長為72 cm 的長方形，當面 積最大時，各邊長應為若干?
解答 :
此長方形的面積 y 和 x 的關係 既然已找到:
Y =x(36-x) =36x – x2= -x2+36x