下载文档原格式
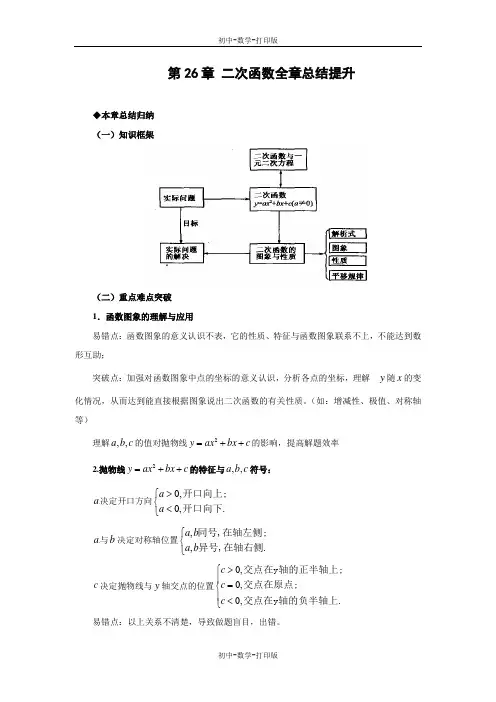
第26章二次函数全章总结提升◆本章总结归纳（一）知识框架（二）重点难点突破1．函数图象的理解与应用易错点：函数图象的意义认识不表，它的性质、特征与函数图象联系不上，不能达到数形互助；突破点：加强对函数图象中点的坐标的意义认识，分析各点的坐标，理解y随x的变化情况，从而达到能直接根据图象说出二次函数的有关性质。
（如：增减性、极值、对称轴等）理解,,a b c的值对抛物线2y ax bx c=++的影响，提高解题效率2.抛物线2y ax bx c=++的特征与,,a b c符号：,,a b c决定开口方向0,0,aa>⎧⎨<⎩开口向上;开口向下.,,a b c与b决定对称轴位置,,a ba b⎧⎨⎩同号,在轴左侧;异号,在轴右侧.c决定抛物线与y轴交点的位置0,0,0,ccc>⎧⎪=⎨⎪<⎩交点在y轴的正半轴上;交点在原点;交点在y轴的负半轴上.易错点：以上关系不清楚，导致做题盲目，出错。
突破点：数形结合，变式训练，特别是,,a b c 与b 一走决定对称轴位置的理解与判定。
3．解析式之间的转化与解析式的求法。
易错点：①将2y ax bx c =++化成顶点式224()24b ac b y a x a a -=++ ②用待定系数法求解时，不能根据不同条件恰当地选取解析式。
突破点：①强调配方的步骤、配方的规律，注意恒等变形与检验。
②比较不同形式的解析式的优劣，应用的环境，加强对顶点式、交点式的理解，并能正确运用。
4．抛物线的平移规律，表达式的变化。
易错点：抛物线的移动，对解析式变化理解不透，不同方向的移动，到底是加还是减判断不清。
突破点：抓住顶点坐标的变化，熟记平移规律，左加右减，上加下减。
5．抛物线与x 轴交点情况。
易错点：此类题综合性较大，对应关系不很明确，隐含条件较多，极易出错。
突破点：抛物线与x 轴交点横坐标就是相应一元二次方程的两根，把交点的个数转化为方程。
根的个数，把交点位置转化为方程根的正负，多加练习，方可过关。
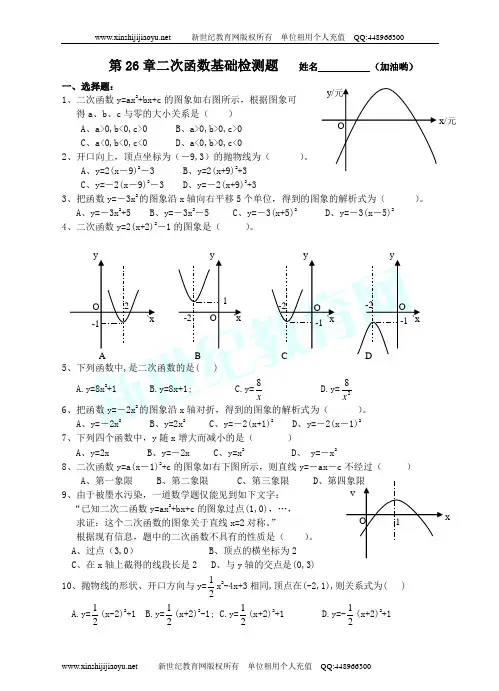
第26章二次函数基础检测题 姓名 （加油哟）一、选择题： 1、二次函数y=ax 2+bx+c 的图象如右图所示，根据图象可得a 、b 、c 与零的大小关系是（ ） A 、a>0,b<0,c>0 B 、a>0,b>0,c>0C 、a<0,b<0,c<0D 、2、开口向上，顶点坐标为（－9,3）的抛物线为（ ）。
A 、y=2(x －9)2－3 B 、y=2(x+9)2+3C 、y=－2(x －9)2－3D 、y=－2(x+9)2+33、把函数y=－3x 2的图象沿x 轴向右平移5个单位，得到的图象的解析式为（ ）。
A 、y=－3x 2+5B 、y=－3x 2－5C 、y=－3(x+5)2D 、y=－3(x －5)24、二次函数y=2(x+2)2－1的图象是（ ）。
5、下列函数中,是二次函数的是( )A.y=8x 2+1B.y=8x+1;C.y=8x D.y=28x 6、把函数y=－2x 2的图象沿x 轴对折，得到的图象的解析式为（ ）。
A 、y=－2x 2B 、y=2x 2C 、y=－2(x+1)2D 、y=－2(x －1)27、下列四个函数中，y 随x 增大而减小的是（ ）A 、y=2xB 、y=－2xC 、y=x 2D 、 y=－x 28、二次函数y=a(x －1)2+c 的图象如右下图所示，则直线y=－ax －c 不经过（ ）A 、第一象限B 、第二象限C 、第三象限D 9、由于被墨水污染，一道数学题仅能见到如下文字：“已知二次二函数y=ax 2+bx+c 的图象过点(1,0)，…，求证：这个二次函数的图象关于直线x=2对称。
”根据现有信息，题中的二次函数不具有的性质是（ ）。
A 、过点（3,0）B 、顶点的横坐标为C 、在x 轴上截得的线段长是2D 、与y 轴的交点是(0,3) 10、抛物线的形状、开口方向与y=12x 2-4x+3相同,顶点在(-2,1),则关系式为( ) A.y=12(x-2)2+1 B.y=12(x+2)2-1; C.y=12(x+2)2+1 D.y=-12(x+2)2+1x/元 xy `x AD y y y `x `x `x 2 -1 O O O O 1 -1 -1 -2 -2 -211、如下左图，抛物线顶点坐标是P(1,3)，则函数y 随自变量x 的增大而减小的x 的取值范围是（ ）。
