7.5多边形内角和与外角和模型专题

初中数学知识归纳多边形的内角和外角在初中数学中，多边形是一个重要的概念。

对于多边形的内角和外角，也是我们需要掌握的基本知识。

本文将对初中数学中多边形的内角和外角进行归纳总结。

一、多边形的定义多边形是由若干条边和若干个顶点组成的图形。

常见的多边形有三角形、四边形、五边形等。

二、多边形的内角和外角1. 内角：多边形内角是多边形内部两条相邻边所形成的角。

对于任意一个n边形，其内角和公式可以表示为：(n-2) × 180°。

例如，三角形的内角和为180°，四边形的内角和为360°。

2. 外角：多边形外角是由多边形边的延长线所形成的角。

对于任意一个n边形，其外角和公式可以表示为：360°。

例如，三角形的外角和为360°，四边形的外角和也为360°。

三、各种多边形的内角和外角1. 三角形：三角形是由三条边和三个顶点组成的多边形。

根据内角和公式，三角形的内角和为180°。

而根据外角和公式，三角形的外角和也为360°。

因为三角形的外角和等于一个圆的周角，所以三角形的外角可以围绕一个点旋转一周。

2. 正多边形：正多边形是指所有边长相等、所有内角相等的多边形。

对于正n边形，其每个内角都可以通过(n-2) × 180° ÷ n来计算。

而对于外角和，根据公式可得360° ÷ n。

例如，正三角形的内角和为180°，外角和为120°；正四边形的内角和为360°，外角和为90°；正五边形的内角和为540°，外角和为72°。

3. 不规则多边形：不规则多边形是指边长和内角均不相等的多边形。

对于不规则多边形，计算内角和需要逐个计算每个内角的度数，然后求和；而外角和则仍然为360°。

四、多边形内角和外角的应用1. 内角和应用：内角和的概念在解决数学题目中经常用到。

七年级数学几何模型大全七年级的小伙伴们，今天咱们来唠唠七年级数学里那些超有趣的几何模型。

一、角平分线模型1. 双角平分线模型- 想象一下，有一个角，然后从这个角的顶点引出两条角平分线。

比如说∠AOB，OC平分∠AOB，OD平分∠AOC。

这里面就有很多好玩的关系哦。

- 如果设∠AOB = 2α，那么∠AOC=α，∠AOD = α/2。

这里面的关键就是根据角平分线的定义，把角之间的关系找出来。

就像分蛋糕一样，角平分线就是把角这个“大蛋糕”分成相等的“小蛋糕”。

- 而且还有个重要的结论呢，如果两个角平分线所夹的角是β，那么β = 1/2∠AOB或者β = 1/2 (∠AOB - ∠COD)，这就看具体的图形情况啦。

2. 邻补角角平分线模型- 当有两个邻补角的时候，它们的角平分线可是很特别的。

比如说∠AOC和∠BOC是邻补角，OE平分∠AOC，OF平分∠BOC。

- 因为∠AOC+∠BOC = 180°，又因为OE和OF是角平分线，所以∠EOC+∠FOC=1/2(∠AOC + ∠BOC)=90°。

这就像两个小伙伴，把相邻的两块“角蛋糕”各自分一半，然后这两半加起来正好是个直角呢。

二、平行线模型1. “Z”字形模型（内错角模型）- 当有两条平行线被第三条直线所截的时候，就会出现像“Z”字一样的图形。

比如说直线a∥b，直线c与a、b相交。

- 这里面的内错角是相等的哦。

就好像在两条平行的铁轨（a和b）上，有一根枕木（c）横过来，形成的内错角就像在铁轨两边对称的位置，它们的大小是一样的。

- 如果∠1和∠2是内错角，那么∠1 = ∠2。

这个结论在证明角相等或者计算角的度数的时候可太有用啦。

2. “F”字形模型（同位角模型）- 还是两条平行线被第三条直线所截，不过这个时候是同位角的关系。

就像“F”字的形状。

- 同位角也是相等的呢。

比如说∠3和∠4是同位角，只要a∥b，那么∠3 = ∠4。

可以想象成在平行的道路（a和b）上，同样位置的标记（∠3和∠4），它们的角度肯定是一样的呀。

龙文教育一对一讲义教师:学生:日期:星期:时段:课题多边形的内角和与外角和学习目标与分析目标：会求多边形的内角和，会根据多边形的外交和求相应的边角关系。

考点：1）多年形内角和公式：（n-2）*18002）多年形外角和为3600学习重点重点：会运用多边形的内角和公式进行相关的计算。

难点：运用外角和定理，内角和公式求多边形的边角关系。

学习方法讲授与练习，归纳与总结学习内容与过程教师分析与批改1.12边形内角和是_______2.已知一个多边形的每个内角为140度则这个多边形是—————边形3.若这多边形边数加1则这多边形的内角和增加——4.在四边形ABCD中四个内角度数比为2:3:4:3则每个内角—————5.下列角中能成为一个多边形内角和的是————A 270度B 560度C 1800度D 1900度6. 如果一个多边形的每个外角都等于40°,则这个多边形的内角和是多少？7.如果一个多边形的每一个内角都等于150°,则这个多边形的边数是多少？8.如图：求正五边形的每一个外角以及每一个内角的度数各是多少度？学习内容与过程教师分析与批改9.如图，D是△ABC的BC边上一点，∠B＝∠BAD，∠ADC＝８0°,∠BAC=70°.求：（1）∠B的度数；（2）∠C的度数.10、一个零件的形状如图所示,按规定∠A应等于900 , ∠B 和∠C应分别是210和320,检验工人量得∠BDC=1480,就断定这个零件不合格.运用你学过的三角形的有关知识说明零件不合格的理由.11. (1）如图(甲)，在五角星图形中，求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数。

（2）把图（乙）、（丙）叫蜕化的五角星，问它们的五角之和与五角星图形的五角之和仍相等吗？为什么？。

多边形内角和与外角和（提高）知识讲解【学习目标】1.理解多边形的概念；2.掌握多边形内角和与外角和公式；3.灵活运用多边形内角和与外角和公式解决有关问题，体验并掌握探索、归纳图形性质的推理方法，进一步培养说理和进行简单推理的能力.【要点梳理】知识点一、多边形的概念1．定义：在平面内不在同一直线上的一些线段首尾顺次联接结所组成的封闭图形叫做多边形．其中，各个角相等、各条边相等的多边形叫做正多边形．2．相关概念：边：组成多边形的各条线段叫做多边形的边．顶点：每相邻两条边的公共端点叫做多边形的顶点．内角：多边形相邻两边组成的角叫多边形的内角，一个n 边形有 n 个内角。

外角：多边形的边与它的邻边的延长线组成的角叫做多边形的外角。

对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线．3.多边形的分类 : 画出多边形的任何一边所在的直线，如果整个多边形都在这条直线的同一侧，那么这个多边形就是凸多边形，如果整个多边形不在直线的同一侧，这个多边形叫凹多边形。

如图：凹多边形凸多边形要点诠释：( 1) 正多边形必须同时满足“各边相等”，“各角相等”两个条件，二者缺一不可；( 2)过 n 边形的一个顶点可以引( n- 3) 条对角线， n 边形对角线的条数为( 3)过 n 边形的一个顶点的对角线可以把n 边形分成 ( n- 2) 个三角形．知识点二、多边形内角和定理n(n3) ；2n 边形的内角和为(n- 2) ·180° ( n≥ 3) ．要点诠释：( 1) 内角和定理的应用：①已知多边形的边数，求其内角和；②已知多边形内角和求其边数；(n2) g180°( 2) 正多边形的每个内角都相等，都等于；n知识点三、多边形的外角和多边形的外角和为 360°．要点诠释：( 1) 在一个多边形的每个顶点处各取一个外角，这些外角的和叫做多边形的外角和．n 边形的外角和恒等于 360°，它与边数的多少无关；( 2) 正 n 边形的每个内角都相等，所以它的每个外角都相等，都等于°360；n( 3) 多边形的外角和为360°的作用是：①已知各相等外角度数求多边形边数；②已知多边形边数求各相等外角的度数．【典型例题】类型一、多边形的概念1．同学们在平时的数学活动中会遇到这样一个问题：把正方形纸片截去一个角后，还剩多少角，余下的图形是几边形，亲爱的同学们，你知道吗【答案与解析】解：这个问题，我们可以用图来说明．?按图 ( 1) 所示方式去截，不经过点 B 和 D ，还剩五个角，即得到一个五边形．按图 ( 2) 所示方式去截，经过点 D ( 或点 B) ．不经过点 B( 或点 D ) ，还剩 4 个角，即得到一个四边形．按图 ( 3) 所示方式去截，经过点D、点 B ，则剩下 3 个角，即得到三角形．答：余下的图形是五边形或四边形或三角形．【总结升华】一个 n 边形剪去一个角后，可能是 ( n+1) 边形，也可能是 n 边形，也可能是 ( n- 1)边形，利用它我们可以解决一些具体问题．举一反三：【变式 1】如图，四边形 ABCD中，∠ B＝ 40°，沿直线 MN剪去∠ B，则所得五边形AEFCD中，∠1+∠ 2＝。

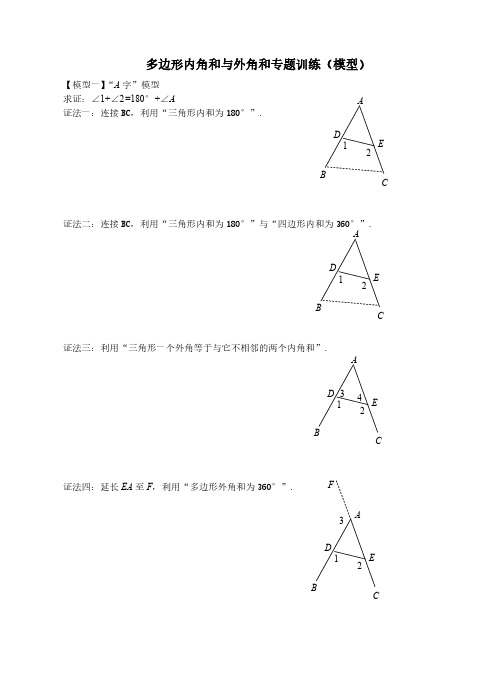
多边形内角和与外角和专题训练（模型）【模型一】“A字”模型求证：∠1+∠2=180°+∠A证法一：连接BC，利用“三角形内和为180°”.证法二：连接BC，利用“三角形内和为180°”与“四边形内和为360°”. 证法三：利用“三角形一个外角等于与它不相邻的两个内角和”.证法四：延长EA至F，利用“多边形外角和为360°”. CAB DE21CAB DE21CAB DE213 4CAB DE213F【模型二】飞镖模型 求证：∠A +∠B +∠C=∠D 证法一、证明：连接BC ，证法二、连接并延长AD ，证法三、连接并延长BD ，交AC 于点E,【模型三】“8字”模型 求证：∠A +∠B=∠C+∠D 证法一、利用“三角形内角和为180°”证法二、利用“三角形任意一个外角等于与它不相邻的两个内角和”A BC D O A B C D 12 A B C D 1 234 A B C D 1E A BC DO 1注意：“8字”模型的变式. 如图，∠1+∠2=∠C+∠D【模型四】“五角星”模型求证：∠A +∠B +∠C+∠D +∠E =180°【模型五】“角平分线”模型 1、 两条内角平分线已知：如图，∠B 、∠C 的平分线BP 、CP 交于点P 求证：∠BPC=90°+21∠A2、两条外角平分线已知：如图，∠CBE 、∠BCF 的平分线BP 、CP 交于点P 求证：∠P =90°-21∠AABCP12PAB C1 2EFDAB OC 1 2 CDEAB3、一条内角平分线和一条外角平分线已知：如图，∠ABC 、∠ACD 的平分线BP 、CP 交于点P 求证：∠P =21∠A【模型六】“高线角平分线”模型求证：∠DCE=21（∠B -∠A ）.（其中∠B >∠A ）【模型七】“折角”模型 求证：∠1+∠2=2∠A求证：∠2-∠1=2∠A求证：∠1-∠2=2∠AP ABC1 2 DCABDE ABCMNA ’2 1MBA ’23D C1NAABCMNA ’ 12 3 D在“填空题”、“选择题”的客观题型中，可以直接运用模型结论解题.注意结论的准确性. 1.☆如图，在△ABC 中，∠A =50°，∠B=65°，则∠ACD= °2.☆如图，∠1+∠2=260°，则∠A= °3.☆如图，∠1=25°，∠2=75°，∠C=65°，则∠D= °4. ☆如图，在△ABC 中，∠A =62°，∠1=20°，∠2=35°，则∠BDC= °5. ☆如图，若∠A=∠B=∠C=∠D=∠E ，则∠A= °6. ☆如图，若∠A=40°，则∠P= °7. ☆如图，△ABC 中，CD ⊥AB ，CE 平分∠ACB ，∠B =50°，∠A =20°,则∠DCE= °8. ☆如图，纸片△ABC 中，∠A =55°，∠B=75°，将纸片的一角折叠，使C 点落在△ABC 内的C ’处，则∠1+∠2= °9. ☆☆如图，∠A +∠B +∠C+∠D +∠E+∠F +∠G= °10. ☆☆如图，∠A +∠B +∠C+∠D = °11. ☆☆如图，BE 、CF 交于点O ，∠EOF =105°，则∠A +∠B +∠C+∠D +∠E+∠F= °. 12. ☆☆如图，∠ABD 与∠ACB 的角平分线相交于点P ，若∠A =50°，∠D =10°，则∠P = °.A B C D 第1题 A B C D 1 2 第2题 D AB OC 1 2 第3题 A B CD 12 第4题AB C PC D EA B 第5题 第6题 C A B D E 第7题 2 C A B C ’1 第8题 AB C D E F G 第9题 ABC D 120100第10A BC DP 第12题A BC105° OD EF第11题在“解答题”中，重现模型证明过程.注意方法的选择.1. ☆☆如图，在∠AMB 的两边AM 、BM 上分别取点P 、Q ，在∠AMB 内取一点N ，连接PN 、QN ，探索∠PNQ 、∠AMB 、∠MPN 、∠MQN 之间的数量关系，并证明你的结论.2. ☆☆如图，∠MON=90°，点A 、B 分别在射线PM 、PN 上，∠MAB 和∠NBA 的平分线相交于点P .点A 和点B 在运动过程中，∠P 的大小是否发生变化？请说明你的理由.3. ☆☆如图，已知AB ∥CD ，BD 平分∠ABC 交AC 于点O ，CE 平分∠DCG.若∠ACE=90°，试判断BD 与AC 的位置关系，并说明理由.A B N O M P A B C D EFA MB A M B AM B4. ☆☆在△ABC 中，内角∠ABC 、∠ACB 的平分线夹角为α，外角∠DBC 、∠ECB 的平分线夹角为β.（1）若α=110°，则∠A = °，（2）若∠A =40°，则β= °，（3）猜想α与β之间的关系，并说明理由.【探索新知】在模型的基础上探索新知，或用与探索模型类似的方法探索新知.注意的模型生成过程. 1. ☆☆如图①，则∠1+∠2+∠3+∠4 = °；如图②，则∠1+∠2+∠3+∠4 +∠5 = °； 如图③，则∠1+∠2+∠3+∠4 +∠5+∠6 = °.2. ☆☆（1）如图（1）,则∠A +∠B +∠C+∠D +∠E+∠F J= °；（2）如图（2），则∠A +∠B +∠C+∠D +∠E+∠F +∠G +∠H J= °； （3）如图（3），则∠A +∠B +∠C+∠D +∠E+∠F +∠G +∠H +∠I +∠J= °.3. ☆☆☆已知：如图，在△ABC 中，BO 1、BO 2是∠ABC 的三等分线，CO 1、CO 2是∠ACB 的三等分线.（1）当∠A =60°时，∠BO 2C = °； （2）探索∠BO 1C 与∠BO 2C 之间的数量关系，并证明你的结论.4. ☆☆☆已知：如图，∠ABC 和∠ACB 的平分线相交于点E . A5 1 2 3 41 2 3 4 6 1 2 3 5 4① ② ③A B C D E F H GF E D C B A A BC D E G H I J F (1) (2) (3)A B C O 1 O 2DA B C EPO（1）若∠D =140°，∠E =110°，则∠A °； （2）求证：∠E =21（∠A +∠D ）5. ☆☆☆☆如图，线段AB 、CD 交于点O ，连接AD 、BC ，我们把形如图1的图形称为“8字形”. （1）如图（1），直接写出∠A +∠D 与∠B+∠C 的关系； （2）如图（2），∠DAB 和∠BCD 的平分线AP 、CP 交于点P ，且分别与AB 、CD 交于点M 、N ，∠D=46°，∠B=30°. 先观察图中还有哪些“8字形”，再利用（1）的结论求∠P 的度数； （3）在（2）中，若∠D=α，∠B=β，直接写出∠P 的度数(用含有α、β的式子表示).6. ☆☆☆☆如图，在△ABC 中，将点A 向下拖动，依次可以得到图1、图2、图3.分别探究图（1）、图（2）、图（3）中∠EAD 、∠B 、∠C 、∠D 与∠E 之间有什么数量关系？7. ☆☆☆☆如图，线段AB 、CD 交于点O .将图（1）中线段AD 上一点E （点A 、D 除外）向下拖AB C A B C D E A B C D E A B C DE （1） （2）（3）A DB C O PM NA D BC O（2）（1）动，依次可以得到图（2）、图（3）、图（4）.分别探究图（2）、图（3）、图（4）中∠A 、∠B 、∠C 、∠D 与∠AED 之间有什么数量关系？8. ☆☆☆☆转化是数学中的重要思想，即把陌生的问题转化成熟悉的问题，把复杂的问题转化简单的问题，把复杂的问题转化为简单的问题，把抽象的问题转化为具体的问题. （1）请你根据学过的知识求出下面星形中∠A +∠B +∠C+∠D +∠E 的度数； （2）若将图（1）中的星形截去一个角，如图（2），请你求出∠A +∠B +∠C+∠D +∠E+∠F 的度数； （3）若再将图（2）中角进一步截去，如图（2），你能由题（2）中的方法或规律，猜想出图（3）中∠A +∠B +∠C+∠D +∠E+∠F +∠G +∠H +∠I +∠J 的度数？（直接写出结果，不需要写出解题过程）10. ☆☆☆☆☆如图，四边形ABCD 中，内角∠ABC 的角平分线与外角∠DCE 的角平分线交于点F ，且∠F 为锐角.设∠A =α，∠D =β.（1） 如图①，α+β>180°，试用α、β表示∠F ；C D E A B A B CD EF G A B C DE F H I J（1） （2） （3）（2） 如图②，α+β<180°，请在图中画出∠F ，并试用α、β表示∠F ；（3） 一定存在∠F 吗？如有，求出∠F 的值；如不一定，指出α、β满足什么条件时，不存在∠F .9. ☆☆☆☆☆如图①，把三角形纸片ABC 折叠，使3个顶点重合于点P ，这时∠α+∠β+∠γ= °，∠1+∠2+∠3+∠4 +∠5 +∠6 = °.如果三角形纸片ABC 折叠后，3个顶点并不重合于点P （如图②），那么（1）中关于“∠1+∠2+∠3+∠4 +∠5 +∠6 ”的结论是否仍然成立？请说明理由. A B C D E F ① AB C D E ② G12 A BCDEF H I34 5 6 α β γP A’ B’ C’ ABCDEF GIH12 3 65 4 4①②。