苏教版高中数学选修1-2 数系的扩充与复数的引入章末小结与测评 学案
- 格式:doc
- 大小:387.00 KB
- 文档页数:7
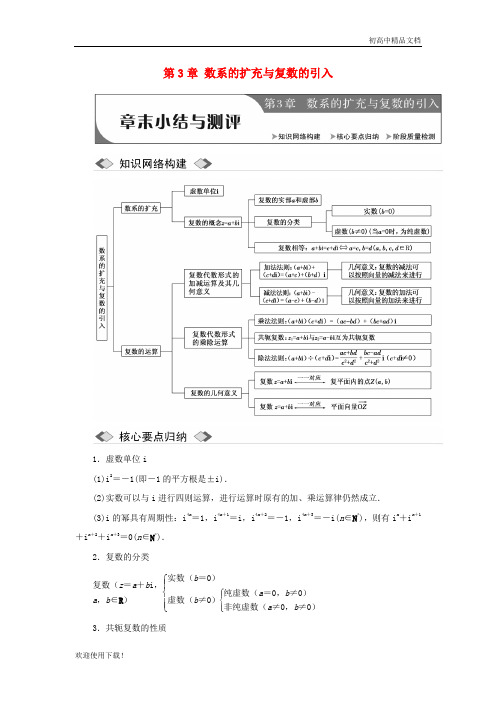
第3章 数系的扩充与复数的引入1.虚数单位i(1)i 2=-1(即-1的平方根是±i).(2)实数可以与i 进行四则运算,进行运算时原有的加、乘运算律仍然成立. (3)i 的幂具有周期性:i 4n=1,i 4n +1=i ,i4n +2=-1,i4n +3=-i(n ∈N *),则有i n +in +1+in +2+in +3=0(n ∈N *).2.复数的分类复数(z =a +b i ,a ,b ∈R )⎩⎪⎨⎪⎧实数(b =0)虚数(b ≠0)⎩⎪⎨⎪⎧纯虚数(a =0,b ≠0)非纯虚数(a ≠0,b ≠0) 3.共轭复数的性质设复数z的共轭复数为z,则(1)z·z=|z|2=|z|2;(2)z为实数⇔z=z,z为纯虚数⇔z=-z.4.复数的几何意义5.复数相等的条件(1)代数形式:复数相等的充要条件为a+b i=c+d i(a,b,c,d∈R)⇔a=c,b=d.特别地,a+b i=0(a,b∈R)⇔a=b=0.注意:两复数不是实数时,不能比较大小.(2)几何形式:z1,z2∈C,z1=z2⇔对应点Z1,Z2重合⇔OZ1―→与OZ2―→重合.6.复数的运算(1)加法和减法运算:(a+b i)±(c+d i)=(a±c)+(b±d)i(a,b,c,d∈R).(2)乘法和除法运算:复数的乘法按多项式相乘进行运算,即(a+b i)(c+d i)=(ac-bd)+(ad+bc)i;复数除法是乘法的逆运算,其实质是分母实数化.(考试时间:120分钟试卷总分:160分)一、填空题(本大题共14小题,每小题5分,共70分)1.(新课标全国卷Ⅱ改编)设复数z1,z2在复平面内的对应点关于虚轴对称,z1=2+i,则z1z2=________.解析:∵z1=2+i在复平面内对应点(2,1),又z1与z2在复平面内的对应点关于虚轴对称,则z2的对应点为(-2,1),则z2=-2+i,∴z1z2=(2+i)(-2+i)=i2-4=-5.答案:-52.(山东高考改编)若a-i与2+b i互为共轭复数,则(a+b i)2=________.解析:根据已知得a=2,b=1,所以(a+b i)2=(2+i)2=3+4i.答案:3+4i3.若复数z 满足 (3-4i)z =|4+3i|,则z 的虚部为________. 解析:∵(3-4i)z =|4+3i|,∴z =|4+3i|3-4i =5(3+4i )(3-4i )(3+4i )=3+4i 5=35+45i ,∴z 的虚部是45.答案:454.已知m1+i =1-n i ,其中m ,n 是实数,i 是虚数单位,则m +n i 等于________.解析:m1+i=1-n i ,所以m =(1+n )+(1-n )i ,因为m ,n ∈R , 所以⎩⎪⎨⎪⎧1-n =0,1+n =m ,所以⎩⎪⎨⎪⎧n =1,m =2,即m +n i =2+i.答案:2+i5.定义运算⎪⎪⎪⎪⎪⎪a b cd =ad -bc ,则满足条件⎪⎪⎪⎪⎪⎪1 -1z z i =4+2i 的复数z 为________. 解析:⎪⎪⎪⎪⎪⎪1 -1z z i =z i +z ,设z =x +y i ,∴z i +z =x i -y +x +y i =x -y +(x +y )i =4+2i , ∴⎩⎪⎨⎪⎧x -y =4,x +y =2,∴⎩⎪⎨⎪⎧x =3,y =-1. ∴z =3-i. 答案:3-i6.在复平面内,复数2-i 1+i 对应的点位于第________象限.解析:2-i 1+i =(2-i )(1-i )(1+i )(1-i )=1-3i 12-i 2=12-32i ,对应的点位于第四象限. 答案:四7.5(4+i )2i (2+i )=________. 解析:5(4+i )2i (2+i )=5(15+8i )-1+2i =5(15+8i )(-1-2i )(-1)2+22=1-38i. 答案:1-38i8.设a 是实数,且a 1+i +1+i2是实数,则a 等于________.解析:∵a 1+i +1+i 2=a (1-i )2+1+i 2=⎝ ⎛⎭⎪⎫a 2+12+(1-a )2i 是实数,∴1-a2=0,即a =1. 答案:19.复数z 满足方程⎪⎪⎪⎪⎪⎪z +21+i =4,那么复数z 的对应点P 组成图形为________. 解析:⎪⎪⎪⎪⎪⎪z +21+i =|z +(1-i)|=|z -(-1+i)|=4. 设-1+i 对应的点为C (-1,1),则|PC |=4,因此动点P 的轨迹是以C (-1,1)为圆心,4为半径的圆.答案:以(-1,1)为圆心,以4为半径的圆10.已知集合M ={1,2,z i},i 为虚数单位,N ={3,4},M ∩N ={4},则复数z =________. 解析:由M ∩N ={4},知4∈M , 故z i =4,∴z =4i =-4i.答案:-4i11.若复数z 满足|z |-z =101-2i ,则z =________.解析:设z =a +b i(a ,b ∈R ),∴|z |-z =a 2+b 2-(a -b i)=a 2+b 2-a +b i , 101-2i =10(1+2i )(1-2i )(1+2i )=10(1+2i )12+22=2+4i , ∴⎩⎨⎧a 2+b 2-a =2,b =4,解得⎩⎪⎨⎪⎧a =3,b =4.∴z =3+4i. 答案:3+4i12.若OA =3i +4,OB =-1-i ,i 是虚数单位,则AB =________.(用复数代数形式表示)解析:由于OA =3i +4,OB =-1-i ,i 是虚数单位, 所以AB =OB -OA =(-1-i)-(3i +4)=-5-4i. 答案:-5-4i13.复数z 满足|z +1|+|z -1|=2,则|z +i +1|的最小值是________.解析:由|z +1|+|z -1|=2,根据复数减法的几何意义可知,复数z 对应的点到两点(-1,0)和(1,0)的距离和为2,说明该点在线段y =0(x ∈[-1,1])上,而|z +i +1|为该点到点(-1,-1)的距离,其最小值为1.答案:114.已知关于x 的方程x 2+(1+2i)x -(3m -1)=0有实根,则纯虚数m 的值是________. 解析:方程有实根,不妨设其一根为x 0,设m =a i 代入方程得x 20+(1+2i)x 0-(3a i -1)i =0,化简得,(2x 0+1)i +x 20+x 0+3a =0,∴⎩⎪⎨⎪⎧2x 0+1=0,x 20+x 0+3a =0,解得a =112,∴m =112i.答案:112i二、解答题(本大题共6小题,共90分) 15.(本小题满分14分)计算:(1)(2+i )(1-i )21-2i ;(2)4+5i (5-4i )(1-i ).解:(1)(2+i )(1-i )21-2i =(2+i )(-2i )1-2i =2(1-2i )1-2i =2.(2)4+5i (5-4i )(1-i )=(5-4i )i(5-4i )(1-i ) =i 1-i =i (1+i )(1-i )(1+i )=i -12=-12+12i.16.(本小题满分14分)求实数k 为何值时,复数(1+i)k 2-(3+5i)k -2(2+3i)分别是:(1)实数;(2)虚数;(3)纯虚数;(4)零.解:由z =(1+i)k 2-(3+5i)k -2(2+3i)=(k 2-3k -4)+(k 2-5k -6)i.(1)当k 2-5k -6=0时,z ∈R , ∴k =6或k =-1.(2)当k 2-5k -6≠0时,z 是虚数,即k ≠6且k ≠-1.(3)当⎩⎪⎨⎪⎧k 2-3k -4=0,k 2-5k -6≠0时,z 是纯虚数,∴k =4.(4)当⎩⎪⎨⎪⎧k 2-3k -4=0,k 2-5k -6=0时,z =0,解得k =-1.综上,当k =6或k =-1时,z ∈R . 当k ≠6且k ≠-1时,z 是虚数.当k =4时,z 是纯虚数,当k =-1时,z =0.17.(本小题满分14分)已知复数z 满足|z |=1+3i -z ,求(1+i )2(3+4i )22z 的值.解:设z =a +b i(a ,b ∈R ),由|z |=1+3i -z , 得a 2+b 2-1-3i +a +b i =0,则⎩⎨⎧a 2+b 2+a -1=0,b -3=0,所以⎩⎪⎨⎪⎧a =-4,b =3,所以z =-4+3i.则(1+i )2(3+4i )22z =2i (3+4i )22(-4+3i )=2(-4+3i )(3+4i )2(-4+3i )=3+4i.18.(本小题满分16分)已知ω=-12+32i.(1)求ω2及ω2+ω+1的值;(2)若等比数列{a n }的首项为a 1=1,公比q =ω,求数列{a n }的前n 项和S n . 解:(1)ω2=⎝ ⎛⎭⎪⎫-12+32i 2=14-32i -34=-12-32i.ω2+ω+1=⎝ ⎛⎭⎪⎫-12-32i +⎝ ⎛⎭⎪⎫-12+32i +1=0.(2)由于ω2+ω+1=0, ∴ωk +2+ωk +1+ωk =ωk (ω2+ω+1)=0,k ∈Z .∴S n =1+ω+ω2+…+ωn -1=⎩⎪⎨⎪⎧0, n =3k ,1, n =3k +1,1+ω, n =3k +2,∴S n=⎩⎪⎨⎪⎧0, n =3k (k ∈Z ),1, n =3k +1(k ∈Z ),12+32i , n =3k +2(k ∈Z ).19.(本小题满分16分)已知z =a -i1-i(a ∈R 且a >0),复数ω=z (z +i)的虚部减去它的实部所得的差等于32,求复数ω的模.解:把z =a -i1-i (a >0)代入ω中,得ω=a -i 1-i ⎝ ⎛⎭⎪⎫a -i 1-i +i =a +12+a (a +1)2i. 由a (a +1)2-a +12=32,得a 2=4. 又a >0,所以a =2. 所以|ω|=|32+3i|=325.20.(本小题满分16分)已知复数z 满足|z |=2,z 2的虚部为2. (1)求复数z ;(2)设z ,z 2,z -z 2在复平面内对应的点分别为A ,B ,C ,求△ABC 的面积. 解:(1)设z =a +b i(a ,b ∈R ),由已知条件得:a 2+b 2=2,z 2=a 2-b 2+2ab i , 所以2ab =2.所以a =b =1或a =b =-1,即z =1+i 或z =-1-i. (2)当z =1+i 时,z 2=(1+i)2=2i ,z -z 2=1-i , 所以点A (1,1),B (0,2),C (1,-1),所以S △ABC =12|AC |×1=12×2×1=1;当z =-1-i 时,z 2=(-1-i)2=2i ,z -z 2=-1-3i. 所以点A (-1,-1),B (0,2),C (-1,-3), 所以S △ABC =12|AC |×1=12×2×1=1.即△ABC 的面积为1.。

高中数学选修1,2《数系的扩充和复数的概念》教案高中数学选修1-2《数系的扩充和复数的概念》教案【一】教学准备教学目标知识与技能1、了解数系扩充的过程及引入复数的需要2、掌握复数的有关概念和代数符号形式、复数的分类方法及复数相等的充要条件过程与方法1、通过数系扩充的介绍,让学生体会数系扩充的一般规律2、通过具体到抽象的过程,让学生形成复数的一般形式情感态度与价值观1、体会数系的扩充过程中蕴含的创新精神与实践精神,感受人类理性思维的作用2、体会类比、分类讨论、等价转化的数学思想方法教学重难点重点:引入复数的必要性与复数的相关概念、复数的分类,复数相等的充要条件难点:虚数单位i的引进和复数的概念教学过程(一)问题引入事实上在实数范围内x和y确实不存在?为什么会这样呢?假设x和y是存在的,那么就肯定是一些不是实数的数,那么,这些数是什么呢?我们能不能解决这个问题呢?这就是我们今天要学习的内容《数系的扩充和复数的引入》(二)回顾数系的扩充历程师:其实对于这种“数不够用”的情况,我们并不陌生。
大家记得吗?从小学到现在,我们一直在经历着数的不断扩充。
现在就让我们来回顾一下,看看我们以前是怎么解决“数不够用”的问题的。
(三)类比,引入新数,将实数集扩充1、类比数系的扩充规律,引导学生找出解决“实数不够用”这个问题的办法生:引入新数,使得平方为负数师:我们希望引入的数的平方为负数,但是负数有无穷多个,我们不肯能一下子引入那么多,只要引入平方为多少就行呢?2、历史重现:3、探究复数的一般形式:(四)新的数集——复数集1.复数的定义(略)2.复数的应用:复数在数学、力学、电学及其他学科中都有广泛的应用,复数与向量、平面解析几何、三角函数等都有密切的联系,是进一步学习数学的基础。
(五)复数的分类(六)复数相等的充要条件复数相等的充要条件可以把复数相等的问题转化为求方程组的解的问题,是一种转化的思想。
课后小结1、由于实际的需要,我们总结数的三次扩充过程的规律,运用类比的方法,我们引进了新的数i,并将实数集扩充到了复数集,认识到了复数的代数形式,并讨论了复数的分类及复数相等的充要条件,并且利用相等的条件把复数问题转化为方程组的解的问题2、那么,复数究竟是什么东西呢?能不能像实数一样在现实中找到它的影子呢?别急,我们的探索脚步并不会停止下去,这是我们下次将要探索的内容。

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……学 习 资 料 专 题3.1 数系的扩充[学习目标] 1.了解引进虚数单位i 的必要性,了解数集的扩充过程.2.理解在数系的扩充中由实数集扩展到复数集出现的一些基本概念.3.掌握复数代数形式的表示方法,理解复数相等的充要条件.[知识链接]为解决方程x 2=2,数系从有理数扩充到实数;数的概念扩充到实数集后,人们发现在实数范围内也有很多问题不能解决,如从解方程的角度看,x 2=-1这个方程在实数范围内就无解,那么怎样解决方程x 2=-1在实数系中无根的问题呢?答 设想引入新数i ,使i 是方程x 2=-1的根,即i·i=-1,方程x 2=-1有解,同时得到一些新数. [预习导引] 1.复数的有关概念(1)复数的概念:形如a +b i 的数叫做复数,其中a ,b ∈R ,i 叫做虚数单位.a 叫做复数的实部,b 叫做复数的虚部.(2)复数的表示方法:复数通常用字母z 表示,即z =a +b i.(3)复数集定义:全体复数所构成的集合叫做复数集.通常用大写字母C 表示. 2.复数的分类及包含关系(1)复数(a +b i ,a ,b ∈R )⎩⎨⎧实数(b =0)虚数(b ≠0)⎩⎪⎨⎪⎧纯虚数(a =0)非纯虚数(a ≠0)(2)集合表示:3.复数相等的充要条件设a ,b ,c ,d 都是实数,那么a +b i =c +d i ⇔a =c 且b =d .要点一 复数的概念例1 请说出下列复数的实部和虚部,并判断它们是实数,虚数,还是纯虚数. ①2+3i ;②-3+12i ;③2+i ;④π;⑤-3i ;⑥0.解 ①的实部为2,虚部为3,是虚数;②的实部为-3,虚部为12,是虚数;③的实部为2,虚部为1,是虚数;④的实部为π,虚部为0,是实数;⑤的实部为0,虚部为-3,是纯虚数;⑥的实部为0,虚部为0,是实数.规律方法 复数a +b i 中,实数a 和b 分别叫做复数的实部和虚部.特别注意,b 为复数的虚部而不是虚部的系数,b 连同它的符号叫做复数的虚部. 跟踪演练1 已知下列命题: ①复数a +b i 不是实数; ②当z ∈C 时,z 2≥0;③若(x 2-4)+(x 2+3x +2)i 是纯虚数,则实数x =±2; ④若复数z =a +b i ,则当且仅当b ≠0时,z 为虚数; ⑤若a 、b 、c 、d ∈C 时,有a +b i =c +d i ,则a =c 且b =d . 其中真命题的个数是________. 答案 0解析 根据复数的有关概念判断命题的真假.①是假命题,因为当a ∈R 且b =0时,a +b i 是实数.②是假命题,如当z =i 时,则z 2=-1<0,③是假命题,因为由纯虚数的条件得⎩⎪⎨⎪⎧x 2-4=0,x 2+3x +2≠0,解得x =2,当x =-2时,对应复数为实数.④是假命题,因为没有强调a ,b ∈R .⑤是假命题,只有当a 、b 、c 、d ∈R 时,结论才成立.要点二 复数的分类例2 求当实数m 为何值时,z =m 2-m -6m +3+(m 2+5m +6)i 分别是:(1)实数;(2)虚数;(3)纯虚数.解 由已知得复数z 的实部为m 2-m -6m +3,虚部为m 2+5m +6.(1)复数z 是实数的充要条件是⎩⎪⎨⎪⎧ m 2+5m +6=0,m +3≠0⇔⎩⎪⎨⎪⎧m =-2或m =-3,m ≠-3⇔m =-2.∴当m =-2时复数z 是实数. (2)复数z 是虚数的充要条件是⎩⎪⎨⎪⎧m 2+5m +6≠0,m +3≠0⇔m ≠-3且m ≠-2.∴当m ≠-3且m ≠-2时复数z 是虚数.(3)复数z 是纯虚数的充要条件是⎩⎪⎨⎪⎧m 2-m -6m +3=0,m 2+5m +6≠0⇔m =3.∴当m =3时复数z 是纯虚数.规律方法 利用复数的概念对复数分类时,主要依据实部、虚部满足的条件,可列方程或不等式求参数.跟踪演练2 实数k 为何值时,复数(1+i)k 2-(3+5i)k -2(2+3i)分别是(1)实数;(2)虚数;(3)纯虚数;(4)零.解 由z =(1+i)k 2-(3+5i)k -2(2+3i)=(k 2-3k -4)+(k 2-5k -6)i. (1)当k 2-5k -6=0时,z ∈R ,即k =6或k =-1. (2)当k 2-5k -6≠0时,z 是虚数,即k ≠6且k ≠-1.(3)当⎩⎪⎨⎪⎧k 2-3k -4=0k 2-5k -6≠0时,z 是纯虚数,解得k =4.(4)当⎩⎪⎨⎪⎧k 2-3k -4=0k 2-5k -6=0时,z =0,解得k =-1.要点三 两个复数相等例3 (1)已知x 2-y 2+2xy i =2i ,求实数x 、y 的值.(2)关于x 的方程3x 2-a2x -1=(10-x -2x 2)i 有实根,求实数a 的值.解 (1)∵x 2-y 2+2xy i =2i ,∴⎩⎪⎨⎪⎧x 2-y 2=0,2xy =2,解得⎩⎪⎨⎪⎧x =1,y =1,或⎩⎪⎨⎪⎧x =-1,y =-1.(2)设方程的实数根为x =m ,则原方程可变为 3m 2-a2m -1=(10-m -2m 2)i ,∴⎩⎪⎨⎪⎧3m 2-a 2m -1=0,10-m -2m 2=0,解得a =11或a =-715.规律方法 两个复数相等,首先要分清两复数的实部与虚部,然后利用两个复数相等的充要条件可得到两个方程,从而可以确定两个独立参数.跟踪演练3 已知M ={1,(m 2-2m )+(m 2+m -2)i},P ={-1,1,4i},若M ∪P =P ,求实数m 的值.解 ∵M ∪P =P ,∴M ⊆P ,∴(m 2-2m )+(m 2+m -2)i =-1或(m 2-2m )+(m 2+m -2)i =4i. 由(m 2-2m )+(m 2+m -2)i =-1得⎩⎪⎨⎪⎧m 2-2m =-1,m 2+m -2=0,解得m =1;由(m 2-2m )+(m 2+m -2)i =4i 得⎩⎪⎨⎪⎧m 2-2m =0,m 2+m -2=4,解得m =2.综上可知m =1或m =2.1.已知复数z =a 2-(2-b )i 的实部和虚部分别是2和3,则实数a ,b 的值分别是________. 答案 ±2,5解析 由⎩⎪⎨⎪⎧a 2=2,-2+b =3,得a =±2,b =5.2.在复数集中,方程x 2+2=0的解是x =________. 答案 ±2i3.如果z =m (m +1)+(m 2-1)i 为纯虚数,则实数m 的值为________. 答案 0解析 由题意知⎩⎪⎨⎪⎧m (m +1)=0,m 2-1≠0,∴m =0.4.下列几个命题:①两个复数相等的一个必要条件是它们的实部相等; ②两个复数不相等的一个充分条件是它们的虚部不相等; ③1-a i(a ∈R )是一个复数; ④虚数的平方不小于0;⑤-1的平方根只有一个,即为-i ; ⑥i 是方程x 4-1=0的一个根; ⑦2i 是一个无理数.其中正确命题的个数为________. 答案 4解析 命题①②③⑥正确,④⑤⑦错误.1.对于复数z =a +b i(a ,b ∈R ),可以限制a ,b 的值得到复数z 的不同情况.2.两个复数相等,要先确定两个复数的实、虚部,再利用两个复数相等的条件进行判断.一、基础达标1.如果z =(m 2-4)+(m -2)i 为纯虚数,则实数m 的值为________. 答案 -2解析 由题意知⎩⎪⎨⎪⎧m 2-4=0m -2≠0,∴m =-2.2.设a ,b ∈R .“a =0”是“复数a +b i 是纯虚数”的________条件. 答案 必要不充分解析 因为a ,b ∈R .“a =0”时“复数a +b i 不一定是纯虚数”.“复数a +b i 是纯虚数”则“a =0”一定成立.所以a ,b ∈R .“a =0”是“复数a +b i 是纯虚数”的必要不充分条件. 3.以-5+2i 的虚部为实部,以5i +2i 2的实部为虚部的新复数是________. 答案 2-2i解析 设所求新复数z =a +b i(a ,b ∈R ),由题意知:复数-5+2i 的虚部为2;复数5i +2i 2=5i +2×(-1)=-2+5i 的实部为-2,则所求的z =2-2i. 4.若(x +y )i =x -1(x ,y ∈R ),则2x +y的值为________.答案 1解析 由复数相等的充要条件知,x +y =0,∴2x +y =20=1.5.z 1=-3-4i ,z 2=(n 2-3m -1)+(n 2-m -6)i ,且z 1=z 2,则实数m =________,n =________. 答案 2 ±2解析 由z 1=z 2得⎩⎪⎨⎪⎧-3=n 2-3m -1,-4=n 2-m -6,解得⎩⎪⎨⎪⎧m =2,n =±2.6.设m ∈R ,m 2+m -2+(m 2-1)i 是纯虚数,其中i 是虚数单位,则m =________. 答案 -2解析 ⎩⎪⎨⎪⎧m 2+m -2=0m 2-1≠0⇒m =-2.7.已知(2x -y +1)+(y -2)i =0,求实数x ,y 的值. 解 ∵(2x -y +1)+(y -2)i =0,∴⎩⎪⎨⎪⎧2x -y +1=0,y -2=0.解得⎩⎪⎨⎪⎧x =12,y =2.∴实数x ,y 的值分别为12,2.二、能力提升8.若(x 3-1)+(x 2+3x +2)i 是纯虚数,则实数x 的值是________. 答案 1解析 由题意,得⎩⎪⎨⎪⎧x 3-1=0,x 2+3x +2≠0,解得x =1.9.若sin2θ-1+i(2cos θ+1)是纯虚数,则θ的值为________. 答案 2k π+π4(k ∈Z )解析 由题意,得⎩⎨⎧sin2θ-1=0,2cos θ+1≠0,解得⎩⎪⎨⎪⎧θ=k π+π4θ≠2k π±3π4(k ∈Z ),∴θ=2k π+π4,k ∈Z . 10.在给出下列几个命题中,正确命题的个数为________. ①若x 是实数,则x 可能不是复数; ②若z 是虚数,则z 不是实数;③一个复数为纯虚数的充要条件是这个复数的实部等于零; ④-1没有平方根. 答案 1解析 因实数是复数,故①错;②正确;因复数为纯虚数要求实部为零,虚部不为零,故③错;因-1的平方根为±i,故④错.11.实数m 分别为何值时,复数z =2m 2+m -3m +3+(m 2-3m -18)i 是(1)实数;(2)虚数;(3)纯虚数.解 (1)要使所给复数为实数,必使复数的虚部为0.故若使z 为实数,则⎩⎪⎨⎪⎧m 2-3m -18=0m +3≠0,解得m =6.所以当m =6时,z 为实数.(2)要使所给复数为虚数,必使复数的虚部不为0.故若使z 为虚数,则m 2-3m -18≠0,且m +3≠0,解得m ≠6且m ≠-3, 所以当m ≠6且m ≠-3时,z 为虚数.(3)要使所给复数为纯虚数,必使复数的实部为0,虚部不为0. 故若使z 为纯虚数,则⎩⎪⎨⎪⎧2m 2+m -3=0m +3≠0m 2-3m -18≠0,解得m =-32或m =1.所以当m =-32或m =1时,z 为纯虚数.12.若m 为实数,z 1=(m 2+1)+(m 3+3m 2+2m )i ,z 2=(4m +2)+(m 3-5m 2+4m )i ,那么使z 1>z 2的m 值的集合是什么?使z 1<z 2的m 的值的集合又是什么? 解 当z 1∈R 时,m 3+3m 2+2m =0, 解得m =0或m =-1或m =-2, ∴z 1=1或z 1=2或z 1=5. 当z 2∈R 时,m 3-5m 2+4m =0, 解得m =0或m =1或m =4, ∴z 2=2或z 2=6或z 2=18.上面m 的公共值为m =0,此时,z 1与z 2同时为实数,且z 1=1,z 2=2. ∴当z 1>z 2时,m 值的集合为空集;当z 1<z 2时,m 值的集合为{0}. 三、探究与创新13.如果log 12(m +n )-(m 2-3m )i>-1,如何求自然数m ,n 的值?解 因为log 12(m +n )-(m 2-3m )i>-1,所以log 12(m +n )-(m 2-3m )i 是实数,从而有错误!由①得m =0或m =3,当m=0时,代入②得n<2,又m+n>0,所以n=1;当m=3时,代入②得n<-1,与n是自然数矛盾,综上可得m=0,n=1.。

第2课时复数代数形式的加减运算及其几何意义1.理解复数代数形式的加减运算规律.2.复数的加减与向量的加减的关系.重点:正确理解复数的加减运算,复数加减运算的几何意义.难点:对比复数加减法与向量加减法的异同,从而理解复数的几何意义.实数可以进行加减运算,并且具有丰富的运算律,其运算结果仍是实数;多项式也有相应的加减运算和运算律;对于引入的复数,其代数形式类似于一个多项式,当然它也应有加减运算,并且也有相应的运算律.问题1:依据多项式的加法法则,得到复数加法的运算法则.设z1=a+b i,z2=c+d i是任意两个复数,那么(a+b i)+(c+d i)=(a+c)+(b+d)i,很明显,两个复数的和仍然是一个确定的复数.问题2:复数的加法满足交换律、结合律.即z1+z2=z2+z1,(z1+z2)+z3=z1+(z2+z3).问题3:利用向量加法讨论复数加法的几何意义向量加法遵循平行四边形法则,在直角坐标系中从横纵坐标上分析就是横纵坐标分别相加.故复数相加就是实部与虚部分别相加得到一个新的复数.问题4:如何理解复数的减法?复数减法是复数加法的逆运算.向量减法遵循三角形法则,在直角坐标系中从横纵坐标上分析就是横纵坐标分别相减.故复数相减就是实部与虚部分别相减得到一个新的复数.十八世纪末十九世纪初,著名的德国数学家高斯在证明代数基本定理“任何一元n次方程在复数集内有且仅有n个根”时,就应用并论述了卡尔丹所设想的新数,并首次引进了“复数”这个名词,把复数与平面内的点一一对应起来,创立了复平面,依赖于平面内的点或有向线段(向量)建立了复数的几何基础.这样历经300年的努力,数系从实数系到复数系的扩张才基本完成,复数才被人们广泛承认和使用.1.设z1=3-4i,z2=-2+3i,则z1-z2在复平面内对应的点位于().A.第一象限B.第二象限C.第三象限D.第四象限【解析】(3-4i)-(-2+3i)=5-7i.【答案】D2.(2-i)+(3+i)+(4+i)+(5+i)-i(其中i为虚数单位)等于().A.10B.10+2iC.14D.14+2i【解析】(2-i)+(3+i)+(4+i)+(5+i)-i=2+3+4+5+(-+1++-)i=14.【答案】C3.复数z1=9+3i,z2=-5+2i,则z1-z2=.【解析】z1-z2=(9+3i)-(-5+2i)=14+i.【答案】14+i4.已知复数z1=7-6i,z1+z2=-4+3i.(1)求z2;(2)求z1-2z2.【解析】(1)z2=(z1+z2)-z1=(-4+3i)-(7-6i)=-11+9i.(2)z1-2z2=(7-6i)-2(-11+9i)=7-6i+22-18i=29-24i.复数代数形式的加减法运算(1)z1=2+3i,z2=-1+2i,求z1+z2,z1-z2;(2)计算:(+i)+(2-i)-(-i);(3)计算:(1-2i)+(-2+3i)+(3-4i)+(-4+5i)+…+(-2019+2019i)+(2019-2019i).【方法指导】依据复数代数形式的加减运算法则以及运算律求解.【解析】(1)z1+z2=2+3i+(-1+2i)=1+5i,z1-z2=2+3i-(-1+2i)=3+i.(2)+i+(2-i)-(-i)=(+2-)+(-1+)i=1+i.(3)(法一)原式=[(1-2)+(3-4)+…+(2019-2019)+2019]+[(-2+3)+(-4+5)+…+(-2019+2019)-2019]i=(-1006+2019)+(1006-2019)i=1007-1008i.(法二)(1-2i)+(-2+3i)=-1+i,(3-4i)+(-4+5i)=-1+i,(2019-2019i)+(-2019+2019i)=-1+i,将以上各式(共1006个)相加可知:原式=1006(-1+i)+(2019-2019i)=1007-1008i.【小结】几个复数相加减,运算法则为这些复数的所有实部相加减,所有虚部相加减.第(3)小题的解法一是从整体上把握,将计算分实部和虚部进行,有机构造特殊数列的和进而求得结果.解法二是从局部入手,抓住了式中相邻两项和的特点,恰当地分组使计算得以简化.复数代数形式加减运算的几何意义在复平面内,A、B、C分别对应复数z1=1+i,z2=5+i,z3=3+3i,以AB、AC为邻边作一个平行四边形ABDC,求D点对应的复数z4及AD的长.【方法指导】根据复数加减运算的几何意义可以把复数的加减运算转化为向量的坐标运算.【解析】如图所示:对应复数z3-z1,对应复数z2-z1,对应复数z4-z1.由复数加减运算的几何意义得=+,∴z4-z1=(z2-z1)+(z3-z1),∴z4=z2+z3-z1=(5+i)+(3+3i)-(1+i)=7+3i,∴AD的长为||=|z4-z1|=|(7+3i)-(1+i)|=|6+2i|=2.【小结】利用向量进行复数的加减运算时,同样满足平行四边形法则和三角形法则.复数加减法运算的几何意义为应用数形结合思想解决复数问题提供了可能.复数加减运算的综合应用已知实数a>0,b>0,复数z1=a+5i,z2=3-b i,|z1|=13,|z2|=5,求z1+z2.【方法指导】利用两复数的模,可求得a,b的值,再求z1+z2.【解析】由题意得∴∴z1=12+5i,z2=3-4i,∴z1+z2=15+i.【小结】本题结合了复数的模与复数的加法,表面看着难,其实难度不大.复数z1=2+3i,z2=4-5i,z3=-6i,求z1+z2-z3,并说明z1+z2-z3在复平面内对应的点所在的象限.【解析】z1+z2-z3=(2+3i)+(4-5i)-(-6i)=6+4i,z1+z2-z3在复平面内对应的点为(6,4),在第一象限.如图所示,平行四边形OABC的顶点O、A、C分别表示0、3+2i、-2+4i.求:(1)表示的复数;(2)表示的复数;(3)表示的复数.【解析】(1)因为=-,所以表示的复数为-3-2i.(2)因为=-,所以表示的复数为(3+2i)-(-2+4i)=5-2i.(3)因为=+,所以表示的复数为(3+2i)+(-2+4i)=1+6i.已知实数a∈R,复数z1=a+2-3a i,z2=6-7i,若z1+z2为纯虚数,求a的值.【解析】z1+z2=(a+2-3a i)+(6-7i)=a+8-(3a+7)i,∴z1+z2为纯虚数,∴∴a=-8.1.复数z1=-3+4i,z2=6-7i,则z1+z2等于().A.3-3iB.3+3iC.-9+11iD.-9-3i【答案】A2.复数(3+i)m-(2+i)对应的点在第三象限内,则实数m的取值范围是().A.m<B.m<1C.<m<1D.m>1【解析】(3+i)m-(2+i)=(3m-2)+(m-1)i,∴点(3m-2,m-1)在第三象限,∴即m<.【答案】A3.复数z1=-2+3i,z2=4+3i,则z1-z2=.【解析】z1-z2=(-2+3i)-(4+3i)=-6.【答案】-64.已知a∈R,复数z1=2+(a+2)i,z2=a2+2a-1+3i,若z1+z2为实数,求z1-z2.【解析】z1+z2=a2+2a+1+(a+5)i,∴a∈R,z1+z2为实数,∴a+5=0,∴a=-5,∴z1=2-3i,z2=14+3i,∴z1-z2=-12-6i.在复平面内,A,B,C三点对应的复数分别为1,2+i,-1+2i.(1)求向量,,对应的复数;(2)判断∈ABC的形状.【解析】(1)=-=(2+i)-1=1+i,=-=(-1+2i)-1=-2+2i,=-=(-1+2i)-(2+i)=-3+i,所以,,对应的复数分别为1+i,-2+2i,-3+i.(2)因为||2=10,||2=8,||2=2,所以有||2=||2+||2,所以∈ABC为直角三角形.1.向量对应的复数是5-4i,向量对应的复数是-5+4i,则+对应的复数是().A.-10+8iB.10-8iC.0D.10+8i【解析】+对应的复数为5-4i+(-5+4i)=0.【答案】C2.复数z1=1-5i,z2=-2+i,则z1-z2在复平面内对应的点在().A.第一象限B.第二象限C.第三象限D.第四象限【解析】z1-z2=(1-5i)-(-2+i)=3-6i,对应的点为(3,-6),该点位于第四象限.【答案】D3.复数z1=5-12i,z2=4+7i,则z1-z2=.【解析】z1-z2=(5-12i)-(4+7i)=1-19i.【答案】1-19i4.已知z1=(3x+y)+(y-4x)i,z2=(4y-2x)-(5x+3y)i(x,y∈R).设z=z1-z2且z=13-2i,求z1,z2.【解析】z=z1-z2=(3x+y)+(y-4x)i-[(4y-2x)-(5x+3y)i]=[(3x+y)-(4y-2x)]+[(y-4x)+(5x+3y)]i=(5x-3y)+(x+4y)i,又z=13-2i,且x,y∈R,则解得故z1=(3×2-1)+(-1-4×2)i=5-9i,z2=4×(-1)-2×2-[5×2+3×(-1)]i=-8-7i.5.复平面内点A,B,C对应的复数分别为i,1,4+2i,由A→B→C→D按逆时针顺序作平行四边形ABCD,则||等于().A.5B.C.D.【解析】如图所示,∈ABCD四个顶点对应复数分别为z1=i,z2=1,z3=4+2i,z4,则有=+,=(z1-z2)+(z3-z2)=2+3i,故||==.【答案】B6.已知复数z1,z2,有|z1|=5,|z2|=12,|z1+z2|=13,则|z1-z2|为().A.8B.10C.12D.13【解析】利用向量结合复数分析可知构成的平行四边形为矩形,故对角线相等.【答案】D7.已知实数a>0,复数z1=a+2i,z2=3+5i,|z1-z2|=5,则a的值为.【解析】z1-z2=a-3-3i(a∈R),∴|z1-z2|=5,∴=25,∴a-3=±4,又a>0,∴a=7.【答案】78.已知f(z)=2z+2-i,z0=1+2i,f(z0-z1)=6-3i,z∈C,求复数z1,f(|z0+z1|).【解析】由已知得2z0-2z1+2-i=6-3i,z0=1+2i,∴2+4i-2z1+2-i=6-3i,即4+3i-2z1=6-3i,∴2z1=(4+3i)-(6-3i)=(4-6)+(3+3)i=-2+6i,∴z1=-1+3i,∴|z0+z1|=|(1+2i)+(-1+3i)|=|5i|=5,∴f(|z0+z1|)=f(5)=2×5+2-i=12-i.9.已知复数z的模为2,则|z-i|的最大值为.【解析】(法一)∴|z|=2,∴|z-i|≤|z|+|i|=2+1=3.(法二)设w=z-i,则w+i=z,∴|w+i|=|z|=2.w表示以点(0,-1)为圆心,以2为半径的圆,由图知,圆上到原点的距离以|OP|为最大,最大值是3.【答案】310.已知a,b∈R,若复数z1=a+b i,|z1|=4,z2=b-a i,求|z1+z2|,|z1-z2|.【解析】∴|z1|=4,∴=4,a2+b2=16.∴z1+z2=(a+b)+(b-a)i,∴|z1+z2|====4.∴z1-z2=(a-b)+(b+a)i,∴|z1-z2|====4.。

高中数学选修1-2《数系扩充和复数概念》教案2篇High school mathematics elective 1-2 "number system expansi on and plural concept" teaching plan高中数学选修1-2《数系扩充和复数概念》教案2篇前言:数学是研究数量、结构、变化、空间以及信息等概念的一门学科,从某种角度看属于形式科学的一种,在人类历史发展和社会生活中,数学发挥着不可替代的作用,是学习和研究现代科学技术必不可少的基本工具。
本教案根据数学课程标准的要求和教学对象的特点,将教学诸要素有序安排,确定合适的教学方案的设想和计划、并以启迪发展学生智力为根本目的。
便于学习和使用,本文档下载后内容可按需编辑修改及打印。
本文简要目录如下:【下载该文档后使用Word打开,按住键盘Ctrl键且鼠标单击目录内容即可跳转到对应篇章】1、篇章1:高中数学选修1-2《数系扩充和复数概念》教案2、篇章2:高中数学选修1-2《数系扩充和复数概念》教案篇章1:高中数学选修1-2《数系扩充和复数概念》教案教学准备教学目标知识与技能1、了解数系扩充的过程及引入复数的需要2、掌握复数的有关概念和代数符号形式、复数的分类方法及复数相等的充要条件过程与方法1、通过数系扩充的介绍,让学生体会数系扩充的一般规律2、通过具体到抽象的过程,让学生形成复数的一般形式情感态度与价值观1、体会数系的扩充过程中蕴含的创新精神与实践精神,感受人类理性思维的作用2、体会类比、分类讨论、等价转化的数学思想方法教学重难点重点:引入复数的必要性与复数的相关概念、复数的分类,复数相等的充要条件难点:虚数单位i的引进和复数的概念教学过程(一)问题引入事实上在实数范围内x和y确实不存在?为什么会这样呢?假设x和y是存在的,那么就肯定是一些不是实数的数,那么,这些数是什么呢?我们能不能解决这个问题呢?这就是我们今天要学习的内容《数系的扩充和复数的引入》(二)回顾数系的扩充历程师:其实对于这种“数不够用”的情况,我们并不陌生。

第1课时数系的扩充和复数的概念1.了解引进复数的必要性,理解并掌握虚数单位i.2.理解复数的代数形式,复数虚部与实部.3.实数集、复数集、虚数集与纯虚数集的关系.重点:掌握复数的实部与虚部;实数、复数、虚数、纯虚数与复数的代数形式的实部、虚部的关系;两复数相等的充要条件.难点:体会复数问题实数化的过程.由于解方程的需要推动了数的发展,为了使类似x+5=3的方程有解,引入了负数;为了使类似5x=3的方程有解,引入了分数;为了使类似x2=3的方程有解,引入了无理数.但引入无理数后,类似x2=-1的方程在实数范围内仍然没解.问题1:为了得到方程x2=-1的解,需引入虚数单位i,试给出虚数单位i的定义?虚数单位i满足它的平方等于-1,即i2=-1.问题2:(1)复数:形如a+b i(a,b∈R)的数叫作复数.(2)复数集:全体复数所成的集合叫作复数集,用字母C表示.(3)复数的代数形式:复数通常用字母z表示,把复数表示成a+b i(a,b∈R)的形式,其中a与b分别叫作复数的实部与虚部.(4)两个复数相等的定义:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.这就是说,如果a、b、c、d∈R,那么a+b i=c+d i∈a=c,b=d.问题3:复数z=a+b i(a,b∈R),当b=0时,复数z是实数;当b≠0时,复数z是虚数;当时,复数z是纯虚数.问题4:两复数可不可以比较大小?当两复数是实数时,两复数可以比较大小;当两复数有一个是虚数时,两复数不能比较大小,只能分析两复数相不相等.“复数”“虚数”这两个名词,都是人们在解方程时引入的.为了用公式求一元二次、三次方程的根,就会遇到求负数的平方根的问题.1545年,意大利数学家卡丹诺在《大术》一书中,首先研究了虚数,并进行了一些计算.1.“a=0”是“复数a+b i(a,b∈R)为纯虚数”的().A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解析】a=0时,a+b i(a,b∈R)可能为纯虚数,也可能为0;a+b i为纯虚数时,a=0.所以答案为B.【答案】B2.复数z=-3-10i的实部是().A.3B.-3C.-10iD.10【解析】复数z=-3-10i的实部是-3.【答案】B3.若复数z1=a+|b|i,z2=c+|d|i(a、b、c、d∈R),则z1=z2的充要条件是.【解析】z1=z2,则它们的实部与虚部分别相等,即a=c且|b|=|d|.【答案】a=c且b2=d2(或写成a=c且|b|=|d|)4.判断下列命题的真假:(1)-1的平方根只有一个;(2)i是1的4次方根;(3)i是方程x6-1=0的根;(4)方程x3-x2+x-1=0的根只有一个.【解析】(1)∵(-i)2=i2=-1,∵-i也是-1的平方根,故(1)为假命题.(2)∵i2=-1,∵i4=i2·i2=(-1)2=1,故(2)为真命题.(3)i6-1=i2·i2·i2-1=(-1)3-1=-2≠0,故(3)为假命题.(4)由x3-x2+x-1=0得(x2+1)(x-1)=0,则x2=-1或x=1,即x=±i或x=1都是方程x3-x2+x-1=0的根,故(4)为假命题.对复数概念的理解已知下列命题:①复数a+b i不是实数;②两个复数不能比较大小;③若(x2-4)+(x2+3x+2)i是纯虚数,其中x∈R,则x=±2;④若复数z=a+b i,则当且仅当b≠0时,z为虚数;⑤若a+b i=c+d i,则a=c且b=d.其中真命题的个数是().A.0B.1C.3D.4【方法指导】根据复数的有关概念来判断命题的真假.【解析】①是假命题,因为当a∈R且b=0时,a+b i是实数.②是假命题,因为两个复数都是实数时,可以比较大小.③是假命题,因为由纯虚数的条件得解得x=2.④是假命题,因为没有强调a,b∈R.⑤是假命题,因为没有强调,a,b,c,d∈R这一重要条件,故选A.【答案】A【小结】对于概念的理解注意一些小细节,比如a+b i中要求a∈R,b∈R.复数概念的应用z=+(m2+5m+6)i,当实数m为何值时,(1)z是实数;(2)z是虚数;(3)z是纯虚数?【方法指导】根据复数的分类方式将问题转化为求实部和虚部应满足什么条件.【解析】(1)若z是实数,则得m=-2.(2)若z是虚数,则得m≠-2且m≠-3且m∈R.(3)若z是纯虚数,则得m=3.【小结】①本题考查复数集的分类,给出的是复数的标准代数形式即z=a+b i(a,b∈R),若不然,应先将其化为标准形式,再根据满足的条件去解;②解题中应时刻注意使式子有意义.复数相等的充要条件(1)已知(2x-1)+i=y-(3-y)i,x,y∈R,求x与y.(2)设z1=1+sin θ-icos θ,z2=+(cos θ-2)i,若z1=z2,求θ.【方法指导】确定两复数的实部与虚部,利用两复数相等的定义列方程组,解方程组.【解析】(1)根据复数相等的充要条件,得方程组解得(2)由已知,得故解得θ=2kπ(k∈Z).【小结】复数问题实数化是解决复数相等问题最基本的也是最重要的思想方法,转化过程主要依据复数相等的充要条件.基本思路是:①等式两边整理为a+b i(a,b∈R)的形式;②由复数相等的充要条件可以得到由两个实数等式所组成的方程组;③解方程组,求出相应的参数.下列命题中正确的有.①若z=a+b i(a,b∈R),则当a=0,b≠0时,z为纯虚数;②若(z1-z2)2+(z2-z3)2=0,则z1=z2=z3;③若实数a与a i对应,则实数集与纯虚数集一一对应.【解析】①正确.②错误,只有当z1,z2,z3∈R时才成立;若z1=1,z2=0,z3=i也满足题意.③错误,若a=0,则0·i=0不再是纯虚数.【答案】①复数z=log2(x2-3x-3)+ilog2(x-3),当x为何实数时:(1)z∈R;(2)z为虚数;(3)z为纯虚数?【解析】(1)因为一个复数是实数的充要条件是虚部为零,所以有由②得x=4,经验证满足①.所以当x=4时,z∈R.(2)因为一个复数是虚数的充要条件是虚部非零,所以有解得即<x<4或x>4.所以当<x<4或x>4时,z为虚数.(3)因为一个复数是纯虚数时其实部为零且虚部不为0,所以有解得方程无解,所以复数z不可能是纯虚数.关于a的方程是a2-a tan θ-2-(a+1)i=0,若方程有实数根,求锐角θ和实数根.【解析】设实数根是a,则a2-a tan θ-2-(a+1)i=0,∵a,tan θ∈R,∵∵a=-1且tan θ=1,又0<θ<,∵θ=,a=-1.1.设集合C={复数},A={实数},B={纯虚数},若全集S=C,则下列结论中正确的是().A.A∈B=CB.∈S A=BC.A∩(∈S B)=∈D.B∩(∈S A)=B【答案】D2.如果复数z=(a2-3a+2)+(a-1)i为纯虚数,则实数a的值为().A.1或2B.1C.2D.不存在【解析】由a2-3a+2=0和a-1≠0,得a=2.【答案】C3.已知复数z=3-2i,则复数z的实部与虚部的积是.【解析】z=3-2i的实部和虚部分别为3,-2,故答案为-6.【答案】-64.实数m为何值时,复数z=(m2-8m+15)+(m2+3m-28)i在复平面内对应的点:(1)位于第四象限;(2)在x轴的负半轴上?【解析】(1)由已知得∵∵-7<m<3.∵当m∈(-7,3)时,z对应的点在第四象限.(2)由已知得解得m=4,即m=4时,z对应的点在x轴的负半轴上.(2019年·上海卷)设m∈R,m2+m-2+(m2-1)i是纯虚数,其中i是虚数单位,则m=.【解析】∵m2+m-2+(m2-1)i是纯虚数,∵∵m=-2.【答案】-21.复数z=-2+3i的虚部是().A.-2B.2C.3D.3i【解析】复数z=-2+3i的虚部是3.【答案】C2.若复数(2x2+5x+2)+(x2+x-2)i为虚数,则实数x满足().A.x=-B.x=-2或-C.x≠-2D.x≠1且x≠-2【解析】由题意得x2+x-2≠0,∵x≠1且x≠-2.【答案】D3.已知集合M={1,2,(m2-3m-1)+(m2-5m-6)i},集合N={-1,3},若M∩N={3},则实数m的值为.【解析】由题设知3∈M,∵m2-3m-1+(m2-5m-6)i=3.∵即∵m=-1.【答案】-14.设复数z=ab+(a2+b2)i(a、b∈R),a、b分别满足什么条件时,z是实数、虚数、纯虚数?【解析】当a、b同时为0时,z为实数;当a、b不全为0时,z是虚数;当a、b有且仅有一个为0时,z为纯虚数.5.如果(x+y)i=x-1,则实数x、y的值分别为().A.x=1,y=-1B.x=0,y=-1C.x=1,y=0D.x=0,y=0【解析】根据复数相等的充要条件,可知解得【答案】A6.下列命题中,正确命题的个数是().①若x,y∈C,则x+y i=1+i的充要条件是x=y=1;②若a,b∈R且a>b,则a+i>b+i;③若x2+y2=0,则x=y=0;④一个复数为纯虚数的充要条件是这个复数的实部等于零;⑤-1没有平方根;⑥若a∈R,则(a+1)i是纯虚数.A.0B.1C.2D.3【解析】由于x,y∈C,所以x+y i不一定是复数的代数形式,不符合复数相等的充要条件,①是假命题.由于两个虚数不能比较大小,∵②是假命题.当x=1,y=i时,x2+y2=0成立,∵③是假命题.因为复数为纯虚数要求实部为零,虚部不为零,故④错.因为-1的平方根为±i,故⑤错.当a=-1时,(a+1)i是实数0,故⑥错.【答案】A7.复数z=(a2+2a-3)+(a2-1)i(a∈R)为纯虚数,则复数z的虚部为.【解析】复数z=(a2+2a-3)+(a2-1)i(a∈R)为纯虚数,∵∵∵a=-3,∵a2-1=8,∵复数z的虚部为8.【答案】88.已知m∈R,复数z=+(m2+2m-3)i,当m为何值时:(1)z∈R;(2)z是虚数;(3)z是纯虚数;(4)z=+4i?【解析】(1)m需满足解得m=-3.(2)m需满足m2+2m-3≠0且m-1≠0,解得m≠1且m≠-3.(3)m需满足解得m=0或m=-2.(4)m需满足解得m∈∈.9.已知m、n∈R,复数z1=m2+2n-3+(m+n)i,z2=2m-3n+2+(2m-n)i,若z1=z2,则m+n=.【解析】∵z1=z2,∵∵∵n=1或n=-,m+n=3n,∵m+n的值为3或-.【答案】3或-10.已知复数z1=sin 2x+λi,z2=m+(m-cos 2x)i(λ,m,x∈R),且z1=z2.若λ=0且0<x<π,求x的值.【解析】∵z1=z2,∵∵λ=sin 2x-cos 2x.若λ=0,则sin 2x-cos 2x=0,得tan 2x=.∵0<x<π,∵0<2x<2π,∵2x=或2x=,∵x=或.。
第三章 数系的扩充与复数的引入【课题】:3.1.1 数系的扩充和复数的概念【学情分析】:从小学接触自然数到扩充至整数范围,进入初中阶段后学生认识到数系从整数到有理数再到实数的第二次扩充.因为现实的需要,高中阶段要进一步实现从实数系到复数系的第三次扩充.学生初次接触复数,会产生一种“虚无缥缈”的感觉.所以要有意识地将实数与复数进行类比学习,学会复数问题向实数问题转化的方法.【教学目标】:(1)知识目标:理解复数产生的必然性、合理性;掌握复数的代数表示形式;掌握复数系下的数的分类. (2)过程与方法目标:从为了解决012=+x 这样的方程在实数系中无解的问题出发,设想引入一个新数i,使i 是方程012=+x 的根.到将i 添加到实数集中去,使新引入的数i 和实数之间能象实数系那样进行加、乘运算;掌握类比的方法,转化的方法。
(3)情感与能力目标:通过介绍数系扩充的简要进程,使同学们感受人类理性思维对数学的发展所起的重要作用,体会数与现实世界的联系。
【教学重点】:复数的概念及其分类。
【教学难点】:虚数单位i 的引入。
【教学突破点】:从解012=+x 方程的需要,引入虚数单位i.及虚数单位i 与实数的融合。
【教法、学法设计】:讲授、练习相结合。
【课前准备】:课件;0)32()43)(2(;217)5()23)(1(=++--=-++i y x i i y x y x .0,,3,2222,55i i i --+-,)43(434.322i n n m m n z -++---=已知复数.,,)2(;,,)1(是实数取什么整数值时是纯虚数取什么整数值时z n m z n mA 组1.写出下列复数的实部与虚部:2.求适合下列各方程的实数:的值和y xB 组1.,,,,().,...()C R M P A PR C B MR CC PM D MR Cφ⊂≠===对于复数集实数集虚数集纯虚数集下列关系正确的是11222.23(log )log 2,___________.z x x x x i x ⎡⎤=--+--⎣⎦使复数是虚部为正数的非纯虚数则实数的取值范围是参考答案:A 组.1.五个复数的实部与虚部依次为:.0,0;1,0;0,3;22,22;5,5--- 2..23,34)2(;7,1).1(-====y x y x 3.;4,1,,4).1(≠-≠∈=m m Z m n;4,1,,14).1(≠-≠∈=-=m m Z m n n 或 B 组. 1.A; 2.B; 3.),3()3,2()41,0(+∞ .第三章数系的扩充与复数的引入【课题】:3.1.2 复数的几何意义【学情分析】:教学对象是高二的学生,学生已经学过代数、解析几何的相关知识,所以本节课要求学生通过类比实数的几何意义自己探索复数的几何意义,由于学生已经学过平面向量及其几何表示、坐标表示,得到用平面向量来表示复数就比较容易了.【教学目标】:(1)知识与技能:了解复数的几何意义,会用复平面的点和向量来表示复数;(2)过程与方法:在解决问题中,通过数形结合的思想方法,加深对复数几何意义的理解;(3)情感态度与价值观:培养学生用联系的观点分析、解决问题的能力。
3.1.1 数系的扩充与复数的概念教学要求: 理解数系的扩充是与生活密切相关的,明白复数及其相关概念。
教学重点:复数及其相关概念,能区分虚数与纯虚数,明白各数系的关系。
教学难点:复数及其相关概念的理解教学过程:一、复习准备:1. 提问:N 、Z 、Q 、R 分别代表什么?它们的如何发展得来的?(让学生感受数系的发展与生活是密切相关的)2.判断下列方程在实数集中的解的个数(引导学生回顾根的个数与∆的关系):(1)2340x x --= (2)2450x x ++= (3)2210x x ++= (4)210x +=3. 人类总是想使自己遇到的一切都能有合理的解释,不想得到“无解”的答案。
讨论:若给方程210x +=一个解i ,则这个解i 要满足什么条件?i 是否在实数集中?实数a 与i 相乘、相加的结果应如何?二、讲授新课:1. 教学复数的概念:①定义复数:形如a bi +的数叫做复数,通常记为z a bi =+(复数的代数形式),其中i 叫虚数单位,a 叫实部,b 叫虚部,数集{}|,C a bi a b R =+∈叫做复数集。
出示例1:下列数是否是复数,试找出它们各自的实部和虚部。
23,84,83,6,,29,7,0i i i i i i +-+--规定:a bi c di a c +=+⇔=且b=d ,强调:两复数不能比较大小,只有等与不等。
②讨论:复数的代数形式中规定,a b R ∈,,a b 取何值时,它为实数?数集与实数集有何关系?③定义虚数:,(0)a bi b +≠叫做虚数,,(0)bi b ≠叫做纯虚数。
④ 数集的关系:0,0)0)0,0)Z a a ⎧⎪≠≠⎧⎨≠⎨⎪≠=⎩⎩实数 (b=0)复数一般虚数(b 虚数 (b 纯虚数(b 上述例1中,根据定义判断哪些是实数、虚数、纯虚数?2.出示例题2:(引导学生根据实数、虚数、纯虚数的定义去分析讨论)练习:已知复数a bi +与3(4)k i +-相等,且a bi +的实部、虚部分别是方程2430x x --=的两根,试求:,,a b k 的值。
2017-2018版高中数学第3章数系的扩充与复数的引入章末复习课学案苏教版选修1-2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017-2018版高中数学第3章数系的扩充与复数的引入章末复习课学案苏教版选修1-2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017-2018版高中数学第3章数系的扩充与复数的引入章末复习课学案苏教版选修1-2的全部内容。
第3章数系的扩充与复数的引入学习目标 1.掌握复数的代数表示形式及其有关概念.2。
掌握复数的模的概念及其计算公式,会用复数模的几何意义解题。
3.理解复数加减法的几何意义,并能进行复数的加减乘除运算.知识点一复数的有关概念1.定义:形如a+b i(a,b∈R)的数叫做复数,其中a叫做________,b叫做________.(i为虚数单位)2.分类:满足条件(a,b为实数)复数的分类a+b i为实数⇔________ a+b i为虚数⇔________a+bi为纯虚数⇔________________3。
复数相等:a+bi=c+d i⇔______________________(a,b,c,d∈R).4.共轭复数:a+b i与c+d i共轭⇔________________(a,b,c,d∈R).5.模:向量错误!的模叫做复数z=a+b i的模,记作______________或________,即|z|=|a+b i|=______________(a,b∈R).知识点二复数的几何意义复数z=a+bi与复平面内的点____________及平面向量OZ,→=(a,b)(a,b∈R)是一一对应关系.知识点三复数的运算1.运算法则:设z1=a+bi,z2=c+d i,a,b,c,d∈R2.几何意义:复数加减法可按向量的平行四边形法则或三角形法则进行.如图给出的平行四边形OZ1ZZ2可以直观地反映出复数加减法的几何意义,即错误!=__________________,错误!=________________.类型一分类讨论思想的应用例1 实数k为何值时,复数(1+i)k2-(3+5i)k-2(2+3i)满足下列条件?(1)是实数;(2)是虚数;(3)是纯虚数.反思与感悟往往以复数分类为载体考查分类讨论思想,复数z=a+bi(a,b∈R)错误!其中纯虚数中“b≠0”这个条件易被忽略,学习中应引起足够的注意.跟踪训练1(1)设i是虚数单位,复数1+a i2-i为纯虚数,则实数a为________.(2)若复数(a2-a-2)+(|a-1|-1)i(a∈R)不是纯虚数,则________.类型二复数的四则运算例2 (1)计算:错误!+(错误!)3 204;(2)已知复数z满足(z+错误!)-3z·错误!i=1-3i,求复数z.反思与感悟(1)进行复数乘除运算,注意i的性质的活用.(2)设出复数的代数形式,转化为实数运算.(3)设ω=-\f(1,2)±错误!i,ω3=1,ω2+ω+1=0,ω2=错误!。
第3章 数系的扩充与复数的引入1.虚数单位i(1)i 2=-1(即-1的平方根是±i).(2)实数可以与i 进行四则运算,进行运算时原有的加、乘运算律仍然成立. (3)i 的幂具有周期性:i 4n=1,i 4n +1=i ,i4n +2=-1,i4n +3=-i(n ∈N *),则有i n +in +1+in +2+in +3=0(n ∈N *).2.复数的分类复数(z =a +b i ,a ,b ∈R )⎩⎪⎨⎪⎧实数(b =0)虚数(b ≠0)⎩⎪⎨⎪⎧纯虚数(a =0,b ≠0)非纯虚数(a ≠0,b ≠0) 3.共轭复数的性质设复数z的共轭复数为z,则(1)z·z=|z|2=|z|2;(2)z为实数⇔z=z,z为纯虚数⇔z=-z.4.复数的几何意义5.复数相等的条件(1)代数形式:复数相等的充要条件为a+b i=c+d i(a,b,c,d∈R)⇔a=c,b=d.特别地,a+b i=0(a,b∈R)⇔a=b=0.注意:两复数不是实数时,不能比较大小.(2)几何形式:z1,z2∈C,z1=z2⇔对应点Z1,Z2重合⇔OZ1―→与OZ2―→重合.6.复数的运算(1)加法和减法运算:(a+b i)±(c+d i)=(a±c)+(b±d)i(a,b,c,d∈R).(2)乘法和除法运算:复数的乘法按多项式相乘进行运算,即(a+b i)(c+d i)=(ac-bd)+(ad+bc)i;复数除法是乘法的逆运算,其实质是分母实数化.(考试时间:120分钟试卷总分:160分)一、填空题(本大题共14小题,每小题5分,共70分)1.(新课标全国卷Ⅱ改编)设复数z1,z2在复平面内的对应点关于虚轴对称,z1=2+i,则z1z2=________.解析:∵z1=2+i在复平面内对应点(2,1),又z1与z2在复平面内的对应点关于虚轴对称,则z2的对应点为(-2,1),则z2=-2+i,∴z1z2=(2+i)(-2+i)=i2-4=-5.答案:-52.(山东高考改编)若a-i与2+b i互为共轭复数,则(a+b i)2=________.解析:根据已知得a=2,b=1,所以(a+b i)2=(2+i)2=3+4i.答案:3+4i3.若复数z 满足 (3-4i)z =|4+3i|,则z 的虚部为________. 解析:∵(3-4i)z =|4+3i|,∴z =|4+3i|3-4i =5(3+4i )(3-4i )(3+4i )=3+4i 5=35+45i ,∴z 的虚部是45.答案:454.已知m1+i =1-n i ,其中m ,n 是实数,i 是虚数单位,则m +n i 等于________.解析:m1+i=1-n i ,所以m =(1+n )+(1-n )i ,因为m ,n ∈R , 所以⎩⎪⎨⎪⎧1-n =0,1+n =m ,所以⎩⎪⎨⎪⎧n =1,m =2,即m +n i =2+i.答案:2+i5.定义运算⎪⎪⎪⎪⎪⎪a b cd =ad -bc ,则满足条件⎪⎪⎪⎪⎪⎪1 -1z z i =4+2i 的复数z 为________. 解析:⎪⎪⎪⎪⎪⎪1 -1z z i =z i +z ,设z =x +y i ,∴z i +z =x i -y +x +y i =x -y +(x +y )i =4+2i , ∴⎩⎪⎨⎪⎧x -y =4,x +y =2,∴⎩⎪⎨⎪⎧x =3,y =-1. ∴z =3-i. 答案:3-i6.在复平面内,复数2-i 1+i 对应的点位于第________象限.解析:2-i 1+i =(2-i )(1-i )(1+i )(1-i )=1-3i 12-i 2=12-32i ,对应的点位于第四象限. 答案:四7.5(4+i )2i (2+i )=________. 解析:5(4+i )2i (2+i )=5(15+8i )-1+2i =5(15+8i )(-1-2i )(-1)2+22=1-38i. 答案:1-38i8.设a 是实数,且a 1+i +1+i2是实数,则a 等于________.解析:∵a 1+i +1+i 2=a (1-i )2+1+i 2=⎝ ⎛⎭⎪⎫a 2+12+(1-a )2i 是实数,∴1-a2=0,即a =1. 答案:19.复数z 满足方程⎪⎪⎪⎪⎪⎪z +21+i =4,那么复数z 的对应点P 组成图形为________. 解析:⎪⎪⎪⎪⎪⎪z +21+i =|z +(1-i)|=|z -(-1+i)|=4. 设-1+i 对应的点为C (-1,1),则|PC |=4,因此动点P 的轨迹是以C (-1,1)为圆心,4为半径的圆.答案:以(-1,1)为圆心,以4为半径的圆10.已知集合M ={1,2,z i},i 为虚数单位,N ={3,4},M ∩N ={4},则复数z =________. 解析:由M ∩N ={4},知4∈M , 故z i =4,∴z =4i =-4i.答案:-4i11.若复数z 满足|z |-z =101-2i ,则z =________.解析:设z =a +b i(a ,b ∈R ),∴|z |-z =a 2+b 2-(a -b i)=a 2+b 2-a +b i , 101-2i =10(1+2i )(1-2i )(1+2i )=10(1+2i )12+22=2+4i , ∴⎩⎨⎧a 2+b 2-a =2,b =4,解得⎩⎪⎨⎪⎧a =3,b =4.∴z =3+4i. 答案:3+4i12.若OA =3i +4,OB =-1-i ,i 是虚数单位,则AB =________.(用复数代数形式表示)解析:由于OA =3i +4,OB =-1-i ,i 是虚数单位, 所以AB =OB -OA =(-1-i)-(3i +4)=-5-4i. 答案:-5-4i13.复数z 满足|z +1|+|z -1|=2,则|z +i +1|的最小值是________.解析:由|z +1|+|z -1|=2,根据复数减法的几何意义可知,复数z 对应的点到两点(-1,0)和(1,0)的距离和为2,说明该点在线段y =0(x ∈[-1,1])上,而|z +i +1|为该点到点(-1,-1)的距离,其最小值为1.答案:114.已知关于x 的方程x 2+(1+2i)x -(3m -1)=0有实根,则纯虚数m 的值是________. 解析:方程有实根,不妨设其一根为x 0,设m =a i 代入方程得x 20+(1+2i)x 0-(3a i -1)i =0,化简得,(2x 0+1)i +x 20+x 0+3a =0,∴⎩⎪⎨⎪⎧2x 0+1=0,x 20+x 0+3a =0,解得a =112,∴m =112i.答案:112i二、解答题(本大题共6小题,共90分) 15.(本小题满分14分)计算:(1)(2+i )(1-i )21-2i ;(2)4+5i (5-4i )(1-i ).解:(1)(2+i )(1-i )21-2i =(2+i )(-2i )1-2i =2(1-2i )1-2i =2.(2)4+5i (5-4i )(1-i )=(5-4i )i(5-4i )(1-i ) =i 1-i =i (1+i )(1-i )(1+i )=i -12=-12+12i.16.(本小题满分14分)求实数k 为何值时,复数(1+i)k 2-(3+5i)k -2(2+3i)分别是:(1)实数;(2)虚数;(3)纯虚数;(4)零.解:由z =(1+i)k 2-(3+5i)k -2(2+3i)=(k 2-3k -4)+(k 2-5k -6)i.(1)当k 2-5k -6=0时,z ∈R , ∴k =6或k =-1.(2)当k 2-5k -6≠0时,z 是虚数,即k ≠6且k ≠-1.(3)当⎩⎪⎨⎪⎧k 2-3k -4=0,k 2-5k -6≠0时,z 是纯虚数,∴k =4.(4)当⎩⎪⎨⎪⎧k 2-3k -4=0,k 2-5k -6=0时,z =0,解得k =-1.综上,当k =6或k =-1时,z ∈R . 当k ≠6且k ≠-1时,z 是虚数.当k =4时,z 是纯虚数,当k =-1时,z =0.17.(本小题满分14分)已知复数z 满足|z |=1+3i -z ,求(1+i )2(3+4i )22z 的值.解:设z =a +b i(a ,b ∈R ),由|z |=1+3i -z , 得a 2+b 2-1-3i +a +b i =0,则⎩⎨⎧a 2+b 2+a -1=0,b -3=0,所以⎩⎪⎨⎪⎧a =-4,b =3,所以z =-4+3i.则(1+i )2(3+4i )22z =2i (3+4i )22(-4+3i )=2(-4+3i )(3+4i )2(-4+3i )=3+4i.18.(本小题满分16分)已知ω=-12+32i.(1)求ω2及ω2+ω+1的值;(2)若等比数列{a n }的首项为a 1=1,公比q =ω,求数列{a n }的前n 项和S n . 解:(1)ω2=⎝ ⎛⎭⎪⎫-12+32i 2=14-32i -34=-12-32i.ω2+ω+1=⎝ ⎛⎭⎪⎫-12-32i +⎝ ⎛⎭⎪⎫-12+32i +1=0.(2)由于ω2+ω+1=0, ∴ωk +2+ωk +1+ωk =ωk (ω2+ω+1)=0,k ∈Z .∴S n =1+ω+ω2+…+ωn -1=⎩⎪⎨⎪⎧0, n =3k ,1, n =3k +1,1+ω, n =3k +2,∴S n=⎩⎪⎨⎪⎧0, n =3k (k ∈Z ),1, n =3k +1(k ∈Z ),12+32i , n =3k +2(k ∈Z ).19.(本小题满分16分)已知z =a -i1-i(a ∈R 且a >0),复数ω=z (z +i)的虚部减去它的实部所得的差等于32,求复数ω的模.解:把z =a -i1-i (a >0)代入ω中,得ω=a -i 1-i ⎝ ⎛⎭⎪⎫a -i 1-i +i =a +12+a (a +1)2i. 由a (a +1)2-a +12=32,得a 2=4. 又a >0,所以a =2. 所以|ω|=|32+3i|=325.20.(本小题满分16分)已知复数z 满足|z |=2,z 2的虚部为2. (1)求复数z ;(2)设z ,z 2,z -z 2在复平面内对应的点分别为A ,B ,C ,求△ABC 的面积. 解:(1)设z =a +b i(a ,b ∈R ),由已知条件得:a 2+b 2=2,z 2=a 2-b 2+2ab i , 所以2ab =2.所以a =b =1或a =b =-1,即z =1+i 或z =-1-i. (2)当z =1+i 时,z 2=(1+i)2=2i ,z -z 2=1-i , 所以点A (1,1),B (0,2),C (1,-1),所以S △ABC =12|AC |×1=12×2×1=1;当z =-1-i 时,z 2=(-1-i)2=2i ,z -z 2=-1-3i. 所以点A (-1,-1),B (0,2),C (-1,-3), 所以S △ABC =12|AC |×1=12×2×1=1.即△ABC 的面积为1.。