[精品]2014-2015学年湖南省长沙市浏阳市洞阳中学七年级(上)数学期中试卷及参考答案

2015年湘教版七年级数学上册期中试题（带答案）一、选择题（每小题3分，共10分）6m3．在﹣2，+3.5，0，，﹣0.7，11中．负分数有（）4．﹣的相反数是（）B娄底市某景区接待游客约为倍大﹣）之后，得到的结果是（A．若x=y，则x+5=y+5 B若a=b，则ac=bc，则11． |﹣2014|= ．12．比较两个数的大小：﹣2．（用“＜、=、＞”符号填空）13．计算：（﹣）×3=．14．计算：﹣3×2+（﹣2）2﹣5= ．15．当x=1时，代数式x2+1= ．16．单项式﹣5x2y的系数是．17．请你写出一个二次三项式：．18．已知x=3是关于x的方程2x﹣a=1的解，则a的值是19．服装店销售某款服装，一件服装的标价为300元，若按标价的八折销售，仍可获利20%，则这款服装每件的进价是元．20．如图，自行车的链条每节长为2.5cm，每两节链条相连接部分重叠的圆的直径为0.8cm，如果某种型号的自行车链条共有60节，则这根链条没有安装时的总长度为 cm。

三、解答题（每小题4分，共28分）21．解方程：3（x+4）=x．22．解方程：．23．先化简，再求值：3（2x2﹣y2）﹣2（3y2﹣2x2）．其中x=1，y=2。

24．计算：（﹣）÷（﹣1）÷（﹣2）2．25．如果规定符号“﹡”的意义是a ﹡b=，求2﹡（﹣3）的值．26．计算：[（﹣3）2﹣（﹣5）2]÷（﹣8）+（﹣3）×（﹣1）27．如图：a ，b 在数轴上如图，化简︱a+b ︱+︱a-b ︱三、应用题（每小题6分，共12分）28．江南生态食品加工厂收购了一批质量为10000千克的某种山货，根据市场需求对其进行粗加工和精加工处理，已知精加工的该种山货质量比粗加工的质量3倍还多2000千克．求粗加工的该种山货质量．0 b a22. 解：方程两边同时乘以6，得：3（1﹣x）=2（4x﹣1）﹣6，去括号得：3﹣3x=8x﹣2﹣6，移项得：8x+3x=3+2+6，合并同类项得：11x=11，系数化为1，得：x=1．23. 解：3（2x2﹣y2）﹣2（3y2﹣2x2）=6x2﹣3y2﹣6y2+4x2=10x2﹣9y2．=-2625.626. 解：原式=（9﹣25）÷（﹣8）+3，=（﹣16）÷（﹣8）+3，=2+3，=5．27.-2b28. 解：设粗加工的该种山货质量为x千克，根据题意，得x+（3x+2000）=10000．解得x=2000．答：粗加工的该种山货质量为2000千克．29.(略)。

七年级（上）期中数学试卷学校:___________姓名：___________班级：___________考号：___________一、选择题（本大题共8小题，共24.0分）1.已知等式x=y，a、b、m、n为任意有理数，则下列等式中，不一定成立的是（）A. x+a=y+aB. x−m=y−mC. −xn=−ynD. xb =yb2.下面说法正确的是（）A. 相反数等于它本身的数只有0B. 绝对值等于它本身的数只有0C. 倒数等于它本身的数只有1D. 任何有理数都有倒数3.对于由四舍五入法得到的近似数8.8×104，下列说法正确的是（）A. 精确到十分位B. 精确到个位C. 精确到千位D. 精确到万位4.下面计算正确的是（）A. 3x2+3x2=6x4B. 3a−a=3C. x3−x2=xD. xy−2xy=−xy5.下列说法正确的是（）A. 13πx2的系数是13B. −2πx2y的次数是3，系数是−2πC. x2y的系数是0D. 3x2y的次数是2，系数是36.在-（-8），（-1）2017，-32，-|-1|，-|0|，-225中，负数共有（）A. 4个B. 3个C. 2个D. 1个7.下列是一元一次方程的是（）A. 2x−3y=6B. x2=5x+1 C. x2−5x+6=0D. 3x+1=08.运算※按下表定义，例如3※2=1，那么（2※4）※（1※3）=（）※123411234214133314244321A. 1B. 2C. 3D. 4二、填空题（本大题共6小题，共12.0分）9.若x=1是方程1-4kx=0的解，则k=______．10.收入870元记作+870元，则支出910元记作______元．11.多项式−15xy2−4x3y+2是______次______项式．12.|-2|的相反数是______．13.如图，圆的周长为4个单位长，数轴每个数字之间的距离为1个单位，在圆的4等分点处分别标上0、1、2、3，先让圆周上表示数字0的点与数轴上表示-1的点重合，再将数轴按逆时针方向环绕在该圆上（如圆周上表示数字3的点与数轴上表示-2的点重合…），则数轴上表示-2013的点与圆周上表示数字______的点重合．14.两个单项式34a3b2m与单项式−23a n b6的和是一个单项式，那么m+n=______．三、计算题（本大题共4小题，共27.0分）15.化简：（x2-y2）-3（x2-2y2）．16.计算：（1）−5−(−11)+213−(−23)；（2）(12−23)×12+32．17.已知：a与b互为相反数，c与d互为倒数，当|x|=2时，求代数式99a+99b-（-cd）2017+x2的值．18.先化简，再求值：3x2y-[2x2y-（xy-x2y）-x2]-xy，其中x=3，y=−11734．四、解答题（本大题共4小题，共34.0分）19.某同学在对方程2x−13=x+a3−2去分母时，方程右边的-2没有乘3，这时方程的解为x=2，试求a的值，并求出原方程正确的解．20.解关于x的方程：（1）12-2（x-5）=1-5x；（2）1-y−32=2y+1321.一辆货车从百货大楼出发负责送货，向东走了4千米到达小明家，继续向东走了1.5千米到达小红家，然后向西走了8.5千米到达小刚家，最后返回百货大楼．（1）以百货大楼为原点，向东为正方向，1个单位长度表示1千米，请你在数轴上标出小明．小红．小刚家的位置．（小明家用点A表示，小红家用点B表示，小刚家用点C表示）（2）小明家与小刚家相距多远？（3）若货车每千米耗油0.5升，那么这辆货车此次送货共耗油多少升？22.已知数a、b、c在数轴上的位置如图所示，（1）用“＞”“＜”“=”填空：a______0；b______0；c______0；（2）用“＞”“＜”“=”填空：a+c______0；a+b______0；c-b______0；（3）化简：|a+c|-|a+b|-|c-b|．答案和解析1.【答案】D【解析】解：A、根据等式的性质1．x=y两边同时加a，得x+a=y+a，故一定成立；B、根据等式的性质1，x=y两边同时减m，得x-m=y-m，故一定成立；C、根据等式2，x=y两边同时乘以-n，得-xn=-yn，故一定成立；D、根据等式性质2，等式两边都除以b时，应加条件b≠0，故不一定成立．故选：D．利用等式的性质对每个等式进行变形即可找出答案．本题主要考查了等式的性质．等式性质1：等式的两边都加上或者减去同一个数或同一个整式，所得结果仍是等式；等式性质2：等式的两边都乘以或者除以同一个数（除数不为零），所得结果仍是等式．2.【答案】A【解析】解：A、只有0的相反数等于它本身0，故本选项正确；B、如|2|=2，等于它本身，故本选项错误；C、1、-1的倒数都等于它本身，故本选项错误；D、0没有倒数，故本选项错误；故选：A．关键相反数、倒数、绝对值的定义求出即可．本题考查了倒数、相反数、绝对值的应用，主要考查学生的理解能力和计算能力．3.【答案】C【解析】解：8.8×104精确到千位．故选：C．根据近似数的精确度进行判断．本题考查了近似数和有效数字：近似数与精确数的接近程度，可以用精确度表示．一般有，精确到哪一位，保留几个有效数字等说法．从一个数的左边第一个不是0的数字起到末位数字止，所有的数字都是这个数的有效数字．4.【答案】D【解析】解：A、3x2+3x2=6x2，故此选项错误；B、3a-a=2a，故此选项错误；C、x3-x2，无法计算，故此选项错误；D、xy-2xy=-xy，正确．故选：D．直接利用合并同类法则计算得出答案．此题主要考查了合并同类项，正确掌握运算法则是解题关键．5.【答案】B【解析】解：A、πx2的系数是，故此选项错误；B、-2πx2y的次数是3，系数是-2π，故此选项正确；C、x2y的系数是1，故此选项错误；D、3x2y的次数是3，系数是2，故此选项错误；故选：B．根据单项式的系数、次数定义：单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数，即可选出正确答案．此题主要考查了单项式的次数与系数，关键是熟练掌握定义，注意π是一个常数，不是字母．6.【答案】A【解析】【分析】直接利用有理数的乘方的性质以及绝对值的性质分别化简得出答案．此题主要考查了有理数的乘方的性质以及绝对值的性质，正确化简各数是解题关键．【解答】解：-（-8）=8，（-1）2017=-1，-32=-9，-|-1|=-1，-|0|=0，-225，负数共有4个．故选A.7.【答案】B【解析】解：A、2x-3y=6，是二元一次方程，故此选项错误；B、=5x+1，是一元一次方程，故此选项正确；C、x2-5x+6=0，是一元二次方程，故此选项错误；D、+1=0，是分式方程，故此选项错误；故选：B．直接利用一元一次方程的定义分析得出答案．此题主要考查了一元一次方程的定义，正确把握定义是解题关键．8.【答案】D【解析】解：∵3※2=1，∴运算※就是找到第三列与第二行相结合的数，∴（2※4）=3，（1※3）=3，∴3※3=4．故选：D．根据题目提供的运算找到运算方法，即：3※2=1就是第三列与第二行所对应的数，按此规律计算出（2※4）※（1※3）的结果即可．本题考查了有理数的混合运算，学生们的阅读理解能力，通过观察例子，从中找到规律，进而利用此规律进行进一步的运算．9.【答案】14【解析】解：把x=1代入方程1-4kx=0，得1-4k=0，解得k=．故答案为．先根据一元一次方程的解的定义把x=1代入方程1-4kx=0，得到关于k的方程，再解此方程即可．本题考查了一元一次方程的解的定义：满足一元一次方程的未知数的值叫一元一次方程的解．10.【答案】-910【解析】解：∵收入870元记作+870元，∴支出910元记作-910元．故答案为：-910．首先审清题意，明确“正”和“负”所表示的意义；再根据题意作答．本题考查了正数和负数，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．11.【答案】4；3【解析】解：多项式是4次3项式，故答案为：4，3．根据多项式的次数是多项式中次数最高的单项式的次数，常数项是不含字母的项，可得答案．本题考查了多项式，多项式的次数是多项式中次数最高的单项式的次数，常数项是不含字母的项，注意项包括符号．12.【答案】-2【解析】解：∵|-2|=2，∴2的相反数是-2．相反数的意义：一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．绝对值规律总结：一个正数的绝对值是它本身，一个负数的绝对值是它的相反数，0的绝对值是0．本题考查了相反数的意义及绝对值的性质：学生易把相反数的意义与倒数的意义混淆．13.【答案】0【解析】解：∵2013÷4=503…1，∴表示-2013的点是第504组的第一个数，即是0．故答案为：0此题注意寻找规律：每4个数一组，分别与0、3、2、1重合，所以需要计算2013÷4，看是第几组的第几个数．此题是借助数轴的一道规律题，寻找规律是关键．14.【答案】6【解析】解：∵两个单项式与单项式的和是一个单项式，∴n=3，2m=6，解得：m=3，故m+n=6．故答案为：6． 直接利用合并同类法则计算得出答案．此题主要考查了合并同类项，正确掌握运算法则是解题关键．15.【答案】解：（x 2-y 2）-3（x 2-2y 2）=x 2-y 2-3x 2+6y 2=-2x 2+5y 2【解析】先去括号，后合并同类项即可．本题考查整式的加减，解题的关键是熟练掌握整式的加减法则，属于中考常考题型．16.【答案】解：（1）原式=-5+11+213+23=6+3=9；（2）原式=12×12-23×12+9 =6-8+9=7．【解析】（1）根据有理数加减混合法则进行计算即可；（2）根据乘法的分配律以及乘方进行计算即可．本题考查了有理数的混合运算，掌握有理数的混合运算的法则是解题的关键．17.【答案】解：∵a 与b 互为相反数，c 与d 互为倒数，|x |=2，∴a +b =0，cd =1，x =±2 ∴x 2=4，∴原式=99（a +b ）-（-1）2017+4=0+1+4=5．【解析】由已知a 与b 互为相反数，c 与d 互为倒数，|x|=2可以先求出a+b ，cd 和x 的值，然后运用整体代入法求值．此题考查了学生对相反数、倒数及绝对值知识点的理解与掌握．解答此类题的关键是根据已知求出a+b 、cd 和x 的值，然后用整体代入法求值，此题比较好．18.【答案】解：原式=3x 2y -[2x 2y -xy +x 2y -x 2]-xy=3x 2y -2x 2y +xy -x 2y +x 2-xy=x 2，当x =3时，原式=32=9．【解析】先去小括号，再去中括号，然后合并同类项得到原式=x 2，然后把x 的值代入计算即可．本题考查了整式的加减-化简求值：给出整式中字母的值，求整式的值的问题，一般要先化简，再把给定字母的值代入计算，得出整式的值，不能把数值直接代入整式中计算．19.【答案】解：根据题意得，x =2是方程2x -1=x +a -2的解，∴把x =2代入2×2-1=2+a -2，得a =3．把a=3代入到原方程中得2x−13=x+33−2，整理得，2x-1=x+3-6，解得x=-2．【解析】某同学在对方程去分母时，方程右边的-2没有乘3，这时方程的解为x=2，说明x=2是方程2x-1=x+a-2的解，把x=2代入求得a的值即可．再把a的值代入原方程，求出原方程正确的解．本题考查了一元一次方程的解法，是基础知识要熟练掌握．20.【答案】解：（1）12-2x+10=1-5x-2x+5x=1-12-103x=-21x=-7；（2）6-3（y-3）=2（2y+1）6-3y+9=4y+2-3y-4y=2-6-9-7y=-13y=137．【解析】（1）根据一元一次方程的解法解答即可；（2）根据一元一次方程的解法解答即可．此题考查解一元一次方程，关键是根据去分母、去括号、移项、合并同类项，系数化为1解答．21.【答案】解：（1）如图所示：A、B、C分别表示小明、小红、小刚家（2）小明家与小刚家相距：4-（-3）=7（千米）；（3）这辆货车此次送货共耗油：（4+1.5+8.5+3）×0.5=17×0.5=8.5（升）．答：小明家与小刚家相距7千米，这辆货车此次送货共耗油8.5升．【解析】（1）根据已知，以百货大楼为原点，以向东为正方向，用1个单位长度表示1千米，一辆货车从百货大楼出发，向东走了4千米，到达小明家，继续向东走了1.5千米到达小红家，然后西走了8.5千米，到达小刚家，最后返回百货大楼，则小明家、小红家和小刚家在数轴上的位置可知．（2）用小明家的坐标减去与小刚家的坐标即可．（3）这辆货车一共行走的路程，实际上就是4+1.5+8.5+3=17（千米），货车从出发到结束行程共耗油量=货车行驶每千米耗油量×货车行驶所走的总路程．本题是一道典型的有理数混合运算的应用题，同学们一定要掌握能够将应用问题转化为有理数的混合运算的能力，数轴正是表示这一问题的最好工具．如工程问题、行程问题等都是这类．22.【答案】＜；＞；＜；＜；＞；＜【解析】解：（1）a＜0，b＞0，c＜0；（2）a+c＜0；a+b＞0；c-b＜0；（3）|a+c|-|a+b|-|c-b|．=-a-c-a-b+c-b=-2a-2b．故答案为＜；＞；＜；＜；＞；＜．（1）利用数轴表示数的方法进行判断；（2）利用有理数的加法判断a+c和a+b的符号，利用有理数的减法判断c-b的符号；（3）先去绝对值，然后合并即可．本题考查了有理数的大小比较：有理数的大小比较比较有理数的大小可以利用数轴，它们从左到有的顺序，即从大到小的顺序（在数轴上表示的两个有理数，右边的数总比左边的数大）；也可以利用数的性质比较异号两数及0的大小，利用绝对值比较两个负数的大小．也考查了绝对值．第11页，共11页。

··10·a ·b初中数学试卷 鼎尚图文**整理制作七年级数学（上册）期中综合测试卷（含答案）一、选择题（30分）1、如果零上2℃记作+2℃，那么零下3℃记作（ ）A. -3℃；B. -2℃；C. +3℃；D. +2℃；2、-2的倒数是（ ）A. 21；B. 21-；C. 2；D. -2；3、下列判断错误的是（ ）A. 1-a -ab 是二次三项式；B. –a 2b 2c 与2ca 2b 2是同类项；C. ab b a 22+是单项式；D. 243a π的系数是π43；4、计算︱-2+3×(-2)︱=( )A. -8；B. 2；C. 4；D. 8；5、有理数ab 在数轴上的位置如图所示，下列式子成立的是（ ）A. a ＞b ；B. a ＜b ；C. ab ＞0；D. b a＞0； 6、据统计，全国每年因吸烟引起疾病致死的人数大约600万，数据600万用科学记数法表示为（ ）A. 0.6×107；B. 6×106；C. 60×105；D. 6×105；7、计算2xy 2+3xy 2的结果是（ ）A. 5xy 2；B. xy 2；C. 2x 2y 4；D. x 2y 4；8、从b a 52+减去b a 44-的一半，应得到（ ）A. b a -4；B. a b -；C. b a 9-；D. b 7；9、数据4604608取近似值，保留三个有效数字，结果是（ ）A. 4.60×106；B. 4600000；C. 4.61×106；D. 4.605×106；10、已知2,5=+=-d c b a ，则)()()(d c a c d b -++-+的值是（ ）A. -5；B. 15；C. -1；D. 1；二、填空题（24分）11、数轴上与表示-3的点的距离为5个单位的点所表示的有理数是 。

湘教版七年级数学上册期中的试卷(含答案)2014年秋季学期七年级数学上册期中试题（90分钟完卷，满分100分）一、选择题（每小题3分，共24分）1.(-1)的结果为（）A。

1B。

-1C。

2D。

-22.据XXX2004年公布的数据显示，益阳市总人口为458.55万人，那么用科学记数法表示为（）人。

A。

4.5855×10^6B。

4.5855×10^8C。

4.5855×10^7D。

4.5855×10^23.下列计算正确的是（）A。

111/(-1)=-12B。

22/3C。

(-1)×(-2)=-2D。

-1+2=-34.当x=1，y=-2时，代数式2x+y-1的值是（）A。

1B。

-2C。

2D。

-15.下列说法不正确的是（）A。

既不是正数，也不是负数B。

1是绝对值最小的数C。

一个有理数不是整数就是分数D。

|0|=06.某商店上月的营业额是a万元，本月比上月增长15%，那么本月的营业额是（）A。

15%（a+1）万元B。

15%a万元C。

（1+15%）a万元D。

（1+15%）2a万元7.若|y|=5，则y=（）A。

5B。

-5C。

5或-5D。

任何数8.已知a、b在数轴上的位置如图所示，那么下面结论正确的是（）二、填空题（每小题3分，共30分）9.规定向东为正，那么向西走2千米记作-2千米。

10.2/3的倒数的相反数是-3/2.11.单项式- a^2b^3的系数是-1.12.钢笔每枝x元，铅笔每枝y元，买3枝钢笔、5枝铅笔共付13元。

13.比较大小：-2/3-0.6<-2/3-0.5，所以-2/3-0.6<0.14.x^2-2x+y=x^2-(2-y)。

15.已知正方体的棱长是a厘米，则它的表面积为6a^2平方厘米。

16.如果|x-3|+(y+2)^2/3=1，那么x-y=4.17.绝对值小于2的整数是-1，0，1.18.若3am-1bc^2和-2a^3bn^-2c^2是同类项，则m+n=-1.三、解答题19.计算（每小题5分，共20分）①。

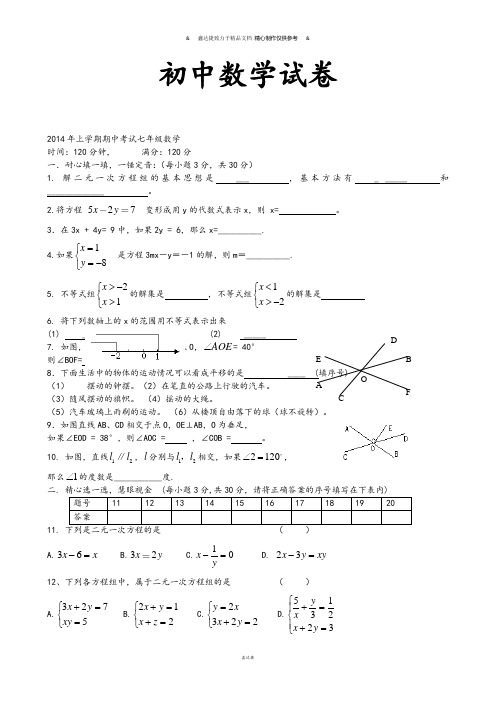
初中数学试卷2014年上学期期中考试七年级数学时间：120分钟， 满分：120分 一．耐心填一填，一锤定音：（每小题3分，共30分）1. 解二元一次方程组的基本思想是 ___ ，基本方法有 _ _____ 和 _____________ 。

2.将方程 527xy 变形成用y 的代数式表示x ，则 x= 。

3．在3x + 4y= 9中，如果2y = 6，那么x=__________. 4.如果⎩⎨⎧-==81y x 是方程3mx －y ＝－1的解，则m ＝__________.5. 不等式组21x x >-⎧⎨>⎩的解集是 , 不等式组12x x <⎧⎨>-⎩的解集是6. 将下列数轴上的x 的范围用不等式表示出来(1) ______ (2) _____7. 如图，直线AB 、CD 、EF 相交于点O ，AOE ∠= 40°则∠BOF= ， AOF ∠ = 。

8．下面生活中的物体的运动情况可以看成平移的是 ____ (填序号)（1） 摆动的钟摆。

（2）在笔直的公路上行驶的汽车。

（3）随风摆动的旗帜。

（4）摇动的大绳。

（5）汽车玻璃上雨刷的运动。

（6）从楼顶自由落下的球（球不旋转）。

9．如图直线AB 、CD 相交于点O ，OE ⊥AB ，O 为垂足， 如果∠EOD = 38°，则∠AOC = ，∠COB = 。

10. 如图，直线12l l ∥，l 分别与12l l ，相交，如果2120∠=，那么1∠的度数是___________度.二. 题号 11 12 13 14 15 16 17 18 19 20 答案11. 下列是二元一次方程的是 （ ） A.x x =-63 B.32xy C.01=-yx D. xy y x =-32 12、下列各方程组中，属于二元一次方程组的是 （ ）A.⎩⎨⎧==+5723xy y xB.⎩⎨⎧=+=+212z x y xC.⎩⎨⎧=+=2232y x x yD.⎪⎩⎪⎨⎧=+=+322135y x y x DA C E OB F13．方程组⎩⎨⎧=-=+13483y x y x 的解是 （ ）A.⎩⎨⎧=-=31y xB.⎩⎨⎧-==13y xC.⎩⎨⎧-=-=13y xD.⎩⎨⎧-=-=31y x14. .如图,不等式组12,39x x -<⎧⎨-≤⎩的解集在数轴上表示正确的是( )30-3A30-3B30C 30D15. 如图，天平右边托盘里的每个砝码的质量都是1千克，则图中显示物体质量的范围是（ ） A 、大于2千克 B 、小于3千克 C 、大于2千克且．小于3千克 D 、大于2千克或．小于3千克 16. 把不等式组 ⎩⎨⎧->≤12x x 的解集表示在数轴上，正确的是 ( )A 、B 、C 、D 、17. 下面四个图形中，∠1与∠2是对顶角的图形的个数有（ ）个 A ．0 B ．1 C ．2 D ．3 18. 如果一个角的补角是150°，那么这个角的度数是（ ） A. 30° B. 60° C.90° D.120° 19. 下列说法错误的是( )A.内错角相等，两直线平行．B.两直线平行，同旁内角互补．C.相等的角是对顶角．D.等角的补角相等．20. 如图a b ∥，M N ，分别在a b ，上，P 为两平行线间一点， 那么123∠+∠+∠=（ ）A ．180B ．270C ．360D ．540三．用心做一做，马到成功：(5+5+10+4+4+4+6+6分,) 21、⎩⎨⎧-=+-=1232y x y x 22、⎩⎨⎧=-=+53y x y x23解不等式组．并在数轴是表示出它的解集(1) 235324x x +<⎧⎨->⎩ (2) ⎪⎩⎪⎨⎧+<-≤+--)1(3151215312x x x x 24.、完成推理填空：如图：直线AB 、CD 被EF 所截，若已知AB//CD ，abM P N123B D E13A CF 2 求证：∠1 ＝ ∠2 。

一、选择题（每题3分，共30分）1. 下列数中，是负数的是：A. -5B. 0C. 5D. -3.52. 如果a > b，那么下列不等式中正确的是：A. a + 2 > b + 2B. a - 2 < b - 2C. a / 2 > b / 2D. a / 2 < b / 23. 一个长方形的长是6cm，宽是3cm，那么它的周长是：A. 12cmB. 18cmC. 24cmD. 36cm4. 下列哪个数是2的平方：A. 4B. 8C. 16D. 325. 在直角坐标系中，点P(2, -3)关于y轴的对称点是：A. (2, 3)B. (-2, 3)C. (2, -3)D. (-2, -3)6. 下列哪个图形是轴对称图形：A. 等边三角形B. 长方形C. 平行四边形D. 等腰梯形7. 一个正方形的边长为a，那么它的面积是：A. aB. a²C. 2aD. 4a8. 如果x² = 25，那么x的值是：A. 5B. -5C. 5 或 -5D. 09. 下列哪个数是无理数：A. √4B. √9C. √16D. √2510. 下列哪个等式是正确的：A. 2 + 3 = 5B. 2 × 3 = 6C. 2 ÷ 3 = 0.666...D. 2 - 3 = -5二、填空题（每题3分，共30分）11. 一个数的倒数是它的什么数？12. 3的平方根是？13. 一个圆的半径是r，那么它的周长是？14. 如果a = 5，b = 3，那么a - b的值是？15. 下列数的绝对值是5的是：A. 5B. -5C. 0D. 10三、解答题（共140分）16. （10分）计算下列各题：(1) 5 - 3 + 2(2) 4 × 3 - 2 × 1(3) (2 + 3) × 417. （10分）解下列方程：(1) 2x + 3 = 11(2) 5 - 2x = 318. （15分）画出一个直角三角形，并标出它的三个顶点A、B、C，其中∠ABC是直角。

七年级（上）期中数学试卷学校: __________ 姓名： ___________ 班级： ___________ 考号： __________ 选择题（本大题共7小题，共21.0分）一个多项式与nf-2n 2的和是5〃上3斥+1,则这个多项式为（）A. 6m 2 — 5n 2 + 1B. -4?n 2 4- n 2 — 1C. 4m 2 — n 2 — 1D. 4m 2 — n 2 -I- 1 据统计，2016年我校师生总人数为8700人，请将这个数据用科学记数法表示为（ ）A. 87 x 102B. 8.7 x 102C. 87 x 103D. 8.7 x 103下列解方程过程屮，变形正确的是（）A. 由 2% - 1 = 3 得 2% = 3 - 1B. 由—-5 =—- 1 得 6% - 5 = 20% - 143C.由_5兀=4得兀=_寸4D.由 ~ — = 1 得 2x — 3x = 6 下列各对数中，互为相反数的是（A. —（+3）与+（—3） C. -3?与（―3）2有理数a 、b 、c 在数轴上的位置如图所示，则\b-a\+\b+c\-\a-c\的化简结果为（ ）填空题（本大题共7小题，共21.0分） 已知\a-2\+ （b+3） 2=0,则 a-b= ___ .若代数式2『+3），+7的值为8,那么代数式6<+9才3的值为 __ .定义新运算：对任意有理数a 、b,都有a®b=cT -b,例如：3®2=32-2=7,那么（3®5）® （-5） = ___ .小明在解关于x 的方程5^=13时，解得方程的解尸2,则a 的值为 __________ .如果.钗卜与2?）严是同类项，则加+”二 ___ 去扌舌号合并同类项：2a- （5a-2） = __ .已知有理数a 、b 满足ab 2<0f 且匕|二3, 0|二2；则a+b 二 ___ .计算题（本大题共4小题，共32.0分）数学老师全老师选派了班上8位同学去参加年级组的数学知识竞赛，试卷满分100 分，我们将成绩中超过90分的部分记为正，低于90分的部分记为负，则这八位同 学的得分如下：+8, +3, -3, -11, +4, +9, -5, -1.）B. -（-4）与 4 D. 一2彳与（一aA.0B.2a下列说法正确的是（）A. -a —定是负数C.正数、负数和0统称为有理数下列说法正确的是（ ）C. 2bD. 2b + 2cB. -a 的绝对值等于aD.整数、分数统称为有理数 A.三是单项式 B. 2nr 的系数是2/r,次数是1次 C. -|a 2Pc 是五次单项式D. ab 2- 2a + 3是四次三项式（1）请求出这8为同学木次数学竞赛的平均分是多少？（2）若得分95以上可以获得一等奖，请求出这8位同学获得一等奖的百分比是多少？16.先化简，再求值(1)x+ (1-x) -2 (2x-4),其中尸扌(2)7X2+3 (-Ixy+y2 ) -2 (3,・3xy+2)?),其中x二丄，y=?3 317.解方程(1)2 (3-x) =-4 (x+3)(2) X-3 2x+l18.已知°、b为常数，且o?・2兀）卄与霁+bx），・4y的差为一次多项式，解关于x 的方程3ax-b=-2（bx-3）.四、解答题（本大题共3小题，共34.0分）19.已知关于x的方程kx+]=3x+2k.（1）当k满足什么条件时，方程有解？（2）若方程有整数解，求正整数£的值?20•计算题(1)6- (+3)・(・4)(2)・1+2一(-》x(_6)(3)(- + ---) x (-12)12 3 4(4)-2 2><(+ 8 一(-2尸(5)3X-3+4X-5X-2X2+4+X(6) 3 (2?-/)-2 (3)1)21.小明买了一套小户型的经济适用房，地面结构如图所示（注：x=a, y=b；单位：m）（1）请用含a、b的式子表示出地面的总面积.（2）如果小明想将卧室和客厅全部铺上木地板，卫生间和厨房全部铺上瓷砖，已知木地板80元加2,瓷砖35元/〃『，则小明一共要花多少钱？（用含a、b 的式子表示）k—3—卧室■p牛'可八客厅X*k一6 —----答案和解析1.【答案】D【解析】解:根据题意得：(5m2-3n2+1) - (m2-2n2) =5m2-3n2+1 -m2+2n2=4m2-n2+1, 故选:D. 根据题意列出关系式，去括号合并即可得到结果.此题考查了整式的加减，熟练掌握运算法则是解本题的关键.2.【答案】D【解析】解:87OO=8.7xlO3.故选:D.用科学记数法表示较大的数时，一般形式为axlO n,其中l<|a|<10, n为整数,据此判断即可.此题主要考查了用科学记数法表示较大的数，一般形式为axlO n,其中l<|a|< 10,确定a与n的值是解题的关键.3.【答案】D【解析】解:A、由2x-l=3,得2x=3+l,错误;B、由21-5=^-1得:6x・60=20x・12,错误；4 .5C、由-5x=4,得:X二;，错误；5D、由得：2x・3x=6,正确，故选:D.各方程整理得到结果，即可作出判断.此题考查了解一元一次方程，以及等式的性质，熟练掌握运算法则是解本题的关键.4.【答案】C【解析】解:A、・(+3)二3、+(-3)=-3,不是互为相反数;B.・(・4)=4与4相等，不是互为相反数；C.-32=-9.(・3)2=9,互为相反数;D.-23=-8. (-2)3-&不是互为相反数；故选:C.分别化简每个选项内的两个数，再根据相反数的定义逐一判断可得.本题主要考查的是相反数的定义，先化简再计算是解题的关键.5.【答案】C【解析】解：由数轴上点的位置得:a<b<O<c, |b|<|c|<|a|,所以b-a>0, b+c〉O, a-c<0,则|b-a|+|b+c|-|a-c|=b-a+(b+c)-(c-a)=b-a+b+c-c+a=2b.故选：C.由数轴上点的位置及有理数的加减法则判断出绝对值里边式子的正负，利用绝对值的代数意义化简，去括号合并即可得到结果.此题考查了整式的加减，数轴，以及绝对值，涉及的知识有:去括号法则，以及合并同类项法则，熟练掌握法则是解本题的关键.6.【答案】D【解析】解:不一定是负数,如-(-2),错误；B、-a的绝对值不一定等于a,如a=-2,错误；C、正有理数、负有理数和0统称为有理数，错误；D、整数、分数统称为有理数，正确；故选：D.根据有理数的定义对各选项分析判断后利用排除法求解.本题考查了有理数的定义，是基础题，熟记概念是解题的关键.7.【答案】B【解析】解:A、:不是数与字母的乘积，不是单项式，此选项错误；B、2;ir的系数是2TI,次数是1次，此选项正确；C、・I a2b3c是六次单项式，此选项错误；D、ab2-2a+3是三次三项式，此选项错误；故选:B.根据单项式的系数、次数:单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数;几个单项式的和叫做多项式，每个单项式叫做多项式的项.多项式中次数最高的项的次数叫做多项式的次数进行分析即可.此题主要考查了单项式，关键是掌握单项式的系数、次数的定义，以及多项式的次数计算方法.8.【答案】5【解析】解:v|a-2|+(b+3)2=0,.*.a=2, b=-3,则a-b=2-(-3)=5.故答案为:5.直接利用绝对值的性质以及偶次方的性质得出a, b的值，进而得出答案.此题主要考查了绝对值的性质以及偶次方的性质，正确得出a, b的值是解题关键.9.【答案】0【解析】解：由题意得:2x2+3y+7=& 可得:2x?+3y=l,6x2+9y=3(2x2+3y)=3,/.6x2+9y-3=0.故答案为:0.根据题意得出2x?+3y的值，进而能得出3(2x2+3y)的值，就能求出代数式6x2+9y-3 的值.本题考查了代数式求值.整体法的运用是解决本题的关键.10.【答案】21【解析】解：3g5=3»5=9・5=4,4®(-5)=42-(-5)=16+5=21.故答案为:21.根据题中的新定义化简，计算即可得到结果.此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键.11.【答案】3【解析】解：把x=2代入方程得:5a-2=13,解得：a=3,故答案为：3把x=2代入方程计算即可求出a的值.此题考查了解一元一次方程，解方程时注意各项都乘以各分母的最小公倍数.12.【答案】・1【解析】解：由题意可知：m=3, n+5=l,••・m=3, n=-4・•・原式=3+(-4)=-l故答案为:・1 根据同类项的定义即可求出m与n的值.本题考查同类项的概念，解题的关键是正确理解同类项的概念，本题属于基础题型.13.【答案】・3d+2【解析】解：原式=2a-5a+2=-3a+2,故答案为:-3a+2.先去括号，再合并同类项即可得.本题主要考查整式的加减，整式的加减的实质就是去括号、合并同类项.- 般步骤是:先去括号，然后合并同类项.14.【答案】・1或・5【解析】解：・.•有理数a、b满足ab2<0,且|a|二3, |b|二2,••・a二3, b=±2.・・・a+b二3+2 或-3+ (-2),•••a+b=・l 或-5,故答案为:・1或・5.根据有理数的乘法，可得a、b的取值范围，根据绝对值的意义，可得冬b的值, 根据代数式求值，可得答案.本题考查了有理数的加法，确定仏b的值是解题关键.15.【答案】解：(1) •・•八位同学的得分如下:+8, +3,・3,・11, +4, +9,・5,・1, ...这8为同学本次数学竞赛的平均分是90+百(8+3-3-11+4+9-5-1) =90+4=94分；(2) •・•得分95以上可以获得一等奖，.••获得一等奖的只有98分和99分，两名同学，・・•这8位同学获得一等奖的百分比是彳二土=25%.8 4【解析】(1)利用计算平均数的分直接求出平均数；(2)先数出得分95分以上的人数，即可得出结论.此题主要考查了平均数，解本题的关键是掌握平均数计算的方法.16.【答案】解：(1)原式=x+l-x-4x+8=-4x+9,当扌时，原式=-4x|+9=-2+9=7 ；乙乙(2)原式=7x2-6xy+3y2-6x2+6xy-4y2=x2-y2,当X=-?尸|时，原式=H=T【解析】(1)先去括号，再合并同类项即可化简原式，再将X的值代入计算即可得；(2)先去括号，再合并同类项即可化简原式，再将x、y的值代入计算即可得. 此题主要考查了整式的化简求值，给出整式中字母的值，求整式的值的问题, 一般要先化简，再把给定字母的值代入计算，得出整式的值，不能把数值直接代入整式中计算.17.【答案】解：(1)去括号得：6-2x=-4x-12,移项合并得：2x=-18,解得：x=-9；(2)去分母得：3x-9-8x-4=12,移项合并得：-5%=25,解得：x=-5.【解析】(1)方程去括号，移项合并，把x系数化为1,即可求出解；(2)方程去分母，去括号，移项合并，把x系数化为1,即可求出解.此题考查了解一元一次方程，解方程时注意各项都乘以各分母的最小公倍数.18.【答案】解：根据题意得：a^-2xy^-x^c'-bxy J r^y=x2- (b+2) xy+x+4y,由差为一次多项式，得到Q=|, b二2,代入方程得：2x+2=-2 (-2x-3),去括号得：2x+2=4x+6,移项合并得：2x=-4f解得：x=-2.【解析】根据题意列出关系式，去括号整理后由差为一次多项式，确定出a与b的值，代入方程计算即可求出解.此题考查了解一元一次方程，解方程时注意各项都乘以各分母的最小公倍数.19.【答案】解：(1) ••心+1二3兀+2£,••・(£・3) x=2k-1,则当心0,即舜3时,方程有解；・・•方程有整数解， ・・・肛3=1或k-3=-1或k~3=5或匕3=・5,解得：B4或小2或"8或r ・2,所以满足条件的正整数k 的值为2或4或8.【解析】⑴由方程变形为(k-3)x=2k-l,据此可得心3时方程有解；⑵由 x= +吕==2+ 昌可知 k-3=l 或 k-3=-l 或 k-3=5 或 k-3=-5,解 之可得. 本题主要考查一元一次方程的解，解题的关键是熟练掌握方程的解的定义. 20.【答案】解：(1)原式=6-3+4=3+4=7(2) 原式=-l+2x (-6) x (-6) =-1+2x36=71(3) 原式=-5-8+9=-4(4) 原式=4x1+844=2+2=4(5) 原式=/+1(6) 原式二6X 2-3>,2-6>,2+4A :2=4X 2-3>,2【解析】(1) 根据有理数运算法则即可求出答案.(2) 根据有理数运算法则即可求出答案.(3) 根据有理数运算法则即可求出答案.(4) 根据有理数运算法则即可求出答案.(5) 根据整式的运算法则即可求出答案.(6) 根据整式的运算法则即可求出答案.本题考查学生的运算能力，解题的关键是熟练运用运算法则，本题属于基础 题型.21.【答案】解：(1)客厅面积为6兀，卫生间面积2y,厨房面积为2x (6-3) =6,卧室 面积为 3x (2+2) =12,所以地面总面积为：6x+2y+18 (w 2)；(2)当却3时, 2k_l 2/c —6+5 小 x= ------= -------=24 5 k_3(2)根据题意知,所花总费用为80 (12+6兀)+35 (2y+6) =480x+70y+l 170 (元)••r【解析】(1)根据图形分别表示岀客厅、卫生间、厨房及卧室的面积即可得；(2)用两部分的费用相加，去括号、合并即可得.本题考查列代数式及代数式求值问题，得到地面总面积的等量关系是解决本题的关键.。

七年级数学上学期期中试题考生注意：本卷共三道大题，总分值120分，时量120分钟一、选择题〔本大题共8个小题，每题3分，总分值24分．请将正确答案的字母代号填在下表中．〕1．12-的绝对值是 A ．-2 B ．12- C ．12 D ．22．如果支出15元记作-15元，那么收入20元记作A ．+5元B ．+20元C ．-5元D ．-20元3．计算4×(-2)的结果是( )A ．8B ．-8C ．6D ．-24．钓鱼岛是位于我国东海钓鱼岛列岛的主岛，被誉为“深海中的翡翠〞，面积约4400000平方米，数据4400000用科学记数法表示为A ．54.410⨯B ．50.4410⨯C ．54410⨯D ．64.410⨯5．以下各组数中，互为相反数的是A ．-1与(-1)2B ．(-1)2与1C ．2与12D ．2与2-6．某服装店新开张，第一天销售服装a 件，第二天比第一天多销售12件，第三天的销售量是第二天的2倍少14件，那么第三天销售了A ．(2a +2)件B ．(2a +20)件C ．(2a +10)件D ．(2a -10)件7．以下各组中，不是同类项的是A ．52与25B ．ab -与baC ．20.2a b 与215a b -D ．23a b 与32a b -8．以下图形都是由同样大小的棋子按一定的规律组成，其中第①个图形有1颗棋子，第②个图形一共有6颗棋子，第③个图形一共有16颗棋子，…，那么第⑧个图形中棋子的颗数为 A ．226 B ． 181 C ．141 D ．106二、填空题〔本大题共8小题，每题3分，总分值24分〕9．比拟大小：0 12- (填“＞〞“＜〞或“＝〞)． 10．多项式222x xy -++次数、项数、第一项的系数分别是 、 、 ．11．如图为我区十二月份某一天的天气预报，该天最高气温比最低气温高 ℃． 12．某校初一〔1〕班有女生a 人，男生人数比女生人数的2倍少5人，那么男生有 人． 1m m +-13．如图，数轴上的点A 表示的数为m ，那么化简的结果为 ．14．假设25(4)0a b ++-=，那么2016()a b +=________．15．计算(-2)2021+(-2)2021的结果是 ．16．观察以下运算过程：S=1+3+32+33+…+32021+32021①，①×3得3S =3+32+33+…+32021+32021②，②-①得2S =32021-1，2014312S -=.运用上面计算方法计算：1+5+52+53+…+52021+52021 = ． 三、解答题〔本大题共8个小题，共计72分〕17．〔本小题总分值6分〕把以下各数：-3，4，-0.5，13-，0.8，0，56-，-7，分别填在相应的大括号里．非负有理数集合：{ …}；整数集合：{ …}；负分数集合：{ …}．18．〔本小题总分值16分〕计算：〔1〕(-5)-(+3)+(-9)-(-8)〔2〕2422()93-÷⨯-〔3〕1571()()36918-+÷- 〔4〕2211363()(2)32----⨯-+-÷19．〔本小题总分值10分〕 化简：〔1〕 (2)(32)x x +--； 〔2〕 (32)(32)xy x xy xy x --+-20．〔本小题总分值6分〕画出数轴，在数轴上表示以下各数，并用“<〞号把这些数连接起来.(4),-- 3.5,-- 1(),2+- 0, ( 2.5),++ 11221．〔本小题总分值8分〕先化简再求值：2211312()()2323x x y x y --+-+，其中1x =，12y =.22．〔本小题总分值8分〕期末检测后，某班抽查了10名同学的数学成绩，以80分为基准，超出的记为正数，缺乏的记为负数，记录的结果如下：+8，-3，+15，-7，-5，-3，-8，+1，0，+10．〔1〕这10名同学中最高分是多少？最低分是多少？〔2〕10名同学中，达优秀〔等于或高于80分〕的所占的百分比是多少？〔3〕10名同学的平均成绩是多少？23．〔本小题总分值10分〕代数式A=2122x xy y ++-，B=2221x xy x -+- 〔1〕求2A-B ；〔2〕当1x =-，2y =-时，求2A-B 的值；〔3〕假设2A-B 的值与x 的取值无关，求y 的值．24．〔本小题总分值8分〕阅读材料：“如果代数式53a b +的值为4-，那么代数式2()4(2)a b a b +++的值是多少？〞我们可以这样来解：原式=2284106a b a b a b +++=+. 把式子534a b +=-两边同乘以2，得1068a b +=-.仿照上面的解题方法，完成下面的问题：〔1〕20a a +=，求22016a a ++的值；〔2〕3a b -=-，求3()5a b a b --++的值；〔3〕222a ab +=-，24ab b -=-，求2225a ab b +-的值.数学参考答案一、选择题〔本大题共8小题，每题3分，总分值24分〕1．C 2．B 3．B 4．D 5．A 6．C 7．D 8．C二、填空题〔本大题共8小题，每题3分，总分值24分〕9．＞ 10．3,3，-1 11．7 12． (25)a -13．21m -+ 14．1 15．22021 16．2017514-三、解答题〔本大题共8个小题，共计72分〕17．非负有理数集合：{ 4, 0.8， 0 …}；…………2分整数集合：{-3,4,0，-7 …}； …………2分负分数集合：{ -0.5，-13 ，56- …}． …………2分 18．(1)原式=-5-3-9+8 …………………3分=-9 …………………4分〔2〕原式=94249-⨯⨯…………………………3分 =-2 ………………………………4分（3）原式=157()(18)369-+⨯-…………………2分 =-6+15-14……………………………3分=-5 ………………………4分〔4〕原式=-9-6+1+8………………3分=-6………………4分19．〔1〕原式=232x x +-+………………3分=31x -………………5分〔2〕原式=3232xy x xy xy x -++-………………3分=56x xy -+………………5分20．数轴2分；描点2分，结论2分。

___2014-2015学年七年级(上)期中数学试卷解析1.的相反数的绝对值是（）2.下列语句中错误的是（）A。

数字也是单项式B。

单项式 -a 的系数与次数都是1C。

xy 是二次单项式3.下列各式计算正确的是（）A。

-(-4) = -16B。

-8 - 2×6 = (-1+6)×(-2)C。

4÷x = 4÷(x)4.如果|a|=3，|b|=1，且a>b，那么a+b的值是（）5.下列说法上正确的是（）A。

长方体的截面一定是长方形B。

正方体的截面一定是正方形C。

圆锥的截面一定是三角形6.如图，四条表示方向的射线中，表示___的是（）A。

B。

C。

7.若，则代数式的值是（）8.下面是___做的一道多项式的加减运算题，但她不小心把一滴墨水滴在了上面。

（-x+3xy-y）-(-x+4xy-y)=-x+2y，阴影部分即为被墨迹弄污的部分。

那么被墨汁遮住的一项应是（）9.下列说法正确的个数为（）1）过两点有且只有一条直线2）连接两点的线段叫做两点间的距离3）两点之间的所有连线中，线段最短4）射线比直线短一半5）直线AB和直线BA表示同一条直线。

10.某电影院共有座位n排，已知第一排的座位为m个，后一排总是比前一排多1个，则电影院中共有座位（）个。

11.比较大小：-π-3.14（选填“＞”、“=”、“＜”）。

12.单项式 -ab 的系数是，单项式 -2 的次数是。

13.在数轴上，点M表示的数是-2，将它先向右移动4.5个单位，再向左移5个单位到达点N，则点N表示的数是。

14.一桶油连桶的重量为a千克，桶重量为b千克，如果把油平均分成3份，每份重量是。

15.如图：三角形有个。

23.正方形的边长为$a$，其中有一直径为$a$的内切圆，阴影部分面积为$S$。

1）求阴影面积$S$；24.计算：1）$\left(-\frac{1}{2}+\frac{3}{4}\right)\times(-12)$；25.1）化简$-2(mn-3m)-[m-5(mn-m)+2mn]$；2）先化简，再求值：$5abc-\{2ab-[3abc-2(2ab-ab)]\}$，当$a=2$，$b=-1$，$c=3$时的值；26.如图，点$P$在线段$AB$上，点$M$、$N$分别是线段$AB$、$AP$的中点，若$AB=16$cm，$BP=6$cm，求线段$NP$和线段$MN$的长度。

la75684321b(3)2014.04| 七年级| 数学 | 第1页| | | | | | | | | | | | | ： | 号 | 考线 | | | | | | | | | | ： | 号 | 位 | 座 | | | | 订 | | | | | | | | | | ： |名 |姓 | | | | | | 装： |级 | 班 | | | | | | | | | | | | | ： |校 | 学 | |七年级期中质量检测试卷——数学时量：120分钟满分：120分一、选择题（3分×10）A．289.224x yxDx x x y+=⎧=⎧⎨⎨-=⎩⎩B．42311..237546x y a b xB Cx y b c y+=-=⎧⎧⎧⎨⎨⎨+=-==⎩⎩⎩C．228423119...23754624x yx y a b xB C Dx y b c y x x y+=+=-=⎧⎧=⎧⎧⎨⎨⎨⎨+=-==-=⎩⎩⎩⎩D．28423119...23754624x yx y a b xB C Dx y b c y x x y+=+=-=⎧⎧=⎧⎧⎨⎨⎨⎨+=-==-=⎩⎩⎩⎩2、如图所示,∠1和∠2是对顶角的图形有12121221A．1个 B．2个 C．3个 D．4个3、下列运算正确的是A．6332xxx=+B．842xxx=∙C．nmnm xxx+=∙D．2045)(xx-=-4、下列各式中从左到右的变形，是因式分解的是A．9-a3)-3)(a(a2=+B．13)2)(x-(x5-xx2++=+C．b)ab(aabba22+=+D．)x1+x(x=1+x25、下列多项式乘法，能用平方差公式进行计算的是A．(x+y)(－x－y) B．(2x+3y)(2x－3z)C．(－a－b)(a－b) D．(m－n)(n－m)6、下列四个多项式是完全平方式的是A．22yxyx++B．222yxyx--C．22424nmnm++D．2241baba++7、若5)a)(x(x--展开式中不含有x的一次项，则a的值为A．0 B．5 C．-5 D．5或-58、如图在边长为a的正方形中挖掉一个边长为b的小正方形(a>b)，把余下的部分剪拼成一个矩形，通过计算两个图形(阴影部分)的面积，验证了一个等式，则这个等式是A．222))(2(babababa-+=-+B．2222)(bababa++=+C．2222)(bababa+-=-D．))((22bababa-+=-9、某校运动员分组训练，若每组7人，余3人；若每组8人，则缺5人；设运动员人数为x人，组数为y组，则列方程组为A．⎩⎨⎧=++=xyxy5837B．⎩⎨⎧=-+=xyxy5837C．⎩⎨⎧+=-=5837xyxyD．⎩⎨⎧+=+=5837xyxy10、若0)5()3(22=+-+-+yxyx，则22yx-的值是A．-15 B．-8 C．15 D．8二、填空题（每小题3 分，共30 分）11、以57xy=⎧⎨=⎩为解的一个二元一次方程是。