初中数学垂径定理(中考题精选)

典型例题分析：例题1、 基本概念1．下面四个命题中正确的一个是（ ）A ．平分一条直径的弦必垂直于这条直径B ．平分一条弧的直线垂直于这条弧所对的弦C ．弦的垂线必过这条弦所在圆的圆心D ．在一个圆内平分一条弧和它所对弦的直线必过这个圆的圆心2．下列命题中，正确的是（ ）．A ．过弦的中点的直线平分弦所对的弧B ．过弦的中点的直线必过圆心C ．弦所对的两条弧的中点连线垂直平分弦，且过圆心D ．弦的垂线平分弦所对的弧例题2、垂径定理1、 在直径为52cm 的圆柱形油槽内装入一些油后，截面如图所示，如果油的最大深度为16cm ，那么油面宽度AB 是________cm.2、在直径为52cm 的圆柱形油槽内装入一些油后，，如果油面宽度是48cm ，那么油的最大深度为________cm.3、如图，已知在⊙O 中，弦CD AB =，且CD AB ⊥，垂足为H ，AB OE ⊥于E ，CD OF ⊥于F .（1）求证：四边形OEHF 是正方形.（2）若3=CH ，9=DH ，求圆心O 到弦AB 和CD 的距离.4、已知：△ABC 内接于⊙O ，AB=AC ，半径OB=5cm ，圆心O 到BC 的距离为3cm ，求AB 的长．5、如图，F 是以O 为圆心，BC 为直径的半圆上任意一点，A 是的中点，AD ⊥BC 于D ，求证：AD=21BF.O A E F例题3、度数问题1、已知：在⊙O 中，弦cm 12=AB ，O 点到AB 的距离等于AB 的一半，求：AOB ∠的度数和圆的半径.2、已知：⊙O 的半径1=OA ，弦AB 、AC的长分别是2、3.求BAC ∠的度数。

例题4、相交问题如图，已知⊙O 的直径AB 和弦CD 相交于点E ，AE=6cm ，EB=2cm ，∠BED=30°，求CD 的长.例题5、平行问题在直径为50cm 的⊙O 中，弦AB=40cm ，弦CD=48cm ，且AB ∥CD ，求：AB 与CD 之间的距离.例题6、同心圆问题如图，在两个同心圆中，大圆的弦AB ，交小圆于C 、D 两点，设大圆和小圆的半径分别为b a ,.求证：22b a BD AD -=⋅.例题7、平行与相似已知：如图，AB 是⊙O 的直径，CD 是弦，于CD AE ⊥E ，CD BF ⊥于F .求证：FD EC =.A B DCE O作 业：一、概念题1．下列命题中错误的有（）（1）弦的垂直平分线经过圆心（2）平分弦的直径垂直于弦（3）梯形的对角线互相平分（4）圆的对称轴是直径A ．1个B ．2个C ．3个D ．4个2、⊙O 的直径为10，弦AB 的长为8，M 是弦AB 上的动点，则OM 的长的取值范围是（ ）（A ）5OM 3≤≤ （B ）5OM 4≤≤（C ）5OM 3<< （D ）5OM 4<<3．如图，如果AB 为⊙O 直径，弦AB CD ⊥，垂足为E ，那么下列结论中错误的是（ ）A ．DE CE =B ．C ．BAD BAC ∠=∠D ．AD AC >4．如图，AB 是⊙O 直径，CD 是⊙O 的弦，CD AB ⊥于E ，则图中不大于半圆的相等弧有（ ）对。

中考数学专题复习《垂径定理》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________ 1．如图 在O 中 直径AB 垂直弦CD 于点E 连接,,AC AD BC 作CF AD ⊥于点F 交线段OB 于点G （不与点,O B 重合） 连接OF ．(1)若1BE = 求GE 的长．(2)求证：2BC BG BO =⋅．(3)若FO FG = 猜想CAD ∠的度数 并证明你的结论．2．如图 AB 是O 直径 直线l 经过O 上一点C 过点A 作直线l 的垂线．垂足为D ．连接AC ．已知AC 平分DAB ∠．(1)求证：直线l 与O 相切(2)若70DAB ∠=︒ 3CD = 求O 的半径．（参考数据：sin350.6︒≈cos350.8︒≈．tan350.7︒≈）3．如图 AC 与BD 相交于点E 连接AB CD CD DE =．经过A B C 三点的O 交BD 于点F 且CD 是O 的切线．(1)连接AF 求证：AF AB =(2)求证：2AB AE AC =⋅(3)若2AE = 6EC = 4BE = 则O 的半径为 ． 4．如图 四边形ABCD 内接于O 对角线,AC BD 交于点E 连接OE ．若,AC BD O ⊥的半径为,r OE m =．(1)若ABC BAD ∠=∠ 求证：OE 平分AEB ∠(2)试用含,r m 的式子表示22AC BD +的值(3)记ADE BCE ABE CDE 的面积分别为1S 2S 3S 4S 当求证：AC BD =．5．如图 AB 是O 的直径 ,C D 是O 上两点 且AD CD = 连接BC 并延长与过点D 的O 的切线相交于点E 连接OD ．(1)证明：OD 平分ADC ∠(2)若44,tan 3DE B == 求CD 的长． 6．已知BC 是O 的直径 点D 是BC 延长线上一点 AB AD = AE 是O 的弦 30AEC ∠=︒．(1)求证：直线AD 是O 的切线(2)若AE BC ⊥ 垂足为M O 的半径为10 求AE 的长．7．已知 在O 中 AB 为弦 点C 在圆内 连接AC BC OC 、、,ACO BCO ∠=∠．(1)如图1 求证：AC BC =(2)如图2 延长AC BC 、交O 于点E D 、 连接DE 求证：AB DE ∥(3)如图3 在（2）的条件下 设O 的半径为,3R DE R = 弦FG 经过点C 连接BG BF 、 72,3,33DBF DBG CG R ∠=∠== 求线段CF 的长． 8．已知点,,A B C 在O 上．(1)如图① 过点A 作O 的切线EF 交BC 延长线于点,E D 是弧BC 的中点 连接DO 并延长 交BC 于点G 交O 于点H 交切线EF 于点F 连接,BA BH ．若24ABH ∠=︒ 求E ∠的大小(2)如图① 若135AOC B ∠+∠=︒ O 的半径为5 8BC = 求AB 的长． 9．如图 A B C D 分别为O 上一点 连AB AC BC BD CD AC 垂直于BD 于E AC BC = 连CO 并延长交BD 于F ．(1)求证：CD CF =(2)若10BC = 6BE = 求O 的半径．10．如图 在 Rt ABC △中 90C ∠=︒，AD 平分 BAC ∠ 交 BC 于点D 点O 是边 AB 上的点 以点O 为圆心 OD 长为半径的圆恰好经过点A 交AC 于点E 弦 EF AB ⊥于点G ．(1)求证：BC 是O 的切线．(2)若 12AG EG ==，，求O 的半径．(3)设O 与AB 的另一个交点为 H 猜想AH AE CE 之间的数量关系 并说明理由． 11．如图 在ABC 中 90ACB ∠=︒ 5AB = 1AD = BD BC = 以BD 为直径作O 交BC 于点E 点F 为AC 边上一点 连接EF 过点A 作AG EF ⊥ 垂足为点G =BAC GAF ∠∠．(1)求证：EG 为O 的切线(2)求BE 的长．12．如图 四边形ABCD 中 90B C ∠=∠=︒ 点E 是边BC 上一点 且DE 平分AEC ∠ 作ABE的外接圆O．(1)求证：DC是O的切线(2)若O的半径为5 2CE=求BE与DE的长．13．如图1 在直角坐标系中以原点O为圆心半径为10作圆交x轴于点A B，（点A⊥（点D在点E上方）连在点B的左边）．点C为直径AB上一动点过点C作弦DE AB∥交圆O于另一点记为点F．直线EF交x轴于点G连接接AE过点D作DF AE，，．OE BF AD(1)若80∠=︒求ADFBOE∠的度数(2)求证：OE BF∥(3)若2=请直接写出点C横坐标．OG CG14．如图AB为O的弦C为AB的中点D为OC延长线上一点连接BO并延长交O于点E交直线DA于点F B D∠=∠．(1)求证：DA为O的切线(2)若42EF=求弦AB的长度．AF=2⊥交O于B C两点．连15．如图在O中M为半径OA上一点．过M作弦BC OA=．接BO并延长交O于点D连接AD交BC于点E．已知EB ED(1)求证：60CD =︒(2)探究线段CE EM 长度之间的数量关系 并证明．参考答案：1．(1)1(3)45︒2．(2)2583．4．(2)()222242AC BD r m +=-5．(2)6．(2)AE =7．(3)21349CF =8．(1)48E ∠=︒ (2)9．51010．(2)52(3)2AH AE CE =+11．(2)16512．(2)6BE = 25DE =13．(1)100︒(3)点C 555-14．28215．(2)2CE EM =。

垂径定理圆心角圆周角定理一选择题：1、如图，⊙O是△ABC的外接圆，∠OBC=42°，则∠A的度数是（）A．42°B．48°C．52°D．58°2.如图，A、B、C、D四个点均在⊙O上，∠AOD=50°，AO∥DC，则∠B的度数为( )A．50° B．55° C．60° D．65°3.如图，点B、D、C是⊙O上的点，∠BDC=130°，则∠BOC是（）A．100° B．110° C．120°D．130°4.如图，⊙O的半径为5，弦AB的长为8，点M在线段AB（包括端点A，B）上移动，则OM取值范围是（）A.3≤OM≤5B.3≤OM＜5C.4≤OM≤5 D.4≤OM＜55、如图所示，AB是⊙O的直径，AD=DE，AE与BD交于点C，则图中与∠BCE相等的角有（）A．2个 B．3个 C．4个 D．5个6.将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B 的读数分别为86°、30°，则∠ACB的大小为( )A．15°B．28° C.29°D．34°7.如图，C为⊙O直径AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是( )8.如图.⊙O 中，AB、AC是弦，O在∠ABO的内部，，，，则下列关系中，正确的是（）A. B. C． D.9.如图，四边形ABCD内接于⊙O，BC是直径，AD=DC，∠ADB=20º，则∠ACB，∠DBC分别为（）A．15º与30º B．20º与35º C．20º与40º D．30º与35º10.图中∠BOD的度数是（）A．55° B．110° C．125° D．150°11.如图，点I为△ABC的内心，点O为△ABC的外心，∠O=140°，则∠I为（）（A）140°（B）125°（C）130°（D）110°12.如图,弦AB∥CD，E为上一点，AE平分，则图中与相等（不包括）的角共有（）A．3个 B．4个 C．5个 D．6个13、如图，已知的半径为1，锐角内接于，于点，于点，则的值等于（）A．的长 B．的长 C．的长 D．的长14.如图，在直角∠O的内部有一滑动杆AB，当端点A沿直线AO向下滑动时，端点B会随之自动地沿直线OB向左滑动，如果滑动杆从图中AB处滑动到A′B′处，那么滑动杆的中点C所经过的路径是（）A.直线的一部分B.圆的一部分C.双曲线的一部分 D.抛物线的一部分15.如图，AB是⊙O的直径，弦BC=2cm，∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动，点Q从A点出发沿着A→C的方向运动，当点P到达点A时，点Q也随之停止运动．设运动时间为t(s)，当△APQ是直角三角形时，t的值为（）A. B. C.或 D.或或16.如图，，在以为直径的半圆上，，在上，为正方形，若正方形边长为1，，，则下列式子中，不正确的是（）A. B. C. D.17.如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=20°，N是弧MB的中点，P是直径AB上的一动点．若MN=1，则△PMN周长的最小值为（）A．4 B．5 C．6 D．718.如图，在△ABC中，AD是高，AE是直径，AE交BC于G，有下列四个结论：•①AD2=BD·CD；②BE2=EG·AE；③AE·AD=AB·AC；④AG·EG=BG·CG．其中正确结论的有（）A．1个 B．2个 C．3个 D．4个19.如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG，DE，FG，，的中点分别是M，N，P，Q。

初中垂径定理试题及答案一、选择题1. 在圆中，垂直于弦的直径是该弦的（）。

A. 垂线B. 垂径C. 弦心距D. 弦长答案：B2. 垂径定理告诉我们，如果一条线段垂直于弦，并且平分弦，那么它也平分弦所对的（）。

A. 弧B. 圆心角C. 弦心距D. 弦长答案：A3. 在圆中，如果一条直径垂直于弦，那么这条直径将弦分成的两段长度（）。

A. 相等B. 不相等C. 无法确定D. 取决于圆的大小答案：A二、填空题4. 在圆中，如果弦AB的中点为M，且直径CD垂直于弦AB于点M，则弦AB所对的弧ACB的度数为______。

答案：90°5. 垂径定理在圆的几何学中非常重要，它说明了垂直于弦的直径将弦平分，并且平分的弦所对的弧是______。

答案：相等的三、解答题6. 已知圆O的半径为10cm，弦AB垂直于直径CD于点M，求弦AB的长度。

答案：由于直径CD垂直于弦AB，根据垂径定理，弦AB被直径CD平分，因此弦AB的长度为圆的直径，即20cm。

7. 在一个圆中，弦AC的长度为12cm，弦BC的长度为8cm，且AC和BC相交于点O，求圆的半径。

答案：由于AC和BC相交于圆心O，根据垂径定理，OA=OC，OB=OA，因此OA=OC=6cm，OB=OA=6cm。

根据勾股定理，圆的半径r满足r^2 =OA^2 + OB^2 = 6^2 + 6^2 = 72，所以r = √72 = 6√2 cm。

四、证明题8. 证明：在圆中，如果一条直径垂直于弦，那么这条直径将弦平分。

答案：设圆心为O，直径为CD，弦为AB，且CD垂直于AB于点M。

要证明CM=MD。

由于CD是直径，所以∠CMO=∠DMO=90°。

根据垂径定理，CM=MD，因此这条直径将弦平分。

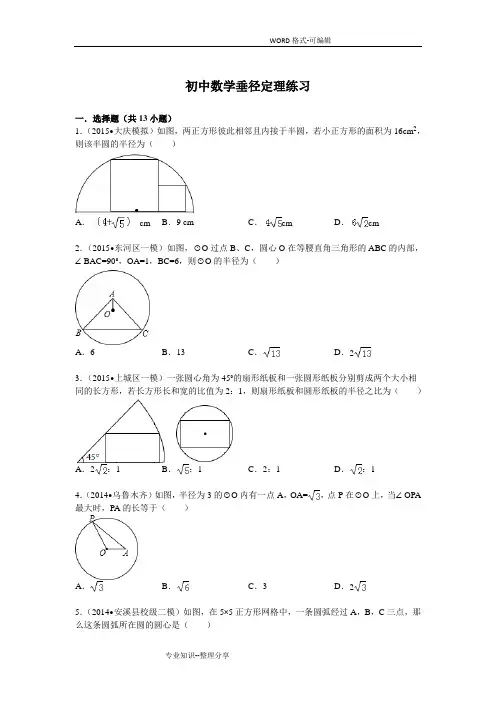
初中数学垂径定理练习一．选择题（共13小题）1．（2015•大庆模拟）如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm2，则该半圆的半径为（）A．cm B．9 cm C．cm D．cm 2．（2015•东河区一模）如图，⊙O过点B、C，圆心O在等腰直角三角形的ABC的内部，∠BAC=90°，OA=1，BC=6，则⊙O的半径为（）A．6B．13 C．D．23．（2015•上城区一模）一张圆心角为45°的扇形纸板和一张圆形纸板分别剪成两个大小相同的长方形，若长方形长和宽的比值为2：1，则扇形纸板和圆形纸板的半径之比为（）A．2：1 B．：1 C．2：1 D．：14．（2014•乌鲁木齐）如图，半径为3的⊙O内有一点A，OA=，点P在⊙O上，当∠OPA 最大时，PA的长等于（）A．B．C．3D．25．（2014•安溪县校级二模）如图，在5×5正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是（）A．点P B．点Q C．点R D．点M 6．（2014•简阳市模拟）如图，⊙O的半径为5，若OP=3，则经过点P的弦长可能是（）A．3B．6C．9D．127．（2014•宝安区二模）如图，将半径为6的⊙O沿AB折叠，与AB垂直的半径OC交于点D且CD=2OD，则折痕AB的长为（）A．B．C．6D．8．（2014•河北区三模）如图，以（3，0）为圆心作⊙A，⊙A与y轴交于点B（0，2），与x轴交于C、D，P为⊙A上不同于C、D的任意一点，连接PC、PD，过A点分别作AE⊥PC 于E，AF⊥PD于F．设点P的横坐标为x，AE2+AF2=y．当P点在⊙A上顺时针从点C运到点D的过程中，下列图象中能表示y与x的函数关系的图象是（）A．B．C．D．9．（2014秋•大竹县校级期末）如图，⊙O的半径为1，点A是半圆上的一个三等分点，点B是弧的中点，P是直径MN上的一个动点，则PA+PB的最小值为（）A．1B．C．D．10．（2014秋•扬中市校级月考）如上图，在直角坐标系中，以点P为圆心为半径的圆弧与x轴交于A、B两点，已知A（2，0），B（6，0），则点P的坐标是（）A．（4，）B．（4，2）C．（4，4）D．（2，）11．（2013•海门市模拟）圆弧形蔬菜大棚的剖面如图所示，AB=8m，∠CAD=30°，则大棚高度CD约为（）A．2.0m B．2.3m C．4.6m D．6.9m12．（2012•天宁区校级模拟）如图，正方形ABCD内接于⊙O，E为DC的中点，直线BE 交⊙O于点F，如果⊙O的半径为，则O点到BE的距离OM=（）A．B．C．D．13．（2012秋•镇赉县校级期末）如图，AB为⊙O的一固定直径，自上半圆上一点C作弦CD⊥AB，∠OCD的平分线交⊙O于点P，当点C在上半圆上（不包括A、B两点）移动时，则对点P的判断正确的是（）A．到CD的距离保持不变B．与点C的距离保持不变D．位置不变C．平分二．填空题（共16小题）14．（2013•宁夏）如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为cm．15．（2011•鄂城区校级模拟）在半径为5的⊙O中，有两平行弦AB．CD，且AB=6，CD=8，则弦AC的长为．16．（2010•海南）如图，将半径为4cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长度为cm．17．（2004•山西）如图，已知Rt△ABC中，∠C=90°，AC=，BC=1，若以C为圆心，CB为半径的圆交AB于点P，则AP=．18．（2003•宁波）如图，AB是半圆O的直径，E是的中点，OE交弦BC于点D，已知BC=8cm，DE=2cm，则AD的长为cm．19．（2008•邵阳）如图，AB，AC分别是⊙O的直径和弦，OD⊥AC于点D，连接BD，BC，AB=5，AC=4，则BD=．20．（2006•龙岩）如图，已知⊙O的半径为5，弦AB=8，P是弦AB上一点，且PB=2，则OP=．21．（2005•中原区）如图，已知⊙O的直径为10，P为⊙O内一点，且OP=4，则过点P且长度小于6的弦共有条．22．（2004•郑州）如图，A、B、C、D是⊙O上的四点，且D是弧AB的中点，CD交OB 于E，∠AOB=100°，∠OBC=55°，那么∠OEC=度．23．（2015•黄冈中学自主招生）如图所示，动点C在⊙O的弦AB上运动，AB=，连接OC，CD⊥OC交⊙O于点D．则CD的最大值为．24．（2015•浠水县校级模拟）如图，AB是⊙O的直径CD是弦，若AB=10cm，CD=8cm，那么A、B两点到直线CD的距离之和为．25．（2015•嘉定区一模）如图，AB、AC都是圆O的弦，OM⊥AB，ON⊥AC，垂足分别为M、N，如果BC=6，那么MN=．26．（2015•泰兴市二模）如图，定长弦CD在以AB为直径的⊙O上滑动（点C、D与点A、B不重合），M是CD的中点，过点C作CP⊥AB于点P，若CD=3，AB=8，PM=l，则l的最大值是．27．（2015•广陵区一模）如图，⊙O的半径是4，△ABC是⊙O的内接三角形，过圆心O 分别作AB、BC、AC的垂线，垂足为E、F、G，连接EF．若OG﹦1，则EF为．28．（2015•滨州模拟）已知圆的两条平行弦分别长6dm和8dm，若这圆的半径是5dm，则两条平行弦之间的距离为．29．（2015春•萧山区校级月考）如图，在平面直角坐标系中，⊙P的圆心坐标是（4，a）（a ＞4），半径为4，函数y=x的图象被⊙P截得的弦AB的长为，则⊙P的弦心距是；a的值是．三．解答题（共1小题）30．（2015•德州）如图，⊙O的半径为1，A，P，B，C是⊙O上的四个点，∠APC=∠CPB=60°．（1）判断△ABC的形状：；（2）试探究线段PA，PB，PC之间的数量关系，并证明你的结论；（3）当点P位于的什么位置时，四边形APBC的面积最大？求出最大面积．2015年07月12日1161622024的初中数学组卷参考答案一．选择题（共13小题）1．C 2．C 3．A 4．B 5．B 6．C 7．B 8．A 9．C 10．C 11．B 12．D 13．C二．填空题（共16小题）14．215．或5或7 16．17．18．19．20．21．0 22．80 23．24．6cm 25．3 26．4 27．28．7dm或1dm 29．14+三．解答题（共1小题）30．等边三角形。

【中考冲刺】垂径定理【中考冲刺】垂径定理一、选择题（共15小题）1．（2012•黄冈）如图，AB为⊙O的直径，弦CD⊥AB于E，已知CD=12，BE=2，则⊙O的直径为（）A．8B．10 C．16 D．202．（2012•毕节地区）下列命题是假命题的是（）A．同弧或等弧所对的圆周角相等B．平分弦的直径垂直于弦C．两条平行线间的距离处处相等D．正方形的两条对角线互相垂直平分3．（2011•牡丹江）已知⊙0的直径AB=40，弦CD⊥AB于点E，且CD=32，则AE的长为（）A．12 B．8C．12或28 D．8或324．（2011•达州）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=10，CD=8，那么线段OE的长为（）A．5B．4C．3D．25．（2011•临沂）如图，⊙O的直径CD=5cm，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OD=3：5．则AB的长是（）A．2cm B．3cm C．4cm D．2cm6．（2009•广元）如图，半径为5的⊙P与y轴相交于M（0，﹣4），N（0，﹣10）两点，则圆心P的坐标为（）A．（5，﹣4）B．（4，﹣5）C．（4，﹣7）D．（5，﹣7）7．（2010•芜湖）如图所示，在圆⊙O内有折线OABC，其中OA=8，AB=12，∠A=∠B=60°，则BC的长为（）A．19 B．16 C．18 D．208．（2010•台湾）如图，AB为圆O的直径，C、D两点均在圆上，其中OD与AC交于E点，且OD⊥AC．若OE=4，ED=2，则BC长度为（）A．6B．7C．8D．99．（2010•绍兴）如图，已知⊙O的直径AB⊥弦CD于点E，下列结论中一定正确的是（）A．A E=OE B．C E=DE C．O E=CE D．∠AOC=60°10．（2009•攀枝花）在圆O中，圆O的半径为5cm，圆心O到弦AB的距离为4cm，则弦AB的长为（）A．3cm B．cm C．2cm D．6cm11．（2010•牡丹江）如图，⊙O的直径AB=10cm，弦CD⊥AB，垂足为P．若OP：OB=3：5，则CD的长为（）A．6cm B．4cm C．8cm D．10cm12．（2009•湘西州）⊙O的半径为10cm，弦AB=12cm，则圆心到AB的距离为（）A．2cm B．6cm C．8cm D．10cm13．（2008•衢州）如图，C是以AB为直径的⊙O上一点，已知AB=5，BC=3，则圆心O到弦BC的距离是（）A．1.5 B．2C．2.5 D．314．（2007•福州）如图，⊙O中，弦AB的长为6cm，圆心O到AB的距离为4cm，则⊙O的半径长为（）A．3cm B．4cm C．5cm D．6cm15．（2008•长春）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=20，CD=16，那么线段OE的长为（）A．10 B．8C．6D．4二、填空题（共15小题）（除非特别说明，请填准确值）16．（2011•孝感）如图，直径分别为CD、CE的两个半圆相切于点C，大半圆M的弦与小半圆N相切于点F，且AB∥CD，AB=4，设、的长分别为x、y，线段ED的长为z，则z（x+y）的值为_________．17．（2011•台州）如图，CD是⊙O的直径，弦AB⊥CD，垂足为点M，AB=20，分别以CM、DM为直径作两个大小不同的⊙O1和⊙O2，则图中阴影部分的面积为_________（结果保留π）．18．（2011•宁德）如图，AB是半圆O的直径，OD⊥AC，OD=2，则弦BC的长为_________．19．（2011•辽阳）如图，AB为⊙O直径，CD⊥AB，∠BDC=35°，则∠CAD=_________．20．（2011•广安）如图所示，若⊙O 的半径为13cm，点P是弦AB上一动点，且到圆心的最短距离为5cm，则弦AB的长为_________．21．（2010•毕节地区）如图，在⊙O中，直径AB的长为，弦CD⊥AB于E，∠BDC=30°则弦CD的长为_________．22．（2011•厦门）如图，⊙O的直径CD垂直于弦AB，垂足为E．若AB=6cm，则AE=_________cm．23．（2011•深圳）如图，在⊙O中，圆心角∠AOB=12O°，弦，则OA=_________cm．24．（2011•黑龙江）如图，已知⊙O的半径为4，OC垂直弦AB于点C，∠AOB=120°，则弦AB长为_________．25．（2010•海南）如图，将半径为4cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长度为_________ cm．26．（2010•玉溪）如图，在半径为10的⊙O中，OC垂直弦AB于点D，AB=16，则CD的长是_________．27．（2010•北京）如图，AB为圆O的直径，弦CD⊥AB，垂足为点E，连接OC，若OC=5，CD=8，则AE=_________．28．（2010•镇江）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=10，CD=8，那么线段OE的长为_________．29．（2010•厦门）⊙O的直径为10，圆心O到弦AB的距离为3，则弦AB的长是_________．30．（2010•文山州）如图，⊙O的弦AB=6，M是AB上任意一点，且OM最小值为4，则⊙O的半径为_________．【中考冲刺】垂径定理参考答案与试题解析一、选择题（共15小题）1．（2012•黄冈）如图，AB为⊙O的直径，弦CD⊥AB于E，已知CD=12，BE=2，则⊙O的直径为（）A．8B．10 C．16 D．20考点：垂径定理；勾股定理．分析：连接OC，可知，点E为CD的中点，在Rt△OEC中，OE=OB﹣BE=OC﹣BE，根据勾股定理，即可得出OC，即可得出直径．解答：解：连接OC，根据题意，CE=CD=6，BE=2．在Rt△OEC中，设OC=x，则OE=x﹣2，故：（x﹣2）2+62=x2解得：x=10即直径AB=20．故选D．点评：本题是对垂径定理和解直角三角形的综合应用，解题的关键是利用勾股定理构造直角三角形．2．（2012•毕节地区）下列命题是假命题的是（）A．同弧或等弧所对的圆周角相等B．平分弦的直径垂直于弦C．两条平行线间的距离处处相等D．正方形的两条对角线互相垂直平分考点：垂径定理；平行线之间的距离；正方形的性质；圆周角定理；命题与定理．分析：分析是否为假命题，可以举出反例；也可以分别分析各题设是否能推出结论，从而利用排除法得出答案．解答：解：A、同弧或等弧所对的圆周角相等，是真命题，故本选项不符合题意；B、平分弦的直径垂直于弦，是假命题，因为只有当该弦不是直径时才成立，故本选项符合题意；C、两条平行线间的距离处处相等，是真命题，故本选项不符合题意；D、正方形的两条对角线互相垂直平分，是真命题，故本选项不符合题意．故选B．点评：主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．3．（2011•牡丹江）已知⊙0的直径AB=40，弦CD⊥AB于点E，且CD=32，则AE的长为（）A．12 B．8C．12或28 D．8或32考点：垂径定理；勾股定理．分析：在直角△OCE中，利用勾股定理即可求得OE的长，则AE=OA+OE或AE=OB﹣OE，据此即可求解．解答：解：如图，连接OC，∵弦CD⊥AB于点E∴CE=CD=16，在直角△OCE中，OE===12，则AE=20+12=32，或AE=20﹣12=8，故AE的长是8或32．故选D．点评：本题主要考查了垂径定理，正确理解应分两种情况讨论是解题关键．4．（2011•达州）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=10，CD=8，那么线段OE的长为（）A．5B．4C．3D．2考点：垂径定理；勾股定理．专题：计算题．分析：连接OC，由垂径定理求出CE的长，再根据勾股定理得出线段OE的长．解答：解：连接OC∵AB是⊙O的直径，弦CD⊥AB，∴CE=CD，∵CD=8，∴CE=4，∵AB=10，∴由勾股定理得，OE===3．故选C．点评：本题考查了垂径定理、勾股定理以及圆中辅助线的作法，是重点知识，要熟练掌握．5．（2011•临沂）如图，⊙O的直径CD=5cm，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OD=3：5．则AB的长是（）A．2cm B．3cm C．4cm D．2cm考点：垂径定理；勾股定理．专题：探究型．分析：先连接OA，由CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为M可知AB=2AM，再根据CD=5cm，OM：OD=3：5可求出OM的长，在Rt△AOM中，利用勾股定理即可求出AM的长，进而可求出AB的长．解答：解：连接OA，∵CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，∴AB=2AM，∵CD=5cm，∴OD=OA=CD=×5=cm，∵OM：OD=3：5，∴OM=OD=×=，∴在Rt△AOM中，AM===2，∴AB=2AM=2×2=4cm．故选C．点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．6．（2009•广元）如图，半径为5的⊙P与y轴相交于M（0，﹣4），N（0，﹣10）两点，则圆心P的坐标为（）A．（5，﹣4）B．（4，﹣5）C．（4，﹣7）D．（5，﹣7）考点：垂径定理；坐标与图形性质；勾股定理．分析：由M（0，﹣4），N（0，﹣10），即可得MN的值，然后连接PM，过点P作PE⊥MN于E，根据垂径定理可得ME的值，然后由勾股定理，即可求得PE的值，则可得圆心P的坐标．解答：解：∵M（0，﹣4），N（0，﹣10），∴MN=6，连接PM，过点P作PE⊥MN于E，∴ME=NE=MN=3，∴OE=OM+EM=4+3=7，在Rt△PEM，PE===4，∴圆心P的坐标为（4，﹣7）．故选C．点评：此题考查了垂径定理，勾股定理的知识．此题难度不大，解题的关键是数形结合思想的应用，注意辅助线的作法．7．（2010•芜湖）如图所示，在圆⊙O内有折线OABC，其中OA=8，AB=12，∠A=∠B=60°，则BC的长为（）A．19 B．16 C．18 D．20考点：垂径定理；等边三角形的判定与性质．分析：延长AO交BC于D，根据∠A、∠B的度数易证得△ABD是等边三角形，由此可求出OD、BD的长；过O作BC的垂线，设垂足为E；在Rt△ODE中，根据OD的长及∠ODE的度数易求得DE的长，进而可求出BE的长；由垂径定理知BC=2BE，由此得解．解答：解：延长AO交BC于D，作OE⊥BC于E；∵∠A=∠B=60°，∴∠ADB=60°；∴△ADB为等边三角形；∴BD=AD=AB=12；∴OD=4，又∵∠ADB=60°，∴DE=OD=2；∴BE=10；∴BC=2BE=20；故选D．点评：此题主要考查了等边三角形的判定和性质以及垂径定理的应用．8．（2010•台湾）如图，AB为圆O的直径，C、D两点均在圆上，其中OD与AC交于E点，且OD⊥AC．若OE=4，ED=2，则BC长度为（）A．6B．7C．8D．9考点：垂径定理；三角形中位线定理；圆周角定理．分析：由垂径定理易知E是AC的中点，而O是AB的中点，则OE是△ABC的中位线，得BC=2OE，由此得解．解答：解：∵半径OD⊥AC，∴E是AC的中点；又∵O是AB的中点，∴OE是△ABC的中位线；∴BC=2OE=8；故选C．点评：此题主要考查了垂径定理及三角形中位线定理的应用．9．（2010•绍兴）如图，已知⊙O的直径AB⊥弦CD于点E，下列结论中一定正确的是（）A．A E=OE B．C E=DE C．O E=CE D．∠AOC=60°考点：垂径定理．分析：根据垂径定理，即垂直于弦的直径平分弦即可判断．解答：解：∵⊙O的直径AB⊥弦CD，∴CE=DE．故选B．点评：本题考查了垂径定理，即垂直于弦的直径平分弦．10．（2009•攀枝花）在圆O中，圆O的半径为5cm，圆心O到弦AB的距离为4cm，则弦AB的长为（）A．3cm B．cm C．2cm D．6cm考点：垂径定理；勾股定理．分析：连接圆心和弦的一端，通过构建直角三角形来求得弦AB的长．解答：解：如图，连接OA；Rt△OAC中，OA=5cm，OC=4cm；由勾股定理，得：AC==3cm；∴AB=2AC=6cm；故选D．点评：此题主要考查了勾股定理及垂径定理的综合应用能力．11．（2010•牡丹江）如图，⊙O的直径AB=10cm，弦CD⊥AB，垂足为P．若OP：OB=3：5，则CD的长为（）A．6cm B．4cm C．8cm D．10cm考点：垂径定理；勾股定理．分析：根据⊙O的直径可得出半径OB的长，也就求出OP的长；连接OC，在Rt△OCP中，运用勾股定理可求出CP的长，进而可依据垂径定理求得CD的长．解答：解：连接OC；∵AB=10cm，∴OB=5cm；∵OP：OB=3：5，∴OP=3cm；Rt△OCP中，OC=OB=5cm，OP=3cm；由勾股定理，得：CP==4cm；所以CD=2PC=8cm，故选C．点评：此题主要考查的是勾股定理及垂径定理的应用．12．（2009•湘西州）⊙O的半径为10cm，弦AB=12cm，则圆心到AB的距离为（）A．2cm B．6cm C．8cm D．10cm考点：垂径定理；勾股定理．分析：画出草图，根据垂径定理和勾股定理求解．解答：解：弦AB=12cm，根据垂径定理可知BE=6．∵OB=10，∴OE=8．（勾股定理）故选C．点评：本题考查了利用勾股定理解直角三角形的能力，但在此题中也要用到垂径定理．13．（2008•衢州）如图，C是以AB为直径的⊙O上一点，已知AB=5，BC=3，则圆心O到弦BC的距离是（）A．1.5 B．2C．2.5 D．3考点：垂径定理；三角形中位线定理．分析：作OM⊥BC，根据三角形的中位线定理弦心距等于AC的一半，再利用勾股定理求出AC的长度，本题即可求出．解答：解：过圆心O作OM⊥BC于M，又根据AB直径，则AC⊥BC∴OM∥AC即OM是△ABC的中位线又AC===4∴OM=AC=2．故选B．点评：本题主要考查了垂径定理的内容，过圆心，且垂直于弦的直线，一定平分弦．14．（2007•福州）如图，⊙O中，弦AB的长为6cm，圆心O到AB的距离为4cm，则⊙O的半径长为（）A．3cm B．4cm C．5cm D．6cm考点：垂径定理；勾股定理．分析：过点O作OC⊥AB于点C．根据垂径定理和勾股定理求解．解答：解：过点O作OC⊥AB于点C∵弦AB的长为6cm，圆心O到AB的距离为4cm∴OC=4，AC=AB=3∴OA==5cm故选C．点评：本题考查了垂径定理和勾股定理的综合应用．15．（2008•长春）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=20，CD=16，那么线段OE的长为（）A．10 B．8C．6D．4考点：垂径定理；勾股定理．分析：先求出DE和圆的半径，再利用勾股定理即可求出．解答：解：∵弦CD⊥AB，垂足为E∴CE=DE=CD=×16=8∴OA是半径OA=AB=×20=10连接OD，在Rt△ODA中，OD=OA=10，DE=8OE===6故选C．点评：此题属简单题目，涉及到垂径定理及勾股定理的运用，需同学们细心解答．二、填空题（共15小题）（除非特别说明，请填准确值）16．（2011•孝感）如图，直径分别为CD、CE的两个半圆相切于点C，大半圆M的弦与小半圆N相切于点F，且AB∥CD，AB=4，设、的长分别为x、y，线段ED的长为z，则z（x+y）的值为8π．考点：垂径定理；勾股定理；切线的性质．专题：计算题．分析：过M作MG⊥AB于G，连MB，NF，根据垂径定理得到BG=AG=2，利用勾股定理可得MB2﹣MG2=22=4，再根据切线的性质有NF⊥AB，而AB∥CD，得到MG=NF，设⊙M，⊙N的半径分别为R，r，则z（x+y）=（CD﹣CE）（π•R+π•r）=（R2﹣r2）•2π，即可得到z（x+y）的值．解答：解：过M作MG⊥AB于G，连MB，NF，如图，而AB=4，∴BG=AG=2，∴MB2﹣MG2=22=4，又∵大半圆M的弦与小半圆N相切于点F，∴NF⊥AB，∵AB∥CD，∴MG=NF，设⊙M，⊙N的半径分别为R，∴z（x+y）=（CD﹣CE）（π•R+π•r），=（2R﹣2r）（R+r）•π，=（R2﹣r2）•2π，=4•2π，=8π．故答案为：8π．点评：本题考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧；也考查了切线的性质和圆的面积公式以及勾股定理．17．（2011•台州）如图，CD是⊙O的直径，弦AB⊥CD，垂足为点M，AB=20，分别以CM、DM为直径作两个大小不同的⊙O1和⊙O2，则图中阴影部分的面积为50π（结果保留π）．考点：垂径定理；勾股定理．专题：计算题．分析：连接CA，DA，根据垂径定理得到AM=MB=10，根据圆周角定理得到∠CAD=90°，易证Rt△MAC∽RtMA2=MC•MD=100；利用S阴影=S⊙O﹣S⊙1部分﹣S⊙2和圆的面积公式进行变形可得到阴影部分的面积=•CM•MD•π，即可计算出阴影部分的面积．解答：解：连接CA，DA，如图，∵AB⊥CD，AB=20，∴AM=MB=10，又∵CD为直径，∴∠CAD=90°，∴∠AMC=∠DMA=90°，∴∠C+∠CAM=90°，∠C+∠D=90°，∴∠CAM=∠D，∴Rt△MAC∽Rt△MDA，∴MA：MD=MC：MA，∴MA2=MC•MD=100；S阴影部分=S⊙O﹣S⊙1﹣S⊙2=π•CD2﹣π•CM2﹣π•DM2=π[CD2﹣CM2﹣（CD﹣CM）2]，=π（CM•CD﹣CM2），=•CM•MD•π，=50π．故答案为：50π．点评：本题考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧；也考查了圆周角定理和三角形相似的判定与性质以及圆的面积公式．18．（2011•宁德）如图，AB是半圆O的直径，OD⊥AC，OD=2，则弦BC的长为4．考点：垂径定理；三角形中位线定理．分析：此题需证出OD∥BC，再根据AO=BO，得出BC=2OD，即可求出答案．解答：解：∵AB是半圆O的直径，∴∠BCA=90°，∵OD⊥AC，∴∠ADO=90°，∴OD∥BC，∵AO=BO，∴OD是△ABC的中位线，∴BC=2OD=4．点评：此题综考查了垂径定理，关键是根据三角形的中位线定理求出答案．19．（2011•辽阳）如图，AB为⊙O直径，CD⊥AB，∠BDC=35°，则∠CAD=70°．考点：垂径定理；圆周角定理．分析：根据AB为⊙O直径，CD⊥AB得出∠BAD=∠BAC=∠BDC=35°，即可求出∠CAD=70°．解答：解：∵AB为⊙O直径，CD⊥AB，∴∠BAD=∠BAC=∠BDC=35°，∴∠CAD=70°．故填70．点评：此题要根据线段垂直平分线的性质证出等边三角形，再熟练运用圆周角定理求解．20．（2011•广安）如图所示，若⊙O 的半径为13cm，点P是弦AB上一动点，且到圆心的最短距离为5cm，则弦AB的长为24cm．考点：垂径定理；勾股专题：计算题．分析：过O点作OC⊥AB于C，连OA，根据垂线段最短得到OC=5cm，根据垂径定理得到AC=BC，再利用勾股定理计算出AC，即可得到AB．解答：解：过O点作OC⊥AB于C，连OA，如图，∴OC=5cm，AC=BC，在Rt△OAC中，OA=13cm，∴AC===12（cm），∴AB=2AC=24cm．故答案为：24cm．点评：本题考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧．也考查了勾股定理．21．（2010•毕节地区）如图，在⊙O中，直径AB的长为，弦CD⊥AB于E，∠BDC=30°则弦CD的长为3．考点：垂径定理；含30度角的直角三角形；勾股定理；圆周角定理；特殊角的三角函数值．分析：连接BD，由∠BDC=30°，即可推出∠BOC=60°，再由AB的长为，求出OC的长度，然后根据特殊角的三角函数值即可推出CE的长度，最后由垂径定理推出CD=2CE，通过计算即可求出CD的长度．解答：解：连接BD，∵∠BDC=30°，∴∠BOC=60°，∵AB=，∴OC=，∵CD⊥AB，∴∠OEC=90°，CD=2CE，∴cos30°==，∵OC=，∴CE=，∴CD=3．故答案为3．点评：本题主要考查圆周角定理，特殊角的三角函数值，垂径定理等知识点，关键在于首先运用圆周角定理推出∠COE的度数，然后根据特殊角的三角函数值推出CE的长度，最后根据垂径定理即可推出CD的长度．22．（2011•厦门）如图，⊙O的直径CD垂直于弦AB，垂足为E．若AB=6cm，则AE=3cm．考点：垂径定理；勾股定理．分析：由⊙O的直径CD垂直于弦AB，AB=6cm，根据垂径定理，即可求得AE的长．解答：解：∵⊙O的直径CD垂直于弦AB，∴AE=AB，∵AB=6cm，∴AE=3cm．故答案为：3．点评：此题考查了垂识．此题比较简单，解题的关键是熟记垂径定理，注意数形结合思想的应用．23．（2011•深圳）如图，在⊙O中，圆心角∠AOB=12O°，弦，则OA=2cm．考点：垂径定理；解直角三角形．分析：过点O作OC⊥AB，根据垂径定理，可得出AC的长，再由余弦函数求得OA的长．解答：解：过点O作OC⊥AB，∴AC=AB，∵AB=2cm，∴AC=cm，∵∠AOB=12O°，OA=OB，∴∠A=30°，在直角三角形OAC中，cos∠A==，∴OA==2cm，故答案为2．点评：本题考查了垂径定理和解直角三角形，是基础知识要熟练掌握．24．（2011•黑龙江）如图，已知⊙O的半径为4，OC垂直弦AB于点C，∠AOB=120°，则弦AB长为4．考点：垂径定理；解直角三角形．专题：计算题．分析：利用等腰三角形的性质和垂径定理得到特殊的直角三角形，然后解直角三角形求得AB的一半AC的长即可求AB的长．解答：解：∵OC垂直弦AB于点C，∴OA=OB，AC=BC，∵∠AOB=120°，∴∠AOC=60°，∵⊙O的半径为4，∴AB=2AC=4cm．故答案为4．点评：本题考查了垂径定理及解直角三角形的知识，解题的关键是利用垂径定理得到直角三角形．25．（2010•海南）如图，将半径为4cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长度为cm．考点：垂径定理；勾股定理．专题：计算题．分析：先过点O作OC⊥AB，垂足为C，连接OA，由题意求得OC，由勾股定理求得AC，再由垂径定理求得AB的值即可．解答：解：如图，过点O作OC⊥AB，垂足为C，连接OA，∵OA=4cm，∴OC=2cm，∴AC=2cm，∴AB=4cm，故答案为：4．点评：本题考查了勾股定理和垂径定理，解答这类题一些学生不会综合运用所学知识解答问题，不知从何处入手造成错解．26．（2010•玉溪）如图，在半径为10的⊙O中，OC垂直弦AB于点D，AB=16，则CD的长是4．考点：垂径定理；勾股定理．分析：连接OA，在Rt△OAD中，由垂径定理易知AD的长，再由勾股定理可求出OD的长；而CD=OC﹣OD，由此得解．解答：解：连接OA；Rt△OAD中，AD=AB=8，OA=10；由勾股定理得：OD==6；∴CD=OC﹣OD=10﹣6=4．故答案为：4．点评：此题主要考查垂径定理及勾股定理的应用．27．（2010•北京）如图，AB为圆O的直径，弦CD⊥AB，垂足为点E，连接OC，若OC=5，CD=8，则AE=2．考点：垂径定理；勾股定理．分析：根据垂径定理可以得到CE的长，在直角△OCE中，根据勾股定理即可求得．解答：解：∵AB为圆O的直径，弦CD⊥AB，垂足为点E．∴CE=CD=4．在直角△OCE中，OE===3．则AE=OA﹣OE=5﹣3=2．点评：此题涉及圆中求半径的问题，此类在圆中涉及弦长、半径、圆心角的计算的问题，常把半弦长，半圆心角，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解，常见辅助线是过圆心作弦的垂线．28．（2010•镇江）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=10，CD=8，那么线段OE的长为3．考点：垂径定理；勾股定理．分析：连接OC，由垂径定理可求出CE的长度，在Rt△OCE中，根据CE和⊙O的半径，即可由勾股定理求出OE的长．解答：解：连接OC；Rt△OCE中，OC=AB=5，CE=CD=4；由勾股定理，得：OE==3；即线段OE的长为3．点评：此题考查的是垂径定理及勾股定理的应用．29．（2010•厦门）⊙O的直径为10，圆心O到弦AB的距离为3，则弦AB的长是8．考点：垂径定理；勾股定理．分析：先求出半径，再利用勾股定理求出半弦长，弦长就可以求出了．解答：解：如图，根据题意，得OA=×10=5，AE===4∴AB=2AE=8．点评：利用半径、半弦长、弦心距构造直角三角形，利用勾股定理求解．30．（2010•文山州）如图，⊙O的弦AB=6，M是AB上任意一点，且OM最小值为4，则⊙O的半径为5．考点：垂径定理；勾股定理．分析：OM最小值为4，即弦AB的弦心距为4，构造直角三角形，根据垂径定理和勾股定理，可求出圆O的半径为5．解答：解：如图，连接OA，OM⊥AB，∴OM=4，∵AB=6，∴AM=BM=AB=3，在Rt△AOM中，OA=，所以⊙O的半径为5．点评：解决与弦有关的问题时，往往需构造以半径、弦心距和弦长的一半为三边的直角三角形，若设圆的半径为r，弦长为a，这条弦的弦心距为d，则有等式r2=d2+（）2成立，知道这三个量中的任意两个，就可以求出另外一个．。

2019年中考数学复习:垂径定理(圆)一、选择题(共１５小题)1、如图,Ａ点是半圆上一个三等分点,B点是弧AＮ的中点,P点是直径MＮ上一动点,⊙O的半径为１,则AP+BＰ的最小值为( )A。

1ﻩB、ﻩC、D、2、如图,梯形ABCD中,AＢ∥DC,ＡＢ⊥BC,AB=２cm,CＤ=４cｍ、以ＢC上一点O 为圆心的圆经过A、Ｄ两点,且∠AＯD=90°,则圆心O到弦AD的距离是( )A、ｃmﻩＢ、ｃm Ｃ、cmﻩD、cm3。

如图,在平面直角坐标系中,⊙Ｐ的圆心坐标是(3,a)(ａ＞3),半径为3,函数y＝ｘ的图象被⊙P截得的弦ＡB的长为,则ａ的值是( )Ａ、４ﻩＢ、ﻩC、D、４、已知⊙O的半径为10,P为⊙O内一点,且OP=6,则过Ｐ点,且长度为整数的弦有( )Ａ。

5条ﻩB。

6条ﻩC、8条D。

１0条5、已知⊙O的半径OA=2,弦AＢ,AC的长分别是2,2,则∠ＢAC的度数为()A、15°Ｂ、7５°C、15°或75°ﻩD、15°或45°6、如图,四边形PAOB是扇形OＭＮ的内接矩形,顶点P在上,且不与M,N重合,当Ｐ点在上移动时,矩形PＡOB的形状、大小随之变化,则ＡB的长度()A、变大Ｂ、变小C、不变D。

不能确定７、给出下列四个命题:(1)假如某圆锥的侧面展开图是半圆,则其轴截面一定是等边三角形;(２)若点A在直线ｙ=２ｘ﹣３上,且点Ａ到两坐标轴的距离相等,则点Ａ在第一或第四象限;(3)半径为５的圆中,弦AB=８,则圆周上到直线AB的距离为２的点共有四个; (４)若A(a,m)、B(a﹣１,n)(a〉0)在反比例函y=的图象上,则m〈ｎ、其中,正确命题的个数是( )A、1个ﻩB。

２个C、3个ﻩＤ、4个８、已知⊙O的半径为10cm,弦AB∥ＣD,AＢ=1２cm,CＤ=１６cｍ,则AB和ＣD 的距离为( )A、2cmﻩB。

１4cmﻩC、2cm或1４ｃmﻩD、１0cm或20cｍ9、已知⊙O的半径为３,△ＡBＣ内接于⊙Ｏ,AB=3,AC=３,Ｄ是⊙O上一点,且AD ＝３,则ＣD的长应是( )Ａ。

垂径定理精选题35道一．选择题（共15小题）1．如图，⊙O的直径AB垂直于弦CD，垂足为E，∠A＝22.5°，OC＝4，CD的长为（）A．2B．4C．4D．82．如图，在平面直角坐标系中，⊙P的圆心坐标是（3，a）（a＞3），半径为3，函数y＝x的图象被⊙P截得的弦AB的长为，则a的值是（）A．4B．C．D．3．如图，AB是⊙O的直径，弦CD交AB于点P，AP＝2，BP＝6，∠APC＝30°，则CD 的长为（）A．B．2C．2D．84．如图，在半径为3的⊙O中，AB是直径，AC是弦，D是的中点，AC与BD交于点E．若E是BD的中点，则AC的长是（）A．B．3C．3D．45．已知⊙O的直径CD＝10cm，AB是⊙O的弦，AB⊥CD，垂足为M，且AB＝8cm，则AC 的长为（）A．2cm B．4cm C．2cm或4cm D．2cm或4 cm6．已知⊙O的直径CD＝10cm，AB是⊙O的弦，AB＝8cm，且AB⊥CD，垂足为M，则AC 的长为（）A．cm B．cm C．cm或cm D．cm或cm7．如图，在⊙O中，半径OC与弦AB垂直于点D，且AB＝8，OC＝5，则CD的长是（）A．3B．2.5C．2D．18．如图，⊙O的直径为10，弦AB的长为6，M是弦AB上的一动点，则线段的OM的长的取值范围是（）A．3≤OM≤5B．4≤OM≤5C．3＜OM＜5D．4＜OM＜5 9．如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC．若∠BAC与∠BOC 互补，则弦BC的长为（）A．3B．4C．5D．610．如图，⊙O的半径OD⊥弦AB于点C，连接AO并延长交⊙O于点E，连接EC．若AB ＝8，OC＝3，则EC的长为（）A．B．8C．D．11．已知如图，AB是⊙O的直径，弦CD⊥AB于E，CD＝6，AE＝1，则⊙O的直径为（）A．6B．8C．10D．1212．点P是⊙O内一点，过点P的最长弦的长为10cm，最短弦的长为6cm，则OP的长为（）A．3cm B．4cm C．5cm D．6cm13．⊙O的半径为5，M是圆外一点，MO＝6，∠OMA＝30°，则弦AB的长为（）A．4B．6C．6D．814．如图，CD为⊙O直径，CD⊥AB于点F，AE⊥BC于E，AE过圆心O，且AO＝1．则四边形BEOF的面积为（）A．B．C．D．15．△ABC中，∠C＝90°，AC＝3，BC＝4，以点C为圆心，CA为半径的圆与AB、BC分别交于点E、D，则AE的长为（）A．B．C．D．二．填空题（共14小题）16．如图，AB是⊙O的直径，点C是⊙O上的一点，若BC＝6，AB＝10，OD⊥BC于点D，则OD的长为．17．如图，在⊙O中，弦AB＝1，点C在AB上移动，连接OC，过点C作CD⊥OC交⊙O 于点D，则CD的最大值为．18．如图，AB是⊙O的直径，CD为⊙O的一条弦，CD⊥AB于点E，已知CD＝4，AE＝1，则⊙O的半径为．19．如图，以G（0，1）为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C，D 两点，点E为⊙G上一动点，CF⊥AE于F，则弦AB的长度为；当点E在⊙G 的运动过程中，线段FG的长度的最小值为．20．如图，方格纸上每个小正方形的边长均为1个单位长度，点O，A，B，C在格点（两条网格线的交点叫格点）上，以点O为原点建立直角坐标系，则过A，B，C三点的圆的圆心坐标为．21．如图，△ABC中，∠BAC＝60°，∠ABC＝45°，AB＝2，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连接EF，则线段EF长度的最小值为．22．已知⊙O的半径为10cm，AB，CD是⊙O的两条弦，AB∥CD，AB＝16cm，CD＝12cm，则弦AB和CD之间的距离是cm．23．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，连接AC．若∠CAB＝22.5°，CD＝8cm，则⊙O的半径为cm．24．如图，在⊙O中，半径OD垂直于弦AB，垂足为C，OD＝13cm，AB＝24cm，则CD＝cm．25．如图，在平面直角坐标系xOy中，直线y＝x+与⊙O相交于A，B两点，且点A在x轴上，则弦AB的长为．26．已知⊙O的直径为10cm，AB，CD是⊙O的两条弦，AB∥CD，AB＝8cm，CD＝6cm，则AB与CD之间的距离为cm．27．如图，圆O的直径AB垂直于弦CD，垂足是E，∠A＝22.5°，OC＝4，CD的长为．28．如图，AB为⊙O的直径，弦CD⊥AB于点H，若AB＝10，CD＝8，则OH的长度为．29．如图所示，在⊙O内有折线OABC，其中OA＝8，AB＝12，∠A＝∠B＝60°，则BC的长为．三．解答题（共6小题）30．如图，AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，MD恰好经过圆心O，连接MB．（1）若CD＝16，BE＝4，求⊙O的直径；（2）若∠M＝∠D，求∠D的度数．31．如图，⊙O中，直径CD⊥弦AB于E，AM⊥BC于M，交CD于N，连接AD．（1）求证：AD＝AN；（2）若AB＝8，ON＝1，求⊙O的半径．32．如图，在圆O中，弦AB＝8，点C在圆O上（C与A，B不重合），连接CA、CB，过点O分别作OD⊥AC，OE⊥BC，垂足分别是点D、E．（1）求线段DE的长；（2）点O到AB的距离为3，求圆O的半径．33．如图，CD为⊙O的直径，CD⊥AB，垂足为点F，AO⊥BC，垂足为点E，BC＝3．（1）求AB的长；（2）求⊙O的半径．34．如图，四边形ABCD内接于⊙O，OC＝4，AC＝4．（1）求点O到AC的距离；（2）求∠ADC的度数．35．筒车是我国古代发明的一种水利灌溉工具，彰显了我国古代劳动人民的智慧，图1，点P表示筒车的一个盛水桶．如图2，当筒车工作时，盛水桶的运行路径是以轴心O为圆心，5m为半径的圆，且圆心在水面上方．若圆被水面截得的弦AB长为8m，求筒车工作时，盛水桶在水面以下的最大深度．垂径定理精选题35道参考答案与试题解析一．选择题（共15小题）1．如图，⊙O的直径AB垂直于弦CD，垂足为E，∠A＝22.5°，OC＝4，CD的长为（）A．2B．4C．4D．8【分析】根据圆周角定理得∠BOC＝2∠A＝45°，由于⊙O的直径AB垂直于弦CD，根据垂径定理得CE＝DE，且可判断△OCE为等腰直角三角形，所以CE＝OC＝2，然后利用CD＝2CE进行计算．【解答】解：∵∠A＝22.5°，∴∠BOC＝2∠A＝45°，∵⊙O的直径AB垂直于弦CD，∴CE＝DE，△OCE为等腰直角三角形，∴CE＝OC＝2，∴CD＝2CE＝4．故选：C．【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了等腰直角三角形的性质和垂径定理．2．如图，在平面直角坐标系中，⊙P的圆心坐标是（3，a）（a＞3），半径为3，函数y＝x的图象被⊙P截得的弦AB的长为，则a的值是（）A．4B．C．D．【分析】PC⊥x轴于C，交AB于D，作PE⊥AB于E，连接PB，由于OC＝3，PC＝a，易得D点坐标为（3，3），则△OCD为等腰直角三角形，△PED也为等腰直角三角形．由PE⊥AB，根据垂径定理得AE＝BE＝AB＝2，在Rt△PBE中，利用勾股定理可计算出PE＝1，则PD＝PE＝，所以a＝3+．【解答】解：作PC⊥x轴于C，交AB于D，作PE⊥AB于E，连接PB，如图，∵⊙P的圆心坐标是（3，a），∴OC＝3，PC＝a，把x＝3代入y＝x得y＝3，∴D点坐标为（3，3），∴CD＝3，∴△OCD为等腰直角三角形，∴△PED也为等腰直角三角形，∵PE⊥AB，∴AE＝BE＝AB＝×4＝2，在Rt△PBE中，PB＝3，∴PE＝，∴PD＝PE＝，∴a＝3+．故选：B．【点评】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理和等腰直角三角形的性质．3．如图，AB是⊙O的直径，弦CD交AB于点P，AP＝2，BP＝6，∠APC＝30°，则CD 的长为（）A．B．2C．2D．8【分析】作OH⊥CD于H，连接OC，如图，根据垂径定理由OH⊥CD得到HC＝HD，再利用AP＝2，BP＝6可计算出半径OA＝4，则OP＝OA﹣AP＝2，接着在Rt△OPH中根据含30度的直角三角形的性质计算出OH＝OP＝1，然后在Rt△OHC中利用勾股定理计算出CH＝，所以CD＝2CH＝2．【解答】解：作OH⊥CD于H，连接OC，如图，∵OH⊥CD，∴HC＝HD，∵AP＝2，BP＝6，∴AB＝8，∴OA＝4，∴OP＝OA﹣AP＝2，在Rt△OPH中，∵∠OPH＝∠APC＝30°，∴∠POH＝60°，∴OH＝OP＝1，在Rt△OHC中，∵OC＝4，OH＝1，∴CH＝＝，∴CD＝2CH＝2．故选：C．【点评】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理以及含30度的直角三角形的性质．4．如图，在半径为3的⊙O中，AB是直径，AC是弦，D是的中点，AC与BD交于点E．若E是BD的中点，则AC的长是（）A．B．3C．3D．4【分析】连接OD，交AC于F，根据垂径定理得出OD⊥AC，AF＝CF，进而证得DF＝BC，根据三角形中位线定理求得OF＝BC＝DF，从而求得BC＝DF＝2，利用勾股定理即可求得AC．【解答】解：连接OD，交AC于F，∵D是的中点，∴OD⊥AC，AF＝CF，∴∠DFE＝90°，∵OA＝OB，AF＝CF，∴OF＝BC，∵AB是直径，∴∠ACB＝90°，在△EFD和△ECB中∴△EFD≌△ECB（AAS），∴DF＝BC，∴OF＝DF，∵OD＝3，∴OF＝1，∴BC＝2，在Rt△ABC中，AC2＝AB2﹣BC2，∴AC＝＝＝4，故选：D．【点评】本题考查了垂径定理，三角形全等的判定和性质，三角形中位线定理，熟练掌握性质定理是解题的关键．5．已知⊙O的直径CD＝10cm，AB是⊙O的弦，AB⊥CD，垂足为M，且AB＝8cm，则AC 的长为（）A．2cm B．4cm C．2cm或4cm D．2cm或4 cm【分析】先根据题意画出图形，由于点C的位置不能确定，故应分两种情况进行讨论．【解答】解：连接AC，AO，∵⊙O的直径CD＝10cm，AB⊥CD，AB＝8cm，∴AM＝AB＝×8＝4（cm），OD＝OC＝5cm，当C点位置如图1所示时，∵OA＝5cm，AM＝4cm，CD⊥AB，∴OM＝＝＝3（cm），∴CM＝OC+OM＝5+3＝8（cm），∴AC＝＝＝4（cm）；当C点位置如图2所示时，同理可得OM＝3cm，∵OC＝5cm，∴MC＝5﹣3＝2（cm），在Rt△AMC中，AC＝＝＝2（cm）．故选：C．【点评】本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．6．已知⊙O的直径CD＝10cm，AB是⊙O的弦，AB＝8cm，且AB⊥CD，垂足为M，则AC 的长为（）A．cm B．cm C．cm或cm D．cm或cm【分析】先根据题意画出图形，由于点C的位置不能确定，故应分两种情况进行讨论．【解答】解：如图，连接AC，AO，∵⊙O的直径CD＝10cm，AB⊥CD，AB＝8cm，∴AM＝AB＝×8＝4cm，OD＝OC＝5cm，当C点位置如图1所示时，∵OA＝5cm，AM＝4cm，CD⊥AB，∴OM＝＝＝3cm，∴CM＝OC+OM＝5+3＝8cm，∴AC＝＝＝4cm；当C点位置如图2所示时，同理可得OM＝3cm，∵OC＝5cm，∴MC＝5﹣3＝2cm，在Rt△AMC中，AC＝＝＝2cm．故选：C．【点评】本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．7．如图，在⊙O中，半径OC与弦AB垂直于点D，且AB＝8，OC＝5，则CD的长是（）A．3B．2.5C．2D．1【分析】根据垂径定理以及勾股定理即可求答案．【解答】解：连接OA，设CD＝x，∵OA＝OC＝5，∴OD＝5﹣x，∵OC⊥AB，∴由垂径定理可知：AD＝4，由勾股定理可知：52＝42+（5﹣x）2∴x＝2，∴CD＝2，故选：C．【点评】本题考查垂径定理，解题的关键是熟练运用垂径定理以及勾股定理，本题属于基础题型．8．如图，⊙O的直径为10，弦AB的长为6，M是弦AB上的一动点，则线段的OM的长的取值范围是（）A．3≤OM≤5B．4≤OM≤5C．3＜OM＜5D．4＜OM＜5【分析】由垂线段最短可知当OM⊥AB时最短，当OM是半径时最长．根据垂径定理求最短长度．【解答】解：如图，连接OA，作OM⊥AB于M，∵⊙O的直径为10，∴半径为5，∴OM的最大值为5，∵OM⊥AB于M，∴AM＝BM，∵AB＝6，∴AM＝3，在Rt△AOM中，OM＝＝＝＝4；此时OM最短，所以OM长的取值范围是4≤OM≤5．故选：B．【点评】本题考查了垂径定理、勾股定理，解决本题的关键是确定OM的最小值，所以求OM的范围问题又被转化为求弦的弦心距问题，而解决与弦有关的问题时，往往需构造以半径、弦心距和弦长的一半为三边的直角三角形，若设圆的半径为r，弦长为a，这条弦的弦心距为d，则有等式r2＝d2+（）2成立，知道这三个量中的任意两个，就可以求出另外一个．9．如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC．若∠BAC与∠BOC 互补，则弦BC的长为（）A．3B．4C．5D．6【分析】首先过点O作OD⊥BC于D，由垂径定理可得BC＝2BD，又由圆周角定理，可求得∠BOC的度数，然后根据等腰三角形的性质，求得∠OBC的度数，利用余弦函数，即可求得答案．【解答】解：过点O作OD⊥BC于D，则BC＝2BD，∵△ABC内接于⊙O，∠BAC与∠BOC互补，∴∠BOC＝2∠A，∠BOC+∠A＝180°，∴∠BOC＝120°，∵OB＝OC，∴∠OBC＝∠OCB＝（180°﹣∠BOC）＝30°，∵⊙O的半径为4，∴BD＝OB•cos∠OBC＝4×＝2，∴BC＝4．故选：B．【点评】此题考查了圆周角定理、垂径定理、等腰三角形的性质以及三角函数等知识．注意掌握辅助线的作法，注意数形结合思想的应用．10．如图，⊙O的半径OD⊥弦AB于点C，连接AO并延长交⊙O于点E，连接EC．若AB ＝8，OC＝3，则EC的长为（）A．B．8C．D．【分析】根据垂径定理求出AC＝BC，根据三角形的中位线求出BE，再根据勾股定理求出EC即可．【解答】解：连接BE，∵AE为⊙O直径，∴∠ABE＝90°，∵OD⊥AB，OD过O，∴AC＝BC＝AB＝＝4，∵AO＝OE，∴BE＝2OC，∵OC＝3，∴BE＝6，在Rt△CBE中，EC＝＝＝2，故选：D．【点评】本题考查了垂径定理，勾股定理，三角形的中位线等知识点，能根据垂径定理求出AC＝BC是解此题的关键．11．已知如图，AB是⊙O的直径，弦CD⊥AB于E，CD＝6，AE＝1，则⊙O的直径为（）A．6B．8C．10D．12【分析】连接OC，根据题意OE＝OC﹣1，CE＝3，结合勾股定理，可求出OC的长度，即可求出直径的长度．【解答】解：连接OC，∵弦CD⊥AB于E，CD＝6，AE＝1，∴OE＝OC﹣1，CE＝3，∴OC2＝（OC﹣1）2+32，∴OC＝5，∴AB＝10．故选：C．【点评】本题主要考查了垂径定理、勾股定理，解题的关键在于连接OC，构建直角三角形，根据勾股定理求半径OC的长度．12．点P是⊙O内一点，过点P的最长弦的长为10cm，最短弦的长为6cm，则OP的长为（）A．3cm B．4cm C．5cm D．6cm【分析】根据直径是圆中最长的弦，知该圆的直径；最短弦即是过点P且垂直于过点P 的直径的弦；根据垂径定理即可求得CP的长，再进一步根据勾股定理，可以求得OP的长．【解答】解：如图所示，CD⊥AB于点P．根据题意，得：AB＝10cm，CD＝6cm．∵AB是直径，且CD⊥AB，∴CP＝CD＝3cm．根据勾股定理，得OP＝＝＝4（cm）．故选：B．【点评】此题综合运用了垂径定理和勾股定理．正确理解圆中，过一点的最长的弦和最短的弦是解题的关键．13．⊙O的半径为5，M是圆外一点，MO＝6，∠OMA＝30°，则弦AB的长为（）A．4B．6C．6D．8【分析】过O作OC⊥AB于C，连接OA，根据含30°角的直角三角形的性质得出OC＝MO＝3，根据勾股定理求出AC，再根据垂径定理得出AB＝2AC，最后求出答案即可．【解答】解：过O作OC⊥AB于C，连接OA，则∠OCA＝90°，∵MO＝6，∠OMA＝30°，∴OC＝MO＝3，在Rt△OCA中，由勾股定理得：AC＝＝＝4，∵OC⊥AB，OC过O，∴BC＝AC，即AB＝2AC＝2×4＝8，故选：D．【点评】本题考查了含30°角的直角三角形的性质，勾股定理，垂径定理等知识点，能熟记垂直于弦的直径平分弦是解此题的关键．14．如图，CD为⊙O直径，CD⊥AB于点F，AE⊥BC于E，AE过圆心O，且AO＝1．则四边形BEOF的面积为（）A．B．C．D．【分析】根据垂径定理求出AF＝BF，CE＝BE，＝，求出∠AOD＝2∠C，求出∠AOD＝2∠A，求出∠A＝30°，解直角三角形求出OF和BF，求出OE、BE、BF，根据三角形的面积公式求出即可．【解答】解：∵CD为直径，CD⊥AB，∴＝，∴∠AOD＝2∠C，∵CD⊥AB，AE⊥BC，∴∠AFO＝∠CEO＝90°，在△AFO和△CEO中∴△AFO≌△CEO（AAS），∴∠C＝∠A，∴∠AOD＝2∠A，∵∠AFO＝90°，∴∠A＝30°，∵AO＝1，∴OF＝AO＝，AF＝OF＝，同理CE＝，OE＝，连接OB，∵CD⊥AB，AE⊥BC，CD、AE过O，∴由垂径定理得：BF＝AF＝，BE＝CE＝，∴四边形BEOF的面积S＝S△BFO+S△BEO＝××+＝，故选：C．【点评】本题考查了垂径定理，圆周角定理，解直角三角形等知识点，能够综合运用定理进行推理是解此题的关键．15．△ABC中，∠C＝90°，AC＝3，BC＝4，以点C为圆心，CA为半径的圆与AB、BC分别交于点E、D，则AE的长为（）A．B．C．D．【分析】在Rt△ABC中，由勾股定理可直接求得AB的长；过C作CM⊥AB，交AB于点M，由垂径定理可得M为AE的中点，在Rt△ACM中，根据勾股定理得AM的长，从而得到AE的长．【解答】解：在Rt△ABC中，∵AC＝3，BC＝4，∴AB＝＝5．过C作CM⊥AB，交AB于点M，如图所示，由垂径定理可得M为AE的中点，∵S△ABC＝AC•BC＝AB•CM，且AC＝3，BC＝4，AB＝5，∴CM＝，在Rt△ACM中，根据勾股定理得：AC2＝AM2+CM2，即9＝AM2+（）2，解得：AM＝，∴AE＝2AM＝．故选：C．【点评】本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．二．填空题（共14小题）16．如图，AB是⊙O的直径，点C是⊙O上的一点，若BC＝6，AB＝10，OD⊥BC于点D，则OD的长为4．【分析】根据垂径定理求得BD，然后根据勾股定理求得即可．【解答】解：∵OD⊥BC，∴BD＝CD＝BC＝3，∵OB＝AB＝5，∴OD＝＝4．故答案为4．【点评】题考查了垂径定理、勾股定理，本题非常重要，学生要熟练掌握．17．如图，在⊙O中，弦AB＝1，点C在AB上移动，连接OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为．【分析】连接OD，如图，利用勾股定理得到CD，利用垂线段最短得到当OC⊥AB时，OC最小，再求出即可．【解答】解：连接OD，如图，∵CD⊥OC，∴∠DCO＝90°，∴CD＝＝，当OC的值最小时，CD的值最大，而OC⊥AB时，OC最小，此时D、B两点重合，∴CD＝CB＝AB＝×1＝，即CD的最大值为，故答案为：．【点评】本题考查了垂线段最短，勾股定理和垂径定理等知识点，能求出点C的位置是解此题的关键．18．如图，AB是⊙O的直径，CD为⊙O的一条弦，CD⊥AB于点E，已知CD＝4，AE＝1，则⊙O的半径为．【分析】连接OC，由垂径定理得出CE＝CD＝2，设OC＝OA＝x，则OE＝x﹣1，由勾股定理得出CE2+OE2＝OC2，得出方程，解方程即可．【解答】解：连接OC，如图所示：∵AB是⊙O的直径，CD⊥AB，∴CE＝CD＝2，∠OEC＝90°，设OC＝OA＝x，则OE＝x﹣1，根据勾股定理得：CE2+OE2＝OC2，即22+（x﹣1）2＝x2，解得：x＝；故答案为：．【点评】本题考查了垂径定理、勾股定理、解方程；熟练掌握垂径定理，并能进行推理计算是解决问题的关键．19．如图，以G（0，1）为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C，D 两点，点E为⊙G上一动点，CF⊥AE于F，则弦AB的长度为2；当点E在⊙G的运动过程中，线段FG的长度的最小值为﹣1．【分析】作GM⊥AC于M，连接AG．因为∠AFC＝90°，推出点F在以AC为直径的⊙M上推出当点F在MG的延长线上时，FG的长最小，最小值＝FM﹣GM，想办法求出FM、GM即可解决问题；【解答】解：作GM⊥AC于M，连接AG．∵GO⊥AB，∴OA＝OB，在Rt△AGO中，∵AG＝2，OG＝1，∴AG＝2OG，OA＝＝，∴∠GAO＝30°，AB＝2AO＝2，∴∠AGO＝60°，∵GC＝GA，∴∠GCA＝∠GAC，∵∠AGO＝∠GCA+∠GAC，∴∠GCA＝∠GAC＝30°，∴AC＝2OA＝2，MG＝CG＝1，∵∠AFC＝90°，∴点F在以AC为直径的⊙M上，当点F在MG的延长线上时，FG的长最小，最小值＝FM﹣GM＝﹣1．故答案为2，﹣1．【点评】本题考查垂径定理、直角三角形30度角的判定和性质、勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考填空题中的压轴题．20．如图，方格纸上每个小正方形的边长均为1个单位长度，点O，A，B，C在格点（两条网格线的交点叫格点）上，以点O为原点建立直角坐标系，则过A，B，C三点的圆的圆心坐标为（﹣1，﹣2）．【分析】连接CB，作CB的垂直平分线，根据勾股定理和半径相等得出点D的坐标即可．【解答】解：连接CB，作CB的垂直平分线，如图所示：在CB的垂直平分线上找到一点D，CD＝DB＝DA＝＝，所以D是过A，B，C三点的圆的圆心，即D的坐标为（﹣1，﹣2），故答案为：（﹣1，﹣2），【点评】此题考查垂径定理，关键是根据垂径定理得出圆心位置．21．如图，△ABC中，∠BAC＝60°，∠ABC＝45°，AB＝2，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连接EF，则线段EF长度的最小值为．【分析】由垂线段的性质可知，当AD为△ABC的边BC上的高时，直径AD最短，此时线段EF＝2EH＝20E•sin∠EOH＝20E•sin60°，因此当半径OE最短时，EF最短，连接OE，OF，过O点作OH⊥EF，垂足为H，在Rt△ADB中，解直角三角形求直径AD，由圆周角定理可知∠EOH＝∠EOF＝∠BAC＝60°，在Rt△EOH中，解直角三角形求EH，由垂径定理可知EF＝2EH．【解答】解：由垂线段的性质可知，当AD为△ABC的边BC上的高时，直径AD最短，如图，连接OE，OF，过O点作OH⊥EF，垂足为H，∵在Rt△ADB中，∠ABC＝45°，AB＝2，∴AD＝BD＝2，即此时圆的直径为2，由圆周角定理可知∠EOH＝∠EOF＝∠BAC＝60°，∴在Rt△EOH中，EH＝OE•sin∠EOH＝1×＝，由垂径定理可知EF＝2EH＝．故答案为：．【点评】本题考查了垂径定理，圆周角定理，解直角三角形的综合运用．关键是根据运动变化，找出满足条件的最小圆，再解直角三角形．22．已知⊙O的半径为10cm，AB，CD是⊙O的两条弦，AB∥CD，AB＝16cm，CD＝12cm，则弦AB和CD之间的距离是2或14cm．【分析】分两种情况进行讨论：①弦AB和CD在圆心同侧；②弦AB和CD在圆心异侧；作出半径和弦心距，利用勾股定理和垂径定理求解即可，小心别漏解．【解答】解：①当弦AB和CD在圆心同侧时，连接OA，OC，过点O作OE⊥AB于点E并延长交CD于点F．如图，∵AB＝16cm，CD＝12cm，∴AE＝8cm，CF＝6cm，∵OA＝OC＝10cm，∴EO＝6cm，OF＝8cm，∴EF＝OF﹣OE＝2cm；②当弦AB和CD在圆心异侧时，如图，∵AB＝16cm，CD＝12cm，∴AF＝8cm，CE＝6cm，∵OA＝OC＝10cm，∴OF＝6cm，OE＝8cm，∴EF＝OF+OE＝14cm．∴AB与CD之间的距离为14cm或2cm．故答案为：2或14．【点评】本题考查了勾股定理和垂径定理的应用．此题难度适中，解题的关键是注意掌握数形结合思想与分类讨论思想的应用，小心别漏解．23．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，连接AC．若∠CAB＝22.5°，CD＝8cm，则⊙O的半径为4cm．【分析】连接OC，如图所示，由直径AB垂直于CD，利用垂径定理得到E为CD的中点，即CE＝DE，由OA＝OC，利用等边对等角得到一对角相等，确定出三角形COE为等腰直角三角形，求出OC的长，即为圆的半径．【解答】解：连接OC，如图所示：∵AB是⊙O的直径，弦CD⊥AB，∴CE＝DE＝CD＝4cm，∵OA＝OC，∴∠A＝∠OCA＝22.5°，∵∠COE为△AOC的外角，∴∠COE＝45°，∴△COE为等腰直角三角形，∴OC＝CE＝4cm，故答案为：4【点评】此题考查了垂径定理，等腰直角三角形的性质，以及圆周角定理，熟练掌握垂径定理是解本题的关键．24．如图，在⊙O中，半径OD垂直于弦AB，垂足为C，OD＝13cm，AB＝24cm，则CD＝8cm．【分析】根据垂径定理，可得AC的长，根据勾股定理，可得OC的长，根据线段的和差，可得答案．【解答】解：由垂径定理，AC＝AB＝12cm．由半径相等，得OA＝OD＝13cm．由勾股定理，得OC＝＝＝5．由线段的和差，得CD＝OD﹣OC＝13﹣5＝8cm，故答案为：8．【点评】本题考查了垂径定理，利用垂径定理得出直角三角形OAC是解题关键，又利用了勾股定理．25．如图，在平面直角坐标系xOy中，直线y＝x+与⊙O相交于A，B两点，且点A在x轴上，则弦AB的长为2．【分析】设直线AB交y轴于C，过O作OD⊥AB于D，先求出A、C坐标，得到OA、OC长度，可得∠CAO＝30°，Rt△AOD中求出AD长度，从而根据垂径定理可得答案．【解答】解：设直线AB交y轴于C，过O作OD⊥AB于D，如图：在y＝x+中，令x＝0得y＝,∴C(0,),OC＝,在y＝x+中令y＝0得x+＝0,解得x＝﹣2,∴A(﹣2,0),OA＝2,Rt△AOC中，tan∠CAO＝＝＝,∴∠CAO＝30°，Rt△AOD中，AD＝OA•cos30°＝2×＝，∵OD⊥AB，∴AD＝BD＝，∴AB＝2，故答案为：2．【点评】本题考查一次函数、锐角三角函数及垂径定理等综合知识，解题的关键是利用tan∠CAO＝得到∠CAO＝30°．26．已知⊙O的直径为10cm，AB，CD是⊙O的两条弦，AB∥CD，AB＝8cm，CD＝6cm，则AB与CD之间的距离为1或7cm．【分析】作OE⊥AB于E，延长EO交CD于F，连接OA、OC，如图，利用平行线的性质OF⊥CD，根据垂径定理得到AE＝BE＝4，CF＝DF＝3，则利用勾股定理可计算出OE＝3，OF＝4，讨论：当点O在AB与CD之间时，EF＝OF+OE；当点O不在AB与CD 之间时，EF＝OF﹣OE．【解答】解：作OE⊥AB于E，延长EO交CD于F，连接OA、OC，如图，∵AB∥CD，OE⊥AB，∴OF⊥CD，∴AE＝BE＝AB＝4cm，CF＝DF＝CD＝3cm，在Rt△OAE中，OE＝＝＝3cm，在Rt△OCF中，OF＝＝＝4cm，当点O在AB与CD之间时，如图1，EF＝OF+OE＝4+3＝7cm；当点O不在AB与CD之间时，如图2，EF＝OF﹣OE＝4﹣3＝1cm；综上所述，AB与CD之间的距离为1cm或7cm．故答案为1或7．【点评】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．注意分类讨论．27．如图，圆O的直径AB垂直于弦CD，垂足是E，∠A＝22.5°，OC＝4，CD的长为4．【分析】根据圆周角定理得∠BOC＝2∠A＝45°，由于⊙O的直径AB垂直于弦CD，根据垂径定理得CE＝DE，且可判断△OCE为等腰直角三角形，所以CE＝OC＝2，然后利用CD＝2CE进行计算．【解答】解：∵∠A＝22.5°，∴∠BOC＝2∠A＝45°，∵⊙O的直径AB垂直于弦CD，∴CE＝DE，△OCE为等腰直角三角形，∴CE＝OC＝2，∴CD＝2CE＝4．故答案为4．【点评】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了等腰直角三角形的性质和圆周角定理．28．如图，AB为⊙O的直径，弦CD⊥AB于点H，若AB＝10，CD＝8，则OH的长度为3．【分析】根据垂径定理由CD⊥AB得到CH＝CD＝4，再根据勾股定理计算出OH＝3．【解答】解：连接OC，∵CD⊥AB，∴CH＝DH＝CD＝×8＝4，∵直径AB＝10，∴OC＝5，在Rt△OCH中，OH＝＝3，故答案为：3．【点评】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．29．如图所示，在⊙O内有折线OABC，其中OA＝8，AB＝12，∠A＝∠B＝60°，则BC的长为20．【分析】延长AO交BC于D，根据∠A、∠B的度数易证得△ABD是等边三角形，由此可求出OD、BD的长；过O作BC的垂线，设垂足为E；在Rt△ODE中，根据OD的长及∠ODE的度数易求得DE的长，进而可求出BE的长；由垂径定理知BC＝2BE，由此得解．【解答】解：延长AO交BC于D，作OE⊥BC于E；∵∠A＝∠B＝60°，∴∠ADB＝60°；∴△ADB为等边三角形；∴BD＝AD＝AB＝12；∴OD＝4，又∵∠ADB＝60°，∴DE＝OD＝2；∴BE＝10；∴BC＝2BE＝20；故答案为20．【点评】此题主要考查了等边三角形的判定和性质以及垂径定理的应用．三．解答题（共6小题）30．如图，AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，MD恰好经过圆心O，连接MB．（1）若CD＝16，BE＝4，求⊙O的直径；（2）若∠M＝∠D，求∠D的度数．【分析】（1）先根据CD＝16，BE＝4，得出OE的长，进而得出OB的长，进而得出结论；（2）由∠M＝∠D，∠DOB＝2∠D，结合直角三角形可以求得结果；【解答】解：（1）∵AB⊥CD，CD＝16，∴CE＝DE＝8，设OB＝x，又∵BE＝4，∴x2＝（x﹣4）2+82，解得：x＝10，∴⊙O的直径是20．（2）∵∠M＝∠BOD，∠M＝∠D，∴∠D＝∠BOD，∵AB⊥CD，∴∠D＝30°．【点评】本题考查了圆的综合题：在同圆或等圆中，相等的弧所对的圆周角相等，直径所对的圆周角为直角；垂直于弦的直径平分弦，并且平分弦所对的弧．31．如图，⊙O中，直径CD⊥弦AB于E，AM⊥BC于M，交CD于N，连接AD．（1）求证：AD＝AN；（2）若AB＝8，ON＝1，求⊙O的半径．【分析】（1）先根据同角的余角相等得到∠CNM＝∠B，利用等量代换得到∠AND＝∠B，利用同弧所对的圆周角相等得到∠D＝∠B，则得∠AND＝∠D，利用等角对等边可得出结论；（2）先根据垂径定理求出AE的长，连接AO，设OE的长为x，则DE＝NE＝x+1，OA ＝OD＝2x+1，在Rt△AOE中根据勾股定理可得出x的值，进而得出结论．【解答】（1）证明：∵CD⊥AB∴∠CEB＝90°∴∠C+∠B＝90°，同理∠C+∠CNM＝90°∴∠CNM＝∠B∵∠CNM＝∠AND∴∠AND＝∠B，∵，∴∠D＝∠B，∴∠AND＝∠D，∴AN＝AD；（2）解：设OE的长为x，连接OA∵AN＝AD，CD⊥AB∴DE＝NE＝x+1，∴OD＝OE+ED＝x+x+1＝2x+1，∴OA＝OD＝2x+1，∴在Rt△OAE中OE2+AE2＝OA2，∴x2+42＝（2x+1）2．解得x＝或x＝﹣3（不合题意，舍去），∴OA＝2x+1＝2×+1＝，即⊙O的半径为．【点评】本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．32．如图，在圆O中，弦AB＝8，点C在圆O上（C与A，B不重合），连接CA、CB，过点O分别作OD⊥AC，OE⊥BC，垂足分别是点D、E．（1）求线段DE的长；（2）点O到AB的距离为3，求圆O的半径．【分析】（1）由OD⊥AC知AD＝DC，同理得出CE＝EB，从而知DE＝AB，据此可得答案；（2）作OH⊥AB于点H，连接OA，根据题意得出OH＝3，AH＝4，利用勾股定理可得答案．【解答】解：（1）∵OD经过圆心O，OD⊥AC，∴AD＝DC，同理：CE＝EB，∴DE是△ABC的中位线，∴DE＝AB，∵AB＝8，∴DE＝4．（2）过点O作OH⊥AB，垂足为点H，OH＝3，连接OA，∵OH经过圆心O，∴AH＝BH＝AB，∵AB＝8，∴AH＝4，在Rt△AHO中，AH2+OH2＝AO2，∴AO＝5，即圆O的半径为5．【点评】本题主要考查垂径定理，解题的关键是掌握垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了中位线定理与勾股定理．33．如图，CD为⊙O的直径，CD⊥AB，垂足为点F，AO⊥BC，垂足为点E，BC＝3．（1）求AB的长；（2）求⊙O的半径．【分析】（1）连接AC，如图，利用垂径定理可判断CD垂直平分AB，则CA＝CB＝3，同理可得AE垂直平分BC，所以AB＝AC＝3；（2）先证明△ABC为等边三角形，则AE平分∠BAC，所以∠OAF＝30°，然后利用含30度的直角三角形三边的关系求出OA即可．【解答】解：（1）连接AC，如图，∵CD⊥AB，∴AF＝BF，即CD垂直平分AB，∴CA＝CB＝3，∵AO⊥BC，∴CE＝BE，即AE垂直平分BC，∴AB＝AC＝3；（2）∵AB＝AC＝BC，∴△ABC为等边三角形，∴∠BAC＝60°，∴AE⊥BC，∴AE平分∠BAC，即∠OAF＝30°，在Rt△OAF中，∵OF＝AF＝×＝，∴OA＝2OF＝，即⊙O的半径为．【点评】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．34．如图，四边形ABCD内接于⊙O，OC＝4，AC＝4．（1）求点O到AC的距离；（2）求∠ADC的度数．【分析】（1）作OM⊥AC于M，根据等腰直角三角形的性质得到AM＝CM＝2，根据勾股定理即可得到结论；（2）连接OA，根据等腰直角三角形的性质得到∠MOC＝∠MCO＝45°，求得∠AOC＝90°，根据圆内接四边形的性质即可得到结论．【解答】解：（1）作OM⊥AC于M，∵AC＝4，∴AM＝CM＝2，∵OC＝4，∴OM＝＝2；（2）连接OA，∵OM＝MC，∠OMC＝90°，∴∠MOC＝∠MCO＝45°，∵OA＝OC，∴∠OAM＝45°，∴∠AOC＝90°，∴∠B＝45°，∵∠D+∠B＝180°，∴∠D＝135°．【点评】本题考查了垂径定理，勾股定理，等腰直角三角形的性质，正确的作出辅助线是解题的关键．35．筒车是我国古代发明的一种水利灌溉工具，彰显了我国古代劳动人民的智慧，图1，点P表示筒车的一个盛水桶．如图2，当筒车工作时，盛水桶的运行路径是以轴心O为圆心，5m为半径的圆，且圆心在水面上方．若圆被水面截得的弦AB长为8m，求筒车工作时，盛水桶在水面以下的最大深度．【分析】过O点作半径OD⊥AB于E，如图，利用垂径定理得到AE＝BE＝4，再利用勾股定理计算出OE，然后计算出DE的长即可．【解答】解：过O点作半径OD⊥AB于E，如图，∴AE＝BE＝AB＝×8＝4（m），在Rt△AEO中，OE＝＝＝3（m），∴ED＝OD﹣OE＝5﹣3＝2（m），答：筒车工作时，盛水桶在水面以下的最大深度为2m．【点评】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．。

垂径定理一、单选题A．82．如图，圆弧形桥拱的跨度A．2米B．43．如图，一个圆柱形的玻璃水杯，将其水平放置，截面是个圆，是弧AB的中点，2CD=cm，杯内水面宽A．6cm4．如图，CD是圆O长为（）A．33A ．45︒6．如图，O 的半径是A ．27．如图是一段圆弧 AB 点．若63,AB CD =A ．6πB ．4π8．如图，在O 中，半径23r =，AB 过点C 作CD OC ⊥交O 于点D ，则A ．4B的直径，11．如图，AB是O==，则CD5,3AB BC的弦，半径12．如图，AB是O中，直径13．如图，在O一点，连AE，过点C作14．如图，在圆O中，弦的直径15．如图．O为．的外接圆，16．如图，⊙O是ABC∠的度数为于点D，连接BD，则D三、解答题17．如图，AB为半圆O点D，若4，==AB AC(1)DE的长．(2)阴影部分的面积．18．如图，AB 为O 的直径，CD 为弦，CD AB ⊥于点E ，连接DO 并延长交O 于点F ，连接AF 交CD 于点G ，CG AG =，连接AC ．(1)求证：AC DF ∥；(2)若12AB =，求AC 和GD 的长．19．如图，在以O 为圆心的两个同心圆中，大圆的弦AB 交小圆于C D 、两点，若16cm 6cm AB CD ==，．(1)求AC 的长；(2)若大圆半径为10cm ，求小圆的半径．∠；(1)连接AD，求OAD(2)点F在 BC上，CDF∠=参考答案：∵OA OB =，C 为弦AB 中点，∴OC AB ⊥，4AC =，∴OE 平分 AB ，∵D 为 AB 的中点，∴点,D E 重合，∴,,O C D 三点共线，设圆的半径为r ，则：2OC OD CD r =-=-，由勾股定理，得：222OA AC OC =+，∴()22242r r =+-，解得：=5r ；故选B ．4．C【分析】本题考查了勾股定理的应用，垂径定理，熟练掌握和运用垂径定理是解决本题的关键．连接OC ，首先根据题意可求得63OC OE ==，，根据勾股定理即可求得CE 的长，再根据垂径定理即可求得CD 的长．【详解】解：如图，连接OC ，∵123AB BE ==，，∴63OB OC OE ===，，∵AB CD ⊥，∵50BOC ∠=︒，OC ∴OCB OBC ∠=∠=∵OC AB ⊥，∴AD BD =，故选：B．7．B【分析】本题考查的是垂径定理，勾股定理及弧长的计算公式，先根据垂径定理求出=长，由题意得OD OAOE AB ⊥ ，132AE BE AB ∴===，22OE OA AE ∴=-=在Rt COE △中，∵AB 是O 的直径，∴152OD OB AB ===∵,6CD AB CD ⊥=，∴13,2DE CD DEO ==∠∴22OE OD DE =-=∵5AB =，∴25OE =，∵DE 切O 于点E ，∴OE DE ⊥，∴90OED ∠=︒，∵1OA =，120AOB ∠=︒，∴30A B ==︒∠∠，AC BC =∴1122OC OA ==，AC =∵直径CD 长为4，∴1422OD =⨯=，∵1OG =，∴1DG OD OG =-=，∴AB 垂直平分OD ，OH 经过圆心O ，12AH BH AB ∴===∴2AO AH OH =+故答案为：5．在Rt AOD 中，12OD OA ==，，1cos 2AOD \Ð=，60AOD ∴=︒∠，OE AC ⊥ ，由垂径定理知，点E是CD的中点，也是AB是 的直径，CD⊥AB∴垂直平分CD，M是OA的中点，∴1122OM OA OD==，OA CD于点M，⊥∴点M是CD的中点，∴垂直平分CD，ABNC ND∴=，Q，∠=︒45CDFNCD NDC∴∠=∠=︒，45∴∠=︒，90CND。

九年级圆的垂径定理与圆心角圆周角的大题精选(含答案)九年级圆的垂径定理与圆心角圆周角的大题精选（含答案）圆的性质大题一、解答题（共25小题）1.如图，⊙O中，弦CD与直径AB交于点H。

1）当∠B+∠D=90°时，求证：H是CD的中点。

证明：∠B+∠D=90°，∠B=90°-∠D，又∠ADC=90°（直径所对的角为直角），所以∠___∠B，因此三角形ADC与三角形BDC相似，所以BD/DC=DC/BD，即BD²=DC²，所以BH=HD，即H为CD的中点。

2）若H为CD的中点，且CD=2，BD=√3，求AB的长。

连接OH，由勾股定理得OH=√3，又因为H为CD的中点，所以CH=1，从而CO=√3+1，又AO=CO，所以AB=2AO=2(√3+1)。

2.如图，∠BAC=60°，AD平分∠___于点D，连接OB、OC、BD、CD。

1）求证：四边形OBDC是菱形。

证明：由角平分线定理得∠OAD=∠OBD，又∠OAB=∠OBA=30°，所以∠OBD=30°，又∠OCD=∠OAD=30°，所以∠___∠OCD，所以BD=CD，又∠___∠OCD=30°，所以∠___∠OBC，所以三角形OBD与三角形OBC全等，所以OB=OC，又∠___∠OCD=30°，所以OB=BC，所以四边形OBDC是菱形。

2）当∠BAC为多少度时，四边形OBDC是正方形？当∠BAC=90°时，∠___∠OCD=45°，所以BD=CD，又∠___∠OCD=45°，所以OB=BC，所以四边形OBDC是正方形。

3.如图，CD是⊙O的直径，∠EOD=84°，AE交⊙O于点B，且AB=OB，求∠A的度数。

由圆心角的性质得∠ACB=2∠A，又∠ACB=90°，所以∠A=45°，所以∠EAB=∠OAB-∠OAE=45°-42°=3°，又∠___∠OAB=45°，所以∠DBA=∠OBD-∠OBA=45°-3°=42°，所以∠C=180°-∠A-∠B=180°-45°-42°=93°。

27.1.2第2课时垂径定理姓名：_______班级_______学号：________1．（2022·云南·中考真题）如图，已知AB是⊙O的直径，CD是OO的弦，AB⟂CD．垂足为E．若AB=26，CD=24，则∠OCE的余弦值为（）A．713B．1213C．712D．13122．（2022·湖北荆门·统考中考真题）如图，CD是圆O的弦，直径AB⊥CD，垂足为E，若AB＝12，BE＝3，则四边形ACBD的面积为()A．363B．243C．183D．723 3．（2023上·安徽合肥·九年级校考阶段练习）如图，AB是O的直径，且经过弦CD的中点H，已知4cos5CDB∠=，5BD=，则OH的长的长度．4．（2022·广东广州·统考中考真题）如图，AB是⊙O的直径，点C在⊙O上，且AC=8，BC=6．(1)尺规作图：过点O作AC的垂线，交劣弧 AC于点D，连接CD（保留作图痕迹，不写作法）；(2)在（1）所作的图形中，求点O到AC的距离及sin∠ACD的值．13．已知：在圆O内，弦AD MN OG．结,题型5垂径定理的推论A．3B的弦AB 15．如图，OA．8A B C在16．已知点,,A．若半径OB平分弦B．若四边形OABCA．4cm B．5cm C．6cm D．7cm21．（2022·浙江宁波·统考模拟预测）AB=，则垂足为M，且8cmA．25cm B．22．筒车是我国古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理，如图已知圆心O在水面上方，且运行轨道的最低点，则点C23．（2023·安徽·统考中考真题）在Rt ABC △中，M 是斜边AB 的中点，将线段MA 绕点M 旋转至MD 位置，点D 在直线AB 外，连接,AD BD ．(1)如图1，求ADB ∠的大小；(2)已知点D 和边AC 上的点E 满足,ME AD DE AB ⊥∥．（ⅰ）如图2，连接CD ，求证：BD CD =；（ⅱ）如图3，连接BE ，若8,6AC BC ==，求tan ABE ∠的值．。

九年级《圆》垂径定理练习一、选择题1. 在Rt△ABC，∠C=90°，BC=5，AB=13，D是AB的中点，以C为圆心，BC为半径作⊙C，则⊙C与点D的位置关系是() A. D在圆内B．D在圆上C．D在圆外D．不能确定2．下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶角的距离相等；④半径相等的两个半圆是等弧．其中正确的有()A．4个B．3个C．2个D．1个3．下面的四个判断中，正确的一个是()A．过圆内的一点的无数条弦中，有最长的弦，没有最短的弦；B．过圆内的一点的无数条弦中，有最短的弦，没有最长的弦；C. 过圆内的一点的无数条弦中，有一条且只有一条最长的弦，也有且只有一条最短的弦；D．过圆内的一点的无数条弦中，既没有最长的弦，也没有最短的弦．4．下列说法中，正确的有()①菱形的四个顶点在同一个圆上；②矩形的四个顶点在同一个圆上；③正方形四条边的中点在同一个圆上；④平行四边形四条边的中点在同一个圆上．A．1个B．2个C．3个D．4个5．如图所示，在⊙0中，直径MN⊥AB，垂足为C，则下列结论中错误的是()A．AC=CB B. C. D. OC=CN6．过⊙O内一点M的最长的弦长为4 cm，最短的弦长为2 c()A．B ． C. 8 cm D ．7．如图所示，AB是⊙O的直径，弦CD⊥AB于点P，CD=10cm，AP：PB=1：5，那么⊙O的半径等于()A．6 cm B ．C．8 cm D ．8．如果⊙O中弦AB与直径CD垂直，垂足为E，AE=4，CE=2，那么⊙O的半径等于()A. 5B.C.D.9. 如图所示，AB是⊙O的一固定直径，它把⊙O分成上、下两个半圆，自上半圆上一点C作弦CD⊥AB．∠OCD的平分线交⊙O于点P，当点C在上半圆(不包括A、B两点)上移动时，点P()A．到CD的距离保持不变B．位置不变C. 等分D．随C点的移动而移动10. 如图所示，同心圆中，大圆的弦AB交小圆于C、D两点，且AC=CD，AB的弦心距等于CD的一半。