当前位置：文档之家 › 直线的两点式截距式方程ppt课件

直线的两点式截距式方程ppt课件

  • 格式：ppt
  • 大小：579.00 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

直线的两点式方程(课件

直线的两点式方程(课件
使用范围
ax＋by＝1
斜率存在且不为 0，不过原点
三．线段的中点坐标公式 若点 P1，P2 的坐标分别为(x1，y1)，(x2，y2)，设 P(x，y)是线段 P1P2 的中点，
x1 x2
y1 y2
则 x＝ 2 ，y＝ 2
．
思考 1： 过点(1，3)和(1，5)的直线能用两点式表示吗？为什么？ 过点(2，3)，(5，3)的直线呢？ 不能，因为 1－1＝0，而 0 不能做分母．过点(2，3)，(5，3)的直 线也不能用两点式表示． 思考 2： 截距式方程能否表示过原点的直线？
二、经典例题
题型一 直线的两点式方程
例 1 如图，已知 A(1,2)，B(－1,4)，C(5,2). ①求线段 AB 中点 D 的坐标； ②求△ABC 的边 AB 上的中线所在的直线方程.
解
①因为 A(1,2)，B(－1,4)，所以线段 AB 中点 D 的坐标为1＋
－1 2
，2＋2 4，
即 D(0,3).
2.2 直线的方程 2.2.2 直线的两点式方程
一、自主学习
一．直线的两点式方程
名称
已知条件
示意图
两点式
P1(x1，y1)，P2(x2，y2)， 其中 x1≠x2，y1≠y2
方程
使用范围
yy2－－yy11＝xx2－－xx11 斜率存在且
不为 0
二．直线的截距式方程
名称
已知条件
在 x，y 轴上的截距 截距式 分别为 a，b 且 a≠0，
三、当堂达标
1.(多选)下列说法正确的是( ) A.不经过原点的直线都可以表示为ax＋by＝1 B.若直线与两轴交点分别为 A、B 且 AB 的中点为(4,1)则直线 l 的方程为8x＋2y＝1 C.过点(1,1)且在两轴上截距相等的直线方程为 y＝x 或 x＋y＝2 D.直线 3x－2y＝4 的截距式方程为4x＋－y2＝1

第二章§2.22.2.2直线的两点式方程课件(人教版)

第二章§2.22.2.2直线的两点式方程课件(人教版)

①
又因为直线 l 过点 P43，2.
所以34a＋2b＝1，整理得 3ab＝6a＋4b.
②
由①②，得ba＝ ＝34， ，
或b＝92， a＝152，
所以直线l的方程为3x＋4y－12＝0或15x＋8y－36＝0.
课堂小结
1.知识清单： (1)直线的两点式方程. (2)直线的截距式方程. 2.方法归纳：分类讨论法、数形结合法. 3.常见误区：利用截距式求直线方程时忽略过原点的情况导致漏解.
解析 因为直线过点(－2,1)和(3，－3)， 所以－y－3－11＝3x－－－－22， 即y－－41＝x＋5 2， 化简得4x＋5y＋3＝0.
(2)已知直线经过点A(1,0)，B(m，1)，求这条直线的方程.
解 由直线经过点A(1,0)，B(m，1)，因此该直线斜率不可能为零，但有 可能不存在. (1)当直线斜率不存在，即m＝1时，直线方程为x＝1； (2)当直线斜率存在，即m≠1时， 利用两点式，可得直线方程为1y－－00＝mx－－11， 即x－(m－1)y－1＝0. 综上可得，当m＝1时，直线方程为x＝1； 当m≠1时，直线方程为x－(m－1)y－1＝0.
二、直线的截距式方程
问题2 若给定直线上两点A(a，0)，B(0，b)(a≠0，b≠0)，你能否得出 直线的方程呢？ 提示 ax＋by＝1
知识梳理
我们把方程 ax＋by＝1 叫做直线的截距式方程，简称截距式.直线与x轴的 交点(a，0)的横坐标a叫做直线 在x轴上的截距 ，此时直线在y轴上的截距 是b .
延伸探究 1.若将点A的坐标改为“A(－3，－4)”，其他条件不变，又如何求解？
解 (1)当直线l在两坐标轴上的截距互为相反数且不为0时， 设直线 l 的方程为ax＋－ya＝1， 又 l 过点 A(－3，－4)，所以－a3＋－－4a＝1，解得 a＝1. 所以直线 l 的方程为1x＋－y1＝1，即 x－y－1＝0.

7.2(2)直线的方程-两点式,截距式.ppt

7.2(2)直线的方程-两点式,截距式.ppt

直线 l 的斜率为 k
由点斜式方程 y y1 y 2 y1 x 2 x1
y 2 y1 x 2 x1
p2
( x x 1 ).
( y1 y 2 )
化简为
y y1 y2 y1

x x1 x2 x1
——直线方程的两点式
例1 、已知直线l于x轴交于点A(a,0), 于y轴 交于B(0, b), (a 0, b 0)，求直线l的方程。
直线 l过点 P ( 4 ,1) 4 1 1 4 b a ab a b
2 4 ab 4 ab ab 16

P(4,1)
A

0
x
S
S min
1
ab 8 （当 a 4 b 即 a 8 , b 2时取等号）
2 x y 8 , 直线 l 方程为 1 x 4y 8 0 8 2
解：
(1)
y 1 3 1 y5 05 y 50

x2 02 x0 50
y 2 x 3.
(2)

y x 5.
5 4
(3)

x 42
y
x.
y y0 k ( x x0 )
应用范围
k存在 k存在
k存在 且k 0
k存在且 0 且不过原点
y kx b
y y1 y2 y1 x x1 x2 x1
x a

y b
1.
课堂练习
1 .求过下列两点的直线的 （1） P1 ( 2 ,1)、 P2 ( 0 , 3 ); ( 2 ) A ( 0 , 5 )、 B ( 5 , 0 ); ( 3 ) C ( 4 , 5 )、 D ( 0 , 0 ). 两点式方程，再化成斜 截式方程：

直线的两点式方程课件

直线的两点式方程课件

2．对直线方程一般式的四点说明 (1)方程是关于 x，y 的二元一次方程． (2)方程中等号的左侧自左向右一般按 x，y 的先后顺序排列． (3)x 的系数一般不为分数和负数． (4)虽然直线方程的一般式有三个系数，但只需两个独立的条件 即可求得直线的方程．
3．五种直线方程形式的比较
名称
已知条件
类型三直线方程的一般式 [例 3] 把直线 l 的一般式方程 x－2y＋6＝0 化成斜截式，求出 直线 l 的斜率以及它在 x 轴、y 轴上的截距，并画出图形．
【解】 将直线 l 的一般式方程化成斜截式 y＝12x＋3，
因此直线 l 的斜率 k＝12，它在 y 轴上的截距是 3，在直线 l 的 方程 x－2y＋6＝0 中，令 y＝0，得 x＝－6，即直线 l 在 x 轴上的截 距为－6.
原点的直线
知识点二 线段的中点坐标公式 若点 P1(x1，y1)，P2(x2，y2)，设 P(x，y)是线段 P1P2 的中点，
则xy＝＝xy11＋ ＋22 xy22， .
知识点三 直线的一般式方程 1．直线与二元一次方程的关系 在平面直角坐标系中的直线与二元一次方程的对应关系如下：
2．直线的一般式方程 式子：关于 x，y 的二元一次方程 Ax＋By＋C＝0； 条件：A，B 不同时为零； 简称：一般式．
|素养提升|
1．对直线的两点式方程的三点说明 (1)如果将直线的两点式方程转化为：(x2－x1)(y－y1)＝(y2－y1)(x －x1)，此时可以表示已知不重合的两个点确定的直线． (2)当已知的两点为 A(a,0)，B(0，b)(a≠0，b≠0)时，由两点式 可得直线方程ax＋by＝1，此方程为直线的截距式． ①其中 a 是直线在 x 轴上的截距，b 是直线在 y 轴上的截距； ②截距式不能表示过原点或与坐标轴垂直的直线． (3)记忆特点： ①左边全为 y，右边全为 x； ②两边的分母全为常数； ③分子，分母中的减数相同．

02教学课件_2.2.2 直线的两点式方程(共25张PPT)

02教学课件_2.2.2 直线的两点式方程(共25张PPT)

可以确定一条直线。
这样，在直角坐标系中，给定一个点p0(x0,y0)和斜率k,可得出直线方程。
若给定直线上两点p1(x1,y1)p2(x2,y2),你能否得出直线的方程呢?
探究新知
1．直线的两点式方程
(1)直线的两点式方程的定义
y－y1 x－x1
＝
y
－y
x2－x1
2
1
__________________就是经过两点
点的坐标还有限制条件吗?
答案:这个方程对两点的坐标没有限制,即它可以表示过任意两点的直线方程.
2.已知直线l过点A(3,1),B(2,0),则直线l的方程为
y-1
x-3
解析:由两点式,得0-1 = 2-3,化简得 x-y-2=0.
答案:x-y-2=0
.
二、直线的截距式方程
点睛：直线的截距式方程是直线的两点式方程的特殊情况,由直线的截距式方程
2
S 取最大值为-3×152+20×15+54 000=54 150(m2).
因此点 P 距 AE 15 m,距 BC 50 m 时所开发的面积最大,
最大面积为 54 150 m2.
归纳总结 二次函数最值问题,一方面要看顶点位置,另一方面还要看定义域的范围.结
合图形求解,有时并非在顶点处取得最值.
当堂检测

不垂直于x、y轴的直线
点P1 ( x1，y1 )和点P2 ( x2，y2 )
y1 y2 x1 x2
在x轴上的截距 a
在y轴上的截距 b
x y
1
a b
不垂直于x、y轴的直线
不过原点的直线
课堂小结
课堂小结：
－3
)

直线的方程-2两点式、截距式)PPT课件

直线的方程-2两点式、截距式)PPT课件

THANKS FOR WATCHING
感谢您的观看
在交通领域，例如在道路规划中，可 以使用这两种方程形式来表示道路的 走向和交点。
在物理学中，例如在电场分析中，可 以使用这两种方程形式来描述电场线 的分布和方向。
04 练习与巩固
基础练习题
01
02
03
题目1
已知两点$P_1(x_1, y_1)$ 和$P_2(x_2, y_2)$，求直 线方程的两点式。
直线的方程。
截距式方程
截距式方程是另一种形式的直线方 程，它表示直线在x轴和y轴上的截 距。
直线方程的应用
了解直线方程在实际问题中的应用， 如几何、物理和工程问题。
学习心得体会
通过学习本章，我掌握了直线方程的两种形式，即两点式和截距式，并 了解了它们在实际问题中的应用。
学习过程中，我遇到了一些困难，如理解截距式方程的推导过程和如何 应用直线方程解决实际问题。但通过反复阅读教材和与同学讨论，我逐
在实际生活中，例如道路修建、桥梁设计等工程领域，常常需要使用到截距式直线 方程来描述道路或桥梁的走向。
在解析几何中，截距式直线方程也是一种重要的直线方程形式，用于解决一些特定 的问题。
03 两种直线方程的比较
异同点比较
相同点
两点式和截距式都是用来表示直线方 程的方法，它们都可以表示直线上的 点。
渐克服了这些困难。
学习本章后，我意识到数学在实际问题中的重要性，并计划在未来的学 习中更加注重数学知识的应用。
下一步学习计划
深入学习直线的其他方程形式， 如点斜式和斜截式。
学习如何利用直线方程解决更复 杂的实际问题，如解析几何和物
理问题。
复习和巩固已学过的直线方程知 识，确保自己能够熟练掌握和应

直线两点式方程的PPT


y y k(x x )
1 1
斜率k和直 线在y轴上 的截距
y kx b
斜 率 必 须 存 在
0
斜率不存在时， 直线方程为：x x
已知直线经过两点P1(x1,y1)，P2(x2,y2)，如何求 出过这两个点的直线方程呢？
经过一点，且已知斜率的直线，可以写出它 的点斜式方程.
可以先求出斜率，再选择一点，得到点斜式 方程.
3.2.2 直线的两点式方程
教学目标：
1﹒掌握直线的两点式方程和截距式方程，以 及各自的适用条件 2﹒会选择适当的方程形式求直线方程 3﹒能将直线的两点式方程化为斜截式方程 或二元一次方程的形式
复习
直线 方程 名称
已知 条件
点 P (x , y ) 和斜率k
1 1 1
直线方程
使用范围
点 斜 式 斜 截 式
练习3.根据下列条件求直线的方程：
(1)在轴上的截距是2，在y轴上的截距为3；
3x+2y-6=0 (2)在x轴上的截距是－5，与y轴的交点为(0, 6). 6x-5y+30=0
练习4.根据下列条件, 求直线的方程： (1)过点(0, 5)，且在两坐标轴上的截距之和为2. 5x-3y+15=0 (2)过点(5, 0)，且在两坐标轴上的截距之差为2. 3x+5y-15=0或7x+5y-35=0
y=-x+5
练习2、三角形的顶点是A(-5,0),B(3,-3),C(0,2)，
求BC边所在直线的方程，以及该边上中线所在直线 y
的方程.
C .
5x+3y-6=0 x+13y+5=0
. A
O
.M

直线的两点式方程 课件

的选取与这两点的顺序无关. (2)当直线斜率不存在(x1=x2)或斜率为零(y1=y2)时,不能 用两点式表示.
(3)如果将直线两点式转化为:(x2-x1)(y-y1)=(y2-y1)(x-x1),此 时只要直线上两点不重合,都可以用该等式表示出来(即这个变 形方程可以表示过任意已知两点的直线).
关于光线的反射问题 【典型例题】 一条光线从点A(3,2)发出,经x轴反射,通过点B(-1,6),求入射 光线和反射光线所在直线的方程.
【解析】点A关于x轴的对称点为A1(3,-2), 点B关于x轴的对称点为B1(-1,-6).因为A1 在反射光线的延长线上,
B1在入射光线的延长线上,
由两点式可得直线A1B的方程为
轴上的截距.
(3)截距式方程是两点式的一种特殊情况(两个点是直线与坐标 轴的交点),在求直线方程时合理地选择形式,会提高解题速度.
类型 一 直线的两点式方程
【典型例题】
1.过点(2，5)，(2，-6)两点的直线方程是( )
A.x=2
B.y=2
C.x+y=5
D.x+y=-6
2.已知A(-3,2)，B(5,-4)，C(0,-2)，在△ABC中，
(1)直线的斜率不存在时，没有两点式方程.( )
(2)与坐标轴平行的直线没有截距式方程.( )
(3)
都是直线的截距式方程.( )
x y 1与 x y 2 35 35
提示：(1)正确.直线的两点式方程应用的前提条件是x1≠x2， y1≠y2，即斜率存在且不等于0. (2)正确.因为截距式方程的应用前提是a≠0,b≠0. (3)错误.不符合截距式方程的标准形式，即左边“+”连接， 右边为1. 答案:(1)√ (2)√ (3)×

2.2.2直线的两点式方程课件(人教版)


− 进行变形？
−
−
=
− −
≠ 且 ≠
−
−
=
−
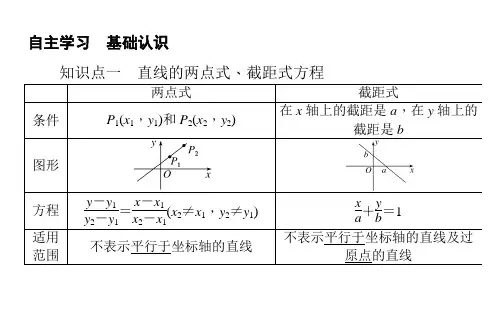
就是经过两点 , ， , (其中 ≠ ，
−
≠ ）的直线的方程.
把它叫做直线的两点式方程，简称两点式.
5
2
2
整理可得x 13 y 5 0,
这就是边BC 上中线AM 所在直线的方程.
知识小结
课堂总结
直线方程
常数的几何意义
斜率不
存在
斜率为 过原
点
0
, 、
,
−
−
是直线上两点
（ ≠ ， ≠ ）的坐标
×
×
√
截距式方程
a b
0 5
截距之和为2, 1, a b 2, 解得a 3, b 5.
a b
x y
所以所求直线的方程为 1, 即5 x 3 y 15 0.
3 5
3.根据下列条件, 求直线的方程
(1)过点(0, 5), 且在两坐标轴上的截距之和为2;
(2)过点(5, 0), 且在两坐标轴上的截距之差为2.
() (，)， , − ;
y 1 x 2
(1)

;
3 1 0 2
() (，)， ,
y5 x0
(2)

.
05 50
探究二：直线的截距式方程
例3 如图，已知直线与轴的交点为(，)，与轴的交点为(，)，
其中 ≠ ， ≠ . 求直线的方程.
这就是边BC 所在直线的方程 .
例4 已知△ABC的三个顶点A( 5, 0), B(3, 3), C (0, 2), 求边BC 所在直线

2.2.2直线的两点式方程 课件(共20张PPT)


所以所求直线方程为： + − 3 = 0或 = 2.
(，0)
Байду номын сангаас


例2 ⑴ 过点(1,2)并且在两个坐标轴上的截距相等的直线有几条?并求其方程．
(2) 过(1,2)并且在两个坐标轴上的截距的绝对值相等的直线有几条? 并求其方程．
解：三条
①当直线的两截距相等过原点时， = 2
②当直线的两截距相等不过原点时， + − 3 = 0




典例剖析
例3 三角形的顶点分别是(−5,0), (3, −3), (0,2)，求边所在直线的方程，以及该边上
中线所在直线的方程.

变式1 求边上的垂直平分线所在直线的方程.
：5 + 3 − 6 = 0 = −

=

1
3
M ,
2
2
+



（1）在轴上的截距为2，在轴上的截距是3；
由截距式得：
x y
1
2 3
整理得：3x 2 y 6
0
（2）在轴上的截距为-5，在轴上的截距是6；
由截距式得：
x
y
1
5 6
整理得： 6 x 5 y 30 0
典例剖析
例2 ⑴ 过点(1,2)并且在两个坐标轴上的截距相等的直线有几条?并求其方程．
斜截式
斜率, 在轴上的纵截距
y kx b
斜
率
必
须
存
在
斜率不存在时，
直线方程为：x x0
思考：已知直线上两点1(1, 1), 2(2, 2)（其中1 ≠ 2, 1 ≠ 2 ），如何求出通过这两点的
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
当k不存在时,直线方程为__x__=__x__0___ 2.直线的斜截式方程___y_=__k__x__+__b______
它表示_斜__率__为__k_，__在__y_轴__上__的__截__距__为__b_的直线. 3.点斜式与斜截式的适用范围是__斜__率__存__在__的__直__线____ 4.斜截式是点斜式的____特__殊__情__况_________
线
一般式 A、B不同时为零 Ax+By+C=
0
15
1、已知直线l 的方程 (2m2 m 3)x (m2 m) y 4m 1 (1)当 m 时，l 的倾斜角是45 (2)当 m 时，l 在 x 轴上的截距是 1 (3)当 m 时，l 平行于 y 轴
思考、若方程(2m2 m 3)x (m2 m) y 4m 1 表 示 一 条 直 线 ， 求 实 数m的 取 值 范 围
求过点 P1( A1 , B1 )，P2 ( A2 , B2 ) (P1P2不重合)
二元一次方程的一般形式是 Ax By C 0 13
新课
直线的方程—一般式
Question：方程 Ax By C 0 总是表示直线吗？
(1)若B 0，则y A x C BB
(2)若B 0，则Ax C 0
1)若A 0，则x C
A
2)若A
0，则0
x
C
若C
0
0，与C
0矛盾
怎么弥补缺陷？
我们推导两点式是通过点斜式的， 还有其他推导方法吗？
利用三点共线，斜率相等 或 共线向量
5
直线方程的两点式和截距式
6
新课
直线的方程—两点式、截距式
特殊地，当直线 l 经过点 A(a,0)，B(0, b)
时的方程为
y0 xa
b0 0a
直线方程的截距式
x y 1 ab
直线方程的截距式不能表示哪些直线？
截距式适用于的_横__、__纵__截__距__都__存__在__且__都__不__为__0__直线.
7
练习
1、三角形的顶点A(5,0)，B(3,3)， C (0,2)，求这个三角形三边所在 的直线方程
变 式1、 求AB边 上 的 中 线 所 在 的 直 线方 程 和ABC的 重 心 坐 标
变式2、求过点B 且在两坐标轴上截距 互为相反数的直线方程
变 式2、 求 过P (2,4)且 与两 坐 标 轴正 方 向 围 成 的 三 角 形 面 积 最 小 的 直线 方 程
变 式3、 过P (2,4)的 直 线 l， 在 两 坐 标 轴上 的 截 距 都 为 正 值 ， 求 截距 之 和 最 小 时 的 直 线 方程
10
练习
直线的方程—两点式、截距式
(x
x1 )
3
新课
直线的方程—两点式、截距式
由方程
y
y1
y2 x2
y1 x1
(x
x1 )
可推得 y y1 x x1 y2 y1 x2 x1
上面的两个方程等价吗？
4
新课
直线的方程—两点式、截距式
直线方程的两点式
y y1 x x1 y2 y1 x2 x1
直线方程的两点式不能表示哪些直线？
8
练习
直线的方程—两点式、截距式
2、求过点 P(2,4)在两坐标轴上的 截距之和为15的直线方程
变 式1、 求 过P (2,4)且 与 两 坐 标 轴正 方 向 围 成 面 积 为18的 三 角 形 的 直 线 方 程
9
练习
直线的方程—两点式、截距式
2、 求 过 点P (2,4)在 两 坐 标 轴 上 的 截 距 之 和 为4的 直 线 方 程
复习
直线的方程—两点式、截距式
1、直线的倾斜角、斜率 2、直线方程的点斜式
y y1 k( x x1 )
3、直线方程的斜截式
y kx b
注意：有缺陷！ 1
【复习回顾】 1.直线的点斜式方程__y__-__y_0_=__k__(_x__-__x_0__)__
它表示___经__过__点__P_0_(x_0_,_y_0)_,_斜__率__为__k___的直线.
2、直线方程的点y斜 y式 1 k( x x1 )
3、直线方程的斜y截 式 kx b
4、直线方程的两yy2点 y式 y11
x x1 x2 x1
5、直线方程的截x距 式 y 1
新课
ab
以上的四种直线方程形式都是 方程，但都有局限性。
那么是否存在某种形式的方程能表示任意的一条直线？
2
新课
直线的方程—两点式、截距式
Question：
我们知道两点可以确定一条直
线，那么经过P1( x1 , y1 )，P2 ( x2 , y2 )两 点的直线方程是什么？
当 x1 x2 时，直线方程为x x1
当 x1
x2
时，直线的斜率为k
y2 x2
y1 x1
直线的方程为
y
y1
y2 x2
y1 x1
3、已知点 A(2,5)，B(4,7)，试在 y 轴 上求一点P，使得| PA|＋| PB |的 值最小
4、已知点 P(6,4)，l：y 4x，点Q在 直线 l上(Q在第一象限 )直线 PQ交 x 轴正半轴于点 M，要使 OMQ 的面积最小，求点 Q 的坐标
11
12
复习
直线的方程—一般式
1、直线的倾斜角、斜率
若C 0，则表示整个平面
结论 当A, B不全为0时，方程Ax By C 0 表示直线
方程 Ax By C 0( A、B不同时为0) 叫做直线方程的一般式
14
新课 直线方程的五种形式 直线的方程—一般式
名称
已知条件
方程
说明
点斜式 点P1(x1,y1)和斜 y-y1=k(x-x1) 不包括y轴和平行于
率k
y轴的直线
斜截式 斜率k和y轴上截 y=kx+b 距
不包括y轴和平行于 y轴的直线
两点式 点P1(x1,y1)和点 P2(x2,y2)
y y1 y2 y1
x x1 x2 x1
不包括坐标轴以及与 坐标轴平行的直线
截距式 在x轴上的截距a 在y轴上的截距b
x a
பைடு நூலகம்
y b
1
不包括过原点的直线 及与坐标轴平行的直
16
2、过点 P(0,1) 的直线 l，它在两直线 l1 : x 3 y 10 0与 l2 : 2x y 8 0 间截得的线段被点P 平分，求直线l 的方程
3、两直线 A1 x B1 y 1 0 (A12 B12 0)和
A2 x
B2
y
1
0 (A22
B
2 2
0)相交于点P(3,2)，