2013_自动控制原理知识点总结

给定值.典型闭坏控制聚统方框圏自动控制原理知识点总结第一章1、 自动控制：是指在无人直接参与的情况下，利用控制装置操纵受控对象，是 被控量等于给定值或按给定信号的变化规律去变化的过程。

2、 被控制量：在控制系统中•按规定的任务需要加以控制的物理量。

3、 控制量：作为被控制量的控制指令而加给系统的输入星•也称控制输入。

4、 扰动量：干扰或破坏系统按预定规律运行的输入量，也称扰动输入或干扰掐 入。

5、 反馈：通过测量变换装置将系统或元件的输出量反送到输入端，与输入信号 相比较。

反送到输入端的信号称为反馈信号。

6负反馈：反馈信号与输人信号相减，其差为偏差信号。

7、 负反馈控制原理：检测偏差用以消除偏差。

将系统的输出信号引回插入端，与输入信号相减，形成偏差信号。

然后根据偏差信号产生相应的控制作用，力图 消除或减少偏差的过程。

8、 自动控制系统的两种常用控制方式是开环控制和闭环控制 。

9、 开环控制：控制装置与受控对象之间只有顺向作用而无反向联系特点：开环控制实施起来简单，但抗扰动能力较差，控制精度也不高。

10、 闭环控制：控制装置与受控对象之间，不但有顺向作用，而且还有反向联系， 既有被控量对被控过程的影响。

主要特点：抗扰动能力强，控制精度高，但存 在能否正常工作，即稳定与否的问题。

11、 控制系统的性能指标主要表现在：（1）、稳定性：系统的工作基础。

（2）、 快速性：动态过程时间要短，振荡要轻。

（3）、准确性：稳态精度要高，误差要 小。

12、 实现自动控制的主要原则有：主反馈原则、补偿原则、复合控制原则。

第二章1、 控制系统的数学模型有： 微分方程、传递函数、动态结构图、频率特性。

2、传递函数：在零初始条件下，线性定常系统输出量的拉普拉斯变换域系统输入量的拉普拉斯变换之比3、求传递函数通常有两种方法：对系统的微分方程取拉氏变换，或化简系统的动态方框图。

对于由电阻、电感、电容元件组成的电气网络，一般采用运算阻抗的方法求传递函数。

@~@自动控制原理知识点总结第一章1.什么是自动控制？（填空）自动控制：是指在无人直接参与的情况下，利用控制装置操纵受控对象，是被控量等于给定值或按给定信号的变化规律去变化的过程。

2.自动控制系统的两种常用控制方式是什么？（填空）开环控制和闭环控制3.开环控制和闭环控制的概念？开环控制：控制装置与受控对象之间只有顺向作用而无反向联系特点：开环控制实施起来简单，但抗扰动能力较差，控制精度也不高。

闭环控制：控制装置与受控对象之间，不但有顺向作用，而且还有反向联系，既有被控量对被控过程的影响。

主要特点：抗扰动能力强，控制精度高，但存在能否正常工作，即稳定与否的问题。

掌握典型闭环控制系统的结构。

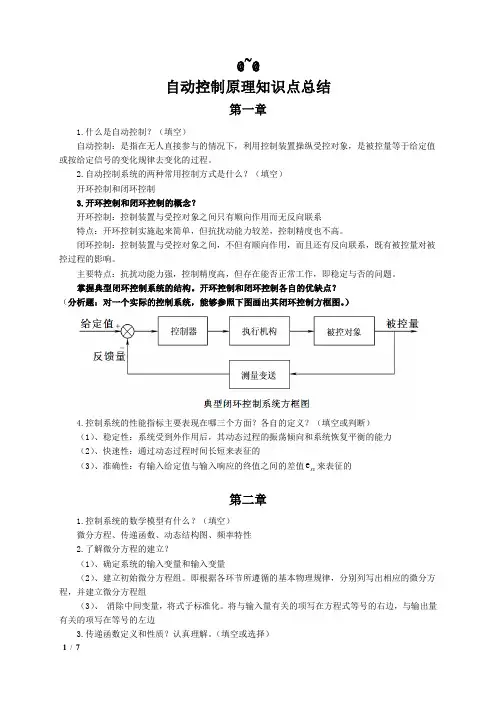
开环控制和闭环控制各自的优缺点？（分析题：对一个实际的控制系统，能够参照下图画出其闭环控制方框图。

）4.控制系统的性能指标主要表现在哪三个方面？各自的定义？（填空或判断）（1）、稳定性：系统受到外作用后，其动态过程的振荡倾向和系统恢复平衡的能力（2）、快速性：通过动态过程时间长短来表征的e来表征的（3）、准确性：有输入给定值与输入响应的终值之间的差值ss第二章1.控制系统的数学模型有什么？（填空）微分方程、传递函数、动态结构图、频率特性2.了解微分方程的建立？（1）、确定系统的输入变量和输入变量（2）、建立初始微分方程组。

即根据各环节所遵循的基本物理规律，分别列写出相应的微分方程，并建立微分方程组（3）、消除中间变量，将式子标准化。

将与输入量有关的项写在方程式等号的右边，与输出量有关的项写在等号的左边3.传递函数定义和性质？认真理解。

（填空或选择）传递函数：在零初始条件下，线性定常系统输出量的拉普拉斯变换域系统输入量的拉普拉斯变换之比5.动态结构图的等效变换与化简。

三种基本形式，尤其是式2-61。

主要掌握结构图的化简用法，参考P38习题2-9（a）、（e）、（f）。

（化简）等效变换，是指被变换部分的输入量和输出量之间的数学关系，在变换前后保持不变。

自动控制原理知识点总结自动控制原理是一门研究自动控制系统的分析与设计的学科，它对于理解和实现各种工程系统的自动化控制具有重要意义。

以下是对自动控制原理中一些关键知识点的总结。

一、控制系统的基本概念控制系统由控制对象、控制器和反馈通路组成。

控制的目的是使系统的输出按照期望的方式变化。

开环控制系统没有反馈环节，输出不受控制，精度较低；闭环控制系统通过反馈将输出与期望的输入进行比较，从而实现更精确的控制。

二、控制系统的数学模型数学模型是描述系统动态特性的工具，常见的有微分方程、传递函数和状态空间表达式。

微分方程是最直接的描述方式，但求解较为复杂。

传递函数适用于线性定常系统，将输入与输出的关系以代数形式表示，便于分析系统的稳定性和性能。

状态空间表达式则能更全面地反映系统内部状态的变化。

三、时域分析在时域中，系统的性能可以通过单位阶跃响应来评估。

重要的性能指标包括上升时间、峰值时间、调节时间和超调量。

一阶系统的响应具有简单的形式，其时间常数决定了系统的响应速度。

二阶系统的性能与阻尼比和无阻尼自然频率有关，不同的阻尼比会导致不同的响应曲线。

四、根轨迹法根轨迹是指系统开环增益变化时，闭环极点在复平面上的轨迹。

通过绘制根轨迹，可以直观地分析系统的稳定性和动态性能。

根轨迹的绘制遵循一定的规则，如根轨迹的起点和终点、实轴上的根轨迹段等。

根据根轨迹，可以确定使系统稳定的开环增益范围。

五、频域分析频域分析使用频率特性来描述系统的性能。

波特图是常用的工具，包括幅频特性和相频特性。

通过波特图，可以评估系统的稳定性、带宽和相位裕度等。

奈奎斯特稳定判据是频域中判断系统稳定性的重要方法。

六、控制系统的校正为了改善系统的性能，需要进行校正。

校正装置可以是串联校正、反馈校正或前馈校正。

常见的校正方法有超前校正、滞后校正和滞后超前校正。

校正装置的设计需要根据系统的性能要求和原系统的特性来确定。

七、采样控制系统在数字控制系统中，涉及到采样和保持、Z 变换等概念。

完整版)自动控制原理知识点汇总自动控制原理总结第一章绪论在自动控制中，被控对象是要求实现自动控制的机器、设备或生产过程，而被控量则是表征被控对象工作状态的物理参量或状态参量，如转速、压力、温度、电压、位移等。

控制器是由控制元件组成的调节器或控制装置，它接受指令信号，并输出控制作用信号于被控对象。

给定值或指令信号r(t)是要求控制系统按一定规律变化的信号，是系统的输入信号。

干扰信号n(t)又称扰动值，是一种对系统的被控量起破坏作用的信号。

反馈信号b(t)是指被控量经测量元件检测后回馈送到系统输入端的信号。

偏差信号e(t)是指给定值与被控量的差值，或指令信号与反馈信号的差值。

闭环控制的主要优点是控制精度高，抗干扰能力强。

但是使用的元件多，线路复杂，系统的分析和设计都比较麻烦。

对控制系统的性能要求包括稳定性、快速性和准确性。

稳定性和快速性反映了系统的过渡过程的性能，而准确性则是衡量系统稳态精度的指标，反映了动态过程后期的性能。

第二章控制系统的数学模型拉氏变换是一种将时间域函数转换为复频域函数的数学工具。

单位阶跃函数1(t)、单位斜坡函数、等加速函数、指数函数e-at、正弦函数sinωt、余弦函数cosωt和单位脉冲函数(δ函数)都有其典型的拉氏变换。

拉氏变换的基本法则包括线性法则、微分法则、积分法则、终值定理和位移定理。

传递函数是线性定常系统在零初始条件下，输出信号的拉氏变换与输入信号的拉氏变换之比，称为系统或元部件的传递函数。

动态结构图及其等效变换包括串联变换法则、并联变换法则、反馈变换法则、比较点前移“加倒数”和比较点后移“加本身”，以及引出点前移“加本身”和引出点后移“加倒数”。

梅森公式是一种求解传递函数的方法，典型环节的传递函数包括比例(放大)环节、积分环节、惯性环节、一阶微分环节、振荡环节和二阶微分环节。

第三章时域分析法时域分析法是一种分析控制系统时域特性的方法。

其中，时域响应包括零状态响应和零输入响应。

自动控制原理知识点总结第1篇频率特性分为两种，分别是A(ω) 幅频特性和 φ(ω) 相频特性。

对于一个一阶线性定常系统对正弦输入信号 Asinωt 的稳态输出 Ysin(ωt +ψ) ，仍是一个正弦信号，其特点：①频率与输入信号相同；②振幅 Y为输入振幅A的 |G(jω)| 倍；③相移为 ψ = ∠G(jω)。

振幅 Y 和相移 ψ都是输入信号频率 ω 的函数，对于确定的 ω 值来说，振幅Y和相移 ψ 都将是常量。

|G(jω)| = Y / A 正弦输出对正弦输入的幅值比—幅频特性∠G(jω) = ψ正弦输出对正弦输入的相移—相频特性理论上可将频率特性的概念推广的不稳定系统，但是，系统不稳定时，瞬态分量不可能消失，它和稳态分量始终同时存在，所以，不稳定系统的频率特性是观察不到的。

（1）幅相曲线：对于一个确定的频率，必有一个幅频特性的幅值和一个幅频特性的相角与之对应，幅值与相角在复平面上代表一个向量。

当频率ω从零变化到无穷时，相应向量的矢端就描绘出一条曲线。

这条曲线就是幅相频率特性曲线，简称幅相曲线。

（2）幅频特性曲线：对数幅频特性曲线又称为伯德图（曲线）。

对数频率特性曲线的横坐标是频率 ω ，并按对数分度，单位是[rad/s] .对数幅频曲线的纵坐标表示对数幅频特性的函数值，线性分度，单位是[dB]，此坐标系称为半对数坐标系。

对数相频特性曲线的纵坐标表示相频特性的函数值，线性分度 , 单位是 (0) 或（弧度），频率特性G(jω) 的对数幅频特性定义如下 L（ω） = 20lg |G(jω)| 对数分度优点：扩大频带、化幅值乘除为加减、易作近似幅频特性曲线图。

（3）对数幅相曲线（又称尼柯尔斯曲线）：其特点是纵、横坐标都线性分度，对数幅相图的横坐标表示对数相频特性的相角，纵坐标表示对数幅频特性的幅值的分贝数。

自动控制原理知识点总结第2篇一阶系统的数学模型（1）单位阶跃响应——输入 r(t) = 1(t)，输出 h(t) = 1 - e-t/T， t >0 特点：●可以用时间常数去度量系统的输出量的数值。

@~@自动控制原理知识点总结第一章1.什么是自动控制？（填空）自动控制：是指在无人直接参与的情况下，利用控制装置操纵受控对象，是被控量等于给定值或按给定信号的变化规律去变化的过程。

2.自动控制系统的两种常用控制方式是什么？（填空）开环控制和闭环控制3.开环控制和闭环控制的概念？开环控制：控制装置与受控对象之间只有顺向作用而无反向联系特点：开环控制实施起来简单，但抗扰动能力较差，控制精度也不高。

闭环控制：控制装置与受控对象之间，不但有顺向作用，而且还有反向联系，既有被控量对被控过程的影响。

主要特点：抗扰动能力强，控制精度高，但存在能否正常工作，即稳定与否的问题。

掌握典型闭环控制系统的结构。

开环控制和闭环控制各自的优缺点？（分析题：对一个实际的控制系统，能够参照下图画出其闭环控制方框图。

）4.控制系统的性能指标主要表现在哪三个方面？各自的定义？（填空或判断）（1）、稳定性：系统受到外作用后，其动态过程的振荡倾向和系统恢复平衡的能力（2）、快速性：通过动态过程时间长短来表征的e来表征的（3）、准确性：有输入给定值与输入响应的终值之间的差值ss第二章1.控制系统的数学模型有什么？（填空）微分方程、传递函数、动态结构图、频率特性2.了解微分方程的建立？（1）、确定系统的输入变量和输入变量（2）、建立初始微分方程组。

即根据各环节所遵循的基本物理规律，分别列写出相应的微分方程，并建立微分方程组（3）、消除中间变量，将式子标准化。

将与输入量有关的项写在方程式等号的右边，与输出量有关的项写在等号的左边3.传递函数定义和性质？认真理解。

（填空或选择）传递函数：在零初始条件下，线性定常系统输出量的拉普拉斯变换域系统输入量的拉普拉斯变换之比5.动态结构图的等效变换与化简。

三种基本形式，尤其是式2-61。

主要掌握结构图的化简用法，参考P38习题2-9（a）、（e）、（f）。

（化简）等效变换，是指被变换部分的输入量和输出量之间的数学关系，在变换前后保持不变。

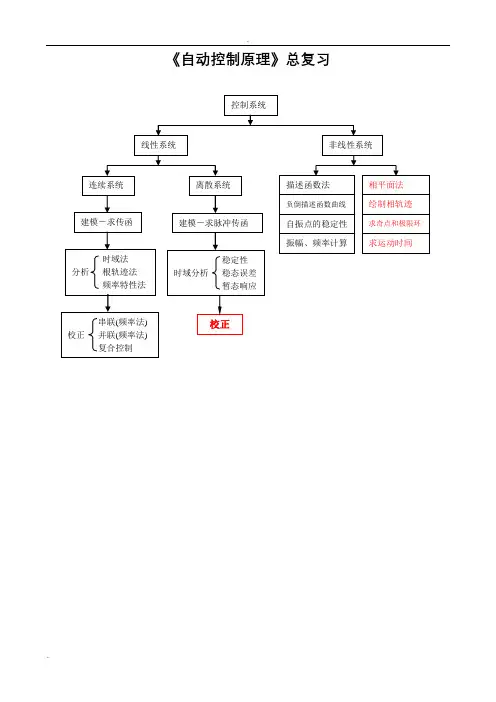
《自动控制原理》总复习第一章自动控制的基本概念一、学习要点1.自动控制基本术语：自动控制、系统、自动控制系统、被控量、输入量、干扰量、受控对象、控制器、反馈、负反馈控制原理等。

2.控制系统的基本方式：①开环控制系统；②闭环控制系统；③复合控制系统。

3.自动控制系统的组成：由受控对象和控制器组成。

4.自动控制系统的类型：从不同的角度可以有不同的分法，常有：恒值系统与随动系统；线性系统与非线性系统；连续系统与离散系统；定常系统与时变系统等。

5.对自动控制系统的基本要求：稳、快、准。

6.典型输入信号：脉冲、阶跃、斜坡、抛物线、正弦。

二、基本要求1.对反馈控制系统的基本控制和方法有一个全面的、整体的了解。

2.掌握自动控制系统的基本概念、术语，了解自动控制系统的组成、分类，理解对自动控制系统稳、准、快三方面的基本要求。

3.了解控制系统的典型输入信号。

4.掌握由系统工作原理图画方框图的方法。

三、内容结构图四、知识结构图第二章 控制系统的数学模型一、学习要点1．数学模型的数学表达式形式（1）物理系统的微分方程描述；（2）数学工具—拉氏变换及反变换； （3）传递函数及典型环节的传递函数；（4）脉冲响应函数及应用。

2．数学模型的图形表示（1）结构图及其等效变换，梅逊公式的应用；（2）信号流图及梅逊公式的应用。

二、基本要求1、正确理解数学模型的特点，对系统的相似性、简化性、动态模型、静态模型、输入变量、输出变量、中间变量等概念，要准确掌握。

2、了解动态微分方程建立的一般方法及小偏差线性化的方法。

3、掌握运用拉氏变换解微分方程的方法，并对解的结构、运动模态与特征根的关系、零输入响应、零状态响应等概念有清楚的理解。

4、正确理解传递函数的定义、性质和意义。

熟练掌握由传递函数派生出来的系统开环传递函数、闭环传递函数、误差传递函数、典型环节传递函数等概念。

（＃）5、掌握系统结构图和信号流图两种数学模型的定义和绘制方法，熟练掌握控制系统的结构图及结构图的简化，并能用梅逊公式求系统传递函数。

自动控制原理知识点归纳1.控制系统的基本概念：-控制对象：需要被控制的对象，可以是一个物理系统、电子设备或生产工艺等。

-控制器：用于监测和调节控制对象的设备或程序，根据输入信号产生输出信号以实现控制。

-反馈：通过采集控制对象的输出信息，并与给定的参考信号进行比较，形成误差信号，作为控制器的输入信号。

-开环控制和闭环控制：开环控制仅根据输入信号直接控制对象，闭环控制则根据反馈信号和误差信号来调节控制器的输出信号。

2.控制系统的数学模型：-状态空间模型：使用微分方程或差分方程描述控制对象的状态变化及其对输入和输出的影响。

-传递函数模型：通过拉普拉斯变换将控制系统描述为输入和输出之间的传递函数。

传递函数描述了系统对输入信号的响应过程。

3.控制系统的稳定性分析：-稳定性定义：稳定性是指控制系统的输出在无穷远处有一个有限的稳定值或震荡在一些范围内。

-稳定性判据：利用特征方程的根的位置或特征值来判断控制系统的稳定性。

- 稳定性分析方法：Bode图法、Nyquist图法、根轨迹法等。

4.控制系统的性能指标：-响应速度：指控制系统从输入信号发生变化到输出信号稳定在其稳定值所需要的时间。

-精度：指控制系统输出信号与给定信号的误差大小。

-稳定度：指控制系统输出信号在稳定状态下的波动程度。

-鲁棒性：指控制系统对参数变化、外部扰动和测量误差的抗干扰能力。

5.控制器的设计方法：-比例控制器：根据误差信号的大小，直接乘以比例系数后作为控制器的输出信号。

-积分控制器：根据误差信号的积分值，乘以积分系数后作为控制器的输出信号，用于消除系统的稳态误差。

-微分控制器：根据误差信号的变化率，乘以微分系数后作为控制器的输出信号，用于提高系统的快速响应能力。

6.控制系统的频域分析：-频率响应：描述控制系统在不同频率下对输入信号的变化如何进行响应的性能。

-奈奎斯特稳定判据：通过绘制控制系统的奈奎斯特曲线，判断系统的稳定性和相位裕度。

-传递函数：利用拉普拉斯变换将控制系统描述为输入和输出之间的传递函数，从而分析系统的频率特性。

自动控制原理知识点笔记(一)自动控制原理知识点基本概念•自动控制系统的定义•控制过程、被控对象、控制器、执行机构等基本元件的介绍•控制系统的闭环结构和开环结构的区别信号与系统•信号的分类和性质•时域和频域的概念•采样定理、傅里叶变换、拉普拉斯变换的定义和计算方法控制系统的数学模型•传递函数、状态方程、框图的概念•不同域的模型之间如何互相转换控制系统稳定性•稳定性的概念和判断方法•入门级的稳定性分析法控制器设计及应用•PID控制器的基本概念和设计方法•优化控制方法的原理和应用•典型的控制器应用案例分析算法和计算机实现•控制算法的种类和原理•基于计算机的实现方式•控制系统仿真的意义和方法典型例题解析•具体的实际控制问题分析和解决思路•相关理论的应用实例解析以上是自动控制原理相关的知识点，需要在学习中注重理解基础概念和理论，掌握相关计算方法，结合实际案例深入理解应用场景，从多维度角度逐渐提升对控制系统的掌控能力。

重要工具•Matlab在控制系统中的应用•Simulink建模和仿真的实现过程系统鲁棒性•系统鲁棒性的概念和应用•参数不确定性、扰动和噪声对系统的影响•鲁棒控制方法的基本原理和应用思路线性系统理论•线性系统的定义和性质•线性正则系统和广义系统的概念•线性系统的稳定性、可控性和可观性等分析方法非线性系统理论•非线性动力学系统的基本概念•多项式、解析和混杂型非线性系统的特征分析•常见的稳定和控制方法在非线性系统中的应用即时控制技术•实时控制技术的基础知识•示波器、逻辑分析仪等工具的使用方法•实时控制系统应用案例分析以上是自动控制原理相关的知识点，需要在学习中注重理解基础概念和理论，掌握相关计算方法，结合实际案例深入理解应用场景，从多维度角度逐渐提升对控制系统的掌控能力。

同时需要关注最新的自动控制技术发展和应用情况，不断地学习和实践，提高对自动控制领域的专业素养和技能水平。

第一章自动控制的一般概念1.1 自动控制的基本原理与方式1、自动控制、系统、自动控制系统◎自动控制：是指在没有人直接参与的情况下，利用外加的设备或装置（称控制装置或控制器），使机器、设备或生产过程（统称被控对象）的某个工作状态或参数（即被控量）自动地按照预定的规律（给定值）运行。

◎系统：是指按照某些规律结合在一起的物体（元部件）的组合，它们相互作用、相互依存，并能完成一定的任务。

◎自动控制系统：能够实现自动控制的系统就可称为自动控制系统，一般由控制装置和被控对象组成。

除被控对象外的其余部分统称为控制装置，它必须具备以下三种职能部件。

•测量元件：用以测量被控量或干扰量。

•比较元件：将被控量与给定值进行比较。

•执行元件：根据比较后的偏差，产生执行作用，去操纵被控对象。

参与控制的信号来自三条通道，即给定值、干扰量、被控量。

2、自动控制原理及其要解决的基本问题◎自动控制原理：是研究自动控制共同规律的技术科学。

而不是对某一过程或对象的具体控制实现（正如微积分是一种数学工具一样）。

◎解决的基本问题：•建模：建立系统数学模型（实际问题抽象，数学描述）•分析：分析控制系统的性能（稳定性、动/稳态性能）•综合：控制系统的综合与校正——控制器设计（方案选择、设计）3、自动控制原理研究的主要内容4、室温控制系统5、控制系统的基本组成◎被控对象：在自动化领域，被控制的装置、物理系统或过程称为被控对象（室内空气）。

◎控制装置：对控制对象产生控制作用的装置，也称为控制器、控制元件、调节器等（放大器）。

◎执行元件：直接改变被控变量的元件称为执行元件（空调器）。

◎测量元件：能够将一种物理量检测出来并转化成另一种容易处理和使用的物理量的装置称为传感器或测量元件（热敏电阻）。

◎比较元件：将测量元件和给定元件给出的被控量实际值与参据量进行比较并得到偏差的元件。

◎放大元件：放大偏差信号的元件。

◎校正元件（补偿元件）：结构参数便于调整的元件，用于改善系统性能。

自动控制原理重点知识点第一章 绪论P1 自动控制系统（由控制装置和被控对象组成）是指能够对被控制对象的工作状态进行自动控制的系统。

P5 自动控制系统分类：1、线性和非线性2、连续和离散3、自动调节和随动（跟踪） P7 控制系统的基本要求：稳定性高、响应速度快、精确度高。

第二章、 数学基础P13 拉普拉斯变换： δ（t ）→1；1（t ）→1s；21t s→.第三章、 控制系统的数学模型P25 控制系统的数学模型是描述系统内部各物理量之间的关系的数学表达式。

建立方法：分析法和实践法。

简化的数学模型通常是一个线性微分方程。

P26 建立步骤：1、 根据系统或元器件的工作原理，确定系统和各元器件的输入/输出变量。

2、 从输入端开始，按信号的传递顺序，依照各变量所遵循的物理或化学定律，按技术要求忽略一些次要因素，并考虑相邻器件的彼此影响，列出微分方程式或微分方程组。

3、 消去中间变量，求得描述输入量与输出量得微分方程式。

4、 标准化，即将与输入变量有关的各项放在等号右侧，将与输出变量有关的各项放在等号左侧，并按降幂顺序排列。

P29 线性定常系统的传递函数定义为：在零初始条件下，输出量与输入量的拉普拉斯变换之比。

P31 传递函数的几点说明：1、 传递函数只适用于线性定常系统。

2、传递函数是真分式函数。

3、与外作用形式无关。

4、对于MIMO 系统没有统一的传递函数。

5、传递函数不能反映非零初始条件下系统的全部运动规律。

6、一定的传递函数有一定的零极点分布图与之对应。

7、传递函数的几种表示形式。

（略） P32典型环节及其传递函数： 1、比例环节（放大环节）：c （t ）=Kr （t ）； G （s ）=K 2、惯性环节：Td c d t()()c t r t +=； G （s ）=11T s +3、积分环节：c （t ）=()r t dt ⎰； G （s ）=1s4、振荡环节： ()()2222d c dc TTc t r t dtdtξ++=；()222221212nn nG s T s Ts s s ωξξωω==++++5、 微分环节：理想、一阶、二阶分别是()()()()()()()()222,,2dr t dr t dr t d r c t c t r t c t r t dtdtdtdtττξτ==+=++()()()22,1,21G s s G s s G s s s ττξτ==+=++P35结构图：1、 并联、串联。

自动控制原理知识点总结一、数学模型与传递函数1.系统的数学模型：数学模型是通过建立系统的数学方程来描述系统的物理特性和行为规律。

2.传递函数：传递函数是描述系统的输入和输出之间关系的函数，它是系统的拉普拉斯变换的比值。

二、系统的稳定性1.稳定性的概念：系统的稳定性是指系统在给定条件下的输出是否能够始终收敛到一个有限的范围内。

2.稳定性判据：稳定性可以通过判断系统的极点位置来确定，例如极点都位于左半平面时系统是稳定的。

3. 稳定性分析方法：常用的稳定性分析方法有根轨迹法、Nyquist稳定判据和Bode稳定判据。

三、系统的时间响应1.系统的单位冲击响应：单位冲击响应是系统对冲激信号的输出响应，它可以通过拉普拉斯变换和反变换求得。

2.系统的单位阶跃响应：单位阶跃响应是系统对阶跃信号的输出响应，它可以通过拉普拉斯变换和反变换求得。

3.响应特性参数：常用的响应特性参数有时间常数、峰值时间、峰值幅值、上升时间、超调量和稳态误差等。

四、控制系统的单一闭环反馈1.开环系统与闭环系统：开环系统是指没有反馈路径的系统，闭环系统是指存在反馈路径的系统。

2.单位负反馈控制系统：单位负反馈控制系统是指闭环系统中反馈信号与输入信号的比例为-1的系统。

3.闭环系统的稳态误差：稳态误差是指系统在达到稳定状态后，输出与期望输出之间的偏差。

4.稳态误差的计算和减小方法：可以通过增大控制增益、引入积分环节或者采用预估控制来减小稳态误差。

五、PID控制器1.PID控制器的结构和原理：PID控制器是由比例环节、积分环节和微分环节组成的控制器。

比例环节根据当前误差来调节输出，积分环节根据累积误差来调节输出，微分环节根据误差变化率来调节输出。

2.PID调节器参数整定方法：常用的整定方法有经验整定法、频域法和模拟优化等。

六、根轨迹法1.根轨迹的概念和性质：根轨迹是描述系统极点运动规律的图形,它是由系统的传递函数特征方程的根随一个参数的改变轨迹而形成的。