位置度最大最小实体计算公式
- 格式:pdf
- 大小:225.31 KB
- 文档页数:4



最大实体补偿位置度的计算方法
最大实体补偿位置度(Maximum Entropy Displacement)是一种用于计
算重新加工工艺在不同工艺参数下的最大可能性的方法。
它是一种可
以对已经被滤波器处理过的执行工艺和数据进行前向运算的计算方法。
1. 分解原始数据:首先,在计算最大实体补偿位置度时,我们需要首
先将原始数据进行分解,以确定可能分解出来的和特征;
2. 根据特征进行重新构建:然后,根据所获得的上述分解结果,对工
艺参数作出恰当的调整,有效地将特征结构重新构建汇集到一起;
3. 用哈希表确定数据的联系:接下来,我们可以通过哈希表的方式来
确定不同特征中引发的数据间的关联,从而形成一个完整的计算模型;
4. 计算最大补偿离散度:在计算最大实体补偿位置度时,我们通过上
述哈希表所形成的模型计算出最大补偿离散度值,以实现最大可能地
减少输入工艺数据中可能存在的错误;
5. 处理成功后,意外发生时的补偿:此外,使用最大实体补偿位置度
可以更好地处理意外发生时的位置补偿,可有效减少对原始数据产生
的影响,使其可以正确地重新编码归类输入。
总之,最大实体补偿位置度是一种可以有效地计算出最大可能性的工艺计算方法,可以帮助原始数据精确地重新分类归类,并在意外发生时可以有效地减少影响,提供更可靠的补偿能力。

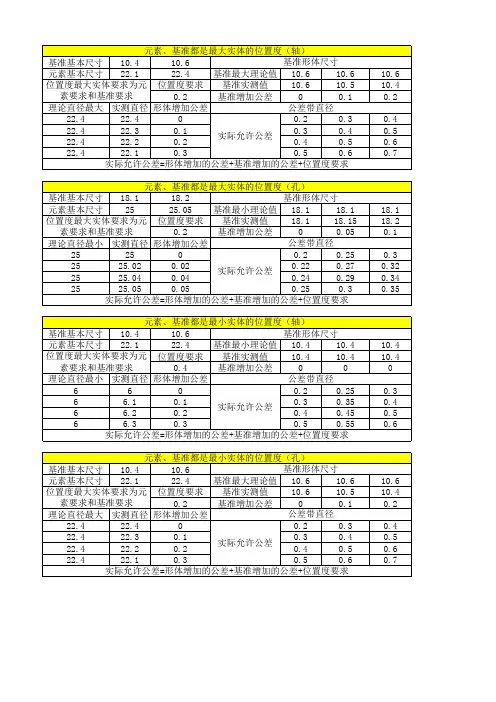
实际允许公差=形体增加的公差+基准增加的公差+图中位置度值
位置度值=2*SQRT((理论X值-实测X值^2+(理论Y值-实测Y值^2
总位置度公差=位置度公差+补偿公差
位置度值=2*SQRT((理论X值-实测X 值^2+(理论Y值-实测Y值^2 位置度值=2*SQRT((理论X值-实测X 值^2+(理论Y值-实测Y值^2 总位置度公差=位置度公差+补偿公差
图中位置度值
0.2
实际允许公差=形体增加的公差+基准增加的
公差+图中位置度值
位置度值=2*SQRT((理论X值-实测X值^2+(理论Y值- 实测Y值^2
孔类与轴类的最大最小实体增加的公差区别:
类轴类最最
轴:最大理论直径-测量直径孔:测量直径-最小理论直径。

位置度公差及其计算一、位置度公差注法的原理•在几何精度设计中,确定中心距是一个重要的方面。
•坐标尺寸注法存在着以下缺点:• 1.加工时产生累积误差;• 2.用两点法测量各个中心距不能保证坐标方向。
•位置度公差注法建立在由理论正确尺寸和几何图框给出的理想位置上。
见图6-1到6-5。
二、位置度公差的标注•单个要素在零件上的定位要求,可以根据基准体系和理论正确尺寸确定的理想位置标注位置度公差来实现。
•要素组在零件上的定位,要考虑该要素组的两种位置关系和两种设计要求。
• 1.孔组位置度公差标注应包含的两项主要内容u孔组的两种位置关系•(1)孔组内各孔的位置关系。
是指几何图框上各孔理想位置之间的关系,各孔之间保持定的坐标位置关系和几何关系。
(各孔位置度公差)•(2)孔组对零件上其他要素的位置关系。
是指孔组或孔组内各孔在零件上的定位要求。
(孔组位置度公差)二、位置度公差的标注u孔组的两种设计要求•(1)第一种设计要求。
装配时不仅要求被连接的两个零件上对应孔组内各孔的位置分别对准,而且要求这两个零件上的某些其他要素也应分别对准。
(对孔组和各孔的位置变动量都应规定较严格的位置度公差。
)•(2)第二种设计要求。
装配时仅要求被连接的两个零件上对应孔组内各孔的位置分别对准,而不要求这两个零件上的某些其他要素也分别对准。
(对各孔的位置变动量应规定较严格的位置度公差,而对孔组位置度公差或定位尺寸公差则应规定的较松。
)•孔组位置度公差与各孔位置度公差的关系:前者一定要不小于后者。
二、位置度公差的标注• 2.孔组位置度公差的基本标注方法u满足第一种设计要求的位置度公差注法•(1)矩形布置孔组。
图6-6。
二、位置度公差的标注•(2)圆周布置孔组。
图6-5。
二、位置度公差的标注• 2.孔组位置度公差的基本标注方法u满足第二种设计要求的位置度公差注法•(1)矩形布置孔组。
•①复合位置度公差注法:指将孔组的两种位置度公差分别用两个公差框格注出。

孔位置度最大实体原则孔位置度最大实体原则是一种在工业设计中常用的设计原则。
该原则的核心思想是,在创建一个产品或物体时,需要将不同的元素或组成部分布置在最佳位置,以实现整体的最佳功能和视觉效果。
该原则通过优化孔形状、大小和布局,以及与其他元素的相互关系,使产品或物体在使用和观察时达到最佳的效果。
为了更好地理解孔位置度最大实体原则,可以从以下几个方面进行说明:1.功能性:孔位置度最大实体原则着重考虑产品的使用功能。
其中一个重要因素是确保孔的布局和位置使得用户可以轻松地访问到需要的操作区域,以实现产品的功能。
例如,对于一个开关板,布置开关孔的位置应考虑到用户的操作习惯和手的舒适程度,使得用户可以方便地轻松操作。
2.视觉效果:孔位置度最大实体原则也关注产品的外观和视觉效果。
通过优化孔的形状和大小,可以创造出更加美观和吸引人的产品。
例如,在一个衣柜的设计中,孔的布局和位置可以使用对称或者非对称的排列方式,以创造出不同的视觉效果和美感。
3.材料和成本:在孔位置度最大实体原则中,设计师还需要考虑到产品的材料选择和成本。
通过合理布置孔的位置,可以使得产品在使用过程中能够最大限度地发挥材料的性能,并降低制造和成本。
例如,在一个汽车设计中,通过优化发动机舱和车身的孔布置,可以有效降低车身的气阻,提高燃油效率。
4.人机工程学:孔位置度最大实体原则的设计也需要综合考虑人机工程学原理。
通过了解用户的需求和习惯,以及其对产品的操作方式和舒适度的要求,可以确定最佳的孔位置度。
例如,在一个手机设计中,可以通过分析用户的人体工程学需求,将音量调节孔和电源按钮孔放在最佳的位置,以方便用户的操作。
5.创新性:孔位置度最大实体原则也鼓励设计师进行创新设计。
通过创新的孔布置和位置,可以为产品或物体带来新颖的功能和视觉效果。
例如,在一个灯具设计中,通过将灯泡孔布置成不规则的形状,可以创造出独特的灯光效果,增加产品的吸引力和艺术性。
总之,孔位置度最大实体原则是一种在工业设计中应用广泛的设计原则。




机械设计名词之最⼤实体边界MMB及最⼩实体边界LMB本⽂参考其他作者的⽂章截取部分发表在博客,仅供⼤家学习、交流。
作者本⼈也是本着学习的态度截取⽂章,以便以后查找和学习。
转载请附出处,谢谢。
最⼤实体边界MMB及最⼩实体边界LMB定义最⼤实体边界MMB(Most Material Boundary)和最⼩实体边界LMB(LeastMaterial Boundary)是2009版标准新引⼊的两个概念,它们的符号与MMC及LMC的符号⼀致。
很多⼈认为没必要去区分MMB和MMC 及LMB和LMC的区别,只要理解MMC及LMC的概念就可以了。
我认为这是完全错误的,新标准引⼊MMB和LMB的概念是有道理的,它的⽬的是为了帮助⼤家更好地理解基准形体的边界及基准漂移(Datum Shift)的来源,它们与MMC、LMC的概念是完全不同的。
MMC及LMC定义的⼀种材料状态,与形位公差⽆关,它们⽤于修正被测形体的形位公差;⽽MMB及LMB定义的是⼀种边界,与形公差有关,它们⽤于修正基准形体。
1. 最⼤实体边界(MMB) —由基准形体尺⼨公差及其它形位公差综合定义的位于实体材料外部的边界。
2. 最⼩实体边界(LMB) —由基准形体尺⼨公差及其它形位公差综合定义的位于实体材料内部的边界。
3. 与材料边界⽆关(RMB) —表⽰模拟基准形体从MMB到LMB渐变以达到与实际基准形体表⾯的最⾼点或最低点接触。
⾸先它们的定义与基准形体相关,也就是说只有基准形体才会⽤到MMB及LMB的概念。
其次它们都与基准形体的尺⼨公差及形位公差有关,MMB是位于材料外部的边界,⽽LMB是位于材料内部的边界。
那么对于孔类零件来说,它的材料外部的边界就等于MMC减去它的形位公差,⽽它的材料内部的边界LMB就等于LMC加上它的形位公差,也就是说它的MMB及LMB分别是基准形体的实效状态VC。
对于轴类基准形体来说,也是⼀样的道理。
因此我们说MMB,LMB边界就是基准形体在MMC或LMC时的VC,孔类基准形体的MMB是它的IB,LMB是它的OB,⽽轴类基准形体的MMB是它的OB,LMB是它的IB。
其实对于这个问题,要先搞清楚下列几个概念:最大实体状态:实际要素在尺寸公差范围内,具有材料最多的状态;最小实体状态:实际要素在尺寸公差范围内,具有材料最少的状态;最大实体尺寸:在最大实体状态时的尺寸;对外表面(轴、凸台等)最大实体尺寸等于最大极限尺寸,对内表面(孔、槽等)最大实体尺寸等于最小极限尺寸。
最小实体尺寸:在最小实体状态时的尺寸;对外表面(轴、凸台等)最小实体尺寸等于最小极限尺寸,对内表面(孔、槽等)最小实体尺寸等于最大极限尺寸。
最大实体边界:在最大实体状态下,具有理想形状的边界;最小实体边界:在最小实体状态下,具有理想形状的边界;实效状态:由图样上给定的被测要素最大实体尺寸和该要素轴线或中心平面的形状公差所形成的极限边界,该极限边界应具有理想形状。
实效尺寸:实效状态的边界尺寸,是最大实体尺寸与形状公差的综合结果;对外表面(轴、凸台等),实效尺寸=最大极限尺寸+形状公差,对内表面(孔、槽等),实效尺寸=最小极限尺寸-形状公差最大实体原则:图样上标注的形位公差值是指在被测要素处于最大实体状态下给定的,当被测要素偏离最大实体状态时,允许增大形位公差值的相互关系原则。
它是针对形位公差来说的,可参考包容原则等内容。
举例说明:例1. 孔径为φ10H8(+0.022/0),它的最大实体尺寸为10,最小实体尺寸为10.022;例2. 轴径为φ10h8(0/-0.022),它的最大实体尺寸为10,最小实体尺寸为9.978;例3. 如果例2中的尺寸φ10h8(0/-0.022)标有轴线的直线度公差φ0.01,且符合最大实体原则(φ0.01后面有一个带圈的M),则它的实效尺寸为10+0.01=10.01;按最大实体原则,当轴处于最大实体状态时,它的直线度误差不得大于0.01;当轴处于最小实体状态时,它的直线度误差可达0.022+0.01=0.032。
转载请注明出自六西格玛品质论坛http://b /,本贴地址:/viewthread.php?tid=139795。
最小坐标与最大坐标引言在数学和计算机科学领域,我们经常需要处理各种形状和对象的坐标。
而在处理坐标时,常常会有求取最小坐标和最大坐标的需求。
本文将介绍最小坐标和最大坐标的概念、应用场景以及如何计算它们。
最小坐标与最大坐标的概念最小坐标和最大坐标是指一组坐标中,具有最小数值和最大数值的坐标点。
通常情况下,这组坐标是二维空间或三维空间中的点集合。
在二维空间中,最小坐标和最大坐标分别是具有最小x和y数值的坐标点以及具有最大x和y数值的坐标点。
类似地,在三维空间中,最小坐标和最大坐标分别是具有最小x、y和z数值的坐标点以及具有最大x、y和z数值的坐标点。
应用场景最小坐标和最大坐标在很多领域都有广泛的应用。
以下是一些常见的应用场景:1.区域边界计算:在地理信息系统或图形学中,最小坐标和最大坐标可以用来计算区域的边界。
通过确定最小和最大坐标,我们可以确定一个区域的范围,进而进行后续的分析和处理。
2.矩形包围盒计算:在计算机图形学中,最小坐标和最大坐标可以用来计算矩形包围盒。
矩形包围盒是一个能够紧密包围一个物体或一组物体的最小矩形。
通过计算最小和最大坐标,我们可以确定矩形包围盒的位置和大小,从而优化物体的渲染和碰撞检测等操作。
3.数据可视化:在数据可视化领域,最小坐标和最大坐标可以用来确定绘图区域的范围。
通过确定最小和最大坐标,我们可以将数据的范围映射到绘图区域的坐标系中,从而实现数据的可视化呈现。
计算最小坐标和最大坐标计算最小坐标和最大坐标的方法取决于具体的应用场景和数据结构。
以下是一些常见方法的示例:方法一:遍历法对于一个给定的点集合,我们可以遍历每个点,同时维护两个变量来保存最小坐标和最大坐标。
具体的步骤如下:1.初始化最小坐标和最大坐标为第一个点的坐标。
2.遍历点集合中的每个点。
3.对于每个点,比较其坐标与当前最小坐标和最大坐标的数值,并更新最小坐标和最大坐标。
4.最终得到的最小坐标和最大坐标即为所求。
实际允许公差=形体增加的公差+基准增加的
公差+图中位置度值
位置度值=2*SQRT((理论X值-实测X值)^2+(理论Y值-实测Y值)^2)
总位置度公差=位置度公差+补偿公差
位置度值=2*SQRT((理论X值-实测X 值)^2+(理论Y值-实测Y值)^2)
位置度值=2*SQRT((理论X值-实测X 值)^2+(理论Y值-实测Y值)^2)
总位置度公差=位置度公差+补偿公差
图中位置度值
0.2
实际允许公差=形体增加的公差+基准增加的
公差+图中位置度值
位置度值=2*SQRT((理论X值-实测X值)^2+(理论Y值-
实测Y值)^2)
孔类与轴类的最大最小实体增加的公差区别:
类轴类最最
轴:最大理论直径-测量直径孔:测量直径-最小理论直径。